1 Introduction

For complex reservoir operation problems, simulation models are very much preferred and widely used in practice, owing to the explicit use of predefined release rules and balancing functions that incorporate the knowledge of the operator and the preferences of the stakeholders and the ease with which detailed performance evaluations can be done considering climate change impacts and plausible social and ecological scenarios. In this regard, the availability of powerful simulation packages such as HEC-ResSim 3.1 (Klipsch and Hurst 2013) and WEAP (Yates et al. 2005) enable the detailed evaluation of the various operation policies/rules (for e.g., Hamlat et al. 2013; Jebbo and Awchi 2016). On the other hand, although mathematical programming models seek to obtain the optimal reservoir operation policy, they are prescriptive in nature and quite often suffer from complexities arising from non-linearity, non-convexity, dimensionality, uncertainty and multiple objectives (Labadie 2004). Moreover, they do not seem to capture social and ecological issues and stakeholder preferences and operator’s changing priorities effectively. In the last two decades, with the emergence of the evolutionary search techniques, the simulation-optimization (S-O) models have gained popularity in dealing with the operation of complex water resources systems problems (Rani and Moreira 2010), utilizing the power of the simulation models effectively. These direct search approaches are based on evolutionary principles and are well suited for arriving at the optimal long-term reservoir operating policy based on performance evaluation obtained from detailed system simulation (Shiau 2009 and Kang et al. 2016). The efficacy of the evolutionary search based genetic algorithms (GAs) for reservoir operation was first demonstrated by Oliveira and Loucks (1997). They derived efficient pre-defined operating rules for multi-reservoir systems, in which the system release rule and the reservoir balancing functions are described as piecewise linear functions. This direct search approach using GA has been further explored by Ahmed and Sarma (2005), Dariane and Momtahen (2009), Afshar et al. (2011). Although the structure of their formulation facilitates the implementation of GA (or other evolutionary search techniques) for reservoir operation and offers significant advantages over the use of traditional optimization techniques, the generation of initial feasible solutions (release rules) poses quite some challenge due to its highly constrained nature arising due to the limitations on release and storage, monotonicity of the release rule curve along the connected linear segments and reservoir mass balance. An added complexity may arise during the local search, since the reproduced solutions obtained through the application of cross-over and/or mutation may fall out of the feasible region necessitating some correction, which may impose restrictions to the search space (Afshar et al. 2011).

Whenever the generated solutions do not lie within the feasible domain, either they are rejected and the generation process is continued until a feasible solution is obtained (Oliveira and Loucks 1997), or the fitness function/s are appropriately penalized during the evaluation process (Afshar et al. 2011). In both the situations, the remedy or the correction is done after the generation of the solution vector, which is likely to result in a less efficient search of the optimality. In case of multi-objective reservoir operation problems, disregarding the infeasible solutions during the stochastic search process may result in loss of diversity, leading to a local Pareto-optimal (P-O) front with lesser stretch and more discontinuity, while in the penalty function approach, finding the appropriate penalty functions for the large number of constraints present is quite challenging (Chang 2008). Moreover, even some of the advanced constraint handling approaches suffer from the common drawback of “premature fitness stagnation” (Kramer 2010). In addition, the presence of equality constraints (such as reservoir storage-continuity) makes the task of finding initial feasible solutions even more challenging.

Hedging rules belong to the class of pre-defined reservoir operating rules used for rationing water supply during droughts with the intent of reducing the risk of unacceptably large water deficits, by allowing a number of smaller magnitude deficits instead. Various hedging rules have been proposed over the years, of which modified two-point hedging rule (Srinivasan and Philipose 1996) and discrete hedging rule (Shih and ReVelle 1995) are being used in direct search based multi-objective S-O models (Shiau 2009 and Kang et al. 2016) to find the Pareto-optimal hedging policies. The direct search based multi-objective time-varying hedging models consist of large number of hedging parameters that make the stochastic search process computationally demanding. One of the commonly adopted practices to reduce the computational effort involved in obtaining a competent P-O front for such complex multi-objective problems is to pre-condition the search by feeding with good initial feasible solutions from heuristic methods that use domain knowledge or from alternate optimization models of a simplified version of the original problem (Maier et al. 2014).

In this research work, it is proposed to adopt the robust piecewise linear operating rule of Oliveira and Loucks (1997) in the context of long-term hedged operation of single water supply reservoir by considering two conflicting objectives, namely, “minimize the total shortage ratio” and “minimize the maximum shortage”. The novelty of this research work is two-fold: i) efficient parameterization of the piecewise linear hedging rule and appropriately structuring the same within a S-O framework, so that the use of constraints is avoided within the optimization segment; and ii) pre-conditioning the stochastic search of the time-varying hedging model by feeding initial feasible solutions sampled from the Pareto-optimal front of a coarser model that has constant hedging parameters, with an intent to improve the Pareto-optimality and increase the computational efficiency.

2 Methodology

2.1 Piecewise Linear Hedging Rule

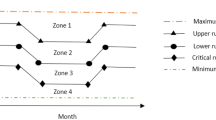
The system release rule proposed by Oliveira and Loucks (1997) is adopted in this research work, by formulating it as a piecewise linear hedging rule (Fig. 1) for water supply reservoir operation. Herein, the feasible solution region for water supply reservoir is bounded by standard operating policy (SOP) on one side and the dashed line shown in Fig. 1 on the other side. The hedging rule is defined using three inflection points (P1 t , P2 t , and P3 t ) in the feasible solution region, and the inflection points are described by the water availability and release at that point (Fig. 1). Herein, Water availability (WA t ) is defined as

$$ W{A}_t={S}_t+{I}_t-{L}_t $$
(1)

where S t is the initial storage, I t is the inflow and L t is the reservoir loss corresponding to period t.

Fig. 1
figure 1

Standard operating policy (SOP) and Piecewise linear hedging rule

Full size image

The parameterization of the piecewise linear hedging rule is formulated using six non-dimensional hedging parameters (α1 t , α2 t , α3 t , β1 t , β2 t  and β3 t ), each ranging between 0 and 1 (Eq. 2). For aesthetic representation of the hedging rule, the carryover storages corresponding to the inflection points are defined as auxiliary variables. With this premise, the inflection points are defined as follows:

$$ \left\{\begin{array}{c}\begin{array}{c} IR{1}_t=\alpha {1}_t\times {D}_t\\ {} IS{1}_{t+1}=\beta {1}_t\times K\\ {} IWA{1}_t= IR{1}_t+ IS{1}_{t+1}\end{array}\\ {}\begin{array}{c} IR{2}_t= IR{1}_t+\alpha {2}_t\times \left({D}_t- IR{1}_t\right)\\ {} IS{2}_{t+1}= IS{1}_{t+1}+\beta {2}_t\times \left(K- IS{1}_{t+1}\right)\\ {} IWA{2}_t= IR{2}_t+ IS{2}_{t+1}\end{array}\\ {}\begin{array}{c} IR{3}_t= IR{2}_t+\alpha {3}_t\times \left({D}_t- IR{2}_t\right)\\ {} IS{3}_{t+1}= IS{2}_{t+1}+\beta {3}_t\times \left(K- IS{2}_{t+1}\right)\\ {} IWA{3}_t= IR{3}_t+ IS{3}_{t+1}\end{array}\end{array}\right. $$
(2)

where D t is the demand during period t, K is the active storage capacity (upper limit of carryover storage); IR1 t , IR2 t and IR3 t are respectively the releases, IWA1 t , IWA2 t and IWA3 t are respectively the water availabilities and, IS1t + 1, IS2t + 1 and IS3t + 1 are respectively the carryover (end-of-period) storages corresponding to the inflection points P1 t , P2 t and P3 t during period t.

The release policy for the piecewise linear hedging rule is given as

$$ \left\{\begin{array}{c}{R}_t=\frac{IR{1}_t}{IWA{1}_t}\times W{A}_{\mathrm{t}}\ when\ 0<W{A}_t\le IWA{1}_t\\ {}{R}_t= IR{1}_t+\frac{IR{2}_t- IR{1}_t}{IWA{2}_t- IWA{1}_t}\times \left(W{A}_t- IWA{1}_t\right)\ when\ IWA{1}_t<W{A}_t\le IWA{2}_t\\ {}{R}_t= IR{2}_t+\frac{IR{3}_t- IR{2}_t}{IWA{3}_t- IWA{2}_t}\times \left(W{A}_t- IWA{2}_t\right)\ when\ IWA{2}_t<W{A}_t\le IWA{3}_t\\ {}{R}_t= IR{3}_t+\frac{D_t- IR{3}_t}{D_t+K- IWA{3}_t}\times \left(W{A}_t- IWA{3}_t\right)\kern0.5em when\ IWA{3}_t<W{A}_t\le \left({D}_t+K\right)\\ {}{R}_t={D}_t\ when\ W{A}_t>\left({D}_t+K\right)\end{array}\right. $$
(3)

where R t is the release and WA t is the water availability during period t.

Once the release is obtained, the carryover storage, St + 1 is calculated as

$$ {S}_{t+1}=\min \left(W{A}_t-{R}_t,\kern0.5em K\right) $$
(4)

and the spill at time t, Spill t , is given as

$$ S{pill}_t=\max \left(0,\kern0.5em W{A}_t-{D}_t-K\right) $$
(5)

The structure of the piecewise linear hedging rule formulation including the parameterization proposed in this research work is adoptable within a simulation-optimization (S-O) framework, without the explicit specification of any of the constraints regarding the location of the inflection points and the system constraints regarding reservoir storage-continuity and upper and lower limits of release and carry-over storage in the optimization module. The piecewise linear hedging rule formulated herein can mimic SOP as well as some of the widely used linear hedging rules like one-point hedging rule, two-point hedging rule (both the traditional SOP based and Type-II (Shiau 2011)) and three-point hedging rule. It also allows the inflection points to lie anywhere on the boundary of the feasible solution domain (SOP and dashed line in Fig. 1 (Zhao et al. 2011; Shiau 2011)). The current formulation also restricts the slope of the hedging line to be between zero and unity, which is necessary to avoid either release or carryover storage decreasing with increasing water availability, which may not be practical.

The parameterization of the piecewise linear hedging rule proposed herein is implemented within the S-O framework as either having constant hedging parameters (CHP) or monthly varying hedging parameters (MVHP). In case of constant hedging parameters, the six hedging parameters are given by

$$ \left\{\begin{array}{c}\alpha {1}_t=\alpha 1\\ {}\alpha {2}_t=\alpha 2\\ {}\alpha {3}_t=\alpha 3\\ {}\beta {1}_t=\beta 4\\ {}\beta {2}_t=\beta 5\\ {}\beta {3}_t=\beta 6\end{array}\kern0.5em \forall t=1,2,\dots \dots, NP\right. $$
(6)

where NP is the number of periods in the operating horizon. In case of monthly varying hedging parameters, the parameterization is implemented as

$$ \left\{\begin{array}{c}\alpha {1}_{12\left(i-1\right)+j}=\alpha {1}_j\\ {}\alpha {2}_{12\left(i-1\right)+j}=\alpha {2}_j\\ {}\alpha {3}_{12\left(i-1\right)+j}=\alpha {3}_j\\ {}\beta {1}_{12\left(i-1\right)+j}=\beta {1}_j\\ {}\beta {2}_{12\left(i-1\right)+j}=\beta {2}_j\\ {}\beta {3}_{12\left(i-1\right)+j}=\beta {3}_j\end{array}\kern0.5em \forall i=1,2,\dots, N;j=1,2,\dots 12\right. $$
(7)

where α1 j , α2 j , α3 j , β1 j , β2 j and β3 j are the hedging parameters for the jth month which are the same for all the N years, thus reducing the dimensionality.

2.2 Objective Functions

While hedging aims to reduce the most critical deficit, it is likely to increase the total deficit volume and/or the total deficit periods over the operating horizon. Hence, in this study, two conflicting objectives, namely, minimizing the total shortage ratio (which represents total deficit volume) and minimizing the vulnerability (which represents the most critical deficit) are considered, leading to a multi-objective optimization problem.

Total Shortage ratio (TSR) is defined as the ratio of the sum of release deficits to the sum of demands over the entire operating horizon.i.e.,

$$ TSR=\frac{\sum \limits_{t=1}^{NP}R{D}_t}{\sum \limits_{t=1}^{NP}{D}_t}\times 100 $$
(8)

where RD t is the release deficit in period t and is given as RD t  = max(D t  − R t , 0).

Vulnerability is defined as the maximum single period deficit in the entire operating horizon and is given as

$$ Vulnerability=\underset{\mathrm{t}}{\min}\left({\mathrm{RD}}_{\mathrm{t}}\right) $$
(9)

2.3 Non-dominated Sorting Genetic Algorithm - II

This study adopts the evolutionary search based non-dominated sorting genetic algorithm (NSGA-II) (Deb et al. 2002), as the driver, which is linked to the simulation engine that invokes the proposed piecewise linear hedging rule within a simulation-optimization (S-O) framework, to derive the Pareto-optimal (P-O) solutions. This algorithm starts by generating the initial population randomly, and keeps improving it over a number generations employing a set of genetic operators namely, selection, crossover and mutation, and utilizing the “elitism” characteristic that ensures the top-ranking solutions to be retained in the subsequent generations unless better solutions are found. It is to be noted that the number of decision variables in case of CHP is only 6, whereas in case of MVHP it is 72. Intuitively, the monthly varying hedging rule (MVHP) is expected to yield a better P-O front when compared with the constant hedging rule (CHP), since the former can account for the monthly variations of inflows and demands. However, it is possible that MVHP with 72 decision variables may get trapped at local optimum, even after very large number of function evaluations and hence may yield an inferior P-O front or a partly inferior front, when compared with that of CHP. To overcome this, in this research work, it is proposed to precondition the NSGA-II in case of MVHP, by seeding part of the initial population from the better P-O solutions of CHP. While these initial P-O solutions provided to MVHP are expected to direct the search to converge to a better P-O front, the elitism characteristic of NSGA-II would enable retaining top-ranking P-O solutions through the generations. The steps of preconditioning adopted in this study are presented below:

  • Step 1: Run the S-O model with constant hedging parameters (CHP) and derive the P-O front and corresponding set of P-O solutions.

  • Step 2: From the set of P-O solutions obtained from the previous step, a pre-specified percent of the population is randomly sampled for feeding as initial solutions to the MVHP case.

  • Step 3: Each of the sampled decision vectors obtained from CHP in Step 2, are replicated for all the 12 months, making the size of the decision vector to be corresponding to MVHP (6 × 12 = 72).

  • Step 4: Run the S-O model with monthly varying hedging parameters (MVHP) to derive the P-O solutions, by seeding part of the initial population with sampled initial solutions obtained in Step 3, and randomly generating the remaining individuals of the population.

Herein, NSGA-II with the preconditioning of initial solutions from CHP, is referred as Seeded Non-dominated Sorting Genetic Algorithm - II (S-NSGA-II).

3 Case Example

The improvement achieved in terms of the Pareto-optimality and the computational efficiency due to the preconditioning of the time-varying piecewise linear hedging model by feeding initial feasible solutions sampled from the Pareto-optimal front of a coarser constant hedging parameter model, is illustrated with the monthly hedged operation of the Dharoi reservoir, a water supply reservoir located on the Sabarmati River in India. The mean annual flow (MAF) at the reservoir site is 868 Mm3 with a high coefficient of variation of 0.82. The reservoir receives about 90% of the annual inflows during the south-west monsoon season, June–September (Fig. 2). The active storage capacity of the reservoir is 775.88 Mm3. The annual demand including evaporation loss is assessed to be 59% MAF (Jain and Bhunya 2008). The monthly demands, which cater to municipal water supply and irrigation (NIH 1987), are also shown in Fig. 2. These are assumed to be same across the years. It may be observed from Fig. 2 that during the period Oct-May, the reservoir receives only around 10% of the annual inflows, while the demand accounts for 73.28% of the annual demand, indicating a significant mismatch.

Fig. 2
figure 2

Index map of Sabarmati River basin and b. Monthly (Jun-May) time series of Inflows and Demands for the period 1935–1975

Full size image

4 Results and Discussion

In this study, the NSGA-II is implemented with binary coding, with 16 bits allocated for each decision variable for both CHP and MVHP cases. For the constant hedging rule (CHP) with 6 hedging parameters, the population size, number of generations, crossover rate and mutation rate are set as 1200, 1600, 0.9 and 0.0104 \( \left(=\frac{1}{no. of decision variables(6)\times bit\ length\ (16)}\right) \), respectively, while for the MVHP with 72 hedging parameters, they are set as 3600, 4800, 0.9 and 0.0009 respectively. It may be noted from Fig. 3 that the P-O front obtained by CHP (NSGA-II CHP) outperforms that obtained by the more flexible MVHP (NSGA-II MVHP) from a TSR of 9.5% onwards, which is counter-intuitive. Such inferior performance of NSGA-II MVHP in certain segments of the P-O front, plausibly implies that the former has got trapped in local optimum.

Fig. 3
figure 3

Comparison of P-O fronts obtained with CHP and MVHP

Full size image

To verify if such trapping in local optima occurs even while using other multi-objective evolutionary algorithms (MOEAs), the MVHP case is implemented with two of the more recent and advanced MOEAs, namely, AMALGAM (Vrugt and Robinson 2007) and Borg MOEA (Hadka and Reed 2012). The AMALGAM uses different heuristic algorithms namely, NSGA-II, particle swarm optimization, adaptive metropolis search and differential evolution, and combines them to adaptively generate the offspring. In the first generation, every heuristic algorithm within AMALGAM generates the same number of off-springs, while in the subsequent generations, the number of off-springs to be mixed from each algorithm is adaptively decided in proportion to the percent of off-springs from the previous generation that have made it to the new population. The Borg MOEA algorithm also employs a similar approach to combine multiple genetic operators, and in addition implements ε-dominance to enable simultaneous convergence and ensure diversity of the P-O solutions, and ε-progress to detect any pre-matured stagnation and to revive the stochastic search process. For more details about AMALGAM and Borg MOEA, the reader is referred to the original works of Vrugt and Robinson (2007) and Hadka and Reed (2012), respectively. It is to be mentioned that the P-O fronts obtained in case of CHP from AMALGAM or Borg MOEA, were identical with NSGA-II, and hence only the results obtained for MVHP are presented here for further discussion. Both AMALGAM and Borg MOEA are implemented with the same number of function evaluations (3600 × 4800 = 17.28 million) as that of NSGA-II.

It may be seen from Fig. 3 that for the MVHP case, the P-O fronts of both AMALGAM MOEA (denoted as AMALGAM MVHP) and Borg MOEA (denoted as Borg MVHP) are better than that of NSGA-II MVHP, while they are found to be inferior when compared with NSGA-II CHP, at lower vulnerabilities. Although Borg MVHP outperforms NSGA-II MVHP at higher TSR values, it is found to be inferior from a TSR of 12% onwards when compared with NSGA-II CHP. On the other hand, even though AMALGAM MVHP is performing better than Borg MVHP and NSGA-II MVHP, it is not able to yield non-dominated solutions with vulnerability lower than 16.5 M cu m, whereas NSGA-II CHP has attained a vulnerability up to 14 M cu m. This indicates that trapping at local optimum is possible even with more advanced hybrid algorithms and a large number of evaluations, especially when a large number of decision variables are involved.

With a view to visualize the effect of preconditioning (seeding from the P-O solutions of CHP), the P-O fronts obtained from the implementation of the constant hedging rule, the monthly varying hedging rule and the seeded monthly varying hedging rule into the NSGA-II based S-O framework, are presented in Fig. 4 and are denoted as NSGA-II CHP, NSGA-II MVHP and S-NSGA-II MVHP, respectively. Four runs have been made for S-NSGA-II MVHP with varying percent (2%, 5%, 10% and 20%) of initial seeding sampled from the P-O front of CHP. Since there is no significant improvement of the resulting P-O front beyond 10% initial seeding (results are not presented herein, for want of space), the same is adopted for comparison. It is evident from Fig. 4 that S-NSGA-II MVHP has significantly gained over NSGA-II MVHP (where the whole initial population is randomly generated), which can be attributed to the good initial feed from NSGA-II CHP (preconditioning). It is also to be mentioned that S-NSGA-II MVHP has taken only 4.32 million function evaluations, while NSGA-II MVHP has taken 17.28 million function evaluations, thus demonstrating the significant gain in terms of computational effort as well.

Fig. 4
figure 4

Comparison of P-O fronts corresponding to NSGA-II MVHP and S-NSGA-II MVHP

Full size image

To further confirm the efficacy of the preconditioning from the P-O front of a coarser level constant parameter model, the same problem is solved for two projected annual demands, namely, 70% MAF and 80% MAF. It is found that with increase in the demand level, the improvement offered by S-NSGA-II also increases in terms of the quality of the P-O front. Moreover, the gain achieved in the computational effort is retained. The results are not presented here due to lack of space.

5 Summary

A multi-objective simulation-optimization (S-O) model with an efficiently parameterized piecewise linear hedging rule is proposed for the long-term hedged operation of a single water supply reservoir. The novelty of the current research work lies in i) the efficient parameterization and the appropriate structuring of the piecewise linear hedging rule that avoids the explicit specification of the constraints (location of the inflection points, mass balance and limits on release and carry-over storage) within the optimization module; and ii) pre-conditioning the stochastic search of the monthly varying hedging model by feeding initial feasible solutions sampled from the Pareto-optimal front of the coarser constant hedging parameter model, with an intent to improve the Pareto-optimality and increase the computational efficiency.

Two conflicting objectives, namely, “minimize the total shortage ratio” and “minimize the maximum shortage” are considered in the simulation-optimization (S-O) framework to derive the Pareto-optimal (P-O) solutions. The improvement achieved in terms of the Pareto-optimality and the computational efficiency due to the preconditioning of the monthly varying piecewise linear hedging model, is illustrated with the operation of the Dharoi reservoir, located on the Sabarmati River in India.

The S-O framework along with the parameterized piecewise linear hedging rule developed in this research work can be extended to multi-purpose and multi-reservoir systems, which is being currently pursued by the authors.