1 Introduction

Scintillator detectors are preferred for a certain class of ionization radiation measurements [1,2,3]. The setup comprised of associated electronics requiring an operator to set several parameters[4]. For example, (a) gain value of amplifier, (b) range of discriminator/energy window, and (c) high voltage of photomultiplier tube (cathode to anode). Generally, the calibration of the typical system is performed onsite, and the range of some of these settings is given a-priori. These setting are widely considered stable, however, may require recalibration as the equipment completes its operational age, employed for different application or exposed to severe conditions [5,6,7,8]. Besides using calibrated settings, there are several other post-processing-related questions which are needed to be considered before measurement. These points usually are left for the operator to decide and may affect the outcome of the experiment, person to person[9]. The calibration process itself requires finding the answer to the following measurement related questions:

  1. 1.

    How many times/instances should one repeat an experiment (the sample size \(M\))?

  2. 2.

    How long should one carry out a single instance of measurement (Time T)?

  3. 3.

    What value should one take, average, median, or mode values of samples?

  4. 4.

    What should be the optimal setting of involved electronics?

Recording multiple instances (for arbitrary times) of the same event is usual practice to achieve better statistical inference. Generally, the mean value of all recorded values is used, assuming that averaging samples would not influence the measurement statistics [10].

Mode is rarely used as multiple local maxima may exist [11]. Median values may be preferred (on case to case basis) over the mean [12] if data is skewed. For the small size of samples, percentile bootstrap bias correction may improve the representation for the bulk of the observations using the median. Hierarchical shift functions are another class of tools as an alternative [13].

The sample size or instance of multiple recordings, if they are subthreshold or small, may affect the reproducibility of the measurement [14,15,16,17].

If a measurement is done for a discrete variable, data from multiple instances is fitted to binary (if the nature of the variable is binary) or Poisson [18]. However, several real-life variables, random in nature, are continuous. The preferred distribution in the field of measurement is the normal distribution, given in Eq. 1.

$$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\overline{x}}{\sigma }\right)}^{2}}$$
(1)

where \(\overline{x}\) is the mean of the distribution, and \(\sigma\) is the standard deviation.

Statistically, if series of variables \({\left.{x}_{i}\right|}_{i=1, \dots , N}\) are repeatedly measured \(M\) times, the average values \({\left.\overline{{x }_{i}}\right|}_{i=1, \dots , N}\) follow a normal distribution with a certain degree (2 or at best three sigmas) of standard deviation. The impractical constraint \(M\in (-\infty\) to \(\infty )\) gets normalized by a limited arbitrary time. The resemblance may improve with as many instances, as allowed, keeping practical limits under control. A widely used approximation is that the Binomial or Poisson distribution of a repeated random variable resembles Gaussian distribution if \(M>20\) [18].

The electronic settings of the radiation count/ events measurement device have a strong influence on the shape of pulses and the resolution of the detector. B. Almutairi et al. performed an experiment using the Geiger Muller counter to show the dependency of applied voltage on pulse shape [19].

The most widely used methods to estimate the optimal voltage and energy discriminator setting of a photomultiplier tube (PMT) of scintillator detector are the gross method [20, 21] and pulse width saturation/ plateau method [19].

The Gaussian nature of measurement noise often corrupts the data imparting non-negligible standard deviation. Central limit theorem (CLT) is another tool to estimate the relative level of precision and accuracy [22, 23].

1.1 Motivation

The information such as the number of samples \(M\), how long each sample was taken T, if the mean, mode, or median was used to get a single value remains absent from the datasheet for respective calibration settings. Information about optimal gain values and energy window range is assumed to be application dependent, and statistically sound criteria to set them are not discussed in the literature in depth. We recalibrated the scintillator detector electronics to explore if above mentioned statistical factors affect the suggested calibration settings.

Five different methods \((N=5)\), namely: (a) two different implementations of CLT, (b) pulse width saturation method, (c) relative comparison using a high accuracy Multi pixel photon counter (MPPC) coupled scintillator gamma radiation detector, and (d) gross method are used. We tested the above methods to find out the best / optimal option to calibrate the electronic setting of the detector and decide for other parameters (like time and number of samples) to measure counts with better accuracy and precision. It is also tested (for the given data set) which one, mean, median, or mode would be an optimal statistical tool for the given data set. Finally, we test which of the electronics settings are more important to pay attention to before one starts the measurement. Brief descriptions about methods, our methodology to test them are discussed, followed by results.

2 Theory

Statistical tools utilizing the saturation in repeating values and probability distribution of radiation count are used in this work. The central limit theorem states that for a sequence of a random independent variable having some finite variance, then the mean of the sequence tends towards Gaussian / normal distribution as the number of variables goes larger [24, 25]. Two methods based on the central limit theorem are used to fit the experimental data into the Gaussian model are curve fitting [26] and Gaussian probability distribution [27]. The Gaussian function has been widely used in modeling and to explain the behavior of physical phenomena in various disciplines of applied physics and engineering. For example, the Gaussian function has been used to model practical microscopic applications [28], LASER heat source in LASER transmission welding[29]. In the field of signal and image processing, the Gaussian function is used to model the approximation of Airy disk [30]. In applied science, the random noise that corrupts the signal can be modeled with the Gaussian function according to the central limit theorem [31]. Following are a brief description:

2.1 Optimal Value Calculation

Method 1 (CLT1):—This method uses Gaussian curve fitting with the following equation (Eq. 2):

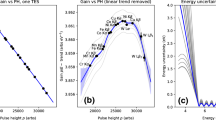
$${C}_{{x}_{i}^{j}}\left(M\right)={A}_{i}^{j}{e}^{-\left(\frac{\left(M-{b}_{i}^{j}\right)}{{c}_{i}^{j}}\right)}+{D}_{i}^{j}{e}^{-\left(\frac{\left(M-{e}_{i}^{j}\right)}{{f}_{i}^{j}}\right)} where \;i=\mathrm{1,2},\dots ,N=5;j=\mathrm{1,2},3,\dots r$$
(2)

To find the optimal setting/value of a particular parameter \({x}_{i}^{j}\), it is varied within its set range (for example, recording time is varied between \(r=5\) till \(30\) sec) while keeping other parameter values at a certain constant value. For each variation, the number of radiation counts \({C}_{{x}_{i}^{j}}\) is recorded. This is repeated \(30\) times (\(M)\). The radiation counts \({C}_{{x}_{i}^{j}}\left(M\right)\) with regards to instance, \(M\) are fitted according to Gaussian. Each plot is fitted into shape controlling parameters, A, \(b, c, D, e,\) and \(f\). The corresponding value of \({x}_{i}^{j}\) with the plot having best-fitting parameters with minimum sum of squared deviation and higher goodness of fit is termed as optimal value \({x}_{i}^{opti.}\). One example is shown in Figure 1a. It is shown that radiation count (normalized w.r.t maximum value) plots vary (shape and amplitude) if the same experiment is repeated multiple times using a different combination of parameters. The one that is having closeness with Gaussian is termed as an optimal combination.

Figure. 1
figure 1

Estimation of Optimal combination by (a) and (b).

Full size image

Method 2 (CLT2):—This method declares the value \({x}_{i}^{j}\) as optimal \({x}_{i}^{opti.}\), if its probability distribution function plot with regards to instances has higher probability values, minimum full-width-half-maxima (FWHM), high peak amplitude, and low standard deviation values. The definition of the normal probability density function is given in the following equation (Eq. 3):

$${p}_{{x}_{i}^{j}}=\frac{1}{{\sigma }_{i}^{j}\surd 2\pi }{e}^{\left(\frac{{-\left({ c}_{i, M}^{j}-{ \overline{c} }_{i,M}^{j}\right)}^{2}}{2{({\sigma }_{i}^{j})}^{2}}\right)}where \;i=\mathrm{1,2},\dots ,N=5;j=\mathrm{1,2},3,\dots r$$
(3)

where \(\sigma\) is standard deviation and \({\overline{x} }_{i,M}^{j}\) is the location parameter (it could be mean, mode or median) of the distribution depending on the respective case study. Probability distribution \({p}_{{x}_{i}^{j}}\) of radiation counts \(c\) with regards to instance \(M\) is plotted for each variation [32]. One example is shown in Figure 1b. The probability distribution function for four data (obtained by setting different combinations of LLD, Voltage, M, T, and Amp. Gain values) are plotted against instances \(M\) (30 values interpolated into 1500 values for better visualization). The combination with the highest peak value with the smallest full width at half max is termed as optimal.

Method 3 (PWS):—This method chooses optimality based on most flat / plateau/saturation region, assuming that the number of counts is less dependent on the setting of parameters. The combination of parameters setting for which flat region is obtained is considered as the optimal setting of the detector.

Method 4 (True counts measurement):—Counts measured for all combinations of parameter variation measured by Na(Tl) based scintillation detector is compared with the counts obtained by MPPC coupled scintillator detector [33]. The corresponding combination of parameters with the least absolute difference is assumed optimal, explained in Eq. 4. This method assumes that counts measured using MPPC coupled scintillator detector \({{\overline{c} }_{T}}_{i,M}^{j}\) are near to true radiation counts.

$${x}_{i}^{opti.}=\left.{ \overline{x} }_{i,M}^{j}\right|\mathrm{min}(\left|{ \overline{c} }_{i,M}^{j}-{ {\overline{c} }_{T}}_{i,M}^{j}\right|)$$
(4)

Method 5 (Gross Method):- According to the definition of this approach, the optimal parameter value would have the highest ratio of the square of gross sample counts rate to background counts rate \({\overline{c} }_{0}\). Its relation is given in Eq. 5:

$${x}_{i}^{opti.}=\left.{ \overline{x} }_{i,M}^{j}\right|\mathrm{max}({\frac{{ \overline{c} }_{i,M}^{j}}{{ {\overline{c} }_{0}}_{i,M}^{j}}}^{2})$$
(5)

3 Methodology

This study is performed under constant atmospheric conditions (25 Degrees centigrade and 65% Humidity). Electronics of most basic detector setup offers buttons/knobs to vary specific parameters. The exhaustive brute force procedure is adopted to find out the optimal combination of these parameters (LLD, amplifier gain, and high voltage applied at PMT), including time. Figure 2 shows the flow of the work.

Figure. 2
figure 2

Flow chart of the adopted methodology.

Full size image

Gamma radiation source Cesium 137 (137Cs) of 1.5µCi and a total of 6 scintillation detectors and associated electronics of two different make/manufacturer is used. Five probe geometry NaI(Tl) scintillator detectors (a crystal of diameter 1 inch) are arranged in a fan-beam to include direction dependency [34]. The measured data is transferred to the computer system using Nuclear Gamma Spectrometer PNS-2™ software, semi-automatically. The experimental setups (automatic, make: Hamamatsu, semi-automatic, make: Electronic Enterprises (India) and manual bins, make: Canberra) are shown in Figure 3. The operational voltage rating\({V}_{cal.}\) (estimated onsite on the date of delivery) and amplifier gain of each scintillator detector is provided by the manufacturer.

Figure. 3
figure 3

Experimental setups for measuring number of counts using scintillation detector: (a) Automatic and Semi-automatic detector and electronics, (b) Detector array and gamma source, and (c) manual Bin.

Full size image

Details are mentioned in Table 1. Another scintillator detector (CsI(Tl) crystal of size: 13 × 13 × 20 mm) coupled with multi-pixel photon counters photomultiplier (MPPC) is used for confirming the readings assuming this detector counts, the radiation resembles true counts. Cathode to anode voltage at PMT, gain at the amplifier, window level of SCA or lower-level discriminator (LLD), Time to count events are assumed to be independent variables. The Brute Force approach is used by varying each of these parameters in apt ranges, one at a time. The ranges of every parameter is given as- Time: 05 s to 30 s with resolution of 5 s, Voltage: 600 V to 900 V with resolution 50 V, Amplifier: 0.4 to 2.8 with resolution 0.4 and LLD: 0.4 to 1.6 with resolution 0.2. The experiment was carried out at every combination of four independent parameters, and consequently, we get 2058 combinations of data set for every single detector. The experiment was repeated 30 times at every combination of settings. The same procedure is repeated for the rest of the detectors.

Table 1 CalibrationSettings from Manufacturer.
Full size table

Gamma CT is used to see the impact of calibration of the detector over the accuracy of the result. The geometry of the gamma CT system is shown in Figure 4. Measurement was performed using a phantom object with a known inner profile (shown in Figure 4) at two different settings: (a) one at the optimal setting calculated by the best method and (b) the other at a random setting. Phantom used in our Gamma CT experiment consists of three different materials: Perspex (\(\upmu\)~1.02), aluminum (\(\upmu\)~0.211), and steel (\(\upmu\)~0.544) where \(\upmu\) is the attenuation coefficient (\({cm}^{-1}\)) of material [35]. Distance between source and detector is kept 68.5 cm, object to the detector is 53.5, fan beam angle was 47.58 cm. and diameter of the object is 12 cm. Data acquired at every rotation angle \({20}^{^\circ }\) up to a complete rotation of \({360}^{^\circ }\).

Figure. 4
figure 4

Geometry of gamma CT system.

Full size image

3.1 Choice of Best Method and Parameters with Major Contribution

Optimal values of LLD, time, amplifier, and voltage of each detector are estimated using 5 different methods. In data processing steps, when a single value is required in few methods (methods 4 and 5), three different case studies/results are created by taking the mean, mode, and median of the same data and estimating the optimal values of parameters. This way, we incorporated and studying optimal settings, having been influenced by these statistical tools. Counts measured at the optimal setting from each method are compared with the count rate. Cesium 137 (137Cs) of present activity 1.5µCi is used. Radioactive source with a relatively higher count rate would require a shorter pulse to discriminate the incidence of a successive individual gamma photon. The coefficient corresponding to amplifier gain is expected to accommodate any associate effect in the case of CLT. For other methods, it is reported that the associated electronics parameter (dead time) does not affect the saturation characteristics[36].

CT measurements (for median, mean, and mode of data) are made for settings estimated from all 5 calibration methods. It is assumed that settings/parameters estimated using the optimal calibration method would give the best reconstruction and would have similar count rates.

Optimal settings of all detectors, calculated by a particular method, are fitted into the multivariate non-linear equation (Eq. 6) to see the major contribution of the parameter. Inbuilt function ‘nlinfit’ of MATLAB® is used for non-linear fitting [37,38,39]. Robust fitting with weight function ‘Talwar’ is used [40]. We note that when the number of outcomes is too small in multivariate non-linear regression, results from the analysis may not be accurate and precise [41]. We choose two different models. The other one has one more independent parameter instance/sample size \((M)\) to testify its influence over measurement results. Following non-linear polynomial equations (Eq. 6 and 7) are used for empirical fitting the data:

$$counts= {b}_{1}({LLD)}^{b2}+{b}_{3}({Time)}^{b4}+{b}_{5}({Amp)}^{b6}+{b}_{7}({Volt)}^{b8}+{b}_{9}$$
(6)
$$counts= {b}_{1}({LLD)}^{b2}+{b}_{3}({Time)}^{b4}+{b}_{5}({Amp)}^{b6}+{b}_{7}({Volt)}^{b8}+{b}_{9}({M)}^{b10}+{b}_{11}$$
(7)

To avoid falling into a local minimum, we ran the codes for several fine boundary conditions of coefficients (\({b}_{1}\) to \({b}_{9})\)or \({b}_{11}\) in between 0.1 to 7.1 with 0.2 resolution. Maximum entropy and minimum \({l}_{2}\) norm is used as an objective function in the above multivariate non-linear constraint optimization analysis [43, 44].

It is assumed that mutually dependent higher-order terms would have a negligible contribution as the parameters are considered independent of each other. As a final check, another practical constraint based on human perception is applied. Out of many solutions with very close values, we chose the one that has positive values of\({b}_{3}\) and \({b}_{7}\) as the time and voltage would increase, counts will increase. The optimizing results having a large contribution of constant-coefficient \({b}_{9}\) or \({b}_{11}\) are rejected to ensure contribution from other parameters/settings. This optimized non-linear equation is used to find the prominent term having a larger contribution to affect the radiation measurement. In the next section, we now discuss the results.

4 Result and Discussion

Detectors are calibrated using five different methods briefly discussed in the theory section. Optimal values of amplifier gain, LLD, high voltage at PMT, Time to measure counts for all detectors are shown in Table 1. The respective counts are shown in Figure 5. Figure 5a, b, c, d, and e shows the counts detected by 5 detectors at optimal setting calculated by method1, method 2, method 3, method 4, and method 5 respectively. It is observed that optimal counts calculated by method 2 (CLT2) are close to the count rate of the radioactive source. Multivariate non-linear equation Eq. 6 modeled to fit optimal setting parameters and corresponding counts calculated by all methods.

Figure. 5
figure 5

Optimal counts Calculated by (a) method 1 (CLT1), (b) method 2 (CLT2), (c) method 3 (PWS), (d) method 4 (True counts measurement), (e) method 5 (Gross method).

Full size image

Entropy, coefficients of time (\({b}_{3}\),\({b}_{4}\)), coefficients of voltage (\({b}_{7}\),\({b}_{8}\)) and constant parameter (\({b}_{9}\)) of 5 different methods are plotted in Figure 6a, b, c, d, e and f respectively. Data are plotted for three statistical tools mean, median, and mode. In Figure 6a, we see that all methods have a comparatively equal value of entropy except for method 5, irrespective of mean, median, and mode. In Figure 6d we got a very large value of \({b}_{9}\) the coefficient for method 3, so we divided this parameter by appropriate value so it will not suppress the value of the coefficient for other methods for easy comparison. It can be observed from Figure 6b, c, d, and e that methods 1, 3, and 4 are dropped out from further discussion due to practical constraints (positive coefficient for voltage and time). We get almost near to zero error values; hence no comparison can be made on the basis of the plot for methods 1, 2, and 4. We observed a large value of root mean square error (RMSE) for methods 3 and 5 compared to other methods, which shows these methods are not fitted well in our modeled equation. The constant term/coefficient \({b}_{9}\) is small as well for method2 for mean (least), median and mode cases. Entropy values are also consistently comparable with maximum values for method2. Figure 6 concludes that method 2 is fitted best in the multivariate non-linear equation and having optimal counts close to the counts rate of the radioactive source. Overall discussion leads to mean as a recommended statistical parameter that preserves the accuracy and precision of the measurement.

Figure. 6
figure 6

For 5 different methods and their mean, median, and mode (a) entropy, (b) time multiplied coefficient, (c) time exponential coefficient, (d) voltage multiplied coefficient, (e) voltage exponential coefficient, and (f)\({b}_{9}\) coefficient.

Full size image

The optimized non-linear eq. for four independent parameters is:

$$Counts=\left(-0.125\right)*({LLD)}^{\left(-13.50\right)}+\left(2.4\right)*({Time)}^{1.67}+\left(-3.09\right)*({Amp)}^{4.93}+\left(0.63\right)*({Volt)}^{1.09}+3.34$$
(8)

Sample number \((M)\) is considered as an independent variable to see an impact on the statistics of the measurement in the next stage of analysis. Up to sample number 25, we got a negative coefficient of sample number. Sample size coefficient negative tells that this is not the threshold sample size. The threshold value of the sample number is observed at 26 in our work. We varied sample numbers from 26 to 30 with resolution 1.

Redoing the above analysis and including \(M\) as an independent variable again resulted in method2 (CLT2) as the best option. Optimal counts and settings are fitted in modeled equation, Eq. 7, and observed that sample number 30 yields the best result, best in the sense it satisfies the criteria that we decided to choose optimal equation. Entropy and coefficient (\({b}_{11}\)) of Eq. 7 are plotted in Figure 7a and b respectively for mean, median, and mode of counts. In this case, we observed that the median optimizes the result. We found that the data has very negligible skewness, and plots are skipped here to maintain the brevity. The optimal non-linear equation for five independent parameters is:

Figure. 7
figure 7

(a) entropy, (b) \({b}_{11}\) the coefficient for modeled Eq. 7.

Full size image
$$Counts=-0.397*({LLD)}^{-11.72}+\left(5.18\right)*({Time)}^{1.46}+\left(-1.74\right)*({Amp)}^{5.60}+ (4.55)*({Volt)}^{0.75}+\left(3.01\right)*({M)}^{1.07}+5.36$$
(9)

4.1 Gamma CT Analysis

The CT phantom profile is a fairly deterministic variable provided that the factors affecting its experimental recovery are optimally chosen /set (w.r.t to error). The inverse estimation of CT Phantom mainly suffers from noise in count measurements and error in the solution of the inverse problem. CT measurement environment is selected to demonstrate that the optimal calibration method (while satisfying the maximum entropy function) provides optimal electronics settings. The optimal electronics settings would minimize the level of noise in count measurement, thus error in reconstruction of CT Phantom.

CT measurements are performed for (a) random parameter values and optimal settings obtained from all methods. Reconstruction results are shown in Figure 8 for random setting and optimal setting obtained from Method2. Upper bottom in Figure 8 shows (a) a real picture of the phantom, (b) a cyber-phantom: the 3-D image of the phantom, and (c) its digital analogs. Figure 8d shows the reconstructed image of the cyber phantom obtained by (d) projection data created using digital analogous / simulation with 0.33% RMSE. Figure 8e shows reconstruction from real data acquired at random settings and Figure 8f at optimal setting calculated by best method 2 (CLT2). The hybrid reconstruction method, MaxenT, is used to obtain reconstructed images [42]. Reconstruction error is minimum for real data measurement when optimal calibration setting is used. Root mean square error is calculated with respect to the cyber phantom image (Figure 8c).

Figure. 8
figure 8

Gamma CT Analysis: (a) camera image of the phantom, (b) 3-D image, (c) cyber phantom, (d) simulation, (e) at random setting, (f) at the optimal setting. The reconstruction with optimal settings has the least RMSE and better visual resemblance with true.

Full size image

Scattering is included in all of the measurements as shielding is not used, and the optimal calibration setting may change. The optimal non-linear equation gives a relationship between counts and the optimal value of LLD, time, Amplifier gain, and high voltage. Both optimal non-linear equation for 4 and 5 independent parameters shows that time to measure the radiation count has a dominant influence over other.

Each detector has different optimal calibration settings owning to the fact that existing fabrication techniques result (structure: electronics, impurities of Thallium in Na) different detectors. Direction dependency may be involved, and further study is required.

Although all detectors are not the same, we are forcing the optimal setting values from all detectors to curve fit Eq. 6 and 7. It is assumed that this would give us bulk characteristics for a major contribution of the parameter. Sparse data set is used to develop Eq. 6. Equation 6 and 7 are made of neglecting several mutual dependent terms, assuming the parameters are independent of each other.

5 Discussion and Conclusion

The proposed general strategy: “vary the involved measurement parameters for radiation counts, apply calibration methods, curve-fit them all for maximum entropy to find optimal parameter values and test for minimum R.M.S.E. in CT reconstruction” can be applied to any other field of radiation measurement using other types of detectors. This algorithm is independent of the type of radiations as well as the type of detectors used. Only the counts and measurement parameters (settings) of the detector are used to study the calibration methods. Different gamma or any other radiation measurement device (detectors) may have different setting parameters to include; however, the strategy may remain the same.

More than two types of scintillator detector setups (manual: nuclear bin type, semi-automatic, and fully automatic) are used for validation. Following are the pointwise conclusions:

  1. 1.

    Median is found to be the best statistical tool in this work if the sample size is included as an independent parameter during the calibration stage. This observation is according to previously reported works. Otherwise, mean as a statistical tool is recommended. Data was found to have negligible skewness limiting the scope to provide comments about utility of mode and median.

  2. 2.

    The second version of the Center Limiting Theorem is found to be the optimal calibration method.

  3. 3.

    The optimal calibration settings correspond to better practical feasibility for precision and accuracy as CT reconstruction is found to be the best.

  4. 4.

    Multivariate non-linear analysis suggests that once the LLD is set (according to photopeak at center), it is essential that time to measure the radiation counts must be optimally obtained. Any random duration for measurement may affect the results. Voltage and sample size are other important parameters to look for. A strategy is presented here for calibration.