1 Introduction

Frictional interaction between contacting bodies gives rise to the effects spanning from the scale of Earth’s tectonic plates [1] to the scale of atoms [2] and sets problems at the interface between physics, chemistry, material science and mechanics [3, 4]. Stick-slip sliding motion [5], which brings pleasure in bowed instruments, annoys in squeaking doors and awakes fear in earthquakes, is an example. Understanding the dynamics of this phenomenon is central in different fields, so evolution of stick-slip events, from preliminary displacement to the onset of sliding and steady motion, has been extensively studied during the last decade [6–14] and much light was shed on this problem.

Surface topography is one of the most important properties affecting the behavior of contacting bodies [3], so modifying the surface geometry is employed literally everywhere from internal combustion engine [15] to biological evolution [16]. The latter has inspired much research on the adhesive effects of splitting up the contact into finer sub-contacts, and hundreds of papers are published to date [17–20]. Surprisingly, it was found that in elastomers, which are usually used as a model material in studies of geometry-controlled adhesion and where stick-slip motion is the most pronounced [21], the effect of stick-slip ceased if contact was split [22–26]. This finding, however important it is, has only recently started being modeled [26, 27].

There are several theoretical models describing the processes that occur at the frictional interface between two bodies in contact [28]. A basis approach was suggested in the Burridge–Knopoff model of earthquakes [29] and further developed in a number of studies [13, 26, 30–34]. Clearly, no model is capable of simulating all features of real process, so main properties only can be isolated [35]. Along this line of thought, based on the classic Burridge–Knopoff approach, here we present a simple toy model that, despite its simplicity, allows explaining the observed effect. Contrary to the most earthquake models where the dynamics of a driven slider chain has been studied and phenomenological laws have been introduced to describe friction at the slider–track interface, here we develop a mass-less (non-inertial) quasi-static (non-viscous) model of stick-slip phenomenon built exclusively on the difference between higher static and lower kinetic friction force between each slider and the track.

2 Theoretical Model

2.1 Single Contact

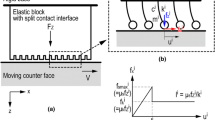
The contact between elastic surface (1) and its rigid counter-face (2) is presented using a simple model including (1) the surface, S, capable of producing static friction, F fr−s, and kinetic friction, F fr−k, the spring describing tangential stiffness of elastic surface, k, and (2) the driving conveyor belt, B, traveling the distance u (Fig. 1a).

Fig. 1
figure 1

Model of the contact between a single-piece (a) and split/rough (b) elastic surface and its rigid counter-face

Full size image

The mechanism of individual stick-slip event is this. Driving belt motion is transmitted through the contact by friction and leads to the quasi-static displacement of the surface, S, while loading the spring. Before the surface starts sliding relative to its counter-face, friction and elastic forces are in equilibrium, growing until elastic force is less than static friction (stick phase). With further displacement of the driving belt, friction cannot hold the surface in the stuck state and elastic force returns the surface toward its original state (slip phase). In doing so, elastic force decreases until it becomes equal to the kinetic friction. At this point, the slip is terminated and the cycle repeats.

2.2 Multiple Contacts

The contact of the rough (or split) elastic surface and its rigid counter-face is presented as a number of separate uncoupled sub-contacts described using the above model, while stiffness and friction of each sub-contact are statistically scattered fractions of those of the whole surface (k, \(F_{{{\text{fr}} - {\text{s}}}}\), \(F_{\text{fr - k}}\)). In the general case, an elastic surface consists of n asperities (or outgrowths) (Fig. 1b), and jth typical asperity is characterized by the following parameters:

$$\begin{gathered} k^{jn} = {k \mathord{\left/ {\vphantom {k n}} \right. \kern-0pt} n} + \delta k^{jn} \hfill \\ F_{\text{fr - s}}^{jn} = {{F_{\text{fr - s}} } \mathord{\left/ {\vphantom {{F_{\text{fr - s}} } n}} \right. \kern-0pt} n} + \delta F_{\text{fr - s}}^{jn} \hfill \\ F_{\text{fr - k}}^{jn} = {{F_{\text{fr - k}} } \mathord{\left/ {\vphantom {{F_{\text{fr - s}} } n}} \right. \kern-0pt} n} + \delta F_{\text{fr - k}}^{jn} \hfill \\ \end{gathered}$$
(1)

where \(\delta k^{jn} ,\, \, \delta F_{\text{fr - s}}^{jn} ,\, \, \delta F_{\text{fr - k}}^{jn}\) are small statistical deviations (positive or negative) of the parameters from their average values \({k \mathord{\left/ {\vphantom {k n}} \right. \kern-0pt} n},\,\,{{F_{{{\text{fr}} - {\text{s}}}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - {\text{s}}}} } n}} \right. \kern-0pt} n},\,\,{{F_{{{\text{fr}} - k}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}} } n}} \right. \kern-0pt} n}\), respectively.

The following numerical algorithm describes stick-slip simulation of the whole set of n asperities with the step-by-step change, Δu, of the counter-face displacement, while at the end of the ith step the displacement is \(u_{i} = u_{i - 1} + \Delta u\). The whole scenario can be represented as follows: (1) At each ith step during the stick phase in jth asperity, the elongation of the respective jth spring increases as \(\Delta l_{i}^{jn} = \Delta l_{i - 1}^{jn} + \Delta u\), so the elastic force equals \(F_{{{\text{el}}, \, i}}^{jn} = k^{jn} \cdot \Delta l_{i}^{jn}\); (2) since the spring is loaded by friction transmitted through the contact, the elastic force, which is equal to friction force, cannot exceed the value of static friction, \(F_{{{\text{fr}} - {\text{s}}}}^{jn}\), so for all asperities the following question should be answered

$$F_{{{\text{el}}, \, i}}^{jn} \mathop = \limits_{ < }^{ > } F_{\text{fr - s}}^{jn} \, ?$$
(2)

(3) The answer defines whether the asperity enters the slip phase. If \(F_{{{\text{el}},i}}^{jn} \le F_{{{\text{fr}} - {\text{s}}}}^{jn}\), the jth asperity is still in stick phase and the spring is further loaded according to point (1) for the next i + 1 step. If \(F_{{{\text{el}},i}}^{jn} > F_{{{\text{fr}} - {\text{s}}}}^{jn}\), the jth asperity enters the slip phase, springing back toward its undeformed state. However, the elastic force cannot drop below the value of kinetic friction, and hence, at this point the slip of jth asperity is terminated. Therefore, the spring deformation becomes \(\Delta l_{i}^{jn} = {{F_{{{\text{fr}} - k}}^{jn} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}}^{jn} } {k^{jn} }}} \right. \kern-0pt} {k^{jn} }}\), and the process is repeated according to point (1) for the next i + 1 step.

Since different asperities are characterized by different statistically scattered parameters, the stick and slip phases in different sub-contacts do not match. Summing up the current values of the elastic forces developed in all asperities, we obtain the current value of the total friction force evaluated versus the counter-face displacement, u.

3 Results and Discussion

Though the presented approach has been formulated to explain the results obtained experimentally [23–26], it is clear that due to its simplicity the model is best suited for qualitative analysis. Therefore, all calculations have been made using the consistent parameters whose units are not specified. The set of the parameters used was as follows. Elastic surface was characterized by the total tangential stiffness k = 1. The interface between the elastic surface and its rigid counter-face was characterized by the total static friction F fr−s = 10 and total kinetic friction F fr−k = 5. The parameters characterizing the individual asperities were chosen using a random number generator from normally distributed pools having mean values \({k \mathord{\left/ {\vphantom {k n}} \right. \kern-0pt} n}\), \({{F_{{{\text{fr}} - {\text{s}}}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - {\text{s}}}} } n}} \right. \kern-0pt} n}\), \({{F_{{{\text{fr}} - k}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}} } n}} \right. \kern-0pt} n}\) and standard deviations \({{0.1 \cdot k} \mathord{\left/ {\vphantom {{0.1 \cdot k} n}} \right. \kern-0pt} n}\), \({{0.1 \cdot F_{{{\text{fr}} - {\text{s}}}} } \mathord{\left/ {\vphantom {{0.1 \cdot F_{{{\text{fr}} - {\text{s}}}} } n}} \right. \kern-0pt} n}\), \(0.1 \cdot {{F_{{{\text{fr}} - k}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}} } n}} \right. \kern-0pt} n}\), where the number of asperities n was chosen between 1 and 5,000 for each numerical test. In each test, the development of the relative displacement between the two surfaces was analyzed by an incremental change in the rigid surface displacement Δu = 0.05. Before the experiment started, the contact was unstressed, which reflected in that all springs were undeformed.

Figure 2a presents a variation of friction force, F fr, during the relative motion between the smooth elastic surface (n = 1) and its rigid counter-face as a function of the counter-face displacement, u. Initially, the contact is unloaded, i.e., the spring is undeformed. At this position, both friction force and displacement are equal to zero. Then, in accordance with the above-described scenario, friction force increases with displacement until it reaches a value of static friction, demonstrating a first (transient) stick phase. After that, friction drops to the kinetic friction value, which represents a first slip phase. Then, steady-state quasi-static stick-slip motion is established. Areas on the graph, corresponding to the increase in the friction force from kinetic to static friction, describe the phases of stick. Areas on the graph, corresponding to the precipitous drop of the friction force from static to kinetic friction, describe the phases of slip.

Fig. 2
figure 2

Friction force between a smooth (a) or rough/split (b, c, d) elastic surface and its rigid counter-face as a function of displacement, u

Full size image

Splitting the elastic surface into two outgrowths (or asperities) having the same properties \({k \mathord{\left/ {\vphantom {k 2}} \right. \kern-0pt} 2}\), \({{F_{{{\text{fr}} - {\text{s}}}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - {\text{s}}}} } 2}} \right. \kern-0pt} 2}\), \({{F_{{{\text{fr}} - k}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}} } 2}} \right. \kern-0pt} 2}\) results in exactly the same behavior of the contact shown in Fig. 2a. However, if the asperity’s properties are chosen randomly from the sample of normally distributed values, the behavior of the system starts changing.

Though the set of two random numbers is a non-representative statistical sample, the case of two outgrowths may be considered to follow the evolution of the split surface behavior. Figure 2b demonstrates the total friction force between the split surface and its counter-face versus the counter-face displacement. Simulation begins from the same initial position as in previous case. Transient response of the system, which is similar to the first stick phase of the non-split surface, continues until friction between one of the two outgrowths and the counter-face reaches the static friction value. It causes the slip of this outgrowth, while the second outgrowth still remains in the stick phase. Then, the turn of the second outgrowth’s slip comes and so on. Figure 2b demonstrates a non-synchronous stick-slip motion of two outgrowths with different parameters, which results in a more random steady-state behavior of the whole system. It is natural to expect that in this case the total friction force will vary around the mean value between static and kinetic friction with slightly smaller amplitude than that in the case of the non-split surface. Actually, the mean value appears slightly smaller than expected, which may be explained by poor statistical representativeness of the sample formed by only two numbers. The following examples, showing the behavior of the surfaces split into much larger number of outgrowths (or asperities), which characterized by different randomly distributed parameters, confirm this hypothesis.

Figure 2c demonstrates the behavior of the elastic surface having 50 asperities. It can be seen that in this case the total friction force really varies about the mean value between static and kinetic friction. The amplitude of the friction force variation is significantly smaller, which provides much more uniform sliding between the rough surface and its counter-face. In that case the surface has 5,000 asperities, the non-synchronous stick-slip motion of individual asperities is nearly not observed (Fig. 2d). Thus, the lack of uniformity in phases of stick and slip between different individual asperities provides smooth sliding between rubbing surfaces in the steady-state regime [27]. The steady-state behavior is independent of the initial conditions, and indeed, no matter what deformation of the springs describing the elastic surface we have started with, the system always approached the same motion state. The system behavior during the transient response, however, did depend on initial conditions, which requires further discussion.

The transient response becomes more visible, the less pronounced is the stick-slip amplitude and manifests itself as a fading wave at the onset of sliding [36], which is best evident in Fig. 2d. This wave appears due to synchronous motion of all asperities that start to be displaced from the same unstressed position, which requires several asynchronous stick-slips of different asperities before the sliding turns to be completely uniform. Considering that real surfaces can hardly be brought in contact without certain tangential prestressing, we can change the above situation by including into our model initial deformations of the springs, \(\Delta l_{0}^{jn}\). This is made when we also choose \(\Delta l_{0}^{jn}\) using a random number generator from a normally distributed pool having mean value 0 and standard deviation 1 (0.1 of preliminary displacement that is approximately equal to 10). The resulting curve appears to be similar to Fig. 2d, while the amplitude of the wave at the onset of sliding decreases twofold. This wave decreases even more when a larger variance of the system parameters is used, leading finally to the more commonly experimentally seen behavior of rough engineering surfaces (as well as biomimetic split surfaces [23–26]), where this wave is completely absent. Figure 3 demonstrates such an example, where we choose the variance of \(k^{jn}\), \(F_{{{\text{fr}} - {\text{s}}}}^{jn}\) and \(F_{{{\text{fr}} - k}}^{jn}\) to have standard deviations of \({{0.3 \cdot k} \mathord{\left/ {\vphantom {{0.3 \cdot k} n}} \right. \kern-0pt} n}\), \({{0.3 \cdot F_{{{\text{fr}} - {\text{s}}}} } \mathord{\left/ {\vphantom {{0.3 \cdot F_{{{\text{fr}} - {\text{s}}}} } n}} \right. \kern-0pt} n}\) and \(0.3 \cdot {{F_{{{\text{fr}} - k}} } \mathord{\left/ {\vphantom {{F_{{{\text{fr}} - k}} } n}} \right. \kern-0pt} n}\), which leads to asynchronous motion of different individual asperities from the very beginning. On the other hand, the appearance of the monotonic part of the transient response (preliminary displacement) is found to be independent of standard deviations of the parameters involved while being defined solely by initial conditions.

Fig. 3
figure 3

Behavior of a rough/split elastic surface characterized by large variance in stiffness and friction of asperities/outgrowths

Full size image

4 Conclusion

The simple mass-less statistical spring/static friction/kinetic friction model presented in this work allows explaining the disappearance of stick-slip motion when elastic surface slid in contact with rigid counter-face is split into large amount of small outgrowths (or asperities). Of course, this toy model is uncapable of simulating all features of real process, such as the aging effects or the fact that some sliding distance is necessary for the transition from static to kinetic friction. However, adjusting the model parameters, it is also possible simulating systems with different transient responses. The results obtained may also be helpful in understanding the variety of sliding behavior of different materials. For instance, in agreement with our findings, in metals, where true contact is usually made at a very large number of areas [37], stick-slip is less pronounced than in rubber-like materials, which, being much more deformable, can better conform the counter-face [38] and, hence, form less contact spots, leading to remarkable stick-slip effects.