1 Introduction

The importance of surface roughness in macroscopic friction is recognized for a long time. As early as in the eighteenth century, Coulomb [1] claimed that the fundamental cause responsible of friction was the interlocking of antagonist asperities. The modern theory of the so-called multi-contact interfaces is due to Bowden and Tabor [2], Archard [3], and Greenwood and Williamson [4]. From these studies, it appears that there is a distinction between the nominal contact area (surface in apparent contact) and the actual contact area (sum of all asperities in contact), the latter being the only one responsible of friction. The actual contact area is proportional to the normal load whatever is the nominal contact area. This is the key to explain Amontons–Coulomb’s laws of friction which states that the friction force is proportional to the normal load but does not depend on the nominal contact area. This behaviour stems from a non-trivial collective phenomenon of microscopic contacts since it has also been checked that this proportionality does not hold for a single contact [5, 6]. The physics of multi-contact interfaces is always an active field of research in both experimental [8] and numerical [7] ways. Recent advances in rapid imaging technology now allow to directly observe the multi-contact interface between sliding solids [9, 10].

But the fundamental question in kinematic friction is how the kinetic energy of the sliding solid is transformed into thermal energy. Microscopic models initiated by Tomlinson [11] have shown the importance of multi-stability [12] in the dissipation process. The energy stored in elastic deformation of microscopic degrees of freedom is suddenly released as vibration. This process is well illustrated by the experiment of Ciliberto and Laroche [13]. The vibration induced by the interaction of asperities is therefore a possible explaination of macroscopic friction [14]. In the meantime, the normal vibration of solids has also a direct effect on the friction force [15, 16]. Hess and Soom [17, 18, 19] have shown that the presence of normal vibration can reduce the mean contact pressure, the contact area and therefore the friction force. All these studies underline the importance of dynamical effects in sliding contact of rough surfaces.

Focusing on the audio frequency range, friction-induced vibration may have several origins [21]. The first origin is the mechanical instabilities such as stick-slip, the ringing of wine glasses [20] for instance. Stick-slip is usually explained by the velocity weakening phenomenon that is the decreasing of friction coefficient during the transition between static and kinematic friction [22]. The second origin, the so-called roughness noise, is a wide band noise produced by light impacts between antagonist asperities. This is a direct effect of the dynamics rough interfaces. Moving a small object on a table or rubbing the hands against each other are two examples of roughness noise.

Experimental studies on roughness noise are rare. They are often included in general studies on friction noise where it is sometimes difficult to separate steady sliding and stick-slip regimes. Let quote the work of Yokoi and Nakai [23], Othman et al. [24], Stoimenov et al. [25], and Ben Abdelounis et al. [26] who have studied the link between the sound pressure level and roughness and sliding speed. They propose a power law \(P_{\rm a}\propto Ra^\alpha V^\beta\) where P a is the acoustical radiated power, V the sliding speed and Ra a roughness parameter.

More recently, the question of the dependence of friction noise with the contact area is tackled in Ref. [27]. The principle of the experiment is the following. Several similar solids with a rough base, called sliders, are pushed on the rough track of a plate, called resonator. The roughness of both track and sliders is the same and the sliding speed is maintained constant. The resulting normal vibration is measured in several points of the resonator. Then, the vibrational level is plotted versus the number of sliders. It has been found that two regimes exist. The first regime is linear. The vibrational energy is directly proportional to the number of sliders, i.e. to the contact area. But, in a second regime, the vibrational energy does not depend on the contact area. All intermediate regimes have also been observed.

In this experiment, no distinction is done between nominal and actual contact areas. When the number of sliders is increased, both nominal and actual contact areas are increased in same proportion. The study of the separate contribution of nominal contact area for instance, would require to maintain constant the actual contact area. This has not been done. Therefore, the evolution of vibrational level versus contact area is rather the evolution of vibration versus the number of identical sources (sliders). Thus, throughout this text, the term contact area must generally be understood as the number of sources.

This experimental result is not obvious. Usually, a larger number of acoustical sources leads to a greater sound pressure level. That evidence applies sometimes but can be violated too, this proves that the acoustic behaviour of rough surfaces deserves a deeper analysis.

This study proposes an explanation of the existence of these two regimes. The aim is to investigate the relationship between the vibrational level and the nominal contact area, the nominal contact pressure being maintained constant. The paper is organized as follows. The first section is concerned with the observation of the two regimes of roughness noise, a constant vibrational level on the one hand, and a proportional vibrational level on the other hand. In Sect. 3, a unified model is proposed and is tested in Section 4 on a system which shows these two regimes. Finally, some conclusions are given in Sect. 5.

2 Observation of the Constancy of Roughness Noise

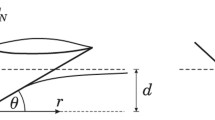
When rubbing two flat steel sheets with hands, the resulting friction noise is an example of roughness noise. This experiment have been proposed by Stoimenov et al. [25] in order to illustrate the dependence of friction noise with roughness. The static load applied by hands is so light that the dynamical coupling is weak. If the movement is applied as shown in Fig. 1, the contact surface can be controlled with the angle between the two pieces. Then, a curious result can be observed: the noise level does not depend on the contact area.

Fig. 1
figure 1

When rubbing two steel pieces, the level of friction sound does not depend on the contact area

Full size image

A similar experiment, may be more convincing, can be achieved with a drum. Rubbing simultaneously several rigid and rough solids, some sugar lumps for instance, on the drum membrane also produces a roughness noise. The drum then plays the role of a resonator. Once again, it can be checked with a sonometer or more simply by hearing the noise, that a larger number of solids does not produce a stronger sound. Results of this experiment are shown in Fig. 2a. The noise level remains constant up to 50 lumps.

Fig. 2
figure 2

Friction noise of sugar lumps. The sound pressure Level (Lp) is measured by a sonometer with a constant sliding speed. a On the drum membrane the friction sound is constant. b On the surface of a wood table the friction sound is proportional to the number of sliders (∼10 dB/decade)

Full size image

This observation is rather paradoxical. The common sense tells us that the greater is the contact area the higher is the sound level. The difference of sound pressure level between a single source and s identical sources is \(\Delta L_{\rm p} = 10 \log_{10} s\) dB that is 10 dB/decade (s = 10). This law simply claims that the power being injected into vibration is proportional to the number of sources, or, in other words, that the sources are uncorrelated.

The additivity of sound sources and its immediate consequence the proportionality of vibrational energy with the number of sliders, applies in some cases. Let re-do the same experiment of sugar lumps on a thick wood table. Results are shown in Fig. 2b. The noise level now increases with a slope near 9  dB/decade which well agrees with the theoretical result of 10 dB/decade. All these simple examples show the link between friction-induced vibration and contact area is more complex that it could be at first sight.

Two regimes exist for roughness noise, a first regime where friction sound is constant and a second one where friction sound is proportional to the number of sliders. These regimes illustrated in these simple experiments, have also been explored on a single steel plate as well as all intermediate regimes [27].

3 Theoretical Development

Roughness noise is generated in three steps. Micro-impacts between asperities at the interface is the fundamental mechanism responsible of the conversion of kinetic energy of the sliding solid into vibrational energy. The resulting vibrations propagate through the solids which then behave as resonators. Finally, the sound is radiated from solids in air.

The final step, the acoustical radiation, is rather well-known [28, 29]. The power being radiated is proportional to the square of the root mean square of vibrational velocity v on the vibrating surface,

$$ P_{\rm rad}=\rho_0 c \sigma v^2 A, $$
(1)

where ρ0 is the air density, c the sound speed in air, σ the so-called radiation factor and A the radiating area. The sound power level (dB) is

$$ L_w=10\log \frac{P_{\rm rad}}{P_0}, $$
(2)

where P 0 = 10−12 W and the base of logarithm is 10. It is therefore directly related to the mean velocity v. The question of sound level then reduces to the knowledge of the mean vibrational velocity v. We shall determine it by applying a power balance on the vibrating system.

The first step is concerned with the excitation mechanism. Without going into details of what happens at the interface, it can expected that the normal vibration stems from the numerous impacts occurring between antagonist asperities. An analytical model of impact of rough surfaces as well as a review of previous ones available in the literature, are presented in Ref. [30]. Several general points can be enounciated. The more important the incident kinetic energy, the stronger the impacts. In particular, an increase of the sliding velocity or the moving mass must lead to a higher vibrational power transfered to the system. Furthermore, due to the random character of the surfaces, all these events are independent i.e. the properties of individual impacts, in particular the transfered energy, are not influenced by other impacts. The vibrational power being injected P inj in the vibrating system is thus proportional to the rate of impacts and therefore the contact area S,

$$ P_{\rm inj} = p S, $$
(3)

where p is the vibrational power being injected per unit area. Indeed, p remains unknown but the important fact is that P inj is proportional to the contact area S.

The vibrational level is controlled by dissipation. Many damping coefficients are used in the literature but in the field of Statistical Energy Analysis [31], the vibrational power being dissipated is,

$$ P_{\rm dis}=\eta\omega mv^2 A. $$
(4)

mv 2 A is the total vibrational energy of the resonator, m being its mass per unit area, A the surface of the resonator and v the mean vibrational velocity. η is the so-called damping loss factor and ω is the central frequency. Indeed, η is a global loss factor which includes all types of dissipation and, in particular, the acoustical radiation. The radiated power P rad is therefore included in the term P dis.

The velocity v is found by applying the power balance P inj = P dis,

$$ mv^2=\frac{pS}{\eta\omega A}. $$
(5)

Since ρ0, c, σ, m and p do not depend on the friction area S, the explaination of the existence of the two regimes must be seek in the possibility of the damping loss factor ηω to depend or not on the contact area S. The physics of η must therefore be detailed.

Several phenomena are responsible of damping of vibration. But they can be classified in two types.

The first type is the dissipation occurring in the overall plate. Dissipation by hysteresis of material is an example. All points of the vibrating system are submitted to a strain cycle and therefore take part in dissipation. The sound radiation also belongs to that type. Beyond the critical frequency, the entire vibrating surface radiates whereas only edges and corners radiate below the critical frequency. Therefore, if in addition the vibrating field is diffuse, all parts of the vibrator are equally responsible of dissipation and the dissipated power is proportional to the plate surface A. We are then lead to introduce the “internal” damping loss factor η i and the power being dissipated by internal damping,

$$ P_{\rm int}=\eta_i\omega m v^2 A. $$
(6)

The internal damping loss factor η i is an intrinsic property of the resonator. Its value just depend on the material and on the shape of the resonator but not on the contact area S.

The second type of dissipation of vibration occurs at the frictional interface. It is well-known for a long time that a mechanical contact can be responsible of a significant increase of the damping loss factor [32]. Several phenomena whose friction, are responsible of dissipation of vibration within the contact. But the most important is certainly the air pumping. The vibrational power being dissipated in the contact is proportional to the contact area S and the square of the mean vibrational velocity v 2 [33]. Let introduce a “contact” damping loss factor η c , the vibrational power being dissipated by friction is,

$$ P_{\rm fric}=\eta_c\omega m v^2 S, $$
(7)

where η c ω is assumed to be a local quantity which depends on the roughness of surfaces in contact, the sliding velocity V and the mass per unit area m but not on the contact area S neither the surface of the resonator A.

The power balance now reads P inj = P fric + P int and therefore,

$$ m v^2=\frac{p S}{\eta_c\omega S+\eta_i\omega A}. $$
(8)

Indeed, the decomposition P dis = P int + P fric and Eqs. (4, 6, 7) implies that η(S) = η i  + η c S/A. Equations (5) and (8) are therefore equivalent, the latter being simply more detailed since the dependance with S is now apparent.

The regime of constant friction sound versus number of sliders experimentally observed, can now be explained by considering that the friction term dominates the internal damping term, η i ω A ≪ η c ωS. Equation (8) then shows that the vibrational energy depends neither on the contact area A nor on the plate area S,

$$ m v^2=\frac{p}{\eta_c\omega}. $$
(9)

On the other hand, the proportionality of friction sound versus number of sliders is recovered when the contact damping term is negligible compared with the internal damping term, η i ωA ≫ η c ωS. Always with Eq. (8) , the vibrational energy is now proportional to the contact area S,

$$ m v^2=\frac{pS}{\eta_i\omega A}. $$
(10)

Let us introduce the dimensionless quantity,

$$ Y=\frac{\eta_c\omega mv^2}{p}, $$
(11)

as the ratio of vibrational power dissipated by friction and injected power. Clearly, Y < 1. With,

$$ X=\frac{\eta_c\omega S}{\eta_i\omega A}, $$
(12)

being the ratio of powers dissipated by friction and by internal damping, Eq. (8) reads,

$$ Y=\frac{X}{X+1}. $$
(13)

The internal damping regime is found when X < 1 leading to the proportionality of friction sound with sources Y = X. And the contact damping regime appears when X > 1, the constancy of friction noise versus sources then reads Y = 1.

4 Experimental Verification

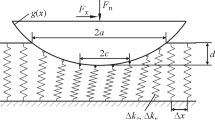
To check the above theory, a simple experiment has been carried out. The experimental set-up is shown in Fig. 3. s rigid sliders of base area S 0 (total friction area S = s S 0) and weight N 0 (total weight N = sN 0) are pulled by a small DC motor with a constant velocity V on an elastic resonator. The base of sliders and the track on the resonator are rough, giving rise to the expected vibration v of the resonator. The sliding velocity V is measured by a magnetic coder on the DC motor. A reductor on the motor ensures a constant sliding speed whatever the number of sliders is. The RMS value v of the vibrational velocity is measured within the frequency band [10 Hz–10 kHz] by a piezo-electric accelerometer. The signal is acquired by a 16-bit A/D board with a sampling frequency 40 kHz. The RMS value of v is computed from the stationary part of the accelerogram within a time window of duration 1 s.

Fig. 3
figure 3

Experimental set-up. Several rigid sliders with base area S and weight N are pulled at a constant velocity V on a rough track located on an elastic resonator. The friction results in a vibrational diffuse field v

Full size image

The sliders are parallelepipedic solids made of stainless steel and have dimensions 2 × 2 × 0.5 cm for the thin one and 2 × 2 × 2 cm for the thick one. Their masses are, respectively, M = 15.5 and 62 g. The first natural frequency of sliders is 35 kHz for the thin one and 75 kHz for the thick one. These values are obtained by finite element method with a volumic mass ρ = 7,800 kg/m3, a Young’s modulus E = 210 GPa and a Poisson’s ratio ν = 0.3. They are largely beyond 10 kHz and therefore the sliders can be considered as being infinitely rigid compared up to the upper frequency 10 kHz of measurement.

The resonator is a rectangular stainless steel plate. Two resonators are used, a steel plate alone and a steel plate covered with a damping material. The dimensions are 150 × 220 × 2 mm with a mass per unit area m = 16.1 kg/m2 for the undamped plate and m = 22.2 kg/m2 for the damped plate. The fundamental frequency of the plates is 200 Hz and about 75 natural frequencies are found within the band [10 Hz–10 kHz]. Consequently, the vibrational field resulting in the resonator is diffuse that is homogeneous and isotropic. The exact position of the accelerometer is of no importance.

The internal damping was assessed with η i ω = 2π × 2.2/T r , where T r is the reverberation time (the time for a decay of 60 dB of the impulse response). The reverberation times of both plates were measured by recording their impulse responses h(t), and plotting the time-reversed integration \(t \mapsto\int_t^\infty h^2(\tau) {\rm d}\tau\) (Schroeder’s plot). Values are given in Table 1.

Table 1 Experimental results
Full size table

The base of sliders and the track on the resonator are prepared by grinding. The size of the particles is about 1 mm and the particles are made of brown corundum. The resulting surfaces have a roughness about R a  = 5μm. The surfaces are cleaned with in two steps. The first cleaning is done with heptan in order to remove all greases. The second cleaning is done with propanol for all residual traces and the surfaces are dried under a nitrogen flux.

During the experiment with sliders, the central frequency is ω = γ/v where γ is the RMS value of the vibrational acceleration and v the RMS value of the vibrational velocity. The value ω/2π = 1,000 Hz is obtained in all experiments.

Four experiments have been realized by combining high and low internal damping with thin and thick sliders. The thickness of sliders is a convenient way to modify the mass of sliders and therefore incident kinetic energy. In all experiments, the vibrational RMS velocity v is measured when pulling from 1 to 8 sliders (S = 4–32 cm2) with a sliding velocity V = 6 cm/s. In Fig. 4 is shown the vibrational velocity v versus contact area S for the four experiments.

Fig. 4
figure 4

Vibrational level v (mm/s) versus contact area S (cm2) for a constant sliding speed V = 6 cm/s for the four combinations thick/thin sliders and undamped/damped resonator. The high damped plate with thin sliders shows the greatest increasing (internal damping regime) whereas the low damped plate with thick sliders rather shows a constant curve (contact damping regime)

Full size image

From Fig. 4, it appears that high damped resonators have a lower vibrational level. This observation well agrees with Eq. (5). The second remark is that the vibrational level is an increasing function of the mass of sliders that is the thickness of sliders. Finally, the slope of the curve v versus S has four different values. The lowest slope is encountered for low damped resonator and highest slider mass while the greatest slope occurs when the damping is high and the mass of sliders is low. The slope λ (dB/decade) as well as the mean vibrational energy \(m\bar{v}^2\) are evaluated from Fig. 4 around the logarithmic mean contact surface (\(\bar{S}=12\) cm2). Results are summarized in Table 1.

Following Eq. (13), the slope λ in dB per decade is,

$$ \lambda=10\frac{\partial \log Y}{\partial \log X}, $$
(14)

with the result

$$ \lambda=\frac{10}{\bar{X}+1}, $$
(15)

where \(\bar{X}\) is the mean value of X. This suggests a way for the determination of the unknown values of η c ω and p. The mean values \(\bar{X}\) and \(\bar{Y}\) follow from

$$ \bar{X}=\frac{10}{\lambda}-1, $$
(16)
$$ \bar{Y}=\frac{\bar{X}}{\bar{X}+1}. $$
(17)

The value of η c ω is thus obtained from

$$ \eta_c\omega=\frac{\bar{X}\eta_i\omega A}{ \bar{S}}, $$
(18)

and the value of p from,

$$ p=\frac{\eta_c\omega m\bar{v}^2}{\bar{Y}}. $$
(19)

Values of η c ω and p are also summarized in Table 1. Results of measurement for the four experiments are re-plotted with dimensionless variables X and Y in Fig. 5.

Fig. 5
figure 5

Vibrational level versus contact area with non-dimensional parameters X and Y. The left part of the curve has a slope of 10 dB/decade (regime of internal damping) and the right part is constant (regime of contact damping). Measurements with two plates (low and high internal damping) and different sliders (thick and thin) well fit the theoretical curve of Eq. (13)

Full size image

It is apparent from Fig. 5 and Table 1 that all regimes from X < 1 to X > 1 are reached in these experiments. The fact that the two regimes (proportionality and constancy) are observed on the same vibrational system, shows that the physical explanation of this phenomenon does not lie in the nature of system (a membrane for the drum and a plate for the wood table), but rather in the friction conditions (contact pressure, sliding velocity, etc.) and the internal damping of the resonator. The value of X (deduced from the slope λ) is multiplied by about 10.4 (respectively 8.6) for thin sliders (respectively thick sliders) when the internal damping η i ω of the resonator is multiplied by 18 (respectively 10). These values are comparable and show that the increase of the vibrational level is effectively driven by the internal damping of the resonator.

A final remark is that the values of injected power per unit area p are greater for heavy sliders. This result reinforces the idea that incident kinetic energy 0.5 MV 2, where M is the mass of sliders and V the sliding speed, is the relevant parameter which controls the vibrational power being injected in the system. It is unfortunately difficult to measure the relative velocity between the slider and the resonator during impacts, but it can be assessed that it is of order of \(V\sin\alpha + v \cos\alpha\) where α is the slope of impacting asperity. Since V = 6 cm/s and v∼1 mm/s, the angle for which both contributions equal is α0 = 1° which is a very low value. For greater angles, the sliding velocity contribution dominates.

5 Conclusion

In this study, it has been shown that the level of normal vibration induced by mechanical impacts during the sliding of rough surfaces, may depend or not on the number of sliders. Two regimes exist for roughness noise. The regime where the contact damping dominates implies that roughness noise level does not depend on the number of sliders. It can be easily observed on drums and, more generally, on any structure highly reverberent. On the other hand, the regime of dominating internal damping implies that the noise level linearly increases with the number of sliders. It can be observed on highly damped resonators, a wood table for instance.

The underlying assumption that has been proposed in this study to explain the constant regime is that the damping of vibration in the interface is a local phenomenon governed by Eq. (7). This is a strong assumption. But this is the only assumption which leads to the energy balance where the contact area vanishes.

The existence of two regimes highlights the fact that the dependence of friction-induced vibration with contact area is more complicated than the similar laws for friction force (Amontons’ law) and wear rate (Achard’s law). However, the vibrational power density being injected (p in Table 1), is always proportional to the nominal contact area and is approximately independent of the internal damping of system. This fact is consistent with Amontons’ law of proportionality of mechanical power being dissipated with normal load.