1 Introduction

The first description of sliding friction in terms of atomistic models was developed by Tomlinson and Prandtl [1, 2]. This model assumes that friction occurs as atoms in the contact slide over some potential barrier where all of the energy is dissipated as the atoms surmount the barrier to move into the adjacent potential minimum. This approach has found its greatest utility in modeling single-asperity contacts, such as might be encountered in atomic force microscope (AFM) experiments [3, 4], and it has provided a phenomenological understanding of the temperature- and velocity dependence of sliding friction, as well as for the atomic stick-slip behavior [5–10]. In this model, the surface is taken to have a sinusoidal sliding potential with height E 0 and a harmonic strain caused by the motion of the contact modifies this simple, periodic sinusoidal potential representing the sliding interface. Therefore, the combined potential leads to a time-dependent height of the barrier ΔE. Temperature and velocity effects are included by incorporating a Boltzmann probability that an atom surmounts the time-dependent potential barrier, where the velocity dependence arises since the potential is time dependent, so that the rate at which the atom surmounts the barrier also depends on time. Semi-empirical, analytical solutions to the Tomlinson/Prandtl model have been obtained by approximating the evolution of the height of the potential ΔE, for small values of ΔE (~kT), as a function of the lateral force F L by:

$$ \Updelta E = {\frac{1}{\beta }}\left( {F^{*} - F_{\text{L}} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} $$
(1)

where the parameter β is a constant of the system [6, 7], and F* is the lateral force required to initiate sliding at 0 K. The value of the parameter β for a pure sinusoidal potential is given by:

$$ \beta_{\sin } = {\frac{{\left( {F^{*} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{{\left( {{\frac{{k_{\text{L}} a^{2} }}{8}} + {\frac{{F^{*} a}}{\pi }}} \right)}}} $$
(2)

where k L is the lateral force constant of the cantilever and a the lattice spacing [11].

Since the rate at which the atom surmounts the time-dependent barrier of height ΔE at some temperature T defines the lateral sliding force, this problem is ideally suited to analysis by Monte Carlo methods. It has been shown that Monte Carlo methods can effectively be used to produce solutions to the Tomlinson/Prandtl model allowing the study of temperature, stick-slip motion [12, 13], and velocity [11] effects on atomic friction. This approach was also used to verify that Eq. 2 yielded the correct form of the value of β [11]. While the Tomlinson/Prandtl model has been extensively utilized to rationalize the load- and velocity dependence of sliding friction in AFM, there is only one instance to our knowledge of quantitative agreement between the results of AFM experiments and the Tomlinson/Prandtl model, for a tungsten tip sliding against a mica surface [7]. The experimental results were fit to the semi-empirical, analytical solution for Tomlinson sliding [7], but required using β as a fitting parameter while, as shown by Eq. 2, it should be completely determined by the parameters in the Tomlinson/Prandtl model. As will be shown below in greater detail, using the analytical model with a value of β determined by Eq. 2 does not agree with experiment and results in a much slower variation in lateral force with sliding velocity than found experimentally. The possible origin for this discrepancy is explored in the following.

2 Results and Discussion

The previously published experimental AFM results that measured the velocity and load dependence of the lateral force for a tungsten tip sliding against a mica surface [7] are shown in Fig. 1. Attempts were made to reproduce the experimental data using the semi-empirical analytical Tomlinson/Prandtl equation with a pure sinusoidal sliding potential, with values of β determined by the experimental parameters (k L) and the surface potential (F*, a) from Eq. 2, and the results are shown plotted as solid lines along with the experimental data in Fig. 1. Clearly this yields a weaker variation in friction force with velocity than found by experiment.

Fig. 1
figure 1

Comparison between the experimental data for the velocity dependence (ln(v)) of the lateral force (F L) at normal loads of 6 (filled square), 8 (filled triangle), 10 (filled diamond), and 12 (filled inverted triangle) nN taken from [7], and the results of the semi-empirical analytical solution to Tomlinson/Prandtl model using a value of β calculated using Eq. 2

Full size image

One possible origin for this discrepancy is that the Tomlinson/Prandtl model, while able to provide qualitative insights into the results of AFM experiments, contains assumptions that preclude it from being used to yield quantitative agreement. It has recently been suggested that the nominally single-asperity contact in AFM really consists of a number of “nano-contacts” at the atomic level [14]. However, periodicity is found in atomic-scale “friction images” and whether these arise from a single or a number of atoms in contact is irrelevant to the Tomlinson/Prandtl model since it only posits a sinusoidal potential and the origin of this potential does not affect the model.

The model also assumes that all of the energy is dissipated during the sliding transition over the potential and that this is the mechanism by which energy is dissipated and from which the friction force arises. If not all of the energy were dissipated, this would lead to a lower friction force than predicted by the model and, depending on how the energy dissipation rate compares with the transit time over the potential, this could result in a velocity dependence of friction curve very different from that found experimentally. That is, the fundamental assumptions underlying the Tomlinson/Prandtl model might be flawed and this possibility cannot be ruled out. Indeed, it was recently found that replacing hydrogen by deuterium reduced the friction of a diamond surface [15] implying that the energy dissipation rate at the surface can play a role, although more recently simulations have suggested this effect could be ascribed to small differences in hydrogen (deuterium) coverage of the two systems [16].

In the following, we propose an alternative possibility that leads to quantitative agreement with the experimental data by using a modified Tomlinson/Prandtl model. Since the surface of mica comprises aluminosilicate rings with a 5.2 Å periodicity where the lattice charge is balanced by an alkali ion located at the center of the ring, this raises the possibility that the sliding potential is not sinusoidal. In the case of either a bare or alkali-covered aluminosilicate lattice, a sharp tip could encounter a sharp change in sliding potential as it passes over the hole or alkali atom. Such a periodic, but non-sinusoidal potential is not easily amenable to a semi-empirical analysis as was done for the Tomlinson/Prandtl model with a sinusoidal potential and is, therefore, analyzed using Monte Carlo methods [11]. This strategy has previously been used to explore velocity effects on sliding friction, and it has been demonstrated that it precisely reproduces the solution to the sinusoidal Tomlinson/Prandtl equation [11]. This, therefore, provides an ideal strategy for exploring sliding with more complex periodic potentials.

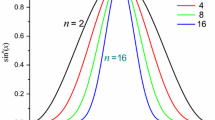
The shape of the surface potential used for the simulation is shown in Fig. 2 and illustrates the strongly non-sinusoidal behavior. The potential is shown with negative excursions. However, it was empirically found that identical results are obtained with positive excursion as long as all parameters remained unchanged. A possible explanation is that, in the Tomlinson model, the lateral force is directly proportional to the instantaneous drop in energy that the system undergoes when the tip slides from one stable position to the next. We have seen that this irreversible drop is directly proportional to the slope between maxima and minima of the potential, and this quantity is the same regardless the sign of the excursions.

Fig. 2
figure 2

Depiction of the non-sinusoidal potential of the modified Tomlinson/Prandtl model used to simulate atomic sliding on a mica surface. The potential was plotted using the equation \( V(x) = E_{0} \cos^{40} \left( {{\frac{\pi x}{a}}} \right) \), where E 0 represents the height of the potential and a the lattice spacing

Full size image

The lateral frictional force was calculated using Monte Carlo strategies as described elsewhere [11, 17], while constraining the experimental lattice constant for mica to be a = 0.52 nm, the lateral cantilever force constant k L to be the measured value of 1.2 N/m, and the frequency factor ν 0 also to be the experimentally determined value of 19.5 kHz [7]. The temperature was fixed at the experimental value of 298 K. Only the height of the Tomlinson/Prandtl potential E 0 was allowed to vary for each value of normal load. There was thus only one variable parameter E 0 used to fit each of the experimental curves of lateral force versus sliding velocity (Fig. 3). The resulting calculated values of the lateral force are also displayed, as solid lines, in Fig. 3 as a function of the sliding velocity for various values of E 0 and are superimposed on the experimental data. Clearly the agreement between the experimental values and the results of the Monte Carlo analysis of the Tomlinson/Prandtl model with a non-sinusoidal potential is very good. While this does not unequivocally prove that the sliding potential is exactly of the form shown in Fig. 2, the results are in good agreement with this postulate. However, these results do show that the shape of the potential can have a profound effect on the lateral sliding force and that such situations can be effectively analyzed using Monte Carlo methods. Finally, Fig. 4 plots the resulting best-fit values of E 0 as a function of the normal load F N. This displays a linear variation, and such load-dependent potentials have been found previously from AFM friction experiments on alkali halide surfaces [9]. This load-dependent sliding potential has been rationalized theoretically as being due to a combination of the change in interaction energy as atoms slide from one stable site to the next (\( E_{0}^{0} \)) and the external work carried out against the normal force F N due to the corrugation of the surface [18] where the vertical displacement is given by δz. In this case, the linear variation of E 0 with normal force F N can be represented as:

$$ E_{0} = E_{0}^{0} + F_{\text{N}} \delta z $$
(3)

where the second term represents the work carried out against the normal force F N and \( E_{0}^{0} \) is the change in internal energy. In this case, a linear fit of Eq. 3 to the data in Fig. 4 indicates that \( E_{0}^{0} \) = 0.22 ± 0.01 eV and δz = 0.040 ± 0.002 Å. The value of δz is relatively small suggesting that even a small corrugation as the tip slides over the surface can have a significant effect on the frictional behavior. The value of \( E_{0}^{0} \) determined here using the potential in Fig. 2 is larger than that found using a simple sinusoidal potential [7] of ~0.93 eV and indicates that the shape of the sliding potential can strongly affect the parameters that are derived from the model. It was also suggested [7] that the shape of the potential might depend on the normal load. The observation that the experimental data can be fit using a single value of \( E_{0}^{0} \) suggests that this is not the case.

Fig. 3
figure 3

Comparison between the experimental data for the velocity dependence (ln(v)) of the lateral force (F L) at loads of 6 (filled square), 8 (filled triangle), 10 (filled diamond), and 12 (filled inverted triangle) nN taken from reference [7], and the results of the Monte Carlo simulations using the surface potential shown in Fig. 2

Full size image
Fig. 4
figure 4

Plot of the values of E 0 used to provide the best fits to the experimental data shown in Fig. 3 for each normal load F N

Full size image

3 Conclusions

The velocity dependence of siding friction of a tungsten tip sliding against a mica surface as a function of normal load was successfully quantitatively modeled by assuming that the periodic surface potential was not sinusoidal but varied much more rapidly. This allowed the experimental velocity-dependent results to be fit using only a single variable, E 0, the height of the sliding potential. It was found that the height of this sliding potential varied linearly as a function of normal load. This is explained by assuming the load-dependent surface potential is due to a combination of the change in interaction energy as atoms slide from one stable site to the next and the external work carried out against the normal force due to the corrugation of the surface.