Introduction

The purpose of this work is to build upon the knowledge of our predecessors and provide an improved chart that will linearize the liquid viscosity of hydrocarbons, halocarbons and liquid metals over an extended temperature and viscosity range. In 1886, Osborne Reynolds [1] wrote “On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, including an Experimental Determination of the Viscosity of Olive Oil” and started the process of scaling the coordinate system to plot liquid viscosities as straight lines. The current ASTM standard viscosity charts, ASTM 341-93 [2], are based on the work of Wright [3], which improved the linearization of hydrocarbons down to 0.18 cSt on charts available from ASTM and to 0.21 cSt with the developed equation in the standard. The new hydrocarbon and halocarbon chart and equation described in this paper will now extend from the low temperature realm of liquid methane to the high temperature, high viscosity realm of petroleum oils. The new chart utilizes the historical work at high viscosities and extends the linearized low viscosity range to 0.04 cSt and below. Using the historical volume based mixing rules, the new chart also allows for calculations of the viscosity of mixtures. An alternate scaling of the temperature axis linearizes the viscosity of metals.

Background

In an attempt to correct problems that have perpetrated through history, a critical literature review is presented to correct the forms of the equations and to correctly reference the authors of those works. Table 1 contains the historical development of viscosity–temperature relations in their original nomenclature. In 1886, Osborne Reynolds found it necessary to know the viscosity of olive oil as a function of temperature and used a simplistic exponential equation to fit the available data over a small temperature range (16–49 °C). In this paper, Reynolds formulated and integrated the hydrodynamic equations that define hydrodynamic lubrication, and derived the Reynolds equation. In his lubricant experiments, Reynolds noted that as the load on the bearing was increased so did the lubricant temperature. The temperature increase generated a new geometric stability, which is based upon a decrease in the fluid viscosity with increasing temperature. It was therefore necessary for the interpretation of the results to know how the viscosity of the lubricant varied with respect to the temperature. At this point in history fluid dynamics were only starting to become understood; Reynolds proposed that fluids have two viscosities, one viscosity for what we now know to be laminar flow and another for turbulent flow to answer problems being probed by Stokes, Poiseuille, and Darcy.

Table 1. Historical development of viscosity–temperature relations in original nomenclature.
Full size table

One of the most misreferenced viscosity equations is that of Vogel [4], which represents the absolute viscosity as:

$$ \eta _{t} = \eta _{\infty } ^{{\frac{{t - t_{1} }} {{t - t_{\infty } }}}} $$
(1)

where η t is the viscosity at a specified temperature t, η∞ is the viscosity as t → ∞, t 1 is the temperature where η = 1, and t ∞ is the temperature where the η → ∞. While Vogel does not note the units used, his choice of fluids (water, mercury, and petroleum oils) indicates that temperature is in degrees Celsius and viscosity is in centipoise (cP). This equation performs reasonably well over a moderate temperature range; however, its nonlinear nature and three fluid specific coefficients make it difficult for generalization. Most referenced works list Vogel’s equation as:

$$ \mu = Ke^{{{\left( {\frac{b} {{t + \theta }}} \right)}}} $$
(2)

or

$$ {\text{log}}_{e} {\left( \mu \right)} = A + \frac{B} {{T - T_{0} }} $$
(3)

which found in [10] and has been carried forward through the lubrication literature; however, these equations are not equivalent to Vogel’s [4] equation. Fulcher [5] is the first to list equation (3) in the analysis of the viscosity of molten glasses. Scherer [14] reviews the history behind the “Fulcher equation” or more standard designation as the VFT (Vogel–Fulcher–Tammann) equation. As noted by Scherer, the VFT equation works well over wide viscosity range for glasses and many liquids, however, like the Vogel equation, its three fluid specific coefficients make it difficult for generalization.

Also in 1921, The Texas Company (Texaco) published a viscosity–temperature chart developed by N. MacCoull in the June edition of Lubrication [15]. This chart linearizes different cuts of crude oil from their cloud point to 40 Saybolt Universal (about 4 cSt). MacCoull’s chart also appears in the 1927 International Critical Tables [16] with dual axes for Saybolt Universal and centistokes. Neither the Lubrication publication nor the International Critical Tables gives the method or equation used to determine the scale of the axes.

In 1928, Walther [6] introduced an equation credited to Le Chatelier.

$$ {\text{log}}{\left( {{\text{log}}{\left( \mu \right)}} \right)} = P - M*t $$
(4)

where μ is the absolute viscosity in centipoise (cP), t is the temperature in degrees Celsius (°C). Walther’s key point is that given two measured points and finding P and M, calculation of the viscosity allows for estimation at other temperatures. Unfortunately, in this equation, viscosities of 1.0 or less cause an undefined double logarithm, and exposes the main drawback of all the double logarithm viscosity–temperature relations that have followed to this date. In 1931, Walther [7,8] published two additional papers where he changed to correlating the kinematic viscosity (ν) with temperature and corrected for the undefined double logarithm by adding a constant of 0.95 to the viscosity allowing viscosities down to 0.05 cSt to be correlated.

$$ {\text{log}}{\left( {{\text{log}}{\left( {\nu + 0.95} \right)}} \right)} = - m*{\text{log}}{\left( {\frac{T} {{T_{{\text{o}}} }}} \right)} + {\text{log}}{\left( {{\text{log}}{\left( {\nu _{{\text{o}}} + 0.95} \right)}} \right)} $$
(5)

The simplification of the above equation has historically been named the “Walther formula” and is of the formFootnote 1:

$$ {\text{log}}{\left( {{\text{log}}{\left( {\nu + \gamma } \right)}} \right)} = a - m*{\text{log}}{\left( T \right)} $$
(6)

where γ is an additive constant and a and m are fluid specific empirical parameters. Allowing a = log(log(a”)), one can also write the Walther formula as:

$$ \nu + \gamma = a^{\prime \prime {{{\left( {T^{{ - m}} } \right)}}}} $$
(7)

In 1932, the American Society for Testing Materials (ASTM) collected all the known charts and correlations for viscosity-temperature relationships in order to develop a standard chart. Geniesse and Delbridge [9] report that “the equation of a straight line on the chart” is:

$$ {\text{log}}{\left( {{\text{log}}{\left( {\nu + 0.8} \right)}} \right)} = a + b*{\text{log}}{\left( T \right)} $$
(8)

The data available at that time allowed for temperatures up to 260 °C and viscosities down to 0.3 cSt with only slight curvature. This report is the first to credit MacCoull with the log–log equation with an additive constant used in constructing his charts. The methodology of a chart based blending rule is presented as previously being applied to the MacCoull chart and an example of two hydrocarbons (gasoline and oil) is illustrated to determine a mixture viscosity.

Erk and Eck [17] correlate the temperature dependence of a dozen crude oils with the Vogel equation, Andrade equation and Walther formula. They note that the Andrade equation does not yield acceptable results, and thus, its application is not pursued. The Walther formula (using a constant of 0.8) correlates the data sets within ±2%, and the Vogel equation is superior above 20 °C with an accuracy of about ±1%; however, below 20 °C, Erk and Eck note that the Vogel equation’s accuracy diminishes. However, their small data sets (3–5 data points) statistically favor the three parameter Vogel equation, while the data viscosity was low enough (<4 cSt) that the Walther formula’s imposed, fixed lower limit of 0.2 cSt influenced its correlation.

Barr [10], while attempting to find a better correlation for oils at high temperatures, published a reduction of Walther’s formula as:

$$ \nu + a = Ae^{{bT^{{ - c}} }} $$
(9)

where A = 1, a = 0.8, and b and c are constants for each oil. Here the additive constant, a, is left as it was approved by Geniesse and Delbridge. Barr, realizing that there is an inadequacy in the formula at high temperatures and low viscosities, attempts a different correlation

$$ {\left[ {\log _{{10}} {\left( {\nu + a} \right)}} \right]}^{{0.3}} = A + \frac{b} {T} $$
(10)

where the scaling of the inverse temperature allows greater spacing than logarithmic temperature at low temperatures and tighter scaling at high temperatures. The new formula gives a better fit to the data of Erk and Eck; however, the additive constant of a = 0.8 was maintained as a strict constant.

Murphy et al. [18] provides a good spectrum of data for lubricating fluids from −40 to 370 °C (−40 to 700 °F) and viscosities from 0.4 to 36,000 cSt. These fluids were plotted on an extended ASTM chart (D 341-43). Murphy et al. noted that the stepwise change in the additive constant that ASTM had at that time introducedFootnote 2 was less than ideal for determining fit coefficients and thus only the chart results are used for analysis. The curvature in some of the datasets was theorized to be the result of uncoiling the molecular structure for the long-chain molecules at high temperatures, while the linearity of most of the fluids is attributed to their straight-chain and/or short-branched structure. At low temperatures, fluids that underwent precipitation of insoluble waxes experienced some curvature on the ASTM chart.

In 1950, MacCoull [19] published a follow-up article in Lubrication in an attempt to clarify the development of his first chart and the chart that appeared in the Critical Tables. In this disclosure, it is explained that because the original chart did not utilize an additive constant in the Walther formula, and it did not extend below 40 Saybolt Universal due to excessive curvature. The 1927 International Critical Tables utilized an additive constant of γ = 0.7 which was determined as a value that best linearized cuts of Pennsylvania and California crude. Based on this report and MacCoull’s original publication, this author will credit charts allowing for the linearization of the viscosity with respect to temperature on the log–log scale as “MacCoull charts”.

Crouch and Cameron [11] formulated a reduction for the Walther formula as:

$$ \nu + \gamma = \beta D^{{T^{{ - c}} }} $$
(11)

where γ = 0.6, and D, β and c are constants. If β is set equal to 1 or if βD = a″, then a correct reduction of the Walther formula is achieved. However, as Stachowiak and Batchelor [20] pointed out in their text, Engineering Tribology, if D is equal to 10 or e and β is the second constant, an incorrect representation of the Walther formula is formulated. Crouch and Cameron compare other viscosity–temperature relationships before attempting to modify the “Vogel” equation, as presented by Barr, with a third constant in developing a generalized equation.

Roelands [12] developed correlations for the viscosity–temperature and viscosity–pressure relationships. Roelands’ viscosity-temperature correlates the absolute viscosity in similar form to the Walther formula:

$$ \log {\left( {\log {\left( {\eta _{{\text{o}}} + 4.2} \right)}} \right)} = - S_{{\text{o}}} \log {\left( {1 + \frac{T} {{135}}} \right)} + \log {\left( {G_{{\text{o}}} } \right)} $$
(12)

Where S o and G o are fluid specific constants. This formulation performs over a narrow temperature range; however, viscosity correlation breaks down over an extended temperature range. Recently, the Roelands’ viscosity–pressure correlation is being scrutinized due to a truncation of data in its derivation of the high-pressure regime [21].

The most significant modification to the Walther formula and MacCoull charts came in 1969. Wright [3] extended the ability to linearize the charting viscosity of hydrocarbons over the temperature range −73–371 °C (−100–700 °F) and viscosities down to 0.21 cSt (0.18 cSt in charts available from ASTM). In order to linearize hydrocarbon data over the temperature range, Wright developed a form of the Walther formula where a function of viscosity f(v) was added to the standard historical constant, γ = 0.7.

$$ {\text{log}}_{{10}} {\left( {{\text{log}}_{{10}} {\left( {\nu + \gamma + f{\left( \nu \right)}} \right)}} \right)} = A - B*{\text{log}}_{{10}} {\left( T \right)} $$
(13)

where

$$ \gamma + f{\left( \nu \right)} = 0.7 + C - D + E - F + G - H $$
(14)

and

$$ \begin{aligned}{} & C = \exp {\left( { - 1.14883 - 2.65868\nu } \right)}{\text{; }}D = \exp {\left( { - 0.00381308 - 12.5645\nu } \right)} \\ & E = \exp {\left( {5.46491 - 37.6289\nu } \right)}{\text{; }}F = \exp {\left( {13.0458 - 74.6851\nu } \right)} \\ & G = \exp {\left( {37.4619 - 192.643\nu } \right)}{\text{; }}H = \exp {\left( {80.4945 - 400.468\nu } \right)} \\ \end{aligned} $$
(15)

As with all the previous double log forms, once the term in the first log term becomes zero, the second log is undefined; this occurs at a viscosity of 0.21 cSt with the Wright formulation. While this equation will not allow the correlation of viscosities below 0.21 cSt, it performs well with hydrocarbons above that threshold. The current state of the art is still based entirely on Wright’s modification to the Walther formula and its charts reflect the improvement.

Manning [13] simplified Wright’s complex form of f(ν) by replacing it with a polynomial and extended the chartable (not linear, due to its basis on Wright’s work) range down to 0.12 cSt.

$$ {\text{log}}{\left( {{\text{log}}{\left( {\nu + 0.7 + \exp {\left( { - 1.47 - 1.84\nu - 0.51\nu ^{2} } \right)}} \right)}} \right)} = A - B*{\text{log}}{\left( T \right)} $$
(16)

While Manning’s new polynomial provides a simplification of Wright’s complex form, it also exhibits non-linear nature below 0.18 cSt due to its derivation. Manning also provides an approximation to find the viscosity knowing the A and B coefficients for the fluid.

$$ \nu = {\left( {Z - 0.7} \right)} - \exp {\left[ { - 0.7487 - 3.295{\left( {Z - 0.7} \right)} + 0.6119{\left( {Z - 0.7} \right)}^{2} - 0.3193{\left( {Z - 0.7} \right)}^{3} } \right]} $$
(17)

where

$$ {\text{log}}{\left( {{\text{log}}{\left( Z \right)}} \right)} = A - B*{\text{log}}{\left( T \right)} $$
(18)

$$ \nu + \gamma = a^{\prime \prime {{{\left( {T^{{ - m}} } \right)}}}} $$ Figure 1 charts the viscosity of pure HFC134a, CO2, propane, HCFC123 and mixture HFC410A. These refrigerants demonstrate nearly linear nature above 0.21 cSt, and the linear correlation breaks down into nonlinear behavior below 0.21 cSt, demonstrative of the Wright and Manning modifications.

Figure 1.
figure 1

ASTM standard D 341-93 (ν ≥ 0.21); Manning equation (ν < 0.21).

Full size image

In order to understand the viscosity–temperature relationships of Vogel, VFT, Walther, and Wright, it is useful to illustrate their boundaries by selecting the saturated liquid viscosity of propane ranging from the triple point to the critical point, [22]. The Vogel equation, figure 2(a), is able to represent the liquid viscosity over a limited temperature range, however, as the temperature approaches the critical point, the formulation is not able to accurately represent the data. The VFT equation, figure 2(b), is also able to represent the viscosity over a limited temperature range; however, the representation falls off near the triple and critical points. While there is not a limit in the temperature field, the Walther formula, figure 2(c), only approximates the viscosity of propane due to its limitation of the viscosity approaches 0.2 cSt as T→∞. The Wright modification to the Walther formula, figure 2(d), does not exhibit an asymptotic behavior as the temperature increases and is able to represent the saturated liquid viscosity above 0.21 cSt; however, it can not be used below a viscosity of 0.21 cSt. The purpose of this work is to find a generalized equation that can be utilized over the entire temperature and viscosity range, figure 2(e).

Figure 2.
figure 2

Viscosity of propane from triple point to critical point, data from Vogel et al. [22].

Full size image

Development of a new improved generalized formulation

It is desired to construct a generalized chart and mathematical formulation that is able to:

  • Cover entire temperature range (low temperatures to high temperatures).

  • Cover entire liquid viscosity range.

  • Linearize fluids that do not exhibit excessive molecular coiling, molecular bonding, or wax precipitation.

  • Maintain the existing ASTM format for lubricants for viscosities greater than 2 cSt.

In choosing to replace the exponential series function of Wright, functions were sought that make up the set of traditional mathematical functions commonly found in fluid mechanics and molecular dynamics. This new function should approximate the shape of the Wright modification in the low viscosity range (0.21 cSt < ν < 2 cSt) and should vanish above 4 cSt to preserve historical precedence. The new modification must also linearize hydrocarbon fluids in the range of 0.04 cSt to their glass transition temperature, and incorporate those hydrocarbons typically seen in natural gas production. The zero order modified Bessel function of the second kind, K 0, was chosen to be the key component of the additive function in the log–log form. The zero order modified Bessel function of the second kind has the form:

$$ K_{0} {\left( x \right)} = {\int_0^\infty {\frac{{\cos {\left( {xt} \right)}dt}} {{{\sqrt {t^{2} + 1} }}}} } $$
(19)

The new function for the viscosity takes the same form as Wright’s function:

$$ {\text{log}}_{e} {\left( {{\text{log}}_{e} {\left( {\nu + \lambda + f{\left( \nu \right)}} \right)}} \right)} = A - B*{\text{log}}_{e} {\left( T \right)} $$
(20)

However, the function of viscosity is now changed in order to extend the viscosity range to ultra-low viscosities:

$$ f{\left( \nu \right)} = e^{{ - \nu }} K_{0} {\left( {\nu + \psi } \right)} $$
(21)

or

$$ {\text{log}}_{e} {\left( {{\text{log}}_{e} {\left( {\nu + \lambda + e^{{ - \nu }} K_{0} {\left( {\nu + \psi } \right)}} \right)}} \right)} = A - B*{\text{log}}_{e} {\left( T \right)} $$
(22)

where ν is the viscosity in cSt, λ and ψ are generalized constants, A and B are coefficients that fit each fluid, and T is the absolute temperature in Kelvin or Rankine. To properly scale the viscosity coordinate as the viscosity approaches zero, it is desired to have the left hand side of the above equation approach negative infinity, −∞.

$$ {\mathop {\lim }\limits_{\nu \to 0} }{\left( {\nu + \lambda + e^{{ - \nu }} K_{0} {\left( {\nu + \psi } \right)}} \right)} = 1 $$
(23)

This scaling condition on viscosity allows λ and ψ to be dependent and the value of λ was optimized using historical lubricant and current fluid viscosity data sets. The optimized constant was determined to be the historical constant, λ = 0.7. Which defines ψ as:

$$ \lambda = 0.7 \to \psi = {\text{1}}{\text{.244 066 584 703}} $$

The new proposed function in its generalized form become:

$$ {\text{log}}_{e} {\left( {{\text{log}}_{e} {\left( {\nu + 0.7 + e^{{ - \nu }} K_{0} {\left( {\nu + 1.244067} \right)}} \right)}} \right)} = A - B*{\text{log}}_{e} {\left( T \right)} $$
(24)
$$ \nu + 0.7 + e^{{ - \nu }} K_{0} {\left( {\nu + 1.244067} \right)} = e^{{A^{\prime T^{{ - B}}} }} $$
(25)

where

$$ A = {\text{log}}_{e} {\left( {A^\prime } \right)} $$
(26)

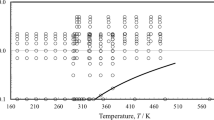
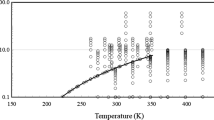
In comparison, the historical additive constants and additive functions, as well as, the proposed additive function are shown in figure 3. This proposed viscosity–temperature relationship is compared to the Wright equation in table 2 and figure 4. It is shown that the new and old equations perform equally well with fluids above 0.21 cSt. Utilizing liquid viscosity data found at the NIST Webbook [23] and extending the range of viscosities to the low-viscosity region yields a chart of refrigerants, table 3 and figure 5; extending to low temperature fluids yields figure 6. Due to their strong hydrogen bonding, water and ammonia are not able to be linearized over their entire temperature range, as shown in figure 7.

Figure 3.
figure 3

Additive function to log–log viscosity–temperature correlations (a). Geniesse and Delbridge, (b) ASTM D341–43, (c) Wright, (d) proposed formulation.

Full size image
Table 2. Comparison of Wright Equation to the proposed equation.
Full size table
Figure 4.
figure 4

Data of different oils on proposed viscosity–temperature chart, table 2.

Full size image
Table 3. Liquid viscosity of halocarbons and low temperature fluids. Fluid data from webbook.nist.gov
Full size table
Figure 5.
figure 5

Proposed viscosity chart with selected hydrocarbons and halocarbons. Fluid data from webbook.nist.gov.

Full size image
Figure 6.
figure 6

Proposed viscosity chart extended to low temperatures. Fluid data from webbook.nist.gov.

Full size image
Figure 7.
figure 7

Viscosity of ammonia and water from the triple point to the critical point. Fluid data from webbook.nist.gov.

Full size image

Mixing rule for liquids

Traditionally, the mixing rule for the Walther formula and MacCoull charts has been a volume fraction based rule.

$$ \Omega = {\sum {V_{i} *{\left( {A_{i} - B_{i} *{\text{log}}_{e} {\left( T \right)}} \right)}} } $$
(27)

where

$$ \Omega = {\text{log}}_{e} {\left( {{\text{log}}_{e} {\left( {\nu _{{{\text{mix}}}} + \lambda + e^{{ - \nu _{{{\text{mix}}}} }} K_{0} {\left( {\nu _{{{\text{mix}}}} + \psi } \right)}} \right)}} \right)} $$
(28)

V i is the volume fraction of each fluid, and A i and B i are the intercept and slope of the fluid on the new chart’s transformed coordinate system, and λ and ψ are constants defined above. This becomes convenient as the mixture viscosity can be estimated when two data points for each fluid in the mixture are known.

The mixture viscosity, as a function using the mass fraction, becomes:

$$ \Omega = {\sum {w_{i} \frac{{\rho _{{{\text{mix}}}} {\left( T \right)}}} {{\rho _{i} {\left( T \right)}}}*{\left( {A_{i} - B_{i} *{\text{log}}_{e} {\left( T \right)}} \right)}} } $$
(29)

where w i is the mass fraction of each fluid, and ρ i is the density of each fluid varying with temperature. To simplify the above equation, if the densities of the fluids and their mixture are assumed to be nearly equal, the density ratio becomes unity and only the mass fraction is used. In another simplification, if the densities of the individual fluids are different and ideal mixing assumed, then one can write:

$$ \rho _{{{\text{mix}}}} {\left( T \right)} = {\left( {{\sum {\frac{{w_{i} }} {{\rho _{i} {\left( T \right)}}}} }} \right)}^{{ - 1}} $$
(30)

To illustrate the mixing rule, the viscosity for the refrigerant mixture HFC407C has been calculated from the individual fluids in the mixture, table 4 and figure 8.

Table 4. Components of HFC407C, figure 8.
Full size table
Figure 8.
figure 8

Refrigerant Mixture HFC407C. Dashed line represents actual HFC407C viscosity. Individual fluid data from webbook.nist.gov. R407C mixture data from NIST REFPROP v.7.

Full size image

If mixture data is available, then using an interaction parameter, ϕ ij , improves the mixture estimate.

$$ \Omega = {\sum\limits_i {{\left( {{\left( {1 + {\sum\limits_j {\varphi _{{ij}} w_{i} w_{j} } }} \right)}*w_{i} \frac{{\rho _{{{\text{mix}}}} {\left( T \right)}}} {{\rho _{i} {\left( T \right)}}}*{\left( {A_{i} - B_{i} *{\text{log}}_{e} {\left( T \right)}} \right)}} \right)}} } $$
(31)
$$ \varphi _{{ii}} = \varphi _{{jj}} = 0 $$
(32)

where ϕ ij can be a constant value, a function of temperature, ϕ ij (T), or a function of temperature and composition, ϕ ij (T,w).

Molten solids and liquid metals

By changing the x-axis scaling, data for molten solids and liquid metals [24−26] can be linearized on a new viscosity chart, table 5 and figure 9. The new equation becomes:

$$ {\text{log}}_{e} {\left( {{\text{log}}_{e} {\left( {\nu + \lambda + e^{{ - \nu }} K_{0} {\left( {\nu + \psi } \right)}} \right)}} \right)} = A - \frac{B} {T} $$
(33)

where the constants λ and ψ are the same as the case of hydrocarbon and halocarbon liquids.

$$ \lambda = 0.7\,{\text{and}}\,\psi = {\text{1}}{\text{.244 066 584 703}} $$
Table 5. Viscosity of liquid metals, figure 9.
Full size table
Figure 9.
figure 9

Viscosity of liquid metals, table 5.

Full size image

Conclusions

A new chart and equation have been developed for use with hydrocarbons, halocarbons and cryogenic fluids. Water and ammonia still pose difficulties to linearize over their temperature range due to theorized molecular bonding. The proposed formulation and chart would correct the low viscosity inadequacy in the current ASTM formulation and charts. Mixture viscosities of low temperature hydrocarbons and halocarbons are now able to be predicted; this also applies to low temperature hydrocarbons mixtures with lubricants and halocarbons with lubricants.