1 Introduction

Coalbed methane (CBM) is an abundant and low-cost fuel that has significant long-term potential for discovery and development. According to reports, the CBM reserves worldwide have been estimated to be 84–262 trillion \(\hbox {m}^{3}\) (Pillalamarry et al. 2011; Liu et al. 2015). Improving the efficiency of CBM development and utilization can not only mitigate the energy crisis, but also ensure mining safety and reduce environmental pollution (Zheng et al. 2016). The most commonly used method for commercial CBM production is reservoir pressure depletion. However, this method is considered inefficient (Shi and Durucan 2005). At present, the \(\hbox {CO}_{2}\)-enhanced CBM (\(\hbox {CO}_{2}\)-ECBM) recovery technique has been proposed as an efficient method to improve CBM recovery (Anggara et al. 2016; Godec et al. 2014; Busch and Gensterblum 2011). The injection of \(\hbox {CO}_{2}\) can not only improve the CBM recovery, but also achieve the purpose of \(\hbox {CO}_{2}\) geological sequestration.

The injection of \(\hbox {CO}_{2}\) into the coal seam and the development of the CBM trigger a series of complex coal–gas interactions, which involve gas adsorption and desorption, eventually resulting in coal deformation (Liu et al. 2011; Palmer and Mansoori 1998; Lin et al. 2016). All these interactions will lead to changes in the coal seam permeability. Therefore, the most important issue for optimizing the CBM recovery is the exploration of the evolution characteristics of coal seam permeability during CBM development.

Laboratory testing of coal core permeability is considered one of the effective methods to understand the evolution of flow field in undisturbed coal seams. Xu et al. (2016) tested the internal structure, containing the distributions of pores and fractures, and directional permeability of coal core in the laboratory, and their relationship was discussed. Yin et al. (2012) studied the coal permeability with a self-developed “Triaxial Stress Thermal-hydrological-mechanical Coal Gas Permeameter” and concluded that the coal permeability decreased with an increase of the effective stress and water content. Wierzbicki et al. (2014) investigated the effect of hydrostatic three-axial state on the coal core permeability, and based on the experimental data, an empirical relationship between coal permeability and confining pressure was identified. In general, these laboratory tests were conducted under the condition of gas adsorption equilibrium. However, in the CBM recovery site, the gas flow under the non-equilibrium state, which involves gas adsorption and desorption, is more common. For example, the injection of \(\hbox {CO}_{2}\) into the coal seam involves \(\hbox {CO}_{2}\) adsorption and the development of CBM involves gas desorption from the coal matrix (Liu et al. 2016; Busch and Gensterblum 2011). Therefore, investigating the gas flow under the non-equilibrium state is of vital importance.

Fig. 1
figure 1

modified from Valliappan and Zhang (1996)

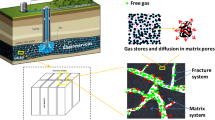
Schematic of gas migration process in coal seams

Full size image

So far, many permeability models have been developed to explore the coal–gas interaction mechanism and gas flow characteristics in coal reservoirs. By idealizing the coal reservoir as a collection of matchsticks, Reiss (1980) developed a permeability model, in which the permeability is directly proportional to the cubic of the coal porosity. Based on the assumption of uniaxial strain, Gray (1987) first incorporated the matrix shrinkage into a coal permeability model. Assuming that the strain changes follow the linear elasticity, Palmer and Mansoori (1998) built another widely used model, which incorporated the effects of matrix shrinkage and effective stress. Shi and Durucan (2004) developed a model for pore pressure-dependent permeability based on the hypothesis that the change of the cleat permeability was dominated by the effective stress normal to the cleats. Cui and Bustin (2005) derived a stress-dependent permeability model by quantifying the effects of reservoir pressure and the volumetric strain caused by gas adsorption on coal seam permeability. At present, based on previous studies, some improved permeability models have been proposed. For example, considering the problem that the exponential function for permeability (McKee et al. 1988) cannot explain the experimental phenomenon that under constant effective stress conditions, matrix shrinkage or swelling affects the measured permeability, Connell (2016) developed an extended exponential model that incorporated the independent effects of pore and confining pressures and the sorption strain. Liu and Rutqvist (2010) developed a permeability model based on improved matchstick geometry, in which the coal matrix blocks are connected by the matrix bridges rather than being completely separated by cleats. This model is thought to be unique for considering the interaction between coal matrix and fracture during coal deformation. Xia et al. (2014a, b) developed a compositional model, coupling the coal deformation, gas flow and transport, and air flow in coal seam, to get a better understanding of the gas drainage processes.

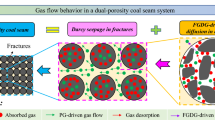
These research findings indicate that laboratory tests conducted previously mainly focused on the permeability measurement under different boundary conditions, such as various confining stresses and gas pressures, with the state of gas adsorption equilibrium, but the gas flow and permeability evolutions under the non-equilibrium state are not clearly understood. Although a certain degree of success has been achieved to explain and match the experimental results with the permeability models developed, a key point is that most of the permeability models developed contain only one gas pressure (Zhi and Elsworth 2016; Pini et al. 2011; Chen et al. 2012; Wei et al. 2016a, b), which cannot be used to model the non-equilibrium process of gas flow. The gas migration process in coal seams can be divided into three stages, namely gas desorption from coal skeleton surface, gas diffusion in coal matrix pores, and gas flow in coal fractures (see Fig. 1) (Valliappan and Zhang 1996; Godec et al. 2014; Liu et al. 2015; Zhou et al. 2016). In this process, gas migration in matrix pores, which is greatly affected by diffusion coefficient, serves as a bridge, connecting the matrix pore and fracture system. In the previous permeability models, the diffusion coefficient of coal was generally viewed as a constant (Yan et al. 2014; Liu et al. 2015; Akkutlu et al. 2016). However, the test results showed that coal specimens have a widely distributed pore system, from a few nanometers to hundreds of microns (Zhao et al. 2017; Zhu et al. 2016), implying variation in coal diffusion coefficient. Moreover, Li et al. (2016) reported that the diffusion coefficient in coal reduced with time. The reason for this phenomenon is that the pores in coal can be viewed as a series structure, at the initial time, the gas escapes from the surface of the coal, and the resistance for gas migration is small, and the diffusion coefficient is relatively large. With an increase of the diffusion time, the gas escapes from the internal pores of coal, and the resistance for gas migration is significantly larger than that at the initial time; therefore, the diffusion coefficient is comparatively small.

In this study, a mathematical model that couples the coal deformation, gas diffusion in matrix pore, and gas flow in fracture has been developed. In the fully coupled permeability model, two gas pressures, namely fracture gas pressure and matrix gas pressure, are considered to model the non-equilibrium flow; additionally, a dynamic diffusion model is introduced to evaluate dynamic diffusion processes in coal seams. The developed model is then verified with the published field data. Based on the verified permeability model, the gas flow processes in coal core during gas adsorption and desorption are investigated and the spatial and temporal evolution of gas pressures and permeability are analyzed. The permeability model and the related results can improve our understanding of the coal–gas interactions under the non-equilibrium state, providing a scientific basis for CBM recovery and \(\hbox {CO}_{2}\) geological sequestration.

2 Governing Equations

2.1 Model Hypothesis

  1. (1)

    The coal reservoir is a dual poroelastic medium, which is composed of coal skeleton, matrix pores, and fractures.

  2. (2)

    The coal containing gas system is under an isothermal condition; the temperature effect is not considered during gas adsorption and desorption.

  3. (3)

    The gas flow in fracture satisfies Darcy’s law and migration in matrix follows Fick’s law.

  4. (4)

    The coal skeleton is incompressible.

Figure 2 shows the physical model for coal structure and its representative elementary volume (REV). The REV is composed of matrix block and fracture. The solid lines represent the REV before deformation, and the dotted lines represent the REV after deformation. \(L_\mathrm{m}\) and \(L_\mathrm{f}\) are the matrix width and fracture width, respectively.

Fig. 2
figure 2

Physical model for dual-porosity continuum a coal structure model and b REV model

Full size image

2.2 Effective Stress Principle for Dual-Porosity Continuum

Without considering the temperature effect during coalbed methane (CBM) recovery, the coal seam deformation is dominated by gas adsorption and desorption and the variation of effective stress (Wu et al. 2011). In this case, the volumetric strain of the coal matrix can be expressed as

$$\begin{aligned} \varepsilon _\mathrm{m} =\underbrace{\varepsilon _\mathrm{L} \left( {\frac{p_\mathrm{m} }{p_\mathrm{L} +p_\mathrm{m} }-\frac{p_{\mathrm{m}0} }{p_\mathrm{L} +p_{\mathrm{m}0} }} \right) }_{{\text {Strain caused by adsorption}}} -\underbrace{\frac{\Delta \sigma _\mathrm{m} }{K_\mathrm{m} }}_{{\text {Strain caused by stress}}} \end{aligned}$$
(1)

where \(\varepsilon _\mathrm{m}\) is the volumetric strain of coal matrix, \(\varepsilon _\mathrm{L}\) is the Langmuir volumetric strain constant, \(p_\mathrm{m}\) is the matrix gas pressure, \(p_\mathrm{m0}\) is the initial matrix gas pressure, \(p_\mathrm{L}\) is the Langmuir pressure, \(\Delta \sigma _\mathrm{m}\) is the acting force of fracture on matrix block, \(K_\mathrm{m}\) is the bulk modulus of coal matrix, \(K_\mathrm{m} =E/3\left( {1-2\nu } \right) \), and E and \(\nu \) are Young’s modulus and Poisson’s ratio of coal, respectively.

In coal seams, the gas adsorption of fracture is negligible, and the fracture deformation can be defined as

$$\begin{aligned} \varepsilon _\mathrm{f} =-\frac{\Delta \sigma _\mathrm{f} }{K_\mathrm{f} } \end{aligned}$$
(2)

where \(\varepsilon _\mathrm{f}\) is the volumetric strain of fracture, \(\Delta \sigma _\mathrm{f}\) is the acting force of matrix block on fracture, \(K_\mathrm{f}\) is the equivalent bulk modulus of fracture, \(K_\mathrm{f} =L_\mathrm{m} K_\mathrm{n}\), \(K_\mathrm{n}\) is the normal stiffness of fracture.

From Fig. 2, we know that the deformation of REV in any direction is composed of fracture deformation and matrix deformation, so strain can be expressed as

$$\begin{aligned} \varepsilon =\frac{\Delta L_\mathrm{m} +\Delta L_\mathrm{f} }{L_\mathrm{m} +L_\mathrm{f} }=\frac{L_\mathrm{m} \varepsilon _\mathrm{m} +L_\mathrm{f} \varepsilon _\mathrm{f} }{3\left( {L_\mathrm{m} +L_\mathrm{f} } \right) } \end{aligned}$$
(3)

where \(\varepsilon \) is the strain of REV in any direction.

Substituting Eqs. (1) and (2) into Eq. (3), we obtain the following equation:

$$\begin{aligned} \varepsilon =\frac{\frac{p_\mathrm{L}L_\mathrm{m} \varepsilon _\mathrm{L}\left( {p_\mathrm{m}-p_{\mathrm{m}0}}\right) }{\left( {p_\mathrm{m} +p_\mathrm{L}}\right) \left( {p_{\mathrm{m}0}+p_\mathrm{L}}\right) }-\frac{L_\mathrm{m}}{K_\mathrm{m}}\Delta \sigma _\mathrm{m}-\frac{L_\mathrm{f}}{K_\mathrm{f}}\Delta \sigma _\mathrm{f}}{3\left( {L_\mathrm{m}+L_\mathrm{f}}\right) } \end{aligned}$$
(4)

The volumetric strain of REV can then be calculated with Eq. (5).

$$\begin{aligned} \varepsilon _V =3\varepsilon =\frac{\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{{m}0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_{m0} +p_\mathrm{L} } \right) }-\frac{L_\mathrm{m} }{K_\mathrm{m} }\Delta \sigma _\mathrm{m} -\frac{L_\mathrm{f} }{K_\mathrm{f} }\Delta \sigma _\mathrm{f} }{\left( {L_\mathrm{m} +L_\mathrm{f} } \right) } \end{aligned}$$
(5)

In the coal seam, the force of fracture on matrix and that of matrix on fracture is equal in size

$$\begin{aligned} \Delta \sigma _\mathrm{m} =\Delta \sigma _\mathrm{f} =\Delta \sigma _e \end{aligned}$$
(6)

where \(\Delta \sigma _e\) is the effective stress exerted on the coal seam.

By substituting Eq. (6) into Eq. (5), we can obtain the governing equation for effective stress

$$\begin{aligned} \Delta \sigma _\text {e} =\frac{K_\mathrm{m} K_\mathrm{f} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\left[ {\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }-\left( {L_\mathrm{m} +L_\mathrm{f} } \right) \varepsilon _\text {V} } \right] \end{aligned}$$
(7)

2.3 Governing Equations for Porosity and Permeability

According to the dual-porosity medium model depicted in Fig. 2, the fracture porosity in the coal seam can be defined as

$$\begin{aligned} \phi _\mathrm{f}= & {} \frac{\left( {L_\mathrm{m} +L_\mathrm{f} } \right) ^{3}-L_\mathrm{m} ^{3}}{\left( {L_\mathrm{m} +L_\mathrm{f} } \right) ^{3}}\cong \frac{3L_\mathrm{f} }{L_\mathrm{m} } \end{aligned}$$
(8)
$$\begin{aligned} \frac{\phi _\mathrm{f} }{\phi _{f0} }= & {} 1+\frac{\Delta L_\mathrm{f} }{L_{f0} } \end{aligned}$$
(9)

where the change of the fracture width can be calculated by Eq. (10).

$$\begin{aligned} \Delta L_\mathrm{f} =-\frac{L_{f0} }{K_\mathrm{f} }\Delta \sigma _e =-\frac{K_\mathrm{m} L_{f0} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\left[ {\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }-\left( {L_\mathrm{m} +L_\mathrm{f} } \right) \varepsilon _\mathrm{V} } \right] \nonumber \\ \end{aligned}$$
(10)

After the substitution of Eq. (10) into Eq. (9), the final fracture porosity equation yields

$$\begin{aligned} \frac{\phi _\mathrm{f} }{\phi _{f0} }=1-\frac{K_\mathrm{m} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\left[ {\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }-\left( {L_\mathrm{m} +L_\mathrm{f} } \right) \varepsilon _\mathrm{V} } \right] \end{aligned}$$
(11)

The cubic law is used to connect porosity with permeability

$$\begin{aligned} \frac{k_\mathrm{f} }{k_{f0} }=\left( {\frac{\phi _\mathrm{f} }{\phi _{f0} }} \right) ^{3}=\left\{ {1-\frac{K_\mathrm{m} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\left[ {\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }-\left( {L_\mathrm{m} +L_\mathrm{f} } \right) \varepsilon _\mathrm{V} } \right] } \right\} ^{3}\nonumber \\ \end{aligned}$$
(12)

The coal matrix is composed of coal skeleton and matrix pore, and its volume can be expressed as \(V=V_\mathrm{s} +V_\mathrm{p}\), where \(V_\mathrm{s}\) is the coal skeleton volume and \(V_\mathrm{p}\) is the matrix pore volume, and the matrix porosity can be defined as

$$\begin{aligned} \phi _\mathrm{m} =\frac{V_\mathrm{p} }{V} \end{aligned}$$
(13)

The differential form of the matrix porosity can be expressed as

$$\begin{aligned} \text {d}\phi _\mathrm{m} =d\left( {\frac{V_\mathrm{p} }{V}} \right) =\frac{V_\mathrm{p} }{V}\left( {\frac{\text {d}V_\mathrm{p} }{V_\mathrm{p} }-\frac{\text {d}V}{V}} \right) =\phi _\mathrm{m} \left( {d\varepsilon _\mathrm{p} -d\varepsilon _\mathrm{m} } \right) \end{aligned}$$
(14)

where \(\varepsilon _\mathrm{p}\) is the strain of matrix pore.

For linear elastic porous media, the matrix porosity can be expressed as \(\phi _\mathrm{m} =\frac{K_\mathrm{p} \left( {K_\mathrm{m} -K} \right) }{KK_\mathrm{m}}\), where K and \(K_\mathrm{p}\) are the bulk moduli of coal seam and matrix pore, respectively (Detournay 1993). Assuming that the volumetric deformation of the matrix pore caused by gas adsorption is equal to that of the matrix, \(\Delta V_\mathrm{p} =\Delta V\), the strain of matrix pore can be expressed as

$$\begin{aligned} \varepsilon _\mathrm{p} =-\frac{\Delta V_\mathrm{p} }{V_\mathrm{p} }=-\frac{\Delta V}{V_\mathrm{p} }=-\frac{\Delta V}{V}\cdot \frac{V}{V_\mathrm{p} }=\frac{\varepsilon _\mathrm{m} }{\phi _\mathrm{m} }=\frac{KK_\mathrm{m} \varepsilon _\mathrm{m} }{K_\mathrm{p} \left( {K_\mathrm{m} -K} \right) } \end{aligned}$$
(15)

Substituting Eqs. (1), (7), and (15) into Eq. (14), the governing equation for matrix porosity can be obtained as follows:

$$\begin{aligned} \phi _\mathrm{m}= & {} \phi _\mathrm{m0} e^{\frac{KK_\mathrm{m} -K_\mathrm{m} K_\mathrm{p} +K_\mathrm{p} K}{K_p \left( {K_\mathrm{m} -K} \right) }\varepsilon _\mathrm{m} }\nonumber \\= & {} \phi _\mathrm{m0} e^{\frac{KK_\mathrm{m} -K_\mathrm{m} K_\mathrm{p} +K_\mathrm{p} K}{K_\mathrm{p} \left( {K_\mathrm{m} -K} \right) }\left\{ {\frac{K_\mathrm{m} L_\mathrm{f} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\frac{p_\mathrm{L} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }+\frac{K_\mathrm{f} \left( {L_\mathrm{m} +L_\mathrm{f} } \right) }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\varepsilon _\mathrm{V} } \right\} } \end{aligned}$$
(16)

where \(\phi _\mathrm{m0}\) is the initial matrix porosity.

2.4 Governing Equation for Gas Migration in Matrix

During the CBM recovery, the gas in fracture first flows into the borehole, which leads to a pressure drop in the fracture. The gas adsorbed in the matrix desorbs and diffuses to the fracture. The mass transfer between the matrix and fracture can be expressed as (Mora and Wattenbarger 2009)

$$\begin{aligned} Q_\mathrm{m} =D_0 \chi \left( {c_\mathrm{m} -\rho _\mathrm{f} } \right) \end{aligned}$$
(17)

where \(Q_\mathrm{m}\) is the mass transfer between the matrix and fracture, \(\chi \) is the shape factor of the matrix, \(\chi =\frac{3\pi ^{2}}{L_\mathrm{m} ^{2}}\), \(c_\mathrm{m}\) and \(\rho _\mathrm{f}\) are the gas concentration in the matrix and the gas density in fracture, respectively. According to the ideal gas equation, we have

$$\begin{aligned} \left\{ {\begin{array}{l} c_\mathrm{m} =\frac{M_\mathrm{C} }{RT}p_\mathrm{m} \\ \rho _\mathrm{f} =\frac{M_\mathrm{C} }{RT}p_\mathrm{f} \\ \end{array}} \right. \end{aligned}$$
(18)

where \(M_\mathrm{C}\) is the molar mass of \(\hbox {CH}_{4}\), R is the gas constant, T is the temperature, \(p_\mathrm{f}\) is the fracture gas pressure, and \(D_0\) is the gas diffusion coefficient, which in previous studies was viewed as a constant, but the research result of Li et al. (2016) showed that the diffusion coefficient of coal decreased with time. Based on the test result in the laboratory, a dynamic diffusion coefficient model was put forward

$$\begin{aligned} D_t =D_0 \exp \left( {-\lambda t} \right) \end{aligned}$$
(19)

where \(\lambda \) is the attenuation coefficient.

Substituting Eqs. (18) and (19) into Eq.(17), we rewrite the governing equation for mass transfer as

$$\begin{aligned} Q_\mathrm{m} =\frac{3\pi ^{2}M_\mathrm{C} \left( {p_\mathrm{m} -p_\mathrm{f} } \right) D_0 \exp \left( {-\lambda t} \right) }{L_\mathrm{m} ^{2}RT} \end{aligned}$$
(20)

The gas content in a unit volume of coal matrix can be expressed as

$$\begin{aligned} m_\mathrm{m} =\frac{abp_\mathrm{m} \rho _c M_\mathrm{C} }{\left( {1+bp_\mathrm{m} } \right) V_\mathrm{m} }+\phi _\mathrm{m} \frac{M_\mathrm{C} p_\mathrm{m} }{RT} \end{aligned}$$
(21)

where \(m_\mathrm{m}\) is the gas content in a unit volume of coal matrix, \(\rho _\mathrm{c}\) is the apparent density of coal, a is the Langmuir volume constant, b is the adsorption equilibrium constant, and \(V_\mathrm{m}\) is molar volume of gas.

Applying a mass balance equation of gas in the coal matrix, we have

$$\begin{aligned} \frac{\partial m_\mathrm{m} }{\partial t}=-\frac{3\pi ^{2}M_\mathrm{C} \left( {p_\mathrm{m} -p_\mathrm{f} } \right) D_0 \exp \left( {-\lambda t} \right) }{L_\mathrm{m} ^{2}RT} \end{aligned}$$
(22)

Substituting Eq. (21) into Eq. (22), we obtain the governing equation for the evolution of matrix gas pressure.

$$\begin{aligned} \frac{\partial p_\mathrm{m} }{\partial t}=-\frac{1}{H}\left[ {\frac{3\pi ^{2}\left( {p_\mathrm{m} -p_\mathrm{f} } \right) D_0 \exp \left( {-\lambda t} \right) }{L_\mathrm{m} ^{2}}+\frac{p_\mathrm{m} \phi _\mathrm{m} K_\mathrm{f} \left( {L_\mathrm{m} +L_\mathrm{f} } \right) \left( {KK_\mathrm{m} -K_\mathrm{m} K_p +K_p K} \right) }{K_p \left( {K_\mathrm{m} -K} \right) \left( {K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} } \right) }\frac{\partial \varepsilon _\mathrm{V} }{\partial t}} \right] \nonumber \\ \end{aligned}$$
(23)

where

$$\begin{aligned} H=\frac{{\textit{ab}}\rho _\mathrm{c} RT}{V_\mathrm{m} \left( {1+bp_\mathrm{m} } \right) ^{2}}+\phi _\mathrm{m} +\frac{K_\mathrm{m} L_\mathrm{f} \left( {KK_\mathrm{m} -K_\mathrm{m} K_p +K_p K} \right) }{K_p \left( {K_\mathrm{m} -K} \right) \left( {K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} } \right) }\frac{p_\mathrm{m} p_\mathrm{L} \phi _\mathrm{m} \varepsilon _\mathrm{L} }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) ^{2}} \end{aligned}$$
(24)

2.5 Governing Equation for Gas Flow in Fracture

Applying the mass conservation law to the gas in fracture, we have (Liu et al. 2015)

$$\begin{aligned} \frac{\partial \left( {\phi _\mathrm{f} \rho _\mathrm{f} } \right) }{\partial t}=Q_\mathrm{m} \left( {1-\phi _\mathrm{f} } \right) -\nabla \left( {\rho _\mathrm{f} V_\mathrm{f} } \right) \end{aligned}$$
(25)

where \(V_\mathrm{f}\) is the gas flow rate in fracture. According to the assumption in Eq. (3), the gas flow in coal fracture follows Darcy’s law

$$\begin{aligned} V_\mathrm{f} =-\frac{k_\mathrm{f} }{\mu }\nabla p_\mathrm{f} \end{aligned}$$
(26)

where \(\mu \) is the dynamic viscosity of gas.

Substituting Eqs. (18), (20), and (26) into Eq. (25), we obtain the governing equation for the evolution of fracture gas pressure.

$$\begin{aligned} \phi _\mathrm{f} \frac{\partial p_\mathrm{f} }{\partial t}+p_\mathrm{f} \frac{\partial \phi _\mathrm{f} }{\partial t}=\frac{3\pi ^{2}D_0 \left( {1-\phi _\mathrm{f} } \right) \exp \left( {-\lambda t} \right) }{L_\mathrm{m} ^{2}}\left( {p_\mathrm{m} -p_\mathrm{f} } \right) +\nabla \left[ {\frac{k_\mathrm{f} }{\mu }p_\mathrm{f} \nabla p_\mathrm{f} } \right] \end{aligned}$$
(27)

2.6 Governing Equation for Coal Seam Deformation

The Navier-type equation for the coal containing gas can be expressed as (Wu et al. 2011)

$$\begin{aligned} Gu_{i,{\textit{jj}}} +\frac{G}{1-2\nu }u_{j,{\textit{ji}}} -\alpha _\mathrm{f} p_{f,i} -\alpha _\mathrm{m} p_{\mathrm{m},i} -\frac{Kp_\mathrm{L} \varepsilon _\mathrm{L} }{\left( {p_\mathrm{m}p_\mathrm{m} +p_\mathrm{L} } \right) ^{2}}p_{\mathrm{m},i} +F_i =0 \end{aligned}$$
(28)

where G is the shear modulus of coal, \(G=E/2\left( {1+\nu } \right) \); \(\alpha _\mathrm{f}\) and \(\alpha _\mathrm{m}\) are the Biot coefficients for fracture and coal matrix, respectively; \(\alpha _\mathrm{f} =1-K/{K_\mathrm{f} }\), \(\alpha _\mathrm{m} =1-K/{K_\mathrm{m}}\), \(u_i\), and \(u_j\) are displacement components; and \(F_i\) is the component of the body force.

3 Model Validations

For the coal reservoir free from the mining disturbance, the four boundaries can be set as the roller boundaries, which restrict the normal displacement. In this condition, the coal permeability model governed by Eq. (12) can be converted into Eq. (29), in which the volumetric strain term for the coal seams is omitted.

$$\begin{aligned} \frac{k_\mathrm{f} }{k_{\mathrm{f}0} }=\left( {\frac{\phi _\mathrm{f} }{\phi _{\mathrm{f}0} }} \right) ^{3}=\left\{ {1-\frac{K_\mathrm{m} }{K_\mathrm{f} L_\mathrm{m} +K_\mathrm{m} L_\mathrm{f} }\left[ {\frac{p_\mathrm{L} L_\mathrm{m} \varepsilon _\mathrm{L} \left( {p_\mathrm{m} -p_\mathrm{m0} } \right) }{\left( {p_\mathrm{m} +p_\mathrm{L} } \right) \left( {p_\mathrm{m0} +p_\mathrm{L} } \right) }} \right] } \right\} ^{3} \end{aligned}$$
(29)

To verify the rationality and feasibility of the permeability model, we use Eq. (29) to match the field test data in San Juan basin. Table 1 lists the data of gas pressure and permeability for ten CBM wells. The basic parameters listed in Table 2 for the coal seams are used for the match. Figure 3 shows the matching results of the field permeability data by the permeability model. Overall, the permeability model matches well with the field data. Comparing Fig. 3a with Fig. 3b, we can find that the permeability for wells A-2, A-4, A-6, A-8, and A-10 is more sensitive to the change of the gas pressure than that of wells A-1, A-3, A-5, A-7, and A-9. This phenomenon indicates that the permeability model developed can be applied to simulate the flow field evolution for CBM wells with different permeability sensitivity to gas pressure reduction.

Table 1 Data measured in San Juan basin Palmer et al. (2005, 2006), Palmer (2009)
Full size table
Table 2 Parameters used for matching the field data in San Juan basin (Shi and Durucan 2005)
Full size table
Fig. 3
figure 3

Matching results of the field permeability data of ten CBM wells in San Juan basin by the permeability model developed

Full size image

4 Numerical Simulation and Discussions

4.1 Numerical Model and Input Parameters

To investigate the permeability distribution and evolution in the coal core, we build a numerical model, which is 100 mm high and 50 mm wide (see Fig. 4b). The model is based on the laboratory tests of coal permeability (see Fig. 4a). The free triangle mesh is selected and 11986 elements are generated in the model. The Mohr–Coulomb criterion is used to control the deformation and failure of the model. To achieve the uniaxial strain condition, the bottom, left, and right sides of the model are set as roller boundaries, which restrict the normal displacement, and the pressure boundary with a pressure of 5 MPa is specified to the top of the model. For gas flow in the fracture, the left and right sides of the model are set as zero flow boundaries, and the top and bottom sides are set as the Dirichlet boundaries with fracture pressures of 1 MPa and 0.1 MPa, respectively. For gas migration in matrix, the zero flow boundaries are specified to the four sides of the model. One measuring line (AB) and nine measuring points \((MP1{-} MP9)\) with an equal spacing of 10 mm are set on the centerline of the model to monitor the variations of the gas pressures and permeability. The parameters input in the model, which are obtained from recently published papers (Wu et al. 2010; Xia et al. 2014a, b), are listed in Table 3. The calculation time is set as 300,000 s, and the time step is set as 100 s.

Fig. 4
figure 4

Numerical model for the simulation. a Sketch map of permeability test system in the laboratory and b sketch map of numerical model

Full size image
Table 3 Basic parameters input in the numerical model
Full size table

In this paper, the non-equilibrium state of gas flow in the coal core is studied, and two cases, gas flow during adsorption and desorption, are discussed:

  1. Case 1:

    In this case, the gas flow during adsorption is simulated. Different from the laboratory tests of the coal permeability, there is nearly no gas adsorbed in the coal core at the initial time, and the initial gas pressures in the fracture and matrix are set as 0.1 MPa.

  2. Case 2:

    In this case, the gas flow during desorption process is simulated. Similar to the permeability tests in the laboratory, the coal core is saturated by gas at the initial time, and the initial gas pressures in the fracture and matrix are set as 1 MPa.

In cases 1 and 2, gas pressures of 1 and 0.1 MPa are specified to the gas inlet and outlet of the model, respectively. During the calculation, both the gas pressures and permeability on line AB and at points \({\text {MP1}}{-}{\text {MP9}}\) are monitored.

4.2 Spatial Distribution of Gas Flow Field During Adsorption Phase

4.2.1 Spatial distribution of gas pressures during adsorption phase

Figure 5 depicts the distributions of fracture and matrix gas pressures in the coal core during the gas adsorption phase. For the fracture gas pressure, the high-pressure area is located at the gas inlet of the coal core at the initial time, and with an increase of time, it expands gradually to the gas outlet. When the time reaches 300,000 s, the distribution of the fracture gas pressure remains unchanged with time. For the matrix gas pressure, the overall variation trend is similar to that of the fracture gas pressure. The difference is that at a given point the increasing rate of the matrix gas pressure is significantly lower than that of the fracture gas pressure. However, with the increase of the time, both fracture and matrix gas pressures tend to have the same distribution.

Fig. 5
figure 5

Distribution of gas pressures in coal under non-equilibrium state

Full size image

To get a better understanding of gas pressure distribution and evolution, we depict the gas pressures on the line AB in Fig. 6. Figure 6a shows that the fracture gas pressure decreases from point A to point B and presents a nonlinear distribution. With an increase of time, the pressure on line AB increases except at points A and B. From Fig. 6b, we can see that the matrix gas pressure also decreases from point A to point B and presents a nonlinear distribution. Comparing Fig. 6a with b, we can find that at the initial time, a relatively large difference exists between the fracture and matrix gas pressures, and with the increase in time, the difference gradually reduces and finally disappears. The possible reason for this phenomenon is that for the larger permeability of the fracture, the gas migrates rapidly into the fracture and reaches a high value in a short period, while at this point, very limited amount of gas is absorbed into the matrix, which can be verified by the fracture and matrix gas pressure distributions at 100 s. Owing to the action of the pressure gradient between the fracture and matrix, the gas in the fracture gradually diffuses into the matrix, leading to an increase of the matrix gas pressure, and the difference between the fracture and matrix gas pressures is reduced gradually.

Fig. 6
figure 6

Distribution of gas pressures in the coal core with different gas adsorption time a fracture gas pressure and b matrix gas pressure

Full size image

4.2.2 Spatial distribution of permeability during adsorption phase

Figure 7 shows the distributions of permeability in the coal core at different time. At 100 s, the permeability reduces gradually from the gas inlet of the model to the gas outlet; with an increase in time, the permeability in the coal core decreases and a low-permeability area appears at gas inlet. At 300,000 s, the permeability remains unchanged with time and shows a distribution of increasing from the gas inlet of the model to the outlet.

Fig. 7
figure 7

Permeability distributions in the coal under the non-equilibrium state

Full size image

During the gas adsorption phase, the permeability on line AB is monitored and depicted in Fig. 8. It can be seen that at the initial time, at 100 s, the permeability in the coal core increases linearly from the gas outlet to the inlet, and the permeability at each point of the sample is higher than the initial value (permeability at point B). The reason is that at 100 s, the fracture gas pressure has increased to a relatively high value, which reduces the effective stress and leads to an increase of permeability. During this time, little changes have occurred on matrix gas pressure, and the matrix swelling caused by gas adsorption is not noticeable. With an increase in time, the permeability decreases overall, and the point closer to the gas inlet of the sample has larger decreasing amplitude. It is because that with the increase of time, the fracture gas pressure keeps rising, which not only reduces the effective stress, but also accelerates the gas diffusion into the matrix. The increase of the matrix gas pressure decreases the effective stress on the one hand, and on the other hand accelerates the gas adsorption and further leads to matrix swelling. In this case, the coal permeability is jointly determined by the reduced effective stress and the increased matrix swelling. Figure 8 shows that when the time is less than 10,000 s, the permeability of the sample is mainly controlled by the effective stress; when the time is more than 10,000 s, the permeability in the part close to the gas inlet is dominated by matrix swelling, whereas that in the part close to the gas outlet is controlled by the effective stress.

Fig. 8
figure 8

Distribution of permeability in the coal core with different gas adsorption times

Full size image
Fig. 9
figure 9

Evolution of gas pressures with time at specific points. a Fracture gas pressure and b matrix gas pressure

Full size image

4.3 Temporal Evolution of Gas Flow Field During Adsorption Phase

From Sect. 4.2, we can find that the gas flow time has a significant effect on the distributions of gas pressures and permeability in the coal core. To get a better understanding of the evolution characteristics of the flow field with time, it is necessary to explore the distributions of gas pressures and permeability at specific points in the time dimension.

4.3.1 Temporal evolution of gas pressures during adsorption phase

The fracture and matrix gas pressures at points \({ MP1}{-}{ MP9}\) are monitored to explore the gas flow behavior at given points, and the results are depicted in Fig. 9. It can be seen that both the fracture and matrix gas pressures show increasing tendencies with the time on the whole, and the point closer to the gas inlet of the coal core has higher gas pressures. From Fig. 9a, we can see that for the points MP1 and MP2, there exist two pressure drop points. The reasons for this phenomenon are that when the gas flows into the coal core, the fracture gas pressure rapidly increases at the initial time (\(t<10 \hbox { s}\)), and then, the high fracture gas pressure promotes the gas to diffuse into the matrix, which leads to a rapid increase of the matrix gas pressure (Fig. 9b) and a slight decrease of the fracture gas pressure. After the pressure drop point, both the fracture and matrix gas pressures increase to a balanced value. In addition, from Fig. 9a, we can see that the time for gas pressure at different points to start to rise is different; for example, the fracture gas pressure of point MP1 begins to rise at 1 s, and that of point MP2 begins to rise at 5 s; after 5 s, the fracture gas pressure at MP3 begins to rise. This phenomenon indicates that the gas flow rate in fracture between two adjacent points is different, and this may be caused by various permeability values.

4.3.2 Temporal evolution of permeability during adsorption phase

Figure 10 shows the permeability evolution with time at different points. It can be seen that at the initial time, the permeability of points close to the gas inlet of the sample increases sharply to relatively high values for the rapid increase of the fracture gas pressure. Moreover, the closer the point to the gas inlet of the sample, the higher the permeability of the point, which can explain the phenomenon that varying periods are needed for the gas to flow between adjacent points. With an increase of time, the permeability of point close to the gas inlet of the sample starts to decrease. This is because with an increase of the matrix gas pressure, the amount of adsorbed gas begins to increase, which results in matrix swelling and further leads to permeability reduction. With the further increase of time, the permeability of the point with greater distance to the gas inlet of the sample starts to decrease. However, we can find that the permeability of different points shows various decreasing amplitudes. This is because the point closer to the gas inlet has a higher matrix gas pressure, which leads to a greater matrix swelling and further results in a lower permeability.

Fig. 10
figure 10

Permeability evolution with time at specific points

Full size image

4.4 Spatial Distribution of Flow Field During Desorption Phase

4.4.1 Spatial distribution of gas pressures during desorption phase

Figure 11 depicts the distributions of fracture and matrix gas pressures in the coal core with different time points. For the fracture gas pressure, at the initial time (100 s), the pressure drop zone appears at the gas outlet of the model, and with an increase of time, it gradually expands to the gas inlet. The variation trend of the matrix gas pressure is similar to that of the fracture gas pressure. The difference is that at the same time, the drop rate of the matrix gas pressure is noticeably lower than that of the fracture gas pressure. However, with an increase of time, this difference narrows gradually, and at 300,000 s, the fracture and matrix gas pressures are similarly distributed along the coal core.

Fig. 11
figure 11

Gas pressures distributions in the coal core during gas desorption processes

Full size image

The gas pressures distributions on line AB are monitored and depicted in Fig. 12. Figure 12a shows that the fracture gas pressure decreases gradually from the gas inlet to the gas outlet on the whole. However, at different periods, there exist obvious differences in the fracture gas distribution. For example, at 100 s, the pressure drop from 0 to 60 mm is not observable, whereas from 60 to 100 mm, a sharp decrease can be observed. With an increase of time, the fracture gas pressure shows a general downward trend. At 300,000 s, the fracture gas pressure reaches the equilibrium state, and the value at each point remains unchanged with the time. Figure 12b depicts the distributions of matrix gas pressure along the coal core at different time points. The overall trend of the matrix gas pressure is similar to that of the fracture gas pressure; the difference is that at the same time and same point, the matrix gas pressure is higher than the fracture gas pressure, and with an increase of time, the difference reduces and disappears finally. When the equilibrium state is reached, both the fracture and matrix gas pressures distribute non-linearly along the coal core.

Fig. 12
figure 12

Gas pressure distributions in the coal core with various time points a fracture gas pressure and b matrix gas pressure

Full size image

4.4.2 Spatial distribution of permeability during desorption phase

It can be seen from Sect. 4.4.1 that the gas pressures show nonlinear distributions along the coal core. From Eq. (12), we know that the change of gas pressure will inevitably lead to a variation of the coal permeability. Therefore, in this section, we study the distributions of permeability in the coal core. Figure 13 shows that at the initial time \((t=100 \hbox { s})\), the high-permeability region locates at the gas inlet side and the low-permeability region locates at the gas outlet side. With an increase of time, the high-permeability region expands to the gas outlet, and at 40,000 s, a high-permeability region appears at the gas outlet side and expands to the gas inlet side.

Fig. 13
figure 13

Permeability distributions in the coal core at various time points

Full size image

Figure 14 depicts the coal permeability on line AB. Overall, the permeability in the coal core increases with time. This is because the decrease of the fracture gas pressure promotes the gas desorption in the coal matrix, which results in matrix shrinkage and further leads to an increase of the coal permeability. At the initial time \((t<10^{4} \hbox { s})\), the coal permeability decreases from point A to point B, and the reason is that the reduction of the fracture gas pressure results in an increase of the effective stress at the gas outlet side, whereas at this moment, the gas desorption in the matrix is negligible and the matrix shrinkage effect is unobvious. When \(t>10^{4}\hbox { s}\), the coal permeability reduces first and then increases from point A to point B. The reason for such permeability distribution is that the coal permeability is jointly determined by the effective stress and matrix shrinkage effect, and for the part close to the gas inlet, the reduction of the fracture gas pressure results in an increase of the effective stress. Because the matrix shrinkage at this part is not obvious, the permeability shows a decreasing trend. For that part close to the gas outlet, the dramatic decrease of the fracture gas pressure accelerates the desorption of the matrix gas, which not only changes the effective stress, but also leads to matrix shrinkage. In this case, the positive effect of matrix shrinkage is greater than the negative effect of the effective stress. Therefore, the coal permeability in this part shows an increasing trend.

Fig. 14
figure 14

Permeability distributions on line AB in the coal core with various time points

Full size image

4.5 Temporal Evolution of Flow Field During Desorption Phase

4.5.1 Temporal evolution of gas pressures during desorption phase

Figure 15 shows the evolution of gas pressures with time at different points. Figure 15a shows that at the initial time, the fracture gas pressure at point MP9 starts to decrease, and with an increase of time, the fracture gas pressure at the points away from the gas outlet begins to reduce in the order of MP8, MP7, MP6, MP5, MP4, MP3, MP2, and MP1. Figure 15b depicts the variations of matrix gas pressure with time at different points. When \(t<100 \hbox { s}\), no changes on matrix gas pressure at each point are observed. By contrast, when \(t>100 \hbox { s}\), the matrix gas pressure at point MP9 starts to reduce for the rapid decrease of the fracture gas pressure. The matrix gas pressures at points away from the gas outlet then begin to fall one by one.

Fig. 15
figure 15

Gas pressure evolutions with time at different points a fracture gas pressure and b matrix gas pressure

Full size image

4.5.2 Temporal evolution of permeability during desorption phase

The variation of gas pressures with time will inevitably lead to a change in coal permeability. In Fig. 16, the evolution of coal permeability at different points is depicted. At the initial time, the permeability at the point close to the gas inlet is greater than that at the point close to the gas outlet, because the reduction of the fracture gas pressure leads to a sharp increase of the effective stress, which further results in a decrease of the coal permeability. For point MP9, the permeability begins to increase at 500 s. When the time reaches 10,000 s, the permeability increases sharply, and when the time is greater than \(2\times 10^{5} \hbox { s}\), the increase in speed becomes slow and reaches equilibrium at \(3\times 10^{5}\hbox { s}\). Reason for the increase of the permeability is that the decrease of the fracture gas pressure promotes the gas desorption in the matrix, which causes the matrix shrinkage. In addition, we can see that the point close to the gas outlet has greater increasing amplitude of the permeability, which resulted from the significant reduction of the matrix gas pressure at this point.

Fig. 16
figure 16

Evolution of permeability with time at different points

Full size image

5 Discussions

In Sect. 4, we discussed the distributions and evolutions of gas flow fields under the non-equilibrium states, including the gas adsorption phase and gas desorption phase. It was found that significant differences exist between the permeability distributions during the adsorption and desorption phases. In this section, we will further discuss the reasons for the differences.

Figure 17 depicts the mechanisms for the permeability evolutions under non-equilibrium states. In this figure, a cross section of the coal core is selected to analyze the permeability evolution mechanisms. In the cross section of the coal core, the coal matrix and fractures are contained. The green and red points represent the adsorbed and free gases, respectively. The blue arrows indicate the gas flow in the fractures, and the black arrows indicate the processes of gas adsorption to or desorption from the matrix. The red line indicates the permeability ratio at the initial time, and the green line represents the permeability ratio during the adsorption and desorption phases.

During the gas adsorption phase, there is no gas in the coal core at the initial time \((t_{0})\), and the permeability ratio along the coal core equals 1. With an increase of the time, the gas flows from the gas inlet to gas outlet. For example, at the time of \(t_{1} (t_{1}<100\hbox { s})\), the gas mainly flows in the fractures, which decreases the effective stress of the coal core. Because the fracture gas pressure decreases from gas inlet to gas outlet (see Fig. 6a), the permeability increases from the gas outlet to the inlet. With the further increase of the time, the gas in the fracture begins to diffuse to the matrix, which leads to adsorption swelling of the matrix. Because the matrix gas pressure decreases from the gas inlet to the gas outlet, the effect of matrix swelling at the gas inlet is more significant than that at the gas outlet. Therefore, the permeability ratio decreases from the gas outlet to the gas inlet.

For the gas desorption phase, at the initial time \((t_{0})\), the coal core is saturated with gas, and the permeability ratio of the coal core can be viewed as 1. With an increase of the time, the gas flow out of the fracture, resulting in a decrease of the fracture gas pressure and an increase of the effective stress. For example, at the time of \(t_{1}\), only the gas in the fracture flows out of the coal core, while there is nearly no gas desorbing from the matrix. In this case, the permeability is mainly controlled by the effective stress. Because the fracture gas pressure decreases from the gas inlet to gas outlet, the permeability reduces from the gas inlet to gas outlet as well. When the time reaches \(t_{2}\), the gas in the matrix desorbs and diffuses to the fracture, which results in matrix shrinkage and permeability rebound at the gas outlet.

From the above analyses, we can deduce that for the \(\hbox {CO}_{2}\) geological sequestration, the initial injection of \(\hbox {CO}_{2}\) will lead to an increase of the coal seam permeability for the decreased effective stress, and later with the adsorption of \(\hbox {CO}_{2}\) to the coal matrix, the coal seam permeability decreases. In contrast, for the CBM recovery, the initial gas production will result in a decrease of the coal seam permeability for the increased effective stress, and later with the desorption of gas from the coal matrix, the matrix shrinkage occurs, resulting in a rebound of the coal seam permeability.

Fig. 17
figure 17

Mechanisms of coal permeability evolutions under non-equilibrium state

Full size image

For the laboratory test of the coal permeability, Eq. (30) is generally used to calculate the coal permeability.

$$\begin{aligned} k=\frac{2\mu p_0 Q_0 L}{A\left( {p_1^2 -p_2^2 } \right) } \end{aligned}$$
(30)

where \(p_{0}\) is the atmospheric pressure, \(Q_{0}\) is the gas flow rate, L is the length of the coal core, A is the sectional area of the coal core, and \(p_{1}\) and \(p_{2}\) are the gas pressures at gas inlet and outlet, respectively.

Equation (30) is obtained by assuming that the gas pressure in the coal core decreases linearly from the gas inlet to the outlet, the gas pressure gradient in the coal core is thought to be a constant of \((p_{1}-p_{2})/L\), and the tested result is the permeability at the middle of the coal core (L / 2). This value is thought to be the average permeability of the coal core and not affected by the gas pressure (see Fig. 18c). However, as shown in Fig. 12 the gas pressure distributes non-linearly in the coal core, and the gas pressure gradient along the coal core is various, instead of a constant. In addition, from Fig. 14, we find that a minimum permeability appears at somewhere close to the gas outlet, and with an increase of the time, the point where the minimum permeability appears gradually shifts toward the gas inlet (see Figs. 18a, b). From the above analyses, we know that both the gas pressure and coal permeability distribute non-linearly in the coal core, which may be caused by the inconstant effective stress and matrix shrinkage. During the laboratory test of the coal permeability, the monitored gas flow rate reflects the value at somewhere (Section B) close to the gas outlet, rather than the value at the middle of the coal core (Section C). Therefore, we think that Eq. (30) is not suitable for the calculation of the coal permeability. Our suggestion for the laboratory test of the coal permeability is that before the tests, a numerical simulation with the parameters obtained from the coal core used should be conducted to determine the position that the minimum permeability appears and its corresponding gas pressure and gas pressure gradient. Then, the coal permeability can be calculated with the gas flow rate monitored in the experiment.

Fig. 18
figure 18

Mechanism for the permeability test of coal core in the laboratory

Full size image

6 Conclusions

To investigate the gas flow behaviors in coal under non-equilibrium state, we developed a new mathematical model that couples gas flow and coal deformation. With this model, both the gas flow during adsorption and desorption phases are discussed. Based on the results of this study, the following conclusions can be drawn:

For gas flow during the adsorption phase, the matrix gas pressure is generally lower than the fracture gas pressure before the equilibrium state is achieved. The main control factor of the permeability varies at different time. At the initial time, the permeability is dominated by the effective stress, and later, the permeability in the part close to gas inlet is mainly controlled by the matrix swelling, whereas that in the part close to outlet is still dominated by the effective stress. For gas flow during desorption phase, the matrix gas pressure is found to be higher than the fracture gas pressure at a given time point. From the gas inlet to the gas outlet, the permeability deceases at the initial time, and when the time is greater than 10,000 s, it shows a decreasing and then an increasing trend. The research results can provide guidance to the optimization of the parameters for \(\hbox {CO}_{2}\) geological sequestration and CBM recovery.

Both the gas pressure and permeability distribute non-linearly along the coal core, which means that the assumptions of linear gas pressure distribution and constant permeability are not appropriate. A method, which is a combination of numerical simulation and laboratory test, has been put forward to get a more accurate test result.

The permeability model is developed with no restrictions on the boundary conditions, implying that this mathematical model can not only simulate the gas flow in the laboratory, but also characterize the flow field evolutions in the CBM reservoir. And the model matches well with the field data. However, the matrix–fracture interaction during coal deformation has not been fully considered in this model, which may lead to an overestimation of the contribution of the matrix deformation to the permeability changes. Besides, in this study the poroelastic model is adopted, while the effect of discrete fracture network is not considered. In the future studies, these issues will be further investigated.