Reactive Transport Modelling of Dolomitisation Using the New CSMP++GEM Coupled Code: Governing Equations, Solution Method and Benchmarking Results

Abstract

Reactive transport modelling (RTM) is a powerful tool for understanding subsurface systems where fluid flow and chemical reactions occur simultaneously. RTM has been widely used to understand the formation of dolomite by replacement of calcite, which can be an important control on carbonate reservoir quality. Dolomitisation is a reactive transport process governed by slow dolomite precipitation and cannot be correctly simulated without a kinetic rate model. The new CSMP++GEM coupled RTM code uses the GEMS3K kernel for solving geochemical equilibria by the Gibbs energy minimisation method with the CSMP++ framework that implements a hybrid finite element–finite volume method to solve partial differential equations. The unique feature of the new coupling is the mineral reaction kinetics, implemented via additional metastability constraints. CSMP++GEM is able to simulate single-phase flow and solute transport in porous media together with chemical reactions at different pressure, temperature, and water salinity conditions. This RTM assures mass conservation which is crucial when simulating transport of solutes with low concentrations over geological time. A full feedback of mineral dissolution/precipitation on the fluid flow is provided via corresponding porosity/permeability evolution and two source terms in the pressure equation. First, the mass source term accounts for the mass of solutes released during mineral dissolution or taken from the solution by mineral precipitation. The second source term attributes to the fact that the solution density is affected by mineral dissolution/precipitation, too. This effect is included through the equivalent water salinity, which is calculated from the total amount of dissolved solutes and is used to update the properties of saline water from the H$_2$O–NaCl equation of state. This paper puts emphasis on the thorough mathematical derivation of the governing equations and a detailed description of the numerical solution procedure. Two sets of benchmarking results are presented. The first benchmark is a well-known 1D model of dolomitisation by MgCl$_2$ solution with thermodynamic reactions. In the second benchmark, CSMP++GEM is compared with TOUGHREACT on a 1D model of dolomitisation by sea water taking into account mineral reaction kinetics. The results presented in this paper demonstrate the ability of the CSMP++GEM code to correctly reproduce dolomitisation effects.

1 Introduction

Dolomitisation (replacement of calcite CaCO$_3$ by dolomite CaMg(CO$_3$)$_2$) is a case of mineral replacement that modifies the volume of the solid phases (Putnis 2002). Dolomite has a higher density than calcite, and 1:1 molar replacement can generate up to 13% additional porosity. On the other hand, dolomite forming as a primary precipitate from supersaturated fluids leads to porosity occlusion. Dolomitisation can also significantly modify permeability by reorganising the pore geometry of the pore network, for example by replacing allochems and matrix with sucrosic dolomite crystals (Gregg 2004). With regard to carbonate-hosted petroleum reservoirs, understanding the spatial distribution of dolomite bodies and the resulting changes in petrophysical properties (porosity–permeability) is key for the accurate estimation of hydrocarbon reserves and improving recovery efficiency.

Dolomitisation has been simulated using reactive transport modelling (RTM) in a number of diagenetic settings, driven by different fluid circulation systems. These include near surface and shallow burial reflux of platform-top evaporative brines (Jones and Xiao 2005; Al-Helal et al. 2012; Gabellone and Whitaker 2015; Lu and Cantrell 2016), intermediate and deep burial geothermal circulation and compactional flow (Wilson et al. 2001; Whitaker and Xiao 2010; Consonni et al. 2010), and high-temperature fluid expulsion through faults and fractures (Corbella et al. 2014).

Dolomitisation is a kinetically controlled, partial equilibrium process (Machel 2004). At near-surface conditions, the precipitation rate of dolomite (Arvidson and Mackenzie 1999) can be a million times slower than that of calcite (at the same supersaturation) or calcium sulphates, whereas the dissolution rates of dolomite and calcite are comparable (Palandri and Kharaka 2004). Slow dolomitisation processes need to be simulated over geological time (hundreds of thousands up to millions of years), which implies long computation times, even if fast numerical methods and algebraic solvers are used. Although RTM has more than 30-year-long history (Lichtner 1985; Steefel and Lasaga 1994; Steefel and MacQuarrie 1996), only now sufficient computational power becomes available to perform long-time 3D simulations on detailed grids; nevertheless, full-scale simulations are still rare. To date, there is only one example of a massively parallel reactive transport code PFLOTRAN (Hammond and Lichtner 2010) that has shown an almost ideal linear scaling on high-performance computers for various problems.

The motivation of this work was to create a versatile run-time coupled RTM code (called CSMP++GEM) by combining the best features of the CSMP++ and GEM families of codes.

Complex Systems Modelling Platform (CSMP++) framework (Matthäi et al. 2001) is an object-oriented software library written in C++ that uses unstructured grids to represent model geometry and finite element–finite volume method to solve partial differential equations. To solve systems of algebraic linear equations CSMP++ uses the SAMG solver (SAMG 2010), which recommended itself for being accurate, robust and fast.

GEMS3K is an open-source stand-alone C++ code for Gibbs energy minimisation that computes (partial) equilibrium chemical speciation in complex heterogeneous multiphase systems from the elemental bulk composition of the system, thermodynamic data for the temperature and pressure of interest, parameters of mixing (Kulik et al. 2013; Wagner et al. 2012), and kinetic rate parameters controlling additional metastability restrictions for certain phases and components. The initial chemical systems for RTM can be set up and tested using the GEM-Selektor v.3 grahical user interface with built-in thermodynamic and model databases and then exported as sets of GEMS3K input files.

The main advantage of CSMP++GEM over the existing CSMP-GEM coupled code (Fowler et al. 2016) is that the current version of the code also implements detailed controls on mineral–water reaction kinetics, which is a crucial issue for modelling reactions such as dolomitisation (Arvidson and Mackenzie 1999).

The choice of the finite volume method for solute transport is important for maintaining the local mass conservation. Unlike the finite element method that is used in OpenGeoSys code (and OpenGeoSys-GEM coupled code (Shao et al. 2009)) for solving both flow and solute transport, in the finite element–finite volume method used in the CSMP++GEM coupling, flux continuity across the finite volume facets guarantees the local mass conservation. The integral finite differences method (IFD) that is used in TOUGHREACT (Xu et al. 2012) is based on the conservation laws, but only allows the use of corner point grids that are much less flexible as unstructured grids.

In codes such as TOUGHREACT, the chemical speciation solver uses the so-called LMA (law of mass action) method, which is based on a selection of master species (usually aqueous ions and water, sometimes minerals) whose amounts enter the material balance equations directly, and product species whose amounts are defined via the LMA equations for reactions of formation of product species from master species and respective equilibrium constants. The systems of material balance and LMA equations are then solved simultaneously using the Newton–Raphson method (Reed 1982). Implicit to the LMA method are the assumptions that the aqueous electrolyte or gaseous mixture phase is predominant in the system; redox state, alkalinity and assemblage of stable phases are known beforehand in some form; and, if a non-ideal solid solution is involved, its equilibrium composition can be obtained from the aqueous-phase composition.

As stated by Reed (1982), the real challenge of LMA method lies in the selection of stable mineral phases, especially solid solutions to be included into the mass balance equations. This is normally done by checking the saturation indices (SI) of the whole list of minerals in the process of solving the LMA speciation task many times and adding/removing mineral phases one by one. Some LMA algorithms, like the Geochemists Workbench (Bethke 2008), cannot solve equilibria with gas mixtures, solid solutions or melts in the material balance, because gases, minerals or melt components are treated as master species.

In contrast to the LMA method, the Gibbs energy minimisation (GEM) method (Karpov et al. 1997; Kulik et al. 2013) finds the unknown phase assemblage and speciation of all phases from the elemental bulk composition of the system by minimising its total Gibbs energy while maintaining the elemental material balance. All species (components) in all phases must be provided with their elemental formulae and standard Gibbs energy per mole; no separation into master and product species is needed.

Compared with LMA, GEM methods do not require any assumptions about the equilibrium state, and are capable of solving equilibria in complex heterogeneous chemical systems with many non-ideal multicomponent solution phases (Wagner et al. 2012; Kulik et al. 2013). This makes possible RTM simulations of complex heterogeneous equilibria with intrinsic redox states, aqueous electrolyte, non-ideal gas mixtures (fluids), mineral solid solutions, melts, adsorption and ion exchange.

The new CSMP++GEM reactive transport code combines relevant features of CSMP++ framework and the GEMS3K stand-alone code for simulation of THC systems with complex geometry and complex chemistry in wide ranges of temperatures, pressures, compositions and various transport regimes.

When simulating thermal–hydrological–chemical (THC) processes, various effects need to be taken into account, such as density changes due to changes in pressure, temperature and salinity, as well as mass sources due to chemical reactions such as aqueous and surface complexation, mineral dissolution or precipitation. This leads to a complex system of coupled flow transport–chemistry equations that can be solved following either a fully implicit approach or an operator-splitting approach. Sequential “operator-splitting” not only allows the use of a chemical speciation solver as a black box, but was also shown to be faster than the fully implicit method, at least for advection-dominated problems in 1D (de Dieuleveult et al. 2009), and was therefore adopted in this study.

This article starts with a mathematical problem statement that includes a derivation of the governing equations for flow, solute transport and chemical reactions. This is followed by a description of numerical methods, used to solve the resulting system of partial differential equations and the Gibbs energy minimisation problem. After that, benchmarking results for a simple 1D model of dolomitisation without and with dolomite precipitation/dissolution kinetics are presented, including the comparison of this RTM with TOUGHREACT. At the end conclusions are briefly outlined.

2 Governing Equations for Single-Phase Flow in Porous Media, Heat and Solute Transport

In this section, the governing equations that describe single-phase multicomponent flow in a fully saturated porous media coupled with chemical reactions are presented. A brief description of the Gibbs energy minimisation method with emphasis on the phase stability index and on how partial equilibria are controlled by the kinetic rates of mineral–water interaction can be found in “Appendix”.

The flow is assumed to be slightly compressible and non-isothermal. Minerals (calcite, dolomite) are either in equilibrium or under kinetic control; their dissolution and/or precipitation result in changes in porosity and permeability.

Chemical composition of the system is defined in terms of the total amounts of so-called independent components (IC), typically chemical elements and electric charge. Each IC can be present in various aqueous ions and molecules dissolved in water, as well as in different minerals of the solid phase. Aqueous concentration $c_i$ is the total amount of moles of the i-th independent component in all species dissolved in the aqueous phase per unit volume.

For each IC, the conservation of mass in the following form holds:

$$\begin{aligned} \frac{\partial (\phi c_i)}{\partial t} + \nabla \cdot (c_i {\mathbf {v}}_i) = q_i,\quad \forall i=\overline{1,N}, \end{aligned}$$

(1)

where $\phi$ is the porosity, ${\mathbf {v}}_i$ is the flow velocity of the i-th independent component, $q_i$ is the source/sink term that accounts for the exchange of i-th IC between solid and aqueous phases due to mineral dissolution/precipitation, and N is the number of independent components. There are no other sources/sinks other then caused by chemical reactions.

Let us define the aqueous solution density $\rho = \sum _{i=1}^{N} c_iM_i$, using $M_i$—the molar mass of the i-th independent component. The solution mass flux is equal to the sum of mass fluxes of individual components:

$$\begin{aligned} \rho {\mathbf {v}} = \sum _{i=1}^{N} c_iM_i{\mathbf {v}}_i. \end{aligned}$$

The sum of the product of Eq. (1) by $M_i$ yields the continuity equation for the aqueous phase:

$$\begin{aligned} \frac{\partial (\phi \rho )}{\partial t} + \nabla \cdot (\rho {\mathbf {v}}) = Q, \end{aligned}$$

(2)

where ${\mathbf {v}}$ is the solution velocity, and Q is the source term that accounts for the mass exchange between aqueous and solid phases due to chemical reactions:

$$\begin{aligned} Q=\sum _{i=1}^{N} q_i M_i. \end{aligned}$$

The fluid velocity is related to the fluid pressure by means of Darcy’s law:

$$\begin{aligned} {\mathbf {v}} = -\frac{k}{\mu }(\nabla p - \rho {\mathbf {g}}), \end{aligned}$$

(3)

where k is the permeability, $\mu$ is the fluid viscosity, p is the fluid pressure, and ${\mathbf {g}}$ is the gravity acceleration vector.

The equivalent salinity is calculated from the chemical composition of a solution:

$$\begin{aligned} X = 1 - \frac{m_w}{m}, \end{aligned}$$

where m is the solution mass, $m_w$ is the mass of pure water (solvent).

We assume that solution density $\rho =\rho (p, T, X)$ depends on pressure $p=p(t, {\mathbf {x}})$, temperature $T=T(t, {\mathbf {x}})$ and chemical composition $X=X(t, {\mathbf {x}})$, and calculate its time derivative:

$$\begin{aligned} \frac{\partial \rho }{\partial t} = \frac{\partial {\rho }}{\partial p}\frac{\partial p}{\partial t} + \frac{\partial \rho }{\partial T }\frac{\partial T}{\partial t } + \frac{\partial \rho }{\partial X }\frac{\partial X}{\partial t } =\rho \beta _f\frac{\partial p}{\partial t} - q_{TX}/\phi , \end{aligned}$$

(4)

where

$$\begin{aligned} \beta _f=-\frac{1}{V} \frac{\partial V}{\partial p} = \frac{1}{\rho } \frac{\partial \rho }{\partial p} \end{aligned}$$

is the isothermal isosaline fluid compressibility, defined as the relative change in the solution volume V (or solution density $\rho$) with a change in pressure, and

$$\begin{aligned} q_{TX} = - \phi \left( \frac{\partial \rho }{\partial T }\frac{\partial T}{\partial t } + \frac{\partial \rho }{\partial X }\frac{\partial X}{\partial t }\right) \end{aligned}$$

is the source term that accounts for the temperature and salinity-induced solution density change at constant pressure.

Neglecting the thermal expansion of the rock, the porosity change is expressed in terms of isothermal pore compressibility:

$$\begin{aligned} \beta _{\phi } = \frac{1}{\phi } \frac{\partial \phi }{\partial p}, \end{aligned}$$

$$\begin{aligned} \frac{\partial {\phi }}{\partial {t}}=\frac{\partial {\phi }}{\partial {p}}\frac{\partial {p}}{\partial {t}}=\phi \beta _{\phi } \frac{\partial {p}}{\partial {t}}. \end{aligned}$$

(5)

Porosity changes caused by chemical reactions are discussed below.

Using Eqs. (4) and (5), the left-hand side of (2) may be rewritten to first get:

$$\begin{aligned} \frac{\partial (\phi \rho )}{\partial t} = \phi \frac{\partial \rho }{\partial t} + \rho \frac{\partial \phi }{\partial t} = \phi \rho \beta _f\frac{\partial p}{\partial t} - q_{TX} + \rho \phi \beta _{\phi }\frac{\partial {p}}{\partial {t}}, \end{aligned}$$

and then inserting (3) into the right-hand side of (2), yields the transient pressure equation:

$$\begin{aligned} \rho \phi ( \beta _f + s\beta _{\phi })\frac{\partial {p}}{\partial {t}}=\nabla \cdot \left( \rho \frac{k}{\mu }(\nabla p - \rho {\mathbf {g}})\right) + q_{TX} + Q. \end{aligned}$$

(6)

The energy conservation equation is written in the following form (Bejan and Kraus 2003):

$$\begin{aligned} (\phi \rho c_{pf}+(1-\phi )\rho _{r}c_{pr})\frac{\partial {T}}{\partial {t}} = \nabla \cdot ( (\phi K_f + (1-\phi )K_r)\nabla T) - \nabla \cdot ( {\mathbf {v}} \rho c_{pf} T ), \end{aligned}$$

(7)

where T is the temperature, $K_f$ and $K_r$ are the fluid and rock thermal conductivities, $c_{pf}$ and $c_{pr}$ are the fluid- and rock-specific heat capacities, respectively; $\rho _{r}$ is the rock density. Thermal effects of the chemical reactions are not taken into account.

Returning to the component transport Eq. (1), we introduce the entity ${\mathbf {J}}_i = c_i({\mathbf {v}}_i - {\mathbf {v}})$—the diffusive mass flux of i-th species with respect to the average flow velocity (Bear 1972).

Using this definition, the second term on the left-hand side of (1) can be written as: $\nabla \cdot (c_i {\mathbf {v}}_i) = \nabla \cdot {\mathbf {J}}_i + \nabla \cdot (c_i {\mathbf {v}}),$ the diffusive flux can be described using Fick’s law ${\mathbf {J}}_i = -D \nabla c_i$, and Eq. (1) can be rearranged in the following form:

$$\begin{aligned} \frac{\partial (\phi c_i)}{\partial t} + \nabla \cdot ({\mathbf {v}} c_i) - \nabla \cdot (D \nabla c_i) = q_i,\; \forall i=\overline{1,N}, \end{aligned}$$

(8)

where D is the diffusion–dispersion coefficient, assumed to be constant and the same for all species.

Equations (6), (7) and (8) together with the equation of state form the total system of equations that describe the non-isothermal slightly compressible single-phase multicomponent transport in porous media. In this work, an equation of state for brine from (Driesner 2007) was used.

3 Solution Method

The resulting system of Eqs. (6), (7) and (8) is solved using a hybrid finite element–finite volume method (Geiger et al. 2006) implemented within the CSMP++ framework software library (Matthäi et al. 2001), an algebraic multigrid solver (SAMG) is used for solving the arising systems of linear algebraic equations (SAMG 2010). The chemical speciation calculations are performed by means of the open-source GEMS3K software library (Kulik et al. 2013).

CSMP++GEM reactive transport code is written in the C++ programming language and has a flexible modular structure that can be configured for particular simulation needs: stationary or transient pressure with/without gravity, constant, stationary or transient temperature, implicit or explicit time stepping. Reactive transport simulations based on 1D, 2D and 3D unstructured grids can be performed.

A consistent initialisation is important for RTM. The initial chemical composition/speciation is read from text-format input files exported from GEM-Selektor (Kulik et al. 2013). Initial and boundary conditions for pressure and temperature are read from a CSMP++ configuration file. Dirichlet, Neumann and mixed boundary conditions for pressure and temperature, as well as fluid and heat sources can be specified. First, initial pressure and temperature distributions across the model are calculated. Next, chemical speciation is computed for each finite volume at the initial pressure–temperature conditions. Last, fluid properties are computed from the equation of state for the given pressure, temperature and salinity.

After the model initialisation, the main time stepping loop is executed. A flow chart for a single time step is shown in Fig. 1, with a detailed description given in the following subsections.

Fig. 1

Flow chart of a single time step as implemented in CSMP++GEM

3.1 Pressure–Temperature Coupling

The pressure Eq. (6) and the heat transport Eq. (7) are solved in a sequential order implicitly in time, as represented by the following semi-discrete Eqs. (9) and (10) in which constant properties lack the superscripts. The rule for the porosity/permeability update is explained below. The pressure equation is solved using the finite element method on an unstructured grid:

$$\begin{aligned} \phi ^{n} \rho ^{n} (\beta _f^{n} + \beta _{\phi }) \frac{p^{n+1}-p^n}{\varDelta t} = \nabla \cdot \left( \left( \rho \frac{k}{\mu } \right) ^{n} (\nabla p^{n+1} - \rho ^{n} {\mathbf {g}} ) \right) + q_{TX}^{n} + Q^{n}, \end{aligned}$$

(9)

where $p^0$ is the initial pressure distribution, $\rho ^0,\; \beta _f^0,\; \mu ^0$ are the initial fluid properties, $\phi ^0,\;k^0$ are the initial rock properties, $q^0=0,\;Q^0=0$.

After the pressure calculation, the density is updated from the equation of state (Driesner 2007): $\rho ^{n+1/2} = \rho (p^{n+1},T^n, X^n)$ and stored for the calculation of $q_{TX}$.

The heat transport equation is solved using the finite volume method on a complementary sub-grid (Geiger et al. 2004):

$$\begin{aligned}&(\phi ^n \rho ^{n}\;c_{pf}^{n}+(1-\phi ^n)\rho _{r}c_{pr})\frac{T^{n+1} - T^{n}}{\varDelta {t}} \nonumber \\&\quad =\nabla \cdot \left( (\phi ^n K_f + (1-\phi ^n)K_r) \nabla T^{n+1} \right) - \nabla \cdot \left( {\mathbf {v}} \rho ^{n}\;c_{pf}^{n}\;T^{n+1} \right) , \end{aligned}$$

(10)

with $T^0$—initial temperature distribution.

After the pressure–temperature calculations, the transport–chemistry calculations are performed, and then the fluid properties: $\rho ^{n+1}\,c_{pf}^{n+1}$, $\mu ^{n+1}$, $\beta _f^{n+1}$ are updated using the equation of state, and new values for $q_{TX}^{n+1}$ and $Q^{n+1}$ are calculated.

3.2 Transport–Chemistry Coupling: Sequential Non-Iterative Approach

The transport Eq. (8) are solved using the sequential non-iterative approach (SNIA) (de Dieuleveult et al. 2009) in two steps:

$$\begin{aligned}&\displaystyle \phi ^{n} \frac{ \left( c^{n+1/2}_i - c^n_i\right) }{\varDelta t} + \nabla \cdot \left( {\mathbf {v}} c^{n+1/2}_i\right) - \nabla \cdot \left( D \nabla c^{n+1/2}_i\right) = 0, \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \phi ^{n} \frac{ \left( c^{n+1}_i - c^{n+1/2}_i\right) }{\varDelta t} = q^{n+1}_i,\;\forall i\in \overline{1,N}. \end{aligned}$$

(12)

This approach allows us to use the GEM chemical partial equilibrium solver as a “black box” to calculate the values for the chemical source $q_i$. The source term $q_i$ in (12) can be expressed as:

$$\begin{aligned} q_i^{n+1} = - \phi ^{n} \frac{f_i^{n+1} - f_i^{n}}{\varDelta t}, \end{aligned}$$

where $f_i$ is the amount of i-th IC in the solid phase per unit pore volume. The negative sign indicates that, as the amount of IC in the solid phase decreases, its amount in the aqueous phase increases, and vice versa.

Calculations are performed in the following way. First, Eq.  (11) are solved using the finite volume method. For each aqueous concentration $c_i$, a transport equation is solved on the entire grid. After that, Eq. (12) are solved using the GEM IPM3 algorithm implemented in the GEMS3K code. Chemical speciation calculations are performed for each finite volume independently. The new values for $c_i^{n+1}$ are computed from:

$$\begin{aligned} ({\mathbf {c}}^{n+1}, {\mathbf {f}}^{n+1}) = F({\mathbf {c}}^{n+1/2}+ {\mathbf {f}}^{n}), \end{aligned}$$

where F denotes the GEMS3K solver that takes as an input the vector of total concentrations (the sum of aqueous and solid concentrations) and yields the vectors of aqueous and solid concentrations: ${\mathbf {c}} = (c_1 \ldots c_{IC})$ and ${\mathbf {f}} = (f_1 \ldots f_{IC})$, respectively.

A new CSMP++ data structure—the Array Variable—is used to store the vectors ${\mathbf {c}}$ and ${\mathbf {f}}$ associated with the nodes. This vector structure allows efficient advective–diffusive transport and chemical speciation computations.

3.3 Porosity/Permeability Feedback from Reactions

The complete discrete form of the equation for species transport would be:

$$\begin{aligned} \frac{ \phi ^{n+1} c_i^{n+1} - \phi ^{n} c_i^{n}}{\varDelta t} + \nabla \cdot \left( {\mathbf {v}}_i c_i^{n+1}\right) - \nabla \cdot \left( D \nabla c_i^{n+1}\right) = - \frac{\phi ^{n+1}f^{n+1}_i - \phi ^n f^n_i}{\varDelta t}. \end{aligned}$$

In this work, we assume as a simplification that porosity is constant during the transport/chemistry computations, solving the following equation instead:

$$\begin{aligned} \phi ^{n} \frac{ {\tilde{c}}_i^{n+1} - c_i^{n}}{\varDelta t} + \nabla \cdot ({\mathbf {v}}_i {\tilde{c}}_i^{n+1}) - \nabla \cdot (D \nabla {\tilde{c}}_i^{n+1}) = - \phi ^{n} \frac{{\tilde{f}}^{n+1}_i - f^n_i}{\varDelta t}. \end{aligned}$$

(13)

After the transport step and the chemical equilibration step, the porosity is updated using the formula:

$$\begin{aligned} \phi ^{n+1} = 1 - V_\mathrm{inert} - \sum ^{N_\mathrm{min}}_{i=1} V^{n+1}_{\mathrm{min}_i}, \end{aligned}$$

where $V_\mathrm{inert}$ is the volume fraction of the non-reactive rock , $V^{n+1}_{\mathrm{min}_i}$ is the new volume fraction of the i-th mineral, calculated by multiplication of $f^{n+1}_i$ with the mineral molar volume, $N_\mathrm{min}$ is the number of minerals.

As a further simplification, the updated value of permeability is obtained from the Kozeny–Carman correlation (Bear 1972):

$$\begin{aligned} k^{n+1} = k^{n} \frac{(1-\phi ^{n})^2}{(1-\phi ^{n+1})^2} \frac{(\phi ^{n+1})^3}{(\phi ^{n})^3} \end{aligned}$$

(14)

The new porosity and permeability values are used in the pressure calculation (9) for the next time level.

In order to maintain the mass balance, the species concentrations $c_i$ and $f_i$ are rescaled with respect to the new porosity, before being used in the transport calculations for the following time step:

$$\begin{aligned} c_i^{n+1} = \frac{\phi ^{n}}{\phi ^{n+1}} {\tilde{c}}_i^{n+1}, \\ f_i^{n+1} = \frac{\phi ^{n}}{\phi ^{n+1}} {\tilde{f}}_i^{n+1}. \end{aligned}$$

3.4 Calculation of $q_{TX}$ and Q

After the transport and chemical speciation calculations are finished, the source terms are determined. The fluid expansion source is calculated from the change in fluid density due to temperature and salinity changes:

$$\begin{aligned} q_{TX}^{n+1} = - \phi ^{n+1} \frac{\rho ^{n+1} - \rho ^{n+1/2}}{\varDelta t} = - \phi ^{n+1} \frac{\rho (p^{n+1},T^{n+1},X^{n+1}) - \rho (p^{n+1},T^{n},X^{n})}{\varDelta t}, \end{aligned}$$

where density is calculated from the equation of state.

As stated above, the chemical source is calculated using the output data from GEMS3K:

$$\begin{aligned} Q^{n+1} = - \phi ^{n+1} \frac{\sum _{i=1}^{N} \left( f^{n+1}_i - f^{n}_i\right) M_i}{\varDelta t} , \end{aligned}$$

where $f^{n+1}_iM_i$ is the new mass of the i-th IC in the solid phase, $f^{n}_iM_i$ is its value at the previous time step.

3.5 Property Values Placement

As described above, porosity is updated based on the mineral amounts that are stored on the nodes, as a consequence of finite volume- (nodal-) based chemical calculations. There is no conservative way to interpolate/extrapolate porosity from the nodes to the elements and back. For this reason, both nodal and elemental porosity are stored. For the permeability update, porosity from the nodes is interpolated to the elements, and then the new element permeability values are calculated using Eq. (14).

The transient pressure Eq. (6) is solved using the linear finite element method. Within the finite element–finite volume framework of CSMP++, fluid properties are stored on the nodes (density, viscosity, fluid compressibility, fluid thermal expansion coefficient), and material properties (rock compressibility, permeability) are stored on the elements. In order to increase the accuracy of the finite element solution of the pressure equation, the following composite (involving node and element variables) properties:

$$\begin{aligned} \rho \phi ( \beta _f + \beta _{\phi }) \end{aligned}$$

—the total system mass compressibility,

$$\begin{aligned} \lambda = \rho \frac{k}{\mu } \end{aligned}$$

—the mass conductivity,

$$\begin{aligned} \rho \frac{k}{\mu } \rho {\mathbf {g}} \end{aligned}$$

—the mass gravity term, are stored on the element integration points. This process is exemplified for the calculation of mass conductivity in Fig. 2. Density and viscosity are placed on the nodes, and permeability is an elemental property. For each element integration point, the value of mass conductivity will be calculated from the density and viscosity values of the corresponding node and a permeability value that is constant on the element.

Fig. 2

Mass conductivity is placed on finite element integration points

Fig. 3

Total mass heat capacity is placed on the finite volume sector integration points

The advection–diffusion heat transport Eq. (7) is solved using the finite volume method, where the finite element integral corresponding to diffusion is accumulated into the same solution matrix (Matthai et al. 2009).

The total mass heat capacity, $C_t = \phi \rho c_{pf}+(1-\phi )\rho _{r}c_{pr}$, is stored on the finite volume sector integration points; the value from the upstream node is used for fluid mass heat capacity $\rho c_{pf}$ calculation. Figure 3 illustrates the calculation of the first, fluid-related term in total mass heat capacity ($\phi \rho c_{pf}$): finite elements are dashed line triangles; finite volume of the dual mesh is drawn in solid lines; porosity $\phi$, density $\rho$ and fluid heat capacity $c_{pf}$ are placed on the nodes; each finite volume sector has one integration point where $c_i = \phi _i \rho c_{pf}$ is stored. The second, rock-related term ($(1-\phi )\rho _r c_{pr}$) is interpolated from finite elements to the finite volume sector integration points.

4 Benchmarking Results

As a first step, CSMP++GEM was benchmarked against the OpenGeoSys-GEM coupled code (that also uses GEM-IPM3 as chemical solver) on a well-known calcite dissolution—dolomite precipitation benchmark without mineral dissolution/precipitation kinetics from Shao et al. (2009).

After that, CSMP++GEM was benchmarked against TOUGHREACT on a 1D dolomitisation model that accounts for kinetics of dolomite.

4.1 Dolomitisation by MgCl$_2$ Without Mineral Kinetics

The test model is a 1D porous medium column of 0.5 m length, with a bulk density $\rho _b=18{,}00$ kg/m$^3$ and porosity $\phi =0.32$. Fluid pressure of 1 bar and temperature of $25\,^\circ \hbox {C}$ are assumed. Pore fluid is initially equilibrated with calcite. The column is flushed from left to right with MgCl$_2$ solution at a flow rate $q = 3 \times 10^{-6}$ m/s, diffusion–dispersion coefficient D is equal to $2 \times 10^{-8}$ m$^2$/s. Initial and boundary concentrations for aqueous species and minerals are presented in Table 1 (Shao et al. 2009). Chloride does not react with solids, but serves as a tracer. Both calcite and dolomite are equilibrium-controlled minerals.

Table 1 Calcite–dolomite benchmark: aqueous and solid boundary and initial concentrations

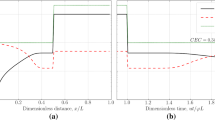
The model domain is discretised into 100 elements of equal length ($\varDelta x=0.005$ m) and a time step $\varDelta t=200$ s is used in the simulation. As the reaction front progresses, dolomite is formed temporarily as a moving zone, and calcite is dissolved. Simulation results after 21,000 s, compared with the results from Shao et al. (2009) for the concentrations of ions and minerals, are presented in Figs. 4 and 5, respectively. The results match well; minor deviations can be explained by different numerical methods used for transport calculations—finite element method (OpenGeoSys) and finite volume method (CSMP++).

Fig. 4

Calcite–dolomite benchmark: concentrations of Ca$^{2+}$, Mg$^{2+}$ and Cl$^-$ ions after 21,000 s

Fig. 5

Calcite–dolomite benchmark: concentrations of calcite and dolomite after 21,000 s

4.2 Dolomitisation by Sea Water with Mineral Kinetics

Following earlier 1D reactive transport simulations of dolomitisation in reflux systems using TOUGHREACT (Gabellone and Whitaker 2015), another 1D benchmark was created in order to compare these results with those obtained using the CSMP++GEM code. The goal was to simulate changes in the mineralogy of a limestone infiltrated by sea water, taking into account the reaction kinetics of dolomite. Kozeny–Carman correlation was applied for calculating the permeability evolution from changing porosity, supported by studies by Ehrenberg (2004, 2006) on Miocene carbonate platforms and Fabricius (2007) on North Sea chalk reservoirs. These studies have demonstrated that carbonates often show a porosity–permeability relationship following the ideal Kozeny–Carman curve, although this can break down, for instance where there is significant vuggy or microporosity.

4.2.1 Description

The simulation model is a 10-m-long vertical column, with a cross section of 1 m$^2$, divided into 50 cells ($\varDelta x = 0.2$ m). Rock properties are listed in Table 2. The initial mineral composition is 99% of calcite and 1% of dolomite. Calcite is under equilibrium control, whereas ordered dolomite is under kinetic control.

Table 2 Rock properties

The column is initially saturated with formation water, and “boundary condition” water is injected at the top. The normal sea water composition (3.5% salinity) was taken from Nordstrom et al. (1979), and is supersaturated to both calcite and dolomite. The initial water composition was derived from this model sea water by equilibrating it with calcite and ordered dolomite, while the boundary water was equilibrated with calcite only.

A thermodynamic database suitable for both CSMP++GEM and TOUGHREACT was not available, and therefore two different databases presenting quite close equilibrium constants for dolomite and calcite (see Table 3) were used. The PSI/Nagra thermodynamic database (Thoenen et al. 2014) was used to prepare the CSMP++GEM input in GEM-Selektor and in the simulation runs, while the THERMODDEM database (Blanc et al. 2012) was used in the TOUGHREACT simulations.

The extended Debye–Huckel activity model with parameters derived by Helgeson et al. (1981) was used in both software packages. Initial and boundary water compositions for CSMP++GEM and TOUGHREACT at $30\,^\circ \hbox {C}$ (in TOUGHREACT input format) are listed in Tables 4 and 5.

Table 3 Thermodynamic data comparison: equilibrium constants at 1 bar, $25\,^\circ \hbox {C}$

Table 4 Initial water compositions for CSMP++GEM and TOUGHREACT runs at 1 bar, $30\,^\circ \hbox {C}$: basic species molalities

Table 5 Boundary water compositions for CSMP++GEM and TOUGHREACT runs at 1 bar, $30\,^\circ \hbox {C}$: basic species molalities

As the precipitation rate of dolomite is very slow at these given temperature conditions (5–6 orders of magnitude less than the dissolution rate of calcite or dolomite), calcite can be assumed to dissolve or precipitate instantly, and thus should be considered as an equilibrium-controlled phase.

We used the kinetic rate of dolomite precipitation:

$$\begin{aligned} r=\kappa A(1-\varOmega ^\theta )^\eta , \end{aligned}$$

where $\kappa$ is the rate constant, A is the reactive surface area, $\varOmega$ is the mineral saturation ratio, $\theta$ and $\eta$ are empirical parameters, and the values of corresponding parameters from Arvidson and Mackenzie (1999). This ensures that simulations are consistent with previous RTM simulations of dolomitisation (Wilson et al. 2001; Jones and Xiao 2005; Al-Helal et al. 2012; Gabellone and Whitaker 2015).

TOUGHREACT has the following built-in temperature correction for the rate constant:

$$\begin{aligned} \kappa =\kappa ^{o} e^{\frac{-E_a}{R}}\left( \frac{1}{T} - \frac{1}{298.15}\right) , \end{aligned}$$

whereas in CSMP++GEM a slightly different but equivalent formulation is used:

$$\begin{aligned} \kappa ={\tilde{\kappa }}^{o}\varLambda e^{\frac{-E_a}{RT}}, \end{aligned}$$

where $E_a$ is the activation energy, $\kappa ^{o}$ and ${\tilde{\kappa }}^{o}$ are rate constants at $25\,^\circ \hbox {C}$, $\varLambda$ is the Arrhenius parameter, R is the universal gas constant. Kinetic parameters for dolomite precipitation are listed in Table 6, and values for the rate constant at $30\,^\circ \hbox {C}$ are compared. A constant specific reactive surface area of 1000 m$^2$/kg was assumed, corresponding to small dolomite rhombs (2.5 $\upmu$m).

Table 6 Kinetic rate parameters for ordered dolomite

The system was assumed to be isothermal; simulations were performed at 30, 40 and $50\,^\circ \hbox {C}$. Dirichlet boundary conditions for pressure at the top and the bottom of the column were assigned, resulting in a flow rate of $\sim$1 m/year ($2.79 \pm 0.25 \times 10^{-8}$ m/s). Essential conditions for the flow simulation are listed in Table 7. In the TOUGHREACT runs, top and bottom cells were infinite volume cells; in CSMP++GEM, Dirichlet boundary conditions were assigned for species concentrations at both column ends. In CSMP++GEM simulations, thermophysical properties of sea water were taken from the equation of state for brine from (Driesner 2007). In TOUGHREACT, the EOS7 module (water, brine, air) was used (Pruess 1991).

Table 7 Essential conditions for the flow simulation

In the RTM simulations, two different time steps were used. In the main time loop, a time step of 10 years was employed, and in the inner loop (solute transport and chemistry), the time increment was chosen according to the Courant–Friedrichs–Lewy (CFL) condition. This is a necessary condition for the convergence of SNIA, as with a $\varDelta t = CFL$ the fluid will move no more than one cell at a time, so it is guaranteed that in the subsequent chemistry calculation the fluid will have had a chance to react with the rock before it leaves the cell.

4.2.2 Results

Three sets of simulations for 30, 40 and $50\,^\circ \hbox {C}$ were performed in CSMP++GEM and TOUGHREACT, and the results were compared after 10k years. Figure 6 shows the results of the simulation at $50\,^\circ \hbox {C}$. Within the first metre of the column, some boundary effects occurred, due to the fact that in both codes the boundary water was slightly undersaturated with respect to calcite and therefore a higher amount of calcite (compared to the rest of the column) dissolved in the first few cells adjacent to the column top.

Apart from the first metre from the top, the changes in mineral amounts are almost constant across the column. After the first few years of injection, the water composition becomes approximately the same along the whole column. Consequently, the kinetic rate of dolomite precipitation and the resulting rate of calcite dissolution are constant, indicating flow rates are high relative to reaction rates. The amount of dissolved calcite is approximately two times greater than the amount of precipitated dolomite, consistent with the stoichiometric assumption, i.e. that two moles of calcite are consumed to form one mole of dolomite.

Fig. 6

Results of the simulation at $50\,^\circ \hbox {C}$: changes in mineral amounts after 10k years

The porosity evolution is shown in Fig. 7. After such a short (in geological timescale) period of time, the change in porosity is minor; the slight increase is due to the differences in molar volumes of calcite and dolomite.

Fig. 7

Results of the simulation at $50\,^\circ \hbox {C}$: porosity after 10k years

Table 8 Results of the simulations at three different temperatures: amount of calcite dissolved, amount of dolomite precipitated and change in porosity

Table 8 compares the results of the simulations at 30, 40 and $50\,^{\circ }\mathrm {C}$, presenting the average values of calcite dissolved, dolomite precipitated, and porosity increase across the column after 10k years of simulation time. The changes in mineral amounts and change in porosity increase by a factor of 8–9 with a change of 10$^{\circ }$ in temperature. These results agree with the saturation indices for dolomite (boundary water) at different temperatures (Table 9), and with the acceleration of dolomite precipitation rates at increasing temperature (Eq. 24). At all three temperatures, calcite dissolution is driven by dolomite growth, and the ratio between the amount of calcite dissolved and dolomite precipitated remains approximately equal to 2. After such a short time, calcite remains dominant (98.6% of mineral phase after 10k years) and dolomitisation rate is limited by reactive surface area.

Table 9 Saturation indices for dolomite at different temperatures

Results using the two different simulators are similar, and minor differences can be explained by (1) different numerical methods for flow and transport (finite difference method in TOUGHREACT and finite element–finite volume method in CSMP++GEM), (2) different numerical methods for chemical reactions (law of mass action in TOUGHREACT and Gibbs energy minimisation in CSMP++GEM), (3) different thermodynamic databases and small differences in aqueous activity models and mineral kinetic rate models, (4) differences in equations of state for the aqueous fluid.

For the $50\,^\circ \hbox {C}$ case, the simulations were run for 200k years, and the evolution of the mineral composition and porosity in two cells with a distance of 1 and 5 m from the top of the column was traced.

Figure 8 shows the changes in mineral amounts in the cell located at 1 m distance from the injection point. Simulations with both codes result in a similar behaviour. The dolomite growth rate (in mol/m$^2$/s) is a function of specific dolomite reactive surface area, temperature and dolomite saturation index. The amount of precipitated dolomite is, however, a function of the total reactive surface area (specific RSA multiplied by the dolomite mass) and therefore a nonlinear function of time. Calcite dissolution and dolomite precipitation occur simultaneously as calcite dissolution is driven by the reduction in Ca$^{2+}$ in the fluid during dolomite precipitation. At the time when all calcite is replaced by dolomite, the amount of precipitated dolomite is equal to half of the original calcite. After all the calcite has dissolved, dolomite continues to precipitate from the aqueous solution at a linear rate determined solely by the degree of the solution oversaturation with respect to dolomite.

Fig. 8

Results of the simulation at $50\,^\circ \hbox {C}$: changes in mineral amounts, plot over time of 200k years at $x=1$ m from the column top

The porosity evolution in the cell located at 1 m distance from the injection point is presented in Fig. 9. After a period of very slow dolomitisation at the start of the replacement phase, the dolomite precipitation rate increases nonlinearly with the increase in reactive surface area (the dolomite saturation index stays constant) and porosity increases from 40 to 47% in CSMP++GEM and to 50% in TOUGHREACT from an initial value of 40%. The highest porosity value coincides with the time of the total calcite replacement, after which porosity starts to decrease due to the formation of dolomite cement.

Fig. 9

Results of the simulation at $50\,^\circ \hbox {C}$: changes in porosity, plot over time of 200k years at $x=1$ m from the column top

At the end of the 200k years simulation, overdolomitisation (primary precipitation of dolomite cement) reduces porosity to 42% in CSMP++GEM and to 47% in TOUGHREACT at the distance of 1m from the top of the column. However, the rate of overdolomitisation is similar in the two models, with porosity reduction at a rate of 0.09%/kyr (CSMP++GEM) and 0.08%/kyr (TOUGHREACT) (calculated from the linear part of the porosity graphs from Fig. 9).

Figure 10 shows the changes in mineral amounts in the cell located at 5 m distance from the model top. In contrast to the cell close to the top of the column (Fig. 8), in the middle of the column almost no overdolomitisation occurs following complete replacement of the calcite, because the solution is depleted in ions by prior precipitation next to the column top. After the complete calcite replacement, dolomite amount in the middle of the column remains nearly constant. Comparing the graphs in Figs. 8 and 10, it can be seen that the time to complete calcite dissolution increases with the distance from the top of the column.

Fig. 10

Results of the simulation at $50\,^\circ \hbox {C}$: changes in mineral amounts, plot over time of 200k years at $x=5$ m from the column top

Changes in porosity in the middle cell are presented in Fig. 11. In agreement with Fig. 10, porosity decreases only slightly after achieving its maximum value, indicating that overdolomitisation takes place close to the injection point and only minor amounts of dolomite cement are present at the 5 m distance from the model top.

Fig. 11

Results of the simulation at $50\,^\circ \hbox {C}$: changes in porosity, plot over time of 200k years at $x=5$ m from the column top

Although the results presented above are in a good agreement during the first 50k years of simulation time (replacement of the first 2–3% of calcite), they progressively diverge thereafter as the amount of precipitated dolomite increases with the increasing total dolomite reactive surface area and the differences between the kinetic rates in two codes get more prominent. The time point of complete calcite replacement is about 25k years delayed for the TOUGHREACT simulation as compared with CSMP++GEM. In the middle of the column, the match between the two codes is closer than at the distance of 1 m. This example shows how even small differences in activity and kinetic rate models can lead to significant differences between model predictions over geological times.

5 Conclusions

The new CSMP++GEMS coupled code is a new tool for reactive transport modelling that allows to take into account mineral dissolution/precipitation kinetics. It differs from RTM codes due to the combination of the finite element–finite volume method for the solution of flow and transport equations and the Gibbs energy minimisation method for chemical equilibrium calculations.

A new reactive transport code CSMP++GEM was benchmarked against OpenGeoSys-GEM and TOUGHREACT. Differences (especially regarding calcite dissolution) can be rationalised in terms of differences in numerical methods for flow (finite element–finite volume vs. finite differences) and chemistry (law of mass action vs. Gibbs energy minimisation), equations of state, kinetic rate models.

The CSMP++GEM coupled framework permits to represent the following effects of dolomitisation. At the replacement stage, the amount of precipitated dolomite is equal to the half of the dissolved calcite; porosity increases in the whole model during the mole per mole replacement, but is subsequently plugged by dolomite cementation in the first few cells close to the model top. Calcite dissolution is a reactive transport phenomenon driven by a slow dolomite precipitation. The models show that the rate of dolomitisation by replacement of calcite increases by factor of 9 with an increase of $10\,^\circ \hbox {C}$ in temperature.

The development of the CSMP++GEM code has just started, there are still many improvements to be made. The use of the sequential iterative approach can increase solution accuracy, but the simulation time will grow proportionally to the number of SIA iterations. Adaptive time stepping, if implemented in the numerical integration of kinetic rates, similar to (Leal et al. 2015), might make the numerical solution more stable. Kinetic rates of mineral precipitation/dissolution depend on the mineral saturation index, time and mineral reactive surface area. Specific surface area correction upon growth or dissolution dependent on the particle/pore size distribution, particle/pore size evolution and shape factor should be implemented in the future, which will make the model more realistic.

The results of this work illustrate the challenges faced when comparing RTM software that uses different methods for transport and chemistry and different thermodynamic databases. The match between two codes is reasonably close, but it can be seen that the discrepancy grows proportional to the increasing amount of precipitated dolomite.

The RTM simulator presented in this paper can be used to check the existing conceptual models of dolomitisation, by trying to reproduce the patterns observed in the case studies and outcrop analogues. The new coupled CSMP++GEM code has proven itself reliable through testing and benchmarking and can be applied to simulations of more complex systems.

Appendices

Appendix 1: Gibbs Energy Minimisation Method

The GEM IPM3 algorithm (Kulik et al. 2013), as implemented in the GEM software (http://gems.web.psi.ch), is capable of thermodynamic modelling of partial equilibria controlled by mineral–water reaction kinetics with multiple reaction pathways. In GEM IPM3, the chemical system is defined by a bulk composition vector, $n^{(b)}$, specifying the input amounts of chemical elements and charge; the standard Gibbs energy per mole for all dependent components (DC, chemical species), $g^o$, at T, p of interest; the parameters of (non)ideal models of mixing in solution phases (Wagner et al. 2012) needed to calculate the activity coefficients $\gamma _j$ of DCs indexed with j; and additional metastability restrictions (AMR) on mole amounts of some DCs in some phases.

The GEM problem consists in finding the (unknown) equilibrium speciation $n^{(x)}$ and phase amounts $n^{(\phi )}$ in the system at p, T, and bulk composition $n^{(b)}$ (i.e. mole amounts of ICs). The number of elements in $n^{(b)}$ vector is n(N), i.e. the number of ICs including the charge; the size of $n^{(x)}$ vector is n(L), i.e. the total number of DCs in all phases.

1.1 The Gibbs Energy Minimisation Problem

Find $n^{(x)} = \left\{ n^{(x)}_j, j\in L \right\}$ such that

$$\begin{aligned} G(n^{(x)}) = \min \left\{ G(n^{(x)}): n^{(x)} \in M_1 \right\} , \nonumber \\ M_1=\left\{ n^{(x)} \in R_1: An^{(x)}=n^{(b)} \right\} , \end{aligned}$$

(15)

where $A=\left\{ a_{ij}, i \in N, j \in L \right\}$ is a matrix composed of the stoichiometry coefficients of ICs in the formulae of DCs; L is the set of n(L) DC indices; $R_1$ is the set of constraints on $n^{(x)}$ composed of trivial non-negativity constraints (set $D_0$), and optional two-side AMRs (set $D_3$),

$$\begin{aligned} R_1 = \left\{ n^{(x)}: \begin{matrix} n^{(x)}_j &{} \ge &{} 0, &{} j \in D_0 \\ {\underline{n}}^{(x)}_j &{} \le &{} n^{(x)}_j \le {\overline{n}}^{(x)}_j, &{} j \in D_3 \end{matrix} \right\} \end{aligned}$$

and sets of indices $D_0, D_3$ are such that $L=D_0 \bigcup D_3$ (Karpov et al. 2001; Kulik et al. 2013). Note that ${\underline{n}}^{(x)}_j \ge 0$; ${\overline{n}}^{(x)}_j \ge 0$, and ${\overline{n}}^{(x)}_j \ge {\underline{n}}^{(x)}_j$.

The normalised total Gibbs energy of the chemical system is a scalar:

$$\begin{aligned} G\left( n^{(x)}\right) = \sum _j {n}^{(x)}_j \mu _j,\,j \in L, \end{aligned}$$

where $\mu _j$ is the normalised chemical potential of the j-th dependent component, written in a simplified dimensionless form as:

$$\begin{aligned} \mu _j = \frac{g^o_j}{RT} + \text {ln} C_j + \text {ln} \gamma _j + \varXi , \, j \in L, \end{aligned}$$

(16)

with $g^o_j$ is the standard chemical potential (Gibbs energy per mole) of j-th DC at p, T of interest; R is the universal gas constant (8.31451 J/K/mol), and $C_j=f({n}^{(x)}_j)$ is the j-th DC concentration relative to the standard concentration scale for the respective phase. For a DC in k-th condensed non-electrolyte solution phase, and for the water–solvent in aqueous electrolyte, $C_j$ is defined as mole fraction $x_j$:

$$\begin{aligned} C_j = x_j = \frac{{n}^{(x)}_j}{n^{(\phi )}_k} = \frac{{n}^{(x)}_j}{\sum _{jp}{n}^{(x)}_{jp}},\quad jp \in l_k, \end{aligned}$$

(17)

where $l_k$ is the subset of indices of all DCs belonging to the k-th phase. For an aqueous electrolyte species (not water–solvent), concentration is defined as molality $m_j$ (moles per kilogram of water–solvent),

$$\begin{aligned} C_j = m_j = \frac{1000}{18.0153} \cdot \frac{x_j}{x_{jw}},\quad j,jw \in l_{aq}, \end{aligned}$$

(18)

where jw is the index of water–solvent, 18.0153 is the molar mass of water in g/mol, and $l_{aq}$ is the subset of indices of DCs in the aqueous electrolyte phase. For gas or plasma or gaseous fluid DCs with indices belonging to the subset $l_g$, the concentration is partial pressure,

$$\begin{aligned} C_j = x_jp,\,j \in l_g, \end{aligned}$$

and for any DC forming a stable pure-substance phase, the concentration is unity,

$$\begin{aligned} C_j = x_j =1,\,j \in l_k\, \text { and }\,n(l_k)=1. \end{aligned}$$

The activity coefficient $\gamma _j$ of the j-th DC in its respective phase is obtained from the chosen model of non-ideal mixing (details in Wagner et al. (2012)). The non-logarithmic asymmetry term $\varXi$ is

$$\begin{aligned} \varXi =1-x_{jw},\quad \forall j \in l_{aq} {\textbackslash } jw \end{aligned}$$

for the aqueous species,

$$\begin{aligned} \varXi =2-x_{jw} - 1/x_{jw},\quad jw \in l_{aq} \end{aligned}$$

for the water–solvent, while $\varXi =0$ for components of condensed mixtures, gaseous, and pure-substance phases (Karpov et al. 2001).

The convex set $M_1$ is called a feasible domain, composed of the system of mass balance constraints, with additional set of constraints $R_1$. If only trivial non-negativity constraints are present in the $R_1$ set, i.e. $D_3 = \varnothing$, then the speciation vector ${\widehat{n}}^{(x)}$ will be the primal solution of the problem (15) only if such a dual solution vector ${\widehat{u}}$ exists such that Karush–Kuhn–Tucker (KKT) necessary and sufficient conditions (written in vector–matrix notation) are satisfied:

$$\begin{aligned} \mu - A^T {\widehat{u}}\ge & {} 0, \nonumber \\ A {\widehat{n}}^{(x)} = n^{(b)},\,{\widehat{n}}^{(x)}\ge & {} 0,\nonumber \\ {\widehat{n}}^{(x)}\left( \mu - A^T {\widehat{u}}\right)= & {} 0, \end{aligned}$$

(19)

where $\,\widehat{ }\,$ denotes optimal. For components with two-side AMRs ($D_3 \ne \varnothing$), the extended KKT conditions (Karpov et al. 2001; Kulik et al. 2013) must be satisfied:

$$\begin{aligned} \mu - A^T {\widehat{u}} + {\widehat{q}}\ge & {} 0,\\ A {\widehat{n}}^{(x)} = n^{(b)},\,{\widehat{n}}^{(x)}\ge & {} 0, \\ \left( {\underline{n}}^{(x)}-{\widehat{n}}^{(x)}\right) \left( \mu - A^T {\widehat{u}} + {\widehat{q}} \right)= & {} 0, \\ {\widehat{q}} \ge 0, \left( {\widehat{n}}^{(x)}-{\overline{n}}^{(x)}\right) {\widehat{q}}= & {} 0, \end{aligned}$$

where ${\widehat{q}}$ is a vector of Lagrange multipliers conjugate to AMRs, and ${\underline{n}}^{(x)}$, ${\overline{n}}^{(x)}$ are vectors of lower and upper AMRs, respectively. These KKT conditions are used by the IPM3 algorithm (Kulik et al. 2013) to iteratively find accurate and precise primal ${\widehat{n}}^{(x)}$ and dual ${\widehat{u}}$ optimal solutions of the GEM problem.

The first condition from (19), rewritten with indices using (16)

$$\begin{aligned}&\frac{g^o_j}{RT} + ln C_j + ln \gamma _j + \varXi - {\widehat{\eta }}_j \ge 0, \nonumber \\&\quad j \in L, \, i \in N, \end{aligned}$$

(20)

implies that, for a j-th DC present in some equilibrium concentration $C_j \ge 0$ in its phase, the primal chemical potential $\mu _j$ must numerically equal the dual chemical potential ${\widehat{\eta }}_j$:

$$\begin{aligned} {\widehat{\eta }}_j = \sum _i a_{ij} {\widehat{u}}_i, \, j \in L, \, i \in N. \end{aligned}$$

(21)

After a GEM run has converged (see more about the GEM IPM3 algorithm in GEMS3K code and its performance compared with LMA codes in Kulik et al. (2013)), the results, namely the primal speciation vector ${\widehat{n}}^{(x)}$ and the dual vector ${\widehat{u}}^{(b)}$ of chemical potentials of chemical elements and charge, provide for concentrations, activities and amounts of all components in each phase.

The stability index $\varOmega _k$ of any phase, even of that absent from the mass balance, is found as a sum of anticipated mole fractions ${\widehat{x}}_j$ of all DCs belonging to this phase:

$$\begin{aligned}&\varOmega _k = \sum _j {\widehat{x}}_j = \sum _j \hbox {exp} \left( {\widehat{\eta }}_j - g^o_j/RT - \text {ln} \gamma _j - \varXi _k \right) , \nonumber \\&\quad j \in l_k. \end{aligned}$$

(22)

Equation (22) follows from combining Eqs. (20, 21), with (17) or (18).

Appendix 2: Modelling Kinetics as Partial Equilibrium

In the GEM IPM3 algorithm, the $\varOmega _k$ index (Eq. 22), which has the physical meaning of a saturation index of a (mineral) phase, is used as a criterion for checking the stability of any phase. If $-\epsilon< \hbox {log}_{10} \varOmega _k < \epsilon$, then the non-negative amount of this phase is in equilibrium with the rest of the system with a numerical tolerance $0< \epsilon \ll 1$. If $\hbox {log}_{10} \varOmega _k < \epsilon$, then the phase is unstable (undersaturated), but may be kept in the mass balance by the lower AMR(s) ${\underline{n}}^{(x)}_j>0$ set on some of its components. If $\hbox {log}_{10} \varOmega _k > \epsilon$, then the phase is over-stable (oversaturated) due to a positive or zero upper AMR(s) ${\overline{n}}^{(x)}_j>0$ set on some or all of its components.

Overall, the GEM output phase stability index $\varOmega _k$ together with input AMRs make the GEMS3K code a versatile tool for simulating phase metastability and kinetics as a series of partial equilibrium states. Thus, lower-AMRs allow stepwise simulation of dissolution of a mineral as long as its $\varOmega _k < 1$; upper AMRs allow stepwise simulation of mineral precipitation as long as $\varOmega _k > 1$. In this way, it is possible to model the kinetics of mineral–aqueous reactions and of trace element uptake (Thien et al. 2014).

In a sequence of partial equilibria, each AMR can be set as a function of the time step duration $\varDelta t$, the time variable t, the surface area $A_{k,t}$ of k-th solid phase, and the (absolute) net kinetic rate $R_{n,k,t}$. In a stepwise simulation, the mole amount $n_{k,t+\varDelta t}$ of the mineral at time $t+\varDelta t$ is set by the upper AMR ${\overline{n}}_{k,t+ \varDelta t}$ for precipitation or by the lower AMR ${\underline{n}}_{k,t+ \varDelta t}$ for dissolution:

$$\begin{aligned} {\overline{n}}_{k,t+ \varDelta t}= & {} n_{k,t} + A_{k,t}R_{k,t} \varDelta t \text { if } \hbox {log}_{10}\varOmega _k > \epsilon \\ {\underline{n}}_{k,t+ \varDelta t}= & {} n_{k,t} - A_{k,t}R_{k,t} \varDelta t \text { if } \hbox {log}_{10}\varOmega _k <- \epsilon \end{aligned}$$

The surface area of k-th solid phase is obtained as

$$\begin{aligned} A_{k,t} = A_{S,k}M_{M,k}n_{k,t}, \end{aligned}$$

where $A_{S,k}$ is the input specific surface area (m$^2$/kg); $M_{M,k}$ is the molar mass (kg/mol); and $n_{k,t}$ is the current amount (mol) of the k-th phase.

Implementation of metastability and kinetics differs from code to code; so far, there is no conventional data structure for kinetic rate parameters. Because the experimental rate constants are typically normalised per unit area, they must be scaled by the current reactive surface area of the mineral, which depends on many factors, some of them are external to the chemical system, and some are related to the particle/pore morphology, initial size distributions, and surface roughness. This is in focus of current research efforts in geochemistry of mineral water interfaces (Marini et al. 2000; Scislewski and Zuddas 2010; Mironenko and Zolotov 2012).

Kinetic rate laws usually contain the so-called activity product term related to a particular reaction mechanism, catalysis, inhibition, etc. (Palandri and Kharaka 2004; Schott et al. 2012). Near-equilibrium kinetic rates also depend on the affinity term based on the phase stability index $\varOmega _k$. Particular forms of this term reflect different nucleation, growth or dissolution mechanisms (Schott et al. 2012).

Some relevant kinetic rate equations for dissolution, precipitation and trace element uptake in solid solutions have been implemented in the TKinMet code library used in the GEM-Selektor and the GEMS3K codes (Kulik et al. 2012; Thien et al. 2014). The mineral–water kinetic rate laws are considered in the general form (with input parameters implemented in phase definition records):

$$\begin{aligned} \frac{dn_k}{dt} = A_{k,t}R_{k,t} = -A_{k,t} \sum _{r}^{N(r)_k} {\theta _{k,r,t}f_1(\kappa ,E)_{k,r}f_2(\varPi a)_{k,r,t}f_3(\varOmega )_{k,r,t}} \end{aligned}$$

(23)

where k is the index of solid phase of interest (pure solid or solid solution); $n_k$ is the mole amount of k-th phase at time t; $A_{k,t}$ is the current surface area of the phase in m$^2$; $R_{n,k,t}$ is the total precipitation or dissolution rate (in mol/m$^2$/s); $N(r)_k$ is the number of parallel reaction mechanisms or pathways that affect the amount of k-th phase; r is the index of a mechanism or pathway (dissolution, nucleation and precipitation can be treated simultaneously as different mechanisms); $\theta _{k,r,t}$ is the effective fraction of surface area of k-th phase assigned to the r-th reaction mechanism.

Time-dependent parameters $A_{k,t}$ and $\theta _{k,r,t}$ may either depend on a built-in model of particle size/area evolution or be externally controlled from the mass transport code.

In Eq. (23),

$$\begin{aligned} f_1(\kappa ,E)=\kappa ^o_{k,r} \varLambda _{k,r} e^{\frac{-E_{k,r}}{RT}} \end{aligned}$$

(24)

is the reaction rate constant term including the temperature correction, where: $\kappa ^o_{k,r}$ is the rate constant at reference temperature ($25\,^\circ \hbox {C}$) in (mol/m$^2$/s) or other appropriate units, having positive sign for dissolution and negative sign for precipitation; T is the temperature in K; $\varLambda _{k,r}$ is the Arrhenius factor (1 by default); and $E_{k,r}$ is the activation energy (J/mol) of r-th reaction mechanism.

The expression $e^{\frac{-E_{k,r}}{RT}}$ in Eq. (24) occurs in the literature in a different form $e^{\frac{-E^{*}_{k,r}}{R}(\frac{1}{T}-\frac{1}{298.15})}$ that involves the reference temperature 298.15 K (Palandri and Kharaka 2004). Both forms are connected as:

$$\begin{aligned} \varLambda _{k,r} e^{\frac{-E_{k,r}}{RT}} = \varLambda ^{*}_{k,r} e^{\frac{-E^{*}_{k,r}}{R}\left( \frac{1}{T}-\frac{1}{298.15}\right) }, \end{aligned}$$

where

$$\begin{aligned} \varLambda _{k,r} = \varLambda ^{*}_{k,r} e^{\frac{-E^{*}_{k,r}}{R \cdot 298.15}} \end{aligned}$$

and $E^{*}_{k,r} = E_{k,r}$.

In Eq. (23), $f(\varPi a)_{k,r,t}$ is the activity product term

$$\begin{aligned} f_2(\varPi a)_{k,r,t}= & {} I^{b_{I,k,r}} pH^{b_{pH,k,r}} pe^{b_{pe,k,r}} Eh^{b_{Eh,k,r}}\nonumber \\&\quad \times \left( \prod _{j}^{n(j)_{k,r}} a^{b_{j,k,r}}_{j,k,r}\right) ^{p_{k,r}} \end{aligned}$$

(25)

is the current (at time t) activity product term, combined to accommodate most of the literature rate laws, where: I is the (effective molal) ionic strength; $b_{I,k,r}$ is the related empirical parameter; $b_{pH,k,r}$ is the empirical parameter related to pH; $b_{pe,k,r}$ is the parameter related to pe; $b_{Eh,k,r}$ is the parameter related to Eh, (V); $p_{k,r}$ is the reaction order parameter; $n(j)_{k,r}$ is the number of (aqueous or gaseous or surface) species from other reacting phases involved; $a_{j,k,r}$ is the activity (fugacity) of j-th species ($a_{H+} = 10^{-pH}, a_e = 10^{-pe})$; $b_{j,k,r}$ is the (reaction stoichiometry coefficient) parameter. Note that in Eq. (25), any term can be disabled, if the respective power coefficient is set to the default value of zero.

Finally, in Eq. (23), $f(\varOmega _{k,r})$ is the affinity term for r-th reaction, which can take several different forms, all using the current (at time t) k-th phase stability index $\varOmega _k$ (Eq. 22). The classic affinity term is taken in the form

$$\begin{aligned} f_3(\varOmega _{k,r}) = \left( 1+u_{k,r}-\varOmega _{k}^{q_{k,r}} \right) ^{m_{k,r}}, \end{aligned}$$

where $q_{k,r}$ and $m_{k,r}$ are the reaction order parameters (default 1; $m_{k,r} = 0$ disables the affinity term); and $u_{k,r}$ is the empirical parameter (default 0).

In Eq. (23), the net rate $R_{k,t}$ is taken in (mol/m$^2$/s) by default. However, in many models of mineral dissolution or growth (Wolthers et al. 2012; Nielsen et al. 2013), the mean orthogonal velocity of surface propagation $R_{L,k,t}$ in (m/s) is considered. $R_{L,k,t}$ is related to $R_{k,t}$ as

$$\begin{aligned} R_{L,k,t} = V_{M,k} R_{k,t} = \frac{M_{M,k}}{\rho _k} R_{k,t}, \end{aligned}$$

where $V_{M,k}$ is the molar volume in m$^3$/mol; $M_{M,k}$ is the molar mass in kg/mol; and $\rho _k$ is the density in kg/m$^3$ of the mineral phase.

Specific surface area of the mineral is defined as $A_{S,k} = A_k/m_k$ in (m$^2$/kg) or $A_{V,k} = A_k / V_k$ in (1/m). Upon growth or dissolution, both $A_{S,k}$ and $A_{V,k}$ values vary with time because of changing particle size, shape and surface roughness. Hence, specific surface areas must be corrected after each time step, either internally in TKinMet functions, or externally by the reactive transport model.

Some parameters, e.g. the dissolution rate constant, the activation energy, the reaction type and order constants for parallel mechanisms, can be considered as chemical properties of the solid phase, kept in the respective phase definition record in GEM-Selektor project database or in GEMS3K input file. Other, “non-chemical” parameters, such as the reactive specific surface area assigned to r-th mechanism, are related to evolving particle or pore size and shape distributions. Such varying parameters should come at each time step into TKinMet calculations from the transport part of the coupled RTM code.