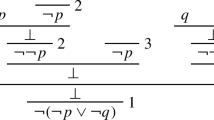On ground and consequence

Abstract

What does it mean that some proposition follows from others? The standard way of spelling out the notion proceeds in modal terms: x follows from y iff necessarily, if y is true, so is x. But although this yields a useful and manageable account of consequence, it fails to capture certain aspects of our pre-theoretical understanding of consequence. In this paper, an alternative notion of logical consequence, based on the idea of grounding, is developed.

1 Introduction

1.1 Modality and source

Analytic philosophy has long overcome its fear of modality. Quinean scepticism concerning modality had been a dominant influence for some decades, but the success of modal logic rehabilitated modal concepts for a broader use in philosophy. Many explications of core philosophical notions were then put forth using modal concepts as their substantial ingredients. To cite but three prominent cases, the following explications became standard proposals in metaphysics¹:

Mod.1:

x makes y true ↔ necessarily, if x exists, y is true

Mod.2:

x essentially has property y ↔ necessarily, if x exists, x has y

Mod.3:

x existentially depends on y ↔ necessarily, if x exists, so does y

The popularity of such explications rests on at least three factors: First, the explications manage to correctly categorise many central examples. Second, their rationale has an intuitive appeal to many philosophers, as they take the very point of such notions to consist in characterising not how things actually are, but how they might or must have been. Third, the explications have proven very useful because they allow us to adopt the technical apparatus of modal logic in order to systematically examine the explicated concepts.

Nevertheless, it has been argued that some conceptual residue of the target notions of truth-making, essence, etc. remains for which the modal explications cannot account. This conceptual loss shows up in a special sort of counterintuitive classifications to which the modal accounts would commit us. Take for illustration a stock example from the debate about truth-makers: Since it is a necessary truth that bachelors are bachelors, it is necessary that if Greg’s fridge exists, bachelors are bachelors. And since it is necessary that 2 + 2 = 4, it is necessary that if Greg’s fridge exists, 2 + 2 = 4. And yet, it seems more than odd to say that the fridge makes it true that bachelors are bachelors, or that it makes it true that 2 + 2 = 4. Modern fridges may have fancier features than the fridges of our ancestors, but to render mathematical propositions true is still not among those features.

Similar examples have been given concerning dependence and essence. To name but one (see Fine 1994, 1995), while Socrates and his singleton plausibly exist in exactly the same possible worlds, the set seems to existentially depend on the man in a way in which he does not depend on the set. And while, given the said assumption, it is necessary that if the man exists, he is a member of his singleton, one may yet deny that the said set-membership is part of his essence.

Apart from producing intuitive counterexamples to the modal explications, their critics have also tried to pin down what aspect of our pre-theoretical understanding got lost. One way of doing so mobilizes a concept of source. Thus, people clearly connote with the concept of making an idea of source or responsibility: if x makes y such-and-so, x should intuitively count as the source of y’s being so, as being responsible for y’s being so.² The same seems to hold of at least one understanding of ‘existential dependence’, so that a dependent entity should owe its existence to that on which it depends. And in his well-received attack on a modal explication of essence, Fine (1994: p. 8f.) also relied on considerations of source: essential truths about an object should have their source in that object. This aspect of the target concepts gets lost once we accept their modal explications. For, there can be necessary connections between facts or things where the source of those connections has nothing, or at least not the right thing, to do with the facts or things in question. Such considerations can then be used to explain the oddity of the cited counter-examples to the modal accounts: while the existence of Greg’s fridge may be necessarily accompanied by the truth of the proposition that 2 + 2 = 4, it is certainly not the source of that truth.

So, unsurprisingly, alternative accounts of the notions of truth-making, dependence, and essence have been developed which are based on the idea that a notion stronger than modality is needed if we want to do full justice to our pre-theoretical concepts.³ Acceptance of this idea, it should be pointed out, is perfectly compatible with taking modal explications to be useful for many purposes. For, wherever fine conceptual niceties do not matter too much, they may still be perfectly valuable theoretical tools even if they do not completely capture the pre-theoretical notions they are meant to explicate.

Another notion which has commonly been spelled out in modal terms is that of strict or broadly logical consequence—or its converse: entailment—, i.e. the relation holding between premises and a conclusion iff the latter strictly follows from the former. Thus, the following definition is standardly employed when the idea of consequence is informally introduced⁴:

Mod.4:

y is a consequence of x ↔ necessarily, if x is true, so is y

I will call this notion modal or also classical consequence. It is logical consequence in only a broad sense of ‘logical’. For, it not only covers formal or purely logical cases which hold merely in virtue of logical constants and/or logical form, but also cases which hold in virtue of analytic and other necessary truths. Symbolic logic then concentrates on an examination of the former sort of case, i.e. of formal consequence, and attempts to model or approximate it in a technically sound framework.⁵

The main aim of this paper is twofold: first, it will be argued that the same sort of reason that motivates the development of non-modal alternative approaches to truth-making, essence, etc. also motivates the development of a non-modal approach to logical consequence (Sect. 2). Second, an alternative account of consequence will be proposed which works with a tool that proved fruitful in the cases of dependence and truth-making: the idea of grounding (Sects. 3, 4). It will be shown that the resulting notion of consequence allows for a rigorous technical implementation in a model-theoretic framework (Sect. 5), and the approach will be briefly compared with that of relevant logics (Sect. 6). The paper concludes with a modest plea for a pluralistic stance towards the notion of logical consequence: It may indeed be useful to keep a plurality of approaches to the notion, as each of them can have its value given particular purposes (Sect. 7).

2 Motivations for an alternative account of consequence

We saw two interrelated worries about the modal approach to essence, etc.: It generates prima facie counterexamples (related to certain necessary truths) and it cannot account for the target concepts’ sensitivity to source. Both worries also arise for the modal approach to consequence.

2.1 Prima facie counter-examples

Despite its popularity and usefulness, the modal explication of consequence makes certain classifications that most philosophers admit to be counterintuitive, at least at first glance. For, it validates the following principles:

EFQ (ex falso quodlibet):

Everything whatsoever is a consequence of a contradiction

VEQ (verum ex quodlibet):

A logical truth follows from any proposition whatsoever

But virtually nobody who first meets these principles acknowledges them as true; when you introduce them in a course on elementary logic, you invariably earn the incredulous stare.

Of course, once we accept the modal explication of consequence, we learn to live with the principles. For given that explication, they can be established straightforwardly. Moreover, EFQ can be argued for by the use of innocent looking inference rules: if ‘P&¬P’ is true, so are ‘P’ and ‘¬P’ (by Conjunction Elimination). But if ‘P’ is true, so is ‘P∨Q’ (by Disjunction Introduction). Now, from ‘P∨Q’ and ‘¬P’ we can infer ‘Q’ (by Disjunctive Syllogism). This argument certainly has lowered our initial resistance to the acceptance of EFQ.

Even if we have stopped worrying, though, we should remember that we indeed had to learn to live with EFQ and VEQ and to accept that a conclusion can count as a consequence of some premises even though they seem completely irrelevant to the conclusion. So EFQ and VEQ are prima facie counterexamples to the modal account of consequence and thereby provide at least some motivation to explore alternatives (this is indeed a driving motivation for relevant logicians).

Finally, one may add that the modal account of consequence also validates a stronger variant of EFQ which says that everything follows from any necessary falsity. The classical argument for EFQ, however, does not support this stronger variant of EFQ. (Equally, the modal definition validates a stronger version of VEQ which says that every necessary truth follows from any premises whatsoever.)

2.2 Lost conceptual aspects of the pre-theoretical notion of consequence

One dominant pre-theoretical explication of the notion of consequence proceeds in terms of a guarantee, so that x is a consequence of y₁ … y_n iff the truth of y₁ … y_n guarantees the truth of x.⁶ Of course, this characterisation is somewhat vague and it is debatable how exactly it should be understood. But it is worth noting that it allows for a reading in which its import is not fully captured by the classical definition of consequence: It is the modal aspect of the definition (necessarily, if the premises are true, so is the conclusion) which is commonly taken to capture the pre-theoretical talk about a guarantee. But the notion of a guarantee is a relational one; a guarantee is always provided by something. And while the pre-theoretical explication of consequence locates the guarantee of the consequence’s truth in the truth of the premises, the modal definition does not locate it anywhere. If x must be true if y is true, this might but need not be because y provides a guarantee for the truth of x. In principle, the guarantee might stem from somewhere else. So, the classic definition neglects a recognisable aspect of the pre-theoretical characterisation.

The same point can be made slightly differently in terms of source: If something is a consequence of something else in a pre-theoretic understanding, then the truth of the former should somehow have its source in the latter. The modal conception of consequence is either wilfully ignorant about this aspect of consequence, or it tries to cash it out in terms of a necessary condition of truth-preservation. But such a connection is too weak for this job, as the above mentioned debates about the notions of truth-making, dependence, or essence have shown.

The described worries about modal consequence parallel those raised with respect to modal accounts of truth-making, etc. Given that the worries provide a good motivation for an alternative approach in one case, they do so in the other case as well. But there are also two further motivations in the case of consequence which deserve being mentioned.

2.3 Systematizing the modal accounts

The first concerns systematicity: The modal explications of consequence, truth-making, etc. should arguably not be regarded as independent of each other. Instead, they constitute a family in which the explication of consequence can be seen as playing a fundamental role. For, the modal approaches to the other notions result from an approach to them in terms of consequence or entailment:

Con.1:

x makes y true ↔ that x exists entails that y is true (conversely put: that y is true is a consequence of x’s existing)

Con.2:

x essentially has property y ↔ that x exists entails that x has y

Con.3:

x existentially depends on y ↔ that x exists entails that y exists

These explications in turn yield the modal explications stated in the introduction, once the modal explication of entailment is plugged in the defining clauses in Con.1 to Con.3. Viewed like that, the modal character of the explication of consequence spreads over to the explications of the other concepts because they are first of all understood via consequence/entailment.⁷ But then the alternative approaches to truth-making etc. which have been developed because of worries about the modal accounts target derived notions; if they are systematically motivated, one should look for a corresponding alternative account of the underlying notion of entailment, which then gives us the alternative accounts of truth-making etc. in the way in which the modal account of consequence gives us the modal accounts of the other notions.

2.4 Ground and consequence

Recently, philosophers such as Kit Fine and Gideon Rosen have influentially argued that it is of utmost importance for metaphysics to acknowledge a relation of grounding, a priority relation holding between derivative facts and their grounds.⁸ But the notion of a ground is the natural correlate of the notion of a consequence; ground stands to consequence as cause stands to effect. So, once grounding has been granted a place in the philosophers’ toolbox, it is tempting to put it to use in an explication of consequence; since it is commonly agreed that grounding is not a modal notion, the resulting notion of consequence will not be either. Moreover, the notion of ground is clearly sensitive to the aspect of source; in fact, it has been employed in the debates about truth-making, etc. in order to find explications of those concepts which are more adequate than the modal ones.⁹ An exploration of a notion of consequence answering to the notion of ground should be of interest to theories both of grounding and of consequence, even if one is not initially dissatisfied with the classical notion of consequence. So, let us see how an account of consequence could build on the notion of ground.

3 Grounding

3.1 The basics

In order to prepare for a ground-theoretical account of consequence, we need a workable notion of grounding; for that purpose I will present

• an informal introduction to the idea of grounding,

• some essentials of the logic of grounding, as well as

• some essentials of the grammar of grounding.¹⁰

First, the informal introduction: Some facts are objectively, but non-causally, prior to others. The former make the latter obtain, and the latter obtain in virtue of the former. The relation of priority at play here is called grounding.¹¹ It is, or corresponds to, a notion of non-causal explanation,¹² and it can be introduced by the connective ‘in virtue of’ (which connects sentences and singular terms) or by the sentential connective ‘because’. (But there are other uses of ‘because’ as well, namely causal and merely evidential ones.¹³) The notion of grounding is therefore grasped—though not always clearly and distinctly—by anyone who understands typical non-causal uses of ‘because’ or ‘in virtue of’, which indeed abound in philosophy. Some examples of commonly accepted grounding truths are:

• (1) That snow is white is true because snow is white.

• (2) A red rose is coloured because it is red.

• (3) A true disjunction is true because of its true disjunct(s).

• (4) The set of Aristotle and Socrates exists because its members exist.

Second, the logic of grounding: it has been shown that grounding allows for a fruitful systematic treatment; a number of authors who independently tackled its logic arrived at very similar general results.¹⁴ Here we can concentrate on some crucial points.

With Fine (2012b: p. 54f.), we may distinguish between the pure and the impure logic of grounding. The former concerns inferences with grounding statements in abstraction from the specific content of the statements which ground or are grounded. The latter takes the content of those statements into account, insofar as it contains logical notions such as truth-functors.

The presently important aspects of the pure logic of ground concern structural properties of grounding. Grounding is a factive priority relation. It is factive, that is, if x grounds y, then both x and y are truths or facts. And it is a priority relation; as such, it is

• irreflexive (nothing is prior to itself) and even

• asymmetrical (if x is prior to y, then y is not prior to x), and it is

• transitive (if x is prior to y, and y is prior to z, then x is prior to z).¹⁵

The presently important aspects of the impure logic of grounding concern the systematic interplay between the notions of grounding and classical truth-functional operators. The interplay is governed by a single core intuition:

Core Intuition:

Classical truth-functional compounds have the truth-values they have because of the truth-values of their components.

For instance, if a disjunction is true, it is so because of the truth of at least one of its disjuncts. And if a double negation is true, it is so because of the truth of the doubly negated statement.

The Core Intuition gives us the impure logic of grounding in its propositional variant (I will not discuss quantifiers here). For the precise statement of the proposal, two preliminary points must be made. First, what grounds a fact need not be a single fact; rather, several facts can jointly do the work. That ‘Ben’ and ‘Jerry’ both contain an ‘e’ is, for instance, jointly grounded in the fact that ‘Ben’ contains an ‘e’ and the fact that ‘Jerry’ contains one. Second, a distinction between partial grounds and full grounds is required. A notion of full grounding will be taken as an undefined primitive here (which is the standard approach in the debate). The corresponding notion of partial grounds is defined in its terms: some facts together partially ground a fact f iff they either fully ground f, or they do so together with some other facts.

Now we can say that any true disjunct of a disjunction is a full ground of it (so, if a disjunction has more than one true disjunct, it is ground-theoretically over-determined). Each conjunct of a true conjunction, on the other hand, is in general only a partial ground of it.¹⁶Jointly, however, the conjuncts constitute a full ground of the conjunction.

So, the following are constitutive principles of the impure logic of grounding, each of which reflects a specific aspect of the Core Intuition:

Disjunction:

If φ is true, then both φ∨ψ and ψ∨φ are fully grounded in φ

Conjunction:

If φ and ψ are true, then φ&ψ is fully and jointly grounded in φ and ψ, and partially grounded in φ, as well as partially grounded in ψ

Double Neg.:

If φ is true, then ¬¬φ is fully grounded in φ

This brief overview of the logic of grounding suffices for what follows.¹⁷

Third, the grammar of grounding. So far, I have talked of grounding as a relation between facts or truths, which is fine for informal purposes. But note there is a controversy about what could be called the Fundamental Question: Is grounding, at bottom level, a relation, and if so, what are its relata, and how finely are they individuated? Henceforth, I will continue to talk about grounding as a relation, and I will regard its relata as fine-grained, structured compounds, which I will without difference call facts or (true) propositions (so I work with what has been called a representational conception of grounding).¹⁸ I do not intend to thereby settle the fundamental question, and be it only for the purposes of this paper. For, it may be wholly legitimate to talk about grounding as a relation between fine-grained facts even if at bottom level, grounding is not a relation, or is a relation between coarse-grained facts. In general, we have many legitimate idioms which just do not reflect the most fundamental ways of being. This does not make statements containing them false. Apart from the fundamental level, there are other, derivative levels of being. If we restricted ourselves to only talking about the fundamental, we’d have to be silent far too often. Applying this general point to the idea of grounding, we may realize that the fundamental level of grounding, whatever it is, can give rise to less fundamental levels of grounding. Thus, even if grounding is non-relational at the fundamental level, such a non-relational notion might be used to define a relation of grounding; and a relation between fine-grained facts may be definable in terms of a relation between coarse-grained facts together with some principles connecting the different grains. So, what is presupposed in this paper is not an answer to the fundamental question; it is only that we can make sense of grounding as a relation between fine-grained facts, whether or not this captures what grounding is at bottom level.

3.2 The relata of consequence and the relata of grounding

When we do logic, we often talk about consequence as a relation between sentences. It is a very useful way of talking: Sentences are strings of letters with which we can easily operate and for which recursive definitions of well-formedness can be given. But we also often talk about consequence as a relation between the contents of sentences, i.e. between propositions. This way of talking has practical disadvantages. Propositions do not have visible or audible tokens, which makes it harder to operate with them. Also, there are notorious controversies about the nature of propositions: are they structured or not? what are their identity conditions? Nevertheless, many philosophers would regard consequence as a relation between propositions to be the more fundamental phenomenon than consequence between sentences. Just as the truth of a sentence is a semantic property owed to the content it expresses (a true sentence is true because it expresses a true proposition), the sentential consequence relation holds between sentences because the propositional consequence relation holds between their contents: if a sentence S is a consequence of S*, it is so because S expresses a proposition P which is a consequence of the proposition expressed by S*.

But I prefer to set issues about priority aside here. What is important to me, however, is to talk of consequence both as a relation between sentences and between propositions, where these two idioms are connected via the following correlation principle: Sentence S is a consequence of sentence S* iff the proposition expressed by S is a consequence of the proposition expressed by S*. Because of that principle, many of the things that we can truly say about consequence on the propositional level have a direct counterpart on the sentential level. For the sake of smooth formulations, it will moreover be helpful to talk about grounding as a relation holding between propositions, as well as between sentences. This talk will also be governed by a correlation principle: Sentence S is a ground of sentence S* iff the proposition expressed by S grounds the proposition expressed by S*.

A final remark: I will, for the purposes of this paper, talk of propositions as entities structured in a way similar to sentences. But the surface structure of a sentence does not always correspond to the structure of the proposition expressed; the logical form of a sentence does.

4 An alternative account of consequence

In Sect. 2, we saw some motivation for exploring alternative approaches to the modal analysis of consequence (despite its undeniable value): The modal explication validates the questionable principles of EFQ and VEQ, it ignores aspects of our pre-theoretical conception (sensitivity to source), and it does not relate the notion of consequence to its natural counterpart, the notion of grounding. What is wanting is an explication of consequence which takes those considerations into account. As a further desideratum, such a notion should be sufficiently similar to the classical one as to count as a promising substitute for it.

4.1 Direct consequence

A straightforward ground-theoretical account of consequence simply defines consequence as the converse of grounding:

DC.1:

x is a consequence of y₁, …, y_n ↔ one or more of the propositions y₁, …, y_n (jointly and fully) ground x.¹⁹

This notion, which will be called simple direct consequence, captures some clear cases of consequence. For instance, it classifies a disjunctive truth to be a consequence of its true disjunct(s), since any disjunctive truth is grounded in its true disjunct(s). Equally, it classifies a doubly negated truth as a consequence of the doubly negated statement.

Moreover, the account does justice to the motivations for seeking an alternative to the classical notion. It yields a notion of consequence which is sensitive to source and which is (obviously) connected to the notion of ground. And it does not validate VEQ; for while it is necessary that Socrates is male or not, it is certainly false that Socrates is male or not because, say, some tulips are red. Nor does the notion validate EFQ. For even if dialetheists are right and, say, the Russell set both contains itself and does not contain itself, it will still be false that because the set contains itself and does not, some tulips are red. Finally, although truth-preservation is not a defining mark of simple direct consequence, it is indeed an outcome of it; the notion does not validate inferences that are classically invalid.

While I think that DC.1 gives us a proper understanding of ‘consequence’, it is of severely limited interest as a notion of consequence in logical theory. A first reason is that since grounding is a factive relation, the defined relation of consequence only holds between true propositions; but in logic we clearly want a kind of consequence that can hold between false propositions as well. A second reason is that since grounding is irreflexive, the defined notion of consequence will be irreflexive too. But we all philosophically grew up with the idea that logical consequence is reflexive, and particularly logicians will not want to give it up unless there are strong reasons to do so. (Let me point out in passing that in so far as intuitive judgements on logical consequence are at issue, there may be disputes over whether consequence should be reflexive or not. However, recall our current task: We set out to define a notion of consequence that takes into account the shortcomings of the standard notion of consequence laid out in Sect. 3, while still serving as a good substitute of the notion. Here one may find reflexivity desirable, so it is worthwhile to see whether we can have such a notion.)

These drawbacks of the current proposal can be overcome by making two amendments to it. In order to take the last point into account, we may resort to a notion of proper or improper grounding, where every truth counts as improperly grounded in itself. To get a grip on this terminology, notice that one can then characterize a fundamental truth as a truth which has no proper ground or, equivalently, as a truth whose only improper ground is itself.

For short, let me use ‘thin grounding’ to cover both proper and improper grounding. I will henceforth work with the notion of thin grounding without always repeating the attribute ‘thin’. Note that talk of thin grounding is merely a simple technical extension of the notion of ground which will make many formulations shorter. But it could be dispensed with; instead of saying that a truth x is a thin ground of y, one could always disjunctively say that x is a (proper) ground of y or x = y. (A cautionary note: thin grounding is not defined as the reflexive closure of a ground, and it is only weakly, not fully reflexive—not every proposition counts as thinly grounded in itself, since thin grounding is still a factive notion; falsities are not grounded at all, not even thinly.)

In order to take the first point on board, we may determine consequence relations always under the hypothesis that the premises are grounded (which implies that they are true).²⁰ A modified definition of consequence would thus look as follows:

DC.2:

x is a consequence of y₁, …, y_n ↔ under the hypothesis that y₁, …, y_n are grounded, one or more of the propositions y₁, …, y_n (jointly, fully, and thinly) ground x

The defined notion can be called broad direct consequence; it is reflexive and it connects propositions independently of their actual truth; apart from that, it works as simple direct consequence.

But it still fares badly as a substitute for the classical account of logical consequence. To see this, consider a conjunction, ‘P&Q’, and one of its conjuncts, ‘P’. On all common treatments of logical consequence, the latter counts as a consequent of the former. But given the present explication of consequence, it does not. A conjunction is grounded in its conjuncts and not vice versa. So on the current ground-theoretical definition of consequence, a conjunction counts as a consequence of its conjuncts, which is fine, but a conjunct does not count as a consequence of a conjunction.

In fact, this is but a symptom of a wide-ranging problem of the current approach. Where truth-functional connectives are involved, the order of grounding always runs from the simpler statements to the logically more complex statements. This is why the current approach only gives us introduction rules for the truth-functional connectives but none of the classical elimination rules. Moreover, since grounding is an asymmetric affair, the present notion cannot allow for any cases of mutual entailment (apart from the reflexive cases). But such cases abound in logic (ranging from the simple case of ‘P’ and ‘¬¬P’, to most complicated ones). So, it may look as if the idea of using grounding to define logical consequence is bound to fail for principled reasons.

4.2 Web consequence

But let’s not be hasty. A notion of consequence which supports classical elimination rules and which allows for mutual instances cannot be the direct converse of an asymmetric priority notion such as grounding. But this does not mean it cannot be defined in terms of it at all. Here is my proposal, informally put: A proposition is a consequence of some premises if, given that they are grounded themselves, they provide a ground of it or bring such a ground along. Now one way of bringing the ground of a conclusion along is by directly grounding it—the ground-theoretical definitions DC.1 and DC.2 focused solely on this way. But there is another way of bringing grounds of x along, namely by being grounded in something which grounds x: Think of the premises and their grounds as a parcel. A conclusion counts as a consequence of some premises if the parcel that they form together with their grounds contains a ground of the conclusion. Less metaphorically put, my proposal is to replace the idea of truth-preservation, which is central to all standard accounts of consequence, with the idea of ground-preservation.

The following definition captures this idea:

WC:

x is a consequence of y₁, …, y_n ↔ under the hypothesis that y₁, …, y_n are grounded, one or more of the (thin) grounds of y₁, …, y_n (jointly, fully, and thinly) ground x

I shall call the defined notion web consequence.²¹ It works by first tracing a way down the grounding web which supports the premises, and then seeking a way up to the conclusion. If the conclusion can be reached via the grounding structure, starting from the premises, then it is a consequence of the premises. It may be pointed out in passing that, since any grounded proposition is a thin ground of itself, broad and simple direct consequence are special cases of web consequence (note that we are still working with the reflexive notion of a thin ground).

Web consequence is a fine notion and a promising substitute for classical consequence. Just as broad direct consequence, it is reflexive, covers relations between false propositions, and covers some core examples of consequence (disjunctions follow from their disjuncts).²²

But it covers many more cases than broad direct consequence. For instance, it allows for downward entailment from a conjunction: consider the conjunction of x and y. Since its conjunct x is one of its grounds, and since x is a thin ground of itself, x is a consequence of the conjunction, just as the conjunction is a consequence of its conjuncts. In fact, web consequence covers the majority of instances of classical consequence (though there is one important exception; it will be discussed in Sect. 5.7). It does not cover, however, VEQ: that Socrates is wise or isn’t is not a web consequence of the proposition that, say, milk is white. For, neither the proposition itself, not any of its grounds are a ground of that tautological truth. Nor does it cover EFQ. Take the conjunctive proposition that Socrates is wise and is not wise. Under the hypothesis that this is grounded, its grounds will be its conjuncts. But while those will ground some propositions, they do not ground any arbitrarily chosen proposition; they will, e.g., not ground the proposition that England is a monarchy.

Web consequence is thereby a more interesting notion for logicians than either simple or broad direct consequence. And it has the desirable features demanded at the outset of this section: (i) it validates a large number of intuitively acceptable inference rules, (ii) it does not validate the problematic rules of VEQ and EFQ, (iii) it is based on the notion of ground (even though less directly than the two forms of direct consequence), and (iv) it connects consequence to the idea of source (a consequence has its source in the grounds of its premises).

Note that, as in the case of classical consequence, we can distinguish between different varieties of web consequence. In particular, the well-received distinction between formal (or: purely logical) and material (or: analytic) consequence can be applied to web consequence: Informally put, a formal web consequence is one which holds on the basis of the interaction of logical notions and the notion of ground. A material web consequence is one which holds, at least partly, on the basis of the interaction of some non-logical notions and the notion of ground. Thus, that Fred exists or grass is green is a formal consequence of Fred’s existing; that his singleton exists is only a material consequence of it. This informal characterization of the distinction should suffice for present purposes. It is a matter of controversy how a precise account of the distinction should look like in the case of classical consequence, and the same points that are controversial there will recur here; but this is not the place to discuss them.

Does web consequence have further desirable virtues? Yes. In particular, it has what it takes to be of genuine use to logicians: it can be formally modeled. In the following section, a model-theoretic account of (formal or purely logical) web consequence will be developed for a propositional logic with standard truth-functional connectives. This will, on the one hand, show that the notion is useful and can be fruitfully treated in a formal system. On the other hand, it will give us a better grasp of the mechanisms of web consequence and allow for distinctions to be made which, among other things, are related to the issue of EFQ.

A final note: For reasons of space, I exclusively focus on propositional logic in this paper. However, even though a proper discussion of the quantifiers has to wait for a future occasion, let me at least comment on a very simple example from quantified logic. Consider the argument ‘Everything is alive. So, Socrates is alive.’ In order to see whether the conclusion counts as a web consequence of the premise, we have to check whether the premise brings along a (thin) ground of the conclusion. Now it is commonly assumed that universal quantifications are, at least partially, grounded in their instances; since the conclusion of the argument is just one of those instances, it is a partial ground of the premise. But the conclusion is also a thin ground of itself. The premise therefore brings along a ground of the conclusion, which is in turn a web consequence of the premise.

4.3 ‘Under the hypothesis’

I want to address two potential worries about my use of the phrase ‘under the hypothesis that’: (i) Is it sufficiently well understood? More particularly, is there an understanding of it that yields the desired results? (ii) Given that there is such an understanding, is it perhaps so loaded that it alone does all the work in avoiding EFQ and VEQ, while no work is left to do for grounding?

There are three independent responses to this. Firstly, I appeal to an intuitive understanding of the phrase. Reasoning under assumptions is something we do all the time; and, as others have pointed out before, we also can reason reliably well under inconsistent assumptions. A good example is provided by interpretations of inconsistent fictions, in which readers successfully can report on what is true in a story and what is false.²³ Admittedly, it may not be easy to spell out precisely how such reasoning works; but this does not mean it must not be employed here.

Secondly, the use of the phrase can be avoided if one adopts Fine’s (2012b: p. 49f.) notion of non-factive grounding (compare above, footnote 20). However, I prefer to work with the factive notion; one reason is that the factive notion is the more familiar one, as it is usually assumed in the current debate about grounding. So I take the above approach to be better accessible to readers that are not deeply into the grounding debate.

Finally, and perhaps most importantly, the phrase ‘under the hypothesis’ is not used in the model theory to be developed now (nor is any substitute of it which might similarly be suspected not to be sufficiently precise). What will be done in the model theory is to quantify over models with well-defined properties; working under the hypothesis that the premises of an argument are grounded corresponds to looking at models in which the premises are grounded. One can then prove further properties of those models. So, the formal model can be taken as implicitly providing a precise rendering of the phrase. At the same time, the model theory shows that the notion of grounding does indeed the crucial work for the defined notion of consequence and its capacity to avoid EFQ (after presenting the theory, it will also be contrasted with First Degree Entailment).

5 Technical implementation: web consequence in propositional logic

5.1 The basic idea

In this section, a model-theoretic notion of consequence is developed. It is a formal counterpart of web consequence in its purely formal mode (i.e. only those consequences are taken into account that hold because of their logical form), and applied to propositional logic (i.e. the only logical constants are the classical truth-functional connectives).

The notion of consequence will, as usual, be defined via a universal relation of premises and consequence in models. However, the present approach deviates from standard approaches in the pertinent relation holding between premises and consequence. Standard accounts take truth-preservation to be the mark of consequence: φ model-theoretically entails ψ iff in every model in which φ is true, ψ is true. In the present account, the notion of truth loses its pivotal role and truth-preservation is replaced by a relation of ground-preservation. So, consequence will be defined along the following lines (recall that by ‘grounds’ I always mean thin grounds, unless indicated otherwise):

φ₁, …, φ_n ⊨ ψ iff:

in every model in which φ₁,…,φ_n are grounded, ψ is fully grounded in (full or partial) grounds of φ₁,…,φ_n

In order to apply this definition, the pertinent notion of a model needs to be defined; they will be called grounding models.

5.2 The languages

A standard object-language with the truth-functional connectives ∨, ¬, & and sentential letters ‘P’, ‘Q’, etc. is used. Small Greek letters ‘φ’, etc. are used as variables of the meta-language ranging over formulas. Corner quotes will not be used unless omitting them leads to serious ambiguities (any quotes will be omitted in the scope of ‘⊨’).

In the meta-language, the symbols ‘≻’ and ‘⋟’ express two varieties of thin ground:

ψ ≻ φ₁,…,φ_n iff:

φ₁,…,φ_n jointly are a thin full ground of ψ

ψ ⋟ φ₁,…,φ_n iff:

φ₁,…,φ_n jointly are a thin partial or full ground of ψ

The lists on the right-hand side of such formulas may consist of a single formula. Moreover, repeated occurrences of the same formula in a list are regarded as redundant; so ‘ψ ≻ φ₁,φ₁’ is equivalent to ‘ψ ≻ φ₁’.

Finally, a formula φ is called grounded—in symbols: Gφ—if there are formulas ψ₁,…,ψ_n such that φ ≻ ψ₁,…,ψ_n.

To avoid any potential misunderstanding, let me point out that the symbols ‘≻’, ‘⋟’, and ‘G’ belong to the meta-language only. In fact, the concept of ground will only be expressed in the meta-language; no expression related to ground is part of the object-language. The present paper puts the notion of ground to use as a tool in formal semantics in order to define a notion of consequence. It presupposes a logic of grounding in order to develop a logic with grounding. The logic of grounding is the topic of other papers and will not be further explored here. Because of that, this paper does not aim at sharpening our grasp of the notion of grounding; a logic of grounding can do that, a logic with grounding requires that grasp, without a claim of deepening it further. It should, however, broaden our sense of the utility of grounding.²⁴

5.3 Grounding models

Informally put, grounding models consist of a grounding structure which distributes the grounding relation over formulas of the object-language, while this distribution is constrained by the logic of grounding sketched above (see Sect. 3.1). Technically, a grounding structure will be defined in a way similar to how truth is defined in standard models: while the latter is defined by an assignment of truth-values to sentential letters together with a recursive truth-definition, the former is defined by a stipulation to the effect that certain literals (i.e. sentential letters and their negations) are grounded together with a recursive grounding-definition.

Every grounding model M contains an evaluation function f_M which determines that at least one member of any pair of corresponding literals (i.e. a sentential letter and its negation) is grounded. Technically, the function can be construed as mapping each pair of corresponding literals to a non-empty (proper or improper) subset of it. If we let Lit be a function that maps a literal to the pair of corresponding literals to which it belongs, we can then stipulate that Gφ in M if φ ∈ f_M(Lit(φ)). In other words, f_M provides a sufficient condition for being grounded (but not a necessary one, as it only concerns literals, not complex formulas).

The distribution of the grounding relation is then defined by recursive clauses (the clauses are all relative to a model, but I will omit the qualification ‘in M’). The first clause reflects that we are working with a notion of thin ground:

G.1—Weak Reflexivity:

If Gφ then φ ≻ φ

The remaining clauses are directly modelled after the propositional logic of ground outlined above in Sect. 3.1; the only differences result from the fact that grounding models do not work with a notion of truth but only with a notion of groundedness. So, talk about truth has been appropriately replaced²⁵:

G.2—Transitivity:

If φ⋟ψ and ψ⋟ξ, then φ⋟ξ

G.3—Factivity:

If φ⋟ψ, then Gφ and Gψ

G.4—Disjunction:

If Gφ then (i) φ∨ψ ≻ φ, and (ii) ψ∨φ ≻ φ

G.5—Neg-disjunction:

If G¬φ and G¬ψ, then ¬(φ∨ψ) ≻ ¬φ, ¬ψ

G.6—Conjunction:

If Gφ and Gψ, then φ&ψ ≻ φ, ψ

G.7—Neg-conjunction:

If G¬φ, then (i) ¬(φ&ψ) ≻ ¬φ, and (ii) ¬(ψ&φ) ≻ ¬φ

G.8—Double.neg:

If Gφ, then ¬¬φ ≻ φ

This completes the recursive grounding definition. Together with the evaluation function, the clauses define the grounding structure of a model which in turn fully determines the model.

The recursive clauses directly construe a grounding structure upwards from some grounded formulas to more complex formulas which are grounded in them. But at the same time, the clauses imply that the following downward claims hold in all grounding models²⁶:

G.4_D—Downw. Dis.:

If Gφ∨ψ then (i) φ∨ψ ≻ φ, or (ii) φ∨ψ ≻ ψ

G.5_D—Downw. Neg-disj.:

If G¬(φ∨ψ) then ¬(φ∨ψ) ≻ ¬φ, ¬ψ

G.6_D—Downw. Conj.:

If Gφ&ψ then φ&ψ ≻ φ, ψ

G.7_D—Downw. Neg-conj.:

If G¬(φ&ψ) then (i) ¬(φ&ψ) ≻ ¬φ, or (ii) ¬(φ&ψ) ≻ ¬ψ

G.8_D—Downw. Double.neg:

If G¬¬φ then ¬¬φ ≻ φ

One representative proof suffices: assume that G¬¬φ holds in a model M. Since a double negation is not a literal, this cannot be an outcome of the evaluation function of M. Instead, it must be due to the recursive clauses. But only clause G.8 determines a ground for a double negation, and thereby that the double negation is grounded. So, if G¬¬φ holds in M, G.8 must be operative and thus ¬¬φ  ≻  φ holds in M, which proves G.8_D.■

The informal reason why the downward claims are entailed is that the grounding models acknowledge no non-logical grounding relations other than the self-groundedness of the literals picked out by the evaluation function. One could allow for more non-logical grounding relations if one included the downward principles as additional, underived recursive clauses in the grounding definition.

5.4 A notion of consequence

Let me use capital Greek letters ‘Γ’, etc. as variables ranging over collections of formulas. ‘Γ ⋟ ξ₁ … ξ_n’ should be understood as saying that each of the ξ₁, …, ξ_n is a full or partial ground of some of the formulas in Γ, i.e. as: for some φ₁ in Γ, φ₁ ⋟ξ₁, and …, and for some φ_n in Γ, φ_n ⋟ ξ_n. Read ‘GΓ’ or ‘Γ is grounded’ as: all formulas in Γ are grounded.

We may now define a notion of consequence as follows:

Γ ⊨ ψ iff in every model M with GΓ, there are ξ₁ … ξ_n such that in M:

(i) Γ⋟ ξ₁ … ξ_n, and (ii) ψ ≻ ξ₁ … ξ_n.

In somewhat plainer English:

Γ ⊨ ψ iff in every model in which Γ is grounded, ψ is fully grounded in grounds of Γ.

5.5 Web consequence examined

Let us study the defined notion of consequence a bit. To get into the mood, we start with some examples. For any formulas φ, ψ, ξ it holds that

(i)	¬¬φ ⊨ φ	(ii)	φ&ψ ⊨ ψ&φ;
(iii)	φ∨ψ ⊨ ψ∨φ	(iv)	(φ&ψ) ∨ (φ&ξ) ⊨ φ & (ψ∨ξ)

Proof of (i): If G¬¬φ holds in M, then ¬¬φ ≻ φ does too (by G.8_D). Therefore, Gφ holds in M (by G.3), and so does φ ≻ φ (by G.1). Hence, there is a formula ξ (namely φ itself) with (i) ¬¬φ ⋟ ξ, and (ii) φ ≻ ξ. ■

Proof of (ii): If Gφ&ψ holds in M, so does φ&ψ ≻ φ, ψ (by G.6_D). Therefore, Gφ and Gψ hold (by G.3), and so does ψ&φ ≻ φ, ψ (by G.6). Hence, there are formulas ξ₁ and ξ₂ (namely φ and ψ) with (i) φ&ψ ⋟ ξ₁, ξ₂ and (ii) ψ&φ ≻ ξ₁, ξ₂.■

The proofs of (iii) and (iv) involve case analyses: since the premises in those claims are disjunctions, we don’t know which disjunct is grounded and so the grounding structure corresponding to each case must be examined. Only the proof of (iv) will be given: If G(φ&ψ) ∨ (φ&ξ) holds in M, either (φ&ψ) ∨ (φ&ξ) ≻ φ&ψ or (φ&ψ) ∨ (φ&ξ) ≻ φ&ξ. Assume the first alternative. Then Gφ&ψ holds (by G.3), and so do φ&ψ ≻ φ,ψ (by G.6) as well as Gφ and Gψ (G.3). By transitivity (G.2), it follows that (φ&ψ) ∨ (φ&ξ) ≻ φ,ψ holds. So φ and ψ have been established as grounds of the premise. Now they are shown to ground the conclusion. Starting from Gψ, G.4 yields (ψ∨ξ) ≻ ψ, so that together with Gφ, G.6 yields in turn φ & (ψ∨ξ) ≻ φ, ψ. So, there are formulas ξ₁ and ξ₂ (namely φ and ψ) with (i) (φ&ψ) ∨ (φ&ξ) ⋟ ξ₁, ξ₂ and (ii) φ & (ψ∨ξ) ≻ ξ₁, ξ₂. The case analysis continues with the second assumption; by reasoning in a strictly parallel fashion, one obtains the result that there are formulas ξ₁ and ξ₂ (namely φ and ξ) with (i) (φ&ψ) ∨ (φ&ξ) ⋟ ξ₁, ξ₂ and (ii) φ & (ψ∨ξ) ≻ ξ₁, ξ₂. Both cases yield the same result, so in every model with G(φ&ψ) ∨ (φ&ξ), there are formulas ξ₁ and ξ₂ with (i) (φ&ψ) ∨ (φ&ξ) ⋟ ξ₁, ξ₂. ■

An interesting result can be established which may improve our grasp of the mechanism of ⊨, as it allows for an instructive reformulation of the conditions under which Γ ⊨ ψ. It can be seen that in every model M, (i) every grounded formula which is not a literal is grounded in a subset of the literals that occur in it, where all the members of that subset are grounded.²⁷ We may call that set of literals the base of φ in M. (ii) Literals can only be trivially grounded in themselves, but not grounded in other formulas; so, the base of a grounded literal is its singleton. (iii) Now let us call a set of formulas a possible base of Γ iff there is a model in which it is the base of Γ. Whether ψ follows from some premises Γ can always be decided via an examination of the possible bases of Γ:

C.0:

Γ ⊨ ψ iff every possible base of Γ contains a full ground of ψ

This is a nice feature as it allows a systematic and fool-proof way of deciding whether the consequence relation holds between Γ and ψ or not: first determine the possible bases of Γ, then determine whether every such base grounds ψ. By covering all ways in which a complex formula can be built up from component formulas, the grounding rules of the models secure that this can be done in a finite number of steps. The following figure illustrates how the procedure is used to establish that P ∨ Q ⊨ Q ∨ P:

Let us turn to some further features of web consequence:

C.1:

The notion is reflexive. That is: φ ⊨ φ

C.2:

The notion is monotonic such that consequence is preserved under the addition of arbitrary premises. That is, if Γ ⊨ ψ, then for any Δ: Γ, Δ ⊨ ψ

(In the theorems, I omit outer universal quantifiers over formulas for ease of presentation.)

The proofs are fairly trivial. So let me be brief:

G.1 gives us C.1. Since full thin grounding is reflexive, in every model with Gφ it also holds that φ ≻ φ. So, there is a formula ψ (namely φ itself) such that φ⋟ψ and φ ≻ ψ. ■

re C.2: Assume Γ ⊨ ψ. Then ψ is fully grounded in some grounds of Γ. But any grounds of Γ are also (partial) grounds of Γ, Δ. So, ψ is fully grounded in grounds of Γ, Δ. Hence Γ, Δ ⊨_C ψ. ■

Now, the most interesting feature of the defined notion of consequence is that it obeys constraints of relevance. In particular, we can see that

C.3:

The defined notion of web consequence does not validate VEQ. That is, given a tautological ψ, it does not hold for every φ that φ ⊨ ψ

A proof by example: P ⊭ Q ∨ ¬Q. For, in every model M in which ‘P’ is grounded, the only ground of ‘P’ is ‘P’ itself. But none of the clauses in the grounding-definition will make ‘P’ a ground of ‘Q ∨ ¬Q’ (which can be shown by a trivial recursive proof).

Moreover, we can see that:

C.4:

Web consequence does not validate EFQ. That is, not for every φ, ψ: φ & ¬φ ⊨ ψ

Again, a simple proof by example: P & ¬P ⊭ Q. For, in every model in which ‘P & ¬P’ is grounded, its only grounds are ‘P’ and ‘¬P’. But ‘Q’ is grounded in neither of them.

Even though a contradiction does not entail everything, it still entails the things it intuitively should entail. It holds for instance that

(i) P&¬P ⊨ P

(ii) P&¬P ⊨ ¬¬(P & ¬P)

(iii) (P&Q) & ¬(P&Q) ⊨ Q

Relatedly to C.3 and C.4, it can be seen that web consequence satisfies a variable sharing principle: a formula ψ can only be a consequence of a premise φ if both share at least one sentential letter. To see this, recall C.0 above; if φ and ψ do not share a sentential letter, then no base of φ is a base of ψ. Since every formula has a possible base, it follows that φ ⊭ ψ.

So far, so good. Web consequence also has a feature, though, which will be far less welcome to many philosophers: it does not validate disjunctive syllogism. This is a disadvantage which deserves a detailed discussion. But before I turn to it, let me say something about the notion of logical truth applied to our current setting.

5.6 Logical truth

In model theory, a tautology or logical truth can be defined as a formula which is true in all models (informally: it is true, come what may). In the present framework, we can easily adopt this definition and call a formula a tautology iff it is grounded in all models (it is grounded, come what may). Then, for instance, ‘P∨¬P’ counts as a logical truth. For, in every grounding model, the evaluation function assigns groundedness to the literal ‘P’ or to the literal ‘¬P’. In either case, by the recursive grounding definition, ‘P∨¬P’ will be grounded. In fact, it can be seen (though the proof must be omitted here) that every classical tautology is grounded in all models, and counts as a logical truth by the present definition.

Note, though, that in classical model theory, an alternative definition declares a logical truth to be a formula which follows from the empty set of premises. This useful (though less natural explication of a logical truth) cannot be applied here, since the empty set does not contain any grounded formulas at all, so nothing can be grounded in their grounds; so the empty set has no ground-theoretical consequences. In the present framework, we should therefore stick to defining logical truth as truth in all models.

5.7 Disjunctive syllogism and possible modifications

As already mentioned, one last noteworthy feature of the defined notion of web consequence is that

C.5:

Web consequence does not validate disjunctive syllogism (or MPP): φ∨ψ, ¬φ ⊭ ψ

To see this, consider whether P∨Q, ¬P ⊭ Q. A countermodel M can easily be constructed: its evaluation function determines that GP and G¬P, but not GQ. Because of G.4, P∨Q ≻ P holds in M, and hence GP∨Q holds too. So, the premises P∨Q and ¬P are grounded in the model; their grounds are ‘P’ and ‘¬P’. But those grounds do not also ground the conclusion ‘Q’ (in fact, nothing does in the model).

Technically, disjunctive syllogism fails because the grounding models can assign groundedness to contradictory literals. But such literals can make a disjunction and the negation of one of its disjuncts true, without making the other disjunct false.

That disjunctive syllogism fails on our notion of consequence is not too surprising, given that EFQ fails too. Since the latter can be established once disjunctive syllogism, disjunction introduction, and conjunction elimination are in play (cf. Sect.  2.1), something has to go. Disjunction introduction and conjunction elimination are in harmony with the logic of grounding, so disjunctive syllogism is the natural candidate to make way. (Conjunction elimination does not play an essential role in arguing for EFQ anyway; even if it was rejected, we could still amend the argument to show that a variant of EFQ holds, namely the principle that a statement together with its negation entail anything whatsoever: start with ‘P’ and ‘¬P’, infer ‘P∨Q’, use disjunctive syllogism.)

It is noteworthy, for what follows, that the only countermodels for disjunctive syllogism are those that assign groundedness to two contradictory literals. Thus they are, in a sense, paraconsistent models; for even though the present framework does not employ a notion of truth in a model in its formal apparatus, the models in question can be said to make two contradictory literals true, in so far as grounding is factive. Let me emphasize that the failure of disjunctive syllogism in such a model is, at least arguably, not an artificial outcome but a reasonable affair. If we seriously envisage a situation in which ‘P’ and ‘¬P’ are true, they will make ‘P∨Q’ true, so we have the premises for an application of disjunctive syllogism. But the application would seem unwarranted, since ‘P’ and ‘¬P’ do not also make ‘Q’ true.

Typical relevance logicians will not be surprised that disjunctive syllogism fails for web consequence; they know the phenomenon from their logic. Nor will they be worried about it; they have learned to live without disjunctive syllogism anyway.²⁸ But some readers will have a different attitude. If a notion of consequence fails to validate disjunctive syllogism, they will regard this as a serious vice, not a virtue. And they will think that if we cannot, at the same time, accept disjunctive syllogism and reject EFQ, then even if EFQ looks counterintuitive at first, the more natural choice is to accept EFQ than to reject disjunctive syllogism.

There is a third way, however, besides just giving up on disjunctive syllogism and accepting EFQ. It starts from a consideration about why we naturally accept disjunctive syllogism as a valid rule. The answer is that we work with the implicit assumption of a consistent background scenario; and if we implicitly presuppose consistency, we can indeed safely rely on disjunctive syllogism. This consideration is used, by some paraconsistent logicians, to justify the rejection of disjunctive syllogism in spite of its intuitive appeal: they would say that in our endorsement of disjunctive syllogism we simply overlook some remote scenarios which are, however, important for the evaluation of certain other entailments (those which involve inconsistent premises). But we may make a different use of the reasoning and construe a modified notion of consequence on its basis. The idea is to introduce a hybrid notion of consequence which works with different sorts of models (differing with respect to the constraints on their evaluation function) depending on whether the premises in an argument are consistent or not. If they are classically inconsistent, paraconsistent models (in which contradictory literals can both be grounded) will be used, but if they are classically consistent, only consistent models (in which only one of two contradictory literals can be grounded) will be used. We can define a notion incorporating this idea as follows:

Γ ⊨_H ψ iff:

(i):

Γ are consistent and in every consistent model M with GΓ, there are ξ₁ … ξ_n such that in M: Γ⋟ξ₁ … ξ_n, and ψ ≻ ξ₁ … ξ_n, or

(ii):

Γ are not consistent and in every model M with GΓ, there are ξ₁ … ξ_n such that in M: Γ⋟ξ₁ … ξ_n, and ψ ≻ ξ₁ … ξ_n.

The result of this somewhat complicated definition is a beautiful notion of consequence in so far as it matches most pivotal intuitions on what should count as a consequence of what. In many cases, it agrees with the judgements of classical logic. But it invalidates VEQ and EFQ, rules which are intuitively problematic. And as long as consistent sets of premises are in play, it respects the validity of disjunctive syllogism. Only if inconsistent premises force us to take into account inconsistent scenarios, it forbids us to rely on that inference rule—which seems reasonable on reflection (see above).

But alas, this beauty does not come for free. Since different sorts of models are evoked depending on whether the premises in an argument are consistent or not, the defined notion of consequence lacks some features one may well find practical and attractive. For example, the notion is not monotonic. For, it holds that P ∨ Q, ¬P ⊨_H Q (since ‘P ∨ Q’ and ‘¬P’ are consistent, ordinary models are used in order to evaluate the claim). But adding another premise can destroy its validity; it happens if we include ‘P’ as a further premise. For, it also holds that P ∨ Q, ¬P, P ⊭_H Q. Since we are now presented with an inconsistent set of premises, we have to resort to paraconsistent models in the evaluation of the claim.

However, two weakened substitutes of monotonicity still hold:

Consistent Mono.:

If Γ and Δ form a set of consistent premises, and Γ ⊨_H ψ, then Γ, Δ ⊨_H ψ

Inconsistent Mono.:

If Γ is a set of inconsistent premises, and Γ ⊨_H ψ, then Γ, Δ ⊨_H ψ

Monotonicity is only one example of complications that arise with the hybrid notion of web consequence. There are more, and they deserve to be systematically studied. But here it suffices to say that while it is nice that the hybrid version of web consequence preserves a version of disjunctive syllogism, the straightforward version of web consequence may well seem more attractive from a technical point of view—there is more than one way in which a theoretical account can exhibit beauty. Hybrid web consequence excels in its proximity to our pre-theoretical intuitions. But the unmodified version of web consequence has the beauty of greater technical simplicity. Since beauty is at least partly in the eye of the beholder, it can be left to the reader to make up her mind on the relative beauty of the two notions.

6 Comparisons: web consequence, FDE, and inexact consequence

6.1 Web consequence and relevance logic

To avoid commitments to EFQ and VEQ, and to develop a notion of consequence which puts constraints of relevance on the connection between premises and their consequences, is one of the driving motivations of the development of relevance logic. Hence, it seems natural that the current proposal should be compared to relevance logic.

But there are many, and in some respects quite diverse varieties of relevance logic. A comprehensive survey of them would clearly go beyond the scope of this paper. Also, to do justice to the different accounts one would have to enter into their technical aspects in a way which is hardly suitable for a paper intended for a general philosophical audience. So I will aim for a more informal comparison here with but a selected variety of relevance logic. Let me focus on Anderson and Belnap’s First Degree Entailment (FDE) as an example of relevance logic and highlight some crucial differences between the approaches.²⁹ An important reason for this choice is that web consequence and FDE are consequence relations that agree extensionally on most cases. The only differences arise when tautological formulas are involved. In FDE, no formula is a tautology (i.e. is true in all models). For, there is a model in which all literals fall into truth-value gaps and thereby make all formulas fall into gaps. But, as already mentioned, there are ground-theoretic tautologies: Every classical tautology is grounded in every grounding model. This difference shows up in the (in)validity of certain arguments: While there is, e.g., no first-degree entailment from ‘P ∨ (Q∨¬Q)’ to ‘Q∨¬Q’, the latter formula is a web consequence of the former formula (in every model in which the former is grounded, its grounds also ground the latter formula).

Despite the extensional similarities between the two notions, though, they are based on different conceptual resources; while relevance logic uses models based on distributions of truth-values, truth-values do not play any role in grounding models. The crucial notion for the latter models is the notion of grounding.

Because of the very different ideology of the two approaches, a further comparison between FDE and web consequence does not immediately get off the ground. To ensure better comparability, it is helpful to extend grounding models by an assignment of truth-values. To do this, we can take the grounding structure of a grounding model to deliver a partial distribution of truth-values to formulas, since grounding is factive; so formulas that are grounded in a model should also be counted as true in the model. But the grounding structures do not, by themselves, entail anything about the falsity of formulas, so that we are left with only a partial distribution of truth-values. An easy way of turning it into a complete one is to stipulate that any ungrounded formula be counted as false.

Now let us start the comparison by recalling crucial features of FDE. As classical consequence, consequence in relevance logic works as truth-preservation in all models. However, unlike the distributions of truth-values in classical models, those in relevant models can be incomplete and inconsistent: The models allow for truth-value gaps (literals without a truth-value) and gluts (contradictory literals which are both true), by which EFQ and VEQ are avoided. Gaps get us around VEQ: In a model in which ‘P’ is neither true not false, ‘P∨¬P’ falls into the truth-value gap, too. Hence it will not be a consequence of ‘Q’, since truth is not preserved from ‘Q’ to ‘P∨¬P’ in all models. Gluts get us around EFQ: Truth is not preserved from {‘P’, ‘¬P’} to ‘Q’ in a model which assigns truth to ‘P’ and ‘¬P’ but falsity to ‘Q’.

Now we can see that the mechanisms in which VEQ is avoided in the relevant and the ground-theoretic framework differ significantly. In the latter, truth-value gaps do not occur. ‘P∨¬P’ is grounded in all models, and if we extend the models with a notion of truth, it will therefore be true in all models. Yet, VEQ fails because even if ‘P∨¬P’ is true in all models, it is not grounded in the grounds of any arbitrarily chosen formula.

When it comes to EFQ, the differences between the relevant scheme and the present are more intricate. What is true is that both approaches need inconsistent models in order to invalidate EFQ. Still, the mechanism of how EFQ fails in an inconsistent model is different: for relevance logicians, it fails because truth is not preserved. In the present framework, the reason is that grounds are not preserved.

While the conceptual difference is clear, it only subtly shows up on the technical surface. To bring it out, we have to consider an unorthodox model-theoretic frame which allows only for consistent distributions of truth-values and a single inconsistent distribution: the one which assigns truth to every formula. In this (admittedly somewhat bizarre) frame, relevant and ground-theoretic consequence come apart with respect to the validity of EFQ. For, assume first the relevant position which treats consequence as truth-preservation in all models. In the strange frame comprising consistent models plus the lonely inconsistent one in which every formula is true, EFQ prevails (no consistent model is a counter-model to the principle, nor is the inconsistent model in which everything is true). Not so in the ground-theoretic framework; it invalidates EFQ even if we allow only for consistent distributions of truth-values plus a single inconsistent one in which every formula is true. EFQ still fails, since even if every formula is true in the single inconsistent model, it does not mean that it is grounded by every other formula in that model. In a model which assigns groundedness (and thus truth) to every literal, ‘Q’ will still not be grounded in either ‘P&¬P’ or its grounds (by the recursive grounding-definition). So, it does not count as a consequence of it, even in our current bizarre model-theoretic frame.

So, while the ground-theoretical framework and the relevant framework both require some inconsistent models in order to invalidate EFQ, for the former framework one such model suffices, whereas the latter requires a whole array of inconsistent models. Hence, the ground-theoretical approach excels in terms of discriminatory power: Its capacity to invalidate EFQ is preserved even if only a single paraconsistent model is allowed, while in such a setting, the relevant notion extensionally collapses into the classical notion (as far as EFQ is concerned).

A tentative diagnosis of the reflections above is this: Just like the ground-theoretical approach, relevance logic (in the form discussed) manages to couple conclusions with premises in a way that respects source. But unlike the ground-theoretical notion of consequence, the relevant notion does not directly trace source; this becomes apparent once we restrict our range of models. Of course, one may find this diagnosis tendentious; certainly the issue has to be studied more carefully, as have to be the differences between relevant and ground-theoretic consequence.

6.2 Web consequence and inexact consequence

An even closer relative of web consequence is Fine’s (2012a: p. 235f.) notion of inexact consequence, a predecessor of which can be found in van Fraassen (1969). Let me briefly mention some differences between those approaches and mine:

First of all, the accounts employ different conceptual frameworks. Inexact consequence is not defined in terms of grounding but in terms of verification or truth-making, i.e. a relation that, unlike grounding, connects propositions with worldly items. This makes the accounts available to different groups of philosophers, depending on what notions they include in their philosophical toolboxes. This difference is also the reason why a detailed comparison of the accounts cannot be given here, since this would require the introduction of the apparatus of truth-maker semantics (future work may show how the current account translates into truth-maker semantics and discuss the merits of such a translation).

Secondly, due to the different conceptual framework employed, the formal apparatus developed above also differs substantially from the one used by Fine.

Thirdly, Fine’s definition of inexact consequence structurally differs from the current account: On Fine’s notion a conclusion counts as a consequence of some premises only if every inexact verifier of the premises is an inexact verifier of the conclusion. Web consequence, however, does not require that every full ground of the premises contain a (full) ground of the conclusion; it only requires that among the grounds of the premises, there is a (full) ground of the conclusion.

This structural difference between the definitions of web and inexact consequence is responsible for two further differences:

On the one hand, for inexact consequence to yield the desired results, one has to exclude the possibility that some truth-functional statements may have irregular truth-makers, i.e. truth-makers that do not operate via the statements connected by the truth-functors. Otherwise, the validity of the elimination rules for truth-functors (e.g. ‘P&Q. So Q’) would not be ensured, since inexact entailment requires that every inexact truth-maker of the premises is an inexact truth-maker of the conclusion. Web consequence, however, does not require an equally strong assumption in order to yield the correct results. For, the ground-theoretical analogue to the requirement that there are no irregular truth-makers would be Fine’s elimination rules for grounding. But those elimination rules are no presupposition of my account. Informally speaking, Fine’s elimination rule for conjunction (Fine 2012b: p. 63ff.) requires that every ground of a conjunction grounds the conjunction through its conjuncts. In contrast, the definition of web consequence only presupposes that every true conjunction has some grounds running through its conjuncts; that way, every true conjunction brings along a thin ground for their conjuncts, so that the entailment of the conjuncts by the conjunction is secured. The said presupposition is a rather weak assumption. Since we are dealing with a conjunction that behaves classically (so that the conjuncts of a true conjunction are true), the introduction rule for conjunction (see Sect. 3) already secures that every true conjunction is grounded in its conjuncts; for, if a conjunction is true, so are its conjuncts; hence, by the introduction rule, the conjuncts ground the conjunction.³⁰ But this does not rule out that some conjunctions have additional grounds which do not run via the conjuncts—whereas this is ruled out by Fine’s elimination rules. To give an example where this may matter: Some philosophers think that a logical truth, say ‘Socrates is wise or isn’t wise’, is grounded in logical laws, say the Law of Excluded Middle. Such a position is excluded by Fine’s elimination rules. But it does not have to be excluded for web consequence to yield the correct results; all that is required here is that ‘Socrates is wise or isn’t wise’ is also grounded in its true disjunct.

On the other hand, the structural difference between the definitions of inexact entailment and web consequence results in some extensional differences between the notions. As remarked in the discussion of FDE, ‘Q∨¬Q’ is a web consequence of ‘P ∨ (Q∨¬Q)’. However, it is not an inexact consequence. For, assume ‘P’ is true; the truth-maker of ‘P’ will then be an inexact verifier of the premise, but it won’t be an inexact verifier of the conclusion.

7 Concluding remarks

Time to take stock: The notion of web consequence has been developed, based on the notion of grounding. The ground-theoretical approach captures certain pre-theoretical intuitions about consequence that get lost in classical treatments; in particular, web consequence does not validate EFQ or VEQ, it is sensitive to aspects of source, and it respects the intimacy between the ideas of ground and consequence. Additionally, it is a useful and flexible notion: We can apply the distinction between formal and material consequence to web consequence, and we can give a model-theoretic account of its formal variety. Let me conclude with some remarks that help to clarify the status of the present project and put it in a wider perspective.

Nowhere have I argued that the classical notion of consequence must be replaced by the ground-theoretic one. In fact, I do not think that we have to choose between the two notions once and for all. Both are theoretically interesting and deserve to be studied in their own right. And each of them may have certain advantages over the other: Classical consequence is easier to handle than web consequence, and since it equates consequence with truth-preservation, it does an excellent job whenever our only interest is to avoid moving from true assumptions to false conclusions. Web consequence, on the other hand, pays better respect to the pre-theoretic intuition that a consequence should be relevantly related to its premises, so that the source of the consequence’s truth can be traced to the premises. We can rest content with having different notions of consequence, designed for slightly different jobs.

I consider it a virtue of the pluralist view that it fits nicely with an Aristotelian idea about proofs. The notions of consequence and proof seem to be intimately related: A genuine proof shows a conclusion to be a consequence of some premises. But Aristotle famously distinguished between two kinds of proof³¹: On the one hand, there are evidential or merely demonstrative proofs which only demonstrate that something is the case. On the other hand, there are explanatory proofs which also show why something is the case; they reveal what brings about a given truth.

It can be instructive to view the distinction between the modal and the ground-theoretical approach to consequence in light of Aristotle’s distinction. Standard modern logic has focussed on proofs of the evidential sort and adopted a corresponding notion of consequence; that a conclusion is a (modal) consequence of something else does in general not reveal why the conclusion holds or by what factors it is brought about. But once the importance of Aristotle’s distinction is acknowledged, it becomes a worthwhile project to look for another concept of consequence which has a closer affinity to explanatory proofs than to evidential ones. And it is the ground-theoretic approach which gives us the desired notion of consequence.

More precisely, the notion of direct consequence (on which consequence is simply the converse of grounding; see Sect. 4.1) strongly corresponds to explanatory proofs: if x is a consequence of y in the explicated sense, x indeed holds because y does. Proofs which establish such consequences thereby also uncover the reasons why the consequences hold.

But how does web consequence relate to Aristotle’s distinction between two kinds of proof? Since web consequence connects a conclusion to premises which need not be its grounds, but only bring along those grounds, it does not directly correspond to explanatory proofs. Establishing that some truth is a web consequence of some premises does not completely reveal the grounds of the truth. But it indicates where those grounds are to be found: among the grounds of the premises. So, web consequence corresponds to proofs which can be called weakly explanatory; the twofold Aristotelian classification of proofs can thus be enriched by a third category.

Similarly, the notion of logical consequence seems to be a natural ingredient in definitions of a variety of other concepts (compare Sect. 2.3 on the concepts truth-making, existential dependence, and essence). While such definitions are often regarded as problematic given the modal explication of consequence, they fare better if they are supplemented with an underlying notion of logical consequence that is stronger than modal consequence. In fact, some existing alternatives to such definitions, which make central use of the notion of grounding, can be seen as incorporating the notion of direct consequence.³² But one might instead use the notion of web consequence here. The resulting definitions would incorporate some relevance constraints and thus be tighter than modally defined notions, but they would be looser than notions defined in terms of direct consequence. Future work may explore this line of thought.

In any case, that many core philosophical notions can be seen as defined in terms of consequence, so that quarrels about the notions can derive from different ideas about consequence, shows the fruitfulness of exploring alternative explications of consequence.³³