Abstract
I present a new approach to the logic and semantics of vagueness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
I wish in this paper to propose a new approach to the topic of vagueness. It is different from the supervaluational approach, which I had previously advocated in Fine (1975), and from almost all other approaches in the literature of which I am aware.Footnote 1 There are two principal respects in which it differs from previous approaches: one concerns the global character of vagueness, of how vagueness relates to a whole range of cases and not merely to a single case; the other concerns the logical character of vagueness, of how it is capable of being conveyed by logical means alone. And so let me say a little more about these two features of the view before proceeding to the account itself.
In order to explain the global character of vagueness, we need to make a distinction that is rarely made or even acknowledged. Take a vague predicate such as ‘bald’. Then we may talk of its vagueness, or indeterminacy, in application to a range of cases. Consider a sorites series, for example, that begins with a completely bald man at one end and proceeds through gradual increments to a very hairy man at the other end. Then we may correctly say that the predicate ‘bald’ is indeterminate, i.e. not completely determinate, in its application to the members of the series. But it also appears as if we may sensibly talk of the indeterminacy in the application of the predicate to a single case. For consider someone in the middle of the sorites series. Then it looks as if we might correctly take the predicate to be indeterminate in its application to this particular man.Footnote 2
Given this distinction, there arises the question of how the two forms of indeterminacy are to be understood and how they are related. The standard view is that indeterminacy in its global aspect is to be understood by reference to its manifestation in particular cases. It is through understanding the notion of a borderline case, where this is a matter of the indeterminacy in the application of a predicate to a single case, that we should understand what it is for a predicate to be vague, where this—at least, in the present context—may be taken to be a matter of the indeterminacy in the application of the predicate to a range of cases. Here is a sampling of authors who have advocated a view of this sort:
However borderline cases should be characterized, it is a datum that vague concepts give rise to them (Wright 2003, p. 93)
Vague predicates have potential or actual borderline cases of application (McLaughin and McGee 1998, p. 221)
It is better to define a predicate as vague if and only if it is capable of yielding borderline cases, where the notion of borderline cases is introduced by examples (Williamson 1994, p. 171)
What does it mean to say that ‘bald’ is vague? Presumably it means that the predicate admits borderline cases (Field 1994, p. 410)
A predicate is extensionally vague if it has borderline cases (Fine 1975, p. 266).Footnote 3
The globalist denies that this is so. For him, global indeterminacy—indeterminacy over a range of cases—is not to be understood by reference to local indeterminacy—the indeterminacy of a single case. Whether the converse holds, and local indeterminacy is to be understood by reference to the global indeterminacy, is another matter. Probably the most plausible position for the globalist is either to deny the existence of local indeterminacy altogether or to claim that, in so far as it exists, it can only be understood by reference to global indeterminacy.
One can get a feel for the globalist position by means of an analogy. Consider some stepping-stones arranged as follows:

The stepping-stones are uneven but no one stepping-stone, considered on its own, is in the relevant sense uneven; the unevenness is a global rather than a local feature of the stepping stones. Or consider the notion of a discontinuous function. No point of discontinuity considered on its own can be said to be discontinuous; rather, it is a matter of the point’s relationship to neighboring points.
These analogies are far from perfect. But they do bring out how the vagueness of a predicate might have to do with its application to a range of cases rather than to a single case; the vagueness of a predicate is, so to speak, an unevenness or ‘singularity’ in its application. And the analogies also bring out how it might still be true, all the same, that some particular case is responsible for the vagueness. Thus if the stepping stones looked like this:

then we could point to the fourth stepping stone as responsible for the unevenness, even though the unevenness itself concerned the general layout of the stones.
The logical question of interest to us relates to how indeterminacy in the application of vague predicates is to be expressed. It has usually been supposed that to do this we will need to make use of a distinctively vagueness-theoretic notion. Thus in addition to the predicate whose indeterminacy is in question and the familiar logical apparatus of the quantifiers and connectives, we will need to make use of some further notion, relating to the general phenomenon of vagueness, if we are to make clear in what the indeterminacy in the application of the predicate is to consist. This further notion has usually been taken to be something like the notion of a borderline case (thereby bringing the present position in line with the localist point of view), though there is no reason in principle why it should not be some other notion, not especially related to the single case.
Once granted the need for this further notion, the question arises as to its status and character. Can it be defined and, if so, then how? And regardless of whether it can be defined, what kind of notion is it? Is it semantic, epistemic, psychological, sociological or perhaps even sui generis? Some of the most hotly debated issues in the literature on vagueness have turned on these questions.
The logicalist denies that any distinctive vagueness-theoretic notion is required in order to give expression to the kind of indeterminacy that is characteristic of vagueness. To state the indeterminacy of a predicate, we need make no use of anything beyond the predicate itself and the familiar apparatus of first-order logic. Indeterminacy, in a word, is a logical phenomenon and no non-logical notions—be they semantic, epistemic psychological, or otherwise—are required in order to give expression to it.
If the logico-globalist position is correct, then it means that the recent literature on vagueness has gone badly astray. The focus on the notion of a borderline case—or on the related notions of determinate or indeterminate truth—is misplaced. The phenomenon of a borderline case—if there is such—is irrelevant to the phenomenon of vagueness; and, consequently, so is all discussion of the nature of borderline cases or all attempts to develop a semantics or logic within which they can be accommodated.
The localist position has become so entrenched that it necessary to restore ourselves to a state of pre-theoretical innocence if we are to appreciate that there is a genuine issue as to whether it should be adopted. We should begin by noting that terms like ‘vague’ and ’borderline case’ are, when used by philosophers, terms of art. A guest may be annoyingly vague as to his intentions, which is not to say that his intention (‘to leave some day next week’) is vague in the philosopher’s sense of the term; a student who barely passes might be said to be a borderline pass even though, by the philosopher’s lights, he would be a clear case of a pass; and a case of law may be borderline simply in the sense of being hard to decide. None of these ordinary uses of the terms correspond to the philosopher’s use; and I doubt that there is any ordinary use that clearly does. The relevant sense of the terms must somehow be made out if it is to be put to philosophical use.
We should note, in the second place, that the core phenomenon of vagueness of interest to the philosophers relates most directly to vagueness in the application of a predicate or term to a range of cases, rather than to a single case. There are two central phenomena that are usually taken to be symptomatic of vagueness. The first is the absence of a sharp cut off between the cases of which the predicate is true and those of which it is false. The other is the susceptibility of vague predicates to soritic reasoning (as when we argue by gradual increments from a hairless man being bald to a hairy man being bald). It is, of course, highly unclear what is meant by a ‘sharp’ cut-off or by a genuine case of soritic reasoning. But however these notions are to be understood, it is clear that they relate to the global application of a predicate to a range of cases rather than to the local application of the predicate to a single case. A cut-off, after all, requires two cases at an absolute minimum, while a piece of soritic reasoning requires at lease three.
In the light of these considerations, it seems clear that the appeal to borderline cases lies more in the nature of a hypothesis than a ‘datum’. It is supposed that what accounts for the indeterminacy in the application of a predicate to a range of cases is the indeterminacy in its application to a single case. The global indeterminacy in the application of the predicate, it is thought, must somehow be made manifest as a localized form of indeterminacy.
Although this is a natural thought, there appears, on further consideration, to be no reasonable way to make it out. Perhaps the most straightforward way to proceed is to say that a predicate is indeterminate in its application to certain objects if it is indeterminate in its application to one of those objects, i.e. if one of those objects is a borderline case of the predicate. But this will not do. For what if no object is a borderline case but one or more of the objects is a borderline borderline case? We can still say that the predicate suffers from some indeterminacy in its application to the objects but not that any one of them is a borderline case.
One might try substituting ‘borderline or borderline borderline case’ for ‘borderline case’ in the account. But a similar difficulty will arise. For what if the object is a borderline borderline borderline case? Indeed, there would appear to be a general difficulty of this sort. For, on the proposed view, the global indeterminacy will be taken to consist in a particular case having a special vagueness-theoretic status—call it ‘schmorderline’. But whatever schmorderlinity might be, it can presumably be borderline whether an object is schmorderline; and, when this is so, we will be in a position to say that the predicate is indeterminate in its application to the objects but not that any of them has that special status. However we attempt to pinpoint the relevant concept of a borderline case, its nature seems forever to elude us.
Nor is this a merely theoretical difficulty to be met by some clever counter-argument. I do not believe that if one surveys the vast literature on the topic one will find a satisfactory account of the vagueness of a predicate in terms of the existence of borderline cases. What one finds is either no account at all or a gesturing towards an account, as in the passages above, that does nothing towards meeting the fundamental difficulty mentioned above.
Let us now turn to a more positive treatment of the pure globalist position. I suspect that, at bottom, the globalist and logicalist positions are the same, and that the most plausible development of either will lead to the other. But let me here explore the logical angle and show how certain purely logical considerations naturally give rise to the hybrid position.
Consider again a sorites series of bald men \(b_{1},\, b_{2},\ldots , b_\mathrm{n}\) going through gradual increments from \(b_\mathrm{1} = \hbox {Baldy}\, \hbox {to } b_\mathrm{n} = \) Hairy. With each member \(b_\mathrm{k}\) of the series we may associate the proposition \(p_\mathrm{k}\) that \(b_\mathrm{k}\) is bald (we shall sometimes also talk of the sentence \(\hbox {p}_ \mathrm{k} = \hbox {Bald}(\hbox {b}_\mathrm{k})\) by which the proposition \(p_\mathrm{k}\) might be expressed); and so corresponding to the series of objects \(b_\mathrm{1},\, b_\mathrm{2}, \ldots , b_\mathrm{n}\) will be a series of propositions \(p_\mathrm{1}\), \(p_\mathrm{2}\), ..., \(p_\mathrm{n}\). Recall that a state-description in the propositions \(p_\mathrm{1},\, p_\mathrm{2}, \ldots , p_\mathrm{n}\) is a conjunction \(q_\mathrm{1} \wedge q_\mathrm{2 }\wedge \cdots \wedge q_\mathrm{n}\) of the propositions \(q_\mathrm{1}\), \(q_\mathrm{2}\), ..., \(q_\mathrm{n}\), where each of the propositions \(q_\mathrm{k}\) is either the proposition \(p_\mathrm{k}\) or its negation \(\lnot p_\mathrm{k}\). We might imagine someone being asked of each man \(b_\mathrm{1}\), \(b_\mathrm{2}\), ..., \(b_\mathrm{n}\) whether or not he is bald. A state-description then corresponds to the respondent providing a ‘yes’ or ‘no’ answer in each case.
We may divide the state-descriptions in the propositions \(p_\mathrm{1}\), \(p_\mathrm{2}\), ..., \(p_\mathrm{n}\) into four classes:
-
(I)
All of the propositions \(p_\mathrm{1}, p_\mathrm{2}, \ldots , p_\mathrm{n}\) are affirmed;
-
(II)
All of the propositions \(p_\mathrm{1}, p_\mathrm{2}, \ldots , p_\mathrm{n}\) are denied;
-
(III)
Some of the propositions \(p_\mathrm{1}, p_\mathrm{2}, \ldots , p_\mathrm{n}\) are affirmed, some denied, and at least one denial is succeeded by an affirmation.
-
(IV)
Some of the propositions \(p_\mathrm{1}, p_\mathrm{2}, \ldots , p_\mathrm{n}\) are affirmed, some denied, but no denial is succeeded by a affirmation.
There is exactly one state-description under (I), viz. \(p_\mathrm{1}\wedge p_\mathrm{2} \wedge \cdots \wedge p_\mathrm{n}\), and exactly one under (II), viz. \(\lnot {p}_\mathrm{1} \wedge \lnot {p}_\mathrm{2} \wedge \cdots \wedge \lnot {p}_\mathrm{n}\). Any state-description under (III) will be of the form \( \cdots \wedge \lnot p_\mathrm{k} \wedge p_\mathrm{k+1} \wedge \cdots \), while any state-description under (IV) will be of the form \(p_\mathrm{1} \wedge p_\mathrm{2} \wedge \cdots \wedge p_\mathrm{k }\wedge \lnot p_\mathrm{k+1} \wedge \lnot p_\mathrm{k+2 } \cdots \wedge \lnot p_\mathrm{n}\).
What of the state-descriptions themselves? Should they be affirmed or denied? We wish to deny that the last man \(b_\mathrm{n}\) in the series is bald. But given that we wish to deny \(p_\mathrm{n}\), we should deny the single state-description \(p_\mathrm{1} \wedge p_\mathrm{2} \wedge \cdots \wedge p_\mathrm{n}\) from the first class. We wish to affirm that the first man \(b_\mathrm{1}\) in the series is bald and hence to deny that he is not bald. But given that we wish to deny \(\lnot p_\mathrm{1}\), we should deny the single state-description \(\lnot p_\mathrm{1} \wedge \lnot p_\mathrm{2} \wedge \cdots \wedge \lnot p_\mathrm{n}\) from the second class. We will wish to deny that a given man \(b_\mathrm{k+1}\) in the series is bald but that his predecessor \(b_\mathrm{k}\), who has fewer hairs on his head, is not bald. But given that we wish to deny \(\lnot p_\mathrm{k}\wedge p_\mathrm{k+1}\), we will wish to deny any state-description \( \cdots \wedge \lnot p_\mathrm{k}\wedge p_\mathrm{k+1} \wedge \cdots \) from the third class. Finally, we will wish to deny that a given man \(b_\mathrm{k}\) in the series is bald but that his successor \(b_\mathrm{k+1}\) is not bald. For how could a miniscule difference in hair coverage make a difference as to whether or not a man is bald? But given that we wish to deny \(p_\mathrm{k} \wedge \lnot p_\mathrm{k+1}\), we will wish to deny any state-description \(p_\mathrm{1} \wedge p_\mathrm{2} \wedge \cdots \wedge p_\mathrm{k }\wedge \lnot p_\mathrm{k+1} \wedge \lnot p_\mathrm{k+2 } \cdots \wedge \lnot p_\mathrm{n}\) from the fourth class.
It therefore looks as if we will wish to deny each of the state-descriptions in the propositions \(p_\mathrm{1}\), \(p_\mathrm{2}\), ..., \(p_\mathrm{n}\); and this I would like to suggest is the hallmark of indeterminacy. Given a predicate F, what it is for the predicate to be indeterminate in its application to the objects \(a_\mathrm{1}\), \(a_\mathrm{2}\), ..., \(a_\mathrm{n}\) is for each of the state-descriptions in the propositions Fa \(_\mathrm{1}\), Fa \(_\mathrm{2}\), ..., Fa \(_\mathrm{n}\) to be false. Or, to state things at the level of the object-language, let us use I(\(\hbox {p}_\mathrm{\mathrm 1}\), \(\hbox {p}_\mathrm{\mathrm 2}\), ..., \(\hbox {p}_\mathrm{n})\), for given sentences \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}\), ..., \(\hbox {p}_\mathrm{n}\), to state that it is indeterminate (i.e. it is not completely determinate) which of \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}\), ..., \(\hbox {p}_\mathrm{n}\) is the case, and let us use I(F; \(\hbox {a}_{1}\), \(\hbox {a}_{2}\), ..., \(\hbox {a}_\mathrm{n})\), for F a predicate and \(\hbox {a}_{1}\), \(\hbox {a}_{2}\), ..., \(\hbox {a}_\mathrm{n}\) names of objects, to state that it is indeterminate (i.e. not completely determinate) which of \(\hbox {a}_{1}\), \(\hbox {a}_{2}\), ..., \(\hbox {a}_\mathrm{n}\) is F. Where \(\hbox {S}_\mathrm{1}\), \(\hbox {S}_\mathrm{2}\), ..., \(\hbox {S}_\mathrm{m}\) are the state-descriptions in \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}\), ..., \(\hbox {p}_\mathrm{n}\), we might then setFootnote 4:
Thus the sentences will be indeterminate if any complete resolution of their truth-values must be false and the predicate will be indeterminate in application to the objects if any complete resolution of its application to those objects will be false.
I take it that most philosophers would be happy with denying each of the state-descriptions from the first three classes but would demur from denying all of the state-descriptions from the fourth class. It would perhaps be agreed that there was something incorrect about asserting any one of the state descriptions from the fourth class, since that would appear to commit one to the view that the predicate was not indeterminate in its application to the given objects. But it would be denied that it was thereby correct to deny any of those state-descriptions, i.e. to assert its negation. It would be incorrect to assert any one of the state-descriptions under the supervaluational approach, for example, since such an assertion would commit one to its being definitely the case and it would be incorrect under the epistemic view since such an assertion would commit one to its being known to be the case. However, that is not to say that one can go on to assert the negation of the state-description, since that might also not be definite or known.
This is an extraordinary and quite counter-intuitive position to adopt. Surely one wants to deny that there is a sharp line between the bald and non-bald cases in the sorites series and what better way to do this than to deny each state-description from the fourth class, given that each such description \(p_{1} \wedge p_{2} \wedge \cdots \wedge p_{k }\wedge {\lnot {p}}_{k+1} \wedge {\lnot {p}}_{k+2 } \cdots \wedge {\lnot {p}}_\mathrm{n}\) draws a sharp line in each of the different ways in which it can arise—either between the first and second, the second and third, ...or the next-to-last and last member of the series. It is only by some devious interpretation of what might be meant by a sharp line or what might be involved in assertion that this natural conclusion can be resisted. It might also be objected that this interpretative maneuver does not remove the difficulty but merely moves it to a higher level. For, as argued in Fine (2008), we will still be stuck with drawing a sharp line, not now between the bald and non-bald cases, but between the definitely bald and not definitely bald, or between the definitely definitely bald and not definitely definitely bald cases, or something else of this sort.
There is an alternative, somewhat more perspicuous, way to express indeterminacy. Instead of forming the state-descriptions from the propositions \(p_{1}\), \(p_{2}\), ..., \(p_\mathrm{n}\), we form the disjunctions \(p_{1 } \vee \lnot p_{1}, p_{2 }\vee \lnot p_{2}, \cdots , p_\mathrm{n }\vee \lnot p_\mathrm{n}\) of each of the propositions with its negation. Indeterminacy may then be expressed as the denial of the conjunction \((p_{1 }\vee \lnot p_{1})\wedge (p_{2 }\vee \lnot p_{2}) \wedge \cdots \wedge (p_\mathrm{n }\vee \lnot p_\mathrm{n})\) of the resulting disjunctions. Or, using an object-language formulation, we may set:
Under certain plausible assumptions,Footnote 5 it can then be shown that the present formulation, in terms of LEM, is equivalent to the previous formulation, in terms of state-descriptions. Each of the conjuncts \(\hbox {p}_\mathrm{k }\vee \lnot \hbox {p}_ \mathrm{k}\) is, of course, an instance of the Law of Excluded Middle (LEM); and so their conjunction will constitute a joint application of LEM. Thus what indeterminacy denies is the joint application of LEM to a number of different sentences \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}, \ldots , \hbox {p}_\mathrm{n}\).
The present formulation in terms of LEM also enables us to say when a predicate is indeterminate over the the domain of quantification:
(it is not the case that every object F’s or doesn’t F) and when it is indeterminate over the objects conforming to a given condition \(\upvarphi \)(x):
(it is not the case that every \(\upvarphi \) F’s or doesn’t F). The special case in which F is indeterminate in its application to the objects \(a_{1}\), \(a_{2}\), ..., \(a_\mathrm{n}\) is simply the one in which \(\upvarphi \)(x) is taken to be the condition \((\hbox {x} = \hbox {a}_{1} \vee \hbox { x} = \hbox {a}_{2} \vee \cdots \vee \hbox { x} = \hbox {a}_\mathrm{n})\) of being identical to \(\hbox {a}_{1}\) or \(\hbox {a}_{2}\) or ...or \(\hbox {a}_\mathrm{n}\).
If these formulations of indeterminacy are correct, then they provide an immediate vindication of the logicalist position, since they only make use of the usual apparatus of the connectives and quantification. In particular, no appeal is made to the notion of determinate truth or the notion of borderline case.
The formulations also lend support to the globalist position. For consider the special case in which the predicate F is taken to be indeterminate in its application to a single object \(a\). The state descriptions in Fa are Fa and \(\lnot {\hbox {Fa}}\), and so the indeterminacy I(F; a) of F in application to the object \(a\) is simply given by \(\lnot {\hbox {Fa}}\wedge \lnot \lnot {\hbox {Fa}}\) under the first formulation, while it will be given by \(\lnot (\hbox {Fa} \vee \lnot {\hbox {Fa}}\)), which is equivalent to \(\lnot {\hbox {Fa}} \wedge \lnot \lnot {\hbox {Fa}}\), under the second formulation. Thus in either case local, or single case, indeterminacy will be provably non-existent. Of course, local indeterminacy might be possible in some other sense of the term, but not in a sense commensurate with the global notion; it cannot simply be understood as the restriction of the global notion to the single case. Perhaps more significantly still, it looks increasingly unlikely, even if there is a coherent notion of local indeterminacy, that global indeterminacy could be understood in terms of local indeterminacy. For what local features of the propositions \(p_{1}\), \(p_{2}\), ..., \(p_\mathrm{n}\) could plausibly account for the failure of LEM to hold of all the instances \(p_{1 }\vee \lnot p_{1}\), \(p_{2 }\vee \lnot p_{2}\), ..., \(p_\mathrm{n }\vee \lnot p_\mathrm{n}\) if not the failure of a single instance?
We see that the most elementary considerations naturally lead to the logico-globalist position. But there is a worry. For can we be sure that the position is coherent. We do not wish to deny a single instance of LEM, since that would lead to contradiction. But we do wish to deny a conjunction of such instances. Yet can we coherently do the one without the other?
Of course, classical logic does not allow us to deny any instance or any conjunction of instances of LEM. Intuitionistic logic does allow us to deny a statement of the form \(\forall \hbox {x}(\hbox {Fx }\vee \lnot \hbox {Fx})\) but it does not allow us to deny a finite conjunction of instances of LEM (since the double negation of such a finite conjunction is an intuitionistic theorem). Paraconsistent logics do allow us to deny a finite conjunction of instances of LEM, but they also allow us to deny a single instance and therefore do not discriminate between the two cases in the way we would like. We therefore appear to be in new logical territory and a new approach to the logic and how it might be modeled would appear to be required.Footnote 6
A convenient starting point from which to understand the new modeling is Kripke’s semantics for intuitionistic logic. Under such a semantics, at least in so far as it relates to vague language, a sentence may be taken to be evaluated relative to an admissible use of the language, where this is a pattern of application that is in conformity with the meaning of our predicates and the facts. Thus given a sorites series \(b_{1},\, b_{2}, \ldots , b_{100}\) for ‘bald’, an admissible use might be one in which ‘bald’ is taken to be true of the first forty men, false of the last forty men, and neither true nor false of the twenty men in the middle. Any admissible use may be required to take ‘bald’ to be true of the first man \(b_{1}\) and to be false of the last man \(b_{100}\), but it may be left open whether it should be true of \(b_{41}\), say, or false of \(b_{60}\), so that there will also be an admissible use in which ‘bald’ is true of \(b_{41}\) and an admissible use in which it is false of \(b_{60}\). One admissible use may ‘extend’ or precisify’ another in an obvious sense; any application sanctioned by the latter will be sanctioned by the former. So, for example, the admissible use in which ‘bald’ is true of \(b_{1},\, b_{2}, \ldots , b_{40}\) and false of \(b_{60},\, b_{61}, \ldots , b_{100}\) (abbreviate this to \(b_{40}/b_{60})\) will extend the admissible use in which it is true of \(b_{1},\, b_{2},\, \ldots , b_{40}\) and false of \(b_{61},\, b_{62}, \ldots , b_{100}\) (abbreviation: \(b_{40}/b_{61})\).
We may then adopt the following clauses for the evaluation of truth-functionally complex statements under an admissible use:Footnote 7
-
(i)
\(\hbox {B } \wedge \hbox { C}\) is true under a use iff B and C are true under that use;
-
(ii)
\(\hbox {B } \vee \hbox { C}\) is true under a use iff B or C is true under the use;
-
(iii)
\(\lnot \hbox {B}\) is true under a use iff B is true under no precisification of that use;
-
(iv)
\(\hbox {B }\supset \hbox { C}\) is true under a use iff C is true under any precisification of that use under which B is true.
This semantics will not serve our purpose, since it validates intuitionistic logic, but a certain modification of it will. The first step is to replace the relation of extension or precisification with the relation of compatibility. Two uses are compatible if they do not conflict; it is not also required that one be an extension of the other. So, for example, the use \(b_{40}/b_{60}\) may well be compatible with the use \(b_{41}/b_{61 }\)even though neither is an extension of the other.
There is a very natural interpretation of incompatibility in terms of disagreement. For with each use may be associated a speaker who adopts that use, i.e. who assents to all and only the sentences true under that use. A case of incompatible uses will then correspond to a case of disagreement, with any speaker who adopts the one disagreeing with any speaker who adopts the other use. One very clear case of incompatibility is when some statement is true under the one use while its negation is true under the other use although, as we shall see, there may be other ways in which incompatibility can arise. It is very plausible, for example, that if the conditional ‘if A then B’ is true under a given use without A being true under that use then any use in which A is true but B is not will also be incompatible with that use.
We now adopt clauses (i)–(iii) above, but using the notion of compatibility in place of precisification:
- \(\mathrm{(i')}\) :
-
\(\hbox {B }\wedge \hbox { C}\) is true under a use iff B and C are true under that use;
- \(\mathrm{(ii')}\) :
-
\(\hbox {B }\vee \hbox { C}\) is true under a use iff B or C is true under the use;
- \(\mathrm{(iii')}\) :
-
\(\lnot \hbox {B}\) is true under a use iff B is true under no use compatible with that use.
We may also write \(\mathrm{(iii')}\) in the form:
- \(\mathrm{(iii'')}\) :
-
\(\lnot \hbox {B}\) is true under a use iff any use under which is true is incompatible with that use.
Thus the clause tells us, in effect, that to assent to \(\lnot \hbox {B}\) is to disagree with anyone who assents to B.
There are a number of significant differences which result from substituting the compatibility relation for the extension relation. In the first place, the two relations satisfy different formal properties. Extension is a reflexive and transitive relation. On the other hand, compatibility is a reflexive and symmetric relation. But it need not be transitive. Thus \(b_{50}/b_{52}\) is compatible with (indeed, an extension of) \( b_{48}/b_{52 }\) and \(b_{48}/b_{52}\) is compatible with \(b_{48}/b_{50}\), but \(b_{50}/b_{52}\) is not compatible with \(b_{48}/b_{50}\) (since ‘bald’ is true of \(b_{50}\) under the one use and false of \(b_{50}\) under the other use). This difference in the formal properties of the underlying relations makes for a significant difference in the resulting logic.
In the second place, there is no general requirement that two compatible admissible uses should have a common admissible extension. Compatibility in the uses does not mean that they can be combined. An example of such a failure arises from the sorites. For there may be an admissible use of the predicate ‘bald’ in which it is true of \(b_{50}\), say, and an admissible use in which it is false of \(b_{51}\) and yet no admissible use in which it is true of \(b_{50}\) and false of \(b_{51}\), since that would be to countenance a sharp cut-off between those of the men who are bald and those who are not bald.
In the third place, a consistent use that is compatible with an admissible use may not itself be admissible. Indeed, we can construct an analogue of the sorites argument to show why must be so. For take an admissible use of ‘bald’ that ends (on the truth side) with \(b_{50}\). Since no admissible use can involve a sharp cut-off, the use must resume (on the false side) after \(b_{51}\). Thus the predicate ‘bald’ will fail to be false of \(b_{51}\) in the given use and so it must be compatible with a use in which the predicate is true of \(b_{51}\) (by the clause for negation). If this further use is admissible, the argument can be repeated to show that it is compatible with a use under which the predicate is true of \(b_{52}\). Proceeding in this way, we can show that there is an admissible use under which the predicate is true of \(b_{100}\), which is clearly impossible.
This argument is not itself a sorites since it is conducted in the precise meta-language. Thus if we are properly to account for the behavior of admissible uses within a precise formal semantics, we must tolerate non-admissible uses and allow admissible uses to be compatible with such uses.
We have not so far given a clause for the conditional. It turns out that the straightforward analogue of the standard clause in the Kripke semantics will not do (one reason is that \(\hbox {A}\,\supset \,\hbox {B}\) would not then follow from A and B, another is that the all-important Possibility Theorem given below would then fail). However, there is a simple modification of the clause that is satisfactory:
- (v\('\)):
-
\(\hbox {B }\supset \hbox { C}\) is true under a use iff either (a) B and C are both true under the use or (b) C is true under any use compatible with a use under which B is true.
Thus \(\hbox {B }\supset \hbox { C}\) will be true under a given use as long as B and C are true under that use, even though there may be a compatible use under which B is true and C is not.
The present semantics delivers the results concerning LEM that we had previously hoped to obtain. First, we should note that the negation of any single instance \(\hbox {p} \vee \lnot \hbox {p}\) will be false, i.e. its double negation \(\lnot \lnot (\hbox {p }\vee \lnot \hbox {p})\) will be true. For \(\lnot (\hbox {p }\vee \lnot \hbox {p}\)) cannot be true under any use \(u\). For either p is true under some use \(v\) compatible with \(u\), in which case \((\hbox {p }\vee \lnot \hbox {p}\)) is true under v and so \(\lnot (p \vee \lnot \hbox {p}\)) is not true under \(u\) or else p is not true under any use compatible with v, in which case \(\lnot \hbox {p}\) and hence \((\hbox {p }\vee \lnot \hbox {p}\)) is true under \(u\) and so, again, \(\lnot (\hbox {p }\vee \lnot \hbox {p}\)) is not true under \(u\). Given that \(\lnot (\hbox {p }\vee \lnot \hbox {p}\)) is not true under any use, it follows that \(\lnot \lnot (\hbox {p }\vee \lnot \hbox {p}\)) is true under every use.
We may also show how a sentence of the form \(\lnot [(\hbox {p }\vee \lnot \hbox {p}) \wedge (\hbox {q }\vee \lnot \hbox {q})]\) can be true under a given use (and similarly for the negations of longer conjunctions of instances of LEM). For consider the model depicted below:

in which we merely take p to be true at the point labeled p and q to be true at the point labeled q and in which the compatibility relation is indicated by the lines. We can then read off the following facts from the model:
-
(a)
neither q nor \(\lnot \hbox {q}\) is true under the point labeled p;
-
(b)
neither p nor \(\lnot \hbox {p}\) is true under the point labeled q;
-
(c)
neither q nor \(\lnot \hbox {q}\) is true under the point labeled \(\lnot \hbox {p}\);
-
(d)
neither p nor \(\lnot \hbox {p}\) is true under the point labeled \(\lnot \hbox {q}\).
It follows that \((\hbox {p }\vee \lnot \hbox {p})\, \wedge (\hbox {q }\vee \lnot \hbox {q})\) is not true under p by (a), not true under q by (b), not true under \(\lnot \hbox {p}\) by (c), and not true under \(\lnot \hbox {q}\) by (d). Thus \((\hbox {p }\vee \lnot \hbox {p}) \wedge (\hbox {q }\vee \lnot \hbox {q})\) is not true under any of the uses; and so \(\lnot [(\hbox {p }\vee \lnot \hbox {p}) \wedge (\hbox {q }\vee \lnot \hbox {q})]\) is true under each of the uses.Footnote 8
One distinctive feature of the present semantics is that the rule of conjunctive syllogism:
is no longer valid. Here is a simple model in which it fails:

For p is true under p; \(\hbox {p }\wedge \hbox { q}\) is not true under p, since q is not true under p, and \(\hbox {p }\wedge \hbox { q}\) is not true under q, since p is not true under q; and so \(\lnot (\hbox {p }\wedge \hbox { q})\) is true at p. But \(\lnot \hbox {q}\) is not true at p, since q is true at q.
Another distinctive feature is the failure of reductio. Reductio holds without side assumptions, i.e. if A entails B and \(\lnot \hbox {B}\) then \(\lnot \hbox {A}\) will be valid. But it fails with side assumptions. From the fact that A with given side assumptions implies both B and \(\lnot \hbox { B}\), it does not follow that the side assumptions themselves will entail \(\lnot \hbox {A}\). Indeed, the failure of Conjunctive Syllogism already indicates why this should be so. For B with side assumptions A and \(\lnot (\hbox {A }\wedge \hbox { B})\) will entail \(\hbox {A }\wedge \hbox { B}\) and \(\lnot (\hbox {A }\wedge \hbox { B})\) but we do not want the side assumptions alone to entail \(\lnot \hbox {B}\).
But perhaps the most distinctive feature of the resulting logic is that it evades the impossibility result of Fine (2008). We would like the indeterminacy of the propositions expressed by the sentences \(\hbox {p}_\mathrm{1},\, \hbox {p}_\mathrm{2}, \ldots , \hbox {p}_\mathrm{n}\) to be incompatible with any sharp cut-off—as might be expressed by \(\hbox {p}_\mathrm{1},\, \hbox {p}_\mathrm{2}, \ldots , \hbox {p}_ \mathrm{k}, \lnot \hbox {p}_ \mathrm{k+1}, \ldots , \lnot \hbox {p}_\mathrm{n}\) or perhaps in some other way, using more complicated constructions on \(\hbox {p}_\mathrm{1},\, \hbox {p}_\mathrm{2}, \ldots , \hbox {p}_\mathrm{n}\) than simple affirmation or denial. What can be shown is that if we take indeterminacy to be the denial of the conjunction of the instances of LEM, then indeterminacy, as so construed, will indeed by incompatible with any sharp cut-off, whether expressed in the original language or in some infinitary extension thereof.Footnote 9
No treatment of vagueness is complete without an account of the sorites. Where does the error in soritic reasoning lie? Why is it an error? And why are we so inclined to make the error?
Let us focus on the sentential rather than the quantificational versions of the soritic arguments, since I doubt that the quantificational versions give rise to any essentially new issues. The usual version of the sentential version, in the case of a soritic series of bald men \(b_{1},\, b_{2}, \ldots , b_\mathrm{n}\) goes as follows: \(\hbox {b}_{1}\) is bald; if \(\hbox {b}_{1}\) is bald then \(\hbox {b}_{2}\) is bald; and so \(\hbox {b}_{2}\) is bald. Continuing in this way, we reach the absurd conclusion that \(\hbox {b}_\mathrm{n}\) is bald. We may exhibit the structure of the argument as follows:

However, there are alternative ways of formulating the major premiss:
-
(i)
as a Conditional: \(\hbox {p}_ \mathrm{k} \supset \hbox {p}_ \mathrm{k+1}\) (as above)
-
(ii)
as a Disjunction: \(\lnot \hbox {p}_ \mathrm{k} \vee \hbox {p}_ \mathrm{k+1}\)
-
(iii)
as the Negation of a Conjunction: \(\lnot (\hbox {p}_ \mathrm{k} \wedge \lnot \hbox {p}_\mathrm{k +1})\).
In the first case, the transitional inference takes the form:
and is an instance of Modus Ponens (from A and \(\hbox {A }\supset \hbox { B}\) infer B).
In the second case, the transitional inference takes the form:
We might break this down into the following further step:

thereby obtaining an instance of Double Negation Introduction (from A infer \(\lnot \lnot \hbox {A}\)), followed by an instance of Disjunctive Syllogism (from \(\lnot \hbox {A}\) and \(\hbox {A }\vee \hbox { B}\) infer B).
If we wish to avoid the application of Double Negation Introduction and simply rely on the rule of Disjunctive Syllogism, then we might run the reasoning backwards as follows:

(in effect going from \(b_\mathrm{k+1 }\) is not bald and either \(b_\mathrm{k }\) is not bald or \(b_\mathrm{k+1 }\)is bald to \(b_\mathrm{k}\) is not bald).
In the third case, the transitional inference takes the form:
Again, we might break this down into a further step:

thereby obtaining an instance of Conjunctive Syllogism (from A and \(\lnot (\hbox {A }\wedge \hbox { B})\) infer \(\lnot \hbox {B}\)) followed by an instance of Double Negation Elimination (from \(\lnot \lnot \hbox {A}\) infer A).
If we wish to avoid the application of Double Negation Elimination and simply rely on the rule of Conjunctive Syllogism, then we might run the reasoning backwards as before:

(in effect going from \(b_\mathrm{k+1 }\) is not bald and it is not the case that \(b_\mathrm{k }\)and \(b_\mathrm{k+1 }\) is not bald to \(b_\mathrm{k}\) is not bald).Footnote 10
Where do these versions of the sorites argument go wrong? I am going to assume that there is nothing amiss with the minor premisses \(\hbox {p}_\mathrm{0}\) and \(\hbox {p}_\mathrm{n}\) (to the effect that Hairless is bald and Hairy is not bald) or with the general structure of the argument (according to which the various transitional inferences may legitimately be chained). The problem is then either with the validity of the transitional inferences or with the major premisses to which they are applied.
It has commonly been assumed that the proper response to the sorites argument is largely indifferent to its formulation. But this is not my own view; and we will therefore go to great care to discuss the different versions of the argument independently of one another.
Let us first discuss the disjunctive formulation of the major premiss. Under this formulation, I assert that either \(b_\mathrm{k }\)(call him Left) is not bald or his neighbor \(b_\mathrm{k+1}\) (call him Right) is bald. But why accept this? It is not directly justified by the intuition that there is no sharp cut-off between the men who are bald and the men who are not bald. And it seems to assume much more determinacy in the application of the predicate ‘bald’ than we are justified in taking to exist. Indeed, if Right is bald then so is Left himself (given that he has fewer hairs on his head). But then the assertion that Left is not bald or Right is bald will commit us to the application of LEM to Left, i.e. to the claim that Left is not bald or Left is bald. Thus in so far as we have any disinclination to assert that Left is not bald or Left is bald, we should have at least as much disinclination to assert that Left is not bald or Right is bald.
The other versions of the major premiss assumptions are more plausible. But it seems to me that the negated conjunctive version of the major premiss is, in its turn, much more plausible than the conditional version. Indeed, the intuitions behind these two versions of the major premiss are rather different. The conditional version rests upon what has sometimes been called the Tolerance Principle:
Tolerance If two cases are sufficiently alike and the first is bald then the second is also bald.
The negative conjunctive version, by contrast, rests upon a Cut-Off Principle:
Cut-Off If two cases are sufficiently alike then it is not the case that the first is bald and the second is not.
Tolerance tells us that the status of being bald will transfer smoothly from one man to his neighbor. Cut-Off tells us that there will be no abrupt transition from a one man being bald to his neighbor not being bald. Of course if there is a smooth transition then there cannot be an abrupt transition. But to deny that there will be an abrupt transition, from bald to not bald, is not to affirm that there will be a smooth transition, from bald to bald, unless we already assume that the neighbor is either bald or not bald.
The point perhaps becomes clearer if stated explicitly in terms of truth or falsity. Tolerance permits us to make the transition from the truth of the antecedent claim (that Left is bald) to the truth of the consequent claim (that Right is not bald), while Cut-Off forbids us from making the transition from the truth of the antecedent claim to the falsity of the consequent claim. But to say that we are forbidden (given the truth of the antecedent claim) to assert the falsity of the consequent claim is not to say that we are permitted to assert the truth of the consequent claim unless we also take for granted that the consequent claim is either true or false.
Given this difference in their import, Cut-off would appear to be much more plausible than Tolerance. For there would appear to be something especially egregious in saying that a given man was bald but that his near neighbor was not bald, in contravention to Cut-Off. This would be to make a distinction when there was no relevant basis for making it. But to say that a given man was bald and yet refuse to say that his near neighbor was bald, in contravention to Tolerance, would not be nearly as egregious and might even appear to be a quite reasonable stand to take as we move from one member in a sorites series to the next .
Of course, in this latter situation, we are also making a distinction—for we are assenting to the one man being bald while not assenting to his near neighbor being bald. But this is a distinction in our response to the cases; it does not in itself commit one to a distinction in the cases themselves. In refraining from saying that a given man is bald, one is not thereby saying that he is not bald; and so it is far from clear that any basis we might have for forming a differentiated response, in which there is assent in the one case yet not in the other, should thereby provide a basis for forming a differentiated judgement, in which there is assent in the one case and dissent in the other.
Thus it seems that the various versions of the major premiss differ greatly in their degree of plausibility. The disjunctive version is not at all plausible; the conditional version is a great deal more plausible; and the negated conjunctive version is highly plausible, perhaps unquestionably so. With the rules of inference involved in the various transitional inferences, it is the reverse: the application of the rules of Modus Ponens and Disjunctive Syllogism is relatively unproblematic while the application of Conjunctive Syllogism is not.
It is true that the rules of Modus Ponens and Disjunctive Syllogism have been questioned in other contexts—Modus Ponens by McGee (1985) in its application to embedded conditionals and Disjunctive Syllogism by certain relevance logicians in its application to inconsistent assumptions. But these reasons for questioning the inferences would appear to have no application to the present context; there are no embedded conditionals and there is no inconsistency in the assumptions (except at the very end, when no further applications of Disjunctive Syllogism need be made).
On the other hand, the application of Conjunctive Syllogism within the context of the reverse sorites is quite problematic. For suppose I assert that:
-
(i)
Right is not bald; and
-
(ii)
it is not the case that Left is bald and Right is not bald.
Am I then entitled to infer that Left is not bald? Clearly, I should not go on to assert that Left is bald and, given that Left is bald or Left is not bald, I am entitled to infer that Left is not bald. But in the absence of that assumption, it is not at all clear that I am entitled to make the inference. In asserting (i) and (ii), I am thereby ruling out that Left is bald. But it is not clear that I am thereby ruling in that Left is not bald.
This suggests that the argument is to be resisted in different ways under the different formulations—by rejecting the major premiss, but not the rule of inference, when the major premiss takes the form of a disjunction or a conditional and by rejecting the rule of inference, but not the major premiss, when the major premiss takes the form of a negative conjunction.
Let us now see how these different versions of the soritical reasoning fare under the compatiblist semantics. It is readily verified that Modus Ponens and Disjunctive Syllogism are valid rules of inference while, as we have already seen, Conjunctive Syllogism will not be valid.Footnote 11 It is also in keeping with our informal account of the semantics in terms of disagreement that Conjunctive Syllogism should fail in its application to the present case. For suppose that I say that Right is not bald (and would thereby ‘object to’, or be in ‘disagreement with’, someone who says that he is bald) and that I also say that it is not the case that Left is bald and Right is not bald (and would thereby object to someone who said both that Left is bald and that Right is not bald). But in objecting to someone saying Right is bald and to someone saying Left is bald and Right is not bald, I am not thereby objecting to someone saying that Left is bald. Of course, I myself would not say that Left was bald, but that is because I have already said that Right is not bald. As long as the other person had made no prior commitment to Right not being bald, I would have no objection to his saying that Left was bald.
The present semantics can also account for our differential judgements concerning the different versions of the major premiss. For it is perfectly compatible with our denying that Left is bald and Right is not bald that we should be unwilling to assent to the proposition that Left is not bald or Right is bald or to the proposition that Right is bald if Left is bald.Footnote 12 Thus the formal modeling is in conformity with our intuitive judgements about the different versions of the soritical reasoning—which is perhaps some kind of argument in its favor.
We come to what is perhaps the most difficult question of all. Why are we inclined to accept an argument that is in fact unsound? Part of what makes the question so difficult is that, whatever our error, it does not appear to be a straightforward mistake in our reasoning or in our judgements as to what is true. For the error appears to be irresistible. No matter how much or in what way we might be disabused of our error, we are still inclined—perhaps as much as we ever were—to make the very same error.
In this respect, we appear to have something like the cognitive analogue of a perceptual illusion, such as The Müller–Lyer illusion. Even if we are told that the one line is not in fact longer than the other and even if we are given an explanation as to why we perceive it as longer, we cannot but help perceive the one line as longer. Our explanation of the soritic error must therefore involve some incurable tendency of the mind just as the Müller–Lyer illusion involves an incurable tendency of our perceptual apparatus.
But this means no satisfactory explanation of the error can attribute it to a straightforward mistake in reasoning (such as affirming the consequent) or a straightforward error of judgement (such as failing to detect an equivocation). For most of us (at least in our more reflective moments) can be disabused of such errors.
Once we are aware of the nature of the difficulty, it becomes clear that most of the usual attempts to account for the error are dismal failures. Let us look at the supervaluational view by way of example (similar criticisms also apply to the epistemic view). According to supervaluationism, the major premisses—whether in conditional, disjunctive, or negative conjunctive form—are not all true. Take the negative conjunctive case. The conjunction of all the major premisses is the following:
(for each man \(b_\mathrm{k}\), k = 1, 2, ..., \(\mathrm{n}-1\), it is not the case that \(b_\mathrm{k}\) is bald and his neighbor \(b_\mathrm{k+1}\) is not bald). We are inclined to regard the conjunction as true and certainly not as false and yet, according to the supervaluational view, it is false (since under any precisification one of the conjuncts will be false). Whence the error in our judgement?
It is very hard to say. It might be thought that we somehow confuse (*) with:
(for each man \(b_\mathrm{k}\), k = 1, 2, ..., \(\mathrm{{n}}-1\), it is not definitely the case that \(b_\mathrm{k}\) is bald and his neighbor \(b_\mathrm{k+1}\) is not bald), which might, with some plausibility, be regarded as true. But this is a pretty gross error. And why would be inclined to make it?
It might be thought that we tend to give a conjunction \((\hbox {A }\wedge \hbox { B})\) under a negation a strong reading as \(\hbox {D}(\hbox {A }\wedge \hbox { B})\). But we do not normally give \((\hbox {A }\wedge \hbox { B})\) under negation a strong reading. When, for example, Herbert is borderline bald and Tim is borderline thin, then we are under no inclination to say that it is not the case that Herbert is bald and Tim is thin. And so why in this case? And even if we do make an error of this sort, why should it be an ineluctable error? We have what appears to be a straightforward misinterpretation of (*) as (**); and so why, once it is pointed out, should we still be inclined to make it?
In the face of these difficulties, I should like to suggest that the error to which we fall prey in the sorites has its source in a transcendental illusion. At its most general, a transcendental illusion is the illusion of thinking that we can attain an external or ‘transcendent’ perspective on some phenomenon or practice when no such perspective is to be had.Footnote 13 Somewhat more specifically, it relates to our finding certain concepts to be intelligible from such a perspective even though their intelligibility cannot be properly grounded in the phenomenon or practice itself. Thus the error is a conceptual error, of taking a concept that is unintelligible to be intelligible, rather than a straightforward logical error or an error of judgement; and what makes the error appear so irresistible is that we are irresistibly drawn to adopting a perspective from which the concept is intelligible.
We can better understand the transcendental illusion at work in the case of the vagueness by comparing it with the transcendental illusion that might plausibly be taken to be operative in the case of the set-theoretic paradoxes. In this case, we are irresistibly drawn towards accepting Unrestricted Comprehension:
(for any condition \(\upvarphi \), there is a set of objects satisfying the condition) even though contradiction is but one step away (through the substitution of \(\lnot (\hbox {x }\in \hbox { x})\) for \(\upvarphi \)(x)). Whence the inclination to accept this logical falsehood?
According to the transcendentalist line of thinking, there is indeed an acceptable principle of Comprehension. It states, loosely speaking, that for any condition on a domain of objects, there will exist a set of the objects from the domain that satisfy the condition. Or, in symbols:
where the first quantifier \({\forall _\mathrm{D}}\hbox {x}\) is relativized to a given domain (or interpretation) D and the second quantifier is relativized to a domain (or interpretation) \(\hbox {D}^{\prime } \) comprising all sets of objects from D. Notice that this principle is schematic both in the condition \(\upvarphi \)(x) and in the specification of the domain D.
It would be too gross an error to confuse the acceptable version (**) of Comprehension with the unacceptable version (*). But there is a transcendental line of thinking that leads from the one to the other. For we may suppose that there is an absolutely unrestricted domain of quantification U. Substituting U for D in the acceptable scheme (**) gives us:
But since U is absolutely unrestricted, we have that every object of \(\hbox {U}^\prime \) is in U:
And from (**)\(_{\mathrm{U}}\) and (***), we obtain:
which is an instance of the unacceptable scheme (*).
The supposition that there is an intelligible concept of absolutely unrestricted quantification arises from our taking an external or transcendental perspective. We observe that our quantifiers are capable of ranging over different domains of objects—these particular objects, those objects and their sets, and so on. We then suppose—and this is the transcendental move—that we can make intelligible to ourselves the concept of an über-domain consisting of all those objects we are capable of quantifying over, so that no further extension of the domain is available to us. We suppose, in other words, that there is a perspective on our ordinary quantificational practice that goes beyond what we appear to be capable of doing from within the practice itself.
When we examine the above transcendental dissolution of the set-theoretic paradoxes, we see that it involves the following three elements. First, there is an unacceptable scheme which we are irresistibly drawn towards accepting. Second, there is another scheme in the neighborhood of the original scheme, which is acceptable. Third, there is a transcendental perspective, which renders intelligible a concept which, when substituted in the acceptable scheme, leads to the unacceptable scheme.
Let us now see how this general picture applies to the sorites. The unacceptable scheme in this case is the Tolerance Principle. For a vague predicate F and a suitable notion of being ‘sufficiently alike’, this states:
Tolerance If two cases are sufficiently alike and the first is F then the second is also F.
This principle is not correct and, indeed, it leads by means of the sorites argument to a contradiction. Yet we are irresistibly drawn to accepting it; and so we must explain why this is so.
The acceptable principle in the neighborhood of the unacceptable principle is:
Cut-Off If two cases are sufficiently alike then it is not the case that the first is F and the second is not F.
One might be tempted at this point to suppose that our mistake is to infer Tolerance from Cut-Off. Now although this inference is classically valid (it is of the form \(\lnot (\hbox {p }\wedge \lnot \hbox {q}) \therefore (\hbox {p }\supset \hbox { q}))\), it is not intuitively valid, as we have seen, and so it is hard to understand why someone who had not already been indoctrinated with classical logic would be inclined to make it. We therefore require a deeper explanation of why we make the inference.
To this end, we need to appeal to a more general version of the Cut-Off principle. This states that when two cases are sufficiently alike, we should not discriminate between them in regard to the status they have (with respect to being F). Thus not only should we not say that the one case is F and the other is not F, we should also not say that the one case is F while the other is borderline F, or that the one case is borderline F while the other is not borderline F, and so on. Say that two statuses with respect to an object’s being F are competing or in competition if we cannot sensibly assent to a single object simultaneously having each status (being F and also not-F, for example, or being F and also borderline F). The general principle then states:
General Cut-Off If two cases are sufficiently alike then it is not the case that the one is \(\upvarphi \) and the other is \(\uppsi \), for competing \(\upvarphi \) and \(\uppsi \).
Of course, there is some unclarity here over what is meant by ‘status’, since it cannot be taken to include any feature of the object whatever. But the applications we make of the principle will all be relatively uncontroversial and will not go beyond its intended import.
We come finally to the transcendental illusion. This can be seen to arise from reflection on the pattern of assertion and denial in the case of a forced march, in which we are required to pass judgement on each successive member of a sorites series \(b_{1}\), \(b_{2}\), ...,\(b_\mathrm{n}\). We eventually find ourselves in a quandary as to what to say in response to the question ‘is the person bald?’. We then suppose—and this is the transcendental move—that we can make intelligible to ourselves a special kind of response, one in which we might correctly say both that it not-true that the person is bald and that it is not-true that the person is not bald (or, alternatively, one in which we might correctly say that the person is a borderline case of bald or that he is neither definitely bald nor definitely not bald). There is, of course, an ordinary or ‘mundane’ sense of not-true in which to say that something is not-true is tantamount to saying that it is not the case. But the present notion is meant to be weaker than the ordinary notion, so that, in saying that something is not-true, we do not thereby commit ourselves to saying that it is not the case. We are therefore in a position to say both that it is not-true that the person is bald and not-true that he is not bald, without thereby committing ourselves to a contradiction.Footnote 14
The supposition that there is such a concept of truth (or being borderline or definite) arises from our taking an external or transcendental perspective on our ordinary practice of forming judgements. Our ordinary practice simply involves forming judgements as to whether or not someone is bald or whether, in the ordinary sense of ‘true’ and ‘false’, it is true or false that the person is bald. But it is supposed, when we have difficulties in forming judgements of this sort, that we can somehow transcend our ordinary practice and arrive at a different sort of judgement, one in which we can meaningfully say that it would be incorrect either to say that the person is bald or that the person is not bald, thereby ruling out whatever basis we might have had for forming an ordinary judgement.
Once we fall prey to the transcendental illusion, it is easy to see how we might make the transition from Cut-Off to Tolerance. For to say that a person is bald and to say that it is not-true that a person bald is to give two competing responses to the question ‘is the person bald?’; one cannot sensibly assent both to a person being bald and to its being not-true that the person is bald. So by General Cut-Off, it will not be the case both that Left is bald and not-true that Right is bald . But from this instance of Cut-Off, we are able to infer that if Left is bald then so is Right. For we are not simply rejecting the abrupt transition from bald to not bald, we are also rejecting the transition to its being not-true that Right is bald; and if, given that Left is bald, we can rule out its not-being-true that Right is bald, in the broad intended sense of ‘not-true’, then it will follow that Right must be bald.Footnote 15
If this line of thought is correct then it means that all (or almost all) extant accounts of vagueness embody the very mistake that led us to accept the sorites argument in the first place. For they all accept a notion of borderline; and it is the acceptance of this very notion, I have argued, that makes the reasoning behind the sorites argument appear so irresistible to us. No wonder, then, that no explanation of the fallacy, within any of these accounts, has been at all convincing.
Of course, there is a way in which my own account also falls prey to a transcendental way of thinking. For the semantics itself embodies—or, at least, comes close to embodying—a transcendental conception of truth or borderline case. Indeed, within our models we can even provide a semantical account of the transcendental concept of not-truth, taking ‘it is not-true that A’ to be true at a use if the statement A is not true at that use; and we might thereby justify the inference from General Cut-Off to Tolerance, which I had gone to such pains to avoid.
But we have here a familiar situation in which we model a given point of view by appeal to elements that are not themselves intelligible from that point of view; and in order to make good use of the model we must then be selective in how these elements are employed. I am not sure what might in the end justify such a way of thinking but there is no doubt that it can be very useful. What is even more important from our own point of view is that the transcendental notions of borderline case and the like are no part of our official doctrine; the core notion of vagueness is global and expressed without the help of local notions. What we appeal to in the semantic modeling is not a dangerous illusion but a useful pretense.
Let me mention, in conclusion, that I believe that the present approach has a number of other useful applications—both to vagueness and to other phenomena.
(1) I have always been sympathetic to the idea of ontological vagueness, i.e. to the idea of vagueness in the world; and I believe that the present logico-global approach also has application to ontological vagueness. This means that we will not express the vagueness of objects by saying that it is indeterminate that one object is identical to another but in some other, more global, way. We thereby have the means of evading a key step in the argument of Evan’s (1978) against ontological vagueness.
(2) The phenomenon of disagreement has recently come under extensive scrutiny and I believe that the present semantical framework enables us to make some useful distinctions that might otherwise go unnoticed. You and I may disagree in the sense that what we are jointly prepared to assert is inconsistent: you are prepared to assert \(\hbox {A}_\mathrm{1}\), \(\hbox {A}_\mathrm{2}\), ..., say, I am prepared to assert \(\hbox {B}_\mathrm{1}\), \(\hbox {B}_\mathrm{2}\), ..., and yet \(\hbox {A}_\mathrm{1}\), \(\hbox {A}_\mathrm{2}\), ...and \(\hbox {B}_\mathrm{1}\), \(\hbox {B}_\mathrm{2}\), ..., taken together, are inconsistent. But you and I may also disagree in the sense that I am prepared to deny something that you are prepared to assert: you are prepared to assert A, for some A, while I am prepared to deny A, i.e. to assert \(\lnot \hbox {A}\).
Call the first type of disagreement moderate and the second type severe. It is usually supposed that any moderate disagreement will be a case of severe disagreement. For suppose you are prepared to assert \(\hbox {A}_\mathrm{1}\), \(\hbox {A}_\mathrm{2}\), .... Then presumably you are prepared to assert the conjunction A = \(\hbox {A}_\mathrm{1} \wedge \hbox {A}_\mathrm{2} \wedge \ldots \hbox {of} \hbox {A}_\mathrm{1}\), \(\hbox {A}_\mathrm{2}\), ...; and similarly, I am prepared to assert the conjunction \(\hbox {B }= \hbox {B}_\mathrm{1} \wedge \hbox {B}_\mathrm{2} \wedge \ldots \hbox {of }\hbox {B}_\mathrm{1},\, \hbox {B}_\mathrm{2}\), .... Given that \(\hbox {A}_\mathrm{1}\), \(\hbox {A}_\mathrm{2}\), ..., \(\hbox {B}_\mathrm{1}\), \(\hbox {B}_\mathrm{2}\), ...are inconsistent, I will presumably be prepared to assert \(\lnot (\hbox {A }\wedge \hbox { B}\)). But since \(\lnot \hbox {A}\) is a logical consequence of B and \(\lnot (\hbox {A }\wedge \hbox { B})\), I will also be prepared to assert \(\lnot \hbox {A}\), i.e. to deny A, and the disagreement will be severe.
But notice that the above line of reasoning rests upon assuming the validity of Conjunctive Syllogism. Under the compatiblist semantics, this rule is not valid and it will be possible to have cases of moderate disagreement which are not severe. Indeed, this is already illustrated by the case of the sorites. For I may assert that Left is bald and deny that Left is bald and Right is not bald while you deny that Right is bald. Our disagreement will then be moderate and yet not severe; although I cannot consistently assert what you assert, I am not prepared to deny anything that you assert.
There may be other cases of this kind of ‘flawless’ disagreement. Suppose you assert rhubarb is tasty, employing your standard of taste, while I deny that rhubarb is tasty, employing my standard of taste. Then you implicitly endorse your standard of taste and hence are prepared to assert that your standard of taste is to be endorsed, while I implicitly endorse my standard of taste and hence am prepared to assert that my standard of taste is to be endorsed. Yet I would not wish to endorse both standards of taste, i.e. I am prepared to deny that both standards of taste are to be endorsed, on the general grounds that two standards of taste that deliver opposing results should not both be endorsed. But then we have a situation structurally similar to the vagueness case, in which there is a moderate disagreement over the standard of taste that is to be endorsed though not a severe disagreement.
(3) Once the logical distinction between \(\lnot (\hbox {p }\wedge \lnot \hbox {q}\)) and \((\hbox {p }\supset \hbox { q})\) is granted, it can be seen to have a wide number of applications to a number of different debates. There is, for example, an issue over whether phenomonal indiscriminability is transitive.Footnote 16 But we may distinguish two notions of indiscriminability. According to the first, two items are indiscriminable if any way the one looks is a way the other looks while, according to second, two items are indiscriminable if it is not the case that one of the items looks one way while the other does not look that way. The first will be transitive and will justify the inference from the one item having a certain look to the other item having that look. However, it is not the notion philosophers have hand in mind and it will not be evident from phenomenal inspection whether the two items are indiscriminable in this sense. The second notion will not be transitive and will not justify the inference from the one item having a certain look to the second item having that look. However, it is, I believe, the notion philosophers have had in mind and its application will be open to phenomenal inspection.
Similarly, one might distinguish two ‘margin of error’ principles of the sort discussed by Williamson (1994, chapter 8). Let p and \(\hbox {p}'\) express neighboring propositions and use KA for ‘the subject knows that A’. Then according to one principle \(\hbox {Kp }\supset \hbox { p}'\); and according to the other \(\lnot (\hbox {Kp }\wedge \lnot \hbox {p}')\). The first leads to untoward results (failure of ‘Transparency’ etc) while the second does not. But it is only the second principle, it may be argued, that is acceptable and properly motivated. Thus the margin of error principle, when properly formulated, can be accepted and the untoward results avoided.
Notes
The one exception appears to be Zardini (2014), although his view appears to be very different from mine in a number of fundamental respects.
The ideas behind my approach were first presented in a seminar on vagueness that I gave at NYU in the Fall of 2008. I should like to thank the participants—including Hartry Field, Stephen Schiffer and Crispin Wright—for many helpful comments. I should also like to thank two referees for the journal and the audiences at talks I gave at Austin Texas, Texas A&M and MIT; and I am, in addition, indebted to Robbie Williams and John Hawthorne for some stimulating conversations. The paper provides only a very brief exposition of the basic ideas; and I hope to give a much fuller exposition of both the philosophical and logical aspects of the theory elsewhere.
I should make clear that I am only interested in the extensional notion of indeterminacy, indeterminacy in so far as it relates to the actual rather than the possible application of the predicate; and, for simplicity, I have focused on the vagueness of predicates, although the discussion is readily extended to other forms of expression.
I am here presupposing a context in which each proposition \(\hbox {p}_ \mathrm{k}\) is equivalent to its double negation \(\lnot \lnot \hbox {p}_ \mathrm{k}\). In the absence of this assumption, the state-descriptions should be formed, not from \(\hbox {p}_\mathrm{1},\, \hbox {p}_\mathrm{2}, \ldots , \hbox {p}_\mathrm{n}\), but from their negations \(\lnot \hbox {p}_\mathrm{1},\, \lnot \hbox {p}_\mathrm{2}, \ldots , \lnot \hbox {p}_\mathrm{n}\).
Principally, the equivalence of \(\lnot (\hbox {p} \vee \hbox {q})\) to \(\lnot \hbox {p}\wedge \lnot \hbox {q}\) and the equivalence of \((\hbox {p}\vee \hbox {q})\wedge \hbox {r to }(\hbox {p}\wedge \hbox {r})\vee (\hbox {q}\vee \hbox {r}).\) I should note that the proof of equivalence will go through within the logic of vagueness given below.
It is perhaps partly for this reason - a failure of logical nerve, so to speak - that the present approach to vagueness has not previously been pursued. The closest semantical framework in the literature of which I am aware is the relational semantics for quantum logic found in Goldblatt (1974), but the motivation and background to the two approaches has been so very different that they have not been connected. There is also a resemblance in motivation between my Compatibility Semantics and Brandom’s Incompatibility Semantics from the fifth of his John Locke Lectures, but the similarity ends there and the development of the same general idea is very different.
For simplicity, I do not consider the semantical treatment of the quantifiers.
The same model can be used to establish the satisfiability of \(\lnot [(\lnot \hbox {p}\vee \lnot \lnot \hbox {p}) \wedge (\lnot \hbox {q}\vee \lnot \lnot \hbox {q})]\).
If we do not assume the equivalence of p and \(\lnot \lnot \hbox {p}\) then, strictly speaking, indeterminacy should be taken to be the denial of a conjunction of instances of the form \(\lnot \hbox {p}_ \mathrm{k} \vee \lnot \lnot \hbox {p}_ \mathrm{k}\).
This kind of move is familiar from the literature. For Putnam (1983) observed that the reasoning above requires the use of Double Negation Elimination and so would not go through in intuitionistic logic; and Read and Wright (1985) then pointed out that the use of Double Negation Elimination might be avoided by running the argument backwards. But, of course, we can see in principle that the adoption of intuitionistic logic is of no help in resisting the derivation of a contradiction, at least when the argument is stated in sentential form. For it is a general result that any contradiction that can be derived classically can also be derived intuitionistically (though not necessarily by the same route). Thus the reverse derivation above just shows how, in this particular case, the alternative derivation might proceed.
Suppose that A and \(\hbox {A }\supset \hbox { B}\) are true under a given use. Then B must also be true under that use by the clause for \(\supset \), thereby establishing the validity of modus ponens. Now suppose that \(\lnot \hbox {A}\) and \(\hbox {A }\vee \hbox { B}\) are true under a given use. Then either A is true under that use or B is by the clause for \(\vee \). But A is not true under the use by the clause for \(\lnot \); and so B must be true under the use, thereby establishing the validity of disjunctive syllogism. Finally, the inference from A and \(\lnot (\hbox {A }\wedge \hbox { B})\) to \(\lnot \hbox {B}\) will be valid under the assumption of \(\hbox {B }\vee \lnot \hbox {B}\). For either B or \(\lnot \hbox {B}\) will be true under the given use; and the former will be impossible given that A and \(\lnot (\hbox {A }\wedge \hbox { B})\) are true under the given use.
More formally, consider the model depicted below:
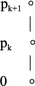
with \(\hbox {p}_ \mathrm{k+1}\)—for \(b_\mathrm{k+1}\) is bald—true at point \(\hbox {p}_ \mathrm{k+1}\hbox { and }\hbox {p}_ \mathrm{k}\)—for \(b_{\mathrm{k}}\) is bald—true at point \(\hbox {p}_ \mathrm{k}\) (and that is all). Then we readily verify that: \(\lnot \hbox {p}_ \mathrm{k+1}\) is true at the base point 0; that \(\hbox {p}_ \mathrm{k}\) is not true at 0 and \(\lnot \hbox {p}_ \mathrm{k+1}\) is not true at \(\hbox {p}_ \mathrm{k}\) and hence that \(\lnot (\hbox {p}_\mathrm{k} \wedge \lnot \hbox {p}_{\hbox {k}+\hbox {1}} )\) is true at the base point; and that \(\hbox {p}_ \mathrm{k}\) is true at \(\hbox {p}_ \mathrm{k}\) and hence that \(\lnot \hbox {p}_ \mathrm{k}\) is not true at 0. This establishes the failure of the relevant instance of Conjunctive Syllogism at 0, with \(\lnot \hbox {p}_ \mathrm{k+1}\) and \(\lnot (\hbox {p}_\mathrm{k} \wedge \lnot \hbox {p}_{\hbox {k}+\hbox {1}} )\) true at 0 but \(\lnot \hbox {p}_ \mathrm{k}\) not true at 0. We also readily verify that: \(\hbox {p}_ \mathrm{k+1}\) is not true at 0 and hence, given that \(\lnot \hbox {p}_ \mathrm{k}\) is not true at 0, that \(\lnot \hbox {p}_\mathrm{k} \vee \hbox {p}_{\hbox {k}+\hbox {1}} \) is not true at 0; and that \(\hbox {p}_ \mathrm{k}\) is true at \(\hbox {p}_ \mathrm{k}\) while \(\hbox {p}_ \mathrm{k+1}\) is not true at \(\hbox {p}_ \mathrm{k}\) and hence, given that \(\hbox {p}_ \mathrm{k}\) is not true at 0, that \(\hbox {p}_\mathrm{k} \supset \hbox {p}_{\hbox {k}+\hbox {1}} \) is not true at 0. This establishes that the disjunctive version \(\lnot \hbox {p}_\mathrm{k} \vee \hbox {p}_{\hbox {k}+\hbox {1}} \) and the conditional version \(\hbox {p}_\mathrm{k} \supset \hbox {p}_{\hbox {k}+\hbox {1}} \) of the major premiss are not true at 0.
I am not so rash as to make any claims about how my conception of a transcendental illusion relates to Kant’s.
I use the phrase ‘not-true’ rather than ‘not true’, since I do not wish to prejudge the question of whether ‘not-true’ is the negation of ‘true’. In fact, the relevant sense of not-true is provably undefinable within our system.
Use \({\bar{\hbox {T}}}\hbox {A}\) for it is not-true that A. We might then justify the inference from \(\lnot \left( \hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B} \right) \) to \(\hbox {A} \supset \hbox {B}\) in terms of the compatibilist semantics. For take \({\bar{\hbox {T}}}\hbox {(A)}\) to be true at a use \(u\) iff A is not true at \(u\). Suppose now that \(\lnot \left( {\hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B}} \right) \) is true at the use \(u\). Take any \(v\) compatible with \(u\) at which A is true. Then B is true at \(v\) since otherwise \({\bar{\hbox {T}}}\hbox {B}\) would be true at \(v\) and, consequently, \(\left( \hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B} \right) \) would be true at v and so \(\lnot \left( {\hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B}} \right) \) would not be true at \(u\) after all.
The response A will also be in competition with \({\bar{\hbox {T}}}\hbox {A}\) in the sense that there is no use of any model in which both are true.
Discussed, for example, in Graff (2001).
Williamson (1994, 1999) and Gaifman (2010) impose reflexivity and symmetry on the accessibility relation in giving a semantics for the definitely operator; and Goldblatt (1974) imposes reflexivity and symmetry on a corresponding compatibility relation in giving a semantics for negation. But we do not use the compatibility relation to provide a semantics for the definitely operator (which we regard as illegitimate); we do not insist upon a double negation interpretation of propositions, as in Goldblatt (1974), and therefore allow ourselves to introduce a choice form of disjunction; and we adopt a novel account of the conditional. Most significantly of all, our semantics is motivated by the desire to avoid the impossibility theorem, which is not something that is aimed for under these alternative approaches.
References
Black, M. (1937). Vagueness: an exercise in logical analysis. Philosophy of Science, 4(4), 427–455.
Evans, G. (1978). Can there be vague objects. Analysis, 38, 208.
Field, H. (1994). Disquotational truth and factually defective discourse. Philosophical Review, 103, 405–452.
Fine, K. (1975). Vagueness, truth and logic. Synthese 30, 265–300. Reprinted in Keefe & Smith (eds.). (1996). Vagueness: A reader. Boston: MIT University Press.
Fine, K. (2008). The impossibility of vagueness. Philosophical Perspectives, 22(1), 111–116.
Gaifman, H. (2010). Vagueness, tolerance and contextual logic. Synthese, 174, 5–46.
Goldblatt, R. (1974). Semantic analysis of orthologic. Journal of Philosophical Logic, 3, 19–35.
Graff, D. (2001). Phenomenal continua and the sorites. Mind, 110(440), 905–935.
Greenough, P. (2003). Vagueness: A minimal theory. Mind, 112(446), 235–281.
McGee, V. (1985). A counter-example to Modus Ponens. Journal of Philosophy, 82(9), 462–471.
Peirce, C. S. (1902). The collected papers. Harvard: Harvard University Press.
Putnam, H. (1983). Vagueness and alternative logic, Erkenntis 19, 297–314. Reprinted in his Realism and reason (pp. 271–86). Cambridge: Cambridge University Press.
Read, S., & Wright, C. (1985). Hairier than Putnam thought. Analysis, 45, 56–58.
Southern Journal of Philosophy, (1998). Distinctions without a difference. 33(Supplement 1995), 203–251.
Williamson, T. (1994). Vagueness. London: Routledge.
Williamson, T. (1999). On the structure of higher order vagueness. Mind, 103, 127–143.
Wright, C. (2003). Vagueness: A fifth column approach. In J. C. Beall & M. Glanzburg (Eds.), Liars and heaps: New essays on paradox (pp. 84–105). Oxford: Oxford University Press.
Zardini E. (2014). First-order tolerant logics. Review of Symbolic Logic (forthcoming).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
We deal with a propositional language in which formulas are formed from an infinite set SL of sentence letters \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}\), ...by means of the connectives \(\vee \), \(\wedge , \lnot ,\) and \(\supset \) We shall also find it convenient to use the falsum constant \(\bot \) in place of \(\lnot \), defining \(\lnot \)A as A \(\supset \bot \).
1.1 Intuitionistic Semantics
We begin by reminding the reader of the Kripke semantics for intuitionistic logic. This will then serve as a foil for our own compatibilist-style semantics.
Under the Kripke semantics, a model M is a triple (\(U\), \(\le \), \(\upvarphi )\), where:
- I(i):
-
\(U\) (‘points’ or ‘uses’) is a non-empty set;
- I(ii):
-
\(\le \) (extension) is a reflexive and transitive relation on U;
- I(iii):
-
\(\upvarphi \) (valuation) is a function from SL into
(U) subject to the Hereditary Condition:
$$\begin{aligned} u\in \upvarphi \left( \hbox {p} \right) \; \mathrm{{and}} \; u \le { {v}} \hbox { implies } { {v}}\in \upvarphi \left( \hbox {p} \right) \hbox { for } \hbox { all } u,{ {v}}\in U \hbox { and } \hbox { p} \in \hbox { SL}. \end{aligned}$$
Intuitively, we may think of \(U\) as consisting of hypothetical uses of the predicates of the language; \(\le \) is the extension relation, where one use extends another when anything taken to be true under the second use is taken to be true under the first; and \(\upvarphi \) tells us which sentence letters are true under any given use.
Relative to a model M, truth of a formula A under the use \(u\) (\(u~{\vert }\!= \hbox {A}\)) is defined by the following clauses:
- T(i):
-
\(u\,|{=\hbox { p iff }} u \in \upvarphi \left( \hbox {p} \right) \)
- T(ii):
-
\(u\,|{=\hbox { B}}\wedge \hbox {C} \hbox { iff }\, u\,\left| \!\,{=\hbox { B} \hbox { and}}\, u\, \right| \!\,{=\,\hbox { C}}\)
- T(iii):
-
\(u\,|{=\hbox { B}}\vee \hbox {C iff }\, u\,\left| \!\,{=\hbox { B or}\, u}\, \right| \!\,{=\hbox { C}}\)
- T(iv):
-
\(u\,|{=\lnot \hbox {B iff not }} { {v}}\,|{=\hbox { B for any }} v \hbox { for which}\, u\le { {v}}\)
- T(v):
-
\(u\,|{=\hbox { B}}\supset \hbox {C iff } { {v}}\,\left| {={\hbox { C whenever}}\, { {v}}} \,\right| {=\hbox { B} \hbox { and}}\, u\,\le { {v}}.\)
We may also employ the following clause for \(\bot \) in place of the clause for \(\lnot \):
- T(vi):
-
\(\hbox {never}\, u\,|\!=\bot .\)
We adopt some standard logical terminology. A is said to be a consequence of \(\Delta \)—in symbols, \(\Delta {\vert }\!=\hbox { A}\)—if, for any model M and point \(u\) of M, A is true at \(u\) in M whenever \(\Delta \) (i.e. each formula of \(\Delta )\) is true at \(u\) in M. We say that A is valid—in symbols, \({\vert }\!= \hbox {A}\)—if A is a consequence of the empty set of formulas \(\oslash \), i.e. if A is true at any point in any model; and we say that A is equivalent to B—in symbols,\(\hbox { A}=\!{\vert }{\vert }\!=\hbox { B}\)—if \(\hbox {A}{\vert }\!=\hbox { B}\) and \(\hbox {B }{\vert }\!=\hbox { A}\). The formulas of \(\Delta \) are said to satisfiable if for some model M and point \(u\) of M, \(\Delta \) is true at \(u\) in M; and the formulas of \(\Delta \) are said to be compatible with the formula A (or with the set of formulas \(\Gamma )\) if \(\Delta \quad \cup \) {A} (or \(\Delta \quad \cup \quad \Gamma )\) is satisfiable (and similarly for unsatisfiability). Clearly, the formulas \(\Delta \) are satisfiable iff not \(\Delta {\vert }\!= \bot \).
1.2 The Compatibilist Semantics
Under the compatibilist semantics, we take a model M to be a triple (\(U\), \(\circ \), \(\upvarphi )\), where:
- C(i):
-
\(U\) (‘points’ or ‘uses’) is a non-empty set;
- C(ii):
-
\(\circ \) (compatibility) is a reflexive and symmetric relation on \(U\);
- C(iii):
-
\(\upvarphi \) (valuation) is a function from SL into
(U).
Our intuitive understanding of \(U\) and of \(\upvarphi \) is as before.
Relative to a model M, truth of a formula A under a use \(u\, (u\, {\vert }=\hbox { A}\)) is defined by the following clauses:
- T(i):
-
\(u\,|{=\hbox { p iff }} u\in \upvarphi \left( \hbox { p} \right) \)
- T(ii):
-
\(u\,|{=\hbox { B}}\wedge \hbox {C iff }\, u\,\left| {=\hbox { B and}\, u} \,\right| {=\hbox { C}}\)
- T(iii):
-
\(u\,|{=\hbox { B}}\vee \hbox {C iff } u\,\left| {=\hbox { B or}\, u}\, \right| {=\hbox { C}}\)
- T(iv):
-
\(u\,\left| {=\lnot \hbox {B iff not}\, { {v}}}\, \right| {=\hbox { B for any}}\, { {v}}\, \hbox {for which }\, u\circ { {v}}\)
- T*(v):
-
\(u\,|{=\hbox { B}}\supset \hbox {C iff either }\left( \hbox {a} \right) \,u\,\left| {=\hbox { B and}\, u} \,\right| {=\hbox { C or }}\left( \hbox {b} \right) { {v}}\left| {=\hbox { C whenever }} { {v}}\, \right| {=\hbox { B and }} u\circ { {v}}\)
- T(vi):
-
\(\hbox {never}\, u\,|{=\bot } .\)
There are two main changes from the semantics for intuitionist logic. The first is in the substitution of the reflexive and symmetric relation \(\circ \) for the reflexive and transitive relation \(\le \) (along with the elimination of the hereditary condition); and the second is in the modification of the clause for the conditional (T*(v) in place of T(v)). The new clause might be regarded as a form of the ‘closest world’ semantics; for either the closest B-world is the actual world \(u\), in which case C must also be true in \(u\), or else the closest B-worlds are the worlds compatible with the actual world, in which case C must also be true in those worlds. Thus there are two ways in which the conditional B \(\supset \) C can be true at a point—either ‘truth-functionally’ with both B and C true or ‘strictly’ with C true whenever B is true.Footnote 17
Logical notions such as validity and consequence transfer in the obvious way to the present semantics. When there is a need to distinguish the semantics in question, we shall talk of compatibilitist or C-validity versus intuitionistic or I-validity; and similarly when other semantical frameworks are in question. We may also define a natural notion of disagreement, where two sets of formulas \(\Delta \) and \(\Gamma \) are said to be in disagreement—\(\Delta \bullet \Gamma \)—if in any model, never \(u\, {\vert }\!= \Delta \), \({ {v}}\ {\vert }\!= \Gamma \) and \(u \circ { {v}}\).
We present three central results—Completeness, Inclusion and Possibility—which we state without proof (further details will be provided elsewhere). Let CL (compatibilist logic) be the system defined by the following axioms and rules of inference (with \(\bot \) as primitive):
1.3 Axioms
-
A1.
\(\hbox {A}\wedge (\hbox {A}\supset \hbox {B})\supset \hbox {B}\)
-
A2.
\(\hbox {A}\supset ((\hbox {A}\supset \hbox {B})\supset \hbox {B})\)
-
A3.
\(\hbox {A}\supset (\hbox {B}\supset \hbox {B})\)
-
A4.
\(\hbox {A}\wedge \hbox {B}\supset (\hbox {A}\supset \hbox {B})\)
-
A5.
\((\hbox {A}\supset \hbox {B}\wedge \hbox {B}\supset \hbox {C})\supset \hbox {B}\vee (\hbox {A}\supset \hbox {C})\)
-
A6.
\(\hbox {A}\wedge \hbox {B}\supset \hbox {A}\)
-
A7.
\(\hbox {A}\wedge \hbox {B}\supset \hbox {B}\)
-
A8.
\((\hbox {A}\supset \hbox {B}\wedge \hbox {A}\supset \hbox {C})\supset (\hbox {A}\supset \hbox {B}\wedge \hbox {C})\)
-
A9.
\(\hbox {A}\supset \hbox {A}\vee \hbox {B}\)
-
A10.
\(\hbox {B}\supset \hbox {A}\vee \hbox {B}\)
-
A11.
\(((\hbox {A}\supset \hbox {C})\wedge (\hbox {B}\supset \hbox {C}))\supset ((\hbox {A}\vee \hbox {B})\supset \hbox {C})\)
-
A12.
\(\hbox {A}\wedge (\hbox {B}\vee \hbox {C})\supset (\hbox {A}\wedge \hbox {B})\vee (\hbox {A}\wedge \hbox {C}).\)
-
A13.
\(\bot \supset \hbox {A}.\)
1.4 Rules of inference
-
R1.
\(\hbox {A},\hbox { A}\supset \hbox {B}/\hbox { B}\)
-
R2.
\(\hbox {A},\hbox { B }/\hbox { A}\wedge \hbox {B}\)
-
R3.
\(\hbox {A}\supset \hbox {B},\hbox { B}\supset \hbox {C }/\hbox { A}\supset \hbox {C}\)
Theorem 1
(Completeness) A formula A is a theorem of the system CL iff it is valid under the compatiblist semantics.
The above axiom system is perhaps a little unnatural, but I believe a much more natural system can be obtained using disagreement—\(\Delta \, {\bullet } \,\Gamma \)—as the basic meta-logical primitive in place of theoremhood; and, indeed, the resulting system may well be regarded as a basic way to formalize the logic of disagreement.
We also have:
Theorem 2
(Inclusion) Any theorem of compatibilist logic is a theorem of intuitionistic logic.
This inclusion is proper, since \(\hbox {p}\wedge \lnot (\hbox {p}\wedge \hbox {q})\supset \lnot \hbox {q}\) is a theorem of intuitionistic logic but not of compatibility logic.
To state the third result, we need some terminology from Fine (2008). A (collective) response is a sequence A(p), A(p),..., A(p) of formulas constructed from the sentence letter p; and \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots , \hbox {A}_\mathrm{n}\) is said to be a (collective)response to \(\hbox {B}_{1}, \hbox {B}_{2}, \ldots , \hbox {B}_\mathrm{n}\) if \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots , \hbox {A}_\mathrm{n}\) are respectively of the form \(\hbox {A}_{1}(\hbox {B}_{1}),\hbox { A}_{2}(\hbox {B}_{2}), \ldots ,\hbox { A}_\mathrm{n}(\hbox {B}_\mathrm{n})\), where \(\hbox {A}_{1}\hbox {(p)},\hbox { A}_{2}\hbox {(p)}, \ldots ,\hbox { A}_\mathrm{n}\hbox {(p)}\) is a collective response. We say that the collective response \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots ,\hbox { A}_\mathrm{n}\) is sharp if:
-
(i)
\(\hbox {A}_\mathrm{i} \ne \hbox {A}_\mathrm{j}\ \hbox {for some i},\hbox { j}\le \hbox {n};\)
-
(ii)
\(\hbox {A}_\mathrm{i}\ \hbox {is incompatible with A}_\mathrm{j}\ \hbox {or A}_\mathrm{i} =\hbox { A}_\mathrm{j}\ \hbox {whenever 1}\le \hbox {i }<\hbox { j}\le \hbox {n}.\)
We may similarly talk of a sharp response to \(\hbox {B}_\mathrm{1}\), \(\hbox {B}_\mathrm{2}\), ..., \(\hbox {B}_\mathrm{n}\). We use:
The indeterminacy operator I* can then be employed to evade the impossibility result of Fine (2008).
Theorem 3
(Possibility) For n \(\ge \) 2, I*(p\(_{1}\), p\(_{2}\), ..., p\(_{\mathrm{{n}}+1}\)) is compatible with \(\{ \mathrm{{p}}_1, \lnot \mathrm {p}_{\mathrm{{n}}+1}\}\) and incompatible with any sharp response to p\(_{1}\), p\(_{2}\), ..., p\(_{\mathrm{{n}}+1}\).
This is a fundamental result and shows how vagueness, as we naturally conceive it, is indeed possible.
Rights and permissions
About this article
Cite this article
Fine, K. The possibility of vagueness. Synthese 194, 3699–3725 (2017). https://doi.org/10.1007/s11229-014-0625-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-014-0625-9