Introduction

Due to wide application of single crystal materials in gas turbine industry for manufacturing of turbine blades, elaboration of adequate models of deformation and fracture criteria for static and especially thermocyclic loading is required. Multiple studies are dedicated to solving these problems [1–15]. Nevertheless, practical calculations are quite often based on deformation models of material, which are suitable only for polycrystalline blades, whereas thermal fatigue durability is estimated via the Manson formula for a universal inclination, which in many cases yields very big errors in the durability estimations.

The present work deals with the analysis of methods for assessing thermal fatigue durability of single crystal materials on the basis of application of deformation criteria with the account of crystallographic orientations (CGO), subdivision of contributions from cyclic and unilaterally accumulated (ratcheting) components of deformation, the separate account of influence of plastic deformations and creep deformations, which make it possible to adequately describe processes of thermal fatigue fracture of materials at complex variable disproportionate high-temperature loading taking into account presence of intermediate exposures. Verification of the developed methods is based on the results of thermal fatigue testing of specimens via the technique described in [8].

1. The Deformation Criterion Formulation. Process of damage accumulation in single crystal materials under thermocyclic loading includes parallelly developing stages: occurrence of slip bands; nucleation and development of microcracks; accumulation of irreversible deformations; formation and propagation of the main crack until fracture of the specimen (machine part). For forecasting the thermal fatigue failure of single crystal materials it is quite rational to use the modifications of the deformation criterion initially proposed in work [16]. As criterion of nucleation of macrocracks, the condition of achievement of the critical value by the total measure of damages is used, which is described by the following equation:

$$ D={D_1}\left( {\varDelta \upvarepsilon_{eq}^p} \right)+{D_2}\left( {\varDelta \upvarepsilon_{eq}^c} \right)+{D_3}\left( {\upvarepsilon_{eq}^p} \right)+{D_4}\left( {\upvarepsilon_{eq}^c} \right)=1. $$
(1)

The proposed criterion (1) is based on linear summation of the damages caused by: plastic deformation variations within a cycle

$$ {D_1}=\sum\limits_{i=1}^n {\frac{{{{{\left( {\varDelta \upvarepsilon_{{e{q_i}}}^p} \right)}}^k}}}{{{C_1}({T_i})}}}, $$
(2)

creep deformations within a cycle

$$ {D_2}=\sum\limits_{i=i}^n {\frac{{{{{\left( {\varDelta \varepsilon_{{e{q_i}}}^p} \right)}}^m}}}{{{C_2}\left( {{T_i}} \right)}},} $$
(3)

creep deformations within a cycle

$$ {D_3}=\mathop{\max}\limits_{{0\leq t\leq {t_{\max }}}}\frac{{\upvarepsilon_{eq}^p}}{{\upvarepsilon_r^p(T)}}, $$
(4)

and unilaterally accumulated creep deformation

$$ {D_4}=\mathop{\max}\limits_{{0\leq t{\leq_{\max }}}}\frac{{\upvarepsilon_{eq}^c}}{{\upvarepsilon_r^c(T)}}, $$
(5)

where C 1, C 2 , k, m, ε r p, and ε r c are the material parameters depending on temperature and CGO. Relations k = 2, m = 5/4, C 1 = (ε r p)k, and C 2 = [(3/4)ε r c]m are frequently used, where ε r p and ε r c are limiting deformations of plasticity and creep under uniaxial tension.

As an equivalent measure of deformations ε eq , various norms of deformation tensor can be considered in Eqs. (1)–(5):

the maximal shear deformation in the slip system with a normal to the slip plane n {111} and slip direction l 〈011〉 :

$$ {\upvarepsilon_{eq }}={{\mathbf{n}}_{{\left\{ {111} \right\}}}}\upvarepsilon {{\mathbf{l}}_{{\left\langle {011} \right\rangle }}}, $$
(6)

the maximal principal strain (the maximum eigenvalue of deformation tensor):

$$ {\upvarepsilon_{eq }}={\upvarepsilon_1}, $$
(7)

strain intensity by Mises:

$$ {\upvarepsilon_{eq }}=\sqrt{{\frac{2}{9}\left[ {{{{\left( {{\upvarepsilon_x}-{\upvarepsilon_y}} \right)}}^2}+{{{\left( {{\upvarepsilon_y}-{\upvarepsilon_z}} \right)}}^2}+{{{\left( {{\upvarepsilon_z}-{\upvarepsilon_x}} \right)}}^2}+\frac{3}{2}\left( {\upgamma_{xy}^2+\upgamma_{xz}^2+\upgamma_{zx}^2} \right)} \right]}}, $$
(8)

and the maximal shear deformation:

$$ {\upvarepsilon_{eq }}=\frac{1}{2}\left( {{\upvarepsilon_1}-{\upvarepsilon_3}} \right). $$
(9)

The equivalent deformation (6) corresponds to crystallographic fracture mode, while the equivalent deformations (7)–(9) correspond to non-crystallographic fracture mode. The choice of the most suitable variant of the equivalent deformation on the basis of comparison of predicted life values with the experimental results was one of the conducted research tasks.

2. Experimental Results. Verification of the proposed deformation criterion (1) was performed on flat hour-glass type specimens from ZhS36 alloy with 〈001〉 , 〈011〉 , and 〈111〉 CGOs. Specimens with and without a central circular hole, which were loaded up to various levels of temperature with various cycle durations, were analyzed. Specimens were cut out from plates (Fig. 1) with various CGOs (Table 1).

Fig. 1
figure 1

Plates from which specimens are cut out.

Full size image
Table 1 Crystallographic Orientations of Plates Used for Production of Specimens
Full size table

It is noteworthy that usage of plates for manufacturing of specimens guarantees that these specimens have identical axial and azimuthal orientations, which is advantageous to the specimens made from circular bars, where coincidence of only axial orientations is provided, while inevitable variations in azimuthal orientation reduce accuracy of results obtained. Moreover, it is rather problematic to to produce specimens with fully conciding axial orientations.

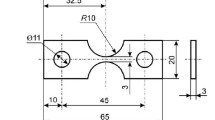
In tests, rigidly fixed specimens with a single polished surface are used. Specimen dimensions and characteristic variation of temperature in its central part are shown in Fig. 2. Tests were conducted in vacuum using loading modes with different maximum (T max = 900–1100°C) and minimum (T min = 200–700°C) temperatures in each cycle, which has made it possible to observe formation of slip bands, nucleation and propagation of cracks, as well as to measure their propagation rate on the specimen polished surface with optical magnification of × 250. Some specimens were subjected to exposure T max with hold times of 2 and 5 minutes. Some specimens had stress concentrators in the form of central circular holes 0.5 mm in diameter. In order to define the CGO, a lowergramme was measured for each specimen, and calculations of Euler’s angles φ, θ, and ψ, axial and azimuthal deviations, as well as the Schmid factor, were perfomed.

Fig. 2
figure 2

Test specimen (a) and temperature variation in its central part (b).

Full size image
Fig. 3
figure 3

Map of fracture mechanisms for specimens of the third set.

Full size image

In the course of tests, relative axial displacements ΔK of two microhardness indentations, which have been made on the border of a working part of specimens with the distance of 4 mm from each other (Table 2), were measured per cycle. On the basis of the data obtained, the estimation of the range of axial mechanical deformations averaged within the specimen working part was conducted

Table 2 Thermal Fatigue Test Results for ZhS36 Alloy Specimens
Full size table

In the course of tests, relative axial displacements _K of two microhardness indentations, which have been made on the border of a working part of specimens with the distance of 4 mm from each other (Table 2), were measured per cycle. On the basis of the data obtained, the estimation of the range of axial mechanical deformations averaged within the specimen working part was conducted

Table 2 contains the experimental data on thermal fatigue life of single crystal specimens for various CGOs and loading modes, which are used for verification of the proposed deformation criterion (1).

3. Governing Equations. In order to estimate the stress-strain state (SSS) of single crystal specimens sublected to complex programs of thermo-mechanical loading, it is expedient to apply physical models of inelastic deformation of the material, which take into account the fact that inelastic deformations occur according to the slip mechanism along the active slip systems and strongly depend on the chrystallographic orientation of a single crystal in relation to the direction of the external factor action. One should be very careful with application of plasticity and creep phenomenological models, which provide the account for anisotropy only for the criterion of plasticity and elastic properties.

It is assumed that plastic flow occurs as the result of possible slip along the octahedric slip systems N, which a characterized by a normal to αth slip plane n α and slip direction l α (α = 1, …, N). For the considered case of single crystals with face-centered cubic (fcc) lattice we have N = 12. The description of processes of inelastic deformation for finite deformations is based on application of the concept of multiplicate decomposition of the strain gradient F [2–7]:

$$ {\mathbf{F}}={{\mathbf{F}}^{*}}{{\mathbf{F}}^p}, $$
(10)

where the plastic component is controlled by the following equations:

$$ {{\mathbf{L}}^p}={{\dot{{\mathbf{F}}}}^{*}}{{\mathbf{F}}^{{{p^{-1 }}}}}=\sum\limits_{{\alpha =1}}^N {{{\dot{\upgamma}}^{\upalpha}}{{\mathbf{l}}^{\upalpha}}{{\mathbf{n}}^{\upalpha}},} $$
(11)
$$ {{\dot{\upgamma}}^{\upalpha}}=f\left( {{\uptau^{\upalpha}},\ldots } \right), $$
(12)
$$ {\uptau^{\upalpha}}=\upsigma \cdot \cdot {{\mathbf{l}}^{\upalpha}}{{\mathbf{n}}^{\upalpha}}, $$
(13)

and the elastic one – by

$$ {{\mathbf{E}}^{*}}=\frac{1}{2}\left( {{\mathbf{c}}-{\mathbf{1}}} \right)=\frac{1}{2}\left( {{{\mathbf{F}}^{*}}{{\mathbf{F}}^{*T }}-1} \right) $$
(14)
$$ {S^{*}}{=^4}{\mathbf{D}}\cdot \cdot {{\mathbf{E}}^{*}}. $$
(15)

Here \( {{\dot{\upgamma}}^{\upalpha}} \) is speed/rate of slip in the α-slip system, which depends on the stressed state (shear stresses τα reduced to the given slip system), and can also depend on a number of internal variables, S * is the Piola–Kirchhoff stress tensor of the 2nd type, which is related the Cauchi stress tensor σ via equality \( {S^{*}}=J{{\mathbf{F}}^{{{*^{-1 }}}}}\upsigma {{\mathbf{F}}^{{{*^{-T }}}}} \) is a unit tensor. The choice of the particular form of expression (12) depends on the investigated phenomena (elastoplastic, viscoplastic, and viscoelastic behaviors), as well as on peculiarities of inelastic deformation of the considered single crystal.

For the viscous-elastic model used for the description of viscous effects in a single crystal below the yield stress level, calculation of multipliers \( {{\dot{\upgamma}}^{\upalpha}} \), which characterize the intensity of inelastic deformation in the α-slip system, was made via the following equations:

$$ {{\dot{\upgamma}}^{\upalpha}}=A{{\left| {{\uptau^{\upalpha}}} \right|}^n}{{\left( {{\upgamma^{\upalpha}}} \right)}^m}\mathrm{sign}\left( {{\uptau^{\upalpha}}} \right). $$
(16)

For the viscous-plastic model used for the description of viscous effects in a single crystal above the yield stress level, calculation of multipliers \( {{\dot{\upgamma}}^{\upalpha}} \) was made as follows:

$$ {{\dot{\upgamma}}^{\upalpha}}=\mathrm{sign}\left( {{\uptau^{\upalpha}}-{X^{\upalpha}}} \right){{\left\langle {\frac{{\left| {{\uptau^{\upalpha}}-{X^{\upalpha}}} \right|-{R^{\upalpha}}-{\uptau_0}}}{K}} \right\rangle}^n}, $$
(17)

where the variables characterizing isotropic and kinematic hardening are controlled by the following equalities:

$$ {R^{\upalpha}}=bQ{\sum_{\upbeta}}{h^{{\upalpha \upbeta}}}{r^{\upbeta}},\quad {{\dot{r}}^{\upalpha}}=\left( {1-b{r^{\upalpha}}} \right){{\dot{\upgamma}}^{\upalpha}},\quad {h^{{\upalpha \upbeta}}}=H\left[ {q+\left( {1-q} \right){\updelta_{ab }}} \right], $$
(18)
$$ {X^{\upalpha}}=C{x^{\upalpha}},\quad {{\dot{x}}^{\upalpha}}=\left[ {\mathrm{sign}\left( {{\uptau^{\upalpha}}-{X^{\upalpha}}} \right)-D{x^{\upalpha}}} \right]{{\dot{\upgamma}}^{\upalpha}}. $$
(19)

In expression (17), the McOili brackets \( \left\langle x \right\rangle =\left\{ {\begin{array}{*{20}{c}} {x,} & {x\geq 0,} \\ 0 & {x<0,} \\ \end{array}} \right. \) are used. In Eqs. (16)–(19), A, n, m, τ0 , K, b, Q, H, q, C, and D are the material constants. Non-diagonal structure of a matrix h αβ makes it possible to consider two-way (latent) hardening of various slip systems.

For the elastoplastic model used for description of irreversible deformation effects under conditions of short-term loading of a single crystal above the yield stress level, calculation of multipliers \( {{\dot{\upgamma}}^{\upalpha}} \) was based on the following equations:

$$ {f^{\upalpha}}=\left| {{\uptau^{\upalpha}}-{X^{\upalpha}}} \right|-{R^{\upalpha}}-{\uptau_0}=0, $$
(20)

where the variables characterizing isotropic and kinematic hardening are controlled by Eqs. (18) and (19). Multipliers \( {{\dot{\upgamma}}^{\upalpha}} \) are determined as solutions of a system of nonlinear algebraic equations, which are derived from (20), (13), (18), and (19).

he further refinement of models can be achieved by incorporation of densities of mobile dislocations and the equations of their evolution [17] into the hardening laws.

For verification of accuracy of solutions using physical models we compared the experimental data on relative displacement within a cycle of specimen basic points (two microhardness indenations) with the calculated ones. Comparison of the experimental data for specimens with no hold time with calculations via the elastoplastic model has shown their good fit (Table 3), while the accuracy of calculations made via viscous-plastic models with account of hold time is somewhat lower, which is attributed to insufficient volume of the input data on creep in the total temperature range.

Table 3 Comparison of Experimental Data on Displacement of Base Points with the Calculated Results
Full size table

4. Deformation Criterion Verification. Thermocyclic loading, which provides spatially nonuniform and nonstationary temperature field, generates non-uniform stress and strain fields in flat hour-glass type specimens from single crystal alloy, both with and without central hole. A possibility of arbitrary orientation of anisotropic material (for the cubic symmetry group) in relation to geometrical axes of the specimen and strongly pronounced physically nonlinear behavior also complicates the problem of deriving simple analytical estimations of the SSS. Therefore for definition of the SSS of specimens we used finite element (FE) solutions in three-dimensional statement with application of inelastic models of the material described in Section 3.

Analysis of the SSS and processes of damage accumulation in hour-glass type specimens was performed using the FE software program complex PANTOCRATOR [18]. Application in calculations of physical models of a material allows one to take into account that inelastic deformations occur according to the slip mechanism along active slip systems and strongly depend on the single crystal crystallographic orientation in relation to the direction of external factor action. In the numerical experiments we used the elastoplastic and viscoelastoplastic material models [6,7] with nonlinear kinematic and isotropic hardening, as well as those with auto-hardening and wo-way (latent) hardening of various slip systems. It has been established that application of viscoelastic models provides unrealistically overestimated stress levels.

The FE calculation results obtained as solutions of three-dimensional nonlinear boundary problems with characteristic non-uniform fields of stresses, strains and damages allow one to determine sites of the most loaded points of the specimen, which are the most probable origins of nucleation of cracks. A typical distribution of the field of damages with use of criterion (1) after the tenth thermal cycle (20 → T max = 900 ↔ T min = 150°C) for specimen 5-1 from ZhS36 alloy with the orientation close to 〈001〉 is presented in Fig. 4. The corresponding curve of cyclic deformation for the central point of specimen 5-1 is shown in Fig. 5.

Fig. 4
figure 4

Distribution of the damage field after the tenth thermal cycle for specimen 5-1 with 〈001〉 orientation.

Full size image
Fig. 5
figure 5

Cyclic deformation curve for the central point of specimen 5-1.

Full size image

Verification of deformation criterion (1) was conducted with use of the experimental data on creep and curves of elastoplastic deformation of ZhS36 alloy [11] on the basis of the FE calculations executed for each specimen taking into account its CGO and the loading mode. Calculations were carried out by the direct step-by-step modeling of cycle-by-cycle kinetics of deformations with automatic determination of damage field variation in the process of problem solving. The number of cycles to formation of the main crack, calculated on the basis of criterion (1) with use of the equivalent deformations (6)–(9), are presented in Table 4. The best accuracy, in comparison with the experimental results, is provided by the criterion with use of the equivalent deformation, which accounts for crystallographic orientation (6), as is shown in Table 4. For criterion (1), the maximum relative error δ in the life predictions does not exceed 130%, an average error being 60%. In case where the fracture criterion is based on the Mises deformation intensities (8), the most conservative estimation is obtained. A close correlation between the results of calculations via (1)–(6) and the experimental values is observed, as is shown in Fig. 6.

Table 4 Comparison of Experimental Data on Life with the Experimental Results
Full size table
Fig. 6
figure 6

Comparison of the calculated number of cycles N in calc to formation of the main crack with use of criterion (1)–(6) with the experimental results N in exp.

Full size image

5. Comparison of the Results Obtained via Criteria ( 1 )–( 6 ) with Predictions by Other Criteria. Let us compare the results obtained using the proposed criterion (1)–(6) with forecasts made via the Coffin and the Manson criteria. We will limit our consideration to the case of short-term loading with on account of contributions from creep deformations. In this case, the deformation criterion (1)–(6) can be reduced to its simplified representation:

$$ \sum\limits_{j=1}^N {{{{\left( {\frac{{\varDelta \upvarepsilon_{eq}^p}}{{{\upvarepsilon_r}}}} \right)}}^k}+\frac{{\max \upvarepsilon_{eq}^p}}{{{\upvarepsilon_r}}}} =1. $$
(21)

The Coffin criterion is described by the following equality:

$$ \sum\limits_{j=1}^N {{{{\left( {\frac{{\varDelta \upvarepsilon_{eq}^p}}{{{\upvarepsilon_r}}}} \right)}}^k}} =1. $$
(22)

The Manson criterion of universal inclinations is given as follows:

$$ \varDelta \upvarepsilon_{eq}^p=1.75\frac{{{\upsigma_u}}}{E}{N^{-0.12 }}+{\upvarepsilon_r}{N^{-0.6 }}, $$
(23)

where σ u is the tensile ultimate strength and E is the elastic module.

Comparison of criteria was performed on the basis of the analysis of the root-mean-square deviation values \( \upchi_{red}^2 \) of the approximating dependences (21)–(23) derived during determination of constants k and ε r by the least squares technique (minimization of , \( \upchi_{red}^2 \)). Results of comparison are presented in Table 5 for three ways of identification of constants: with the fixed values k = 2 and \( {\upvarepsilon_r}=\upvarepsilon_r^{p* } \) (\( \upvarepsilon_r^{p* } \) is the limiting plastic deformation under tensile loading), with the fixed value \( {\upvarepsilon_r}=\upvarepsilon_r^{p* } \) and variable value k, and with two variable parameters k and ε r

Table 5 Comparison of Criteria for Various Ways of Determination of Parameters k and ε r
Full size table

The results of comparing the criteria of macrocracks’ initiation under thermal fatigue conditions for the considered class of problems using various ways of determination of constants show that the most exact solution is provided by the combined criterion (21). However, this conclusion requires further experimental verification for various loading conditions and other single crystal alloys.

Conclusions. Various modifications of deformation-based fracture criterion for single crystal alloys under thermocyclic loading conditions are proposed. Verification of the criterion for single crystal ZhS36 alloy is presented on the basis of comparison with the experimental data obtained on hour-glass type specimens with various orientation of crystallographic axes (〈001〉, 〈011〉, and 〈111〉 ) at different temperatures (150–1050°C) and cycle durations (20–385 s). A high accuracy of thermal fatigue life prediction by means of the proposed criterion is established.

The importance of taking into account the unilaterally accumulated inelastic deformation along with its range within a cycle is demonstrated in calculations of the number of cycles to macrocrack initiation. It is established that usage in the fracture criterion of the equivalent deformations related to the maximum shear in the slip planes, yields more exact life forecast, than usage of the equivalent deformations which prproved no explicit account of the crystallographic orientations. Application of the Mises deformation intensities results in the most conservative estimation.

For determination of the stress-strain state of single crystal specimens we have executed FE calculations by means of physical models of plasticity and creep by postulating that inelastic deformation of a single crystal occurs according to the available active slip systems and is controlled by the crystallographic orientation. Distribution of damage fields in the specimen and history of their variation are analyzed, which allows one to directly identify the potential initiation sites of thermal fatigue macrocracks, as well as to estimate the respective number of cycles to initiation. As a result of combined experimental and calculation studies, a strongly pronounced sensitivity of thermal fatigue life of single crystals to crystallographic orientation of specimens is proved.

The results obtained are recommended to be used in calculations of thermal fatigue life of gas turbine blades produced from single crystal alloys.

This research is executed with the Russian Fund of Fundamental Investigations support (Project No. 12-08-00943).