1 Introduction

The magnetic activity of the Sun, generated via an \(\alpha -\omega \) dynamo, exhibits variations across a very wide range of time scales, encompassing seconds and minutes up to the evolutionary scales of the star (Hathaway 2010; Usoskin 2017; Vecchio et al. 2017; Biswas et al. 2023). Within this broad interval, the Sun displays several scales of variability, but, among the others, two key characteristic time scales stand out: the solar rotation period (\(\sim 27\) days) and the Schwabe cycle (also known as 11-year solar cycle). In particular, the former time scale is usually used to discern between Space Weather and Space Climate (see, e.g., Mursula, Usoskin, and Maris 2007). Strong signatures of variations at these time scales have been found in several indices used to quantify the magnetic activity of the Sun, such as SunSpot Number (SSN), SunSpot area, F10.7 cm, chromospheric proxies, etc. (see, e.g., Lean and Brueckner 1989; Chowdhury, Khan, and Ray 2009; Roy et al. 2019; Kotzé 2021). The imprints of these periodicities (i.e., rotation period and 11-year cycle) are visible also in geomagnetic indices and near-Earth solar wind data. Indeed, the advent of the “space era” has led to a growing wealth of data, enabling to find the presence of a solar wind cycle, with a characteristic time scale comparable to the Schwabe one, in several near-Earth solar wind parameters (e.g., King 1979; Neugebauer 1981; El-Borie 2002; Dmitriev, Suvorova, and Veselovsky 2013; Li, Zhang, and Feng 2017; Hajra et al. 2021; Reda, Giovannelli, and Alberti 2023). Such a discovery has stimulated a long-standing discussion to understand the still not completely clear relation between the solar wind cycle and the solar activity one, which is marked by a time delay (on average ∼ 3 yrs) of the former respect to the latter (Köhnlein 1996; Li, Zhanng, and Feng 2016; Venzmer and Bothmer 2018; Samsonov et al. 2019; Reda et al. 2023). These outcomes stem from cross-correlation analysis, whose peculiarity consists in measuring the degree of synchronization as a function of the time delay between the time series peaks, which does not ensure a cause-effect relationship. However, such constraint has recently been overcome by Reda et al. (2024), who, making use of a technique from information theory (i.e., Transfer Entropy), found the presence of an information flow from Ca II K index to solar wind parameters marked by time lags compatible to those previously found. A further point of interest is represented by the fact that such a lagged response has been found to be not the same for each cycle. Indeed, it is characterized by cycle-to-cycle variations, with solar wind parameters almost anticorrelated to solar activity along Solar Cycles 20 and 21, whereas a tendency toward smaller time lags has been observed in the subsequent Cycles 22, 23, and 24 (see Samsonov et al. 2019; Reda, Giovannelli, and Alberti 2023).

The approach we propose here, to study the relation between solar activity and solar wind properties, is different and is based on the analysis of their phases. Indeed, investigating how the solar coronal flux is related in phase to solar activity variations is crucial in the context of Space Climate studies. The examination of phase dynamics in complex systems, such as the heliosphere, assumes particular significance due to the potential emergence of synchronization in nonlinearly connected quantities. This synchronization can result in the locking of their respective phases, even as their amplitudes exhibit chaotic and uncorrelated behavior (see, e.g., Rosenblum, Pikovsky, and Kurths 1996). In the context of the heliosphere, a complex interplay exists between solar activity indicators like the Ca II K index and solar wind properties near Earth. Understanding the phase relationships within this system unveils insights into the underlying dynamics, which may not be evident when solely considering amplitude variations.

This work seeks to explore the phase-relation of a solar activity physical proxy, the Ca II K index, with two solar wind parameters, speed and dynamic pressure, as a function of the time scales. This is possible by using a robust tool such as the Hilbert–Huang transform (Huang et al. 1998; Huang and Wu 2008). Notably, its distinct feature lies in its ability to firstly decompose the signals into their time scale components and subsequently extract their amplitude, phase, and frequency as functions of time. Such last step, which is of relevance also in Space Weather contexts, has recently been used by Chapman et al. (2020) to build up a solar cycle “clock”, enabling them to examine over a uniform time base the occurrence of geomagnetic storms in relation to solar cycle phases. In recent years, the Hilbert–Huang transform and its first step (i.e., the empirical mode decomposition) have been widely employed for various applications in the fields of both solar and space physics (Li et al. 2007; Nakariakov et al. 2010; Deng et al. 2013; Stangalini et al. 2014; Deng et al. 2015; Kolotkov et al. 2015; Kolotkov, Broomhall, and Nakariakov 2015; Lovric et al. 2017; Vecchio et al. 2017; Deng et al. 2019; Alberti et al. 2020, 2022), with use also in the study of multicomponent stellar activity cycles (Velloso et al. 2023).

The paper is organized as follows. In Section 2, we describe the dataset used in this work. In Section 3, we present the results of the analysis, which are subsequently discussed in Section 4. A description of the methodology used is left to Appendix A. Finally, in Section 5, we summarize the conclusions of the work.

2 Data

The proxy employed here to quantify the magnetic activity of the Sun is the Ca II K 0.1-nm emission index.Footnote 1 In particular, we exploit the composite by Bertello et al. (2016), which contains data with monthly resolution starting from almost the beginning of the twentieth century (February 1907) up to October 2017. Nevertheless, such a composite has been extended to April 2021 by Reda et al. (2021, 2023) by using the Mg II index composite from the Bremen University,Footnote 2 thus providing a complete cover for the Solar Cycle 24. The Ca II K 0.1-nm emission index (hereafter indicated simply as Ca II K index) is based on the intensity of the Ca II’s K line at 393.4 nm, which originates in the solar chromosphere. For this reason, the Ca II K index provides a physical measure of the average properties of the solar chromospheric emission. Unlike a synthetic index as the Sunspot Number, which is biased by the presence of highly concentrated magnetic structures (the sunspots), the Ca II K index has been demonstrated to quantify the intensity of the solar magnetic field throughout all phases of the solar cycle, even in the absence of sunspots, such as during solar minima (see, e.g., Schrijver et al. 1989; Pevtsov et al. 2016; Kahil, Riethmüller, and Solanki 2017, 2019). Specifically, different studies have highlighted the ability of this index to trace the line-of-sight (LoS) unsigned magnetic flux density (Ortiz and Rast 2005; Chatzistergos et al. 2019), which, in turn, is also connected to the solar wind power (Schwadron and McComas 2008). For these reasons, the use of a physical indicator as the Ca II K index constitutes a reasonable choice for analyzing the long-term phase relationship between solar activity and solar wind properties.

The availability of direct measurements of solar wind quantities is directly connected to the birth of the “space era”. Indeed, data concerning solar wind speed are dated back to 1963 (IMP spacecraft launch), whereas measurements of other parameters start only from 1965. The analysis we perform here regards two dynamic plasma parameters of the solar wind: the solar wind speed (hereafter also indicated as \(v_{sw}\)) and the solar wind dynamic pressure (hereafter also indicated as \(P_{d,sw}\)), which is defined as \(P_{d,sw}=1/2\,\rho _{i,sw}v_{sw}^{2}\), where \(\rho _{i,sw}\) is the solar wind ion density. Since to compute the latter quantity, we need both speed and ion density measurements, the solar wind dataset used spans the time interval July 1965 – April 2021. Such data have been downloaded at hourly resolution from the OMNI databaseFootnote 3 (accessed in May 2021) and later binned to obtain monthly averages. OMNI is a large database containing intercalibrated multisource data, both in low and high resolution (King and Papitashvili 2005). It provides solar wind magnetic field and plasma measurements, energetic proton fluxes, and several geomagnetic indices, representing a data container widely used by the solar and heliospheric community.

As previously explained, the main constraint related to the temporal window explored in this work comes from the absence of direct solar wind data before 1965. Nevertheless, the study covers a significant time interval, ranging from July 1965 to April 2021, enabling a five solar cycles analysis, one of the longest conducted in this framework up to now.

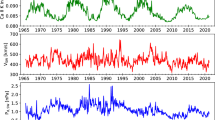
Figure 1 shows the monthly values of the time series used for the present analysis and their probability distribution functions (PDFs). The Ca II K index, as expected, clearly shows the presence of the 11-year cycle, whereas in the case of the solar wind parameters (both speed and dynamic pressure), such a periodicity is covered by the high-frequency variability. The maximum and minimum values of Ca II K index are 0.082 and 0.097, respectively, whereas the mean value is \(0.087\pm 0.003\). For the solar wind speed, the average value is \(439\pm 50\) km s−1, whereas the maximum and minimum values are 318 km s−1 and 644 km s−1, respectively. Finally, in the case of solar wind dynamic pressure, the lowest value is 0.45 nPa, the highest value is 2.59 nPa, whereas the mean monthly one is \(1.10\pm 0.31~\mathrm{nPa}\). Looking at the PDFs, it is possible to notice that in the case of solar wind speed and dynamic pressure, the distribution is asymmetric, with the peak leaning toward small values, as previously found (see, e.g., Tokumaru, Kojima, and Fujiki 2010; Li, Zhanng, and Feng 2016; Venzmer and Bothmer 2018; Larrodera and Cid 2020). The PDF of the Ca II K index also exhibits asymmetry and, in addition, shows the presence of two peaks: one at very small values (representing the values at the solar cycle minima) and the other at intermediate values (mainly accounting for the values at the ascending and descending phases of the cycle).

Figure 1
figure 1

Time series analyzed in this work and corresponding PDFs: Ca II K index (top panels), solar wind speed (middle panels), and solar wind dynamic pressure (bottom panels).

Full size image

3 Results

The results shown in this section arise from the application of the Hilbert–Huang transform (HHT) to the time series of Figure 1. This method is based on the empirical mode decomposition (EMD, Huang et al. 1998), a data-adaptive method that allows us to decompose a signal into its physical components, and on the Hilbert spectral analysis, useful to associate with each component its typical time scale, as well as to obtain its instantaneous phase, amplitude, and frequency (Huang and Wu 2008). A description of this method is left to Appendix A, whereas in this section, we simply present the results of the data analysis.

In Table 1, we summarize the characteristic (or mean) time scale of each EMD mode. Thus \(<\tau _{i}>\) denotes the period of the ith intrinsic mode function (IMF) averaged over time, whereas the associated error represents the standard deviation value. Since the number of the IMF is already reported in the first column of Table 1, we simply use the notation \(<\tau >\) to refer to the mean time scale. It is worth highlighting that the IMFs, whose decomposition bases are not prescribed a priori, are characterized by amplitudes and frequencies that can vary with time. Furthermore, since the characteristic time scale is computed starting from the instantaneous frequencies, as described in Appendix A, the associated error bar should be interpreted as a bandwidth of time scales around its mean value, due to the time-dependent nature of the instantaneous frequencies, in a similar way to the bandwidth of frequencies for Fourier or wavelet transforms. This property explains the large values of the errors associated with the period estimates.

Table 1 Characteristic time scales of the IMFs (or EMD modes) of the three signals analyzed in this work and their standard deviation values.
Full size table

The algorithm identifies 6 IMFs in Ca II K index and 7 ones in both \(v_{SW}\) and \(P_{d,SW}\). In particular, for all the signals, we find: two IMFs under the year scale; one IMF that can be associated with variations occurring on a time scale ∼ 2 years (IMF 3 in Ca II K index, IMF 4 in SW speed and SW dynamic pressure), indicative of quasi-biennial oscillations (QBOs); one IMF on an intermediate scale between QBOs and solar cycle; one IMF at solar cycle scale; a further one describing variations on time scales longer than that of the solar cycle. Further information on the same decomposition can be found in Reda et al. (2024). The IMF 5 in Ca II K index represents the component corresponding to the Schwabe cycle. As expected, modes with a comparable time scale are also present in solar wind speed and dynamic pressure (IMF 6 in both cases).

3.1 Phase Analysis

Once the signals have been decomposed into their components, it is possible to obtain, by making use of the Hilbert transform, the instantaneous phase, the instantaneous amplitude, and the instantaneous frequency of each of them. Exploiting the phase values of each IMF, we compute the unwrapped phase differences \(\Delta \phi _{i,j}(t)\) between the \(i\)th IMF of Ca II K index and the \(j\)th IMF of solar wind speed (or dynamic pressure). The obtained phase differences between the modes of Ca II K index and those of solar wind parameters have been subsequently normalized to the interval \([-\pi , \pi ]\), following the approach used by Donner and Thiel (2007). Then we compute the standard deviation of the normalized phase differences, and thus \(\sigma (\Delta \phi _{i,j})\) indicates the standard deviation of the phase differences between the \(i\)th IMF of Ca II K index and the \(j\)th IMF of solar wind parameters. We compute such a quantity for all IMFs of the Ca II K index with those of both \(v_{sw}\) and \(P_{d,sw}\), thus obtaining two \(6\times 7\) matrices.

Figure 2 shows the probability density function (PDF) and the cumulative density function (CDF) of \(\sigma (\Delta \phi )\) on the left panel for the pair Ca II K index–solar wind speed and on the right panel for the pair Ca II K index-solar wind dynamic pressure. We consider here the standard deviation of the phase difference since it is a statistical feature useful to quantify the phase coherence between time series (see, e.g., Donner and Thiel 2007). As the EMD enables us to decompose the signals in their time scale components, this approach lets to quantify the phase coherence as a function of the time scale \(\tau \), not only at the similar ones but across the whole time scales obtained through the decomposition.

Figure 2
figure 2

Probability density function (PDF) and 1-cumulative density function (1-CDF) of the standard deviations of the phase differences of Figure 3. Left panel: \(\sigma (\Delta \phi )\) of the IMFs of Ca II K index and those of SW speed. Right panel: \(\sigma (\Delta \phi )\) of the IMFs of Ca II K index and solar wind dynamic pressure.

Full size image

Figure 3 shows the values of the standard deviation of the phase differences \(\sigma (\Delta \phi )\) of Ca II K index modes with those of solar wind speed (left panel) and with those of solar wind dynamic pressure (right panel). For an easier understanding, we report the characteristic scale of each IMF in the plot labels. To obtain a statistical significance upper limit for the phase coherence, we look at the PDFs and CDFs of Figure 2. We consider as the upper limit for \(\sigma (\Delta \phi )\) the first bin of the PDFs, corresponding to the value 0.09 in both cases. Since it accounts for almost 30% of probability, such a bin is evidently the dominant one of the two PDFs. The values of \(\sigma (\Delta \phi ) \leq 0.09\) are highlighted in Figure 3 with a white color annotation. By fixing such a threshold it is possible to see that in both plots of Figure 3 the phase differences seem to look coherent at similar time scales up to time scales corresponding to QBOs. Instead, going to larger time scales (\(\tau >\) 2 yrs), also adjacent modes seem to maintain a significant phase coherence.

Figure 3
figure 3

Map of the standard deviation of the phase differences of Ca II K index and solar wind parameters IMFs. Left panel: solar wind speed (\(x\)-axis) vs. Ca II K index (\(y\)-axis). Right panel: solar wind dynamic pressure (\(x\)-axis) vs. Ca II K index (\(y\)-axis). The color map shows the value of the standard deviation, whose values are also reported as annotations. For each IMF, the characteristic time scale is reported on the axis label. The values annotated in white are the ones within the coherence threshold.

Full size image

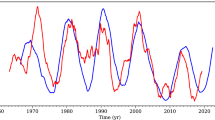
Decomposing the time series into sets of IMFs, each with its characteristic time scale, enables the filtering out of the contribution of time scales not of interest for the analysis at hand. This is necessary in the case of signals oscillating on multiple time scales, as those here analyzed. In particular, here we focus on the solar cycle time scales by considering only the contribution of IMFs 4 – 5 for Ca II K index and the contribution of IMFs 5 – 6 for both \(v_{sw}\) and \(P_{d,sw}\). We aim to study how the phase of the solar wind properties changes over time with respect to the solar cycle. To achieve this, we utilize the Ca II K index as a reference clock for Space Climate scales. Consequently, we compute the phase difference between solar cycles IMFs of the Ca II K index and the two solar wind parameters \(v_{sw}\) and \(P_{d,sw}\). To visually investigate this relation, we plot on the left panels of Figure 4 the filtered \(v_{sw}\) (top-left) and \(P_{d,sw}\) (bottom-left) as functions of time, highlighting with a color map the phase difference values with respect to Ca II K index. Here the quantity \(\delta \phi _{X_{SW}-K}\) is defined as follows:

$$ \delta \phi _{X_{SW}-K} = \Delta \phi _{X_{SW}-K} - < \Delta \phi _{X_{SW}-K}>, $$

where \(\Delta \phi _{X_{SW}-K}\) is the unwrapped phase difference between a solar wind quantity (here simply indicated with \(X_{SW}\)) and Ca II K index, whereas \(<\Delta \phi _{X_{SW}-K}>\) is its average value. Thus the value \(\Delta \phi _{X_{SW}-K}=0\) in the color map corresponds to the average phase difference between the time series over the analyzed time interval. Please note that to avoid boundary effects, we have excluded 3 years of data at the beginning and end of the dataset. We observe that the variations of the phase difference are in general smaller for the solar wind dynamic pressure than for the solar wind speed with respect to the Ca II K index. Moreover, the average phase difference is reached around 2000 for solar wind speed, whereas it is in 1990 for the dynamic pressure. In the right panels of Figure 4, instead, we show \(\Delta \phi _{X_{SW}-K}\) modulo \(\pi \) as a function of time. Besides small fluctuations, the dynamic pressure (bottom panel) is almost in antiphase to Ca II K index up to 1987 (\(\Delta \phi _{avg} = -0.9 \; \pi \)), whereas, after a change occurring around 1990, it moves to a more in-phase state (smaller phase difference, \(\Delta \phi _{avg} = -1.0 \; \frac{\pi}{2}\)). Larger fluctuations are observed in the case of the speed, for which we find a significant change in 2001. However, also for the speed, on average, there seem to be two states (marked by dashed lines): one almost in antiphase up to around 1985 (\(\Delta \phi _{avg} = -0.8 \; \pi \)) and one characterized by a smaller phase difference later 1990 (\(\Delta \phi _{avg} = -0.9 \; \frac{\pi}{2}\)). By adopting an average solar cycle duration of 11 years we can link the phase difference values to time delays. Specifically, the respective time lags for the two states of phase differences are as follows: 4.6 years and 2.4 years for solar wind speed and 5.0 years and 2.8 years for solar wind dynamic pressure. These results, based on a phase analysis, confirm the previous findings reported by Samsonov et al. (2019) and Reda, Giovannelli, and Alberti (2023) through cross-correlation analysis. Overall, both \(P_{d,SW}\) and \(v_{SW}\) are always characterized by delayed (negative phase differences) variations with respect to the Ca II K index. This behavior points out that at the solar cycle time scales the solar wind properties, as measured near the Earth, do not promptly respond to solar activity variations.

Figure 4
figure 4

Top-left: Sum of solar wind speed IMFs 5 – 6 plotted as a function of time, with the color map showing the phase difference with the IMFs 4 – 5 of the Ca II K index. Bottom-left: Same as top-left, but showing the IMFs 5 – 6 of solar wind dynamic pressure. Top-right: Phase difference of solar wind speed to Ca II K index modulo \(\pi \); Bottom-right: Phase difference of solar wind dynamic pressure to Ca II K index modulo \(\pi \). In the right panels the dashed lines show the two “states” of the phase difference.

Full size image

3.2 Dependence of the Dynamical Properties on the Characteristic Time Scales of the System

Having the different time scale components of the signals is very useful. Indeed, it not only enables us to filter out the contribution of scales not of interest, but also to investigate how the relationship between solar activity (Ca II K index) and solar wind parameters evolves when adding or removing the contribution of various scales. After having considered a mean phase difference between the signals (same across all the scales), indicative of the time delayed response of solar wind properties to solar activity, we plot in Figure 5 the relation of Ca II K with solar wind speed (left panels) and with solar wind dynamic pressure (right panels). Here moving from top to bottom corresponds to adding the contribution of increasing time scale components. It is interesting to notice that in both cases, adding the contribution of larger scale components results in a shift from negligible correlation to a weak correlation (see the subplots on the bottom).

Figure 5
figure 5

Scatter plots showing the relationship of Ca II K index with solar wind speed (left panels) and with solar wind dynamic pressure (right panels), with the latter delayed by a mean time lag. Moving from top to bottom corresponds to adding the contribution of increasing time scales. The color map is used to describe the time dependence.

Full size image

Exploring the impact of adding scales in the opposite direction, and hence starting from large scales and adding the contribution of ever smaller time scales, reveal also intriguing dynamics. This relationship is shown in Figure 6 for Ca II K index with solar wind speed (left panels) and with solar wind dynamic pressure (right panels). In this case, at least a weak correlation is preserved when the contribution of smaller scales is introduced. Additional information provided by the plots of Figures 5 and 6 about the physics governing the relationship between the Ca II K index and the speed and dynamic pressure of the solar wind will be discussed in the next section.

Figure 6
figure 6

Scatter plots showing the relationship of Ca II K index with solar wind speed (left panels) and with solar wind dynamic pressure (right panels), with the latter delayed by a mean time lag. Moving from top to bottom corresponds to adding the contribution of decreasing time scales. The color map in each subplot is used to describe the time dependence.

Full size image

4 Discussion

The Hilbert–Huang transform stands out as a powerful technique, with one of its advantages being the possibility to decompose a nonlinear and nonstationary signal into its components (i.e., IMFs), each one associated with its characteristic time scale. By applying this method to the monthly time series on Ca II K index, solar wind speed (\(v_{SW}\)) and solar wind dynamic pressure (\(P_{d,SW}\)), we find seven IMFs in the latter two and six IMFs in the former one. In particular, in all of them, it is possible to identify two modes under the year scale, one mode that can be linked to QBOs, one mode with characteristic time scale ∼ 11-year (solar cycle component), and a further one describing longer time scale variations. The presence of clear solar-cycle modulation in \(v_{SW}\) and \(P_{d,SW}\) is in agreement with previous findings (El-Borie 2002; Dmitriev, Suvorova, and Veselovsky 2013; Li, Zhang, and Feng 2017; Reda, Giovannelli, and Alberti 2023), confirming the presence of a link between solar activity and solar wind properties at 11-year scale (Venzmer and Bothmer 2018; Samsonov et al. 2019; Reda et al. 2023).

The advantages of having separated for each signal the contribution of the different time scales are multiple. For example, it allows us to easily obtain the phase of each component, providing the opportunity to explore their relationship. Studying the solar activity–solar wind relation in terms of phases, rather than in terms of amplitudes as usually done, is particularly convenient when dealing with time series that merge measurements from different instruments or satellites. This is actually the case of the OMNI solar wind database that is based on inter-calibrated data from several satellites, as mentioned in Section 2, potentially introducing amplitude-related issues.

The presence of cycle-to-cycle differences has been studied for different solar activity indicators (see, e.g., Karak 2023), as well as for global solar wind (e.g., Owens, Lockwood, and Riley 2017) and coronal mass ejections (e.g., Zhang et al. 2023, 2024). However, although this cycle dependence in the relationship of solar activity proxies with solar wind parameters has been already pointed out (e.g., Samsonov et al. 2019; Reda, Giovannelli, and Alberti 2023), this is the first time in which their instantaneous time-dependent phase difference has been investigated by taking advantage of the instantaneous and adaptive nature of the HHT. The study of the phase difference between solar wind properties and the Ca II K index clearly indicates a shift in phase, transitioning from almost antiphase during Solar Cycles 20 and 21 to a quadrature phase from Solar Cycles 22 onward. The change in phase is more pronounced during the minimum following Solar Cycle 21 and the rising phase of Solar Cycle 22. The result is also consistent with a two-component solar wind source, one in antiphase and one in quadrature, capable of replicating the observed phase shift over the last five solar cycles. This finding is particularly intriguing in the context of establishing a connection between the solar wind and the solar dynamo and will be further investigated in future research.

The availability of cross-scale phase values opens the possibility to analyze their phase coherence, quantified in terms of standard deviation of normalized phase differences \(\sigma (\Delta \phi )\) as a function of the time scale \(\tau \). Our results suggest that Ca II K index and both \(v_{SW}\) and \(P_{d,SW}\) are coherent in phase along each comparable time scale, whereas the coherence seems to be preserved also between adjacent components when moving to \(\tau >\) 2 yrs. The maximum phase coherence is found near the solar cycle time scale (\(\tau \sim \) 11 yrs), pointing out a significant degree of connection between solar activity and solar wind properties on time scales that are relevant in the context of Space Climate studies.

Figures 5 and 6 shed light on the intricate relationship between solar activity, as represented by the Ca II K index, and solar wind parameters, specifically solar wind speed and dynamic pressure. The analysis focuses on the impact of varying time scale components, offering valuable insights into the nuanced dynamics governing the solar-atmospheric coupling.

In Figure 5, we observe a noteworthy trend as the contribution of larger time scale components is successively added, revealing a systematic evolution. Initially characterized by a negligible correlation, the relationship transforms into a weak-to-moderate correlation as larger time scale components are incorporated. This observation suggests a complex interplay between solar activity and solar wind parameters, which becomes more discernible with the inclusion of longer time scale components.

Conversely, Figure 6 investigates the effects of introducing ever smaller time scale components in the opposite direction. When starting from larger scales and progressively adding smaller time scale contributions, a contrasting behavior emerges. This implies that fine-scale variations in solar activity may indeed influence the observed correlations, underscoring the intricate nature of the solar-atmospheric interaction. In particular, it is possible to observe a transition from a more ordered cyclic behavior to a less coherent orbit when incorporating the time scales under the solar cycle (Figure 6, fifth row) with a tendency toward disorder when the time scales under the year are added (Figure 6, sixth and seventh rows).

The observed divergence in correlation strength with varying time scales suggests the existence of distinct dynamical regimes. This transition from negligible to weak correlation, and vice versa, points to a sensitivity to the temporal hierarchy of underlying processes, indicative of a potential bifurcation phenomenon. Recent studies in fluid turbulence and stochastic dynamical systems have reported similar phenomena (Alberti et al. 2023a,b).

Our findings align with the evolving concept of attractors, traditionally viewed as sets of states toward which a system evolves over time. We introduce the notion of a chameleon attractor, where properties vary with scale, capturing the emergence of an intrinsic time scale closely related to the solar cycle. This time scale governs the geometrical and topological attributes of phase-space trajectories. Remarkably, it is responsible for a fundamental shift in the nature of system equilibria—from an unstable saddle at shorter time scales to two stable nodes at larger ones.

Our study underscores the critical role of temporal scales in Space Climate research. The ability to selectively include or exclude contributions from different time scales enhances our understanding of underlying mechanisms and hints at the presence of dynamical transitions shaping observed correlations. Future investigations should delve deeper into these dynamics, elucidating the mechanisms driving the observed bifurcation and developing simple models. These models, inspired by dynamical systems with two stable equilibria and an unstable one, could provide insights into the observed behavior. Unlike classical dynamical systems, the unique feature here is that the bifurcation parameter is the time scale itself, introducing an intriguing dynamic balance across temporal dimensions.

The stability landscape of such a dynamical system, shaped by the interplay of stable and unstable equilibria, not only influences its long-term behavior but also offers valuable insights into the system adaptability across varying time scales. This understanding is pivotal for unraveling the complex dynamics of solar-atmospheric interactions and has implications for predicting and interpreting phenomena in Space Climate studies.

5 Summary and Conclusions

Investigating the relation of solar activity with solar wind is of significant importance for understanding the interaction among the different solar atmospheric layers. Additionally, it plays a crucial role in unveiling the dynamics of solar activity within the heliosphere. In this work, by exploiting five solar cycles data, we investigate how the Ca II K index is related in phase to two solar wind parameters, the solar wind speed \(v_{SW}\) and the solar wind dynamic pressure \(P_{d,SW}\). By using the Hilbert–Huang transform we decompose the signals into their intrinsic modes of oscillation (i.e., IMFs) and explore the relationship among their phases. Phase coherence of solar wind dynamic pressure (speed) with Ca II K index is found at the same time scales up to ∼ 2 yrs, whereas it extends over broader time scales when moving to those > 2 yrs.

By focusing on the solar cycle time scale components we highlight the phase differences of \(v_{SW}\) and \(P_{d,SW}\) with Ca II K index. Both parameters exhibit delayed variations to Ca II K index. Despite minor fluctuations, two consistent mean phase differences (or state) are observed: one predominantly in antiphase until 1985, followed by quadrature phase differences later on. Further analysis to investigate the physical processes dominating this behavior is needed.

Finally, we focus our attention on the relation between the designed solar wind parameters and the Ca II K index as a function of the time scales contribution. Adding the contribution of increasing (decreasing) time scales components has the effect of making more discernible (less discernible) the connection between solar activity and solar wind. This observation has implications on the dynamical regime of solar activity–solar wind connection, for which the time scale seems to act as a bifurcation parameter.

The findings of this study, combined with insights from prior papers, are planned to be used for building up a dynamical model in the context of Space Climate predictions.