The added value of management skill in the explanation of the distribution of firm size

Abstract

The stochastic explanations of skewed distribution of firm size question the value added of management theories that trace differences in market share and profits of firms to strategy and organization choices, which are in turn linked to better entrepreneurial skills. This paper explains the distribution of firm size as the market equilibrium outcome of individual occupational choices of working as entrepreneurs or employees. The distribution of size and profit of firms in the equilibrium is directly related to the distribution of skills within the group of individuals who, in the same equilibrium, choose to work as entrepreneurs, restoring the importance of management choice in the performance of firms. The paper highlights the importance of having a theoretical model as guidance in the interpretation of regularities observed in the distribution of firm size, and the ability to distinguish between “resembling” and “true” power laws of such distributions.

1 Introduction

Observed empirical regularities in the distribution of organization variables challenge the theories of individual and group behavior that must explain the “stylized facts.” This paper is concerned with the theoretical understanding—from individual occupational choices of working as employees or as entrepreneur-managers—of the long-term, empirically established regularity that the distribution of firm size (DFS from now on) follows a power law (Simon, 1955; Axtell, 2001). Existing explanations of why the size of the firm and other organization variables are distributed as a power law appeal to stochastic, multiplicative, or additive cumulative shocks to the value of the reference variable (Andriani and McKelvey, 2009; Gabaix, 2016).¹ This paper takes a different stance and proposes an explanation of the distribution of firm size that follows Axtell’s (2001:1820) request for a “microeconomic model in which individual agents interact to form productive teams (that can explain) … the undisputed empirical evidence that the size of firms in the US follows a Zipf distribution” (a special case of power law distribution). To this end, we propose an explanation of the DFS with entrepreneurial-managerial skill as a main determinant.

The proposed microeconomic explanation of the DFS draws on occupational choice theory (Lucas, 1978; Rosen, 1982), where management teams compete for control of resources to produce goods and services until the market equilibrium is reached. Individuals in the economy differ in attributes important for income-maximizing occupational choices that in this paper are summarized in the construct “entrepreneurial skills” (Lucas, 1978; Jovanovic, 1994). The way that the entrepreneurial skill determines the income from working as employee (salary) or as entrepreneur-manager (profit), implies that in the market equilibrium, individuals in the upper tail of the distribution of skill choose to work as entrepreneur-managers and the rest as employees. The profit-maximizing inputs and output quantities of each entrepreneur-firm depend on the skill of the respective entrepreneur-manager. A correspondence is then established between the distribution of skills in the population, the truncated upper tail (from the skill level of the less skilled entrepreneur) of this distribution that corresponds to the distribution of skills for the sub-group of individuals who work as entrepreneurs, and the distribution of the profit-maximizing values of the outcome variables of firms such as sales, employees, capital, and profits - each a function of the respective entrepreneur’s skill. From this correspondence, under the assumptions of the model, the DFS will be a power law only when the distribution of skill in the population is also a power law.

The purely stochastic or “chance” explanation of the distribution of variables, such as growth rate and size of the firm, that has dominated the literature, particularly that around the explanation of the power law distribution attributed to the variable size of the firm (Andriani and McKelvey, 2009), and that Axtell (2006) qualifies “more as fables of firm growth than as credible explanations,” question the “value added” of theories of Management. Such theories trace the differences in performance among firms to better strategy and organization choices linked to better managerial skills (Geroski 2000; Denrell et al. 2014; Knudsen et al. 2017). The representation of the firm in occupational choice models explicitly incorporates the input of the entrepreneur (quality of strategic decisions and skill-weighted monitoring time) as determining the organization’s production output and performance (profit), in combination with direct labor and capital. Consequently, in the explanation of the heterogeneity observed in the size and performance of firms from occupational choice models, entrepreneur-managers’ skills matter, and the value added of management theory is restored. In this respect, the entrepreneur in occupational choice models is characterized as a director of resources (Coase, 1937; Penrose, 1959), rather than as an individual involved in the introduction of innovations and new ventures (Schumpeter, 1934).²

In the empirical section, we use Axtell’s (2001) data about the size of firms, from the US census, to test some predictions from the theory, and to compare these predictions with the results from assuming that the firm size data follows a power low (Axtell’s assumption). The research interest is similar to that of Joo et al. (2017) on whether the taxonomy of non-normal distributions that fits individual output variables includes distributions other than the power law. The difference, in our paper, is that, first, we connect the empirical results with the predictions from a model of individual and collective behavior; in particular, we derive the DFS in the market equilibrium assuming that the distribution of skill in the population is lognormal and then fit the distribution to the actual data. And second, it is possible to relate the parameters of the distribution of outcome variables with the parameters of the theoretical model.

This paper contributes to the literature that aims to explain the causal processes underlying observed patterns of heterogeneity across firms, particularly in their size and profits, with new views from occupational choice models that complement the existing explanations, mainly coming from complexity science (Andriani and McKelvey, 2009). The repetition of the same pattern of a highly skewed-to-the-right distribution of the values of organization and entrepreneurial variables has led to the conclusion that the description of a social world is far from “normality.” The paper then complements the existing explanations of the social world of power laws, with an explanation of the heterogeneity in size and performance of firms from a model of rational individual behavior and team production that responds to the request of Axtell (2001), and restores the value of management and entrepreneurial inputs as determinants of size and performance of firms.

Entrepreneurship research, see Crawford et al. (2015), Aguinis et al. (2018), and Joo et al. (2017), has established empirical links between the distribution of entrepreneurial inputs (one of these being entrepreneurial skill) and the distribution of entrepreneurial outcomes (one of these being the size of the firm). The occupational choice model presented in this paper complements this literature with a market equilibrium distribution of firm size (outcome) that is the result of a transformation of the distribution of skill (input). Specifically, for the standard formulation of the production function of firms, the DFS will be a convex transformation of the left-truncated distribution of entrepreneurial skills in the population, and the probability density function of the DFS will generally be strictly (strictly) decreasing and convex. The visual examination of the function will resemble that of a power law, but the sufficient conditions for the size distribution of firms being a strict power law are more restrictive, as this paper shows. The lower bound and the shape of the DFS will depend, among other things, on parameters of the distribution of skills in the population, and on parameters of the production and organization technologies.³

Although the occupational choice theory is well established and has been influential in the literature (Lucas’ 1975 paper has more than 4000 citations in Google), its practical relevance is conditioned by the difficulty of directly measuring the entrepreneurial skill of individuals. The use of human capital data, i.e., education, training, and experience of entrepreneur-managers (Storey, 1994; Roper, 1998; Ferrante, 2005) as proxies of entrepreneurial skill, leaves out many personal attributes that differentiate entrepreneurs from salaried employees. This difficulty may explain why the predictions from the theory have been tested in indirect ways. For example, the positive association between size of the firm and compensation of managers has been interpreted as evidence that the higher productivity of the management team (more volume of managed resources) is rewarded with higher compensation (Rosen, 1981, 1982; Gabaix and Landier, 2008). Ferrante (2005) finds that the time entrepreneurs dedicate to entrepreneurial tasks increases with their skills, which is interpreted as evidence that the return from the time dedicated to entrepreneurial tasks increases with skill. Vendrell-Herrero et al. (2014) find a positive correlation between total factor productivity, their proxy for entrepreneurial talent, and the rate of return in a sample of technological firms. Although there are ways to overcome the difficulty of directly measuring entrepreneurial skills, more needs to be done for occupational choice theory becoming more relevant for policy and management.

The rest of the paper is organized as follows. Section 1 presents a brief introduction to power laws. Section 2 introduces the basic theory of the size distribution of firms from occupational choices. Section 3 extends the results to outside occupational choice models. Section 4 re-examines the empirical tests of whether the size distribution of firms in the USA, with census data, follows a Zipf distribution. The Conclusions summarize the main findings of the paper and draw some theoretical and empirical implications as well as extensions of future research.

2 Power laws

The term power law is used in statistics, the natural sciences, and the social sciences to refer to relationships between two quantities or variables that can be mathematically described by power functions. Thus, a power law defines a functional relationship between two variables, y and x, such that the value of y is equal or proportional to a value of x risen to a power parameter. More formally, a power law is usually represented by a function of the form y = c x^−a with c, a > 0. In statistics, the distribution of a variable x is said to follow a power law if and only if its probability density function f(x) (or its survival function) is a power function.

A distinctive feature of the power function is that the elasticity of y to changes in x is constant and equal to a for all values of x (a log-linear relationship of variables y and x). Power functions have the property that, if g(x) and h(x) are power functions, then g ' (x)and h(g(x)) are also power functions. Mathematically, if $g(x)={c}_1{x}^{a_1}$ and $h(x)={c}_2{x}^{a_2}$, then $g\hbox{'}(x)={c}_1{a}_1{x}^{a_1-1}$, $h\hbox{'}(x)={c}_2{a}_2{x}^{a_2-1},$ and $h\left(g(x)\right)={c}_2{c}_1^{a_2}{x}^{a_1{a}_2}$.

The only random variables whose probability density functions are power functions in a strict sense are the Pareto distribution and the Zeta (also known as Zipf distribution), the former being a continuous version of the latter.⁴ Their probability density functions are given by:

$$ \mathrm{Pareto}\ \mathrm{distribution}:\kern0.5em f(x)=\alpha {e_m}^{\alpha }{x}^{-1-\alpha}\kern0.5em \left(\alpha >0,x\ge {e}_m>0,x\in \mathrm{\mathbb{R}}\right) $$

$$ \mathrm{Zeta}\ \mathrm{distribution}\kern0.5em p(x)=\frac{x^{-1-\rho }}{\zeta \left(1+\rho \right)}\kern2em \left(\rho >0,x\ge 1,x\in \mathrm{\mathbb{N}}\right) $$

where ζ(x) is the Riemann zeta function.

2.1 Power laws of individual and organizational variables

Most of the explanations of why entrepreneurial and organizational variables, including firm size, follow a true or apparent power law include some stochastic element. A common reference, see Crawford et al. (2015) and Crawford (2018), is Andriani and McKelvey (2009) that explains power law distributions as an outcome consistent with the predictions from complexity science, with extensions to theories of organizational change and development that are “scale-free,” i.e., there is one primary driver that explains the relationship between inputs and outputs at multiple levels, regardless the scale at which the phenomenon is measured.⁵ These authors view organization development as the outcome of independent-multiplicative causal elements that operate as the system complexity increases, or as the result of random events that are interdependent, interactive, or both. In these situations, “Pareto distributions dominate because the positive feedback (and other processes) leading to extreme effects occur more frequently than “normal” Gaussian-based statistics lead us to expect” (p. 1055).

Gabaix (2016) considers two mechanisms that generate power laws in the distribution of firm size: random growth, and “transfer” of that power from another variable via matching and optimization. The random growth model that generates power laws of firm sizes is the proportional random growth of Gibrat (1931) complemented with other assumptions, for example a minimum firm size required for survival (Ijiri and Simon 1967). The random growth rates that interact multiplicatively generate bell-shaped but skewed distributions (lognormal distribution). With a lower bound of the size variable the bell shape is lost, and the distribution converges to the Pareto one. The “scale free” condition in these papers is that of constant returns to scale in the production technology, so that unit production cost is constant for all values of size (i.e., differences in size do not become differences in unit costs).

The matching and optimization explanation of the power law of firm size draws from Rosen’s (1981) “economics of superstars” that provides a market explanation of the positive correlation between compensation of managers and size of the respective firm (Gabaix and Landier, 2008). Firms with different sizes compete for hiring managers of different talent; the outcome of the competition process assigns the most talented person to the largest firm and so on. The distribution of managers’ talent is not known but, under certain assumptions, given the ordering of talent, the approximate difference of talent between two adjacent managers varies like a power law of their rank. The matching and optimization processes imply that the power law distribution of the rank of managerial talent is “transferred” to the distribution of firm size, and to the distribution of managers’ compensation.

The matching explanation of the power law distribution of firm size is somehow related to the matching between entrepreneurial skills and firm sizes in occupational choice models, although this relation has not yet been formally established. The model presented in the following section summarizes the heterogeneity of the working population in the construct “entrepreneurial skills.” The heterogeneity of skills in the population will explain the occupational choice of working as salaried employee or as entrepreneur-manager, as well as the differences in the number of employees working under the direction of each entrepreneur (different firm size).

The condensation of the heterogeneity in the working population into the single attribute of entrepreneurial skill responds to tractability reasons. Entrepreneurship is a multidimensional phenomenon and the list of variables that have been used to characterize entrepreneurs in the working population is rather long (Shepherd et al., 2019). Conceptually at least, the occupational choice theory and the predictions from the market equilibrium could be extended substituting the single construct of entrepreneurial skill, for a vector z of attributes (skills, risk attitude, preference for independent work, empathy...), with joint cumulative distribution functions in the population, H(z). The individuals who choose to work as entrepreneurs in the market equilibrium will occupy a region R of the space of attributes determined from supply and demand conditions, similar to what happens with the single construct of skill. The outcome variables from the market equilibrium (production inputs labor and capital, output, profits) would then depend on the values of the variables in z, and the cumulative distribution functions of those outcome variables would continue being a function (transformation) of the joint distribution function H with the values of the attributes z restricted to values in the region R.

3 Occupational choices explanation of firm size

The main premise of occupational choice models is that the distribution of firm size is the equilibrium outcome in a market where individuals with different skills compete for the control of productive resources, labor, and capital. This section presents a summary of the basic results of occupational choice models (Lucas 1978; Rosen 1982; Jovanovic 1994) on the determinants of the distribution of firm size in the economy.

3.1 Market equilibrium and distribution of firm sizes

Consider a production technology that uses two inputs⁶ to produce a quantity of output, labor services supplied by employees, and the skill-weighted time of the entrepreneur who manages the production process. The skill of the entrepreneur is fixed, and employees can be hired in the market at a given salary. Output produced is sold in the market at a normalized price of one. The working time is normalized to one unit. The entrepreneur earns the profit of the firm and employees receive a market-determined salary.

Let Q = g(e, L) be the production technology, where Q is the total output produced; e is a number that represents the skill of the entrepreneur; L is the number of employees; and g() is the production function, increasing in e and L, and concave in L. The production function is formally derived from the aggregation of outputs from individual job, each occupied by an employee monitored by a single entrepreneur of given skill, as in Rosen (1982). The entrepreneur decides how to allocate the skill-weighted limited working time among the employees-jobs; in the optimal solution the output in each job depends on the entrepreneur’s monitoring time and of the direct working time of the employee. The aggregate output of the entrepreneur-team of employees is further leveraged by the quality of the strategic decisions of the entrepreneur that contribute equally to the productivity of all employees. The monitoring function of the entrepreneur-manager takes place under decreasing returns to scale (which capture the organizational size diseconomies that limit the growth of firms in Penrose’s (1959) theory of the growth of the firm). The quality of strategic decisions is a “public good” that affects positively the output of all jobs equally. The contribution to the total productivity of the group from the quality of the decisions of the entrepreneur increases with the level of skill. Occupational choice models modify the neoclassical production function to incorporate the contribution to the total output (from quality of decisions and from monitoring of their implementation) of the skill-weighted working time of the entrepreneur who manages the production team.

If w is the market salary for employees, the profit/income of the entrepreneur of skill e is Π = g(e, L) − w L. The profit-maximizing number of employees satisfies the condition of marginal revenue equal to marginal costs, $\frac{\partial\;g\left(e,L\right)}{\partial\;L}=w\kern0.5em$. Solving this equation, the demand for labor as a function of the entrepreneur’s skill and employees’ salary is given by L = h(e; w), increasing with skills e and decreasing with the salary, w. Substituting into the profit function, the maximum profit for an entrepreneur of skill e is equal to Π^∗(e; w) = g(e, h(e; w)) − w h(e; w).

Individuals with different skills choose between working as employees and earning the market salary or working as entrepreneurs and earning a profit. The distribution of skills in the population is taken as given. Let F(e) and f(e) denote the cumulative distribution function (CDF) and the probability density function (PDF) of entrepreneurial skills with support [e_m, e_M], where e_M may be equal (or tend) to +∞.

The market equilibrium is determined by two equations, one on the level of entrepreneurial skills e^∗ that characterizes the individual who is indifferent between working as employee or as entrepreneur, and the other on the market salary w^∗ for which the supply of employees is equal to the demand:

$$ {\displaystyle \begin{array}{c}{\varPi}^{\ast}\left({e}^{\ast };{w}^{\ast}\right)={w}^{\ast}\\ {}\underset{e_m}{\overset{e^{\ast }}{\int }} dF(e)=\underset{e^{\ast }}{\overset{e_M}{\int }}h\left(e;{w}^{\ast}\right) dF(e)\end{array}} $$

(1)

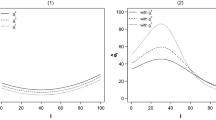
Figure 1 shows the market equilibrium; more specifically, it shows the salary of employees and profits of entrepreneurs-managers for the equilibrium salary w^∗. Since the maximum profit is increasing with e, for each w there will be a skill value e^∗ such that an individual with this skill will be indifferent between working as employee or as entrepreneur (first equation). Individuals with skills above the threshold will earn higher income as entrepreneurs, while individuals with lower skills will earn higher income as employees (see Fig. 1). If the demand for employees is higher than the supply, the market salary will increase, reducing the demand and increasing the supply of individuals who want to work as employees. The salary will adjust until supply equals demand.

Fig. 1

Market income and occupational choices in the market equilibrium (as a function of skills). Wages and profits (vertical axis) versus level of skill (horizontal axis). The hump-shaped curve is the probability density function of the distribution of skills, lognormal in this figure

The distribution of skills in the group of entrepreneurs is just the left-truncated distribution of skills in the population, so that its support is [e^*, e_M] for e_M finite, and [e^*, +∞] otherwise. When we measure firm size S by the number of employees L, then firm size is a function of the entrepreneur’s skill, S = L = h(e; w^*), where “e” is the skill of an entrepreneur hiring L = h(e; w^*) employees. The distribution of firm size, measured by the number of employees, is just a transformation of the distribution of the entrepreneurs’ skills.

Consequently, the distribution of firm size is just a transformation of the left-truncated distribution of skills in the whole population. The following claim characterizes the probability cumulative function and the probability density function of the distribution of firm size.

Claim 1.

Mathematically, the probability cumulative function and the probability density function of the distribution of entrepreneurs’ skills are characterized by

$$ {F}_{ent\kern0.28em skills}(e)=\frac{F(e)-F\left({e}^{\ast}\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)},{f}_{ent\kern0.28em skills}(e)=\frac{f(e)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\kern1em \left(\forall e\ge {e}^{\ast}\right) $$

Then the probability cumulative function and the probability density function of the distribution of firm size are characterized by

$$ {F}_S(s)=\frac{F\left({h}^{-1}(s)\right)-F\left({e}^{\ast}\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)},{f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{\mathrm{d}\kern0.28em {h}^{-1}(s)}{\mathrm{d}\kern0.28em s}\kern1em \forall s\ge {S}_{\mathrm{min}} $$

(2)

Where S_min is the minimum firm size, S_min = h(e^∗; w^∗).

Proof of Claim 1:

See Appendix 1.

Mathematically, the shape of the DFS is determined by: (i) the shape of the left tail of the distribution of entrepreneurial skills in the population, and (ii) the shape of the (individual) labor demand as a function of the entrepreneur’s skill, which is increasing and convex with skills for all reasonable production functions.

3.2 Distributions of firm size for different distributions of skills

We now illustrate the implications of Claim 1 by solving for the DFS from different distributions of skills and a particular production function. In its simplest form, from the way the input of the entrepreneur enters the production function, the aggregate output from L employees-jobs managed by an entrepreneur of skill e is given by,

$$ Q=\theta \kern0.5em {e}^{\left(\tau +\beta \right)}{L}^{1-\beta } $$

(3)

The parameter θ captures the general level of total factor productivity different from the contribution of the skill of the entrepreneur. The term e^τ (τ > 0) is the contribution of the skills of the entrepreneur from the quality of the entrepreneurial and managerial decisions (public good effect). The term e^βL^1 − β is the contribution from the aggregation of the output at the job level, of the input of the employee and the skill-weighted individualized monitoring time of the entrepreneur. The parameter 1 > β > 0 determines the degree of organizational size diseconomies from the technology used in the supervision of employees’ work.

The first order conditions of profit maximization, $\frac{\partial\;g\left(e,L\right)}{\partial\;L}=w\kern0.5em$, lead to the optimal labor demand function,

$$ L=h\left(e;w\right)={\left(\frac{\theta \left(1-\beta \right)}{w}\right)}^{\frac{1}{\beta }}{e}^{\left(\beta +\tau \right)/\beta } $$

This is a power function of the skill, h(e; w) = a e^b, where a = (θ(1 − β)/w)^1/β and the power parameter is b = (β + τ)/β.

The market equilibrium from occupational choices is characterized by [1], with Π^∗(e^∗; w^∗) = θ e^{(τ + β)}[h(e^∗; w^∗)]^1 − β − w^∗h(e^∗; w^∗). After substituting the optimal labor demand $h\left(e;w\right)={\left(\frac{\theta \left(1-\beta \right)}{w}\right)}^{\frac{1}{\beta }}{e}^{\left(\beta +\tau \right)/\beta }$, we obtain the system of equations

$$ {\displaystyle \begin{array}{c}\beta {\theta}^{\frac{1}{\beta }}{\left(\frac{1-\beta }{w^{\ast }}\right)}^{\frac{\left(1-\beta \right)}{\beta }}{\left({e}^{\ast}\right)}^{\frac{\left(\beta +\tau \right)}{\beta }}={w}^{\ast },\\ {}\kern0ex \underset{e_m}{\overset{e^{\ast }}{\int }} dF(e)={\left(\frac{\theta \left(1-\beta \right)}{w^{\ast }}\right)}^{\frac{1}{\beta }}\underset{e^{\ast }}{\overset{e_M}{\int }}{e}^{\left(\beta +\tau \right)/\beta } dF(e)\end{array}} $$

From the first equation, the equilibrium salary is w^∗ = θβ^β(1 − β)^{(1 − β)}(e^∗)^{(β + τ)}, where the skill threshold e^∗ is the solution to the following equation (which has no closed-form solution, except for some specific distributions of skills, like the Pareto):

$$ \beta {\left({e}^{\ast}\right)}^{\left(\beta +\tau \right)/\beta}\underset{e_m}{\overset{e^{\ast }}{\int }} dF(e)=\left(1-\beta \right)\underset{e^{\ast }}{\overset{e_M}{\int }}{e}^{\left(\beta +\tau \right)/\beta } dF(e) $$

We consider six alternative probability density functions of entrepreneurial skills in the population, f(x), and, for each of them, we obtain the distribution of firm size, f_s(x). In all cases (except for the uniform distribution) the support of the distribution of firm size is [S_min, +∞), with S_min = h(e^∗; w^∗) = a(e^∗)^b, a = θ^1/β((1 − β)w^∗)^−1/βand b = (β + τ)/β.

The probability density functions of the six distributions of skill, the corresponding distributions of firm size, and the Zipf plot of the size distribution (a graph of the logarithmic transformation of the survival function as a function of the logarithmic of size), often used to represent the DFS, are represented graphically in Table 1. The continuation of Table 1 also shows the respective functional form for each of the six distributions of skill and of firm size.

Table 1. Graphical representations of the distributions of skills and firm size, for six alternative distribution of skills.

Although the distributions of skills considered have very different shapes, the probability density function of the firm size distribution is strictly decreasing and convex in all cases (even in the case of the Uniform distribution of skills). Different distributions of skill turn into quite similar, at least from the visual observation, distributions of firm size. In fact, since in all cases the distribution is a decreasing and convex function of size, all distributions “resemble” a power law, and would be considered as such under a “loose” definition of power law distributions. However, technically, only in the case where the distribution of skills is a Pareto distribution, the distribution of firm size is indeed a Pareto, with lower bound a (e^∗)^b and power parameter $\frac{\alpha }{b}$. The Pareto distribution of skill is also the only one for which the Zipf plot of the distribution of firm size is a linear function. In the other size distributions, the logarithm of the survival function is a decreasing and concave (non-linear) function of the logarithm of size.⁷

In conclusion, since the size distribution of firms is a power transformation of the truncated upper tail of the distribution of skills in the population, and the upper tail of many distributions will be decreasing and convex with values of the random variable, the size distribution of firms will also be decreasing and convex with size. This would lead to the belief that the distribution follows a power law, although this will only be strictly true if the distribution of skills is also a power law. The importance of the distinction between “resemblance” and “true” power law distribution may depend on the research context. In the context of this paper, with an explicit model of the formation of firms and the match between entrepreneur-managers and firms in the economy, whether the distribution of the variables of interest are true power laws or not would be particularly relevant in testing predictions of, say, how the distribution of entrepreneurial skills in the population determines the distribution of size and performance variables.

4 Generalization

The expressions in [2] are valid for any distribution of skills and for any labor demand function. In order to obtain some general hints about the properties of the DFS, we must impose some reasonable conditions on the functions of labor demand L(e) and distribution of skills, F(e). From the way the skills of the entrepreneur enter into the production function, i.e., as part of the total factor productivity term, the labor demand will be increasing and convex in the entrepreneur’s skill, $L=h\left(e;w\right),\frac{\partial h}{\partial e}>0,\frac{\partial^2h}{\partial {e}^2}>0.$ Moreover, for commonly used production functions (Cobb Douglas and CES production functions), the demand for labor is an increasing and convex power function of entrepreneurial skills h(e; w) = a e^b (with a > 0 and b > 1), Medrano-Adan et al., 2015, 2019).

Since there are individuals with extremely high levels of skill (the superstars), we can reasonably assume, for modeling purposes, that the maximum skill in the population is unbounded e_M →  + ∞, and that the support of the distribution is [e_m, +∞). But then, its probability density function must be strictly decreasing and convex in the right tail (for sufficiently high values of e, see Lemma 1 in the Appendix), since probability values must be non-negative and the limit of the cumulative distribution must be equal to one.

To sum up, for commonly used production functions, the labor demand function will be increasing and convex in the level of skills; and, for reasonable distributions of skills, the probability density function is decreasing and convex. The following claim mathematically proves that, given these conditions, the probability density function of the DFS will be strictly decreasing and convex for all size values.

Claim 2.

If $\frac{\partial h}{\partial e}>0,\frac{\partial^2h}{\partial {e}^2}>0,$ and f '(x) < 0, f''(x) > 0, for x ≥ e₁, then f'_S(s) < 0 and (in general) f ''_S(s) > 0 (∀s > S_min).

Proof of Claim 2:

See Appendix 1.

The distribution of firm size inherits the properties of the right tail of the skill distribution: it will be (bounded from below and) strictly decreasing and convex, i.e., similar in graphical appearance to a power law (a power function with negative power parameter). On the other hand, even if the distribution of skills is bell-shaped (normal, lognormal, etc) the probability density of the DFS will be strictly decreasing and convex (losing its bell shape because only those in the right tail of the distribution of skills become entrepreneurs) and will resemble a power law.

In fact, we can prove that if the labor demand function is a power function of skills, then the distribution of skills being a Pareto distribution is a necessary and sufficient condition for the DFS to be a power law.

Claim 3.

If the labor demand is a power function of skills, then the distribution of firm size is a power law if and only if the distribution of skills is Pareto.

Proof of Claim 3:

See Appendix 1.

Consequently, in the framework of occupational choice models, with individuals who differ in their levels of skill, the distribution of firm size will follow a power law only if both the labor demand function and the distribution of skills are power functions. For other labor demand functions and/or other distributions of skills, the distribution of firm size will not strictly follow a power law, although its graphical appearance may resemble a power law (probability density function will be decreasing and convex).

What are the a priori assumptions about the distribution of entrepreneurial skill in the population? One reasonable proxy of the variable skill is the human capital of the working population. The OECD-PIAAC project measures the cognitive skills of the working population across OECD countries in a standardized way. The published reports on the results of the project show that in all countries the distribution of cognitive skills in the population is “bell-shaped” but non-symmetric (Broecke et al. 2017). Since the entrepreneurial input in the production function is in related with quality of the decisions and monitoring time, it is reasonable to expect that the variable entrepreneurial skill will be monotonically increasing with the level of cognitive skill, and then, its distribution will also be bell-shaped but non-symmetric. Specifically, in the empirical analysis (section 4), we will assume that the distribution of entrepreneurial skill in the population is lognormal and estimate the corresponding distribution of firm size that results from the market equilibrium.

Occupational choice models explain the heterogeneity among firms via the heterogeneity in the indivisible skill of their respective entrepreneur-managers. Other studies highlight the heterogeneity observed in the total factor productivity, TFP, of firms and production plants (Moral Benito 2018; Decker et al. 2018), and still others attribute the heterogeneity in TFP, at least in part, to the high dispersion observed in the quality of management within and across countries around the world (Bloom and Van Reenen, 2007). Although no direct connection has yet been established, the observed heterogeneity in TFP and in management skills among firms within a country and across countries could just be the reflection of differences in the construct variable entrepreneurial skill among those compared. In fact, the skill input in Eq. [3] above is part of the TFP term of the production function, together with the general productivity parameter θ. Ortín-Ángel and Vendrell-Herrero (2010), Vendrell-Herrero et al. (2014) explicitly use the TFP of firms as a measure of entrepreneurial talent. Medrano-Adán et al. (2019) provide evidence that the observed distribution of TFP among Spanish firms in Moral Benito (2018) is very much in line with the distribution predicted from an occupational choice model with values of the parameters calibrated for the Spanish economy.

Crawford et al. (2015) explain the power law distribution of entrepreneurs’ outcomes, such as size of firms, as the result of power law distributed inputs grouped into “endowment” (i.e., human capital of entrepreneurs), “engagement” (i.e., entrepreneur’s working time), “expectations” (i.e., future growth projections of the venture) and “environments” (i.e., sales in different industries) variables. Occupational choice models can explain the link between input and outcome variables in the market equilibrium for input variables that condition the occupational choice of working as entrepreneur or as employee, and that enter as inputs of the entrepreneur in the production function. The endowment, engagement, expectations, and environment variables could all eventually be part of the vector of variables z mentioned above that could condition the occupational choice. Endowment variables such as human capital of the entrepreneur, together with engagement variables such as working time of the entrepreneur, would qualify as entrepreneurial inputs of the production function and be part of the “skill” variable. However, expectations and environment variables as inputs of the entrepreneur in the production function would be more difficult to justify.

In any case, the occupational choice theory supports the view that there will be a link between the distribution of entrepreneurial inputs and the distribution of entrepreneurial outputs and formally derives what such link will be. In the context of the model the necessary condition for the outcome being distributed as a power law is that the input be distributed as a power law too. There is supporting evidence of the skewedness of the distribution of entrepreneurial input and output variables but as Joo et al. (2017) show not all right-skewed distributions that “resemble” power laws are in fact “true” power law distributions. Stochastic additive and multiplicative shocks (Andriani and McKelvey, 2009) explanations of the distribution of entrepreneurial and organizational variables, and theories that explain the emergence of outliers in such distributions (Crawford, 2018) will predict links between entrepreneurial input and output variables that at this point occupational choice models could not explain.

5 Empirical tests of the distribution of firm size

In this section, we use the Axtell (2001) data about the size distribution of firms, from the US census, to test some predictions from the theory and to compare the results of the empirical analysis with those obtained directly when assuming that the distribution of firm size follows a power law. The exposition will be divided in two parts. First, we follow the conventional approach of fitting a power law distribution to the data and applying some conventional test of model specification to reject, or not, the null hypothesis that the firm size distribution variable in the USA follows a power law distribution. Second, we estimate the distribution of firm sizes predicted from our occupational choice model, assuming that the distribution of entrepreneurial skills in the population is lognormal, and compare the goodness of fit with that obtained when assuming that the variable is distributed according to a power law.⁸ The use of Axtell’s firm size data from the USA is because it is easily available and because Axtell’s paper is probably the most-cited paper supporting the view that the firm size variable is distributed according to a power law. (In Appendix 3, we provide complementary evidence with Spanish data.)

5.1 Test of the null hypothesis: The distribution of firm size is a power law

We first replicate the conventional empirical analysis of the distribution of firm size, ignoring the predictions from the theory above. Under the null hypothesis that firm size, measured by number of employees L, follows a Pareto distribution, with power parameter α > 0 and minimum size L_min> 0, the probability density function, the cumulative distribution function, and the survival function of the size variable are given by:

$$ {\displaystyle \begin{array}{c}f(x)=\alpha \kern0.28em {L}_{\mathrm{min}}^{\alpha }{x}^{-1-\alpha },\kern1em F(x)=1-{L}_{\mathrm{min}}^{\alpha }{x}^{-\alpha },\\ {}\kern0ex SF(x)=1-F(x)={L}_{\mathrm{min}}^{\alpha }{x}^{-\alpha}\kern1em \left(\alpha >0,x\ge {L}_{\mathrm{min}}\right)\end{array}} $$

Taking logarithms of f(L) and SF(L) we have the log-linear functions,

$$ \ln \left[f(x)\right]=\ln \left[\alpha\;{L}_{\mathrm{min}}^{\alpha}\right]-\left(1+\alpha \right)\ln \left[x\right] $$

(4.a)

$$ \ln \left[ SF(x)\right]=\alpha \ln \left[{L}_{\mathrm{min}}\right]-\alpha \ln \left[x\right] $$

(4.b)

Axtell (2001) fitted Eq. [4.b] to US Census binned data on firm size, concluding that the distribution of firm sizes in the USA follows a power law, with a power parameter close to one (Zipf distribution). The 1997 US Census data on the distribution of firm size that Axtell used in testing the power law is reported in the first three columns of Table 2. With binned data, Eq. [4.b] is written as,

$$ \ln \left[1-\frac{N_i}{N}\right]={c}_0-\alpha \ln \left[{L}_i\right] $$

(5)

where N is the (total) number of firms and N_i denotes the cumulative number of firms with L_i employees or fewer.

Table 2 Axtell’s (2001) US Census 1997 data on firm size distribution, and predicted number of firms in size classes, from different distributions and estimated parameters

The Newey-West Least Squares, LS, estimation of [5] with the data from Table 2 gives the following results: estimated slope $\hat{\alpha}$ = 1.0598 (SE = 0.0555, p value = 0.0000); estimated constant ${\hat{c}}_0$= 0.7125 (SE = 0.3745, p value = 0.0862); and R-squared of 0.987. Axtell (2001) reported practically the same estimated value for the slope parameter α = 1.059 (the estimated constant is not reported), and the same high R-squared, and from these results concluded: “the power law distribution well describes the data” (page 1819).

Is this sufficient to conclude that the distribution of firm size in the USA is a power law? The answer could be yes if we only want to test that the distribution “resembles” a power law, but not to test that the distribution is a “true” power law. First, consider the constant c₀ with informative value since it provides an estimate of the lower bound of the distribution or minimum firm size. From the regression results, ${\hat{L}}_{\mathrm{min}}=\mathrm{Exp}\left[{\hat{c}}_0/\hat{\alpha}\right]$ = 1.96. With this minimum, the probability of observing firms with 1 employee would be close to zero. However, from Table 2, more than 20% of firms in the USA have one employee. The introduction of the restriction that the minimum firm size is one in the estimation, implies setting the constant c₀ in model [5] is equal to zero:

$$ \ln \left[1-\frac{N_i}{N}\right]=-\alpha \ln \left[{L}_i\right] $$

(6)

The estimated slope from [6] is $\hat{\alpha}$ = 0.9782 (SE = 0.0342 and R² = 0.979), close to 1. With the restriction of a minimum size equal to one, the distribution of the firm size continues to “resemble” a power law.

From an econometric point of view, a very high R-squared is not sufficient for a correct model specification. The residuals show an inverted-U pattern for both models, [5] and [6], which suggests a better fit for a nonlinear model, as can be seen in Fig. 2, which also plots the residuals from the log-quadratic model [7] and from the DFS predicted from the occupational choice model, Eq. [10] below. In fact, the Ramsey RESET specification test⁹ (Ramsey, 1969) rejects the null hypothesis of correct specification for models [5] and [6] with p value of 0.0005.

Fig. 2

Residual Plot. Residuals ${\hat{u}}_i=\ln \left[1-{N}_i/N\right]-\hat{\ln}\left[1-\hat{F}\left({L}_i\right)\right]$ from the estimation of the (transformed) logarithms of survival Functions, Eqs. [5], [6], [7], and [10]. Horizontal axis: firm size measured by the logarithm of the number of employees. Vertical axis: Values of the residuals ${\hat{u}}_i={y}_i-{\hat{y}}_i$, where y_i = ln[1 − N_i/N] and the fitted values ${\hat{y}}_i$ from the estimations of Eqs. [5], [6], [7], and [10] are shown in the Notes of Fig. 3

Furthermore, the columns in the right-hand side of Table 2 show the number of firms predicted in each bin of the size variable from a power law distribution with parameter values equal to those estimated from eqs. [5] and [6], and those predicted from a Zipf distribution, with power parameter values equal to 1 and the estimated by maximum likelihood,¹⁰${\hat{\alpha}}_{ML}$= 0.501547. The prediction errors are substantial in all cases, although they tend to concentrate differently, depending on the estimation method (in the upper tail in the ML estimation, and in the lower tail in the other estimations). It is worth noticing that the residuals are very low (consistent with R-squared higher than 0.979) in the log-log models [5]–[6], where the residuals are defined as ${\hat{u}}_i=\ln \left[1-\frac{N_i}{N}\right]-\left({\hat{c}}_0-\hat{\alpha}\ln \left[{L}_i\right]\right)$, while they are “large” when calculated with the original, untransformed, values of the size variable, $\hat{u}{\hbox{'}}_i={N}_i-{\hat{N}}_i$. This evidence casts doubt on the rightness of using measures of goodness of fit, i.e., R² values, of the log-log model specification (survival function) to test whether the distribution of firm size is a power law, or not.

The last specification test is equivalent to one of possible omitted explanatory variables. The log-linear transformation of the survival function, Eq. [5], could be generally written as a Taylor’s second-order approximation of an unknown functional form, as follows.

$$ \ln \left[1-\frac{N_i}{N}\right]={c}_0-\alpha \ln \left[{L}_i\right]+\delta {\left(\ln \left[{L}_i\right]\right)}^2 $$

(7)

The power law distribution is a special case of [7] with δ = 0. If the estimated value of δ is different from zero, the condition from the power law that the logarithm of the survival function is a linear function of the size variable in logarithms, would be violated. The fit of [7] to the US Census data gives estimated values of $\hat{a}$ = 0.680 (SE = 0.0715) and $\hat{\delta}$ = − 0.030 (SE = 0.00584 and p value = 0.0006). Therefore, the hypothesis of δ = 0 is rejected at a high level of significance (higher than 99.9%). The hypothesis of log-linearity between the value of the survival function and the value of the size variable is rejected. Consequently, the specification tests do not support the conclusion that the data on the distribution of firm size in the USA follows a power law.

5.2 Estimation of firm size distribution predicted by the model

We now estimate the distribution of firm size predicted by the occupational choice model and lognormal distribution of entrepreneurial skills in the population. From Section 2, the probability density function of the distribution of firm size is given by:

$$ {f}_S(x)=\frac{1}{1-\frac{1}{2} Erfc\left[\frac{\mu -\log \left[{e}^{\ast}\right]}{\sigma \sqrt{2}}\right]}\frac{1}{b\;x}\frac{1}{\sqrt{2\pi}\sigma}\mathrm{Exp}\left[\frac{-1}{2{\sigma}^2}{\left(\frac{1}{b}\log \left[\frac{x}{a}\right]-\mu \right)}^2\right] $$

With probability cumulative function,

$$ {F}_S(x)=\frac{Erfc\left[\frac{b\mu +\ln (a)-\ln (x)}{b\sigma \sqrt{2}}\right]- Erfc\left[\frac{\mu -\ln \left({e}^{\ast}\right)}{\sigma \sqrt{2}}\right]}{2- Erfc\left[\frac{\mu -\ln \left({e}^{\ast}\right)}{\sigma \sqrt{2}}\right]} $$

where $Erfc\left[z\right]=1-\frac{2}{\sqrt{\pi }}\underset{0}{\overset{z}{\int }}\mathrm{Exp}\left[-{t}^2\right] dt$. Or, equivalently, as

$$ {F}_S(x)=\frac{1}{2-2{c}_3}\left( Erfc\left[\frac{c_1-\ln (x)}{c_2}\right]-2{c}_3\right) $$

(8)

wherec₁ = bμ + log[a], ${c}_2= b\sigma \sqrt{2}$, and ${c}_3=\frac{1}{2} Erfc\left[\frac{\mu -\log \left[{e}^{\ast}\right]}{\sigma \sqrt{2}}\right]$.

The parameters (c₁, c₂, c₃) of the cumulative probability distribution F_s depend on the values of the primitive parameters of the model (a, b, μ, σ, e^∗). For example, knowing the parameters of the distribution of skills (μ, σ), the other parameters of the model could be calculated as follows: ${e}^{\ast }= Exp\left(\mu -\sqrt{2}\sigma {Erfc}^{-1}\left[2{c}_3\right]\right)$, $b=\frac{c_2}{\sqrt{2}\sigma }$, and a = Exp(c₁ − bμ).

For the estimation of the parameters of the cumulative probability distribution from the binned data on firm sizes in the USA (third column of Table 2), Eq. [8] is written as,

$$ \frac{N_i}{N}=\frac{1}{2-2{c}_3}\left( Erfc\left[\frac{c_1-\ln \left({L}_i\right)}{c_2}\right]-2{c}_3\right) $$

(9)

Or in logarithms of the survival function, 1-F_s,

$$ \ln \left[1-\frac{N_i}{N}\right]=\ln \left[\frac{1}{2-2{c}_3}\left(2- Erfc\left[\frac{c_1-\ln \left({L}_i\right)}{c_2}\right]\right)\right] $$

(10)

where, as before, N is the (total) number of firms and N_i denotes the accumulated number of firms with L_i employees, or fewer.

We estimate the parameters (c₁, c₂, c₃) of the predicted-by-the-model distribution from the untransformed model, Eq. [9], and from the log-log model, Eq. [10], for the purpose of illustrating the relevance of the logarithmic transformation for the distribution of the values of the residuals.¹¹ Since both models, [9] and [10] are non-linear, we estimate them by nonlinear least squares (NLS). Since the proportion of firms with employees in the sample data is 5%, we introduce this restriction, c₃ =1 – 0.05 = 0.95 in the estimation of the other two parameters. The restriction has two purposes. One, to take advantage of information available from sources external to the model, and the other to estimate the model with the same degrees of freedom as when estimating the parameters, two, of the power law distribution, thus making the results more comparable.

To compare with the results from model [9], it is interesting to fit the data to the (untransformed) distribution function of the Pareto distribution

$$ \frac{N_i}{N}=1-{\left(\frac{L_{min}}{L_i}\right)}^{-\alpha }+{u}_i $$

(11)

The NLS estimates of α and L_min are $\hat{\alpha}$ = 0.5637 and ${\hat{L}}_{\mathrm{min}}$= 0.6896.

The results of these estimations using non-linear least square estimation methods are presented in Table 3, together with the estimated values of the parameters of the power law, again with both untransformed (model [11]) and transformed (model [5]) values of the variables.

Table 3 Estimations of the distributions of firm sizes (from Axtell’s US Census 1997 data): predicted by the model (under lognormal skills) versus Pareto DFS

Figure 3 shows the plot of observed values of the survival function,¹² ln[1 − N_i/N], and fitted values of the four logarithmic models analyzed: the log-linear models from the Pareto distribution, [5] and [6], the log (non-linear) quadratic model, [7], and the logarithm of the survival function of the DFS predicted from the occupational choice model, Eq. [10]. The superior fit of the logarithmic nonlinear functional form, [7] and [10], is evident.

Fig. 3

Observed data on firm size distribution (Axtell’s 2001 US Census 1997) and fitted values from the Logarithms of the Survival Functions, Eqs. [5], [6], [7], and [10]. Vertical axis: Observed CENSUS data y_i = ln[1 − N_i/N] and fitted values of the Logarithm of the Survival Functions, ${\hat{y}}_i=\hat{\ln}\left[1-{N}_i/N\right]=\hat{\ln}\left[\hat{SF}\left({L}_i\right)\right]$, from the estimations of Eqs. [5], [6], [7], and [10]. Fitted values from model [5]: ${\hat{y}}_i={\hat{c}}_0-\hat{\alpha}\ln \left[{L}_i\right]$, with $\hat{\alpha}$= 1.0598, ${\hat{c}}_0$= 0.7125. Fitted values from model [6]: ${\hat{y}}_i=-\hat{\alpha}\ln \left[{L}_i\right]$, with $\hat{\alpha}$= 0.9782. Fitted values from model [7]: ${\hat{y}}_i={\hat{c}}_0-\hat{\alpha}\ln \left[{L}_i\right]+\hat{\delta}{\left(\ln \left[{L}_i\right]\right)}^2$ with ${\hat{c}}_0$= − 0.0359, $\hat{\alpha}$= 0.6801, and $\hat{\delta}$= − 0.0301. Fitted values from model [10]: ${\hat{y}}_i=\ln \left[1-\frac{1}{2\left(1-0.95\right)}\left(2+ Erfc\left[\frac{{\hat{c}}_1-\ln \left({L}_i\right)}{{\hat{c}}_2}\right]\right)\right]$, with ${\hat{c}}_1$= − 6.290, ${\hat{c}}_2$= 5.067

For the distribution of firm sizes predicted by the occupational choice model and a lognormal distribution of skill, the estimated values of the parameters in the estimation with untransformed variables and in the estimation with log-transformed values of the variables (survival function) are very similar. On the contrary, when we fit the data to a Pareto distribution of firm sizes, as if the power law were the true distribution of the size variable, the estimated values of the parameter vary between the two estimations: estimated parameter α equal 0.5637, with untransformed values of the variables, and equal to 1.0598 with the transformed ones.

Table 4 shows the fitted number of firms for each size class, obtained from the estimations reported in Table 3, which correspond to the DFS predicted by the occupational choice model, Eqs. [9] and [10], and to the DFS when assuming it follows a power law, Eqs. [5] and [11]. Table 4 also shows the 1997 US Census data on firm sizes used by Axtell (2001). The fitted values obtained from the DFS predicted by the occupational choice model are closer to the observed data than those obtained from the estimated power laws, in both cases: when directly estimating the cumulative distribution function, and when estimating the logarithm of the survival function.

Table 4 Axtell’s (2001) US Census 1997 data on firm size distribution and predicted number of firms in size classes, from different distributions and estimated parameters

Figure 4 displays the observed values of the cumulative number of firms and values of the fitted (untransformed) CDFs corresponding to the Pareto distribution, Eqs. [11], and the DFS predicted by the occupational choice model, Eq. [9]. While Fig. 3 shows the fitted values for logarithms of the survival function, Fig. 4 displays the fitted values from directly fitting the data to the cumulative distribution functions.

Fig. 4

Observed data, N_i, on firm size distribution (Axtell’s 2001 US Census 1997) and fitted values, ${\hat{N}}_i$, from the untransformed Cumulative Distribution Functions, Eqs. [9] and [11]. Vertical axis: observed, N_i, and fitted values, ${\hat{N}}_i=N\;{\hat{y}}_i=N\;\hat{F}\left({L}_i\right)$, of the cumulative number of firms with L_i employees or less. N = 4,821,940. Fitted values from estimation of Eq. [9]: ${\hat{N}}_i=N\;{\hat{y}}_i$ with ${\hat{y}}_i=\frac{1}{2\left(1-0.95\right)}\left(2+ Erfc\left[\frac{-7.5285-\ln \left({L}_i\right)}{6.099}\right]\right)$. Fitted values from estimation of Eq. [11]: ${\hat{N}}_i=N\;{\hat{y}}_i$ with ${\hat{y}}_i=1-{\left(\frac{{\hat{L}}_{min}}{L_i}\right)}^{-\hat{\alpha}}$, $\hat{\alpha}$= 0.564 and ${\hat{L}}_{\mathrm{min}}$= 0.690. Horizontal axis: number of employees, L_i

Finally, Fig. 5 depicts the residual plot of models [9] and [11]. Both, Table 4 and Fig. 5, show that the prediction errors from the estimated theoretical model are smaller in each and all size classes than the errors from the estimations of a power law.

Fig. 5

Residual Plot. Residuals ${\hat{u}}_i=\left({N}_i/N\right)-\hat{F}\left({L}_i\right)$from the estimation (by non-linear least squares) of the untransformed cumulative distribution functions, Eqs. [9] and [11]. Horizontal axis: firm size measured by the number of employees. Vertical axis: Values of the residuals ${\hat{u}}_i={y}_i-{\hat{y}}_i$, where y_i = N_i/Nand the fitted values ${\hat{y}}_i$ from the estimations of Eqs. [9], and [11] are shown in the Notes of Fig. 4

Although these results do not prove that the “true” distribution of skills in the population is lognormal, they do show that (i) the distribution of firm size predicted by the occupational choice model, assuming a lognormal distribution of skill, fits the data better than a power law; and (ii) the fact that a visual observation of the empirical distribution of values of the outcome variable, in this case the size of the firm, suggests that the distribution “resembles” a power law, is not sufficient for the actual distribution being a power law. Having a theoretical model of what determines the distribution of the variable firm size helps to discern when the apparent and the true distributions will coincide.

To sum up, the fact that the log-quadratic model [7] and DFS predicted by the occupational choice model, Eqs. [9] and [10], fit the data significantly better than the Pareto distribution, together with the results of the Ramsey RESET tests, the observation of the (non-random) residuals’ plots, and the statistical significance of the quadratic term in model [7], are all evidence that question Axtell’s conclusion that the distribution of firm size in the USA is a power law.

6 Conclusion and implications

The occupational choice theory has been, surprisingly, missing from explanations of the so-called “pervasiveness” of power law distributions among organizational and entrepreneurial variables, including the distribution of firm size, even though the pioneering paper of Lucas (1978) explicitly models the distribution of firm size. Occupational choice models go beyond the purely stochastic or chance explanation of the distribution of the organizational variables and restore the value added of management theory to explain differences in size and performance across firms. The paper establishes a correspondence between the distribution of skill in the subset of entrepreneurs and the distribution of firm size. The distribution of firm size turns out to be a truncated non-linear transformation of the distribution of skills (convex power transformation in our case). In fact, in the context of the occupational choice model, the paper provides conditions for the distribution of skills and for the production technology, under which the distribution of firm size in the market equilibrium will be a “true” power law (a result that could be extended to heterogeneity in input variables other than skill).

6.1 Implications for theory

The explanation of the distribution of firm size and other organizational/entrepreneurial variables as a market equilibrium from competing profit-maximizing entrepreneurs, rather than more or less complex processes of stochastic growth, will shift the researcher’s attention towards characteristics of these teams (their production technology, internal organization, relation to external markets, particularly financial markets), and to modeling the input of the entrepreneur-manager in the output of the team, when explaining observed regularities in the distribution of such variables. So far, such regularities have led to a recognition from the outset that the “social world seems to be organized according to power law distributions” (Crawford et al., 2015: 705 and references therein) and, from this result, the research focus has narrowed to the investigation of causal processes from complexity science that can generate such power law distributions (Andriani and McKelvey, 2009). Occupational choice models then provide microeconomic team production explanations of power law-like distribution of organization variables such as firm size, as requested by Axtell (2001, 2006), that complement other approaches, where the micro-organization of production is treated as a “black box.”

In the occupational choice models of Lucas (1978) and Rosen (1982), from which we draw in this paper, the power law-like distribution observed in entrepreneurial output variables such as size and profit of firms, and therefore the difference between low performing and extremely high performing firms, are very much related to the way the entrepreneurial input enters into the production function, from the job to the firm levels. In the market equilibrium, there is a lower bound in skill that determines the size and profit of the smaller firm with employees and a continuum of firm sizes and profits as a function of the skills of the respective entrepreneur-managers. Therefore, occupational choice models can explain the whole range of size and performance of firms, a feature of the theories of entrepreneurship that are particularly valued (Crawford et al., 2015). Two forces are in place: one from scale economies of skills that push towards concentration of more resources under the direction of fewer higher-skilled entrepreneurs; the other, from organizational size diseconomies (a la Coase and Penrose) that limit the growth of the firm and push towards dispersion of production in more numerous and smaller firms. Entrepreneurship theories should then further investigate these two forces and the other factors that intervene in the final outcome mediating effects (shape of the distribution of skills, parameters of the production technology, cost of capital, neutral technological progress).

6.2 Implications for empirical research

The theoretical findings have implications for empirical analysis that examine the pervasiveness of the power law distribution across economic variables, and in particular for research on the distribution of firm size. For example, Clauset et al. (2009) empirically find that the hypothesis of a power law distribution cannot be rejected for values of the respective variable above an empirically determined minimum value. A purely empirical analysis cannot determine the relevance of this result because there is no theory about what the minimum value of the variable should be. In the occupational choice model, the market equilibrium determines the size of the smallest firm and this result should be accounted for when testing for power law distributions. The same argument applies when testing whether the size distribution predicted from the model is rejected, or not, by the empirical data.

Theoretical and empirical advances to distinguish between distributions that “resemble” power law and “true” power law are relevant for conducting empirical tests of proposed theories, particularly if the results can have policy implications. For example, a power law distribution of firm size implies that the firm size elasticity of the survival function is constant, while the model presented in the paper predicts that the absolute value of the elasticity will be monotonically increasing with size. Size-conditioned public policies for firms can be different in one case and in the other.

The paper highlights the difference between comparing the goodness of fit to a dataset of a normal distribution and of a power law distribution (as in Clauset et al., 2009 and Joo et al., 2017), and testing the hypothesis that the distribution is a true power law. In the latter case, the necessary and sufficient condition for the distribution being a power law is that the log of the survival function is a linear function of the logarithm of the value of the variable. Therefore, the strong empirical test of a power law should be formulated and implemented as a model specification test, in line with the test of Eq. [7] above. The text also points out the limitations of using the R², goodness of fit, as a criterion to test for a power law, as well as the precautions that should be taken when working with binned data. The supplementary on-line document discusses in more detail some methodological issues that arise in the empirical estimation of the distribution of firm size that could be extended to other economic variables.

Having a theoretical model of team production and management from which to make predictions about the endogenous distribution of relevant organizational variables, for example firm size, allows for enriching interactions between the theory and the evidence in empirical research. For example, the parameter of the explanatory variable of the log-linear transformation of the survival function can be directly related to values of the parameters of the model, particularly parameters of the production technology and the internal organization of firms. To make economic sense, the values of these parameters must be within certain bounds, something that can be tested as a way of strengthening the conclusions from the empirical research. Comparative static analysis around the market equilibrium of changes in the distribution of size resulting from changes in the parameters of the model can help to explain differences in the distribution of size of firm across countries and/or changes in the distribution in one country, over time. At a higher level, the model may predict a distribution of the endogenous values of the relevant organization variable that can be directly tested in the empirical analysis, as we do in this paper. Once again, the theory will impose restrictions on the empirical distribution, for example on the choice of the lower bound of the values of the random variable (minimum size of the firm predicted by the model and observed minimum size, in our case).

6.3 Implications for management and policy

The occupational choice models restore the value of the management input in determining the size and performance of firms. The distribution of entrepreneurial skill in the population will be reasonably given in the midterm. However, the model identifies another variable that managers control and that can alter the market equilibrium from occupational choices, namely the diseconomies of organizational size. In the model, these diseconomies have to do with the intensity of supervision of employees by the entrepreneur at the job level (Rosen, 1982). More generally, organizational size diseconomies are related to the limits to the growth-size of the firm that Penrose (1959) attributed to the (fixed) management input, to management costs when the entrepreneur takes the place of the price system in the direction of resources (Coase, 1937), and to costs from “loss of control” in hierarchical organizations. Managers must be aware that the internal organization of firms, for example more delegation of decision power and less intensity of supervision in environments of higher goal congruence, will mitigate the organizational size diseconomies and will affect the equilibrium distribution of firm size, with more output concentrated in fewer large firms. The model is stylized on the details about the internal organization of firms (for example, the number of hierarchical levels and the role of intermediate managers) but it is sufficient to highlight the importance—for the performance of the firm—of organizational design variables, jointly with strategic ones.

In the market equilibrium from occupational choices, where entrepreneurs compete for control of production resources, the total output produced is maximized, within the total resource constraints. Policy makers should then be concerned about the actual working of the market for entrepreneur-managers, including the market for corporate control, and the financial markets that provide funds to talented but non-wealthy would-be entrepreneurs. Concentration forces in markets, driven by efficiency factors, i.e., more efficient firms, and firms managed by more skilled entrepreneurs concentrating a high volume of resources, with the corresponding concentration of power and profits, may raise policy concerns in terms of limits to competition and/or increasing income inequality. In other circumstances, the policy concerns may focus on the other side of the income distribution and public authorities may make policy decisions regulating labor markets, for example with the introduction of minimum wages. Caution should be taken, however, so that regulations and government policies do not create opportunities for rent seeking that attract talent that, in the absence of these opportunities, would be allocated to productive entrepreneurial tasks (Murphy et al. 1991). Then, a better understanding of the efficiency-driven determinants of the distribution of firm size and the possible distributional consequences of the free-market equilibrium results, as well as the potential opportunity costs of diverting talented individuals from productive entrepreneurial tasks, will be relevant for better-informed public policies that must consider the tradeoff between economic efficiency and other social goals.

6.4 Future research

The occupational choice model as formulated in this paper is highly stylized, static, and based on strong assumptions, mainly because we want to produce some robust predictions on the results. Moreover, the occupational choice model is not the only way to open the “black box” of microeconomics that can explain the regularities observed in the distribution of important organization variables, such as the size and performance of firms. Therefore, from the perspective of this paper, future research should be directed mainly towards generalizing the assumptions of the model and testing for the robustness of old and new predictions. In this respect, the proposed occupational choice model should not be viewed as an alternative to complexity science in the explanation of regularities observed in important organization variables, but as a complementary one. Incorporating complex stochastic dynamics from out-of-equilibrium situations in extensions of the static occupational model, including the possibility of changes in the distribution of skill over time from rational individual decisions on investment in human capital, could be a very fruitful area of research. For example, Knudsen et al. (2017) model the dynamics of convergence to the Cournot-Nash target in an oligopoly market with frictions; the same set-up could be replicated to model the convergence to the size of a firm in the occupational equilibrium and/or convergence to the size distribution equilibrium.

In addition to being static, and only looking at market equilibrium solutions, i.e., ignoring out-of-equilibrium results, another limitation of the paper is that all heterogeneity among individuals that determines the occupational choice is summarized in the single variable of entrepreneurial skill. We outline in the text how, conceptually, the paper could be generalized to accommodate situations with multiple sources of heterogeneity; more particularly, the analysis could be generalized to differentiate between the endowment of individuals of skill to perform operational tasks, and skill to perform entrepreneurial tasks, in line with Jovanovic (1994). Fuchs-Schündeln and Schündeln (2005) find supporting evidence that risk aversion is an important variable in explaining the occupational choice of working as employee or as self-employed, in line with the theoretical prediction of Kihlstrom and Laffont (1979). Thus, the model could be extended to include heterogeneity in skill and in risk aversion in the same theoretical model. In a similar vein, the analysis could be generalized to solve for the market equilibrium when the performance of entrepreneurs improves with more balanced, multiple skills, rather than a single one (Lazear, 2004). Another realistic assumption in future generalizations of the results could be to allow for the possibility that individuals “learn” about their entrepreneurial skills from trial and error and from noisy signals of performance from firms that they establish, as in Jovanovic (1982), Hopenhayn (1992), and Melitz (2003), with the extension to open economies. The extended model would expand the outcome from entrepreneurial decisions to entry and exit of firms, and to entrepreneurs that fail or succeed.

Appendices

Appendix 1. Proofs of the claims

Lemma 1.

If x is a random variable with support [x_m, +∞), then there exists an x* > 0 such that the probability density function (PDF) is strictly decreasing and convex for all x > x*.

Proof. The demonstration is made by reductio ad absurdum (reduction to absurdity). Consider a random x variable with support [x_m, +∞) (x_m may be any real number or −∞).

The probability density function satisfies that $\underset{-\infty }{\overset{+\infty }{\int }}f(x) dx=1,f(x)\ge 0\kern0.5em \forall x$. If f(x) is not decreasing in the right tail (and the support is [x_m, +∞)), then there exist δ > 0 and x* > 0, such that f(x) > δ for all x > x*, but then $\underset{x^{\ast }}{\overset{+\infty }{\int }}f(x) dx>\underset{x^{\ast }}{\overset{+\infty }{\int }}\delta dx=+\infty$, which is absurd. Consequently, f(x) is decreasing in the right tail; more precisely, there exists x* such that f(x) is strictly decreasing for all x > x*. Moreover, if f(x) is concave for all x > x*, then there is a value x** such that f(x**) = 0, which is absurd, since we are assuming that f(x) > 0 for all x ∈ [x_m, +∞). Therefore, f(x) must be strictly decreasing and convex in the right tail. ■.

Proof of claim 1

In equilibrium, the individuals who become entrepreneurs are those with skill levels higher or equal to e*, so that the distribution of skills in the group of entrepreneurs is just the left-truncated distribution of skills in the population. Therefore, its support is [e^∗, e_M] for e_M finite, and [e^∗, +∞) otherwise; and its probability cumulative function and density probability function are characterized by.

${F}_{ent\; skills}(e)=\frac{F(e)-F\left({e}^{\ast}\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)},\kern0.75em {f}_{ent\; skills}(e)=\frac{f(e)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\kern1em \left(\forall e\ge {e}^{\ast}\right)$ (*).

since, for any continuous random variable X with support [x_m, x_M] and probability density function g(x) and cumulative distribution function G(x), the truncated distribution of X for the values in [a, b] (x_m ≤ a < b ≤ x_M) is characterized by ${g}_{truncated}(x)=\frac{g(x)}{G(b)-G(a)}$ and ${G}_{truncated}(x)=\frac{G(x)-G(a)}{G(b)-G(a)}$ (for any x such that a ≤ x ≤ b).

On the other hand, Firm size S, measured by number of employees, is a function of the entrepreneur’s skills e, S = h(e; w^∗), for e ≥ e*; so that the distribution of firm size is just the transformation (by “h”) of the distribution of the entrepreneurs’ skills. And, for any continuous random variable X with probability density function f_X(x) and cumulative distribution function F_X(x), and Y = h(X), where h is invertible (and monotonous and differentiable), the probability cumulative function and the density probability function of Y are characterized by F_Y(y) = F_X(h⁻¹(y)) and ${f}_Y(y)={f}_X\left({h}^{-1}(y)\right)\frac{d\kern0.1em {h}^{-1}(y)}{dy}$. By applying these expressions to the distribution of entrepreneurs’ skills, expression (*) above, and S = h(e; w^∗), we directly obtain that the probability cumulative function and PDF of S are characterized by

$$ {F}_S(s)=\frac{F\left({h}^{-1}(s)\right)-F\left({e}^{\ast}\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)},{f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{\mathrm{d}\kern0.28em {h}^{-1}(s)}{\mathrm{d}\kern0.28em s}\kern1em \forall s\ge {S}_{\mathrm{min}} $$

Where S_min = h(e^∗; w^∗). ■.

Proof of claim 2.

On the one hand, for reasonable production functions, the (individual) labor demand will be increasing and convex in the entrepreneur’s skill, $L=h\left(e;w\right),\frac{\partial h}{\partial e}>0,\frac{\partial^2h}{\partial {e}^2}>0$, so that its inverse, h⁻¹(), will be strictly increasing and concave, $\frac{dh^{-1}(s)}{ds}>0$ and $\frac{d^2{h}^{-1}(s)}{ds^2}<0$. On the other hand, for reasonable distributions of skills, with support [e_m, +∞), there exists e₁ such that f ' (x) < 0 and f ''(x) > 0, for x ≥ e₁ ≥ e_m. So that, by assumption,

$\frac{d{h}^{-1}(s)}{ds}>0,\frac{d^2{h}^{-1}(s)}{d{s}^2}<0,f\hbox{'}(x)<0,f\hbox{'}\hbox{'}(x)>0.$ (*)

From [2], the probability density function of the distribution of firm size is ${f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{dh^{-1}(s)}{ds}$ and its first derivative is

$$ \frac{\mathrm{d}{f}_S(s)}{\mathrm{d}s}=\frac{1}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\left[f^{\prime}\left({L}^{-1}(s)\right)\frac{d{L}^{-1}(s)}{ds}\frac{d{L}^{-1}(s)}{ds}+f\left({L}^{-1}(s)\right)\frac{d^2{L}^{-1}(s)}{d{s}^2}\right] $$

It directly follows, from the assumptions (*), that f ' (h⁻¹(s)) < 0, $\frac{dh^{-1}(s)}{ds}$ > 0, f(h⁻¹(s))>0 $\frac{d^2{h}^{-1}(s)}{ds^2}$ < 0, and then both summands in the above expression of $\frac{\mathrm{d}{f}_S(s)}{\mathrm{d}s}$ are negative; i.e. f_S(s) is strictly decreasing.

On the other hand, the second derivative is given by

$$ {\displaystyle \begin{array}{l}{\beta \theta}^{\frac{1}{\beta }}{\left(\frac{1-\beta }{w^{\ast }}\right)}^{\frac{\left(1-\beta \right)}{\beta }}{\left({e}^{\ast}\right)}^{\frac{\left(\beta +\tau \right)}{\beta }={w}^{\ast }},\\ {}\underset{e_m}{\overset{e^{\ast }}{\int }} dF(e)={\left(\frac{\theta \left(1-\beta \right)}{w^{\ast }}\right)}^{\frac{1}{\beta }}\underset{e^{\ast }}{\overset{e_m}{\int }}{e}^{\left(\beta +\tau \right)/\beta } dF(e)\end{array}} $$

$$ {\displaystyle \begin{array}{c}\frac{{\mathrm{d}}^2{f}_S(s)}{\mathrm{d}{s}^2}=\frac{1}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\left[f"\left({h}^{-1}(s)\right){\left(\frac{d{h}^{-1}(s)}{ds}\right)}^3+\right.\\ {}\kern1.75em +2f^{\prime}\left({h}^{-1}(s)\right)\left(\frac{d{h}^{-1}(s)}{ds}\right)\frac{d^2{h}^{-1}(s)}{d{s}^2}+\\ {}\begin{array}{l}+f^{\prime}\left({h}^{-1}(s)\right)\frac{d{h}^{-1}(s)}{ds}\frac{d^2{h}^{-1}(s)}{d{s}^2}+\\ {}\left.+f\left({h}^{-1}(s)\right)\frac{d^3{h}^{-1}(s)}{d{s}^3}\right]\end{array}\end{array}} $$

From the assumptions, expression (*) above in this proof, it is obvious that the three first summands in the above expression are positive. The fourth one is also positive for labor demands of power function (or polynomial) type. Consequently, f_S''(s) > 0. ■

Proof of claim 3.

If the individual labor demand is a power function, $h\left(e;w\right)={a}_1\kern0.5em {e}^{b_1}$, then 

${h}^{-1}(s)={\left(s/{a}_1\right)}^{1/{b}_1}$ and $\frac{dh^{-1}(s)}{ds}=\frac{1}{b_1{a}_1}{\left(\frac{s}{a_1}\right)}^{\left(1-{b}_1\right)/{b}_1}$.

Sufficient condition: (if f(x) is a power law, then f_S(x) is also a power law).

On the one hand, if the distribution of skills follows a power law, then its probability density function may be written asf(x) = C x^{−1 − α} (where e_M =  +  ∞ , C = αe_m^α, F(e_M) − F(e^∗) = e_m^α(e^∗)^−α and F(e^∗) =  − e_m^α(e^∗)^−α), and from [3], the probability density function of the distribution of size is given by

$$ {f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{d{h}^{-1}(s)}{ds}=\frac{C\;{\left({\left(s/{a}_1\right)}^{1/{b}_1}\right)}^{-1-\alpha }}{\left[F\left({e}_M\right)-F\left({e}^{\ast}\right)\right]{b}_1{a}_1}{\left(\frac{s}{a_1}\right)}^{\left(1-{b}_1\right)/{b}_1}=C^{\prime }{\left(\frac{s}{a_1}\right)}^{-1-\left(\alpha /{b}_1\right)} $$

which is a power law as well, but with constant parameter $C\hbox{'}=\frac{C\;}{\left[F\left({e}_M\right)-F\left({e}^{\ast}\right)\right]{b}_1{a}_1}$ and power parameter (α/b₁).

Necessary condition: (if f_S(x) is a power law, then f(x) must be a power law as well).

First, remember that the DFS follows a power law if and only if the elasticity of its probability density function is constant (and let us denote this elasticity κ_S):

$$ {\eta}_S=\frac{s}{f_S(s)}\frac{\mathrm{d}{f}_S(s)}{\mathrm{d}s}={\kappa}_S $$

Let us assume that this elasticity is constant and equal to κ_S. From [3], ${f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{dh^{-1}(s)}{ds}$, so that the above elasticity is given by

$$ {\eta}_S=\frac{s}{f_S(s)}\frac{\mathrm{d}{f}_S(s)}{\mathrm{d}s}=\frac{s\frac{1}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\left[f^{\prime}\left({h}^{-1}(s)\right)\frac{d{h}^{-1}(s)}{ds}\frac{d{h}^{-1}(s)}{ds}+f\left({h}^{-1}(s)\right)\frac{d^2{h}^{-1}(s)}{d{s}^2}\right]}{\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{d{h}^{-1}(s)}{ds}}={\eta}_S=\frac{s\;f^{\prime}\left({h}^{-1}(s)\right)}{f\left({h}^{-1}(s)\right)}\frac{d{h}^{-1}(s)}{ds}+\frac{s\frac{d^2{h}^{-1}(s)}{d{s}^2}}{\frac{d{h}^{-1}(s)}{ds}} $$

Remember that, if labor demand is a power function, $h\left(e;w\right)={a}_1\kern0.5em {e}^{b_1}$, then ${h}^{-1}(s)={\left(s/{a}_1\right)}^{1/{b}_1}$, ${h}^{-1}(s)={\left(\frac{s}{a_1}\right)}^{1/{b}_1}$, $\frac{dh^{-1}(s)}{ds}=\frac{1}{b_1{a_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-1}$ and $\frac{d^2{h}^{-1}(s)}{ds^2}=\frac{\left(1-{b}_1\right)/{b}_1}{b_1{a_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-2}$. Note also that ${h}^{-1}(s)={b}_1s\frac{dh^{-1}(s)}{ds}$ or equivalently, $\frac{dh^{-1}(s)}{ds}=\frac{1}{b_1{a_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-1}=\frac{1}{b_1s}{\left(\frac{s}{a_1}\right)}^{\left(1/{b}_1\right)}=\frac{1}{b_1s}{h}^{-1}(s)$.

By substituting $\frac{dh^{-1}(s)}{ds}=\frac{1}{b_1{a_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-1}$, $\frac{d^2{h}^{-1}(s)}{ds^2}=\frac{\left(1-{b}_1\right)/{b}_1}{b_1{a_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-2}$, and ${h}^{-1}(s)={b}_1s\frac{dh^{-1}(s)}{ds}$, into the last expression of the last elasticity of η_S we get

$$ {\eta}_S=\frac{s\;f^{\prime}\left({h}^{-1}(s)\right)}{f\left({h}^{-1}(s)\right)}\frac{h^{-1}(s)}{b_1\;s}+\frac{s\frac{\left(1-{b}_1\right)/{b}_1}{{b_1{a}_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-2}}{\frac{1}{{b_1{a}_1}^{1/{b}_1}}{s}^{\left(1/{b}_1\right)-1}}=\frac{1}{b_1}\frac{\;{h}^{-1}(s)}{f\left({h}^{-1}(s)\right)}f^{\prime}\left({h}^{-1}(s)\right)+\frac{1-{b}_1}{b_1} $$

Let us now make the change of variable x = h⁻¹(s). Then,

$$ {\eta}_S=\frac{1}{b_1}\frac{x}{f(x)}f\hbox{'}(x)+\frac{1-{b}_1}{b_1} $$

The DFS follows a power law if this elasticity is constant,

$$ {\displaystyle \begin{array}{c}{\eta}_S=\frac{1}{b_1}\frac{x}{f(x)}f\hbox{'}(x)+\frac{1-{b}_1}{b_1}={\kappa}_S\iff \\ {}\frac{x}{f(x)}f\hbox{'}(x)={b}_1\left({\kappa}_S+1\right)-1\end{array}} $$

This is a simple differential equation, and the “unique” solution is $f(x)={C}_1{x}^{b_1\left({\kappa}_S+1\right)-1}$, which is the density probability function of a Pareto distribution (for an appropriate value of the constant C₁).

Alternatively, we can prove that f(x) must be a power law as follows. If labor demand is a power function and the distribution of size follows a power law, f_S(s) = C₁ s^{−1 − k}, then, from [3]

$$ {f}_S(s)={C}_1\kern0.28em {s}^{-1-k},\kern.5em \mathrm{and}{f}_S(s)=\frac{f\left({h}^{-1}(s)\right)}{F\left({e}_M\right)-F\left({e}^{\ast}\right)}\frac{d{h}^{-1}(s)}{ds}\Rightarrow {C}_1\kern0.28em {s}^{-1-k}=\frac{1}{\left[F\left({e}_M\right)-F\left({e}^{\ast}\right)\right]{b}_1{a}_1}{\left(\frac{s}{a_1}\right)}^{\left(1-{b}_1\right)/{b}_1}f\left({\left(s/{a}_1\right)}^{1/{b}_1}\right) $$

After rearranging some terms, we get

$$ f\left({\left(s/{a}_1\right)}^{1/{b}_1}\right)={C}_1\left[F\left({e}_M\right)-F\left({e}^{\ast}\right)\right]{b}_1{a_1}^{-k}{\left({\left(s/{a}_1\right)}^{1/{b}_1}\right)}^{\left(-1-{kb}_1\right)} $$

So that the probability density function of the distribution of skills may be written as (after changing variables, $x={\left(s/{a}_1\right)}^{1/{b}_1}$)

$$ f(x)=C\;{x}^{\left(-1-{kb}_1\right)} $$

which is a power law as well (but with power parameter k b₁ and constant/scale parameter C = C₁[F(e_M) − F(e^∗)]b₁a₁^1 − k. ■.

Appendix 2. A closed equilibrium solution from occupational choices and power law distribution of entrepreneurial skills

The Pareto distribution of skills has the advantage that it allows for closed solutions to the occupational choice equilibrium, which facilitates the comparative static analysis of changes in the DFS to changes in the parameters of the model. In this appendix, we present the market equilibrium solution from occupational choices for the simple production function Q = θ e^(1 + β)L^1 − β and a distribution of entrepreneurial skill in the working population that follows a Pareto distribution (with minimum value e_m and power parameter α). It can be shown that equilibrium exists and is unique for values of the parameters that satisfy the condition¹³ (α − 1)β > 1. The level of skill for which the individual is indifferent between working as employee or working as an entrepreneur and the equilibrium salary are given by (see Medrano-Adán et al. (2019) for the details):

$$ {e}^{\ast }={e}_m{\left(\frac{\alpha -\beta -1}{\left(\alpha -1\right)\beta -1}\right)}^{1/\alpha }{w}^{\ast }=\theta {\left(1-\beta \right)}^{1-\beta }{\beta}^{\beta }{e_m}^{\beta +1}{\left(\frac{\alpha -\beta -1}{\left(\alpha -1\right)\beta -1}\right)}^{\left(\beta +1\right)/\alpha } $$

The distribution of firm size is (also) a Pareto distribution with power parameter $\frac{\alpha\;\beta }{\left(\beta +1\right)}$ and minimum size value ${S}_{\mathrm{min}}=h\left({e}^{\ast };{w}^{\ast}\right)=a\;{\left({e}^{\ast}\right)}^b=\frac{\left(1-\beta \right)}{\beta }$. The probability density function and cumulative distribution function are given by (for x ≥ S_min = (1 − β)/β)

$$ {f}_S(x)=\frac{\alpha\;\beta }{\left(\beta +1\right)}{S}_{\mathrm{min}}^{\frac{\alpha\;\beta }{\left(\beta +1\right)}}{x}^{-1-\frac{\alpha\;\beta }{\left(\beta +1\right)}},\kern2.00em {F}_S(x)=1-{\left(\frac{S_{\mathrm{min}}}{x}\right)}^{\frac{\alpha\;\beta }{\left(\beta +1\right)}} $$

The density and distribution functions only depend on the power parameter of the distribution of skills α, and on the parameter of the organization technology, β. We can easily prove the following analytical results:

• 1. The average firm size, given by $\overline{S}=\frac{\alpha \left(1-\beta \right)}{\left(\alpha -1\right)\beta -1}$, is strictly decreasing in α, the concentration of the distribution of skills, and in the organizational size diseconomies parameter, β.

• 2. The minimum firm size is strictly decreasing in β,

• 3. The power parameter of the distribution function of firm size $\frac{\alpha\;\beta }{\left(\beta +1\right)}$ is strictly increasing in both α and β.

• 4. The quantiles of the firm size distribution $Quantile(q)=\frac{\left(1-\beta \right)}{\beta }{\left(1-q\right)}^{-\frac{1+\beta }{\alpha \beta}}$ are strictly decreasing in both α and β).

The average size of firms in the occupational choice equilibrium increases with lower organizational size diseconomies, i.e., with lower intensity of time of the entrepreneur in the supervision of the employees under direction, lower β, and with higher dispersion of skills in the population, lower α. Lower organizational size diseconomies, lower β, also implies larger minimum firm size, i.e., lower number of micro firms in the market equilibrium. The proportion of employees in larger firms, for example in the top 1% quantile of the size distribution, decreases with α and with β.

The survival function of the DFS, the complementary of the cumulative distribution function, is a power function:

$$ S{F}_S(x)=1-{F}_s(x)={\left(\frac{S_{\mathrm{min}}}{x}\right)}^{\frac{\alpha\;\beta }{\left(\beta +\tau \right)}}\kern1em \left(\forall x\ge {S}_{\mathrm{min}}=\left(1-\beta \right)/\beta \right) $$

So that its plot in logarithmic scale (the so-called Zipf plot) is linear; there is a negative linear relationship between the log of the proportion of firms with L or more employees and the number of employees L.

$$ \ln \left[1-{F}_S(x)\right]=\frac{\alpha\;\beta }{\left(\beta +\tau \right)}\left[\ln \left({S}_{\mathrm{min}}\right)-\ln (x)\right] $$

The DFS satisfies the property of power law distributions of constant elasticity, equal to $\frac{\alpha\;\beta }{\left(\beta +1\right)}$, between the proportion of firms above a value of the variable L and the value of L. In the Zipf distribution the power parameter would be equal to 1, $\frac{\alpha\;\beta }{\left(\beta +1\right)}$= 1, which implies that (α − 1)β = 1. For values of the parameters satisfying this condition, the occupational choice equilibrium would not have a finite equilibrium (average size of firms tends to infinity, for example). In other words, for economically meaningful occupational choices equilibrium, the parameters of the model must satisfy (α − 1)β > 1 and the power parameter must be greater than one. Axtell (2001) estimated a power parameter $\frac{\alpha\;\beta }{\left(\beta +1\right)}$= 1.059, greater than one, although, as we show in the main text, we reject the null hypothesis that the US distribution of firm size really follows a power law.

Appendix 3. Test of the power law with Spanish data on firm size

For robustness purpose we present empirical results additional to those in section 4 on the power law distribution of firm size, now with Spanish data. The Spanish official statistical office, INE, publishes annual binned data from 1999 till 2019 on the distribution of firm size (see https://www.ine.es/jaxiT3/Tabla.htm?t=299&L=0), with number of firms in each of the 11 size classes with limits {1, 2, 5, 9, 19, 49, 99, 199, 499, 999, 4999, more than 5000}. For each of the years we estimate Eqs. [5] and [7] in the main text and perform the Ramsey RESET and omitted variable specification tests.

For each of the 21 years considered (1999–2019), the estimated value of δ is in the interval (− 0.0133, − 0.0328), and the p value of the test of the mull hypothesis that δ = 0 is always lower than 0.00604 (with mean value equal to 0.00070). The Ramsey RESET test gives similar results, with p values lower than 0.0051 (with mean value equal to 0.0006). Table 5 shows a summary of the estimation results: the hypothesis of δ = 0 is rejected at a high level of significance (higher than 99%) for all the years.

Consequently, the specification tests do not support the conclusion that the data on the distribution of firm size in Spain follows a power law, similar to the result in the main text for US firm size data.

Table 5 Estimations of the distributions of firm size with Spanish data: log-linear and log-quadratic model: selected years in the period 1999 to 2019