Asymptotics for the Green’s functions of a transient reflected Brownian motion in a wedge

Abstract

We consider a transient Brownian motion reflected obliquely in a two-dimensional wedge. A precise asymptotic expansion of Green’s functions is found in all directions. To this end, we first determine a kernel functional equation connecting the Laplace transforms of the Green’s functions. We then extend the Laplace transforms analytically and study its singularities. We obtain the asymptotics applying the saddle point method to the inverse Laplace transform on the Riemann surface generated by the kernel.

1 Introduction

Context Since its introduction in the 1980s, reflected Brownian motion in a cone has been extensively studied [29, 31, 45], particularly due to its deep links with queuing systems as an approximate model in heavy traffic [27, 41]. Seminal work has determined the recurrent or transient nature of this process in dimension two [34, 46] and in higher dimensions [3, 4, 6, 8]. The literature on the stationary distribution in the recurrent case, in particular the study of the asymptotics, is wide and vast [10, 11, 23, 28, 40, 42]. Numerical methods have been explored in [7, 9] and explicit expressions for the stationary density have been given in [1, 2, 12, 19, 21, 24, 25, 33]. The transient case, which is less studied, is also considered by several articles which study the escape probability along the axes [20], the absorption probability at the vertex [15, 26], or the corresponding Green’s functions [14, 22].

In this article, we consider a transient obliquely reflected Brownian motion in a cone of angle $\beta \in (0, \pi )$ with two different reflection laws from two boundary rays of the cone. We denote by $\widetilde{g}(\rho \cos (\omega ), \rho \sin (\omega ) )$ the Green’s function of this process in polar coordinates; Green’s functions are used to study the distribution of time that the process spends at a point on the cone. The article determines the asymptotics of $\widetilde{g}(\rho \cos (\omega ),\rho \sin (\omega ))$ as $\rho \rightarrow \infty$ and $\omega \rightarrow \omega _0$ for any given angle $\omega _0 \in [0, \beta ]$. See Theorem 1 when $\omega _0\in (0,\beta )$ and Theorem 2 when $\omega _0=0$ or $\beta$. This extends results of [14] in two aspects. Firstly, asymptotic results are obtained in any convex two-dimensional cone with two different reflection laws from its boundaries. While in [14] the authors are able to easily calculate an explicit Laplace transform of the Green’s function for the half plane, the same is certainly not true for RBM in the cone. Laplace transforms of Green functions in this case are expressed in [22] in terms of integrals as solutions of Riemann boundary problems. Secondly, Theorem 1 provides Green function’s asymptotics for any direction of the cone and not only along straight rays as in [14], namely when the angle $\omega$ above tends to a given angle $\omega _0$. The asymptotics depend on the rate of convergence of $\omega \rightarrow \omega _0$ and enables us to determine the Martin boundary of the process.

In [23] the asymptotics of the stationary distribution for recurrent Brownian motion in a cone is found along all regular directions $\omega _0 \in (0, \beta )$, while some special directions $\omega _0$ were left open for future work. The asymptotics are obtained by studying the singularities and applying the saddle point method to the inverse Laplace transform of the stationary distribution. This article applies the approach of [23] to Green’s functions and provides new techniques which enable us to treat all special directions where the asymptotics depend of the convergence rate of $\omega$ to $\omega _0$ rather to that of r tending towards infinity. This is the case when $\omega _0=0$ or $\beta$ (see Theorem 2), and also when the saddle point meets a pole of the boundary Laplace transform (see Theorem 3).

The tools used in this paper are inspired by methods introduced by Malyshev [39], who studied the asymptotic of the stationary distribution for random walks in the quarter plane. Articles studying asymptotics in line with Malshev’s approach include [36], which studies the Martin boundary of random walks in the quadrant; [37], which extends these methods to the join-the-shorter-queue issue; and [35], which studies the asymptotics of the occupation measure for random walks in the quarter plane with drift absorbed at the axes. Fayolle and Iasnogorodski [16] also developed a method to determine explicit expressions for generating functions using the Riemann and Carleman boundary value problems. Then, in the seminal book [17], Fayolle, Iansogorodski and Malyshev merged their analytic approach for random walks in the quadrant. The work [23] was the first to extend their approach to continuous stochastic processes in the quadrant to compute asymptotics of stationary distributions, and [14] was the first one to study the asymptotics of Green’s functions using this analytic approach.

Fig. 1

The cone of angle $\beta$, the reflection angles $\delta$ and $\varepsilon$ and the drift $\widetilde{\mu }$ with its direction $\theta$. The point $\tilde{z}$ with polar coordinates $\rho$ and $\omega$ is displayed

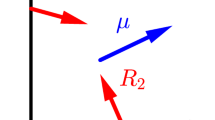
Main results We consider an obliquely reflected standard Brownian motion in a cone of angle $\beta \in (0,\pi )$ starting from $\widetilde{z_0}$, with reflection angles $\delta \in (0,\pi )$ and $\varepsilon \in (0,\pi )$ and of drift $\widetilde{\mu }$ of angle $\theta \in (0,\beta )$ with the horizontal axis, see Fig. 1. We assume that

$$\begin{aligned} \delta +\varepsilon <\beta +\pi . \end{aligned}$$

This well known condition ensures that the process is a semi-martingale reflected Brownian motion [47, 48]. The reflected Brownian motion will be properly defined in the next section. The process is transient since we have assumed that $\theta \in (0,\beta )$ which means that the drift belongs to the cone. If we assume that $\widetilde{p_t}$ is the transition probability of this process, the Green’s function is defined for $\widetilde{z}$ inside the cone by

$$\begin{aligned} \widetilde{g}(\widetilde{z})=\int _0^\infty \widetilde{p_t}(\widetilde{z_0},\widetilde{z})\textrm{d}t. \end{aligned}$$

(1.1)

For $\omega \in (0,\beta )$ and $\rho >0$ we will denote $\widetilde{z} = (\rho \cos \omega ,\rho \sin \omega )$ the polar coordinates in the cone. Note that the tilde symbol $\widetilde{\,}$ stands for quantities linked to the standard reflected Brownian motion in the $\beta$-cone. The same notation without the tilde symbol will stand for the corresponding process in the quadrant ${\mathbb R}_+^2$.

In the next remark we explain how to go from a standard Brownian motion reflected in a convex cone to a reflected Brownian motion reflected in a quadrant by adjusting the covariance matrix. This will be useful because our strategy of proof is to first establish our results in the quadrant for a general covariance matrix, and then to extend the results to all convex cones. The proof of the main Theorems 1, 2 and 3 stated below in the case of a cone can be found at the very end of Sect. 11 and are based on Theorems 4, 5 and 6, which determine the asymptotics in the case of a quadrant.

Remark 1.1

(Equivalence between cones and quadrant) There is a bijective equivalence between the following two families of models:

• Standard reflected Brownian motions (i.e. identity covariance matrix) in any convex cone of angle $\beta \in (0,\pi )$,

• Reflected Brownian motions in a quadrant of any covariance matrix of the form

  $$\begin{aligned} \left( \begin{array}{cc} \displaystyle 1 &{} -\cos \beta \\ -\cos \beta &{} \displaystyle 1 \end{array}\right) . \end{aligned}$$

In Sect. 11 this equivalence is established by means of a simple linear transformation defined in (11.2). Therefore, all the results established for one of these two families can be applied directly to the other family.

Furthermore, any reflected Brownian motion in a general convex cone and with a general covariance matrix can always be reduced via a simple linear transformation to a Brownian motion of one of the two families of models mentioned above (see Remark 1.3 below).

Before presenting our results in more detail, we pause to make the following remark.

Remark 1.2

(Notation) Throughout this article, we will use the symbol $\sim$ to express an asymptotic expansion of a function. If for some functions f and $g_k$ we state that $f(x)\sim \sum _{k=1}^n g_k(x)$ when $x\rightarrow x_0$, then $g_k(x)=o(g_{k-1}(x))$ and $f(x)- \sum _{k=1}^n g_k(x)=o(g_n(x))$ when $x\rightarrow x_0$.

We now state the main result of the article. We define the angles

$$\begin{aligned} \omega ^*:=\theta -2\delta \quad \text {and}\quad \omega ^{**}:=\theta +2\epsilon . \end{aligned}$$

Note that $\omega ^{*}<\theta <\omega ^{**}$.

Theorem 1

(Asymptotics in the general case) We consider a standard reflected Brownian motion in a wedge of opening $\beta$, with reflection angles $\delta$ and $\varepsilon$ and a drift $\widetilde{\mu }$ of angle $\theta$ (see Fig. 1). Then, the Green’s function $\widetilde{g}(\rho \cos \omega ,\rho \sin \omega )$ of this process has the following asymptotics when $\omega \rightarrow \omega _0\in (0,\beta )$ and $\rho \rightarrow \infty$, for all $n\in \mathbb {N}$:

• If $\omega ^{*}<\omega _0<\omega ^{**}$ then

  $$\begin{aligned} \widetilde{g} (\rho \cos \omega ,\rho \sin \omega ) \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow \omega _0 \end{array}}{\sim } e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{\omega -\theta }{2} \right) } \frac{1}{\sqrt{\rho }} \sum _{k=0}^n \frac{\widetilde{c_k}(\omega )}{ \rho ^{k}}. \end{aligned}$$

  (1.2)

• If $\omega _0<\omega ^*$ then

  $$\begin{aligned} \widetilde{g} (\rho \cos \omega ,\rho \sin \omega ) \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow \omega _0 \end{array}}{\sim } c^{*} e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( {\omega +\delta -\theta } \right) } + e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{\omega -\theta }{2} \right) } \frac{1}{\sqrt{\rho }} \sum _{k=0}^n \frac{\widetilde{c_k}(\omega )}{ \rho ^{k}}. \end{aligned}$$

  (1.3)

• If $\omega ^{**}<\omega _0$ then

  $$\begin{aligned} \widetilde{g} (\rho \cos \omega ,\rho \sin \omega ) \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow \omega _0 \end{array}}{\sim } c^{**}e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( {\omega -\epsilon -\theta } \right) } + e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{\omega -\theta }{2} \right) } \frac{1}{\sqrt{\rho }} \sum _{k=0}^n \frac{\widetilde{c_k}(\omega )}{ \rho ^{k}}. \end{aligned}$$

  (1.4)

where $c^*$ and $c^{**}$ are positive constants and $c_k(\omega )$ are constants depending on $\omega$ such that $\widetilde{c_k}(\omega )\underset{\omega \rightarrow \omega _0}{\longrightarrow } \widetilde{c_k}(\omega _0)$.

There are four cases which are illustrated by Fig. 2.

Fig. 2

Asymptotics of the Green’s function determined in Theorem 1 according to the direction $\omega _0$: four different cases according to the value of angles $\omega ^{*}=\theta -2\delta$ and $\omega ^{**}=\theta +2\epsilon$.When $\omega _0$ belongs to the gray region, the asymptotics are given by (1.2); in the purple region, they are given by (1.3); in the orange region, they are given by (1.4)

Our second result states the asymptotics along the edges when $\omega \rightarrow 0$ or $\omega \rightarrow \beta$.

Theorem 2

(Asymptotics along the edges) We now assume that $\omega _0=0$ and let $\rho \rightarrow \infty$ and $\omega \rightarrow \omega _0=0$. In this case, we have $\widetilde{c_0}(\omega )\underset{\omega \rightarrow 0}{\sim }\ c' \omega$ and $\widetilde{c_1}(\omega )\underset{\omega \rightarrow 0}{\sim }\ c''$ for some non-negative constants $c'$ and $c''$ which are non-null when $\omega ^* <0$. Then, the Green’s function $\widetilde{g}(\rho \cos \omega ,\rho \sin \omega )$ has the following asymptotics:

• When $\omega ^{*}<0$ the asymptotics are still given by (1.2). In particular, we have

  $$\begin{aligned} \widetilde{g} (\rho \cos \omega ,\rho \sin \omega ) \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow 0 \end{array}}{\sim } e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{\omega -\theta }{2} \right) } \frac{1}{\sqrt{\rho }} \left( c' \omega + \frac{c''}{\rho } \right) . \end{aligned}$$

• When $\omega ^{*}>0$ the asymptotics given by (1.3) remain valid. In particular, we have

  $$\begin{aligned} \widetilde{g} (\rho \cos \omega ,\rho \sin \omega ) \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow 0 \end{array}}{\sim } c^{*} e^{-2\rho |\widetilde{\mu }| \sin ^2 \left( {\omega +\delta -\theta } \right) }. \end{aligned}$$

  where $c^*$ is the same constant as in Theorem 1.

Therefore, when $\omega ^* < 0$, there is a competition between the two first terms of the sum $\sum _{k=0}^n \frac{\widetilde{c_k}(\omega )}{ \rho ^{k}}$ to know which one is dominant between $c'\omega$ and $\frac{c''}{\rho }$. More precisely:

• If $\rho \sin \omega \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow 0 \end{array}}{\longrightarrow } \infty$ then the first term is dominant.

• If $\rho \sin \omega \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow 0 \end{array}}{\longrightarrow } c>0$ then both terms contribute and have the same order of magnitude.

• If $\rho \sin \omega \underset{\begin{array}{c} \rho \rightarrow \infty \\ \omega \rightarrow 0 \end{array}}{\longrightarrow } 0$ then the second term is dominant.

A symmetric result holds when we take $\omega _0=\beta$. The asymptotics are given by (1.2) when $\beta <\omega ^{**}$ and by (1.4) when $\omega ^{**}<\beta$. The first two terms of the sum compete to be dominant, and this depends on the limit of $\rho \sin (\beta -\omega )$.

We will explain later in Propositions 11.1 and 11.2 that $\omega ^*$ and $\omega ^{**}$ correspond in some sense to the poles of the Laplace transforms of the Green’s functions and that $\omega$ corresponds to the saddle point obtained when we will take the inverse of the Laplace transform. Our third result states the asymptotics when the saddle point meets the poles, which occurs when $\omega \rightarrow \omega ^*$ or $\omega \rightarrow \omega ^{**}$.

Throughout, we let $\Phi (z):= \frac{2}{\sqrt{\pi }} \int _0^z \exp (-t^2)dt$.

Theorem 3

(Asymptotics when the saddle point meets a pole) We now assume that $\omega _0=\omega ^{*}=\theta -2\delta$ and let $\omega \rightarrow \omega ^{*}$ and $\rho \rightarrow \infty$. Then, the Green’s function $\widetilde{g}(\rho \cos \omega ,\rho \sin \omega )$ has the following asymptotics:

• When $\rho (\omega -\omega ^{*})^2\rightarrow 0$ the asymptotics are given by (1.3) with the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}$.

• When $\rho (\omega -\omega ^{*})^2\rightarrow c>0$ for some constant c then:

  • If $\omega <\omega ^{*}$ the asymptotics are still given by (1.3) with the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}(1+\Phi (\sqrt{c}A))$ for some constant A.

  • If $\omega >\omega ^{*}$ the asymptotics are still given by (1.3) with the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}(1-\Phi (\sqrt{c}A))$ for some constant A.

• When $\rho (\omega -\omega ^{*})^2\rightarrow \infty$ then:

  • If $\omega <\omega ^{*}$ the asymptotics are given by (1.3)

  • If $\omega >\omega ^{*}$ the asymptotics are given by (1.2) and we have $\widetilde{c_0}(\omega )\underset{\omega \rightarrow \omega ^{*}}{\sim }\frac{c}{\omega -\omega ^{*}}$ for some constant c.

A symmetric result holds when we assume that $\omega _0=\omega ^{**}=\theta +2\epsilon$.

These main asymptotic results are very similar to those obtained in the article [23] on the stationary distribution in the recurrent case when the drift points towards the apex of the cone. This makes sense given that the Green’s functions and the stationary distribution measure the time or proportion of time that the process spends at a point. However, the analysis of Green’s functions is more complex because of their dependence on the initial state of the process.

In the three previous theorems, we considered a Brownian motion which is standard, i.e. of covariance matrix identity. But all the results stated above may easily be extended to all covariance matrices by the the simple linear transformation mentioned in the previous remark. The next remark explains how to proceed, in line with what is stated in Sect. 11.

Remark 1.3

(Generalisation to any covariance matrix in any convex cone) Consider $\widehat{Z}_t$ an obliquely reflected Brownian motion in a cone of angle $\widehat{\beta }_0\in (0,\pi )$ starting from $\widehat{z_0}$, with reflection angles $\widehat{\delta }$ and $\widehat{\varepsilon }$, of drift $\widehat{\mu }$ of angle $\widehat{\theta }$ and of covariance matrix $\widehat{\Sigma }$. We introduce the angle $\widehat{\beta }_1:=\arccos \left( -\frac{\widehat{\sigma }_{12}}{\sqrt{\widehat{\sigma }_{11}\widehat{\sigma }_{22}}} \right) \in (0,\pi )$ and the linear transformation

$$\begin{aligned} \widehat{T}:= \left( \begin{array}{cc} \displaystyle \frac{1}{\sin \widehat{\beta }_1} &{} \cot \widehat{\beta }_1\\ 0 &{} 1 \end{array} \right) \left( \begin{array}{cc} \displaystyle \frac{1}{\sqrt{\widehat{\sigma }_{11}}} &{} 0\\ 0 &{} \displaystyle \frac{1}{\sqrt{\widehat{\sigma }_{22}}}. \end{array}\right) \end{aligned}$$

Then, the process $\widetilde{Z}_t:=\widehat{T} \widehat{Z}_t$ is an obliquely reflected standard Brownian motion in a cone of angle $\beta \in (0,\pi )$ starting from $\widetilde{z_0}:=\widehat{T} \widehat{z}_0$, with reflection angles $\delta$ and $\varepsilon$ and of drift $\widetilde{\mu }:=\widehat{T} \widehat{\mu }$ of angle $\theta$. The angle parameters are in $(0,\pi )$ and are determined by

$$\begin{aligned}{} & {} \tan \beta =\frac{\sin \widehat{\beta }_1}{\frac{1}{\tan \widehat{\beta }_0}\sqrt{\frac{\widehat{\sigma }_{22}}{\widehat{\sigma }_{11}}} +\cos \widehat{\beta }_1} \, \qquad \tan \theta =\frac{\sin \widehat{\beta }_1}{\frac{1}{\tan \widehat{\theta }}\sqrt{\frac{\widehat{\sigma }_{22}}{\widehat{\sigma }_{11}}} +\cos \widehat{\beta }_1} \,\\{} & {} \tan \delta =\frac{\sin \widehat{\beta }_1}{\frac{1}{\tan \widehat{\delta }}\sqrt{\frac{\widehat{\sigma }_{22}}{\widehat{\sigma }_{11}}} +\cos \widehat{\beta }_1} \, \qquad \tan (\beta -\varepsilon ) =\frac{\sin \widehat{\beta }_1}{\frac{1}{\tan (\widehat{\beta }_0 -\widehat{\varepsilon })}\sqrt{\frac{\widehat{\sigma }_{22}}{\widehat{\sigma }_{11}}} +\cos \widehat{\beta }_1}. \end{aligned}$$

The linear transformation $\widehat{T}$ gives the following relation between the Green’s function of $\widehat{Z}_t$ denoted by $\widehat{g}( \widehat{z})$ for $\widehat{z}$ inside the cone of angle $\widehat{\beta }_0$ and the Green’s function of $\widetilde{Z}_t$ denoted by $\widetilde{g}( \widetilde{z})$ for $\widetilde{z}$ inside the cone of angle $\beta$:

$$\begin{aligned} \widehat{g}( \widehat{z})= \frac{1}{\sqrt{\det \widehat{\Sigma }}} \widetilde{g} (\widehat{T} \widehat{z}). \end{aligned}$$

Therefore, the previous formula allows us to extend our results from $\widetilde{g}$ to $\widehat{g}$.

The following remark concerns the Martin boundary.

Remark 1.4

(Martin boundary) The Martin boundary associated to this process can be computed from the asymptotics of the Green’s function obtained in the previous theorems. The corresponding harmonic functions can also be obtained utilizing the the constants of the dominant terms of the asymptotics. See Section 6 of [14] which briefly reviews some elements of this theory in a similar context.

1.1 Plan and strategy of proof

In this article, the results will be first established in a quadrant for any covariance matrix and then will be extended to a cone in the last section.

The first step in solving our problem is to determine a functional equation relating the Laplace transforms of Green’s functions in the quadrant and on the edges (see Sect. 2). In Sect. 3, we continue to study these Laplace transforms, in particular their singularities. Then, we use the inversion Laplace transform formula combined with the functional equation to express the Green’s functions as a sum of simple integrals (see Sect. 4). To determine the asymptotics, we first use complex analysis to obtain Tauberian results, which links the poles of the Laplace transforms to the asymptotics of the Green’s functions. Then, we use a double refinement of the classical saddle-point method: the uniform method of the steepest descent. One of the reference books on this classical approach is that of Fedoryuk [18]. Appendix A, which gives a generalized version of the classical Morse Lemma by introducing a parameter dependency, will be useful in understanding the refinement of the saddle-point method. Section 5 studies the saddle point and Sect. 6 explains how we shift the integration contour, thus determining the contribution of the encountered poles to the asymptotics. Section 7 identifies which parts of the new integration contour are negligible. Section 8 establishes the contribution of the saddle point to the asymptotics and states the main result. Section 9 studies the asymptotics along axes and Sect. 10 studies the asymptotics in the case where the saddle point meets a pole. Appendix B states a technical result useful to this section. Finally, Sect. 11 explains how to transfer the asymptotic results obtained in the quadrant to any convex cone and thus concludes the proof of Theorems 1, 2 and 3.

2 Convergence of Laplace transforms and functional equation

2.1 Transient reflected Brownian motion in a cone

Let $(Z_t)_{t\ge 0} = (z_0 + \mu t + B_t + RL_t)_{t\ge 0}$ be a (continuous) semimartingale reflected Brownian motion (SRBM) in ${\mathbb R}^2_+$ on a filtered probability space where $\mu =(\mu _1,\mu _2)^\top \in {\mathbb R}^2$ is the drift, $\Sigma$ is the covariance matrix associated to the Brownian motion B, $R=(r_{ij})_{1\leqslant i,j\leqslant 2}\in \mathbb {R}^{2\times 2}$ is the reflection matrix, and $(L_t)_{t\ge 0} = ((L^1_t, L^2_t)^\top )_{t\ge 0}$ is the bivariate local time on the edges associated to the process. We will assume that $\det (\Sigma ) > 0$, i.e. that $\Sigma$ is positive-definite. See Fig. 3 to visualize the parameters of this process. We recall the following classical result concerning the existence of such a process, see for example [43, 47].

Proposition 2.1

(Existence and uniqueness of SRBM) There exists an SRBM with parameters $(\mu ,\Sigma , R)$ if and only if $\Sigma$ is a covariance matrix and R is completely-$\mathcal {S}$, i.e.

$$\begin{aligned} r_{11}> 0,\; r_{22}> 0, \;\,\text {and}\, \;\text {[}\det (R)> 0 \quad \text {or}\quad r_{21},\; r_{12 } > 0\,\text {]}. \end{aligned}$$

(2.1)

In this case, the SRBM is unique in law and defines a Feller continuous strong Markov process.

Condition (2.1) will therefore be required throughout the article. The recurrence and transience conditions of those processes are well known, see [34, 46]. In our case, the SRBM will be transient because of the following assumption of positive drift, which we assume to hold throughout the sequel.

Assumption 1

(Positivity of the drift) We assume that $\mu _1 > 0$ and $\mu _2 > 0$.

Note that this assumption is equivalent to that made in the introduction: $\theta \in (0,\beta )$. Under Assumption 1, the reflected Brownian motion is transient by [34].

Fig. 3

SRBM parameters in the quadrant: drift $\mu$, reflection vectors $R^1$ and $R^2$ and covariance matrix $\Sigma$

2.2 Green’s function

As in (1.1), recall that the Green’s measure G inside the quadrant is defined by

$$\begin{aligned} G(z_0,A):= {\mathbb E}_{z_0}\left[ \int _0^\infty \mathbbm {1}_A(Z_t)dt\right] \end{aligned}$$

for $z_0 \in {\mathbb R}_+^2$ and $A\subset \mathbb {R}^2$. For $i \in \{1,2\}$, we define $H_i$ the Green’s measures on the edges of the quadrant by

$$\begin{aligned} H_i(z_0,A):= {\mathbb E}_{z_0}\left[ \int _0^\infty \mathbbm {1}_A(Z_t)dL^i_t \right] . \end{aligned}$$

The measure $H_1$ has its support on the vertical axis and $H_2$ has its support on the horizontal axis.

Proposition 2.2

Green measures G (resp. $H_1, H_2$) have densities g (resp. $h_1, h_2$) with respect to the two dimensional (resp. one dimensional) Lebesgue measure.

We then have $G(z_0,A) =\int _A g(z) dz$ for $A\subset \mathbb {R}^2$, $H_1(z_0,B\times \{0\})=\int _B h_1(z) dz$ for $B\subset \mathbb {R}$ and $H_2(z_0,\{0\}\times C)=\int _C h_2(z) dz$ for $C\subset \mathbb {R}$.

In the sequel it should be kept in mind that in the notations g and $h_i$ we have omitted the dependence on the starting point $z_0$.

Proof

In the recurrent case, Harrison and Williams proved in [32] that the invariant measure has a density with respect to the Lebesgue measure. The proof in that article extends to the transient case and justifies the existence of a density with respect to the Lebesgue measure for the Green’s measures. Indeed, the proof of Lemma 9 of section 7 in [32] shows that for a Borel set A of Lebesgue measure 0, we have

$$\begin{aligned} {\mathbb E}\left[ \int _0^{+\infty }\mathbbm {1}_{A}(Z_t)dt\right] = 0. \end{aligned}$$

This is even an equivalence, although we will not need it in the present article. Since the proof does not require the recurrence property, this gives the desired result by the Radon Nikodym theorem. The same argument applies to the densities of $H_i$ for $i=1,2$, see theorem 1, section 8 in [32].

In the following, we denote $\mathbb {R}_+=[0,\infty )$ and $\mathbb {R}^*_+=(0,\infty )$.

Remark 2.3

(Partial differential equation) Let us denote $\mathcal {L} = \frac{1}{2}\nabla \cdot \Sigma \nabla + \mu \cdot \nabla$ the generator of the SRBM inside the quadrant and $\mathcal {L}^* = \frac{1}{2}\nabla \cdot \Sigma \nabla - \mu \cdot \nabla$ its dual operator. Then, the Green’s function g satisfies

$$\begin{aligned} \mathcal {L}^*g = -\delta _{z_0} \end{aligned}$$

in the sense of distributions $\mathcal {D'}(({\mathbb R}^*_+)^2)$.

Let us define the matrix $R^*=2\Sigma -R \ \text {diag}(R)^{-1}\text {diag}(\Sigma )$. We denote $R_1^*$ and $R_2^*$ the two columns of $R^*$. Then, the following boundary conditions hold

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{R_1^*}g(z)-2\mu _1 g(z)=0 \text { for } z\in \{0\}\times \mathbb {R_+} \\ \partial _{R_2^*}g(z)-2\mu _2 g(z)=0 \text { for } z\in \mathbb {R_+}\times \{0\} \end{array}\right. } \end{aligned}$$

where $\partial _{R_i^*}=R_i^* \cdot \nabla$.

Sketch of proof of the remark

The partial differential equation of the Green’s function and its boundary conditions are derived from the forward equation of the transition kernel established in [29], see Equation (8.3). However, we provide here a direct elementary proof of the fact that $\mathcal {L}^*g = -\delta _{z_0}$. Let $\varphi \in C^\infty _c(({\mathbb R}_+^*)^2)$. Applying Ito’s formula and taking expectations, we obtain

$$\begin{aligned} {\mathbb E}[\varphi (Z_t)] = \varphi (z_0) + {\mathbb E}\left[ \int _0^{t}\mathcal {L}\varphi (Z_s)ds\right] . \end{aligned}$$

One may remark that there are no boundary terms since the functions $\varphi$ will cancel on a neighborhood of the boundaries. Since we are in the transient case and since $\varphi$ is bounded, the left term converges to 0 as t tends towards infinity by the dominated convergence theorem. Since successive derivatives of $\varphi$ are bounded, $\mathcal {L}\varphi (a, b)$ is bounded by an exponential function up to a multiplication constant. Due to the convergence domain of the Laplace transform (see Proposition 2.6 below), we obtain by dominated convergence that $\varphi (z_0) = - {\mathbb E}\left[ \int _0^{+\infty }\mathcal {L}\varphi (Z_s)ds\right] = - \int _{{\mathbb R}_+^2}\mathcal {L}\varphi (z)g(z) dz$ which implies that $\mathcal {L}^*g = -\delta _{z_0}$.

Furthermore, it is preferable to have continuity of the Green’s function when investing their asymptotic behaviour. This is the content of the following comment.

Remark 2.4

(Smoothness of Green’s functions) By the strictly elliptic regularity theorem (see for instance the Hypoelliptic theorem 5.1 in [30]), we may deduce from $\mathcal {L}^*g = -\delta _{z_0}$ that the density g has a $\mathcal {C}^\infty$ version on $(0,+\infty )^2\backslash \{ z_0\}$. We will not go into more detail here about the proof of this result. In the remainder of this article, we will assume that g is continuous on $[0, +\infty )^2{\setminus } \{0, z_0\}$.

2.3 Laplace transform and functional equation

Definition 2.5

(Laplace transform of Green’s functions) For $(x, y) \in {\mathbb C}^2$ we define the Laplace transforms of the Green’s measures by

$$\begin{aligned} \varphi (x, y):= {\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x, y)\cdot Z_t}dt\right] =\int _{\mathbb {R}_+^2} e^{(x,y)\cdot z}g(z) dz \end{aligned}$$

and

$$\begin{aligned}{} & {} \varphi _1(y):= {\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x,y)\cdot Z_t}dL^1_t\right] =\int _{\mathbb {R}_+} e^{y b}h_1(b) db, \\{} & {} \varphi _2(x):= {\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x,y)\cdot Z_t}dL^2_t\right] =\int _{\mathbb {R}_+} e^{x a}h_2(a) da. \end{aligned}$$

Let us remark that $\varphi _1$ does not depend on x and $\varphi _2$ does not depend on y. Recall the dependence on the starting point $z_0$ even though it is omitted in the notation.

Since Green’s measures are not probability measures, the convergence of their Laplace transforms are not guaranteed. For example, $\varphi (0)$ is not finite. Convergence domains for Laplace transforms of Green’s functions have been studied in [22] but we need stronger results. The following proposition establishes the convergence when the real parts of x and y are negative.

Proposition 2.6

(Convergence of the Laplace transform) Assuming that $\mu _1>0$ and $\mu _2 > 0,$

• $\varphi _1(y)$ converges (at least) on $y \in \{y \in {\mathbb C}, \Re (y) < 0\}$

• $\varphi _2(x)$ converges (at least) on $x \in \{x \in {\mathbb C}, \Re (x) < 0\}$

• $\varphi (x, y)$ converges (at least) on $(x, y) \in \{(x,y) \in {\mathbb C}^2, \Re (x)< 0\; \text {and}\; \Re (y) < 0\}.$

Before proving this proposition, we state the functional equation that will be central in this article. First, we need to define for $(x, y) \in {\mathbb C}^2$ the following polynomials

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma (x, y) = \frac{1}{2}(x, y)\cdot \Sigma (x, y) + (x, y)\cdot \mu = \frac{1}{2}(\sigma _{11}x^2 + 2\sigma _{12}xy + \sigma _{22}y^2) + \mu _1 x + \mu _2 y\\ \gamma _1(x, y) = R^1\cdot (x, y) = r_{11}x + r_{21}y \\ \gamma _2(x, y) = R^2\cdot (x, y) = r_{12}x + r_{22}y \end{array}\right. } \end{aligned}$$

where $R^1, R^2$ are the two columns of the reflection matrix R. The polynomial $\gamma$ is called the kernel.

Proposition 2.7

(Functional equation) If $\Re (x) < 0$ and $\Re (y) < 0$, then

$$\begin{aligned} - \gamma (x, y)\varphi (x, y) = \gamma _1(x, y)\varphi _1(y) + \gamma _2(x, y)\varphi _2(x) + e^{(x, y)\cdot z_0}. \end{aligned}$$

(2.2)

The proofs of these two proposition are directly related, so we will prove both together.

Proof of Propositions 2.6 and 2.7

The main idea of the proof is to take the expectation of Itô’s formula applied to the SRBM and to use a sign argument to justify the limit when $t \rightarrow +\infty$. The beginning of the proof is inspired by the Proposition 5 of [22].

Letting $(x, y) \in ({\mathbb R}_-^*)^2$, Itô’s formula applied to $f(z):= e^{(x, y)\cdot z}$ gives

$$\begin{aligned} f(Z_t) - f(z_0)&= \int _0^t\nabla f(Z_s).dB_s + \int _0^t\mathcal {L}f(Z_s)ds + \sum _{i=1}^2\int _0^t R_i\cdot \nabla f(Z_s)dL^i_s\end{aligned}$$

(2.3)

$$\begin{aligned}&= \int _0^t \nabla f(Z_s).dB_s + \gamma (x, y)\int _0^te^{(x, y)\cdot Z_s}ds + \sum _{i=1}^2\gamma _i(x, y)\int _0^t e^{(x, y)\cdot Z_s}dL^i_s \end{aligned}$$

(2.4)

where $\mathcal {L} = \frac{1}{2}\nabla \cdot \Sigma \nabla + \mu \cdot \nabla$ is the generator of the Brownian motion. Since $(x,y) \in ({\mathbb R}_-^*)^2$, the integral $\int _0^t\nabla f(Z_s).dB_s$ is a martingale (its quadratic variation is bounded by C.t for a constant $C > 0$) and its expectation cancels out. Therefore,

$$\begin{aligned}{} & {} {\mathbb E}_{z_0}\left[ e^{(x, y)\cdot Z_t}\right] - e^{(x, y)\cdot z_0} - \gamma (x, y){\mathbb E}_{z_0}\left[ \int _0^t e^{(x, y)\cdot Z_s}ds\right] \nonumber \\{} & {} \quad = {\mathbb E}_{z_0}\left[ \gamma _1(x, y)\int _0^t e^{(x, y)\cdot Z_s}dL^1_s +\gamma _2(x, y)\int _0^t e^{(x, y)\cdot Z_s}dL^2_s\right] . \end{aligned}$$

(2.5)

The expectations in the left-hand side of the previous equation are finite because for $(x, y) \in ({\mathbb R}_-^*)^2$, the first expectation is bounded by 1 and the second expectation is bounded by t. This implies that the expectation of the right-hand side is also finite.

The aim now is to take the limit of (2.5) when t goes to infinity to show the finiteness of the Laplace transforms and the functional equation. First, since $(x, y)\in ({\mathbb R}^*_-)^2$ and $\left|\hspace{-0.66666pt}\left|Z_t \right|\hspace{-0.66666pt}\right| \underset{t \rightarrow \infty }{\longrightarrow }+\infty$ a.s., the expectation ${\mathbb E}_x\left[ e^{(x, y)\cdot Z_t}\right]$ converges toward 0 when $t \rightarrow \infty$ by the dominated convergence theorem. Secondly, by the monotone convergence theorem, the expectation ${\mathbb E}_{z_0}\left[ \int _0^t e^{(x, y)\cdot Z_s}ds\right]$ converges in $[0,\infty ]$ to $\varphi (x,y)={\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x, y)\cdot Z_s}ds\right]$.

We now prove by contradiction that $\varphi (x_0, y_0)$ is finite. For the sake of contradiction, let us assume that it is possible to choose $(x_0,y_0)\in ({\mathbb R}^*_-)^2$ such that $\gamma (x_0,y_0)<0$, $\gamma _1(x_0,y_0)<0$ and $\gamma _2(x_0,y_0)<0$ and ${\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x_0, y_0)\cdot Z_s}ds\right] = + \infty$. Since $\gamma (x_0,y_0)<0$, the left-hand side of (2.5) will be positive for large enough t. But, since $\gamma _1(x_0,y_0)<0$ and $\gamma _2(x_0,y_0)<0$, the right-hand side of (2.5) is always negative. We have thus obtained a contradiction, allowing us to conclude that $\varphi (x_0,y_0)={\mathbb E}_{z_0}\left[ \int _0^\infty e^{(x_0, y_0)\cdot Z_s}ds\right]$ is finite. Hence, the limit of the right-hand side of (2.5) is also finite and converges by the monotone convergence theorem to $\gamma _1(x_0,y_0)\varphi _1(y_0)+\gamma _2(x_0,y_0)\varphi _2(x_0)$. We deduce that $\varphi _1(y_0)$ and $\varphi _2(x_0)$ are also finite and that the functional equation (2.2) is satisfied for $(x_0,y_0)$. This implies that for all x and y in $\mathbb {C}$ such that $\Re x <x_0$ and $\Re y <y_0$ the Laplace transforms $\varphi (x,y)$, $\varphi _1(y)$ and $\varphi _2(x)$ are finite and the functional equation (2.2) is satisfied by taking the limit of (2.5) when $t\rightarrow \infty$.

All that remains is to show that we can always choose $x_0$ and $y_0$ as close to 0 as we like, such that $(x_0, y_0) \in ({\mathbb R}_-^*)^2$, $\gamma (x_0,y_0)<0$, $\gamma _1(x_0,y_0)<0$ and $\gamma _2(x_0,y_0)<0$ and the proof of Propositions 2.6 and 2.7 will be complete. Let us denote by $\mathcal {E}$ the ellipse of equation $\gamma (x, y)=0$. One may observe that the interior of the ellipse $\mathcal {E}$ defined by $\gamma (x, y)< 0$ contains a neighbourhood of 0 intersecting $({\mathbb R}^*_-)^2$ by Assumption 1 on the positivity of the drift. Indeed, the drift is an external normal to the ellipse at (0, 0). We consider two cases coming from the existence condition of the process (2.1). The first case is given by $r_{11}>0$, $r_{22}>0$, $r_{12} > 0$ and $r_{21} > 0$ (see Fig. 4a). In this case, one may see directly see that $\gamma _1(x, y) < 0$ and $\gamma _2(x, y) <0$ on $({\mathbb R}^*_-)^2$. It is therefore easy to pick $(x_0,y_0)$ close enough to (0, 0) which satisfies the required conditions. The second case is given by $r_{11}>0$, $r_{22}>0$ and $\det (R) > 0$ (see Fig. 4b). In this case, the cone defined by $\gamma _1 < 0$ and $\gamma _2 < 0$ has a non-empty intersection with $({\mathbb R}^*_-)^2$. Hence, we can still choose $(x_0, y_0)$ as close as we want to (0, 0) inside the desired cone and the ellipse $\mathcal {E}$.

Fig. 4

Illustration of the domain where $\gamma _1 < 0$ and $\gamma _2 < 0$

Remark 2.8

(Dependency on the initial state) The main difference compared to the recurrent case [23] comes from the additional term $e^{(x,y)\cdot z_0}$ in the functional equation. With the exception of this one term, it is coherent that Green’s functions in the transient case have similar asymptotic behaviors that those of the stationary densities in the recurrent case.

The following proposition follows from the functional equation and states that the boundary Green’s densities $h_1$ and $h_2$ are equal, up to some constant, to the bivariate Green’s function g on the axes.

Proposition 2.9

(Green’s densities on the boundaries) The Green’s density g is related to the boundary Green’s densities $h_i$ by the formulas

$$\begin{aligned} r_{11}h_1(b)=\frac{\sigma _{11}}{2} g(0,b) \quad \text {and}\quad r_{22}h_2(a)=\frac{\sigma _{22}}{2} g(a,0). \end{aligned}$$

Proof

The initial value formula of a Laplace transform gives

$$\begin{aligned} x\varphi (x,y) \underset{x\rightarrow -\infty }{\longrightarrow }\ -\int _0^\infty e^{yb} g(0,b)db. \end{aligned}$$

Therefore, by dividing the functional equation (2.2) by x and taking the limit when x tends to infinity, we obtain

$$\begin{aligned} \frac{1}{2}\sigma _{11} \int _0^\infty e^{yb} g(0,b)db = r_{11}\varphi _1(y)=r_{11} \int _0^\infty e^{yb} h_1(b)db \end{aligned}$$

which implies the result.

3 Continuation and properties of $\varphi _1(x)$ and $\varphi _2(y)$

The first step of the analytical approach [14, 17] is to study the kernel.

Lemma 3.1

(Kernel study)

• (i) Equation $\gamma (x,y)=0$ determines an algebraic function Y(x) [resp. X(y)] with two branches

  $$\begin{aligned} Y^{\pm } (x)= \frac{1}{\sigma _{22 }}\Big (-\sigma _{12} x -\mu _2 \pm \sqrt{(\sigma _{12}^2 -\sigma _{11} \sigma _{22}) x^2 + 2 (\mu _2 \sigma _{12}- \mu _1 \sigma _{22})x + \mu _2^2} \Big ). \end{aligned}$$

  The function Y(x) [resp. X(y)] has two branching points $x_{min}$ and $x_{max}$ [resp. $y_{min}$ and $y_{max}$] given by

  $$\begin{aligned} x_{min}= & {} \frac{\mu _2\sigma _{12} - \mu _1\sigma _{22} - \sqrt{D_1}}{\det (\Sigma )}, \quad x_{max} = \frac{\mu _2\sigma _{12} - \mu _1\sigma _{22} + \sqrt{D_1}}{\det (\Sigma )},\\ y_{min}= & {} \frac{\mu _1\sigma _{12} - \mu _2\sigma _{11} - \sqrt{D_2}}{\det (\Sigma )}, \quad y_{max} = \frac{\mu _1\sigma _{12} + \mu _2\sigma _{11} - \sqrt{D_2}}{\det (\Sigma )}, \end{aligned}$$

  where $D_1 = (\mu _2\sigma _{12} - \mu _1\sigma _{22})^2 + \mu _2^2\det (\Sigma )$ and $D_2 = (\mu _1\sigma _{12} - \mu _2\sigma _{11})^2 + \mu _1^2\det (\Sigma )$. Both of them are real and $x_{min}<0<x_{max}$ [resp. $y_{min}<y_{max}$]. The branches of Y(x) [resp. X(y)] take real values if and only if $x\in [x_{min}, x_{max}]$ [resp. $y \in [y_{min}, y_{max}]$]. Furthermore $Y^{-}(0)= -\frac{2\mu _2}{\sigma _{22}}<0$, $Y^-(x_{max})<0$, $Y^{+}(0)=0$, $Y^+(x_{max})<0$. See Fig. 5.

• (ii) For any $u \in {\mathbb {R}}$

  $$\begin{aligned}{} & {} \textrm{Re} Y^{\pm }(u+iv) \\ {}{} & {} \quad = \frac{1}{\sigma _{22 }}\Big (-\sigma _{12} u -\mu _2 \pm \frac{1}{\sqrt{2}} \sqrt{ (u-x_{min}) (x_{max}-u)+v^2 +| (u+iv - x_{min})(x_{max}-u-iv ) | } \Big ). \end{aligned}$$

• (iii) Let $\delta =\infty$ if $\sigma _{12}\ge 0$ and $\delta = -\mu _2/\sigma _{12} -x_{max}>0$ if $\sigma _{12}<0$. Then for some $\epsilon >0$ small enough

  $$\begin{aligned} \textrm{Re} Y^{-}(u+iv)<0 \ \ \ \text {for}\ u \in ] -\epsilon , \ x_{max}+\delta [,\ \ v \in {\mathbb {R}}. \end{aligned}$$

Proof

Points (i) and (ii) follow from elementary considerations. The fact that $Y^{+}(x_{max})<0$ implies the inequality $-\sigma _{12}x_{max}- \mu _2<0$, so that $\delta >0$. Furthermore, by (ii) $\textrm{Re}\, Y^{-}(u+iv) \le \textrm{Re} Y^{-}(u)$ which is strictly negative for $u \in ]-\epsilon , x_{max} +\delta [$ by the analysis in (i).

Lemma 3.2

(Continuation of the Laplace transform) Function $\varphi _2(x)$ can be meromorphically continued to the (cut) domain

$$\begin{aligned} \{x = u+iv \mid u < x_{max}+\delta , v \in {\mathbb {R}} \} \setminus [x_{max}, x_{max}+\delta ] \end{aligned}$$

(3.1)

by the formula:

$$\begin{aligned} \varphi _2(x)= \frac{ -\gamma _1(x,Y^-(x)) \varphi _1(Y^-(x)) -\exp \big (a_0 x + b_0 Y^{-}(x) \big )}{\gamma _2(x, Y^{-}(x))} \end{aligned}$$

(3.2)

where $z_0 = (a_0, b_0)$. A symmetric continuation formula holds for $\varphi _1$.

Proof

By Lemma 3.1 (iii) for any $x=u+iv$ with $u \in ] -\epsilon , 0[$ the following equation holds

$$\begin{aligned}{} & {} - \gamma (x, Y^{-}(x)) \varphi (x, Y^{-}(x)) = \gamma _1(x,Y^-(x)) \varphi _1(Y^-(x))+ \gamma _2(x,Y^-(x)) \varphi _2(x) \\{} & {} \quad + \exp (a_0 x + b_0 Y^{-}(x)). \end{aligned}$$

Since $\gamma (x, Y^{-}(x))=0$, the statement follows.

We now define

$$\begin{aligned} x^* = 2\frac{\mu _2\frac{r_{12}}{r_{22}} - \mu _1}{\sigma _{11} - 2\sigma _{12}\frac{r_{12}}{r_{22}} + \sigma _{22}\left( \frac{r_{12}}{r_{22}}\right) ^2} \quad \text {and} \quad y^{**} = 2\frac{\mu _1\frac{r_{21}}{r_{11}} - \mu _2}{\sigma _{11}\left( \frac{r_{21}}{r_{11}}\right) ^2 - 2\sigma _{12}\frac{r_{21}}{r_{11}} + \sigma _{22}}. \end{aligned}$$

(3.3)

Proposition 3.3

(Poles of the Laplace transform, necessary condition)

• (i) $x=0$ is not a pole of $\varphi _2(x)$, and $\varphi _2(0) = {\mathbb E}[L^2_\infty ] < +\infty$. The local time spent by the process on the horizontal axis is finite.

• (ii) If x is a pole of $\varphi _2(x)$ in the domain (3.1), then $x = x^*$ and $(x^*, Y^{-}(x^*))$ is a unique non-zero solution of the system of two equations

  $$\begin{aligned} \gamma (x,y)=0, \ \ \ \ \gamma _2(x,y)= r_{12}x+ r_{22}y=0. \end{aligned}$$

  (3.4)

  In this case, $x_{max}r_{12} + Y^{\pm }(x_{max})r_{22} > 0,$ $x^*$ is real and belongs to $(0, x_{max})$.

• (iii) If y is a pole of $\varphi _1(y)$, then $y = y^{**}$ and $(X^{-}(y^{**}), y^{**})$ is a unique non-zero solution of the system of two equations

  $$\begin{aligned} \gamma (x,y)=0, \ \ \ \ \gamma _1(x,y)=r_{11}x+ r_{21}y=0. \end{aligned}$$

  (3.5)

  In this case, $y_{max}r_{21} + X^\pm (y_{max})r_{11} > 0$, $y^{**}$ is real and belongs to $(0, y_{max})$.

Finally, we define

$$\begin{aligned} y^*:=Y^+(x^{*}) \quad \text {and}\quad x^{**}:=X^+(y^*). \end{aligned}$$

See Fig. 5 below, which depicts the poles $x^*$ and $y^{**}$ when they are both poles.

Fig. 5

In the real plane (x, y), graphical representation of poles $x^{*}$ and $y^{**}$ when both exist

Proof

(i) The observation that $\gamma _2(0, Y^{-}(0))=r_{22} \times Y^{-}(0) \ne 0$ implies the first statement.

(ii) If x is a pole of $\varphi _2$, then $(x, Y^{-}(x))$ should be a solution of the system (3.4) above by the continuation formula (3.2) and the continuity of $\varphi _{1}$ [resp. $\varphi _2$] on $\{\Re y \le 0\}$ [resp. $\{\Re x \le 0\}$]. This system has one solution (0, 0) and the second one $(x^\circ ,y^\circ )$, which is necessarily real. Then $x^\circ \in [x_{min}, x_{max}]$ and $y^\circ$ is either $Y^{-}(x^\circ )$ or $Y^{+}(x^\circ )$. But $x^\circ$ can be a pole of $\varphi _2(x)$, if only it is within $]0, x_{max}]$ and $y^\circ =Y^{-}(x^\circ )$. This last condition implies $\frac{r_{12}}{r_{22}} >\frac{ - Y^{\pm } (x_{\max }) }{x_{max}}$.

Proposition 3.4

(Poles of the Laplace transforms, sufficient condition) The point $x^*$ (resp. $y^{**}$) is a pole of $\varphi _2$ (resp. $\varphi _1$) if (and only if) $x_{max}r_{12} + Y^{\pm }(x_{max})r_{22} > 0$ (resp. $y_{max}r_{21} + X^\pm (y_{max})r_{11} > 0$).

Proof

The inequalities above are necessary by the previous proposition. The next two lemmas prove sufficiency. In those, we denote the dependence of Laplace transforms with the initial condition $z_0$ by $\varphi _1^{z_0}, \varphi _2^{z_0}$ instead of $\varphi _1, \varphi _2$. The proof is done for $x^*$, but is of course symmetrical for $y^{**}$.

Lemma 3.5

(Existence of the pole for a starting point) If $x_{max}r_{12} + Y^{\pm }(x_{max})r_{22} > 0$, there exists $z_0 \in {\mathbb R}_+^2$ such that $x^*$ is a pole of $\varphi _2^{z_0}$.

Proof

The denominator of the continuation formula (3.2) vanishes since we assume that $x_{max}r_{12} + Y^{\pm }(x_{max})r_{22} > 0$. We are looking for a $z_0$ such that the numerator doesn’t vanish at $x^*$, which will imply that $z_0$ is a pole of $\varphi _2$. If $\gamma _1(x^*, Y^-(x^*)) \ge 0$, this is obvious due to the exponential term and since $\gamma _1(x^*, Y^-(x^*)\varphi _1(Y^-(x)) \ge 0$. We suppose now that $-C:= \gamma _1(x^*, Y^-(x^*)) < 0$. We proceed with a proof by contradiction. For the sake of contradiction, assume that

$$\begin{aligned} \forall z_0=(a_0, b_0) \in {\mathbb R}_+^2, \quad -C\varphi _1^{(a_0, b_0)}(Y^-(x^*)) + e^{a_0x^* + b_0Y^-(x^*)} = 0. \end{aligned}$$

(3.6)

Let T be the stopping time defined by the first hitting time of the axis $\{x = 0\}$, i.e. $T = \inf \{t \ge 0, Z^{1}_t = 0\}$ with $Z = (Z^1, Z^2)$. (It is possible that $T = +\infty$). Firstly, since the Stieltjes measure $dL^1$ is supported by $\{Z^1 = 0\}$ and since Z is a strong Markov process, for a starting point $z_0=(a_0,b_0)$ we have:

$$\begin{aligned} \varphi _1^{(a_0, b_0)}(Y^-(x^*))&= {\mathbb E}_{(a_0, b_0)}\left[ \int _T^{+\infty }e^{Z^2_t.Y^-(x^*)}dL^1_t\mathbbm {1}_{T<+\infty }\right] \end{aligned}$$

(3.7)

$$\begin{aligned}&= {\mathbb E}_{(a_0, b_0)}\left[ {\mathbb E}_{Z_T}\left[ \int _0^{+\infty }e^{Z^2_t.Y^-(x^*)}dL^1_t\right] \mathbbm {1}_{T<+\infty }\right] \end{aligned}$$

(3.8)

$$\begin{aligned}&= {\mathbb E}_{(a_0, b_0)}\left[ \varphi _1^{(0, Z^2_T)}(Y^-(x^*))\mathbbm {1}_{T<+\infty }\right] . \end{aligned}$$

(3.9)

Conditioning by the value of $Z^2_T$, using (3.6) and $Y^-(x^*) \le 0$, we get:

$$\begin{aligned} \varphi _1^{(a_0, b_0)}(Y^-(x^*))&= \int _{0}^{+\infty }\varphi _1^{(0,b)}(Y^-(x^*)){\mathbb P}_{(a_0, b_0)}({T<+\infty }, Z^2_T = db)\end{aligned}$$

(3.10)

$$\begin{aligned}&= \int _0^{+\infty } \frac{1}{C}e^{0.x^* + bY^-(x^*)}{\mathbb P}_{(a_0, b_0)}(T< +\infty , Z^2_T = db) \le \frac{1}{C}{\mathbb P}_{(a_0, b_0)}(T < +\infty ) \le \frac{1}{C}. \end{aligned}$$

(3.11)

But, $(a_0, b_0)$ can be chosen such that $e^{a_0x^* + b_0Y^-(x^*)}$ is as large as desired because $x^* > 0$. This is in contradiction with (3.6).

Lemma 3.6

(Existence of a pole for all starting points) If $x^*$ is a pole of $\varphi _2^{z_0}$ for some $z_0 \in {\mathbb R}^2_+$, then $x^*$ is a pole of $\varphi _2^{z_0'}$ for every $z_0' \in {\mathbb R}^2_+$.

The proof of Lemma 3.6 requires Proposition 3.8 to be established and is therefore postponed until after Proposition 3.8.

Lemma 3.7

(Nature of the branching point of $\varphi _2$) Letting $x \rightarrow x_{max}$ with $x < x_{max}$, we have

• If $\gamma _2(x_{max}, Y^-(x_{max})) = 0$, i.e. $x^*=x_{max}$, then

  $$\begin{aligned} \varphi _2(x) = \frac{C}{\sqrt{x_{max} - x} }+ O(1) \end{aligned}$$

  for a constant $C > 0.$

• If $\gamma _2(x_{max}, Y^-(x_{max})) \ne 0$, then

  $$\begin{aligned} \varphi _2(x) = C_1 + C_2\sqrt{x_{max} - x } + O(x_{max} - x) \end{aligned}$$

  for constants $C_1 \in \mathbb {R}$ and $C_2 >0$.

Proof

By Lemma 3.1, $Y^-$ can be written as $Y^-(x) = Y^-(x_{max}) - c\sqrt{x_{max} - x} + O(x_{max} - x)$ where $c > 0$. We proceed to calculate an elementary asymptotic expansion of the quotient of the continuation formula (3.2). Firstly,

$$\begin{aligned} \frac{1}{\gamma _2(x, Y^-(x))}&= \frac{1}{\gamma _2(x_{max}, Y^-(x_{max})) - r_{22}c\sqrt{x_{max} - x} + O(x_{max} - x)} \\&= {\left\{ \begin{array}{ll} \frac{-1}{r_{22}c\sqrt{x_{max} - x}} &{}\text {if} \; \gamma _2(x_{max}, Y^-(x_{max}) = 0, \\ \frac{1}{\gamma _2(x_{max}, Y^-(x_{max}))}\left( 1 + \frac{r_{22}c \sqrt{x_{max} - x} }{\gamma _2(x_{max}, Y^-(x_{max}))}+ O(x_{max} - x)\right) &{}\text {if} \; \gamma _2(x_{max}, Y^-(x_{max})) \ne 0. \end{array}\right. } \end{aligned}$$

Secondly, for the numerator,

$$\begin{aligned}{} & {} \gamma _1(x, Y^-(x))\varphi _1(Y^-(x)) + e^{a_0x + b_0Y^-(x)} =\nonumber \\{} & {} \quad \left( \gamma _1(x_{max}, Y^-(x_{max})) - r_{21}c\sqrt{x_{max} - x} + O(x_{max} - x)\right) \nonumber \\{} & {} \quad \times \left( \varphi _1(Y^-(x_{max})) - c\varphi _1'(Y^-(x_{max}))\sqrt{x_{max} - x} + O(x_{max} - x) \right) \nonumber \\{} & {} \quad + e^{a_0x_{max} + b_0Y^-(x_{max})}(1 - cb_0\sqrt{x_{max} - x} + O(x_{max} - x)) \end{aligned}$$

(3.12)

Combining the two asymptotic expansions, we obtain the desired formula with

$$\begin{aligned} C = \frac{\gamma _1(x_{max}, Y^-(x_{max}))\varphi _1(Y^-(x_{max})) + e^{a_0x_{max} + b_0Y^-(x_{max})}}{r_{22}c} \end{aligned}$$

and

$$\begin{aligned} C_2= & {} \frac{1}{\gamma _2(x_{max}, Y^-(x_{max}))} \Big [r_{21}c\varphi _1(Y^-(x_{max})) + c\gamma _1(x_{max}, Y^{-}(x_{max}))\varphi '_1(Y^-(x_{max})) + cb_0e^{a_0x_{max} + b_0Y^-(x_{max})}\\{} & {} - \frac{r_{22}c}{\gamma _2(x_{max}, Y^-(x_{max}))}\left( \gamma _1(x_{max}, Y^-(x_{max}))\varphi _1(Y^-(x_{max})) + e^{a_0x_{max} + b_0Y^-(x_{max})} \right) \Big ]. \end{aligned}$$

The following proposition states the asymptotics of the Green’s functions $h_1$ and $h_2$ on the boundaries. We note that we obtain the same asymptotics as in Theorem 2 and 5 with $\alpha \rightarrow 0$, which is consistent with the link made between $h_1$, $h_2$ and g in Proposition 2.9.

Proposition 3.8

(Asymptotics of the Green’s functions on the boundary $h_1$ and $h_2$) In this proposition we denote by c a constant which is allowed to vary from one line to the next.

• 1. Suppose that we have a pole $x^* \in ]0, x_{max}[$ for $\varphi _2$. Then, the Green’s function $h_2$ has the following asymptotics

  $$\begin{aligned} h_2(u) \underset{u\rightarrow \infty }{\sim }\ c e^{-x^* u}. \end{aligned}$$

• 2. Suppose that $x^* = x_{max}$, then

  $$\begin{aligned} h_2(u) \underset{u\rightarrow \infty }{\sim }\ c u^{-1/2}e^{-x_{max} u}. \end{aligned}$$

• 3. Suppose that there is no pole in $]0, x_{max}[$ and that $x^* \ne x_{max}$, then,

  $$\begin{aligned} h_2(u) \underset{u\rightarrow \infty }{\sim }\ c u^{-3/2}e^{-x_{max} u}. \end{aligned}$$

A symmetric result holds for $h_1$.

Proof

The result directly follows from classical Tauberian inversion lemmas which link the asymptotic of a function at infinity to the first singularity of its Laplace transform (which is here given in Lemma 3.7). We refer here to Theorem 37.1 of Doetsch’s book [13] and more precisely we apply the special case stated in Lemma C.2 of [10]. To apply this lemma, we have to verify the analyticity and the convergence to 0 at infinity of $\varphi _2$ in a domain $\mathcal {G}_\delta (x_{max}):=\{z\in \mathbb {C}:z\ne x_{max}, |\arg (z-x_{max})|>\delta \}$ for some $\delta \in (0,\pi /2)$. But this follows directly from the continuation procedure of Lemma 3.2:the exponential part of the continuation formula (3.2) tends to 0 in a domain $\mathcal {G}_\delta (x_{max})$ for some $\delta \in (0,\pi /2)$ by using (ii) of lemma 3.1. Note that the convergence to 0 also follows from Lemma B.2. Then, Lemma 3.7 gives the nature at the branching point $x_{max}$ which is the smallest singularity except in the case where there is a pole in $]0,x_{max}[$, where the pole $x^*$ is the smallest singularity.

Remark 3.9

We remark in the proof of Lemma 3.7 that O(1) and $O(x_{max} - x)$ of this lemma are locally uniform according to $z_0$. This means that $\sup _{z'_0 \in V}\left| \varphi _2^{(z'_0)}(x) - \frac{C^{(z'_0)}}{\sqrt{x_{max} - x} }\right| = O(1)$ as $x \rightarrow x^*$ when $\gamma _2(x_{max}, Y^-(x_{max})) = 0$ for a sufficiently small neighborhood V of $z_0$ (and the same holds for $O(x_{max} - x)$ in the other case). This implies that the results of Proposition 3.8 hold locally uniformly in $z_0$. Indeed, it is enough to adapt the Tauberian lemmas of [13] used in the proof of Proposition 3.8. Note that the constants c of this proposition depend continuously on $z_0$.

Proof of Lemma 3.6

Let $z_0=(a_0,b_0)$ be a starting point such that $x^*$ is a pole of $\varphi _2^{z_0}$. Then, the continuation formula (3.2) implies that $-\gamma _1(x^*,Y^-(x^*)) \varphi _1^{z_0}(Y^-(x^*)) -\exp \big (a_0 x^* + b_0 Y^{-}(x^*) \big ) \ne 0$. By continuity with respect to the starting point (which follows from the integral formula given in [22] or from [38]), there exists a neighbourhood V of $z_0$ such that $-\gamma _1(x^*,Y^-(x^*)) \varphi _1^{z_0'}(Y^-(x^*)) -\exp \big (a_0' x^* + b_0' Y^{-}(x^*) \big ) \ne 0$ for all $z_0'=(a_0',b_0') \in V$. Therefore, by the continuation formula, $x^*$ is a pole of $\varphi _2^{z_0'}$ for all $z_0' \in V$. From Proposition 3.8 and by continuity of the constant of this proposition according to $z'_0$ we conclude the following. If $x^*$ is a pole of $\varphi _2^{z_0'}$, there exists a constant c such that for all $z_0' \in V$ we have $h_2^{(z_0')}(u) = c e^{-x^*u} (1+o(1))$ (notice that o(1) is uniform in $z_0'$ in the sense of Remark 3.9 and that c is continuous in $z_0'$). For $z_0''\in \mathbb {R}^2$ we introduce the stopping time

$$\begin{aligned} T_V:=\inf \{ t >0: Z_t^{z_0''} \in V \} \end{aligned}$$

where $Z_t^{z_0''}$ denotes the process starting from $z_0''$. By the strong Markov property applied to $T_V$ we have for some constant C and when $u\rightarrow \infty$,

$$\begin{aligned} h_2^{z_0''}(u) \geqslant \mathbb {P}_{z_0''}(T_V < \infty ) \inf _{z_0'\in V} h_2^{z_0'}(u) = C e^{-x^*u} (1+o(1)). \end{aligned}$$

We deduce by Proposition 3.8 that $z_0''$ is necessarily a pole.

We conclude this section with the following lemma which will be needed in Sect. 6.

Lemma 3.10

(Boundedness of the Laplace transform) Let $\eta \in ]0, \delta [$, we have

$$\begin{aligned} \sup _{\begin{array}{c} u \in [X^{\pm }(y_{\max })-\eta , x_{max}+\eta ] \\ |v|>\epsilon \end{array}} |\varphi _2(u+iv)| <\infty . \end{aligned}$$

Proof

Clearly, for any $x=u+iv$ with $u<0$, $|\varphi _2(u+iv)|\le \varphi _2(u)$. Then for any $\epsilon >0$,

$$\begin{aligned} \sup _{ u \in [X^{\pm }(y_{\max })-\eta , -\epsilon ]} |\varphi _2(u+iv)| <\infty . \end{aligned}$$

(3.13)

For any $x=u+iv$ with $u \in [-\epsilon , x_{max}+\eta ]$ Lemma 3.2 applies and gives the representation (3.2). Let us consider all its terms. By Lemma 3.1 (ii), for any fixed $u \in {\mathbb {R}}$, the function $\textrm{Re} Y^{-}(u+iv)$ is strictly decreasing as |v| goes from 0 to infinity. Moreover, for any $u \in [-\epsilon , x_{max} +\delta ]$

$$\begin{aligned} \textrm{Re} Y^{-} (u+iv) \le -\frac{1}{\sqrt{2} \sigma _{22}} |v|. \end{aligned}$$

Then,

$$\begin{aligned} |\varphi _1(Y^{-}(u+iv))| \le \varphi _1 (\textrm{Re}\,Y^{-}(u+iv)) \le \varphi _1 \left( \frac{-1}{\sqrt{2} \sigma _{22}} |v|\right) \le \varphi _1(0). \end{aligned}$$

(3.14)

By Proposition 3.3 (i) $\varphi _1(0)<\infty$. It follows that

$$\begin{aligned} \sup _{ u \in [-\epsilon , x_{max} +\delta ] }\varphi _1(Y^{-}(u+iv)) <\infty . \end{aligned}$$

(3.15)

By Lemma 3.1 (i) there exists a constant $d_1>0$ such that

$$\begin{aligned} |\gamma _1(u+iv, Y^{-}(u+iv))| \le d_1 |v|, \ \ \forall u \in [-\epsilon , x_{max}+\eta ], \ |v| \ge \epsilon . \end{aligned}$$

(3.16)

Note that $|\gamma _2(u+iv, Y^{-}(u+iv))| \ge |r_{12} u + r_{22} \textrm{Re} Y^{-}(u+iv)|$. Then by Lemma 3.1 (ii) and also by Proposition 3.3 (ii) there exists a constant $d_2>0$ such that

$$\begin{aligned} |\gamma _2(u+iv, Y^{-}(u+iv))| \ge d_2 |v|, \ \ \forall u \in [-\epsilon , x_{max}+\eta ], \ |v|\ge \epsilon . \end{aligned}$$

(3.17)

Finally by Lemma 3.1 (ii)

$$\begin{aligned}{} & {} |\exp (a_0 (u+iv)+ b_0 Y^{-}(u+iv))| = \exp (a_0 u + b_0 \textrm{Re}\, Y^{-} (u+iv) ) \nonumber \\{} & {} \quad \le \exp \left( \left( a_0 {- b_0\frac{\sigma _{12}}{\sigma _{22}}} \right) u - \frac{b_0 }{ \sqrt{2} \sigma _{22} } |v| \right) \end{aligned}$$

(3.18)

for any $u \in [-\epsilon , x_{max}+ \eta ]$ and v with $|v|>\epsilon$. Then the estimate (3.13), the representation (3.2) combined with the estimates (3.15), (3.16), (3.17) and (3.18) lead to the statement of the lemma.

4 Inverse Laplace transform: from a double integral to simple integrals

By the Laplace transform inversion formula ([13, Theorem 24.3 and 24.4] and [5]), for any $\epsilon >0$ small enough,

$$\begin{aligned} g(a,b)= \frac{1}{(2\pi i)^2 } \int _{-\epsilon -i \infty }^{-\epsilon + i \infty } \int _{-\epsilon - i \infty }^{-\epsilon + i \infty } \varphi (x,y) \exp (-a x -by) dxdy, \end{aligned}$$

in the sense of principal value convergence.

Lemma 4.1

(Inverse Laplace transforms as a sum of simple integrals) Let $z_0=(a_0,b_0)$ be the starting point of the process. For any $(a,b)\in \mathbb {R}_+^2$ where either $a>a_0, b>0$ or $b>b_0, a>0$ the following representation holds:

$$\begin{aligned} g(a,b)= I_1(a,b)+ I_2(a,b) + I_3(a,b) \end{aligned}$$

where

$$\begin{aligned} I_1(a,b)= & {} \frac{1}{2 \pi i } \int _{-\epsilon - i \infty }^{- \epsilon + i \infty } \varphi _2 (x) \gamma _2 (x, Y^{+} (x)) \exp ( -a x - b Y^{+}(x)) \frac{dx}{\gamma '_y(x, Y^{+}(x)) },\\ I_2(a,b)= & {} \frac{1}{2 \pi i } \int _{-\epsilon - i \infty }^{- \epsilon + i \infty } \varphi _1 (y) \gamma _1 ( X^{+} (y), y) \exp ( -a X^{+}(y)-by) \frac{dy}{\gamma '_x( X^{+}(y), y)},\\ I_3(a,b)= & {} \frac{1}{2\pi i } \int _{-\epsilon - i \infty }^{- \epsilon + i \infty } \exp (a_0 x + b_0 Y^{+}(x)) \exp ( -a x - b Y^{+}(x)) \frac{dx}{\gamma '_y(x, Y^{+}(x)) } \ \ \hbox { if }b>b_0,\\ I_3(a,b)= & {} \frac{1}{2\pi i } \int _{-\epsilon - i \infty }^{- \epsilon + i \infty } \exp (a_0 X^{+}(y) + b_0 y ) \exp ( -a X^{+}(y) - b y ) \frac{dy}{\gamma '_x(X^{+}(y), y) } \ \ \hbox { if }a>a_0. \end{aligned}$$

The two different formulas for $I_3$ will be useful in Sect. 9 in studying the asymptotics along the axes.

Proof

For any $\epsilon >0$ small enough $\gamma (-\epsilon , -\epsilon )<0$. Then

$$\begin{aligned} \textrm{Re} \gamma (-\epsilon +iv_1, -\epsilon + iv_2) <0 \ \ \forall v_1, v_2 \in {\mathbb {R}} \end{aligned}$$

(4.1)

since $\Sigma$ is a covariance matrix. Then, by (2.2)

$$\begin{aligned}{} & {} g(a,b)= \frac{-1}{(2 \pi i)^2 } \int _{-\epsilon -i \infty }^{-\epsilon + i \infty } \int _{-\epsilon -i\infty }^{-\epsilon + i\infty }\\ {}{} & {} \quad \frac{\gamma _1(x,y) \varphi _1(y)+ \gamma _2(x,y) \varphi _2(x)+ \exp (a_0 x + b_0 y)}{\gamma (x,y)} \exp (-a x -by)dxdy. \end{aligned}$$

Now, let us consider for example the second term. It can be written as

$$\begin{aligned} \frac{-1}{(2 \pi i)^2} \int _{-\epsilon -i \infty }^{-\epsilon +i \infty } \varphi _2(x) \exp (-ax) \Big ( \int _{-\epsilon -i \infty }^{-\epsilon + i\infty } \frac{\gamma _2(x,y)}{\gamma (x,y)} \exp (-by) dy \Big ) dx. \end{aligned}$$

Note that the convergence in the sense of the principal value of this integral can be guaranteed by integration by parts.

Now, it just remains to show that

$$\begin{aligned} \frac{-1}{2 \pi i } \int _{-\epsilon -i\infty }^{-\epsilon + i\infty } \frac{\gamma _2(x, y)}{\gamma (x,y)} \exp (-by)dy = \frac{\gamma _2(x, Y^{+}(x))}{\gamma '_y (x, Y^{+}(x))}\exp \big (-b Y^{+}(x)\big ). \end{aligned}$$

(4.2)

Let $x=-\epsilon$. The equation $\gamma (-\epsilon , y)=0$ has two solutions, $Y^{+}(-\epsilon )>0$ and $Y^{-}(-\epsilon )<0$. (In fact, for $\epsilon >0$ small enough $Y^{+}(-\epsilon )$ is close to $Y^{+}(0)=0$ staying positive and $Y^{-}(-\epsilon )$ is close to $Y^{-}(0)= - 2\mu _2/\sigma _{22}<0$). Let $x=-\epsilon + iv$. The functions $Y^{+}(-\epsilon +iv)$ and $Y^{-}(-\epsilon +iv)$ are continuous in v. By (4.1) their real parts do not equal $-\epsilon$ for any $v \in {\mathbb {R}}$. Thus $\textrm{Re} Y^{+}(-\epsilon + iv)>-\epsilon$ and $\textrm{Re} Y^{-}(-\epsilon + iv)<-\epsilon$ for all $v \in {\mathbb {R}}$. Let us construct the contour $[-\epsilon -i R, -\epsilon + i R] \cup \{ t + i R, \mid t \in [-\epsilon , 0] \} \cup \{R e^{it} \mid t \in ]-\pi /2 + \pi /2[ \} \cup \{ t - i R, \mid t \in [-\epsilon , 0] \}$, see Fig. 6.

Fig. 6

Integral contour in the complex plane ${\mathbb C}_y$, with the pole $Y^+(x)$

For any fixed $x=-\epsilon +iv$, the integral over this contour taken in the counter-clockwise direction of the function $\frac{\gamma _2(x,y)}{\gamma (x,y)} \exp (-by)$ equals the residue of this function multiplied by $2\pi i$, which is exactly the result in (4.2). It suffices to show that the integral over $\{ t + i R \mid t \in [-\epsilon , 0] \} \cup \{R e^{it} \mid t \in ]-\pi /2 + \pi /2[ \} \cup \{ t - i R \mid t \in [-\epsilon , 0] \}$ converges to zero as $R \rightarrow \infty$. The integral over the half of the circle $\{R e^{it} \mid t \in ]-\pi /2 + \pi /2[ \}$ equals

$$\begin{aligned} \int _{-\pi /2}^{\pi /2} \frac{\gamma _2(x, Re^{it})}{ \gamma (x, Re^{it})} \exp (-b R e^{it}) iRe^{it} dt. \end{aligned}$$

We have $\sup _{R>R_0} \sup _{t \in ]-\pi /2, \pi /2[} \Big | \frac{\gamma _2(x, R e^{it}) }{\gamma (x, R e^{it}) } i R e^{it} \Big |<\infty$ for $R_0 = R_0(x) > 0$ large enough, while $|\exp (-b R e^{it}) | = \exp (-b R \cos t) \rightarrow 0$ as $R \rightarrow \infty$ for any $t \in ]-\pi /2, \pi /2[$ since $b>0$. Hence, the integral over the half of the circle converges to zero as $R \rightarrow \infty$ by the dominated convergence theorem. Let us look at the integral over segment $\{ t + i R \mid t \in [-\epsilon , 0]\}$. For any fixed $x=-\epsilon +iv$, there exists a constant $C(x)>0$ such that for any R large enough

$$\begin{aligned} \sup _{u \in [-\epsilon , 0]}\Big | \frac{\gamma _2(x, u+ i R)}{\gamma (x, u+ iR)} \Big | \le \frac{C(x)}{R}. \end{aligned}$$

Therefore

$$\begin{aligned} \Big |\int _{-\epsilon }^0 \frac{\gamma _2(x, u+ iR) }{ \gamma (x, u+ iR) } \exp (- b (u+ i R)) du \Big | \le \epsilon \exp ( b \epsilon ) \frac{C(x)}{R} \underset{R\rightarrow \infty }{\longrightarrow }\ 0. \end{aligned}$$

The representation of $I_1(a,b)$ follows.

The reasoning is the same for the third term. The integral over the half of the circle equals

$$\begin{aligned} \int _{-\pi /2}^{\pi /2} \frac{\exp (-(b-b_0) R e^{it}) }{ \gamma (x, Re^{it})} iRe^{it} dt. \end{aligned}$$

We have $\sup _{R>R_0} \sup _{t \in ]-\pi /2, \pi /2[} \Big | \frac{1 }{\gamma (x, R e^{it}) } i R e^{it} \Big |<\infty$ while $|\exp (-(b-b_0) R e^{it}) | = \exp (-(b-b_0) R \cos t) \rightarrow 0$ as $R \rightarrow \infty$ for any $t \in ]-\pi /2, \pi /2[$ since $b-b_0>0$. The integral over the half of the circle converges to zero as $R \rightarrow \infty$ by the dominated convergence theorem once again. For any fixed $x=-\epsilon +iv$, there exists a constant $C(x)>0$ such that for any R large enough

$$\begin{aligned} \sup _{u \in [-\epsilon , 0]}\Big | \frac{1}{\gamma (x, u+ iR)} \Big | \le \frac{C(x)}{R^2}. \end{aligned}$$

Therefore

$$\begin{aligned} \Big |\int _{-\epsilon }^0 \frac{\exp (- (b-b_0)(u+ i R)) }{ \gamma (x, u+ iR) } du \Big | \le \epsilon \exp ( (b-b_0) \epsilon ) \frac{C(x)}{R^2} \rightarrow 0, \ \ R \rightarrow \infty . \end{aligned}$$

The representations for $I_2(a,b)$ and $I_3(a,b)$ with $a>a_0$ are obtained in the same way.

Remark. Let us introduce the notation a, b, c, $\widetilde{a}$, $\widetilde{b}$, $\widetilde{c}$ by

$$\begin{aligned} \gamma (x,y)= a(x)y^2 +b(x)y+c(x) = \widetilde{a}(y)x^2+ \widetilde{b}(y) x + \widetilde{c}(y). \end{aligned}$$

(4.3)

Then functions in the integrand can be represented as

$$\begin{aligned}{} & {} \gamma '_y(x, Y^+(x))= a(x) (Y^+(x)- Y^-(x)) = 2 a(x) Y^+(x) + b(x)= \sqrt{b^2(x)-4a(x) c(x)} \end{aligned}$$

(4.4)

$$\begin{aligned}{} & {} \gamma '_x(X^+(y), y)= \widetilde{a}(y) (X^+(y)- X^-(y)) = 2 \widetilde{a}(y) X^+(y) + \widetilde{b}(y)= \sqrt{ \widetilde{b}^2(y)-4\widetilde{a}(y) \widetilde{c}(y)}. \end{aligned}$$

(4.5)

5 Saddle point and contour of the steepest descent

Our aim is to study the integrals $I_1$, $I_2$ and $I_3$ of Lemma 4.1 using the saddle point method (see, for example, Fedoryuk [18]).

5.1 Saddle point

For $\alpha \in [0,2\pi [$ we define

$$\begin{aligned} (x(\alpha ), y(\alpha )):= \textrm{argmax}_{(x,y): \gamma (x,y)=0}(x \cos \alpha + y \sin \alpha ). \end{aligned}$$

(5.1)

We will see that this point turns out to be the saddle point of the functions inside the exponentials of the integrals $I_1$, $I_2$ and $I_3$. See Fig. 7 for a geometric interpretation of this point.

Fig. 7

Graphical representation of the saddle point. We denote $e_{\alpha } = (\cos (\alpha ), \sin (\alpha ))$

The map $\alpha : [0, 2\pi [ \rightarrow \{(x,y): \gamma (x,y)=0\}$ is a diffeomorphism. The functions $x(\alpha ), y(\alpha )$ are in the class $C^\infty ([0, 2\pi ])$. For any $\alpha \in [0, \pi /2]$ the function $\cos (\alpha ) x + \sin (\alpha ) Y^{+}(x)$ reaches its maximum at the unique point on $[X^{\pm } (y_{max}), x_{max}]$ called $x(\alpha )$. This function is strictly increasing on $[X^{\pm }(y_{max}), x(\alpha )]$ and strictly decreasing on $[x(\alpha ), x_{max}]$. The function $\cos (\alpha ) X^{+}(y) + \sin (\alpha ) y$ reaches its maximum on $[Y^{\pm }(x_{max}), y_{max}]$ at the unique point $y(\alpha )$. It is strictly increasing on $[Y^{\pm }(x_{max}), y(\alpha )]$ and strictly decreasing on $[y(\alpha ), y_{max}]$.

Thus $x(0)=x_{max}$, $y(0)= Y^{\pm } (x_{max})$, $x(\pi /2)= X^{\pm }(y_{max})$, $y(\pi /2)= y_{max}$. Finally, $x(\alpha )=0$ and $y(\alpha )=0$ if $(\cos (\alpha ), \sin (\alpha ))= \left( \frac{\mu _1}{\sqrt{\mu _1^2 + \mu _2^2}},\frac{\mu _2}{\sqrt{\mu _1^2 + \mu _2^2}}\right)$. We denote the direction corresponding to the drift by $\alpha _\mu$.

Let us define the functions

$$\begin{aligned} F(x,\alpha )= & {} - \cos (\alpha ) x - \sin (\alpha ) Y^{+}(x) + \cos (\alpha ) x(\alpha ) + \sin (\alpha ) y(\alpha ),\\ G(y, \alpha )= & {} -\cos (\alpha ) X^{+}(y)- \sin (\alpha ) y + \cos (\alpha ) x(\alpha ) + \sin (\alpha ) y(\alpha ).\nonumber \end{aligned}$$

(5.2)

We see that the function F is (up to a constant) the function inside exponential of the integral $I_1$, and the function G is (up to a constant) the function inside the exponential of the integral $I_2$, see Lemma 4.1. We have

$$\begin{aligned} F(x(\alpha ), \alpha )=0 \ \ \forall \alpha \in [0, \pi /2] \end{aligned}$$

and

$$\begin{aligned} F'_x(x(\alpha ), \alpha )=0 \ \ \forall \alpha \in ]0, \pi /2], \hbox { but not at }\alpha =0. \end{aligned}$$

In the same way $G(y(\alpha ), \alpha )=0$ for any $\alpha \in [0, \pi /2]$ and $G'_y(y(\alpha ), \alpha )=0$ for any $\alpha \in [0, \pi /2[$ but not at $\alpha =\pi /2$. Then $(Y^{+}(x(\alpha )))' = -\textrm{ctan }(\alpha )$ and $(X^{+}(y(\alpha )))' = -\textrm{tan }(\alpha )$.

Using the identities $\gamma (x, Y^{+}(x)) \equiv 0$ and $\gamma (X^+(y), y) \equiv 0$, we get:

$$\begin{aligned} (Y^{+}(x))'\Bigm |_{x=x(\alpha )}= & {} - \frac{ \gamma '_x(x(\alpha ), y(\alpha )) }{ \gamma '_y(x(\alpha ), y(\alpha ))} = -\frac{\cos (\alpha )}{\sin (\alpha )}, \ \ \ \alpha \in ]0, \pi /2]\\ (X^{+}(y))'\Bigm |_{y=y(\alpha )}= & {} - \frac{ \gamma '_y(x(\alpha ), y(\alpha )) }{ \gamma '_x(x(\alpha ), y(\alpha ))} = -\frac{\sin (\alpha )}{\cos (\alpha )}, \ \ \alpha \in [0, \pi /2[\nonumber \\ (Y^{+}(x))''\Bigm |_{x=x(\alpha )}= & {} -\frac{ \sigma _{11} + 2\sigma _{12} (-\textrm{ctan}\,(\alpha )) + \sigma _{22} (-\textrm{ctan}\,(\alpha ))^2 }{ \gamma '_y(x(\alpha ), y(\alpha ) )}\nonumber \\ (X^{+}(y))''\Bigm |_{y=y(\alpha )}= & {} -\frac{ \sigma _{11} (-\textrm{tan } (\alpha ))^2 + 2\sigma _{12} (-\textrm{tan}\,(\alpha )) + \sigma _{22} }{ \gamma '_x(x(\alpha ), y(\alpha ) )}\nonumber \end{aligned}$$

(5.3)

$$\begin{aligned} F''_{x}(x(\alpha ), \alpha ) = \frac{ \sigma _{11}\sin ^2(\alpha ) - 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha ) }{ \gamma '_y(x(\alpha ), y(\alpha ) ) \sin \alpha }>0 \ \ \alpha \in ]0, \pi /2], \end{aligned}$$

(5.4)

$$\begin{aligned} G''_{y}(y(\alpha ), \alpha )=\frac{ \sigma _{11}\sin ^2(\alpha ) - 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha ) }{ \gamma '_x(x(\alpha ), y(\alpha ) ) \cos (\alpha ) }>0 \ \ \alpha \in [0, \pi /2], \end{aligned}$$

where the strict inequality arises from (4.4), (4.5) and the positive-definite form of $\Sigma$.

Fig. 8

Level sets of $\Re (F)$ in purple and of $\Im (F)$ in orange. The saddle point $x(\alpha )$ is represented in blue and the branch point $x_{max}$ is in red

The values of $x(\alpha )$ and $y(\alpha )$ are given by the following formulas.

$$\begin{aligned} x(\alpha )= & {} \frac{(\mu _2 \sigma _{12} - \mu _1 \sigma _{22})}{\det (\Sigma )} + \frac{{1}}{\det (\Sigma )} (\sigma _{22} - \tan (\alpha ) \sigma _{12}) \sqrt{{\frac{{\mu _2^2 \sigma _{11} - 2 \mu _1 \mu _2 \sigma _{12} + \mu _1^2 \sigma _{22}}}{{\sigma _{11} \tan ^2(\alpha ) - 2 \sigma _{12} \tan (\alpha ) + \sigma _{22}}}}} \end{aligned}$$

(5.5)

$$\begin{aligned} y(\alpha )= & {} \frac{{(\mu _1 \sigma _{12} - \mu _2 \sigma _{11})}}{\det (\Sigma )} + \frac{{1}}{\det (\Sigma )} \left( \sigma _{11} - \frac{1}{\tan (\alpha )} \sigma _{12}\right) \sqrt{{\frac{{\mu _1^2 \sigma _{22} - 2 \mu _1 \mu _2 \sigma _{12} + \mu _2^2 \sigma _{11}}}{{\frac{{\sigma _{22}}}{\tan ^2(\alpha )} - 2 \frac{\sigma _{12}}{\tan (\alpha )} + \sigma _{11}}}}}. \end{aligned}$$

(5.6)

Indeed, using the same calculations as in section 4.2 of [23], the equation $0=\frac{d}{dx}\left[ \gamma (x, Y^+(x))\right] |_{x = x(\alpha )}$ combined with the first equation of (5.3) gives a linear relationship between $x(\alpha )$ and $y(\alpha )$. Injecting this condition in the polynomial equation $\gamma (x(\alpha ), y(\alpha ))=0$, we get two possible values for $x(\alpha )$ and $y(\alpha )$. The choice of sign then depends on $\alpha$.

5.2 Contour of the steepest descent

Before continuing, the reader should read Appendix A which states a parameter dependent Morse lemma. The usual Morse Lemma enables one to find steepest descent contours for a function at a critical point. The parameter dependent Morse lemma treats the case of a family of functions $(f_\alpha )_{\alpha }$ which have critical points $x(\alpha )$ (with smooth dependency in $\alpha$). This lemma tells us that the contours of steepest descents of $f_\alpha$ at $x(\alpha )$ are also smooth in $\alpha$. This property is necessary to obtain the asymptotic behaviour where $r\rightarrow +\infty$ and $\alpha \rightarrow \alpha _0$. Let $\alpha _0 \in ]0, \pi /2]$. We apply Lemma A.1 to F defined in (5.2). Let us fix any $\epsilon \in ]0, K[$ and consider any $\alpha$ such that $|\alpha -\alpha _0 |<\eta$, where constants K and $\eta$ are taken from the definition of $\Omega (0, \alpha _0)$ in Lemma A.1. Then, for any $\alpha$ we can construct the contour of the steepest descent

$$\begin{aligned} \Gamma _{x,\alpha } =\{x(it, \alpha ) \mid t \in [-\epsilon , \epsilon ] \}. \end{aligned}$$

Clearly,

$$\begin{aligned} F(x(it, \alpha ), \alpha )= -t^2. \end{aligned}$$

We denote by $x^+_\alpha = x(i\epsilon , \alpha )$ and $x^{-}_\alpha = x(-i\epsilon , \alpha )$. Then

$$\begin{aligned} F(x^+_\alpha , \alpha )=-\epsilon ^2, \ \ F(x^-_\alpha , \alpha )=-\epsilon ^2. \end{aligned}$$

(5.7)

Since $F''_x(x(\alpha ), \alpha ) \ne 0$, the contours in a neighborhood of $x(\alpha )$ where the function F is real are orthogonal, see Fig. 8. One of them is the real axis. The other is the contour of the steepest descent, which is the orthogonal to the real axis. It follows that $\textrm{Im}x_{\alpha _0}^+>0$ and $\textrm{Im} x_{\alpha _0}^-<0$. By continuity of $x(i \epsilon , \alpha )$ on $\alpha$ for any $\eta >0$ small enough, there exists $\nu >0$ such that

$$\begin{aligned} \textrm{Im}\,x_{\alpha }^+>\nu , \ \ \textrm{Im}\,x_{\alpha }^-<-\nu \ \ \forall \alpha : |\alpha -\alpha _0|<\eta . \end{aligned}$$

(5.8)

In the same way, for any $\alpha \in [0, \pi /2[$, we may define by the generalized Morse lemma the function $y(\omega , \alpha )$ w.r.t. $G(y, \alpha )$. Let $\alpha _0 \in [0, \pi /2[$. We can construct the contour of the steepest descent

$$\begin{aligned} \Gamma _{y,\alpha } =\{y(it, \alpha ) \mid t \in [-\epsilon , \epsilon ] \} \end{aligned}$$

with end points $y^+_\alpha = y(i\epsilon , \alpha )$ and $y^{-}_\alpha = y(-i\epsilon , \alpha )$ and the property analogous to (5.8).

We note that for any $\alpha =]0,\pi /2[$

$$\begin{aligned} \Gamma _{x, \alpha }= \underrightarrow{\overleftarrow{X^+ (\Gamma _{y, \alpha })}},\ \ \Gamma _{y, \alpha } = \underrightarrow{\overleftarrow{Y^+ (\Gamma _{x, \alpha })}}. \end{aligned}$$

(5.9)

The arrows mean that the direction has to be changed because of the facts that $(X^+(y))'\Bigm |_{y=y(\alpha )}<0$ and $(Y^+(x))'\Bigm |_{x=x(\alpha )}<0$. This notation comes from [17] (chapter 5.3, p 137).

Fig. 9

Steepest descent contour for $\Re (F)$ according to $\alpha$. As $\alpha$ gets closer to zero, the corresponding contours appear in lighter shades of green. When $\alpha \rightarrow 0$ this contour tends to the half line $[x_{max},\infty )$

5.2.1 Case where $\alpha _0=0$

In this case $\Gamma _{y, 0}$ is now well-defined, but not $\Gamma _{x, 0}$ (since $F_x''(x(0),0)=\infty$), see Fig. 9. Thus we define

$$\begin{aligned} \Gamma _{x,0}=\underrightarrow{\overleftarrow{X^{+}(\Gamma _{y,0})}} \end{aligned}$$

with end points $x^+_0 = X^+(y^{+}_{0})= x_{max}+ \epsilon ^2$ and $x^{-}_0=X^+(y^{-}_{0})=x_{max}+\epsilon ^2$. In fact, for $\alpha =0$, we have $G(y, 0)=-X^+(y)+x_{max}$ and $G(y(i\epsilon , 0), 0)=-\epsilon ^2$. Thus $\Gamma _{x,0}$ runs the real segment from $x_{max}+\epsilon ^2$ to $x_{max}$ and back to $x_{\max }+ \epsilon ^2$. Figure 9 illustrates why this phenomenon happens when $\alpha =0$. Again by continuity on $\alpha$ we may find $\eta >0$ and $\nu >0$ small enough, such that

$$\begin{aligned} Re x_\alpha ^+-x_{max}>\nu , \ \ Re x_\alpha ^- - x_{max}>\nu , \ \ \forall \alpha \in [0, \eta ]. \end{aligned}$$

(5.10)

If $\alpha _0=\pi /2$, $\Gamma _{x, \pi /2}$ is well-defined, but not $\Gamma _{y, \pi /2}$. We then let

$$\begin{aligned} \Gamma _{y,\pi /2}=\underrightarrow{\overleftarrow{ Y^{+}(\Gamma _{x,\pi /2}) }} \end{aligned}$$

with endpoints $y^+_\alpha = Y^+(x^{+}_{\alpha })$ and $y^-_\alpha =Y^+(x^{-}_{\alpha })$.

6 Shift of the integration contours and contribution of the poles

We will now define the integration contours of $I_1$, $I_2$ and $I_3$ using the contours of the steepest descent studied in the previous section. First, let

$$\begin{aligned} S^+_{x, \alpha }= & {} \{x^+_{\alpha } +it \mid t \ge 0 \ \},\ \ S^-_{x, \alpha }=\{x^-_{\alpha } - it \mid t \ge 0 \},\\ S^+_{y, \alpha }= & {} \{y^+_{\alpha } +it \mid t \ge 0 \}, \ \ S^-_{y, \alpha }=\{y^-_{\alpha } - it \mid t \ge 0 \}. \end{aligned}$$

Now, let us construct the integration contours $T_{x, \alpha }= S^-_{x, \alpha }+ \Gamma _{x, \alpha } + S^+_{x, \alpha }$ and $T_{y, \alpha }= S^-_{y, \alpha }+ \Gamma _{y, \alpha } + S^+_{y, \alpha }$ for any $\alpha \in [0, \pi /2]$. See Fig. 10 which illustrates these integration contours.

Fig. 10

In the complex plane ${\mathbb C}_x$, shift of the integration contour passing through the saddle point along the steepest line

6.1 Case where the saddle point meets the pole

The only exception in defining these contours will be for $\alpha \in [0, \pi /2]$ such that $x(\alpha )=x^* \in ]0, x_{max}[$ is a pole of $\varphi _2(x)$ and $y(\alpha )=y^{**} \in ]0, y_{max}[$ is a pole of $\varphi _1(y)$. We call these directions $\alpha ^*$ and $\alpha ^{**}$, so that $x(\alpha ^*)=x^*$, $y(\alpha ^*)=Y^{+}(x^*)=y^*$, $y(\alpha ^{**})=y^{**}$, $x(\alpha ^{**})= X^+(y^{**})=x^{**}$. When $x^*$ and $y^{**}$ are poles, we recall that by the Lemma 3.3:

$$\begin{aligned} x^* = 2\frac{\mu _2\frac{r_{12}}{r_{22}} - \mu _1}{\sigma _{11} - 2\sigma _{12}\frac{r_{12}}{r_{22}} + \sigma _{22}\left( \frac{r_{12}}{r_{22}}\right) ^2} \quad \text {and} \quad y^{**} = 2\frac{\mu _1\frac{r_{21}}{r_{11}} - \mu _2}{\sigma _{11}\left( \frac{r_{21}}{r_{11}}\right) ^2 - 2\sigma _{12}\frac{r_{21}}{r_{11}} + \sigma _{22}}. \end{aligned}$$

(6.1)

We also recall that

$$\begin{aligned} y^*:=Y^{+}(x^*) \quad \text {and}\quad x^{**}:= X^+(y^{**}). \end{aligned}$$

(6.2)

We remark that we have $y^* = -\frac{r_{12}}{r_{22}}x^*$ (resp. $x^{**} = -\frac{r_{21}}{r_{11}}y^{**}$) if and only if $x^*$ (resp $y^{**}$) is not a pole of $\varphi _2$ (resp. $\varphi _1$) because of the condition on $x^*$ and $y^{**}$ to be poles.

Remark 6.1

If $x^*$ is a pole, then $\alpha ^* \in ]0, \alpha _\mu [$, and if $y^{**}$ is a pole, then $\alpha ^{**} \in ]\alpha _\mu , \pi /2[$. We denote $\alpha ^*=-\infty$ if $x^*$ is not a pole and $\alpha ^{**}=+\infty$ if $y^{**}$ is not a pole.

If $\alpha =\alpha ^* \in ]0, \alpha _\mu [$, we modify in the definition of $T_{x,\alpha }$ the contour $\Gamma _{x, \alpha }$ by $\widetilde{\Gamma }_{x, \alpha }$, which is the half of the circle centered at $x(\alpha ^*)$ going from $x^{+}_{\alpha ^*}$ to $x^{-}_{\alpha ^*}$ in the counter-clockwise direction. The same modification is made for $\alpha =\alpha ^{**} \in ]\alpha _\mu , \pi /2[$.

The next lemma performs the shift of the integration contour and takes into account the contribution of the crossed poles. Recall that $I_1$, $I_2$ and $I_3$ are defined in Lemma 4.1.

Lemma 6.2

(Contribution of the poles to the asymptotics) Let $\alpha \in [0, \pi /2]$. Then for any $a,b>0$

$$\begin{aligned} I_1(a,b)= & {} \frac{ \big (\mathrm{-res}_{x=x^*} \varphi _2(x) \big ) \gamma _2(x^*, y^*)}{ \gamma '_y(x^*, y^*)} \exp (-ax^* -b y^* ) \times \textbf{1}_{ \alpha <\alpha ^*}\\{} & {} + \frac{1}{ 2 \pi i } \int \limits _{T_{x, \alpha }} \frac{\varphi _2(x) \gamma _2(x, Y^+(x))}{\gamma '_y(x, Y^+(x))} \exp (-ax -b Y^+(x))dx,\\ I_2(a, b)= & {} \frac{ \big (\mathrm{-res}_{y=y^{**}} \varphi _1(y) \big ) \gamma _1(x^{**}, y^{**})}{ \gamma '_x(x^{**},y^{**})} \exp (-ax^{**} -by^{**}) \times \textbf{1}_{ \alpha>\alpha ^{**}}\\{} & {} + \frac{1}{2\pi i } \int \limits _{T_{y, \alpha }} \frac{\varphi _1(y) \gamma _1(X^+(y), y)}{\gamma '_x(X^+(y), y)} \exp (-aX^+(y) -b y)dy,\\ I_3(a,b)= & {} \frac{1}{2\pi i } \int \limits _{T_{x, \alpha }} \exp ((a_0-a) x + (b_0-b) Y^{+}(x)) \frac{dx}{\gamma '_y(x, Y^{+}(x)) } \ \ \hbox { if }b>b_0\\ I_3(a,b)= & {} \frac{1}{2\pi i }\int \limits _{ T_{x, \alpha }} \exp ((a_0-a) X^{+}(y) + (b_0-b) y ) \frac{dy}{\gamma '_x(X^{+}(y), y) } \ \ \hbox { if }a>a_0. \end{aligned}$$

We remark that we have $\gamma _2(x^*, y^*)\textrm{res}_{x^*}\varphi _2<0$ and $\gamma _1(x^{**}, y^{**})\textrm{res}_{y^{**}}\varphi _1<0$.

Proof

We start from the result of Lemma 4.1, and we use Cauchy theorem to shift the integration contour. We take into account the poles by the residue theorem noting that $x^*<x(\alpha )$ if and only if $\alpha <\alpha ^*$ and that $y^{**}<y(\alpha )$ if and only if $\alpha ^{**}<\alpha$. In order to get the representation of $I_1$ by shifting the contour, we want to show that the integrals on the dotted lines of Fig. 10 tend to 0 when these lines go to infinity. To do so, it suffices to show that for any $\eta >0$ small enough,

$$\begin{aligned}{} & {} \sup _{ u \in [X^+(y_{max})-\eta , x_{max}+ \eta ]} \Big | \frac{ \varphi _2(u+iv) \gamma _2(u+iv, Y^+(u+iv))}{ \gamma _y'(u+iv, Y^+(u+iv))} \\ {}{} & {} \quad \exp (-a(u+iv) - b Y^+(u+iv)) \Big | \rightarrow 0, \ \ \hbox { as } v\rightarrow \infty . \end{aligned}$$

It suffices to study the supremum on $[- \epsilon , x_{max}+ \eta ]$. By Lemma 3.10 for any $\epsilon >0$,

$$\begin{aligned} \sup _{ u \in [X^+(y_{max})-\eta , x_{max}+ \eta ], |v| \ge \epsilon } |\varphi _2(u+iv)|<\infty . \end{aligned}$$

Let us observe that by (4.4)

$$\begin{aligned} \gamma '_y(x, Y^{+}(x))=\sqrt{b^2(x)-4 a(x) c(x)} = \sqrt{ (\sigma _{12}^2 -\sigma _{11} \sigma _{22})x^2 + 2 (\mu _2 \sigma _{12} - \mu _1 \sigma _{22}) x + \mu _2^2}. \end{aligned}$$

(6.3)

This function equals zero only at real points $x_{min}$ and $x_{max}$ and grows linearly in absolute value as $|{\Im } x| \rightarrow \infty$. By Lemma 3.1 (i) the function $|\gamma _2(x, Y^{+}(x))|$ grows linearly as $|{\Im } x | \rightarrow \infty$. Then for any $\epsilon >0$

$$\begin{aligned} \sup _{\begin{array}{c} u \in [X^+(y_{max})-\eta , x_{max}+ \eta ],\\ |v| \ge \epsilon \end{array}} \Big |\frac{ \gamma _2(u+iv, Y^+(u+iv))}{ \gamma _y'(u+iv, Y^+(u+iv))} \exp (-a (u+iv)) \Big | <\infty .\ \ \end{aligned}$$

Finally,

$$\begin{aligned}{} & {} \sup _{ u \in [X^+(y_{max})-\eta , x_{max}+ \eta ]} |\exp (-b Y^+(u+iv))| \\ {}{} & {} = \sup _{ u \in [X^+(y_{max})-\eta , x_{max}+ \eta ]} \exp (-b \textrm{Re } Y^+(u+iv)) \rightarrow 0, \end{aligned}$$

as $|v| \rightarrow \infty$ due to Lemma 3.1 (ii) and the fact that $b>0$. The other representations are obtained in the same way. In the representations of $I_3(a,b)$ we have used the facts that $a-a_0>0$ and $b-b_0>0$.

7 Exponentially negligible part of the asymptotic

Let us recall the integration contours $T_{x, \alpha }= S^-_{x, \alpha }+ \Gamma _{x, \alpha } + S^+_{x, \alpha }$ and $T_{y, \alpha }= S^-_{y, \alpha }+ \Gamma _{y, \alpha } + S^+_{y, \alpha }$ for any $\alpha \in [0, \pi /2].$ This section establishes a domination of the integrals on the contours $S_{x,\alpha }^\pm$ and $S_{y,\alpha }^\pm$. This domination will be useful in the following sections to show that these integrals are negligible. We will see that the asymptotics of integrals $I_1$, $I_2$ and $I_3$ of contour $T_{x, \alpha }$ and $T_{y, \alpha }$ are given by the integrals on the lines of steepest descent $\Gamma _{x, \alpha }$ and $\Gamma _{y, \alpha }$.

Lemma 7.1

(Negligibility of the integrals on $S_{x,\alpha }^\pm$ and $S_{y,\alpha }^\pm$) For any couple $(a,b) \in {\mathbb {R}}_+^2$ we may define $\alpha (a,b)$ as the angle in $[0,\pi /2]$ such that $\cos (\alpha ) = \frac{ a }{ \sqrt{a^2+b^2}}$ and $\sin (\alpha ) = \frac{ b }{\sqrt{a^2+ b^2}}$.

• Let $\alpha _0 \in ]0, \pi /2]$. Then for any $\eta$ small enough and any $r_0>0$ there exists a constant $D>0$ such that for any couple (a, b) where $\sqrt{a^2+b^2}>r_0$ and $|\alpha (a,b) -\alpha _0|<\eta$ we have

  $$\begin{aligned} \Big |\int \limits _{S^{+}_{x, \alpha }} \frac{\varphi _2(x) \gamma _2(x, Y^+(x))}{\gamma '_y(x, Y^+(x))} \exp \big (-ax -b Y^+(x)\big )dx \Big | \le \frac{D}{b} \exp \Big (-a x(\alpha ) -b y(\alpha ) - \epsilon ^2 \sqrt{a^2+b^2} \Big ). \end{aligned}$$

  (7.1)

  Furthermore, if $b>b_0$ we have

  $$\begin{aligned} \Big | \int \limits _{S^{+} _{x, \alpha }} \exp ((a_0-a) x + (b_0-b) Y^{+}(x)) \frac{dx}{\gamma '_y(x, Y^{+}(x)) } \Big | \le \frac{D}{b-b_0} \exp \Big (-a x(\alpha ) -b y(\alpha ) -\epsilon ^2\sqrt{a^2+(b-b_0)^2}\Big ). \end{aligned}$$

  (7.2)

• Let $\alpha _0 \in [0, \pi /2[$. Then for any $\eta$ small enough and any $r_0>0$ there exists a constant $D>0$ such that for any couple (a, b) such that $\sqrt{a^2+b^2}>r_0$, $|\alpha (a,b) -\alpha _0| \le \eta$ we have

  $$\begin{aligned} \Big |\int \limits _{S^{+}_{y, \alpha }} \frac{\varphi _1(y) \gamma _1(X^+(y), y)}{\gamma '_x(X^+(y), y)} \exp \big (-aX^+(y) -b y \big )dy \Big | \le \frac{D}{a} \exp \Big (-a x(\alpha ) -b y(\alpha ) - \epsilon ^2\sqrt{a^2+b^2}\Big ). \end{aligned}$$

  (7.3)

  Furthermore, if $a>a_0$ we have

  $$\begin{aligned} \Big | \int \limits _{S^{+} _{y, \alpha }} \exp ((a_0-a) X^+(y) + (b_0-b) y ) \frac{dy}{\gamma '_x(X^+(y), y) } \Big | \le \frac{D}{a-a_0}\exp \Big (-a x(\alpha ) -b y(\alpha ) -\epsilon ^2\sqrt{(a-a_0)^2+b^2}\Big ). \end{aligned}$$

  (7.4)

The same estimations hold for $S^{-}_{x, \alpha }$ and $S^{-}_{y, \alpha }$.

Proof

First, with definition (5.2) and the notation in (5.7), the estimate (7.1) can be written as

$$\begin{aligned} \Big |\int \limits _{v>0} \frac{\varphi _2(x_\alpha ^+ +iv) \gamma _2(x_\alpha ^+ + iv, Y^+(x_\alpha ^+ + iv))}{\gamma '_y(x_\alpha ^++iv, Y^+(x_\alpha ^+ + iv))} \exp \big (-\sqrt{a^2+b^2}\big (F(x_\alpha ^+ +iv,\alpha ) -F(x_\alpha ^+, \alpha )\big )dx\Big |\le \frac{D}{b} \end{aligned}$$

(7.5)

with $\alpha =\alpha (a,b)$.

Let be $\alpha _0 \in ]0, \pi /2]$. If $\alpha _0 \ne \pi /2$, let us fix $\eta >0$ sufficiently small such that $\alpha _0 - \eta >0$, and $\alpha _0+\eta \le \pi /2$. If $\alpha _0 =\pi /2$, let us fix any small $\eta >0$ and consider only $\alpha \in [\pi /2-\eta , \pi /2]$.

By Lemma 3.10 and equation (5.8)

$$\begin{aligned} \sup _{v\ge 0, |\alpha -\alpha _0| \le \eta } |\varphi _2(x_\alpha ^+ + iv)| < \infty . \end{aligned}$$

(7.6)

By the observation (4.4) $\gamma '_y(x, Y^+(x))=0$ only if $x=x_{min}, x_{max}$. Then by (5.8) we have

$$\begin{aligned} \inf _{v \ge 0, |\alpha -\alpha _0|\le \eta } |\gamma '_y(x_\alpha ^+ + iv, Y^+(x_\alpha ^+ + iv))|>0. \end{aligned}$$

(7.7)

Again by (6.3) and Lemma 3.1 (ii) we have

$$\begin{aligned} \sup _{ v\ge 0, |\alpha -\alpha _0|\le \eta } \Big | \frac{\gamma _2(x_\alpha ^+ + iv, Y^+(x_\alpha ^+ + iv))}{\gamma '_y(x_\alpha ^++iv, Y^+(x_\alpha ^+ + iv))} \Big | <\infty . \end{aligned}$$

(7.8)

Finally

$$\begin{aligned} |\exp \big (-\sqrt{a^2+b^2}(F(x_\alpha ^+ +iv,\alpha ) -F(x_\alpha ^+, \alpha )) \big )|=\exp \big (- b (\textrm{Re} Y^{+}(x_\alpha ^++iv)- \textrm{Re} Y^{+} (x_\alpha ^+) ) \big ). \end{aligned}$$

(7.9)

By Lemma 3.1 (ii), the function $\textrm{Re} Y^{+}(x_\alpha ^++iv)- \textrm{Re} Y^{+} (x_\alpha ^+)$ equals 0 at $v=0$ is strictly increasing as v goes from zero to infinity. Moreover, it grows linearly as $v\rightarrow \infty$: there exists a constant $c>0$ such that for any $\alpha$ such that $|\alpha -\alpha _0|\le \eta$ and any v large enough

$$\begin{aligned} \textrm{Re} Y^{+}(x_\alpha ^++iv)- \textrm{Re} Y^{+} (x_\alpha ^+) \ge c v. \end{aligned}$$

(7.10)

It follows from (7.6), (7.8), (7.9) and (7.10) that the left-hand side of (7.5) is bounded by

$$\begin{aligned} C \int _0^{\infty } \exp (- bcv ) dv = C \times (cb)^{-1} \end{aligned}$$

with some constant $C>0$ for all couples (a, b) with $|\alpha (a,b)-\alpha _0| \le \eta$.

As for the integral (7.2), we make the change of variables $B=b-b_0>0$. Next, we proceed exactly as we did in (7.1). The only different detail is the elementary estimation $\sup _{|\alpha -\alpha _0|\le \eta , v>0} |\exp (a_0 (x_\alpha ^++iv))| <\infty$. We then obtain the bound $\frac{D'}{B} \exp (-a x(\alpha ) - B y(\alpha ) -\epsilon \sqrt{a^2 + B^2} )$ with some $D'>0$. Then with $D=D' \exp (b_0 y(\alpha ))$ the estimation (7.2) follows.

The proofs for (7.3) and (7.4) are symmetric.

The previous lemma will be useful in Sect. 8 in establishing the asymptotics when $\alpha _0\in ]0,\pi /2[$. In the next lemma we will show the negligibility of the integrals in the two cases where $\alpha _0=0$ or $\pi /2$. This will be useful in Sect. 9.

Remark 7.2

(Pole and branching point) In the next lemma and in Sect. 9 and 10, we exclude the case $\gamma _2(x_{max}, Y^{\pm }(x_{max})) = 0$ [resp. $\gamma _1(X^{\pm }(y_{max}),y_{max}) = 0$] such that the branching point and the pole of $\varphi _2(x)$ coincides. This case corresponds to $x^*=x_{max}$ [resp. $y^*=y_{max}$], i.e. $\alpha ^{*}=0$ [resp. $\alpha ^{**}=\pi /2$]. Note that we already obtained the asymptotics of $h_1$ and $h_2$ in these specific cases in Proposition 3.8.

Lemma 7.3

(Negligibility of the integrals on $S_{x,\alpha }^\pm$ and $S_{y,\alpha }^\pm$, case where $\alpha _0=0$ or $\pi /2$)

For any $\eta >0$ small enough and any $r_0>0$ there exists a constant $D>0$ such that for any couple (a, b) where $\sqrt{a^2+b^2}>r_0$ and $0<\alpha (a,b)<\eta$ we have

$$\begin{aligned} \Big |\int \limits _{S^{+}_{x, \alpha }} \frac{\varphi _2(x) \gamma _2(x, Y^+(x))}{\gamma '_y(x, Y^+(x))} \exp \big (-ax -b Y^+(x)\big )dx \Big | \le D \exp \Big (-a x(\alpha ) -b y(\alpha ) - \epsilon ^2 \sqrt{a^2+b^2} \Big ). \end{aligned}$$

(7.11)

Furthermore, if $b>b_0$ we have

$$\begin{aligned} \Big | \int \limits _{S^{+} _{x, \alpha }} \exp ((a_0-a) x + (b_0-b) Y^{+}(x)) \frac{dx}{\gamma '_y(x, Y^{+}(x)) } \Big | \le D \exp \Big (-a x(\alpha ) -b y(\alpha ) -\epsilon ^2\sqrt{a^2+(b-b_0)^2}\Big ). \end{aligned}$$

(7.12)

The same estimations hold for $S^{-}_{x, \alpha }$. For any couple (a, b) such that $\sqrt{a^2+b^2}>r_0$ and $0< \pi /2-\alpha (a,b)<\eta$, a symmetric result holds for the integrals on $S^{+}_{y, \alpha }$ and $S^{-}_{y, \alpha }$.

Proof

Let $\alpha _0=0$ so that $x(\alpha _0)=x_{max}$. Our aim is to prove (7.11), which is then reduced to the estimate

$$\begin{aligned} \Big |\int _{v>0} \frac{ \varphi _2(x_\alpha ^++ iv) \gamma _2(x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) }{\gamma '_y (x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv))} \exp \big (-aiv - b (Y^+(x_\alpha ^+ +iv) -Y^+(x_\alpha ^+)) \big ) dv \Big | \le D. \end{aligned}$$

(7.13)

Let us fix any $\eta >0$ small enough and consider $\alpha \in ]0, \eta ]$. By (4.4) the denominator $\gamma '_y(x, Y^{+}(x))$ is zero at $x=x_{max}$ but not at other points in a neighborhood of $x_{max}$. Then by (5.10) we have

$$\begin{aligned} \inf _{0\le \alpha \le \eta }|\gamma '_y(x_\alpha ^+, Y^{+} (x_\alpha ^+))|>0. \end{aligned}$$

(7.14)

The function $\varphi _2(x)$ has a branching point at $x_{\max }$. But it follows from the representation (3.2) that it is bounded in a neighborhood of $x_{max}$ cut along the real segment due to Remark 7.2. Hence, this integral has no singularity at $v=0$ for any $\alpha \in ]0, \eta ]$ so that

$$\begin{aligned} \sup _{ 0 \le \alpha \le \eta } \frac{\varphi _2(x_\alpha ^+) \gamma _2(x_\alpha ^+, Y^+(x_\alpha ^+ )) }{\gamma '_y (x_\alpha ^+, Y^+(x_\alpha ^+))} <\infty . \end{aligned}$$

(7.15)

Let us consider the asymptotics of the integrand in (7.13) as $v \rightarrow \infty$. It is clear that $Y^+(x_\alpha ^+ + iv)$ grows linearly as $v \rightarrow \infty$ and so do functions $\gamma _2$ and $\gamma '_y$ of this argument. The function $\varphi _2(x_\alpha +iv)$ is defined by the formula of the analytic continuation

$$\begin{aligned} \varphi _2(x_\alpha + iv)= -\frac{ \gamma _1 (x_\alpha ^++iv, Y^-(x_\alpha ^+ + iv)) \varphi _1 (Y^- (x_\alpha ^++iv)) + \exp \big ( a_0(x_\alpha ^+ +iv) + b_0 Y^-(x_\alpha ^+ +iv) \big ) }{ \gamma _2 (x_\alpha ^+ +iv, Y^-(x_\alpha ^+ + iv)) }. \end{aligned}$$

(7.16)

We know that $Y^-(x_\alpha ^+ +iv)$ varies linearly as $v \rightarrow \infty$, and moreover $Re Y^- (x_\alpha +iv) \le -c_1-c_2 v$ for all $v \ge 0$ and $\alpha \in ]0, \eta ]$ with some $c_1,c_2>0$. Then by Lemma B.2 in Appendix C

$$\begin{aligned} |\varphi _2(x_\alpha ^+ +iv)| \le C v^{\lambda -1} \end{aligned}$$

(7.17)

for any $\alpha \in ]0, \eta ]$ and $v>V_0$ with some $C>0$, $V_0>0$ and $\lambda <1$. Hence, the integrand

$$\begin{aligned} \frac{\varphi _2(x_\alpha ^+ + iv) \gamma _2(x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) }{\gamma '_y (x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv))} \end{aligned}$$

is $O(v^{\lambda -1})$ as $v \rightarrow \infty$. The positivity of $\textrm{Re} Y^+(x_\alpha ^+ +iv) -\textrm{Re} Y^+(x_\alpha ^+)$ for any $v\ge 0$ and the inequality (7.10) in the exponent stay valid for any $\alpha \in ]0, \eta ]$, so that the exponential term is bounded in absolute value by $\exp (-c b v )$ with some $c>0$. But for $\eta$ small enough, the assumption $\alpha (a,b) \in ]0, \eta ]$ implies the arbitrary smallness of b. In the limiting case $b=0$ the integral in the l.h.s of (7.13) is not absolutely convergent. In order to prove the required estimate (7.13), we proceed by integration by parts. This integral equals

$$\begin{aligned}{} & {} \frac{\varphi _2(x_\alpha ^+ + iv) \gamma _2(x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) }{\gamma '_y (x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) (-ai-b (Y^+(x_\alpha ^++iv))'_v) }\exp \Big ( -aiv - b (Y^+(x_\alpha ^+ +iv) -Y^+ (x_\alpha )) \Big ) \Bigm |_{v=0}^{v=\infty } \end{aligned}$$

(7.18)

$$\begin{aligned}{} & {} - \int _0^\infty \Big ( \frac{\varphi _2(x_\alpha ^+ + iv) \gamma _2(x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) }{\gamma '_y (x_\alpha ^+ +iv, Y^+(x_\alpha ^++iv)) (-ai-b (Y^+(x_\alpha ^++iv))'_v)} \Big )'_v \exp \big ( -aiv - b (Y^+(x_\alpha ^+ +iv) - Y^+ (x_\alpha ^+)) \big ) dv.\nonumber \\ \end{aligned}$$

(7.19)

Note that although in this case $x^+_{\alpha _0}= x_{max}$ which is a branching point for $Y^+(x)$, the first and second derivatives are bounded

$$\begin{aligned} \sup _{\alpha \in [0, \eta ]} \Big |Y(x_\alpha ^+ +iv)'\Bigm |_{v=0} {\Big |}<\infty , \ \ \sup _{\alpha \in [0, \eta ]} \Big |Y(x_\alpha ^+ +iv)''\Bigm |_{v=0} {\Big |} <\infty \end{aligned}$$

(7.20)

by remark (5.10). Furthermore, $Y^\pm (x_\alpha ^+ +iv)'$ is of the constant order and $Y^\pm (x_\alpha ^+ +iv)''$ is not greater than O(1/v) as $v \rightarrow \infty$.

The term (7.18) at $v=0$ is bounded in absolute value by some constant due to (7.15) and (7.20). It converges to zero as $v \rightarrow \infty$ by the statements above for any $\alpha \in [0, \infty ]$, $a,b\ge 0$. To evaluate (7.19), we compute the derivative in its integrand and show that it is of order $O(v^{\lambda -2})$ as $v \rightarrow \infty$. We skip the technical details of this computation but outline the fact that $\varphi _2(x_\alpha ^++iv)'_v$ is computed via the representation (7.16) and $|\varphi _1( Y^-(x_\alpha ^++iv))'_v|$ is evaluated again by Lemma B.2. Namely, it is of order not greater than $O(v^{\lambda -2})$ as $v \rightarrow \infty$. Thus, the integral (7.19) is absolutely convergent for any $a, b\ge 0$ and can be bounded by some constant as well. This finishes the proof of (7.11). The proof of (7.12) is symmetric.

Note that the proof of Lemma 7.1 essentially uses the result of Lemma 3.10 which bounds the Laplace transforms. The proof of Lemma 7.3 uses a stronger result stated in Appendix C which gives a more precise estimate of the Laplace transform near infinity.

Following the lines of the proof we could establish a better estimate, namely the one that the integral is bounded by some universal constant divided by a, but we do not need it for our purposes.

Remark 7.4

(Negligibility) When $\alpha (a,b) \rightarrow \alpha _0 \in ]0, \pi /2[$, Equations (7.1), (7.2), (7.3), (7.4) of Lemma 7.1 give quite satisfactory estimates which prove the negligibility of the integrals on the contours $S_{x,\alpha }^\pm$ and $S_{y,\alpha }^\pm$ with respect to integrals on contours $\Gamma _{x,\alpha }$ and $\Gamma _{y,\alpha }$, see Lemma 8.1 below. In fact

$$\begin{aligned}{} & {} \frac{ \exp (-a x(\alpha ) -b y (\alpha ) -\epsilon ^2 \sqrt{a^2+b^2} ) }{b} = o\Big (\frac{\exp (-a x(\alpha )-b y(\alpha )) }{\root 4 \of {a^2+b^2}} \Big ),\\{} & {} \frac{ \exp (-a x(\alpha ) -b y (\alpha ) -\epsilon ^2 \sqrt{a^2+b^2} ) }{a} = o\Big (\frac{\exp (-a x(\alpha )-b y(\alpha )) }{\root 4 \of {a^2+b^2}} \Big ). \end{aligned}$$

When $\alpha (a,b) \rightarrow 0$ or $\pi /2$, Equations (7.11) and (7.12) of Lemma 7.3 give satisfactory estimates which prove the negligibility which will be useful in Sect. 9 when computing the asymptotics along the axes.

8 Essential part of the asymptotic and main theorem

This section is dedicated to the asymptotics of $g(a,b)=I_1+I_2+I_3$ when $\alpha (a,b) \rightarrow \alpha _0 \in ]0, \pi /2[$. The next lemma determines the asymptotics of the integrals on the lines of steepest descent $\Gamma _{x,\alpha }$ and $\Gamma _{y,\alpha }$ of the shifted contours.

For any couple $(a,b) \in {\mathbb {R}}_+^2$ we define $\alpha (a,b)$ as the angle in $[0,\pi /2]$ such that $\cos (\alpha ) = \frac{ a }{ \sqrt{a^2+b^2}}$ and $\sin (\alpha ) = \frac{ b }{\sqrt{a^2+ b^2}}$ and we define $r\in \mathbb {R}_+$ such that $r=\sqrt{a^2+b^2}$.

Lemma 8.1

(Contribution of the saddle point to the asymptotics) Let $\alpha _0 \in ]0, \pi /2[$. Let $\alpha (a,b) \rightarrow \alpha _0$ and $r=\sqrt{a^2+b^2} \rightarrow \infty$. Then for any $n \ge 0$ we have

$$\begin{aligned}{} & {} \frac{1}{ 2 \pi i } \int \limits _{\Gamma _{x, \alpha }} \frac{\varphi _2(x) \gamma _2(x, Y^+(x))}{\gamma '_y(x, Y^+(x))} \exp (-ax -b Y^+(x))dx + \frac{1}{2\pi i } \int \limits _{\Gamma _{y, \alpha }} \frac{\varphi _1(y) \gamma _1(X^+(y), y)}{\gamma '_x(X^+(y), y)} \exp (-aX^+(y) -b y)dy\nonumber \\{} & {} \qquad + \frac{1}{2\pi i } \int \limits _{\Gamma _{x, \alpha }} \exp ((a_0-a) X^+(y) + (b_0-b) y) \frac{dy}{\gamma '_x(X^+(y), y) } \nonumber \\{} & {} \qquad \sim \exp (-ax(\alpha (a,b)) -b y (\alpha (a,b))) \sum _{k=0}^n \frac{c_k(\alpha (a,b))}{ \root 4 \of {a^2+b^2}(a^2+b^2)^{k/2}} \end{aligned}$$

(8.1)

with some constants $c_0(\alpha ), c_1(\alpha ), \ldots , c_n(\alpha )$ continuous at $\alpha _0$. Namely

$$\begin{aligned} c_0(\alpha ) = \frac{ \gamma _1(x(\alpha ), y(\alpha )) \varphi _1(y(\alpha ))+ \gamma _2(x(\alpha ), y(\alpha )) \varphi _2(x(\alpha ))+ \exp (a_0 x(\alpha )+ b_0 y(\alpha ))}{ \sqrt{2\pi ( \sigma _{11}\sin ^2(\alpha ) + 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha ))} } \times C(\alpha ), \end{aligned}$$

(8.2)

where

$$\begin{aligned} C(\alpha )= \sqrt{ \frac{ \sin (\alpha )}{ \gamma '_y(x(\alpha ), y(\alpha )) }} = \sqrt{ \frac{ \cos (\alpha ) }{ \gamma '_x( x(\alpha ), y(\alpha ) } }. \end{aligned}$$

Proof

Consider the first integral. We make the change of variables $x=x(it, \alpha )$, see Sect. 5 and Appendix A. Then the sum of integrals becomes

$$\begin{aligned} \frac{\exp (-ax(\alpha ) - by(\alpha ))}{2\pi }\int _{-\epsilon }^\epsilon f(it, \alpha ) \exp (-\sqrt{a^2+b^2} t^2)dt \end{aligned}$$

where

$$\begin{aligned} f(it, \alpha )= \frac{ \varphi _2(x(it, \alpha )) \gamma _2(x(it, \alpha ), Y^+(x(it, \alpha )) ) }{ \gamma '_y(x(it, \alpha ), Y^+(x(it, \alpha ))) } x'_\omega (it, \alpha ). \end{aligned}$$

We take $\Omega (\alpha _0)$ from Lemma A.1 where K and $\eta$ are defined in this lemma. For any $\alpha \in [\alpha _0-\eta ,\alpha _0+ \eta ]$ and $t \in [-\epsilon , \epsilon ]$ we have

$$\begin{aligned} \Big | f(it, \alpha ) - \sum _{l=0}^{2n} f^{(l)} (0, \alpha )\frac{(it)^l}{l!}\Big | \le C |t|^{2n+1} \end{aligned}$$

with the constant

$$\begin{aligned} C= \sup _{\begin{array}{c} |\omega |=K, \\ |\alpha -\alpha _0|\le \eta \end{array}} \Big | \frac{ f(\omega , \alpha ) - \sum _{l=0}^{2n} f^{(l)} (0, \alpha )\frac{\omega ^l}{l!} }{\omega ^{2n+1} } \Big | \end{aligned}$$

by the maximum modulus principle and the fact that $f(\omega , \alpha )$ is in class $C^{\infty }$ in $\Omega (\alpha _0)$. The integral

$$\begin{aligned} \int _{-\epsilon }^{\epsilon } t^{l} \exp (-\sqrt{a^2+b^2} t^2)dt \end{aligned}$$

equals 0 if l is odd. By the change of variables $s=\root 4 \of {a^2+b^2}t$ it equals

$$\begin{aligned} \frac{(l-1)(l-3)...(1)}{2^{l/2}} \frac{\sqrt{\pi } }{ (\root 4 \of {a^2+b^2})^{l+1} } + O\Big ( \frac{ \exp (-\sqrt{a^2+b^2} \epsilon ) }{ (\root 4 \of {a^2+b^2})^{l+1}}\Big ), \ \ \sqrt{a^2+b^2} \rightarrow \infty \end{aligned}$$

if l is even. The constant comes from the fact that $\int _{-\infty }^{+\infty }t^le^{-s^2}ds = \frac{(l-1)(l-3)...(1)}{2^{l/2}}\sqrt{\pi }$. By the same reason

$$\begin{aligned} \int _{-\epsilon }^{\epsilon } |t|^{2n+1} \exp (-\sqrt{a^2+b^2} t^2)dt = O \Big ( \frac{ 1 }{ (\root 4 \of {a^2+ b^2})^{2n+2} } \Big ), \ \ \sqrt{a^2+b^2} \rightarrow \infty . \end{aligned}$$

The representation (8.1) for the first integral follows with the constants

$$\begin{aligned} c_l^1(\alpha ) = \frac{(l-1)(l-3)...(1)}{2^{l/2}} \frac{\sqrt{\pi }}{2\pi } \frac{(-1)^l f^{(2l)}(0, \alpha )}{ (2l)!}. \end{aligned}$$

In particular

$$\begin{aligned} c^1_0(\alpha ) = \frac{1}{2 \sqrt{\pi } } \times \frac{ \gamma _2(x(\alpha ), y(\alpha )) \varphi _2(x(\alpha ))}{ \gamma '_y(x(\alpha ), y(\alpha ))} \times x'_\omega (0, \alpha ). \end{aligned}$$

Using the expressions (A.1) and (5.4), we get

$$\begin{aligned} c^1_0(\alpha )= \frac{\gamma _2(x(\alpha ), y(\alpha )) \varphi _2(x(\alpha ))}{ \sqrt{2\pi ( \sigma _{11}\sin ^2(\alpha ) + 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha )) }} \times \sqrt{ \frac{ \sin (\alpha )}{ \gamma '_y(x(\alpha ), y(\alpha )) }}. \end{aligned}$$

In the same way, using the variable y instead of x, we get the asymptotic expansions of the second and the third integral with constants $c^2_0(\alpha ), \ldots , c_{n}^2(\alpha ), c^3_0(\alpha ), \ldots , c^3_n(\alpha )$. Namely,

$$\begin{aligned} c^2_0(\alpha ) + c^3_0(\alpha )= & {} \frac{\gamma _1(x(\alpha ), y(\alpha )) \varphi _1(y(\alpha )) + \exp (a_0 x(\alpha ) + b_0 y(\alpha )) }{ \sqrt{2\pi ( \sigma _{11}\sin ^2(\alpha ) + 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha ))} } \\ {}{} & {} \quad \times \sqrt{ \frac{ \cos (\alpha )}{ \gamma '_x(x(\alpha ), y(\alpha )) }}. \end{aligned}$$

By (5.3) $\sin (\alpha ) \gamma '_x(x(\alpha ), y(\alpha )) = \cos (\alpha ) \gamma '_y (x(\alpha ), y(\alpha ))$. This implies the representation (8.1) and concludes the proof with $c_k(\alpha )=\sum _{i=1}^3 c_k^i(\alpha )$.

We will justify later that the constants $c_0(\alpha )$ are not zero. We now turn to the main result of the paper.

Theorem 4

(Asymptotics in the quadrant, general case) We consider a reflected Brownian motion in the quadrant of parameters $(\Sigma , \mu , R)$ satisfying conditions of Proposition 2.1 and Assumption 1. Then, the Green’s density function $g(r\cos (\alpha ), r\sin (\alpha ))$ of this process has the following asymptotics for all $n \in \mathbb {N}$ when $\alpha \rightarrow \alpha _0\in (0,\pi /2)$ and $r\rightarrow \infty$:

• If $\alpha ^*<\alpha _0<\alpha ^{**}$ then

  $$\begin{aligned} g(r\cos (\alpha ), r\sin (\alpha )) \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow \alpha _0 \end{array}}{\sim } e^{-r(\cos (\alpha )x(\alpha ) + \sin (\alpha )y(\alpha ))} \frac{1}{\sqrt{r}} \sum _{k=0}^n \frac{c_k(\alpha )}{ r^{k}}. \end{aligned}$$

  (8.3)

• If $\alpha _0<\alpha ^{*}$ then

  $$\begin{aligned} g(r\cos (\alpha ), r\sin (\alpha )) \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow \alpha _0 \end{array}}{\sim } c^{*}e^{-r(\cos (\alpha )x^* + \sin (\alpha )y^*)} + e^{-r(\cos (\alpha )x(\alpha ) + \sin (\alpha )y(\alpha ))}\frac{1}{\sqrt{r}} \sum _{k=0}^n \frac{c_k(\alpha )}{ r^{k}}. \end{aligned}$$

  (8.4)

• If $\alpha ^{**}<\alpha _0$ then

  $$\begin{aligned} g(r\cos (\alpha ), r\sin (\alpha )) \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow \alpha _0 \end{array}}{\sim } c^{**} e^{-r(\cos (\alpha )x^{**} + \sin (\alpha )y^{**})} + e^{-r(\cos (\alpha )x(\alpha ) + \sin (\alpha )y(\alpha ))} \frac{1}{\sqrt{r}} \sum _{k=0}^n \frac{c_k(\alpha )}{r^{k}} \end{aligned}$$

  (8.5)

where explicit expressions of the saddle point coordinates $x(\alpha )$ and $y(\alpha )$ are given by (5.5) and (5.6), the coordinates of the poles $x^*$, $y^*$, $y^{**}$, $x^{**}$ are given by (6.1) and (6.2), and the constants are given by

$$\begin{aligned} c^* = \frac{(-res_{x = x^*}\varphi _2(x))\gamma _2(x^*,y^*)}{\gamma '_y(x^*, y^*)}>0 \quad \text {and}\quad c^{**} = \frac{(-res_{y = y^{**}}\varphi _1(y))\gamma _1(x^{**},y^{**})}{\gamma '_y(x^{**}, y^{**})} >0 \end{aligned}$$

where the $c_k$ are constants depending on $\alpha$ and such that $c_k(\alpha )\underset{\alpha \rightarrow \alpha _0}{\longrightarrow } c_k(\alpha _0)$ where $c_0(\alpha )$ is given by (8.2). We have $c_0(\alpha ) > 0$ at least when $\alpha ^*<\alpha _0<\alpha ^{**}$ where it gives the dominant term of the asymptotics in (8.3).

Proof

The theorem follows directly from combining several lemmas. By Lemma 4.1 the inverse Laplace transform g(a, b) can be expressed as of the sum of three simple integrals $I_1 + I_2 + I_3$. Those integrals have been rewritten in Lemma 6.2 by the residue theorem as the sum of residues and integrals whose contour locally follows the steepest descent line through the saddle point. This has been done in Sect. 6 using Morse’s Lemma, see Appendix A. Residues are present if $0< x^* < x(\alpha )$ or $0< y^{**} < y(\alpha )$. In addition, we proved in Lemma 7.1 the negligibility of the integrals of the lines $S^{\pm }_{x,\alpha }$ and $S^{\pm }_{y,\alpha }$ compared to the integrals on the steepest descent lines. The main asymptotics are then given by the poles plus the asymptotics of the steepest descent integrals. A disjunction of cases concerning the pole’s contributions gives the three cases of the theorem (recall that $\alpha ^* < \alpha ^{**}$). In the second case, when $\alpha _0 < \alpha ^*$, $\varphi _2$ has a pole and then $c^* \ne 0$ because we have $\frac{r_{12}}{r_{22}} > \frac{-Y^{\pm }(x_{max})}{x_{max}}$ which implies $\gamma _2(x^*, y^*) \ne 0$. The same holds for $c^{**}$. Finally, Lemma 8.1 gives the desired asymptotic expansion of the integrals on the lines of the steepest descent. The fact that $c_0(\alpha _0) \ne 0$ when $\alpha ^*<\alpha _0<\alpha ^{**}$ is postponed to Lemma 8.2 and Lemma 8.3.

The constants $c_0(\alpha )$ shall not be zero at least when $\alpha ^*<\alpha _0<\alpha ^{**}$, that is when the poles are not involved in the asymptotics. We divide the proof into two lemmas.

Most of the quantities studied so far depend on the starting point of the process, even if this dependence is not explicit in the notation. In the following, we add a power $z_0$ (or $(a_0, b_0)$) in the notation of the objects which correspond to a process whose starting point is $z_0=(a_0, b_0)$. For example, we will note $h_1^{z_0}$ or $\varphi _1^{z_0}$ when we want to emphasise the dependency on the starting point.

Lemma 8.2

(Non nullity of the constant $c_0(\alpha )$ for at least a starting point) If $\alpha \in \left( 0, \frac{\pi }{2}\right) {\setminus }{\{\alpha ^*,\alpha ^{**}\}}$, there exists some starting point $z_0 \in {\mathbb R}_+^2$ such that $c_0^{z_0}(\alpha ) \ne 0$.

Proof

Let $z_0=(a_0, b_0)$ the starting point of the process. We proceed by contradiction assuming that $c_0^{(a_0, b_0)}(\alpha ) = 0$ for all $a_0, b_0 \ge 0.$ Since $x(\alpha ) \le 0$ or $y(\alpha ) \le 0$, we suppose without loss of generality that $y(\alpha ) \le 0.$ We have then, by (8.2) and the continuation formula:

$$\begin{aligned} c_1\varphi _1^{(a_0,b_0)}(y(\alpha )) - c_2\varphi _1^{(a_0,b_0)}(Y^-(x(\alpha )))= & {} \gamma _2(x(\alpha ), y(\alpha ))e^{a_0x(\alpha )+b_0Y^-(x(\alpha ))}\nonumber \\ {}{} & {} - \gamma _2(x(\alpha ), Y^-(x(\alpha )))e^{a_0x(\alpha )+b_0y(\alpha )}\nonumber \\ \end{aligned}$$

(8.6)

with $c_1 = \gamma _1(x(\alpha ), Y^-(x(\alpha )))\gamma _2(x(\alpha ), y(\alpha ))$ and $c_2 = \gamma _1(x(\alpha ), Y^-(x(\alpha )))\gamma _2(x(\alpha ), Y^-(x(\alpha )))$. We remark that $\gamma _2(x(\alpha ), Y^-(x(\alpha ))) \ne 0$ since we have assumed $\alpha \ne \alpha ^*$. The right term of (8.6) is unbounded on the set of all $(a_0, b_0)$ belonging to ${\mathbb R}_+^2$ since $Y^-(x(\alpha )) < y(\alpha ) = Y^+(x(\alpha ))$. Then, it is sufficient to show that the supremum of the left term is bounded according to $(a_0, b_0)$. We denote by $h_1^{(a_0,b_0)}$ the density of $H_1$ according to the Lebesgue measure corresponding to the starting point $(a_0, b_0)$. We have then

$$\begin{aligned}{} & {} c_1\varphi _1^{(a_0,b_0)}(y(\alpha )) - c_2\varphi _1^{(a_0,b_0)}(Y^-(x(\alpha ))) \nonumber \\ {}{} & {} \quad = \int _0^\infty \left( c_1e^{y(\alpha )z} - c_2e^{Y^-(x(\alpha ))z}\right) h_1^{(a_0,b_0)}(z)dz =: I. \end{aligned}$$

(8.7)

Similarly to the proof of Lemma 3.5, we introduce T as the first hitting time of the axis $\{x = 0\}$. By the strong Markov property, we obtain in the same way:

$$\begin{aligned} I&= {\mathbb E}_{(a_0, b_0)}\left[ \mathbbm {1}_{T < +\infty }{\mathbb E}_{(0, Z^2_T)}\left[ \int _0^{+\infty }\mathbbm {1}_{\{0\}\times {\mathbb R}_+}(Z_t)\left( c_1e^{y(\alpha )Z^2_t} - c_2e^{Y^-(x(\alpha ))Z^2_t}\right) dL^1_t\right] \right] \end{aligned}$$

(8.8)

$$\begin{aligned}&=\int _0^{+\infty }\int _0^{+\infty }\left( c_1e^{y(\alpha )z} - c_2e^{Y^-(x(\alpha ))z}\right) h_1^{(0,y)}(z)dz{\mathbb P}(T < +\infty , Z^2_T = dy)\end{aligned}$$

(8.9)

$$\begin{aligned}&= \int _0^{+\infty } \left( c_1\varphi _1^{(0,y)}(y_\alpha ) - c_2\varphi _1^{(0,y)}(Y^-(x_\alpha ))\right) {\mathbb P}(T < +\infty , Z^2_T = dy). \end{aligned}$$

(8.10)

Using the identity (8.6) in (8.10) (where we see the relevance of going to the y-axis), we get the bound

$$\begin{aligned} |I| \le |\gamma _2(x(\alpha ), y(\alpha ))| + |\gamma _2(x(\alpha ), Y^-(x(\alpha )))| \end{aligned}$$

(8.11)

since $y(\alpha ) \le 0.$ The right term of (8.6) is therefore bounded in $(a_0, b_0)$, and thus a contradiction has been reached. This completes the proof.

Lemma 8.3

(Non nullity of the constant $c_0(\alpha )$ for all starting points) For all $\alpha \in \left( 0, \frac{\pi }{2}\right)$ such that $\alpha ^*< \alpha < \alpha ^{**}$ and $z_0 \in {\mathbb R}_+^2$, we have $c_0^{z_0}(\alpha ) \ne 0$.

Proof

Denote $z_0 = (a_0, b_0)$ the point obtained in Lemma 8.2 such that $c_0^{z_0}(\alpha ) \ne 0$. By continuity of the Laplace transforms $\varphi _1^{z_0}$ and $\varphi _2^{z_0}$ in $z_0$ (see the proof of Lemma 3.6) $c^{z'_0}(\alpha ) \ne 0$ for all $z'_0$ in an open neighborhood V of $z_0.$ Let $z''_0 \in {\mathbb R}_+^2$ be the starting point of the process $Z^{(z''_0)}$ and let $T = \inf \{t \ge 0, Z^{(z''_0)}_t \in V\}$ be the hitting time of V. We have ${\mathbb P}_{z''_0}(T < +\infty ) = p > 0$. By the strong Markov property,

$$\begin{aligned} g^{z''_0}(r\cos (\alpha ),r\sin (\alpha ))&\ge p\inf _{z'_{0}\in V}g^{z'_0} (r\cos (\alpha ),r\sin (\alpha ))\end{aligned}$$

(8.12)

$$\begin{aligned}&\ge p\inf _{z'_{0}\in V}\left[ c_0^{z'_0}(\alpha ) (1 + o_{r\rightarrow \infty }(1))\right] e^{-r(\cos (\alpha )x(\alpha ) + \sin (\alpha )y(\alpha ))} \frac{1}{\sqrt{r}}. \end{aligned}$$

(8.13)

Furthermore, V can be chosen bounded and such that $\inf _{z'_{0}\in V}c_0^{z'_0}(\alpha ) > 0$. The issue is that the term $o_{r\rightarrow \infty }(1)$ may depend on $z'_0$. We then refer to the proof of Lemma 7.1. We remark that the only quantity depending on the initial condition is the constant D of Lemma 7.1, which is based on Lemma 3.10. If the supremum on $z'_0 \in V$ of the quantity of Lemma 3.10 is finite, then the result holds. This fact is verified easily from the proof of this lemma, because V is bounded and $\varphi _1^{z'_0}(0)$ is continuous in $z'_0.$

9 Asymptotics along the axes: $\alpha \rightarrow 0$ or $\alpha \rightarrow \frac{\pi }{2}$

In this section, we study the asymptotics of the Green’s function g along the axes. We recall the assumptions $\alpha ^*\ne 0$ and $\alpha ^{**}\ne \pi /2$ made in Remark 7.2.

Let us recall that for any couple $(a,b) \in {\mathbb {R}}_+^2$ we define $r=\sqrt{a^2+b^2}$ and $\alpha (a,b)$ as the angle in $[0,\pi /2]$ such that $\cos (\alpha ) = \frac{ a }{ \sqrt{a^2+b^2}}$ and $\sin (\alpha ) = \frac{ b }{\sqrt{a^2+ b^2}}$.

Lemma 9.1

(Contribution of the saddle point to the asymptotics when $\alpha \rightarrow 0$ or $\pi /2$)

• (i) Let $a \rightarrow \infty$, $b>0$ and $\alpha (a, b) \rightarrow 0$. Then the asymptotics of (8.1) remain valid with $c_0(\alpha )\rightarrow 0$ as $\alpha \rightarrow 0$. Moreover, we have $c_0(\alpha ) \sim c'\alpha$ and $c_1(\alpha ) \sim c''$ as $\alpha \rightarrow 0$ where $c'$ and $c''$ are non-null constants at least when $\alpha ^* = -\infty$ (i.e. when there is no pole for $\varphi _2$).

• (ii) When $b \rightarrow \infty$, $a>0$ and $\alpha (a, b) \rightarrow \pi /2$ the same result holds.

Remark 9.2

(Competition between the two first term of the asymptotics) The previous lemma states that when $\alpha \rightarrow 0$ and $r\rightarrow \infty$, there is a competition between the first two terms of the sum of the asymptotic development given in (8.1). Namely, the first term $\frac{c_0(\alpha )}{\sqrt{r}} \sim \frac{c' \alpha }{\sqrt{r}}\sim \frac{c' b}{r\sqrt{r}}$ and the second term $\frac{c_1(\alpha )}{r\sqrt{r}}\sim \frac{c''}{r\sqrt{r}}$ may have the same order of magnitude. If $b \rightarrow 0$, the second term is dominant. If $b\rightarrow c$ where c is a positive constant, they both contribute to the asymptotics. If $b \rightarrow \infty$ (and also $b=o(a)$ since $\alpha \rightarrow 0$), the first term is dominant.

Proof

We first prove (i). For any $\alpha$ close to 0, $\Gamma _{x, \alpha }$ lies in a neighborhood of $x(\alpha )$. Using the continuation formula of $\varphi _2(x)$ (3.2), the definition of F (5.2), and the fact that $\Gamma _{x, \alpha }= \underrightarrow{\overleftarrow{X^+ (\Gamma _{y, \alpha })}}$ (5.9), the first integral of (8.1) becomes

$$\begin{aligned}{} & {} \frac{e^{-a x(\alpha ) -b y (\alpha ) } }{2i\pi } \int _{ \underrightarrow{\overleftarrow{ X^+(\Gamma _{y, \alpha } ) } } } \frac{ \gamma _2(x, Y^+(x)) \Big (-\gamma _1(x, Y^{-}(x)) \varphi _1 (Y^-(x))-e^{a_0 x +b_0 Y^{-}(x)} \Big )}{\gamma _2(x, Y^{-}(x) ) \gamma '_y(x, Y^+(x)) }\\{} & {} \qquad \quad \quad \quad \times \exp \big (\sqrt{a^2 + b^2} F(x, \alpha )\big ) dx. \end{aligned}$$

Let us make the change of variables $x=X^+(y)$. Taking into account the fact that $Y^+(X^+(y))=y$, the relation $\gamma '_x(X^+(y), y)(X^+(y))'+ \gamma '_y(X^+(y), y)\equiv 0$ and the direction of $\underrightarrow{\overleftarrow{ X^+(\Gamma _{y, \alpha } ) } }$, the first integral becomes

$$\begin{aligned}{} & {} \frac{e^{-a x(\alpha ) -b y (\alpha ) } }{2i\pi } \int _{ \Gamma _{y, \alpha } }\frac{ \gamma _2(X^+(y), y) \Big (-\gamma _1(X^+(y), Y^{-}(X^{+}(y))) \varphi _1 (Y^-( X^+(y)))-e^{a_0 X^+(y) +b_0 Y^{-}(X^+(y))} \Big )}{\gamma _2(X^+(y), Y^{-}(X^+(y) ) ) \gamma '_x(X^+(y), y) }\nonumber \\{} & {} \qquad \quad \quad \quad \times \exp \big (\sqrt{a^2 + b^2} G(y, \alpha )\big ) dy. \end{aligned}$$

(9.1)

For the second and the third integral, we use the representation valid for $a>a_0$. We then have to find the asymptotics of the integral

$$\begin{aligned}{} & {} \frac{e^{-a x(\alpha ) -b y (\alpha ) } }{2i\pi }\int _{ \Gamma _{y, \alpha } } \nonumber \\ {}{} & {} \frac{ \gamma _2(X^+(y), Y^{-}(X^{+}(y))) H(X^+(y),y) - \gamma _2(X^+(y), y) H(X^+(y), Y^{-}(X^{+}(y))) }{\gamma _2(X^+(y), Y^{-}(X^+(y) ) ) \gamma '_x(X^+(y), y) }\\{} & {} \quad \times \exp \big (\sqrt{a^2 + b^2} G(y, \alpha )\big ) dy \end{aligned}$$

where

$$\begin{aligned} H(X^+(y),y) = \gamma _1(X^+(y),y) \varphi _1(y)+\exp (a_0 X^+(y) + b_0 y). \end{aligned}$$

Finally, note that with notation in (4.3)

$$\begin{aligned} Y^{-}(X^+(y)) = \frac{ c(X^{+}(y)) }{ a (X^{+}(y) ) \times Y^+(X^+(y))} = \frac{\sigma _{11} (X^+(y))^2 + 2 \mu _1 X^+(y)}{ \sigma _{22} y }. \end{aligned}$$

The function $X^+(y)$ is holomorphic in a neighborhood of $Y^{\pm }(x_{max})$. By (4.5) we have $\gamma _x'(X^+(y), y)= \sqrt{\widetilde{b}^2(y)-4 \widetilde{a}(y) \widetilde{c}(y)}$ which is holomorphic in a neighborhood of $Y^{\pm }(x_{max})$ and different from zero. Finally, $\gamma _2(x_{\max }, Y^{\pm } (x_{max})) \ne 0$ by our assumption in Remark 7.2. It follows that the integrand in (9.1) is a holomorphic function in a neighborhood of $Y^{\pm }(x_{max})$. Then, we can apply the saddle point procedure of Lemma 8.1 to $G(y, \alpha )$ with $\alpha =0$ and where we replace the function $f(it, \alpha )$ by

$$\begin{aligned} f(it, \alpha ) = [\gamma _2(X^+(y(it, \alpha )),&Y^{-}(X^{+}(y(it, \alpha )))) H(X^+(y(it, \alpha )),y(it, \alpha )) \\&-\gamma _2(X^+(y(it, \alpha )), y(it, \alpha )) H(X^+(y(it, \alpha )), Y^{-}(X^{+}(y(it, \alpha ))))]\\&\times \frac{y'_\omega (it, \alpha )}{\gamma _2(X^+(y(it, \alpha )), Y^{-}(X^+(y(it, \alpha )) ) ) \gamma '_x(X^+(y(it, \alpha )), y(it, \alpha ))} \end{aligned}$$

where $y(it, \alpha )$ is the path given by the parameter-dependent Morse Lemma (see Lemma A.1). We get the asymptotic development (8.1) as $\alpha \rightarrow 0$ and then have a competition $c_0(\alpha ) + \frac{c_1(\alpha )}{r} + O\left( \frac{1}{r^2}\right)$ between $c_0(\alpha ) = \frac{1}{2\sqrt{\pi }} f(0, \alpha )$ and $c_1(\alpha ) = -\frac{1}{4\sqrt{\pi }} \frac{f''_\omega (0, \alpha )}{4!}$. When $\alpha \rightarrow 0$, we have $c_0(\alpha )\sim c' \alpha$ and $c_1(\alpha )\sim c''$ for non-null constants $c'$ and $c''$, see Lemma 9.3 and Remark 9.4 below.

The proof of (ii) is exactly the same, except that we use the other representation of $I_3(a,b)$.

Lemma 9.3

(Non nullity of $c'$) When $\alpha \rightarrow 0$ we have $c_0(\alpha )\sim c' \alpha$ and the constant $c'$ is non-null at least when $\alpha ^* = -\infty$ (i.e. when there is no pole for $\varphi _2$).

Proof

It is clear that $c_0(0)=0$ because $c_0(\alpha )$ coincides with (8.2) by uniqueness of asymptotic development, and this expression tends to 0 as $\alpha$ goes to 0 due to $C(\alpha )$. Let us now consider the behaviour of $c_0(\alpha )$ when $\alpha \rightarrow 0$. Recall that $c_0(\alpha ) = \frac{1}{2\sqrt{\pi }} f(0, \alpha )$ with the notation of the proof of Lemma 9.1. Invoking Lemma 3.1, we obtain

$$\begin{aligned} y(\alpha )-Y^{-}(X^+(y(\alpha )))&= Y^+(X^+(y(\alpha ))- Y^-(X^+(y(\alpha ))) \\&= \frac{2}{\sigma _{22}}\sqrt{(\sigma _{11}\sigma _{22} -\sigma _{12}^2) (x_{max} - X^+(y(\alpha )) (X^+(y(\alpha )) -x_{min})}. \end{aligned}$$

We also remark that $(X^+(y))'\Bigm |_{y=y(0)}=0$ and $(X^+(y))''\Bigm |_{y=y(0)} = -\frac{\sigma _{22}}{\gamma '_x(x_{max}, Y^{\pm }(x_{max} ))}$, so that

$$\begin{aligned} x_{max} - X^+(y(\alpha )) = \frac{\sigma _{22}}{2\gamma '_x(x_{max}, Y^{\pm }(x_{max} ))} \alpha ^2(1+o(1)), \hbox { as }\alpha \rightarrow 0. \end{aligned}$$

Finally

$$\begin{aligned} y(\alpha )-Y^-(X^+(y(\alpha ))) \sim \sqrt{ \frac{ 2(\sigma _{11}\sigma _{22} -\sigma _{12}^2) (x_{max} -x_{min}) }{ 2 \sigma _{22} \gamma '_x(x_{max}, Y^{\pm } (x_{max})) } } \times \alpha \sim \Pi \times {\alpha }, \end{aligned}$$

where $\Pi$ is defined as the constant in front of $\alpha$.

Since $\gamma _2(x, y)=r_{12}x + r_{22}y$ and $\gamma _2(x_{max}, Y^-(x_{max}))\gamma '_x(x_{max}, Y^-(x_{max})) \ne 0$, we obtain

$$\begin{aligned} c_0(\alpha )&= \frac{-r_{22} H(x_{max}, Y^{\pm } (x_{max}))\times (\Pi \alpha ) + \gamma _2 (x_{max}, Y^{\pm }(x_{max})) H'_y(x_{max}, Y^{\pm } (x_{max})) \times (\Pi \alpha ) + o(\alpha )}{\gamma _2(x_{max}, Y^-(x_{max}))\gamma '_x(x_{max}, Y^-(x_{max})) + o(1)} \\&= \alpha (c' + o(1)) \end{aligned}$$

as $\alpha \rightarrow 0$ where $c'$ is the corresponding constant.

Let us prove that $c' \ne 0$. We have to show that

$$\begin{aligned} -r_{22} H(x_{max}, Y^{\pm } (x_{max})) + \gamma _2 (x_{max}, Y^{\pm }(x_{max})) H'_y(x_{max}, Y^{\pm } (x_{max})) \ne 0 \end{aligned}$$

i.e. that

$$\begin{aligned} -r_{22}&\Big (\gamma _1(x_{max}, Y^{\pm } (x_{max}))\varphi _1(Y^{\pm }(x_{max})) + e^{a_0x_{max} + b_0Y^{\pm }(x_{max})} \Big ) + \gamma _2 (x_{max}, Y^{\pm }(x_{max}))\\&\times \Big (r_{21}\varphi _1(Y^{\pm }(x_{max})) + \gamma _1(x_{max}, Y^{\pm }(x_{max}))\varphi _1'(Y^{\pm }(x_{max})) + b_0e^{a_0x_{max} + b_0Y^{\pm }(x_{max})}\Big ) \ne 0. \end{aligned}$$

The equation can be rewritten as

$$\begin{aligned} c_1\varphi _1(Y^{\pm }(x_{max})) + c_2 \varphi '_1(Y^{\pm }(x_{max})) \ne (c_3 + c_4 b_0)e^{a_0x_{max} + b_0Y^{\pm }(x_{max})} \end{aligned}$$

(9.2)

with $c_1, c_2, c_3, c_4$ constants not depending on the initial conditions. Note that $c_3 = -r_{22} \ne 0$ by (2.1) and $c_4 = \gamma _2(x_{max}, Y^{\pm }(x_{max})) \ne 0$ by the assumption in Remark 7.2. Furthermore, with the same method employed in the proof of Lemmas 3.5 and 8.2, the left term of (9.2) is bounded in $(a_0, b_0)$. Since $x_{max} > 0$ and $Y^{\pm }(x_{max}) < 0$, the right term of (9.2) is not bounded in $(a_0, b_0)$. Hence, (9.2) holds for at least one $(a_0, b_0)$. By a similar argument developed in the proof of Lemmas 3.6 and 8.3 (using the fact that $\alpha ^* = -\infty$), since $c' \ne 0$ at least for one starting point $(a_0, b_0)$, $c' \ne 0$ for all starting points. Finally, (9.2) holds for every initial condition. This concludes the proof that $c_0(\alpha )\sim c' \alpha$ for a non-null constant $c'$.

Remark 9.4

(Non nullity of $c''$) We note here that $c'' \ne 0$. A proof inspired by what has been done in the previous lemma to show that $c' \ne 0$ would work. The same techniques have also been employed in Lemmas 3.5 and 3.6 to characterize the poles by showing the non nullity of a constant, and in Lemmas 8.2 and 8.3 to show the non nullity of $c_0(\alpha )$.

We now have everything we need to prove our second main result, which states the full asymptotic expansion of the Green’s function g along the edges.

Theorem 5

(Asymptotics along the edges for the quadrant) We now assume that $\alpha _0=0$ and let $r\rightarrow \infty$ and $\alpha \rightarrow \alpha _0=0$. In this case, we have $c_0(\alpha )\underset{\alpha \rightarrow 0}{\sim }\ c' \alpha$ and $c_1(\alpha )\underset{\alpha \rightarrow 0}{\sim } c''$ for some constants $c'$ and $c''$ which are non-null at least when $\alpha ^* = -\infty$ (i.e. when there is no pole for $\varphi _2$). Then, the Green’s function $g(r\cos (\alpha ), r\sin (\alpha ))$ has the following asymptotics:

• When $\alpha ^{*} < 0$ the asymptotics given by (8.3) remain valid. In particular, we have

  $$\begin{aligned} g(r\cos (\alpha ), r\sin (\alpha )) \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow 0 \end{array}}{\sim } e^{-r(\cos (\alpha )x(\alpha ) + \sin (\alpha )y(\alpha ))} \frac{1}{\sqrt{r}} \left( c'\alpha + \frac{c''}{r} \right) . \end{aligned}$$

• When $\alpha ^{*} > 0$ the asymptotics given by (8.4) remain valid. In particular, we have

  $$\begin{aligned} g(r\cos (\alpha ), r\sin (\alpha )) \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow 0 \end{array}}{\sim } c^{*}e^{-r(\cos (\alpha )x^* + \sin (\alpha )y^*)}. \end{aligned}$$

Therefore, when $\alpha ^* = -\infty$, there is a competition between the two first terms of the sum $\sum _{k=0}^n \frac{c_k(\alpha )}{r^{k}}$ to know which of $c'\alpha$ and $\frac{c''}{r}$ is dominant. More precisely:

• If $r \sin \alpha \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow 0 \end{array}}{\longrightarrow } \infty$ then the first term is dominant.

• If $r \sin \alpha \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow 0 \end{array}}{\longrightarrow } c>0$ then both terms contribute and have the same order of magnitude.

• If $r \sin \alpha \underset{\begin{array}{c} r\rightarrow \infty \\ \alpha \rightarrow 0 \end{array}}{\longrightarrow } 0$ then the second term is dominant.

A symmetric result holds when we take $\alpha _0 = \frac{\pi }{2}$. The asymptotics given by (8.3) remain valid when $\frac{\pi }{2}<\alpha ^{**}$ and (8.5) remain valid when $\alpha ^{**}<\frac{\pi }{2}$ and there is a competition between the two first terms of the sum to know which one is dominant which in turn depends on the limit of $r \cos (\alpha )$.

Proof

The theorem follows directly from several lemmas put together. First, in Lemma 4.1 we invert the Laplace transform and we express the Green’s function g as the sum of three integrals. Then, in Lemma 6.2 we shift the integration contour of the integrals to reveal the contribution of the poles to the asymptotics by applying the residue theorem. In Lemma 7.3 we show the negligibility of some integrals which implies that the asymptotic expansion is given by the integrals on the contour of steepest descent. Finally, Lemma 9.1 states the asymptotic expansion of these integrals given by the saddle point method.

10 Asymptotics when a pole meets the saddle point: $\alpha \rightarrow \alpha ^*$ or $\alpha \rightarrow \alpha ^{**}$

In this section we study the asymptotics of the Green’s function $g(r\cos \alpha ,r\sin \alpha )$ when $\alpha \rightarrow \alpha _0$ in the special cases where $\alpha _0=\alpha ^*$ or $\alpha _0=\alpha ^{**}$, that is when the pole meets the saddle point.

We introduce the following notation

$$\begin{aligned} R(\alpha )= & {} x'_\omega (0,\alpha )= \sqrt{ \frac{ 2}{F''_{xx}(x(\alpha ), \alpha ) } } = \sqrt{ \frac{ 2}{-\sin (\alpha ) (Y^+(x))''\mid _{x(\alpha )} } }\\= & {} \sqrt{ \frac{2\sin (\alpha ) \gamma '_y(x(\alpha ), y(\alpha )) }{ \sigma _{11}\sin ^2(\alpha ) + 2\sigma _{12} \sin (\alpha ) \cos (\alpha ) + \sigma _{22} \cos ^2(\alpha ) } }.\nonumber \end{aligned}$$

(10.1)

We recall that for $(a,b) \in {\mathbb {R}}_+^2$ we define $r=\sqrt{a^2+b^2}$ and we let $\alpha (a,b)$ be the angle in $[0,\pi /2]$ such that $\cos (\alpha ) = \frac{ a }{ \sqrt{a^2+b^2}}$ and $\sin (\alpha ) = \frac{ b }{\sqrt{a^2+ b^2}}$.

Lemma 10.1

(Asymptotics of the integral on steepest descent line when $\alpha \rightarrow \alpha ^*$) Letting $\alpha (a,b) \rightarrow \alpha ^*$ as $r=\sqrt{a^2+b^2 } \rightarrow \infty$. Then

$$\begin{aligned} I:= \frac{1}{2\pi i} \int \limits _{\Gamma _{x,\alpha }} \frac{\gamma _2(x, Y^+(x)) \varphi _2(x) }{ \gamma '_y(x, Y^+(x)) } \exp \Big (\sqrt{a^2+b^2} F(x, \alpha (a,b)) \Big ) dx \end{aligned}$$

has the following asymptotics.

• (i) If $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow 0$, then

  $$\begin{aligned}{} & {} I \sim \frac{-1}{2} \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)} \ \ \ \hbox { if } \alpha (a,b) >\alpha ^*,\\{} & {} I \sim \frac{1}{2} \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)} \ \ \hbox { if } \alpha (a,b) <\alpha ^*. \end{aligned}$$

• (ii) If $\sqrt{a^2+b^2} (\alpha (a,b) - \alpha ^*)^2 \rightarrow c>0$. Further, let

  $$\begin{aligned} A(\alpha ^*)= \frac{-x'_\alpha (\alpha ^*) }{R(\alpha ^*)}. \end{aligned}$$

  (10.2)

  Then

  $$\begin{aligned}{} & {} I \sim \frac{-1}{2}\exp (c A^2(\alpha ^* )) \Big (1-\Phi \Big (\sqrt{c} A(\alpha ^* )\Big )\Big ) \times \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)} \ \ \ \hbox { if } \alpha (a,b) >\alpha ^*,\\{} & {} I \sim \frac{1}{2}\exp (c A^2(\alpha ^* )) \Big (1-\Phi \Big (\sqrt{c} A(\alpha ^* )\Big )\Big ) \times \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2}{ \gamma '_y(x^*, y^*)} \ \ \ \hbox { if } \alpha (a,b)<\alpha ^* \end{aligned}$$
  $$\begin{aligned} \Phi (z)= \frac{2}{\sqrt{\pi }} \int _0^z \exp (-t^2)dt. \end{aligned}$$

  (10.3)

• (iii) Let $\sqrt{a^2+b^2}( \alpha (a,b)-\alpha ^*)^2 \rightarrow \infty$. Then

  $$\begin{aligned} I \sim \frac{ \gamma _2(x^*, y^*) R(\alpha ^*) }{2\sqrt{\pi } \gamma _y'(x^*, y^*) } \times \frac{ { \mathrm res}_{x=x^*}\varphi _2 }{ (x(\alpha (a,b))-x(\alpha ^*))} \times \frac{1}{ \root 4 \of {a^2+b^2}}. \end{aligned}$$

Proof

Proceeding as we did in Lemma 8.1, we obtain that

$$\begin{aligned} I\sim \frac{1}{2\pi } \int \limits _{-\epsilon }^{ \epsilon } f(it, \alpha (a,b))\exp (-\sqrt{a^2+b^2} t^2)dt \end{aligned}$$

(10.4)

where

$$\begin{aligned} f(it, \alpha (a,b)) =\frac{ \gamma _2(x(it, \alpha ), Y^+(x(it, \alpha )))\varphi _2(x(it, \alpha ))}{\gamma '_y (x(it, \alpha ), Y^+(x(it, \alpha )))} \times x'_\omega (it,\alpha ). \end{aligned}$$

The function $\varphi _2$ is a sum of a holomorphic function and of the term $\frac{\textrm{res}_{x^*} \varphi _2}{x-x^*}$ which after the change of variables takes the form $\frac{\textrm{res}_{x^* } \varphi _2}{x(it, \omega )-x^*}$.

We have $x(0, \alpha ^* )=x(\alpha ^*)$. By the implicit function theorem there exists a function $\omega (\alpha )$ in the class $\mathcal {C}^\infty$ such that

$$\begin{aligned} x(\omega (\alpha ), \alpha ) \equiv x^* \ \ \ \forall \alpha : |\alpha -\alpha ^* |\le \tilde{\eta }\ \ \ \ \ \ \end{aligned}$$

for some $\tilde{\eta }$ small enough where $\omega (\alpha ^*)=0$. Furthermore, differentiating this equality, we get

$$\begin{aligned} \omega '(\alpha )= \frac{ -x'_\alpha (\omega (\alpha ), \alpha ) }{x'_\omega (\omega (\alpha ), \alpha ) }, \end{aligned}$$

so that

$$\begin{aligned} \omega '(\alpha ^* )= -\frac{x'_\alpha (\alpha ^*)}{x'_\omega (0, \alpha ^* )}. \end{aligned}$$

The formula

$$\begin{aligned} \omega (\alpha ) = \frac{(x(\alpha ^*)-x(\alpha ))}{x'_\omega (0, \alpha ^*)}(1+o(1)) = \frac{(x(\alpha ^*)-x(\alpha ))}{ R(\alpha ^*)}(1+o(1)) \ \ \hbox { as } \alpha \rightarrow \alpha ^* \end{aligned}$$

(10.5)

provides the asymptotics of $\omega (\alpha )$ as $\alpha \rightarrow \alpha ^*$. Note also that the main part of $\omega (\alpha )$ is real.

Let us introduce the function

$$\begin{aligned} \Psi (\omega , \alpha ) = \left\{ \begin{array}{cc} \frac{\omega -\omega (\alpha )}{x(\omega , \alpha ) - x(\omega (\alpha ), \alpha ) } &{}\hbox { if } \omega \ne \omega (\alpha ) \\ \frac{1}{x'_\omega (\omega (\alpha ), \alpha ) } &{} \hbox { if } \omega = \omega (\alpha ). \end{array} \right. \end{aligned}$$

This function is holomorphic in $\omega$ for any fixed $\alpha$ and continuous as a function of three real variables. Note that the integral (10.4) can be written as

$$\begin{aligned} \frac{1}{2\pi i} \int \limits _{-\epsilon }^{\epsilon } f(it, \alpha )(it-\omega (\alpha )) \frac{\exp (-\sqrt{a^2+b^2}t^2)}{t+i\omega (\alpha )}dt. \end{aligned}$$

Furthermore, there exists a constant $C>0$ such that

$$\begin{aligned}{} & {} \Big |f(it, \alpha )(it-\omega (\alpha )) - f(0, \alpha )(0-\omega (\alpha ))\Big | \le C|t|. \ \ \forall (it, \alpha ) \in \widetilde{\Omega }(0, \alpha ^*) \nonumber \\ {}{} & {} \quad = \{(\omega , \alpha ) : |\omega | \le K, |\alpha -\alpha ^*|\le \min (\eta , \tilde{\eta })\}. \end{aligned}$$

(10.6)

Indeed, it suffices to take C as the maximum of the modulus of

$$\begin{aligned} (f(\omega , \alpha )(\omega -\omega (\alpha )) - f(0, \alpha )(0-\omega (\alpha )))\omega ^{-1} \end{aligned}$$

on $\{(\omega , \alpha ): |\omega |= K, |\alpha -\alpha ^*|\le \min (\eta , \tilde{\eta })\}$ for $\eta$ small enough. Moreover since ${\Im } \omega (\alpha ) =o({\Re } \omega (\alpha ))$ as $\alpha \rightarrow \alpha ^*$, then by Lemma (B.1) (i) for any $\alpha$ close to $\alpha ^*$ the inequality

$$\begin{aligned} \frac{|t|}{|t +i\omega (\alpha ) |} \le 2 \end{aligned}$$

holds for all $t \in {\mathbb {R}}$. The integral

$$\begin{aligned} \int _{\mathbb {R}} 2 \exp (-\sqrt{a^2+b^2} t^2)dt =O(\frac{1}{\root 4 \of {a^2+b^2} }) \end{aligned}$$

is of smaller order than the asymptotics announced in the statement of the lemma. Hence, it suffices to show that the integral

$$\begin{aligned} \frac{1}{2\pi i }\int \limits _{-\epsilon }^{\epsilon } f(0, \alpha )(0-\omega (\alpha )) \frac{\exp (-\sqrt{a^2+b^2}t^2)}{t+i\omega (\alpha )} dt \end{aligned}$$

has the expected asymptotics. Note that by (10.5)

$$\begin{aligned} \varphi (x(\alpha )) (-\omega (\alpha )) x'_\omega (0, \alpha ) \rightarrow \textrm{res}_{x^*} \varphi \hbox { as }\alpha \rightarrow \alpha ^*, \end{aligned}$$

so that

$$\begin{aligned} f(0, \alpha )(-\omega (\alpha )) \rightarrow \frac{ \gamma _2(x^*, y^*) }{\gamma '_y(x^*, y^*) } \times \textrm{res}_{x^*}\varphi . \end{aligned}$$

It remains to study

$$\begin{aligned} \frac{1}{2\pi i} \int \limits _{-\epsilon }^{\epsilon } \frac{\exp (-\sqrt{a^2+b^2}t^2)}{t+i \omega (\alpha )}dt. \end{aligned}$$

For any $t \in {\mathbb {R}} \setminus [-\epsilon , \epsilon ]$ the denominator in the integral is bounded from below

$$\begin{aligned} |t+i\omega (\alpha )|\ge ||t|-\omega (\alpha ) |\ge \epsilon -\omega (\alpha ) \ge \epsilon /2 \end{aligned}$$

for any $\alpha$ close enough to $\alpha ^*$ while

$$\begin{aligned} \int _{\mathbb {R}} \exp (-\sqrt{a^2+b^2}t^2)dt= O(\frac{1}{\root 4 \of {a^2+b^2}}) \end{aligned}$$

is of smaller order than the one stated in the lemma. Finally, it suffices to prove that

$$\begin{aligned} \frac{1}{2\pi i } \int _{-\infty }^\infty \frac{\exp (- \sqrt{a^2+b^2}t^2)}{t+i \omega (\alpha (a,b))}dt \end{aligned}$$

(10.7)

has the right asymptotics. By a change of variables, equation (10.7) equals

$$\begin{aligned} \frac{1}{2\pi i }\int _{-\infty }^\infty \frac{\exp (-s^2)}{s+i \omega (\alpha ) \root 4 \of {a^2+b^2}}ds. \end{aligned}$$

(10.8)

Now let $\alpha >\alpha ^*$ [resp. $\alpha < \alpha ^*$]. Then $x(\alpha )<x(\alpha ^*)$ [resp. $x(\alpha )>x(\alpha ^*)$] and by (10.5) ${\Re } \omega (\alpha )>0$ [resp. ${\Re } \omega (\alpha )<0$]. By Lemma B.1 (iii) this integral evaluates to

$$\begin{aligned}{} & {} \frac{-1}{2} \exp (\sqrt{a^2+b^2} \omega ^2 (\alpha )) \Big (1-\Phi (\root 4 \of {a^2+b^2}\omega (\alpha )) \Big ) \ \ \ \hbox { if }\alpha >\alpha ^*\\{} & {} \frac{1}{2} \exp ( \sqrt{a^2+b^2} \omega ^2(\alpha ) ) \Big (1-\Phi (-\root 4 \of {a^2+b^2}\omega (\alpha ))\Big ) \ \ \ \hbox { if }\alpha < \alpha ^*. \end{aligned}$$

If $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^* )^2 \rightarrow c\ge 0$ then by (10.5) $\sqrt{a^2+b^2} \omega (\alpha (a,b))^2 \rightarrow c A^2(\alpha ^*)$ and the results of (i) and (ii) are immediate. Now let $\sqrt{a^2+b^2}(\alpha (a,b)-\alpha ^*)^2 \rightarrow \infty$. Then by Lemma B.1 (ii) the asymptotics of this integral are

$$\begin{aligned} \frac{\sqrt{\pi } }{2\pi i \times (i \omega (\alpha (a,b)))\root 4 \of {a^2+b^2}} \end{aligned}$$

where the asymptotics of $\omega (\alpha (a,b))$ have been stated in (10.5). The result follows.

It is useful to note that

$$\begin{aligned}{} & {} -\cos (\alpha ) x^*- \sin (\alpha ) y^* = -\cos (\alpha ) x(\alpha ) -\sin (\alpha ) Y^+(x(\alpha )) + R^{-2}(\alpha ^*)(x(\alpha )-x^*)^2 (1+o(1)) \nonumber \\{} & {} \quad = -\cos (\alpha ) x(\alpha ) -\sin (\alpha ) Y^+(x(\alpha )) + A^2(\alpha ^*)(\alpha -\alpha ^*)^2 (1+o(1)), \ \ \ \alpha \rightarrow \alpha ^*\nonumber \\ \end{aligned}$$

(10.9)

with the notation $R(\alpha )$ and $A(\alpha )$ above in (10.1) and (10.2).

By Taylor expansion at $x(\alpha )$ and and by the definition of a saddle point (the first derivative is zero):

$$\begin{aligned}{} & {} -\cos (\alpha ) x^* -\sin (\alpha ) y^* = -\cos (\alpha ) x(\alpha ) -\sin (\alpha ) Y^{+}(x(\alpha )) \nonumber \\ {}{} & {} \quad - \frac{1}{2} \sin (\alpha ) (Y^+(x))''\mid _{x=x(\alpha )}(x(\alpha )-x^*)^2 (1+o(1)), \ \ \alpha \rightarrow \alpha ^*. \end{aligned}$$

We remind the reader that

$$\begin{aligned} - \frac{1}{2} \sin (\alpha ) (Y^+(x))''\mid _{x=x(\alpha )} = (R(\alpha ))^{-2} = R(\alpha ^*)^{-2} (1+o(1)), \ \ \alpha \rightarrow \alpha ^*. \end{aligned}$$

The following lemma is useful in determining the asymptotics of the value of $I_1$ found in Lemma 6.2.

Lemma 10.2

(Combined contribution of the pole and saddle point to the asymptotics when $\alpha \rightarrow \alpha ^*$) Let $r=\sqrt{a^2+b^2} \rightarrow \infty$ and $\alpha (a,b) \rightarrow \alpha ^*$. The sum

$$\begin{aligned} I:= & {} \frac{ \big (\mathrm{-res}_{x=x^*} \varphi _2(x) \big ) \gamma _2(x^*, y^*)}{ \gamma '_y(x^*, y^*)} \exp (-ax^* -b y^* ) \times \textbf{1}_{ \alpha <\alpha ^*}\nonumber \\ {}{} & {} + \frac{1}{2i\pi } \int _{\Gamma _{x, \alpha }} \frac{\gamma _2(x, Y^+(x))\varphi _2(x)}{\gamma _y'(x, Y^+(x))} \exp (-a x -b Y^+(x))dx \end{aligned}$$

(10.10)

has the following asymptotics.

• (i) If $\alpha >\alpha ^*$ and $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow \infty$. Then

  $$\begin{aligned}{} & {} I \sim \frac{\exp (-a x(\alpha (a,b)) -b y(\alpha (a,b)))}{\root 4 \of {a^2+b^2} } \\ {}{} & {} \quad \frac{\gamma _2(x^*, y^*)}{ \sqrt{2\pi } \sqrt{\sigma _{11}\sin ^2(\alpha ^*) + 2\sigma _{12} \sin (\alpha ^*) \cos (\alpha ^*) + \sigma _{22} \cos ^2(\alpha ^*)} } \\ {}{} & {} \quad \times \frac{ \textrm{res}_{x^*}\varphi _2 }{x(\alpha (a,b))-x^* } \times C(\alpha ^*), \end{aligned}$$

  where

  $$\begin{aligned} C(\alpha ^*)= \sqrt{ \frac{ \sin (\alpha ^*)}{ \gamma '_y(x^*, y^*) }} = \sqrt{ \frac{ \cos (\alpha ^*) }{ \gamma '_x( x^*, y^*) } }. \end{aligned}$$

• (ii) If $\alpha >\alpha ^*$ and $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow c>0$, then

  $$\begin{aligned} I \sim \frac{-1}{2} \exp (-a x^* -b y^*) \Big (1-\Phi \Big (\sqrt{c} A(\alpha ^* )\Big )\Big ) \times \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)}. \end{aligned}$$

  where $A(\alpha ^*)$ and $\Phi$ are defined in (10.2), (10.1) and (10.3).

• (iii) If $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow 0$, then

  $$\begin{aligned} I \sim \frac{-1}{2} \exp (-a x^* -b y^*) \times \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)}. \end{aligned}$$

• (iv) If $\alpha <\alpha ^*$ and $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow c>0$, then

  $$\begin{aligned} I \sim \frac{-1}{2} \exp (-a x^* -b y^*) \Big (1+\Phi \Big (\sqrt{c} A(\alpha ^* )\Big )\Big ) \times \frac{ \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi _2 }{ \gamma '_y(x^*, y^*)}. \end{aligned}$$

• (v) If $\alpha <\alpha ^*$ and $\sqrt{a^2+b^2} (\alpha (a,b) -\alpha ^*)^2 \rightarrow \infty$, then

  $$\begin{aligned} I \sim \exp (-a x^* -b y^*) \times \frac{ - \gamma _2(x^*, y^*) \textrm{res}_{x=x^*} \varphi }{ \gamma '_y(x^*, y^*)}. \end{aligned}$$

Proof

Let us note that

$$\begin{aligned} \int _{\Gamma _{x, \alpha }} \frac{\gamma _2(x, Y^+(x))\varphi _2(x)}{\gamma _y'(x, Y^+(x))} \exp (-a x -b Y^+(x))dx \end{aligned}$$

(10.11)

$$\begin{aligned} = \exp ( - a x(\alpha ) -b y (\alpha ) ) \int \limits _{\Gamma _{x,\alpha }} \frac{\gamma _2(x, Y^+(x))\varphi _2(x)}{\gamma _y'(x, Y^+(x))} \exp \big (\sqrt{a^2+b^2} F(x, \alpha (a,b)) \big ) dx \end{aligned}$$

• (i) The result follows from the representation (10.11) and Lemma 10.1 (iii) with $R(\alpha ^*)$ defined in (10.1).

• (ii) Invoking (10.9) the representation (10.11) can be also written as

  $$\begin{aligned}{} & {} \exp ( - a x^* -b y^* - \sqrt{a^2+b^2} A^2(\alpha ^*)(\alpha (a,b) -\alpha ^*)^2(1+o(1))) \nonumber \\ {}{} & {} \int \limits _{\Gamma _{x, \alpha } } \frac{\gamma _2(x, Y^+(x))\varphi _2(x)}{\gamma _y'(x, Y^+(x))} \exp (\sqrt{a^2+b^2} F(x,\alpha (a,b)) )dx \end{aligned}$$

  (10.12)

  The result follows from Lemma 10.1 (ii).

• (iii) We will consider three subcases. If $\alpha (a,b)>\alpha ^*$, the announced result follows from Lemma 10.1 (i) and from the representation (10.12) where $\sqrt{a^2+b^2} A^2(\alpha ^*)(\alpha (a,b) -\alpha ^*) \rightarrow 0$. If $\alpha =\alpha ^*$, then the contour $\Gamma _{x,\alpha }$ is special and a direct computation leads to the result. We refer to Lemma 19 of [14] which deals with a similar case. If $\alpha (a,b)<\alpha ^*$, then by Lemma 10.1 (i) the asymptotics of the second term of (10.10) are the same as in the case $\alpha (a,b)>\alpha ^*$ but with the opposite sign. It should be summed with the first term. The sum of their constants $1/2-1$ provides the result.

• (iv) By the representation (10.12) and Lemma 10.1 (ii) the asymptotics of the second term of (10.10) are the same as in the case (ii) but with opposite sign. It should be summed with the first term. The sum of their constants $\frac{1}{2} (1-\Phi (\sqrt{c} A(\alpha ^*)))-1$ leads to the result.

• (v) By Lemma (10.1) (iii) and the representation (10.12) the second term of (10.10) has the asymptotics

  $$\begin{aligned}{} & {} \exp \Big ( - a x^* -b y^* - \sqrt{a^2+b^2} A^2(\alpha ^*)(\alpha (a,b) -\alpha ^*)^2(1+o(1)) \Big )\\{} & {} \quad \times \frac{\gamma _2(x^*, y^*) R(\alpha ^*) }{2\sqrt{\pi } \gamma _y'(x^*, y^*) } \times \frac{ \textrm{res}_{x=x^*}\varphi }{ (x(\alpha (a,b))-x(\alpha ^*))} \times \frac{1}{ \root 4 \of {a^2+b^2}}. \end{aligned}$$

  Since $\frac{\exp (-\sqrt{a^2+b^2} A^2(\alpha ^*)(\alpha (a,b) -\alpha ^*)^2)}{ (\alpha (a,b)-\alpha ^* ) \root 4 \of {a^2+b^2}}$ converges to 0 in this case, the order of the second term in (10.10) is clearly smaller than the one of the first term which dominates the asymptotics.

Remark 10.3

(Consistency of the results) The results of (i) and (v) are perfectly “continuous” with asymptotics along directions $\alpha \rightarrow \alpha ^*, \alpha < \alpha ^*$ and $\alpha \rightarrow \alpha ^*, \alpha > \alpha ^*$. Namely, if in (i) we substitute $\varphi (x(\alpha ))$ instead of $\frac{res_{x^*} \varphi }{x(\alpha (a,b)) - x^*}$, we obtain the asymptotics for angles greater than $\alpha ^*$. The result (v) remains valid for angles less than $\alpha ^*$.

We now summarize the previous results to obtain our final main result.

Theorem 6

(Asymptotics in the quadrant when the saddle point meets a pole) We now assume that $\alpha _0=\alpha ^{*}$ and let $\alpha \rightarrow \alpha ^{*}$ and $r\rightarrow \infty$. Then, the Green’s density function $g(r\cos \alpha , r \sin \alpha )$ has the following asymptotics:

• When $r(\alpha - \alpha ^{*})^2\rightarrow 0$ then the principal term of the asymptotics is given by (8.4) but the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}$.

• When $r(\alpha -\alpha ^{*})^2\rightarrow c>0$ for some constant c then:

  • If $\alpha <\alpha ^{*}$ the principal term of the asymptotics is still given by (8.4) but the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}(1+\Phi (\sqrt{c}A))$ for some constant A.

  • If $\alpha >\alpha ^{*}$ the principal term of the asymptotics is still given by (8.4) but the constant $c^{*}$ of the first term has to be replaced by $\frac{1}{2}c^{*}(1-\Phi (\sqrt{c}A))$ for some constant A.

  Note that above $\Phi (z)= \frac{2}{\sqrt{\pi }} \int _0^z \exp (-t^2)dt$.

• When $r(\alpha -\alpha ^{*})^2\rightarrow \infty$ then:

  • If $\alpha <\alpha ^{*}$ the principal term of the asymptotics is given by (8.4).

  • If $\alpha >\alpha ^{*}$ the principal term of the asymptotics is given by (8.3) and we have ${c_0}(\alpha )\underset{\alpha \rightarrow \alpha ^{*}}{\sim }\frac{c}{\alpha -\alpha ^{*}}$ for some constant c.

A symmetric result holds when we assume that $\alpha _0=\alpha ^{**}$.

Proof

The theorem follows directly from several lemmas put together. The Green’s function g is still given by the sum $I_1 + I_2 + I_3$, see Lemma 4.1. We again apply Lemma 6.2 to take into account the contribution of the poles and Lemma 7.1 which shows the negligibility of some integrals in the final asymptotics. Furthermore, by the proof of Lemma 8.1, $I_2 + I_3 = O\left( \frac{e^{-r\cos (\alpha ^*)x(\alpha ^*) - r\sin (\alpha ^*)y(\alpha ^*))}}{\sqrt{r}}\right)$ when $r \rightarrow \infty$ and $\alpha \rightarrow \alpha ^*$ (recall that $\alpha ^*< \alpha ^{**}$). With Lemma 10.2, we see in each case that $I_2 + I_3$ is negligible compared to $I_1$ when $r\rightarrow \infty$ and $\alpha \rightarrow \alpha ^*$. Indeed, in the case $\alpha > \alpha ^*$ and $r(\alpha - \alpha ^*)^2 \rightarrow \infty$, the domination of $I_1$ is due to the term $\frac{1}{x(\alpha ) - x^*}$. For the other cases, the domination of $I_1$ is due to the factor $\frac{1}{\sqrt{r}}$ in the asymptotics of $I_2 + I_3$.

The proof is similar for $\alpha _0 = \alpha ^{**}$.

11 Asymptotics in a cone

11.1 From the quadrant to the cone

Let us describe the linear transformation which maps the reflected Brownian motion in the quarter plane (of covariance matrix $\Sigma$ and reflecting vectors $R^1$ and $R^2$) to a reflected Brownian motion in a wedge with identity covariance matrix. We take

$$\begin{aligned} \beta =\arccos \left( -\frac{\sigma _{12}}{\sqrt{\sigma _{11}\sigma _{22}}} \right) \in (0,\pi ) \end{aligned}$$

(11.1)

and we define

$$\begin{aligned} T= \left( \begin{array}{cc} \displaystyle \frac{1}{\sin \beta } &{} \cot \beta \\ 0 &{} 1 \end{array} \right) \left( \begin{array}{cc} \displaystyle \frac{1}{\sqrt{\sigma _{11}}} &{} 0\\ 0 &{} \displaystyle \frac{1}{\sqrt{\sigma _{22}}} \end{array}\right) \end{aligned}$$

(11.2)

which satisfies $T\Sigma T^\top = \text {Id}$. Then, if $Z_t$ is a reflected Brownian motion in the quadrant of parameters $(\Sigma ,\mu ,R)$, the process $\widetilde{Z_t}=TZ_t$ is a reflected Brownian motion in the cone of angle $\beta$ and of parameters $(T\Sigma T^\top ,T\mu ,TR)=(\text {Id},\widetilde{\mu },TR)$. The new reflection matrix TR correspond to reflections of angles $\delta$ and $\epsilon$ defined in $(0,\pi )$ by

$$\begin{aligned} \tan \delta = \frac{\sin \beta }{\frac{r_{12}}{r_{22}}\sqrt{\frac{\sigma _{22}}{\sigma _{11}}}+\cos \beta } \qquad \text {and} \qquad \tan \varepsilon = \frac{\sin \beta }{\frac{r_{21}}{r_{11}}\sqrt{\frac{\sigma _{11}}{\sigma _{22}}}+\cos \beta }. \end{aligned}$$

(11.3)

The new drift has an angle $\theta =\arg \widetilde{\mu }$ with the horizontal axis and satisfies

$$\begin{aligned} \tan \theta =\frac{\sin \beta }{\frac{\mu _1}{\mu _2}\sqrt{\frac{\sigma _{22}}{\sigma _{11}}} +\cos \beta }. \end{aligned}$$

(11.4)

The assumption $\mu _1>0$ and $\mu _2>0$ is equivalent to $\theta \in (0,\beta )$.

11.2 Green’s functions in the cone

Let us denote $g^{z_0}$ the density of $G(z_0,\cdot )$. For $z\in \mathbb {R}_+^2$ we have

$$\begin{aligned} g^{z_0}(z)=\int _0^\infty p_t(z_0,z)\textrm{d}t. \end{aligned}$$

Let us recall that we have denoted $\widetilde{G}(\widetilde{z_0},\widetilde{A})$ the Green measure of $\widetilde{Z_t}$ and $\widetilde{g}^{\widetilde{z_0}}(\widetilde{z})$ its density. It is straightforward to see that for $A\in \mathbb {R}_+^2$ we have $G(z_0,A)=\widetilde{G}(T{z_0},TA)$ and then

$$\begin{aligned} g^{z_0}(z)= |\det T| \widetilde{g}^{T{z_0}}(Tz)=\frac{1}{\sqrt{\det \Sigma }}\widetilde{g}^{\widetilde{z_0}}(\widetilde{z}) \end{aligned}$$

(11.5)

where $\widetilde{z_0}=Tz_0$ and $\widetilde{z}=Tz$.

11.3 Polar coordinates

For any $z=(a,b)\in \mathbb {R}_+^2$ we may define the polar coordinate in the quadrant $(r,\alpha )\in \mathbb {R}_+ \times [0,\frac{\pi }{2}]$ by

$$\begin{aligned} z=(a,b)=(r\cos \alpha ,r\sin \alpha ). \end{aligned}$$

(11.6)

We now define the polar coordinates in the $\beta$-cone $(\rho ,\omega )$ by

$$\begin{aligned} \widetilde{z}=(\rho \cos \omega , \rho \sin \omega ). \end{aligned}$$

(11.7)

For $\widetilde{z}=Tz$ we obtain by a direct computation that

$$\begin{aligned} (r\cos \alpha ,r\sin \alpha )=(\rho \sqrt{\sigma _{11}} \cos (\beta -\omega ), \rho \sqrt{\sigma _{22}}\sin \omega ). \end{aligned}$$

(11.8)

and that

$$\begin{aligned} \tan \omega = \frac{\sin \beta }{\frac{1}{\tan \alpha }\sqrt{\frac{\sigma _{22}}{\sigma _{11}}}+\cos \beta }. \end{aligned}$$

(11.9)

We deduce that

$$\begin{aligned} \widetilde{g}^{\widetilde{z_0}}(\rho \cos \omega , \rho \sin \omega )=\sqrt{\det \Sigma } \ g^{z_0}(\rho \sqrt{\sigma _{11}} \cos (\beta -\omega ), \rho \sqrt{\sigma _{22}}\sin \omega ). \end{aligned}$$

(11.10)

11.4 Saddle point

The ellipse $\mathcal {E}=\{(x,y)\in \mathbb {R}^2: \gamma (x,y)=0\}$ can be easily parametrized by the following,

$$\begin{aligned} \mathcal {E}=\left\{ (\widetilde{x}(t),\widetilde{y}(t)): t\in [0,2\pi ] \right\} , \end{aligned}$$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \widetilde{x}(t)=\frac{x_{max}+x_{min}}{2}+\frac{x_{max}-x_{min}}{2}\cos (t), \\ \widetilde{y}(t)=\frac{y_{max}+y_{min}}{2}+\frac{y_{max}-y_{min}}{2}\cos (t-\beta ) . \end{array}\right. } \end{aligned}$$

(11.11)

see Proposition 5 of [23]. Noticing that

$$\begin{aligned} -\cos \theta = \frac{x_{max}+x_{min}}{x_{max}-x_{min}}, \quad \text {and} \quad -\cos (\beta -\theta ) = \frac{y_{max}+y_{min}}{y_{max}-y_{min}} \end{aligned}$$

and that

$$\begin{aligned} 2|\widetilde{\mu }|=\sqrt{\sigma _{11}}(x_{max}-x_{min})\sin \beta =\sqrt{\sigma _{22}}(y_{max}-y_{min})\sin \beta \end{aligned}$$

we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \widetilde{x}(t) = \frac{|\widetilde{\mu }|}{\sqrt{\sigma _{11}} \sin \beta }(\cos t-\cos \theta ) = \frac{2|\widetilde{\mu }|}{\sqrt{\sigma _{11}}\sin \beta } \sin (\frac{\theta -t}{2})\sin (\frac{t+\theta }{2}) \\ \widetilde{y}(t) = \frac{|\widetilde{\mu }|}{\sqrt{\sigma _{22}}\sin \beta }(\cos (t-\beta )-\cos (\theta -\beta )) = \frac{2|\widetilde{\mu }|}{\sqrt{\sigma _{22}}\sin \beta } \sin (\frac{\theta -t}{2})\sin (\frac{t+\theta -2\beta }{2}) . \end{array}\right. } \end{aligned}$$

(11.12)

The following result gives an expression of the saddle point in terms of the polar coordinate in the cone.

Proposition 11.1

(Saddle point in polar coordinate) For $\alpha \in (0,\frac{\pi }{2})$ and $\omega \in (0,\beta )$ previously defined and linked by (11.9) we have

$$\begin{aligned} (x(\alpha ),y(\alpha ))=(\widetilde{x}(\omega ),\widetilde{y}(\omega )) \end{aligned}$$

(11.13)

where $(x(\alpha ),y(\alpha ))$ is the saddle point defined in (5.1).

Proof

Letting $\alpha \in (0,\frac{\pi }{2})$, we are looking for the point $(x(\alpha ),y(\alpha ))$ which maximizes the quantity $x\cos \alpha +y \sin \alpha$ for (x, y) in the ellipse $\mathcal {E}=\{(x,y)\in \mathbb {R}^2: \gamma (x,y)=0\}$. We search for a $t\in (0,\beta )$ cancelling the derivative of $\widetilde{x}(t)\cos \alpha + \widetilde{y}(t)\sin \alpha$ w.r.t t. By (11.12) we obtain that $\widetilde{x}'(t)\cos \alpha + \widetilde{y}'(t)\sin \alpha = 0$ if and only if

$$\begin{aligned} -\frac{1}{\sqrt{\sigma _{11}}}\sin t \cos \alpha -\frac{1}{\sqrt{\sigma _{22}}} \sin (t-\beta )\sin \alpha =0. \end{aligned}$$

Writing $\sin (t-\beta )=\sin t \cos \beta -\cos t \sin \beta$ it directly leads to $\tan t = \frac{\sin \beta }{\frac{1}{\tan \alpha }\sqrt{\frac{\sigma _{22}}{\sigma _{11}}}+\cos \beta }$. Then by (11.9) we obtain $\tan t=\tan \omega$ and we deduce that $t=\omega$ maximizes $\widetilde{x}(t)\cos \alpha + \widetilde{y}(t)\sin \alpha$ and therefore $(x(\alpha ),y(\alpha ))=(\widetilde{x}(\omega ),\widetilde{y}(\omega ))$.

11.5 Poles

Let us recall that $x^*$ is the pole of $\varphi _2(x)$ (when $x^* > 0$), and $y^{**}$ is the pole of $\varphi _1(y)$ (when $y^{**}> 0$), see Proposition 3.4. We defined $\alpha ^*$ and $\alpha ^{**}$ such that $x(\alpha ^*)=x^*$ and $y(\alpha ^{**})=y^{**}$. Now, we may define the corresponding $\omega ^*$ and $\omega ^{**}$ linked by formula (11.9) and such that

$$\begin{aligned} x^*=\widetilde{x}(\omega ^*)=\widetilde{x}(-\omega ^*) \quad \text {and}\quad y^{**}=\widetilde{y}(\omega ^{**})=\widetilde{y}(2\beta -\omega ^{**}). \end{aligned}$$

(11.14)

Proposition 11.2

(Poles in polar coordinate) We have

$$\begin{aligned} \omega ^*=\theta -2\delta \quad \text {and}\quad \omega ^{**}=\theta +2\epsilon . \end{aligned}$$

(11.15)

We have, $\alpha <\alpha ^*$ if and only if $\omega <\omega ^*$, and $\alpha >\alpha ^{**}$ if and only if $\omega >\omega ^{**}$. Then, $x^*$ is the pole of $\varphi _2(x)$ if and only if $\theta -2\delta >0$, and $y^{**}$ is a pole of $\varphi _1(y)$ if and only if $\theta +2\epsilon <\beta$.

Proof

When the pole of $\varphi _2$ exists, we have $\gamma _2(x^*,Y^-(x^*))=0$. Let us recall that in (6.2) we defined $y^*:=Y^+(x^*)=\widetilde{y}(\omega ^*)$. Therefore, we have $Y^-(x^*)=\widetilde{y}(-\omega ^*)$. We are looking for the solutions of the equation

$$\begin{aligned} \gamma _2(\widetilde{x}(t),\widetilde{y}(t))=0, \end{aligned}$$

(11.16)

which is the intersection of the ellipse $\mathcal {E}$ and the line $\gamma _2=0$. There are two solutions, the first one is elementary and is given by $t=\theta$, that is $(\widetilde{x}(t),\widetilde{y}(t))=(0,0)$. The second one is by definition $(\widetilde{x}(-\omega ^{*}),\widetilde{y}(-\omega ^{*}))=(x^{*},Y^-(x^{*}))$. By (11.12), the Eq. (11.16) gives

$$\begin{aligned} r_{12}\frac{1}{\sqrt{\sigma _{11}}}\sin \left( \frac{-\omega ^{*}+\theta }{2}\right) +r_{22} \frac{1}{\sqrt{\sigma _{22}}}\sin \left( \frac{-\omega ^{*}+\theta }{2} -\beta \right) =0 \end{aligned}$$

With some basic trigonometry, we obtain that

$$\begin{aligned} \tan \frac{-\omega ^{*}+\theta }{2} = \frac{\sin \beta }{\frac{r_{12}}{r_{22}} \sqrt{\frac{\sigma _{22}}{\sigma _{11}}}+\cos \beta }=\tan (\delta ). \end{aligned}$$

We deduce that $\omega ^{*}=\theta -2\delta$. A symmetric computation leads to $\omega ^{**}=\theta +2\epsilon$. The necessary and sufficient condition for the existence of the poles comes from Proposition 3.4. The inequalities on $\alpha$ transfer to $\omega$ by equation (11.9).

11.6 Asymptotics in the cone

We now compute the exponential decay rate in terms of the polar coordinate in the cone.

Proposition 11.3

(Exponential decay rate) For $\alpha$ and $\omega$ previously defined and linked by (11.9) we have

$$\begin{aligned} r\cos (\alpha ) x(\alpha )+ r\sin (\alpha ) y(\alpha )=2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{\omega -\theta }{2} \right) \end{aligned}$$

(11.17)

and

$$\begin{aligned} r\cos (\alpha ) x(\alpha ^*)+ r\sin (\alpha ) y(\alpha ^*)=2\rho |\widetilde{\mu }| \sin ^2 \left( \frac{2\omega -\omega ^*-\theta }{2} \right) . \end{aligned}$$

(11.18)

Proof

By Equations (11.8) and (11.13) we obtain the desired result.

Proofs of Theorems 1, 2 and 3

Equation (11.5) and Propositions 11.1, 11.2, 11.3 combined to Theorem 4 (resp. Theorems 5 and 6), lead to Theorem 1 (resp. Theorems 2 and 3).

Appendices

Appendix A: Parameter-dependent Morse lemma

The following lemma is a parameter-dependent Morse lemma. Although it is an intuitive result, we could not find it in the existing literature.

Lemma A.1

Assume that $\alpha _0\in \mathbb {R}$ is a constant, $\alpha \mapsto x(\alpha )$ is a function which is $\mathcal {C}^\infty$ near $\alpha _0$, and $(x,\alpha )\mapsto F(x,\alpha )$ is a function which is analytic as a function of the first variable x and $\mathcal {C}^\infty$ as a function of the second variable $\alpha$ near $(x(\alpha _0),\alpha _0)$. Furthermore, assume that for all $\alpha$ near $\alpha _0$ we have

$$\begin{aligned} F(x(\alpha ), \alpha )=0, \quad F'_x(x(\alpha ), \alpha )=0, \quad F''(x(\alpha ), \alpha )>0. \end{aligned}$$

There exists a neighborhood of $(0, \alpha _0)$ in ${\mathbb {C}} \times {\mathbb {R}}$

$$\begin{aligned} \Omega (0, \alpha _0)=\{ (\omega , \alpha ) \in {\mathbb {C} \times \mathbb {R}}: |\omega |\le K, |\alpha -\alpha _0|\le \eta \} \end{aligned}$$

with some $K, \eta >0$ and a function $x(\omega , \alpha )$ defined in $\Omega (0, \alpha _0)$ such that

$$\begin{aligned}{} & {} F(x(\omega , \alpha ), \alpha ) =\omega ^2, \ \ \forall \omega : |\omega |\le K\\{} & {} x(0, \alpha ) = x(\alpha ) \ \ \forall \alpha : |\alpha -\alpha _0| \le \eta . \end{aligned}$$

Furthermore $x(\omega , \alpha )$ is in the class $\mathcal {C}^\infty$ as function of three real variables ${\Re }\omega , {\Im } \omega , \alpha$ and holomorphic of $\omega$ for any fixed $\alpha$. Finally

$$\begin{aligned} x'_\omega (0, \alpha ) = \sqrt{\frac{2}{F''_x(x(\alpha ), \alpha )) } } . \end{aligned}$$

(A.1)

Proof

This is an adaptation of Morse’s lemma to the dependence of the parameter $\alpha$. Consider $T(z,\alpha )=F(z+x(\alpha ), \alpha )$. Then $T(0, \alpha )=0$, $T'_z(0, \alpha ) =0$ and $T''_z(0, \alpha ) = F''_x(x(\alpha ), \alpha )>0$ for any $\alpha$ close to $\alpha _0$. Then the following representation holds

$$\begin{aligned} T(z, \alpha )=z^2 F''_x(x(\alpha ), \alpha )/2 +z^3 h(z, \alpha ) \end{aligned}$$

(A.2)

which allows us to define

$$\begin{aligned} S(z,\alpha )= z\sqrt{ F''_x(x(\alpha ), \alpha )/2 + z h(z,\gamma )} \end{aligned}$$

with one of two branches of the square root. Let us choose the one that takes the value $+F''_x(x(\alpha ), \alpha )/2$ at $z=0$. Due to elementary properties of the function F and the fact that $x(\alpha )$ is in class $\mathcal {C}^\infty$, the function $h(z,\alpha )$ in the representation of T above is in class $\mathcal {C}^\infty$ in a neighborhood of ${\mathcal O}(0, \alpha _0) \subset {\mathbb {C}} \times {\mathbb {R}}$ as a function of three real variables and also holomorphic in z for any fixed $\alpha$. Furthermore,

$$\begin{aligned} S'_z (0, \alpha _0) = F''_x(x(\alpha _0), \alpha _0)/2 \ne 0. \end{aligned}$$

(A.3)

Then by the implicit function theorem (the real one to establish the announced properties in ${\mathbb {R}}^3$ and the complex one to show the holomorphicity), there exists a function $z(\omega , \alpha )$ in a neighborhood of $(0, \alpha _0)$ which is in the class $\mathcal {C}^\infty$ in three variables and holomorphic in $\omega$ such that

$$\begin{aligned} S(z(\omega , \alpha ), \alpha ) \equiv \omega , \ \ \ \ z(0, \alpha _0)=0. \end{aligned}$$

(A.4)

This means that $T(z(\omega , \alpha ), \alpha )\equiv \omega ^2$ for any couple $(\omega , \alpha )$ in this neighborhood. In particular, the function $z(0, \alpha )$ solves the equation $S(z, \alpha ) \equiv 0$ in the variable z. Since $S'_z(0, \alpha _0)\ne 0$, a function in the class $\mathcal {C}^\infty$ of a real variable $\alpha$ satisfying this equation and vanishing at $\alpha _0$ is unique by the implicit function theorem. But we know already that $S(0, \alpha )=0$ for any $\alpha$ close to $\alpha _0$. Hence, $z(0, \alpha )\equiv 0$ for any $\alpha$ close to $\alpha _0$.

Now, let

$$\begin{aligned} x(\omega , \alpha )=z(\omega , \alpha )+ x(\alpha ), \end{aligned}$$

where $x(\alpha )$ is in the class $\mathcal {C}^\infty$. It satisfies all expected properties. Furthermore $F(x(\omega , \alpha ), \alpha )\equiv \omega ^2$. Differentiating this identity twice, we obtain (A.1).

Appendix B: Technical results

This following lemma is useful in Sect. 10 for finding out how the asymptotics behave as the saddle point approaches the pole.

Lemma B.1

• (i) If $C>0$ is such that $C^2 \ge 1 + \frac{B^2}{A^2}$, then

  $$\begin{aligned} \frac{|s|}{|s+i (A+i B)|} \le C \ \ \forall s \in {\mathbb {R}}. \end{aligned}$$

• (ii) Let $|A| \rightarrow \infty$ and $B=o(A)$ as $|A| \rightarrow \infty$. Then

  $$\begin{aligned} \int _{-\infty }^{\infty } \frac{\exp (-s^2)}{s+i(A+iB)} ds \sim \frac{\sqrt{\pi }}{i(A+iB)}. \end{aligned}$$

• (iii) Let

  $$\begin{aligned} \Pi (w)= \int _{-\infty }^{\infty } \frac{\exp (-s^2)}{s+iw}ds \end{aligned}$$

  with $\Re w \ne 0$. This function is holomorphic in each half plane $\{ w: {\Re }\, w>0\}$ and $\{w: {\Re }\, w<0\}$ and can be made explicit:

  $$\begin{aligned} \Pi (w)= & {} \pi i \exp (w^2)(1-\Phi (-w)) \ \ \forall w: \ {\Re } w<0\\ \Pi (w)= & {} -\pi i \exp (w^2)(1-\Phi (w)) \ \ \forall z: \ {\Re } w>0 \end{aligned}$$

  where $\Phi (w)=\frac{2}{\sqrt{\pi }} \int _0^w \exp (-s^2)ds.$

Proof

• (i) Elementary computation.

• (ii) We have $\int _{-\infty }^{\infty }\frac{\exp (-s^2)}{i(A+ i B)}ds= \frac{\sqrt{\pi } }{i(A+iB )}.$ It suffices to show that

  $$\begin{aligned} \int _{\mathbb {R}} \frac{ |s|}{|s+i(A+iB) |} \exp (-s^2)ds \end{aligned}$$

  converges to 0 for any A with absolute value large enough to have $\frac{|A|}{|B|}\ge 1$. Then by (i) $\frac{|s|}{|s +i(A+iB)|} \le 2$ for any $s \in {\mathbb {R}}$. Since the integral $\int _{\mathbb {R}} 2 \exp (-s^2)ds$ converges, the dominated convergence theorem applies and we get the stated asymptotics.

• (iii) Let us define for any $z>0$ and $w>0$

  $$\begin{aligned} \Pi (z, w)= \int _{-\infty }^\infty \frac{\exp (-zs^2)}{s+i w} ds. \end{aligned}$$

  Then

  $$\begin{aligned} \Pi '_z(z,w)&= \int _{-\infty }^{\infty } \frac{-s^2 \exp (-z s^2) }{s+iw } ds = \int _{-\infty }^\infty \frac{((iw)^2-s^2-(iw)^2)\exp (-z s^2)}{s+iw } ds\\&= \int _{-\infty }^{\infty } (iw-s) \exp (-z s^2)ds + w^2\int _{-\infty }^\infty \frac{ \exp (-z s^2) }{s+iw}ds \\&=iw \sqrt{\frac{\pi }{z}} + w^2 \Pi (w,z). \end{aligned}$$

  Solving this differential equation, we get that $\Pi (w,z)=c(w,z)\exp (w^2z)$ where $c'_z(w,z)= iw \sqrt{\frac{\pi }{z}}\exp (-w^2z)$. Taking into account the fact that $\Pi (+\infty , w)=0$, we obtain

  $$\begin{aligned}{} & {} \Pi (z,w)= -i w \sqrt{\pi } \exp (w^2 z) \int _z^\infty t^{-1/2} \exp (-w^2 t )dt= - i w \sqrt{\pi } \exp (w^2z) \\ {}{} & {} \quad \int _{w\sqrt{z}}^\infty \exp (-s^2)ds\\{} & {} \quad = -i w \pi \exp (w^2 z) \Big (1-\Phi (w \sqrt{z})\Big ). \end{aligned}$$

  Now let $z=1$. Then

  $$\begin{aligned} \Pi (1, w)= -\pi i \exp (w^2) (1-\Phi (w)) \end{aligned}$$

  for any real positive w. The holomorphicity of $\Phi (w)$ in $\{w \in {\mathbb {C}}: \Re w>0 \}$ allows us to prove statement (iii). Finally, we note that for any w with $\Re w<0$, $\Pi (-w)=-\Pi (w)$.

Appendix C: Green’s functions near zero and Laplace transforms near infinity

We introduce the parameter

$$\begin{aligned} \lambda =\frac{\delta +\epsilon -\pi }{\beta } \end{aligned}$$

where $\beta$ is the angle of the cone, and $\epsilon$ and $\delta$ are the angles of reflection which can be expressed in terms of the covariance matrix $\Sigma$ and the reflection matrix R, see Sect. 11. This parameter $\lambda$ is well known in the SRBM literature and is usually denoted by $\alpha$ but to avoid any confusion of notation we have called it $\lambda$ in this article. It is well known that existence conditions of the SRBM stated in (2.1) are equivalent to

$$\begin{aligned} \lambda <1. \end{aligned}$$

Lemma B.2

(Laplace transforms behaviour near infinity and Green’s functions near zero) For some constants $C_1$ and $C_2$, the Laplace transforms $\varphi _1$ and $\varphi _2$ satisfy

$$\begin{aligned} \varphi _1(y)\sim C_1y^{\lambda -1} \text { when } |y|\rightarrow \infty \quad \text {and}\quad \varphi _2(x)\sim C_2x^{\lambda -1} \text { when } |x|\rightarrow \infty \end{aligned}$$

(B.1)

and their derivatives satisfy

$$\begin{aligned} \varphi _1'(y)\sim C_1(\lambda -1)y^{\lambda -2} \text { when } |y|\rightarrow \infty \quad \text {and}\quad \varphi _2'(x)\sim C_2(\lambda -1)x^{\lambda -2} \text { when } |x|\rightarrow \infty . \end{aligned}$$

(B.2)

Furthermore, the Green’s functions on the boundaries $h_1$ and $h_2$ satisfy

$$\begin{aligned} h_1(v)\sim C_1 \Gamma (-\lambda +1) v^{-\lambda } \text { when } |v|\rightarrow 0 \quad \text {and}\quad h_2(u)\sim C_2 \Gamma (-\lambda +1) u^{-\lambda } \text { when } |u|\rightarrow 0, \end{aligned}$$

(B.3)

where $\Gamma$ is the gamma function.

We give the sketch of the proof of the previous Lemma which relies on the resolution of Boundary Value Problem studied in [22]. This lemma is not crucial for establishing the results of this article. It is only used to simplify the proof of Lemma 7.3 which is useful only in the special case where we are looking for the asymptotics along the axes.

Sketch of proof

The article [22] states in Theorem 11 an explicit expression for the Laplace transform $\varphi _1$. This result is obtained by solving a Carleman Boundary Value Problem coming from the functional equation (2.2). The solution is the product of the solution of the corresponding homogeneous problem and an integral, namely,

$$\begin{aligned} \varphi _1(y)=X(W(y))\left( \frac{1}{2\pi }\int _{\mathcal {R}^-} \frac{g(t)}{X^+(t)}\frac{dt}{W(y)-W(t)}+C \right) , \end{aligned}$$

where we have taken the notation of Theorem 11 in [22] and its proof. Since $\frac{g(t)}{X^+(s)}$ converges to 0 when t tends to infinity, the integral $\frac{1}{2\pi }\int _0^1 \frac{g(t)}{X^+(t)}\frac{dt}{W(y)-W(t)}$ converges to a constant when $y\rightarrow \infty$ by classical complex analysis results, see (5.2.17) of [17]. The function X(W(y)) is the solution to the corresponding homogeneous BVP which is studied in detail in the recurrent case in [25]. Proposition 19 of [25] shows that $X(W(y)))\sim y^{\lambda -1}$ when y tends to infinity, which concludes the proof of (B.1).

Integral Hardy-Littlewood Tauberian theorems (see for example Karamata’s theorem and Ikehara’s theorem [44, §7.4 & 7.5] and [13, Thm 33.3 & 33.7]) state that, with some hypotheses, for a function f and its Laplace transform $\mathcal {L}(f)$, for $\lambda \geqslant -1$, $f(t)\sim C t^{-\lambda }$ when $t\rightarrow 0$ is equivalent to $\mathcal {L}(f)(x)\sim C \Gamma (-\lambda +1) x^{\lambda -1}$ when $x\rightarrow \infty$. Equation (B.3) follows from a Tauberian theorem and from (B.1).

The proof of (B.2) follows from (B.3), from a Tauberian theorem and from the properties of the derivative of the Laplace transform, namely $\mathcal {L}(tf(t))=\frac{d}{dx}\mathcal {L}(f)(x)$.