A note on “new quantum key agreement protocols based on Bell states”

Abstract

We remark that the quantum key agreement protocol (Yang et al. in Quantum Inf Process 18(10):322, 2019) is flawed. It is unnecessary for Bob to prepare his secret key $K_B$, because it is finally announced and accessible to adversaries. We find, $K_B$ has no relation to the confidentiality of the final agreed key $K_{AB}=K_A\oplus K_B$. It is just a key transfer scheme, not a general key agreement scheme. We also find there is short of a code for Bob to extract bits from the measured results.

1 Introduction

Very recently, Yang et al. [4] have presented a quantum key agreement protocol based on Bell states. It relies on that the intended receiver, Bob, cannot discriminate between the particles in Bell states and decoy particles. If two particles Bob measures with Bell basis are uncorrelated, the measurement result can be any of the four Bell states with equal probability.

Though the Yang et al.’s scheme is interesting, we find it is flawed. Since Bob’s secret key $K_B$ is finally announced and accessible to adversaries, $K_B$ has no relation to the confidentiality of the final agreed key $K_{AB}=K_A\oplus K_B$. Naturally, it is just a key transfer scheme, not a general key agreement scheme. We also find it does not specify a code for Bob to extract bits from the measured results.

2 Review of the scheme

There are two entities, Alice and Bob, who randomly generate the secret keys $K_A$ and $K_B$, respectively

$$\begin{aligned} K_A=\{k_1^A, k_2^A, \ldots , k_{2N}^A\}, ~ K_B=\{k_1^B, k_2^B, \cdots , k_{2N}^B\}, \end{aligned}$$

where $k_i^A, k_i^B\in \{0, 1\}$. The intended receiver, Bob, will measure the decoy particles with X or Z basis randomly, where

$$\begin{aligned} X=\left[ \begin{array}{cc} 0 &{}\quad 1 \\ 1 &{}\quad 0 \\ \end{array} \right] ,~~ Z= \left[ \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad -1 \\ \end{array} \right] . \end{aligned}$$

Alice is responsible for generating the Bell states,

$$\begin{aligned} |\beta _{ij}\rangle =\frac{1}{\sqrt{2}} \left( |0\,j\rangle +(-1)^i|1\,\bar{j}\rangle \right) , \end{aligned}$$

where $i, j\in \{0, 1\}, \bar{j}=j\oplus 1$. The scheme can be described as follows.

• 1. Alice prepares the sequence $S_A$ of N Bell states. For the i-th Bell state, where $i\in \{1, 2, \cdots , N\}$, she prepares it in the state

  $$\begin{aligned} |\beta _{k^A_{2i-1}k^A_{2i}\rangle }=\frac{1}{\sqrt{2}}\left( |0k^A_{2i}\rangle +(-1)^{k^A_{2i-1}}|1\overline{k^A_{2i}}\rangle \right) \end{aligned}$$

  and prepares 2N decoy particles each of which is randomly chosen from the four non-orthogonal states $\{|0\rangle , |1\rangle , |+\rangle , |-\rangle \}$. She inserts them into $S_A$ randomly to obtain a new sequence $S_A^{\prime }$. Send $S_A^{\prime }$ to Bob via the quantum channel.

• 2. Bob announces $K_B$ to Alice via an authenticated classical channel.

• 3. Alice tells Bob the positions of decoy particles in the sequence $S_A^{\prime }$, and computes the agreement key $K_{AB}=K_A\oplus K_B$.

• 4. Bob measures the corresponding decoy particles with X or Z basis randomly. Publish his measurement outcomes and the basis corresponding to the decoy particles.

• 5. Alice computes the error rate. If it exceeds the preset threshold, she abandons the process and restart.

• 6. Bob removes the decoy particles from the sequence $S_A^{\prime }$ to recover $S_A$. He then performs Bell-basis measurement on the N Bell states to recover $K_A$ and obtain $K_{AB}=K_A\oplus K_B$.

Table 1 Yang et al.’s quantum key agreement scheme

Table 2 The code for basis and polarizations in BB84 protocol

3 Analysis

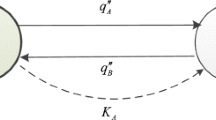
The Yang et al.’s scheme can be depicted as below (see Table 1). We now remark that the scheme has some shortcomings.

$\bullet$ It is unnecessary for Bob to prepare his secret key $K_B$. As we see, $K_B$ is finally announced and accessible to the adversary. If it is not accessible to the adversary, there must be a secure channel between Alice and Bob, which ensures the confidentiality of $K_B$. In this case, Alice can simply make use of the secure channel to transfer $K_A$.

Table 3 Prototype of Yang et al.’s quantum key agreement scheme

$\bullet$ It is not a general key agreement scheme. We find that $K_B$ has no relation to the confidentiality of the final agreed key $K_{AB}=K_A\oplus K_B$ because $K_B$ is universally accessible. Actually, it is just a key transfer scheme, not a key agreement scheme. As for the differences between key transfer and key agreement, we refer to [3]. More precisely, we want to stress that the scheme is a quantum encryption [2], which can be directly used to encrypt the classical message $K_A$.

$\bullet$ There is short of a code for Bob to extract bits from the measured results. In the end, Bob has to measure the sequence $S_A$ in order to extract the encoded key $K_A$. These measurements are not deterministic, otherwise the adversary can figure out $K_A$ by man-in-middle attack. We want to stress that a classical signal state, s, can be uniquely represented as a bit, i.e., $s\rightarrow \{0, 1\}$. A quantum signal state qs, however, should be compounded with the measuring basis B so as to be represented as a bit, i.e., $(qs, B) \rightarrow \{0, 1\}$. The strength of BB84 [1] just comes from the bilingual code (Table 2), and that an unknown polarization cannot be deterministically measured by the adversary, even by the intended receiver, Bob. But the scheme has forgotten to specify such a code.

$\bullet$ The phrase of authenticated classical channel is misunderstood. In the classical cryptography, an authenticated channel can be used to authenticate either the transferred message or the identities of sender and receiver. To construct an authenticated channel, it is usual to make use of message authentication code (MAC) or public key encryption. But for a quantum cryptographic scheme, it always assumes that the current public key encryption based on mathematical intractability is insecure. Thus, one needs to use MAC to construct the authenticated classical channel in quantum key agreement schemes. This is a PARADOX, because MAC requires that the sender and receiver share a same password. Clearly, there does not exist such a shared password in the quantum key agreement scheme. That is to say, Alice and Bob need to use other methods, for instance, voice or video communication, to authenticate each other.

$\bullet$ The claim that the security against passive attack from the outside eavesdropper is not sound. It wrote:

In the proposed protocol, Alice’s key $K_A$ is transmitted via the quantum channel while $K_B$ is announced by Bob via the authenticated classical channel. If $K_A$ is kept secret and $K_B$ is generated independently, an outside attacker is unable to derive $K_{AB}$ where the security is ensured by the one-time pad.

Apparently, it argues that the confidentiality of $K_{AB}$ is ensured by the one-time pad. The claim is false, because $K_B$ which is universally accessible cannot be viewed as one-time secret key.

In fact, the prototype of Yang et al.’s scheme can be depicted as below (see Table 3). The parameter, $K_B$, has no relation to the subsequent operations, such as Alice’s computation of the error rate, Bob’s measuring of the decoy particles and publishing of the measurement outcomes and basis. It is only used to combine the key $K_{AB}=K_A\oplus K_B$. As we stressed before, the parameter $K_B$ is public. So, the true confidentiality results from that whether Bob can remove the decoy particles from $S_A^{\prime }$ to recover the original sequence $S_A$, after Alice discloses the positions of decoy particles in $S_A^{\prime }$.

4 Conclusion

We show that the Yang et al.’s quantum key agreement scheme is flawed, and some popular phrases in the classical cryptography have been unconcernedly used. We hope this note could correct some misunderstandings about such quantum key agreement schemes.