1 Introduction

The notion of quantum entanglement was first described by Einstein et al. [1] and Schrödinger [2] as one of the most peculiar phenomenon of quantum mechanics in which the global states of a compound quantum system cannot be written as a product of the states of individual subsystems [3]. Since then, this strange phenomenon has been recognized as an indispensable resource for many potential applications in quantum computing [4], quantum information processing [5,6,7] and quantum technologies [8, 9]. However, the practical utilization of entanglement in the above-mentioned fields is hardly constrained by the obstacle imposed by the environmental decoherence, stemming from the fact that every real quantum system is never truly isolated from its external environment, which leads to the degradation of quantum coherence and consequently the destruction of entanglement and in the worst of the case its complete disappearance. Therefore, in order to understand how the system loses entanglement to the external environment and search effective techniques to recover entanglement and enhance its robustness, it is of great importance to study the effects of various noisy environments described either in their classical or quantum mechanical pictures, on the dynamics of entanglement. So far, some approaches such as quantum error correction [10, 11] and quantum Zeno effect [12, 13], and also preparing the input state of the system in the decoherence-free subspace [14] which effectively decouples the system dynamics from its environment [15] have been proposed in the literature to reverse the detrimental effects of the environment. Nevertheless, in recent years the evolution of entanglement under several models of environment has been a subject of active research for both bipartite and multipartite quantum systems [16,17,18,19,20,21,22,23,24]. However, a number of theoretical works examining the dynamics of entanglement in multipartite systems are focused only on the entanglement among different bipartite cuts (bipartitions) of the global system [25,26,27,28]. This is mainly due to the fact that apart for bipartite systems in pure state [4] and two-qubit system in mixed states [29], the quantification and characterization of the exact value of entanglement in multipartite quantum systems remain a very hard task [30] and have been calculated only for particular models of decoherence and particular quantum states [7]. However, due to recent progress in the theory of multipartite entanglement, some efficient and calculable entanglement measures that can capture the global information of multipartite systems such as the lower bounds of concurrence [31] and the multipartite negativity [32] have been designed.

In recent years, a number of theoretical works have analyzed the dynamics of quantum correlations in two uncoupled qubits interacting with an external classical environment characterized either by a Gaussian [33] or by a non-Gaussian noise [34,35,36]. More precisely, two relevant classes of non-Gaussian noise, namely the random telegraph noise (RTN) with a Lorentzian spectrum and the low-frequency noise with \( 1/f^{\alpha } \) spectrum, have been widely examined. Motivated by the recent progress in the theory of multipartite quantum correlations, some of the above-mentioned works have been extended from two-qubit systems to multi-qubit systems and some results which add interesting insights on the topics of the dynamics of multipartite quantum system in classical environments have been obtained. For instance, Buscemi et al. [30] have discussed the time evolution of quantum discord and entanglement in a model of three non-interacting qubits under local and non-local RTN. Also, Kenfack et al. [17, 18] have investigated the effects of classical static noise on the dynamics of quantum correlations for a system of three qubits and have demonstrated that suitable environment engineering allows preservation of quantum correlations indefinitely. However, to our knowledge, the evolution of quantum correlations in multi-qubit systems interacting with the low-frequency noise with \( 1/f^{\alpha } \) spectrum has not been investigated yet.

In the present paper, by using approaches already used elsewhere [34, 35, 37, 38] for a two-qubit system, we intend to analyze the dynamics of entanglement in a physical model consisting of three uncoupled qubits subject to a classical colored noise, i.e., \( 1/f^{\alpha } \) noise, in a common environment (CE), mixed environments (ME) and independent environments (IE). The \( 1/f^{\alpha } \) noise is introduced as a stochastic process affecting the single-qubit transition amplitudes. Three different input configurations of the qubit, namely the GHZ-type states, the W-type states and the mixed states composed of a GHZ and a W state, are investigated for two different configurations of the noise. In the first configuration, the \( 1/f^{\alpha } \) noise arises from the interaction of each qubit with a single random bistable fluctuator (RBF) with an undetermined switching rate, whereas in the second case it stems from the interaction of each qubit with a large number N of RBFs with fixed switching rates, distributed according to a proper distribution function. However, it is worth noting that even if similar works have already been investigated for a two-qubit system [34, 35], the study for a three-qubit system seems quite promising since here the entanglement derives from a more complex scenario, and consequently, more strange phenomena are expected.

The interest of studying the \( 1/f^{\alpha } \) noise arises from the fact that it is a ubiquitous noise in nature and affects almost all superconductor and semiconductors nanodevices. Concretely speaking, it is a serious interference that limits the proper working of electronic devices at low frequencies since it represents the main sources of decoherence in superconducting and solid-state qubits [39,40,41,42]; magnetic, silicon and vortex matter systems [43,44,45]. It is interesting to note that the \( 1/f^{\alpha } \) noise was first observed in 1925 by Johnson while studying the current fluctuations of electronic emission in a thermionic tube [46] and that the color of the noise depends upon the value of the exponent \( \alpha \) which is always a positive number. More precisely, two interesting cases, namely \( \alpha =1 \) and \( \alpha =2 \), are often examined. The former corresponds to the so-called pink or 1 / f noise which is obtained from a set of random telegraph fluctuators weighted by the inverse of the switching rate [34], while the latter corresponds to the so-called brown or \( 1/f^{2} \) noise. The evolution of the three-qubit system under the effect of the noise is obtained by performing two ensemble averages operation on the evolved density matrix of the global system: the first average operation is over all the possible realizations of the noise phase and the second one is over all the possible choices for the switching rates. Once the three-qubit density matrix in the three different scenarios of CE, ME and IE coupling is obtained, we employ the tripartite negativity and suitable entanglement witnesses to characterize the effects of the noise on the evolution of the initial entanglement existing between the three qubits.

This paper is structured as follows: In Sect. 2, we briefly review the definition of the tripartite negativity and entanglement witnesses. In Sect. 3, we describe the physical model consisting of three uncoupled qubits subject to a classical colored noise generated either by a single RBF or by a collection of RBFs. In Sect. 4, we provide the time evolution of entanglement for the three different setups of the qubit–noise coupling. Finally, we summarize the paper in Sect. 5.

2 Measures of entanglement in tripartite systems

In this section, we briefly illustrate the correlations measures adopted in our work to quantify and characterize the tripartite entanglement. Note that the material presented in this section is already known in the literature and we cite it appropriately. As mentioned previously, in order to quantify, characterize and detect the tripartite entanglement we employ the tripartite negativity and the concepts of entanglement detection.

2.1 Tripartite negativity

For a tripartite system in mixed states \( \rho \equiv \rho _{123} \), the tripartite negativity is defined as [47]

$$\begin{aligned} {\mathcal {N}}^{(3)}(\rho _{123})=\root 3 \of {{\mathcal {N}}_{1-23} {\mathcal {N}}_{2-13}{\mathcal {N}}_{3-12}}, \end{aligned}$$
(1)

By virtue of this equation, \( {\mathcal {N}}^{(3)}(\rho ) \) is nonzero if and only if the system contains genuine or full tripartite entanglement, i.e., entanglement between any bipartition cut is nonzero. \( {\mathcal {N}}_{I-JK}=-\,2\sum \nolimits _{\imath }|\lambda _{\imath }(\rho ^{T_{I}})|\) characterizes the bipartite negativity between the subsystem I and the compound system JK with \( I\in \{1, 2,3\}\) and \( JK\in \{12, 13, 23\}\), respectively. \( \left\{ \lambda _{\imath }(\rho ^{T_{I}})\right\} \) are the negative eigenvalues of the partial transpose of the total density matrix \( \rho \) with respect to the subsystem I. It is interesting to note that the tripartite negativity given in Eq. (1) is the geometric average of the bipartite negativity that corresponds to the possible bipartite cuts of the system and that it cannot be used to discriminate different classes of tripartite entanglement. In addition, apart from pure states, null tripartite negativity could indeed not imply the absence of entanglement [30].

2.2 Entanglement witnesses

Nowadays, it is well established that entanglement witnesses are one of the main methods to detect entanglement experimentally [48]. As the tripartite negativity, the density matrix is requisite to decide whether the state is entangled or not. An observable \( {\mathcal {W}} \) is called an entanglement witness if it satisfies the following properties [48]: \( {{\mathrm{Tr}}}({\mathcal {W}}\rho _{s})\ge 0\) for every separable state \( \rho _{s} \) and \( {{\mathrm{Tr}}}({\mathcal {W}}\rho _{e})<0 \) for at least one entangled state \( \rho _{e} \). Therefore, for any given mixed state \( \rho \), if we measure \( {{\mathrm{Tr}}}({\mathcal {W}}\rho )<0 \) we conclude that the state \( \rho \) is entangled. However, \( {{\mathrm{Tr}}}({\mathcal {W}}\rho )<0 \) is a sufficient but not a necessary condition for identifying the state \( \rho \) as an entangled state, i.e., \( {{\mathrm{Tr}}}({\mathcal {W}}\rho )\ge 0\) do not guarantee the absence of entanglement. Some details about the construction of entanglement witnesses can be found in Ref. [48]. For the three-qubit GHZ- and W-type states, the appropriate witnesses that we will use in this paper are, respectively [49, 50]

$$\begin{aligned} {\mathcal {W}}_\mathrm{GHZ}=\dfrac{1}{2}{\mathbb {I}}_{8}-|\hbox {GHZ}\rangle \langle \hbox {GHZ}|, \end{aligned}$$
(2)

and

$$\begin{aligned} {\mathcal {W}}_{W}=\dfrac{2}{3}{\mathbb {I}}_{8}-|W\rangle \langle W|. \end{aligned}$$
(3)

where \( |\hbox {GHZ}\rangle =\dfrac{1}{\sqrt{2}}\left( |000\rangle +|111\rangle \right) \) and \( |W\rangle =\dfrac{1}{\sqrt{3}}\left( |001\rangle +|010\rangle +|100\rangle \right) \), respectively. Let us note that \( {\mathcal {W}}_\mathrm{GHZ} \) is a GHZ class witness that distinguishes GHZ-type states from separable states and likewise, \( {\mathcal {W}}_{W} \) is a W class witness that distinguishes W-type states from separable states.

3 The physical model

The model which we intend to study in this paper consists of three non-interacting qubits, initially entangled, subject to a noisy classical environment with noise spectra of the type \( 1/f^{\alpha } \), which are realized by different configurations of RBF. As shown in Fig. 1, three different setups of the qubit–environment (Q-E) coupling, namely IE, ME and CE, are investigated: in the first setup, each qubit locally interacts with its external environment; in the second setup, two of the three qubits locally interact with a unique common external environment and the remaining qubit with its own local external environment, and finally, in the third setup all the three qubits are coupled with a unique common external environment. Each local external environment is constituted by a collection of N RBFs.

Fig. 1
figure 1

Schematic representations of the different qubit–environment coupling configurations studied in this paper: a independent environments (IE), b mixed environments (ME) and c common environment (CE). The blue, yellow and green dotted lines represent the entanglement among the qubits, while the wavy lines show the interaction of each qubit with a collection of N classical bistable fluctuators. Let us note that, in the case of IE and ME coupling, there is an indirect interaction between the local environments due to the initial correlations existing between the states of the qubits. On the other hand, in the IE coupling setup, the whole system has 3N degree of freedom, while in the other configurations, it has 2N (ME coupling) and N (CE coupling) degrees of freedom, respectively (Color figure online)

Full size image

In the above Q-E coupling setups, the evolution of the three-qubit is governed by the following effective Hamiltonian (in units of \( \hbar =1 \))

$$\begin{aligned} {\mathcal {H}}(t)={\mathcal {H}}_{1}(t)\otimes {\mathbb {I}}_{2} \otimes {\mathbb {I}}_{3}+{\mathbb {I}}_{1}\otimes {\mathcal {H}}_{2}(t) \otimes {\mathbb {I}}_{3}+{\mathbb {I}}_{1}\otimes {\mathbb {I}}_{2}\otimes {\mathcal {H}}_{3}(t), \end{aligned}$$
(4)

where \( {\mathbb {I}}_{l} (l=1,2,3)\) stands for the identity operator acting on the subspace of the qubit l, \({\mathcal {H}}_{l}(t) \) denotes the Hamiltonian of a single qubit interacting with a collection of N RBFs and can be explicitly expressed as

$$\begin{aligned} {\mathcal {H}}_{l}(t)=\omega _{0}{\mathbb {I}}_{l}+\sigma _{x}^{l} \sum \limits _{j=1}^{N}\lambda _{j}\vartheta _{j}^{l}(t). \end{aligned}$$
(5)

In the above equation, \( \omega _{0} \) is the qubit energy in the absence of noise (energy degeneracy is assumed), \( \sigma _{x}^{l} \) represents the spin-flip Pauli matrix in the subspace of the qubit l, \( \lambda _{j} \) characterizes the strength of the interaction of each single qubit with the jth RBF and \(\vartheta _{j}^{l}(t) \) denotes the stochastic process describing the jth RBF with a switching rate \( \gamma _{l,j} \) distributed according to a specific probability law. The model Hamiltonian of Eq. (5) can describe an effective evolution of a quantum particle trapped in a symmetric double-well potential [51] and coupled to a spin-chain environment in which each spin behaves as a RBF.

As mentioned in introduction, two different kinds of noise are analyzed: the pink ( \( \alpha =1 \)) and brown (\( \alpha =2 \)) noises. In the former, the probability distribution of each switching rate \( \gamma _{l,j} \) can be written as [34, 35]

$$\begin{aligned} {{\mathrm{P}}}(\gamma _{l,j})=\dfrac{1}{\gamma _{l,j}\ln (\gamma _{\max }/ \gamma _{\min })}, \end{aligned}$$
(6)

while in the latter, it takes the following form

$$\begin{aligned} {{\mathrm{P}}}(\gamma _{l,j})=\dfrac{1}{\gamma _{l,j}^{2}} \left[ \dfrac{\gamma _{\min }\gamma _{\max }}{\gamma _{\max }-\gamma _{\min }}\right] . \end{aligned}$$
(7)

In the previous equations, \( \gamma _{\min } \) and \( \gamma _{\max } \) are, respectively, the minimum and the maximum values of the switching rate considered. On the other hand, it is worth nothing that the stochastic processes \( \vartheta _{j}^{1} \), \( \vartheta _{j}^{2} \) and \( \vartheta _{j}^{3} \) are totally uncorrelated in the case of IE coupling, whereas they are totally correlated for the case of CE coupling. Hence, for the sake of simplicity, we will assume that \( \vartheta _{j}^{1}\ne \vartheta _{j}^{2}\ne \vartheta _{j}^{3} \) in the case of IE coupling and that \( \vartheta _{j}^{1}= \vartheta _{j}^{2}= \vartheta _{j}^{3} \) in the case of CE coupling. However, in the case of ME coupling, we will assume that \( \vartheta _{j}^{1}= \vartheta _{j}^{2}\ne \vartheta _{j}^{3} \). Due to the random nature of the noise parameter \( \vartheta _{j}^{l}(t) \), the time-dependent Hamiltonian of Eq. (5) is stochastic and leads to a stochastic evolution of the quantum states [30]. Therefore, in order to evaluate the density matrix describing the system under the influence of \( 1/f^{\alpha } \) noise, we need to perform two average operations, one over the different choices of the stochastic process \( \vartheta _{l}(t) \) and the other one over the different choices of the switching rate \( \gamma _{l} \). The evolution of the initial state of the system can thus be written as

$$\begin{aligned} \rho (t)=\left\langle \left\langle {\mathcal {U}}(\left\{ \vartheta _{l}\right\} ,t )\rho (0){\mathcal {U}}(\left\{ \vartheta _{l}\right\} ,t )^{\dagger }\right\rangle _{\left\{ \vartheta (t)\right\} } \right\rangle _{\left\{ \gamma \right\} }, \end{aligned}$$
(8)

where \( \rho (0) \) is the initial state of the system and

$$\begin{aligned} {\mathcal {U}}(\left\{ \vartheta _{l}\right\} ,t )={\mathcal {U}}(\vartheta _{1},t )\otimes {\mathcal {U}}(\vartheta _{2},t )\otimes {\mathcal {U}}(\vartheta _{3},t ), \end{aligned}$$
(9)

stands for the global unitary time evolution operator of the system at time t for a given noise configuration \( \left\{ \vartheta (t)\right\} =\left\{ \vartheta _{1},\vartheta _{2},\vartheta _{3}\right\} \) with \( \vartheta _{l}(t)=\sum \nolimits _{j=1}^{N}\vartheta _{j}^{l}(t) \). As initial state of the system, we will consider the following states: the GHZ-type states given by

$$\begin{aligned} \rho _\mathrm{GHZ}(0)=r|\hbox {GHZ}\rangle \langle \hbox {GHZ}|+\dfrac{1-r}{8}{\mathbb {I}}_{8}, \end{aligned}$$
(10)

the W-type states given by

$$\begin{aligned} \rho _{W}(0)=r|W\rangle \langle W|+\dfrac{1-r}{8}{\mathbb {I}}_{8}, \end{aligned}$$
(11)

and finally the mixed states composed of a GHZ state and a W state given by

$$\begin{aligned} \rho _{\mathrm{GHZ}-W}(0)=p|\hbox {GHZ}\rangle \langle \hbox {GHZ}|+(1-p)|W\rangle \langle W|. \end{aligned}$$
(12)

In the previous initial states, r is the initial state purity ranging from 0 to 1, \( {\mathbb {I}}_{8} \) is the identity matrix of dimension 8, the parameter p is the mix probability of the GHZ and W states, \( |\hbox {GHZ}\rangle =\dfrac{1}{\sqrt{2}}\left( |000\rangle +|111\rangle \right) \) and \( |W\rangle =\dfrac{1}{\sqrt{3}}\left( |001\rangle +|010\rangle +|100\rangle \right) \). It is worth noting that when the probability \( p=1 \), the mixed state of Eq. (12) becomes the pure GHZ state, while when \( p=0 \) it becomes the pure W state.

In the following, we will assume that all the RBFs have roughly the same coupling constant with the qubits, i.e., \( \lambda _{j}\equiv \lambda \). With the help of the Hamiltonian given in Eq. (5), we can write the single-qubit time-evolution operator \({\mathcal {U}}(\vartheta _{l},t ) \) as

$$\begin{aligned} {\mathcal {U}}(\vartheta _{l},t )=e^{-i\int \limits _{0}^{t}{\mathcal {H}}_{l}(t')\,dt'} =\exp \left[ -\,i\left( \omega _{0}t{\mathbb {I}}_{l}+\varphi _{l}(t)\sigma _{x}^{l}\right) \right] , \end{aligned}$$
(13)

where \( \varphi _{l}(t)=\sum \nolimits _{j=1}^{N}\lambda \int \limits _{0}^{t}\vartheta _{j}^{l}(t')\,dt' \) is the total noise phase picked up during the time interval [0, t] and characterized by the following distribution \( {{\mathrm{P}}}(\varphi _{l},t)=\prod \nolimits _{j=1}^{N}{{\mathrm{P}}}(\varphi _{j}^{l},t) \) with \( {{\mathrm{P}}}(\varphi _{j}^{l},t) \) the probability distribution of the noise phase \( \varphi _{j}^{l}(t)= \lambda \int \limits _{0}^{t}\vartheta _{j}^{l}(t')\,dt'\) induced in the state of each single qubit by the jth RBF and whose explicit form can be written as [38, 52]

$$\begin{aligned} P\left( \varphi _{j}^{l},t\right)= & {} \frac{1}{2}e^{\displaystyle -\gamma _{l,j} t}\Bigg \{\Big [\delta (\varphi _{j}^{l}-\lambda t) +\delta (\varphi _{j}^{l}+\lambda t)\Big ]+\frac{\gamma _{l,j}}{\lambda }\Bigg [\begin{aligned}&\varTheta (\varphi _{j}^{l}+\lambda t)\\&\quad +\varTheta (\varphi _{j}^{l}-\lambda t) \end{aligned}\Bigg ]\Bigg \} \nonumber \\&\times \Bigg [\frac{I_{1}\Big (\gamma _{l,j} t\sqrt{1-(\varphi _{j}^{l}/\lambda t)^{2}}\Big )}{\sqrt{1-(\varphi _{j}^{l}/\lambda t)^{2}}}+I_{0}\Big (\gamma _{l,j} t\sqrt{1-(\varphi _{j}^{l}/\lambda t)^{2}}\Big )\Bigg ]. \end{aligned}$$
(14)

where \(\delta (x)\) is the Dirac delta function, \(I_{k}(x)\) is the modified Bessel function and \(\varTheta (x)\) is the Heaviside step function. In Eq. (8), \( \left\langle \ldots \right\rangle _{\left\{ \vartheta (t)\right\} } \) denotes the average over the different choices of the stochastic process \( \vartheta (t) \) and corresponds to the integral

$$\begin{aligned} \left\langle \ldots \right\rangle _{\left\{ \vartheta (t)\right\} }\equiv \left\langle \ldots \right\rangle _{\left\{ \varphi (t)\right\} } =\int (\ldots ){{\mathrm{P}}}\left( \left\{ \varphi \right\} ,t\right) \,d\left\{ \varphi \right\} , \end{aligned}$$
(15)

with

$$\begin{aligned} {{\mathrm{P}}}\left( \left\{ \varphi \right\} ,t\right) \,d\left\{ \varphi \right\} =\prod \limits _{j=1}^{N}\left( \prod \limits _{k}^{}{{\mathrm{P}}}(\varphi _{j}^{k},t)\,\mathrm{d}\varphi _{j}^{k}\right) , \end{aligned}$$
(16)

where \( k=1,2,3 \) in the case of IE coupling, \( k=1,3 \) in the case of ME coupling and finally \( k=1 \) in the case of CE coupling. On the other hand, \( \left\langle \ldots \right\rangle _{\left\{ \gamma \right\} } \) is the average over the possible choices of the switching rate and corresponds also to the integral

$$\begin{aligned} \left\langle \ldots \right\rangle _{\left\{ \gamma \right\} }=\int _{\gamma _{\min }}^{\gamma _{\max }}(\ldots ){{\mathrm{P}}}\left( \left\{ \gamma \right\} \right) \,d\left\{ \gamma \right\} , \end{aligned}$$
(17)

with

$$\begin{aligned} {{\mathrm{P}}}\left( \left\{ \gamma \right\} \right) \,d\left\{ \gamma \right\} =\prod \limits _{j=1}^{N}\left( \prod \limits _{k}^{}{{\mathrm{P}}}(\gamma _{k,j})\,\mathrm{d}\gamma _{k,j} \right) . \end{aligned}$$
(18)

It is worth noting that in order to evaluate the time-evolved density matrix of Eq. (8), we need to estimate the averages of the type \( \left\langle \left\langle \left[ \cos (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \right\rangle _{\left\{ \gamma \right\} } \) and \( \left\langle \left\langle \left[ \sin (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \right\rangle _{\left\{ \gamma \right\} } \). By following the approach of Ref. [38], the averaged terms of the type \( \left\langle \left[ \cos (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \) and \( \left\langle \left[ \sin (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \) can be expressed in terms of the characteristic function of the total noise phase

$$\begin{aligned} \left\langle \exp \left[ \pm \, in\varphi _{l}(t)\right] \right\rangle = \left\langle \prod \limits _{j=1}^{N}\exp \left[ \pm \, in\varphi _{j}^{l}(t)\right] \right\rangle , \end{aligned}$$
(19)

which, in turn, can be expressed as

$$\begin{aligned} \left\langle \exp \left[ \pm in\varphi _{l}(t)\right] \right\rangle =\prod \limits _{j=1}^{N} G_{n\lambda }(\gamma _{l,j},t), \end{aligned}$$
(20)

where the function \( G_{n\lambda }(\gamma _{l,j},t) \) is the characteristic function of the noise phase induced in the state of each single qubit by the jth RBF and can be expressed as

$$\begin{aligned} G= \left\{ \begin{aligned}&\displaystyle e^{\displaystyle -\gamma _{l,j} t}\left[ \cosh (\delta _{n\lambda } t)+\dfrac{\gamma _{l,j}}{\delta _{n\lambda }}\sinh (\delta _{n\lambda } t)\right] \quad \text {for}\;\,\dfrac{\gamma _{l,j}}{n\lambda }>1 \\\\&\displaystyle e^{\displaystyle -\gamma _{l,j} t}\left[ \cos (\delta _{n\lambda } t)+\dfrac{\gamma _{l,j}}{\delta _{n\lambda }}\sin (\delta _{n\lambda } t)\right] \quad \text {for}\;\,\dfrac{\gamma _{l,j}}{n\lambda }<1 \end{aligned} \right. \end{aligned}$$
(21)

where \( G\equiv G_{n\lambda }(\gamma _{l,j},t) \) and \(\delta _{n\lambda }=\sqrt{|\gamma ^{2}-n^{2}\lambda ^{2}|}\). Hence, from Eq. (20) we can easily compute that

$$\begin{aligned} \begin{aligned}&\left\langle \left[ \cos (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} }=\prod \limits _{j=1}^{N}G_{n\lambda }(\gamma _{l,j},t)\,\, \text {and}\, \\&\left\langle \left[ \sin (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} }=0. \end{aligned} \end{aligned}$$
(22)

Having computed the first average over the different choices of the total noise phase (Eq. (22)), we obtain after performing the calculations from Eq. (17) that

$$\begin{aligned} \left\{ \begin{aligned}&\left\langle \left\langle \left[ \cos (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \right\rangle _{\left\{ \gamma \right\} }= \left[ \int \limits _{\gamma _{\min }}^{\gamma _{\max }}G_{n\lambda }(\gamma ,t){{\mathrm{P}}}(\gamma )\,\mathrm{d}\gamma \right] ^{N}=\eta _{n}(t); \\\\ {}&\left\langle \left\langle \left[ \sin (n\varphi _{l}(t))\right] \right\rangle _{\left\{ \varphi \right\} } \right\rangle _{\left\{ \gamma \right\} }=0. \end{aligned} \right. \end{aligned}$$
(23)

The explicit evaluations of the time-evolved states \( \rho _\mathrm{GHZ}(t) \), \( \rho _{W}(t) \) and \( \rho _{GHZ-W}(t) \), for the different setups of the Q-E coupling, are reported in “Appendices A, B and C”, respectively.

In the following, we will analyze in detail the dynamics of entanglement in the case of pink and brown noises generated either by a single RBF \( (N=1) \) or by a collection of RBFs \( (N>1) \).

4 Results and discussion

In this section, we present and discuss the numerical results of the evolution of entanglement of qubits subjected to \( 1/f^{\alpha } \) noise. Three different setups of the Q-E coupling, namely IE, ME and CE, corresponding to the interaction of the qubits with a single RBF or a collection of RBFs are analyzed. The evolution of entanglement is quantified in terms of the evolution of tripartite negativity and suitable entanglement witnesses. The qubits are initially prepared either in the GHZ-type states, W-type states or in the mixed states given in Eq. (12).

4.1 Colored noise generated by a single random bistable fluctuator \( (N=1) \)

Here, we analyze the case where the \( 1/f^{\alpha } \) noise is due to the interaction of each qubit with a single RBF with an unknown switching rate \( \gamma \) extracted from a distribution \( 1/\gamma \) (Eq. 6) for the case of pink noise and \( 1/\gamma ^{2} \) (Eq. 6) for the case of brown noise. The qubits are affected only by one source of noise, and therefore, only one decoherence channel is present [34]. Note that, what differentiates this case with the case of RTN studied in Ref. [30] is the fact that the switching rate is not known a priori.

4.1.1 GHZ-type states as initial state of the qubits

Here, the effects of colored noise due to a single RBF on the state of Eq. (10) are investigated. Following the time-evolved states \( \rho _\mathrm{GHZ}^{IE}(t) \), \( \rho _\mathrm{GHZ}^\mathrm{ME}(t) \) and \( \rho _\mathrm{GHZ}^\mathrm{CE}(t) \) given in Eqs. (A.1), (A.2) and (A.3), respectively, we can write the analytical forms of tripartite negativity and the average value of the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness as

$$\begin{aligned} \left\{ \begin{aligned}&{\mathcal {N}}^{(3)}_{CE}(t)=\dfrac{1}{8}\left[ \sum \limits _{k=1}^{2}\sum \limits _{m=1}^{2}\varOmega _{k}^{m}(t)-4\right] ; \\ {}&{\mathcal {N}}^{(3)}_{IE}(t)= \dfrac{1}{8}\sum \limits _{k=1}^{2}\varTheta _{k}+\dfrac{1}{4}\Big | r\left( 2\eta _{2}^{2}(t)-1\right) -1\Big |+\dfrac{1}{2}\left( r\eta _{2}^{2}(t)-1\right) ; \\ {}&{\mathcal {N}}^{(3)}_{ME}(t)=\dfrac{1}{2} \root \displaystyle 3 \of {\left[ \sum \limits _{k=1}^{2}\sum \limits _{m=1}^{3}\varphi _{k}^{m}(t)-1\right] ^{2} \left[ \sum \limits _{k=1}^{2}\left( \varTheta _{k}(t)+\varOmega _{k}^{2}(t)\right) -4\right] }. \end{aligned} \right. \end{aligned}$$
(24)

where

$$\begin{aligned}&\varOmega _{k}^{1}(t)=\left| r\left[ 1+2\cos (k\pi )\sqrt{2(1+\eta _{4}^{2}(t))} \right] -1\right| ,\\&\varOmega _{k}^{2}(t)=\left| r\left[ 2\eta _{4}(t)+\cos (k\pi )\right] +\cos (k\pi )\right| ,\\&\varTheta _{k}(t)=\left| r(4\eta _{4}^{2}(t)-\cos (k\pi ))+\cos (k\pi )\right| ,\\&\varphi _{k}^{1}(t)=\dfrac{1}{8}\left| r\Big (\eta _{4}(t)+\cos (k\pi )\sqrt{4\eta _{2}^{4}(t)+(\eta _{4}(t)-1)^{2}}\Big )+1\right| ,\\&\varphi _{k}^{2}(t)=\dfrac{1}{8}\left| r\Big (2+\eta _{4}(t)+\cos (k\pi )\sqrt{4\eta _{2}^{4}(t)+(\eta _{4}(t)-1)^{2}}\Big )-1\right| ,\\&\varphi _{k}^{3}(t)=\dfrac{1}{4}\Big |r\Big (2\eta _{2}^{2}(t)+\cos (k\pi )\Big )+\cos (k\pi )\Big |, \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{aligned}&{{\mathrm{Tr}}}\left[ {\mathcal {W}}_\mathrm{GHZ}\rho _\mathrm{GHZ}^\mathrm{CE}(t)\right] =-\dfrac{3r}{8}\left[ \eta _{4}(t)+\dfrac{4}{3}\right] +\dfrac{3}{8}; \\&{{\mathrm{Tr}}}\left[ {\mathcal {W}}_\mathrm{GHZ}\rho _\mathrm{GHZ}^\mathrm{IE}(t)\right] =\dfrac{1}{4}\left[ 3r\eta _{2}^{2}(t)-\dfrac{3-r}{2}\right] ; \\&{{\mathrm{Tr}}}\left[ {\mathcal {W}}_\mathrm{GHZ}\rho _\mathrm{GHZ}^\mathrm{ME}(t)\right] =-\dfrac{r}{4}\left[ \dfrac{2\eta _{2}^{2}(t)+\eta _{4}(t)}{2}+1\right] +\dfrac{3}{8}. \end{aligned} \right. \end{aligned}$$
(25)
Fig. 2
figure 2

First column: time evolution of tripartite negativity \({\mathcal {N}}^{(3)}(t)\) as a function of the initial state purity r, for three qubits interacting with a single RBF with 1 / f spectrum in independent (a), mixed (c) and common (e) environment(s) when \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \) and the qubits initially in the state \( \rho _\mathrm{GHZ}(0) \). Second column: same as in the first column, but for three qubits interacting with a single RBF with \( 1/f^{2} \) spectrum in independent (b), mixed (d) and common (f) environment(s)

Full size image

In Fig. 2, we report the tripartite negativity \( {\mathcal {N}}^{(3)}(t) \) as a function of the dimensionless time \( \lambda t \) and the purity r of the initial state, for the case of pink (first column) and brown (second column) noise. The integral \( \eta _{n}(t) \) (n = 1, 2) has been computed numerically in the range \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). However, note that if different ranges of integration are considered, different time behaviors for the entanglement can arise. First of all, both for the IE and ME coupling, we find that entanglement decays with damped oscillations. Indeed, for both Q-E couplings, we observe that entanglement is stressed by alternating sudden death and revivals phenomena during its dynamical evolution. These revivals are hardly due to the non-Markovian character of the colored noise which has already been studied in Ref. [53]. However, the amplitudes of oscillation are more prominent in the case of brown noise than in the one of pink noise, demonstrating that the degree of non-Markovianity of the brown noise (i.e., its proficiency to enable recoherence phenomena, such as entanglement revivals) is higher than the one of the pink noise; or in other words, that the amount of information that the system can recover because of the presence of classical memory in the environment (characterized by the revivals of entanglement) is higher in the case of brown noise with respect to the case of pink noise. This is in good agreement with the corresponding results described in Ref. [53]. In contrast to the case of IE and ME couplings, we observe that for an initial state with purity r ranging from 1 to 1/4, entanglement in the case of CE coupling can be indefinitely preserved regardless of the case of pink noise or the case of brown noise. In fact, we observe that entanglement decays with time until reaching an asymptotic value depending upon the purity r and then exhibits oscillations with damped amplitudes. The preservation of entanglement in the limit of sufficiently long but finite time as shown by the evolution of tripartite negativity is in accordance with what is found in Ref. [30] for the case of RTN and with the same model, but represents the major discrepancy with what was found in the two-qubit form of the model studied in this paper [34]. Note that, the long-lived entanglement has also been observed in two-qubit systems interacting with environments described in their quantum-mechanical pictures [12, 16, 54]. According to the authors of Ref. [30], the preservation of entanglement can be attributed to the indirect interaction among the qubits stemming from the coupling of the global system to a common noisy environment. Indeed, unlike the case of IE and ME couplings, here the environment is no longer only the source of decohering effects, but also represents a sort of interaction mediator between the qubits, what in one way or another prevent the destruction of entanglement. In all the Q-E coupling setups studied, we observe that the initial amount of entanglement decreases with the decrease in the purity r. This latter result is not surprising and can be explained by noticing that the smaller is the value of the purity of the initial state, the more enhanced is its degree of mixedness. On the one hand, we observe that the periods as well as the amplitudes of entanglement revival increase with the increase in the purity r. On the other hand, for fixed value of the purity r, the period of entanglement revival as well as the decay rate of entanglement in the case of pink noise is higher than in the case of brown noise, demonstrating that the 1 / f noise is more fatal to the survival of entanglement than the \( 1/f^{2} \) noise and that the degree of non-Markovianity of an environment can be a key factor in the process of classical environment engineering. Overall, we observe that entanglement is not only affected by the kind of noise considered but also by Q-E coupling configuration considered. More precisely, we found that the CE coupling followed by the ME coupling hinders more the degradation of entanglement than the IE coupling. Finally, having compared for \( r=1 \) the results obtained in this subsection with those of Ref. [18], it is possible to conclude that different ranges of integration \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda \) give rise to different time behaviors for the entanglement.

Fig. 3
figure 3

First column: time evolution of the opposite of the average value of the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness as a function of the initial state purity r, for three qubits interacting with a single RBF with 1 / f spectrum in independent (a), mixed (c) and common (e) environment(s) when \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). Second column: same as in the first column, but for three qubits interacting with a single RBF with \( 1/f^{2} \) spectrum in independent (b), mixed (d) and common (f) environment(s)

Full size image

In Fig. 3, the evolution of the opposite of the expectation value of the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness as a function of the dimensionless time \( \lambda t \) and the purity r, for the different Q-E coupling setups, is reported. The first column corresponds to the case of system subjected to 1 / f noise, whereas the second one is for the case of system subjected to \( 1/f^{2} \) noise. We observe immediately that no matter what the Q-E coupling setup or the kind of noise considered is, the amount of entanglement quantified by the tripartite negativity \( {\mathcal {N}}^{(3)} \) is always higher than the one detected by the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness. We observe that at initial time, i.e., at \( t=0 \), the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness can only detect the states with \( r>3/7 \) this means that any state with \( r<3/7 \) is not in the W-B class. On the one hand, we find that for an initial pure GHZ state, i.e., a state with \( r=1 \), the \( {\mathcal {W}}_\mathrm{GHZ} \) witness in the case of CE coupling is able to detect the survival of entanglement at sufficiently long but finite time which is known to be present via the tripartite negativity measure. In the case of IE and ME couplings, we also find that the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness undergoes a sudden death type phenomenon (i.e., becomes positive) before the tripartite negativity, demonstrating that there is remaining entanglement in the system beyond the detection of the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness. It is interesting to note that the period of \( {\mathcal {W}}_\mathrm{GHZ} \) witness revival is equal to the one of the tripartite negativity \( {\mathcal {N}}^{(3)} \), both for the case of pink and brown noises, demonstrating that there is a connection between these two estimators. On the other hand, the fact that we have sudden death and revivals type phenomena with respect to the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness [49] for states with \( r<3/7 \) clearly shows that there is a flow of information from the system to the environment and vice versa.

4.1.2 W-type states as initial state of the qubits

Here, the situation in which the three qubits are initially prepared in a W-type state and then subjected to a colored noise generated by a single RBF is examined. Note that in contrast to the GHZ-type states where tracing out any one of the qubits destroys all the entanglement, the remaining two qubits will still be entangled for W-type states. In particular, the evolution of entanglement initially in the state \( \rho _{W}(0) \) is investigated for the case of IE, ME and CE couplings. After performing the calculations, we find that the density matrices describing the evolution of the system under the effect of the noise for the above-mentioned Q-E coupling setups can be expressed as in Eqs. (B.1), (B.2) and (B.3), respectively. Because of lack of compact expressions, the analytical forms of tripartite negativity are not presented in this section. However, the expectation value of the \( {\mathcal {W}}_{W} \) entanglement witness in case of IE, ME and CE couplings can, respectively, be expressed as in Eq. (26).

$$\begin{aligned} \left\{ \begin{array}{l} {{\mathrm{Tr}}}\left[ {\mathcal {W}}_{W}\rho _{W}^\mathrm{IE}(t)\right] =-\,\dfrac{5r}{24}\left[ \dfrac{7}{5}\eta _{2}^{3}(t)+\eta _{2}^{2}(t)+\eta _{2}(t)+\dfrac{4}{5}\right] +\dfrac{13}{24}; \\ \\ {{\mathrm{Tr}}}\left[ {\mathcal {W}}_{W}\rho _{W}^\mathrm{ME}(t)\right] =-\,\dfrac{2r}{9}\left[ \begin{aligned} &{}\eta _{2}^{2}(t)+\dfrac{\eta _{2}(t)}{32}(39\eta _{4}(t)+33)\\ {} &{}\quad -\dfrac{3}{32}\eta _{4}(t)+\dfrac{25}{32} \end{aligned} \right] +\dfrac{13}{24}; \\ \\ {{\mathrm{Tr}}}\left[ {\mathcal {W}}_{W}\rho _{W}^\mathrm{CE}(t)\right] =-\,\dfrac{3r}{16}\left[ \begin{aligned} &{}\dfrac{7}{16}\eta _{2}(t)+\eta _{4}(t)+\eta _{2}(t)\\ {} &{}\quad +\dfrac{3}{2}\eta _{6}(t)+1 \end{aligned}\right] +\dfrac{13}{24}; \end{array} \right. \end{aligned}$$
(26)
Fig. 4
figure 4

First column: time evolution of tripartite negativity \( {\mathcal {N}}^{(3)}(t) \) as a function of the initial state purity r, for three qubits interacting with a single RBF with 1 / f spectrum in independent (a), mixed (c) and common (e) environment(s) when \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \) and the qubits initially in the state \( \rho _{W}(0) \). Second column: same as in the first column, but for three qubits interacting with a single RBF with \( 1/f^{2} \) spectrum in independent (b), mixed (d) and common (f) environment(s)

Full size image

In Fig. 4, we plotted for the case of pink (first column) and brown (second column) noises the tripartite negativity \( {\mathcal {N}}^{(3)}(t) \) with respect to the dimensionless times \( \lambda t \) and the purity r for \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). In Fig. 4, we can observe that in contrast to the case of GHZ-type states analyzed in the previous subsection, entanglement is completely suppressed when the qubits are coupled in a common environment both for the case of pink and for the case of brown noises. Concretely speaking, we observe that at sufficiently long but finite time, entanglement is completely destroyed, regardless of the Q-E coupling or the kind of noise considered. Also for this input configuration, we observe that entanglement is hardly affected by the Q-E coupling setups and the noise spectrum considered. Indeed, in the case of CE coupling setup we observe that entanglement decays with damped oscillations either with sudden death (pink noise) or not (brown noise) and completely disappear in the limit of long but finite time. However, in the other Q-E configurations (IE and ME), we observe that entanglement decays exponentially with time to zero and exhibits multiple collapses and revivals with damped amplitudes. Once more, the frequency of entanglement revival as well as the revival amplitudes is higher in the case on brown noise than in the case of pink noise, demonstrating again that the pink noise has the most destructive influence on the entanglement than the brown one. In fact, for pink noise the switching rates are more uniformly distributed over the range \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda \) than in the case of brown noise, thus leading to massive destructive interference [34]. On the other hand, we observe that the smaller the value of the degrees of freedom of the overall system is, the longer is the time required for the initial state to become separable. This means that the CE coupling followed by the ME coupling is less detrimental against entanglement than the IE coupling. However, for the case of IE and ME couplings, we notice in the case of both pink and brown noises that the period of entanglement revival for GHZ-type states is always higher than the one of W-type states. This remark together with the fact that the entanglement initially present in the W-type states is completely suppressed in the case CE coupling clearly shows that the GHZ-type states preserve more entanglement than the W-type states. Such a result has also been observed when studying the same model as the one studied in this paper, but both in the case of RTN [30] and static noise [17]. Nevertheless, it has been found in the literature that for certain environmental noise models such as, for instance, the Pauli channel \( \sigma _{z} \) [55], the fermionic [56] and spin-chain [57, 58] environments, the entanglement initially present in the W-type states is more robust/resistant than the entanglement initially present in the GHZ-type states. Therefore, one can conclude that the robustness of entanglement in the GHZ-type states with respect to W-type states is here closely related to the classical nature of the environmental noise.

Fig. 5
figure 5

First column: time evolution of the opposite of the average value of the \( {\mathcal {W}}_{W} \) entanglement witness as a function of the initial state purity r, for three qubits interacting with a single RBF with 1 / f spectrum in independent (a), mixed (c) and common (e) environment(s) when \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). Second column: same as in the first column, but for three qubits interacting with a single RBF with \( 1/f^{2} \) spectrum in independent (b), mixed (d) and common (f) environment(s)

Full size image

Figure 5 displays the evolution of the opposite of the average value of the \( {\mathcal {W}}_{W} \) entanglement witness as a function of the dimensionless time \( \lambda t \) and the purity r, for the different Q-E coupling setups. The first column corresponds to the case of system subjected to 1 / f noise, whereas the second one is for the case of system subjected to \( 1/f^{2} \) noise. We can immediately observe that in contrast to the case of brown noise, the entanglement witness in the case of pink noise does not exhibit revival. At \( t=0 \), we find that the \( {\mathcal {W}}_{W} \) entanglement witness can detect only the states with \( r>13/21 \). Also for the W-type states, we find that the \( {\mathcal {W}}_{W} \) entanglement witness is successful in detecting entanglement only up to a certain point despite the continued presence of tripartite entanglement measured by \( {\mathcal {N}}^{(3)} \).

Fig. 6
figure 6

First column: time evolution of the tripartite negativity \( {\mathcal {N}}^{(3)}(t) \) as a function of the mix probability p, when the qubits (initially prepared in the state \( \rho _{GHZ-W}(0) \)) are in interaction with a single RBF with 1 / f spectrum in independent (a), mixed (c) and common (e) environment(s) when \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). Second column: same as in the first column, but for three qubits interacting with a single RBF with \( 1/f^{2} \) spectrum in independent (b), mixed (d) and common (f) environment(s)

Full size image
Fig. 7
figure 7

First column: 2D view of \( {\mathcal {N}}^{(3)}(t) \) as a function of the probability p, when the qubits (initially prepared in the state \( \rho _{GHZ-W}(0) \)) are coupled in independent (a), mixed (c) and common (e) environment(s), in the case of 1 / f noise and with the same parameters as in Fig. 6. Second column: same as in the first column but in the case of \( 1/f^{2}\) noise in independent (b), mixed (d) and common (f) environment(s)

Full size image

4.1.3 Mixed states composed of a GHZ and a W state as initial state of the qubits

Here, we study the evolution of entanglement of a three-qubit undergoing the action of a single RBF in IE, ME and CE couplings; when the qubits are initially prepared in the mixed states composed of a GHZ and a W state as given in Eq. (12). We note that the evolution of entanglement of a three-qubit system initially prepared in the state of Eq. (12) and then subjected to the action of a classical RTN [19], multipartite cavity-reservoir [59] and various noisy channels [60] has already been investigated. In Fig. 6, we report the time evolution of the tripartite negativity \( {\mathcal {N}}^{(3)} \) as a function of the dimensionless time \( \lambda t \) and the mix probability p for the different Q-E coupling setups and for the case of pink (first column) and brown (second column) noise. Also, in Fig. 7 we report the two-dimensional (2D) view of \( {\mathcal {N}}^{(3)} \) versus the probability p.

The observation of Fig. 6 shows that entanglement is not only affected by the noise spectrum considered, but also by the Q-E coupling setups as well as the mix probability p. Beyond this, we observe that for an initial mixed state with the parameter p ranging from 1 to 0.27, the entanglement can be indefinitely conserved in the case of CE coupling in both the pink and brown spectra. As we have already pointed out in case of GHZ- and W-type states, the amplitudes of entanglement revival are higher in the case of brown noise than in the case of pink noise. However, unlike GHZ- and W-type states in which the initial state entanglement decreases in a linear way to zero with the increasing of the purity, here we observe that at \(t=0\), the entanglement exhibits a parabolic behavior when the probability p increases. Note that the minimum of the initial entanglement is located at \(p=0.5\). Moreover, we observe that in the case of IE and ME couplings, entanglement decays in an exponential manner while in the case of CE coupling, it decays with damped oscillations. On the one hand, we find both in the case of IE and ME couplings that no matter what the value of the mix probability p is, entanglement always undergoes entanglement sudden death (ESD) and entanglement revivals (ER) phenomena. However, this is not so when the qubits are initially prepared in the GHZ-type or W-type states. In, fact we find that unlike the initial states analyzed in the two previous subsections in which the revival amplitude of entanglement always decreases with the purity r decreasing, here, we find that the revival amplitudes of entanglement can either increase or decrease with the mix probability p decreasing. Indeed, we find that for initial mixed states with p ranging from 1 to 0.5 the revival amplitudes of entanglement decrease with the decreasing of the probability p; meanwhile, the situation is completely reversed for initial states with p ranging from 0.5 to 0. On the other hand, for the probability \(0.89\le p<1\) and purity \(0.89\le r<1 \), we find that an initial mixed state of Eq. (12) has an equal initial entanglement to that of the corresponding GHZ-type state. However, in these ranges, we find that the entanglement of an initial GHZ-type state experiences ESD before the one of an initially mixed state composed of a GHZ and a W state (12). Thus, we can conclude that the initial mixed states of Eq. (12) preserve more entanglement than the GHZ-type states.

Overall, we find that the initially mixed states composed of a GHZ state and a W state followed by the GHZ-type states stays entangled for a very long time than the W-type states.

4.2 Colored noise generated by a collection of random bistable fluctuators \( (N>1) \)

Here, we study the evolution of entanglement of qubits subjected to a collection of N RBFs. In order to compare the robustness of the entanglement initially present in the states of Eqs. (10), (11) and (12) under the effects of colored noise arising from a collection of RBFs, we report for the different Q-E coupling configurations the evolution of the tripartite negativity as a function of the dimensionless time \(\lambda t\) and for the case of pink and brown noises.

Fig. 8
figure 8

Upper panels: time evolution of tripartite negativity for the different Q-E coupling setups when the qubits are initially prepared in the pure GHZ state (a), pure W state (b) and mixed GHZ-W state (12) with \( p=1/4 \) (c) and then subjected to a collection of \( N=20 \) (solid lines) and \( N=100 \) (dashed lines) RBFs with 1 / f spectrum. The range of integration is \( \left[ \gamma _{\min },\gamma _{\max }\right] /\lambda =\left[ 10^{-2},10^{2}\right] \). Lower panels: time evolution of the opposite of the expected values of \( {\mathcal {W}}_\mathrm{GHZ} \) (d) and \( {\mathcal {W}}_{W}\) (e) with the same parameter as in the upper panels

Full size image

4.2.1 Pink noise \( (\alpha =1) \)

In Fig. 8, we have plotted the time evolution of entanglement for the different Q-E coupling configurations in the case of \( N=20 \) and \( N=100 \) fluctuators. We remark immediately that entanglement is strongly affected both qualitatively and quantitatively by the number of fluctuators or decoherence channels used to model the environment. In fact, we observe that when the qubits are affected only by one decoherence channel (first column of Figs. 2, 3, 4, 5, 6, 7), entanglement quantified in terms of \( {\mathcal {N}}^{(3)} \) or detected by means of suitable entanglement witnesses may experience revivals, depending on the Q-E coupling setup, whereas when they are affected by many decoherence channels, no revivals of entanglement are observed. Interestingly, we find that the survival of entanglement, which occurs for the GHZ state when the qubits are coupled in a common environment, persists also for increasingly larger numbers of RBF. Moreover, no matter are the Q-E coupling configuration and the input configuration of the qubits, we observe that the decay rate of entanglement increases when the number of decoherence channels realizing the environment increases. That is, the bigger is the number of RBFs, the more enhanced is the decay rate of entanglement. Such a result is not surprising and can be explained by noticing that adding more noises in the system \( (N\gg 1) \) just leads to the increase in the overall detrimental effects and thus to the faster decay of entanglement. On the other hand, in the case of GHZ state, we find that the entanglement quantified by the tripartite negativity \( {\mathcal {N}}^{(3)} \) as well as the one detected by the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness is less degraded by the CE coupling configuration followed by the ME coupling configuration with respect to the IE coupling configuration. However, the situation is totally reversed in the case of W state. Furthermore, we note that when a bigger number of fluctuators or decoherence channels are considered, the action of IE, ME or CE coupling has almost the same effects on the robustness of entanglement when the input configuration of the qubits is the W state or the mixed state (12) with the probability \( p=1/4 \). Moreover, whatever the Q-E coupling setup considered is, entanglement quantified by \( {\mathcal {N}}^{(3)} \) undergoes ESD in the case of W state while in the case of GHZ state, entanglement decays exponentially with time and vanish asymptotically, except for the CE coupling setup.

Fig. 9
figure 9

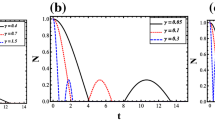
Upper panels: time evolution of tripartite negativity, when the three qubits, initially prepared in the GHZ state, are coupled to a collection of \( N=10 \) (black solid line) and \( N=20 \) (red dashed line) RBFs with \( 1/f^{2} \) spectrum in independent (a), mixed (b) and common (c) environment(s). Lower panels: same as in upper ones, but rather for the time evolution of the opposite of the expectation value of \( {\mathcal {W}}_\mathrm{GHZ} \) in the case of independent (d), mixed (e) and common (f) environments (Color figure online)

Full size image
Fig. 10
figure 10

Upper panels: time evolution of tripartite negativity, when the three qubits, initially prepared in the W state, are coupled to a collection of \( N=10 \) (black solid line) and \( N=20 \) (red dashed line) RBFs with \( 1/f^{2} \) spectrum in independent (a), mixed (b) and common (c) environment(s). Lower panels: same as in upper ones, but rather for the time evolution of the opposite of the expectation value of \( {\mathcal {W}}_{W} \) in the case of independent (d), mixed (e) and common (f) environments (Color figure online)

Full size image
Fig. 11
figure 11

Time evolution of tripartite negativity when the three qubits, initially prepared in the mixed state of Eq. (12) with \( p=1/4 \), are coupled to a collection of \( N=10 \) (black solid line) and \( N=20 \) (red dashed line) RBFs with \( 1/f^{2} \) spectrum in independent (a), mixed (b) and common (c) environment(s) (Color figure online)

Full size image

4.2.2 Brown noise \( (\alpha =2) \)

In Figs. 9, 10 and 11, we plot the time evolution of tripartite negativity and entanglement witnesses for the different Q-E coupling setups and for three different input configurations, namely the GHZ state, the W state and the mixed state composed of a GHZ state and a W state. If we compare these figures with those obtained in Sects. 4.1.1 and 4.1.2 for \( r=1 \) (Figs. 2, 4) and 4.1.3 (Fig. 6) for \( p=1/4 \), we find immediately that the evolution of entanglement is not only affected by the color of the noise, the input configuration and the Q-E coupling setup, but also by the number of decoherence channels used to describe the environment. Indeed, as in the case of pink noise, we observe that entanglement quantified in terms of tripartite negativity as well as the one detected by the witnesses decreases faster when the number of decoherence channels modeling the environment increases. Moreover, we find that the longtime survival of entanglement as shown by the tripartite negativity (Fig. 9c) can be efficiently detected by the \( {\mathcal {W}}_\mathrm{GHZ} \) entanglement witness (Fig. 9f). Nevertheless, unlike pink noise in which entanglement exhibits a monotonic decay, here we find that entanglement decays with damped oscillation either with the presence or absence of ESD and ER phenomena. On the other hand, for W state we find that in contrast to the case of pink noise, entanglement is less degraded by the CE coupling with respect to the other Q-E couplings. Comparing Fig. 9 with Fig. 10, respectively, we see that the entanglement of the GHZ state is more robust than the entanglement of the W states, regardless of the Q-E coupling or the number of bistable fluctuators modeling the external environment.

5 Conclusions

In this paper, we have investigated in detail the evolution of entanglement for a three-qubit system interacting with an outside classical environment characterized by a noise spectrum of the form \( 1/f^{\alpha } \). In particular, we have addressed the evolution of entanglement for two different configurations of the outside environment: In the first configuration, the outside environment is modeled as a single RBF with an undetermined switching leading to an overall \( 1/f^{\alpha } \) spectrum, while in the second configuration the outside environment is modeled as an ensemble of many RBFs, with fixed switching rates chosen from a specific interval and a specific distribution. For each configuration, we have studied the evolution of entanglement for the case of \( \alpha =1 \) (1 / f spectrum or pink noise) and \( \alpha =2 \) (\( 1/f^{2} \) spectrum or brown noise). We have analyzed three different input configurations of the qubits, namely the Greenberger–Horne–Zeilinger (GHZ)-type states, W-type states and mixed states composed of a GHZ state and a W state. Beyond this, three different setups of the qubit–environment (Q-E) interaction, namely IE, ME and CE, have been investigated for each input configuration of the qubits. We have accessed the entanglement by means of suitable entanglement witnesses and compared the evolution of their detection efficiencies with the evolution of the tripartite negativity.

Our analysis shows that the evolution of entanglement is extremely influenced not only by the input configuration of the qubits, the spectrum of the environment and the Q-E coupling setup considered, but also by number of RBFs modeling the environment. More precisely, we found that depending on the input configuration and the Q-E coupling considered, entanglement can be indefinitely preserved and that the decay rate of entanglement increases with the number of RBFs modeling the external environment. On the one hand, we found that the 1 / f spectrum is more fatal to the survival of entanglement than the \( 1/f^{2} \) one, regardless of the setup of the Q-E coupling, the input configuration of the qubits or the number of RBF modeling the environment. Moreover, we found that the proficiency of the tripartite entanglement witnesses to detect entanglement is weaker than that of the tripartite negativity. On the other hand, we found that the mixed states (12) followed by the GHZ-type states preserve entanglement better than the W-type states (which is in good agreement with previous results obtained with different classical noise models [17, 19, 30]) and that the IE, ME and CE coupling may play opposite roles in the improvement of entanglement robustness depending on the input configuration of the qubits considered and the number of RBF or decoherence channels used to model the external environment. Specifically, for an initial GHZ-type state with \( 1<r\le 0.25 \) as well as for an initial mixed state (12) with \( 1<p\le 0.27 \), we found that when the qubits are coupled in a common external environment, entanglement can be indefinitely preserved even for increasingly larger number of decoherence channels. Furthermore, for these input configurations we found that when the noise is described as an ensemble of many RBFs with \( 1/f^{2} \) spectrum, the CE coupling followed by the ME coupling degrades entanglement among the qubits more weakly than the IE coupling. However, the situation is completely reversed in the case of 1 / f spectrum when the qubit is initially prepared in the W state or in the mixed state of Eq. (12) with larger values of the probability p. Specifically for the pure W state and mixed state, we found that when the external environment is modeled by a sufficiently large number of random bistable fluctuator with 1 / f spectrum, the action of IE, ME or CE coupling has almost the same effects on the robustness of entanglement.

Especially in the case of pink noise, we found that when the environment is described as a single RBF, the entanglement sudden collapses and revivals phenomena occur, whereas when an ensemble of many RBFs is considered, no revival of entanglement is observed.

Overall, we found that engineering environments toward the CE coupling setup and also preparing the input state of the system either in the mixed states composed of a GHZ state and a W state or in the GHZ-type states, is useful to preserve entanglement as well as to improve its robustness against the detrimental effects of the external environment.

Finally, we believe that these results shed a new light on the use of multipartite entangled states for practical applications.