1 Introduction

A quantum computer possesses great processing power and can speed up the solution of mathematical issues significantly. Quantum logic gates play a great important role in the development of quantum information processing, because they are essential for building a quantum computer, including the conventional parallel quantum computation [1,2,3,4,5,6,7] and the hyperparallel photonic quantum computation [8,9,10,11]. It is well known that any quantum entangling gate supplementing with single-qubit operations is sufficient for universal quantum computing [12]. Controlled-NOT (CNOT) gate is one of the universal gates [3, 5, 6, 12,13,14,15,16,17,18,19,20], which has been realized in both theory and experiment. It has been proved that almost all n-qubit operators can be constructed by a circuit with at least \([\frac{1}{4}(4^{n}-3n-1)]\) CNOT gates [21]. However, in experiment, it is difficult to construct multi-qubit gates with CNOT and one-qubit gates, which also increases the possibility of errors. Therefore, it is meaningful to find an efficient way to realize multi-qubit gates directly [5, 6]. In the field of multi-qubit gates, Fredkin gate and SWAP gate have attracted great attention. It is well known that an arbitrary multi-qubit operation can be decomposed into a sequence of Fredkin and Hadamard gates [22, 23]. The SWAP gate itself is not universal; however, it can be widely used to construct optimal quantum circuits, store quantum information, and teleport the quantum state [24]. Moreover, they have a great influence on complex quantum algorithms (such as the Shor algorithm [25] and the famous Grover/Long algorithm [26, 27]), fault tolerant quantum circuits [28], error correction [29], and phase estimation [30].

Quantum computation plays a critical role in quantum information processing [12, 31,32,33]. To realize quantum computation, researchers need to implement the accurate coherent control of a sequence of qubits [34,35,36,37,38,39]. In the last decades, cavity quantum electrodynamics (CQED) has become one of the main approaches to implement quantum logic gates, which provides the platform for strong quantum interface between photons and atoms. By far, some remarkable progress on the study of gate operations has been reported in both theory and experiment [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]. In 2004, based on cavity-assisted interaction between single-photon pulses, Duan and Kimble [57] put forward a scheme for scalable photonic quantum computation. In 2006, by exploiting a single resonant interaction in cavity QED, Chen et al. [58] put forward a practical protocol to realize a three-qubit Toffoli gate without using two-qubit CNOT gates. Meanwhile, Deng et al. [59] presented a scheme to realize a nonlocal N-qubit conditional phase gate with the single-photon interference. In 2010, an interesting scheme for a photon–photon \(\sqrt{\text{ SWAP }}\) gate is proposed by Koshino, Ishizaka, and Nakamura [60], in which a three-level \(\Lambda \) system is adopted as the temporary memory for photons. In 2013, Wei and Deng [47] gave some important schemes for the compact quantum circuits to implement the CNOT, Toffoli, and Fredkin gates on the diamond nitrogen-vacancy (NV) centers confined inside cavities, assisted by some input–output processes of a single photon. In 2014, Wang et al. [61] constructed a deterministic hybrid hyper-controlled-not (hyper-CNOT) gate assisted by quantum dots in optical double-sided microcavities. Later, based on a nitrogen-vacancy center coupled with a whispering-gallery-mode microresonator, Wang and Wang [7] investigated the construction of two universal three-qubit quantum gates in a hybrid system.

In recent years, quantum logic gates for the hybrid photon–atom system in high-quality optical microcavities play a leading role in the exploration of quantum communication and computing. Due to its potential scalability and stability, atoms in optical cavities have recently been one of the most appealing candidates for quantum computation and network [62,63,64,65]. Meanwhile, flying photons are usually chosen to realize quantum information processing over long distance, since their decoherence with atmosphere can be neglected. In 2013, Wei and Deng [5] proposed some deterministic schemes to construct universal compact quantum gates, including the CNOT, Toffoli, and Fredkin gates, between flying photon qubit and stationary electron-spin qubits assisted by quantum dots inside double-sided optical microcavities. In 2015, they [66] designed a compact quantum circuit for implementing the \((\text{ SWAP })^a\) gate for \(0 < a \le 1\) on two diamond NV centers by using some input–output processes of a single photon.

In this work, by utilizing the photonic Faraday rotation, we have proposed two feasible experimental schemes for constructing Fredkin gate and SWAP gate on hybrid photon–atom systems. In our scheme, the control qubits of our compact quantum gates are encoded on the two polarization states of a single photon, denoted by the right-circularly polarized photon \(|R\rangle \) and the left-circularly polarized photon \(|L\rangle \), while the target qubits are encoded on the states \(|0\rangle \) and \(|1\rangle \) of an atom confined in an optical microcavity. It is worth pointing out that the storage time exceeding 15 seconds for a single atom in high-finesse optical cavity has been achieved [67], which is suitable for multi-time operations between the photon and the atoms in our protocols. Different from the schemes with a double-sided optical microcavity, our schemes based on single-sided optical microcavities need not meet the condition that the transmission for the uncoupled cavity is balanceable with the reflectance for the coupled cavity [16]. We analyze the feasibility of the protocols, which shows that our gates can be achieved with high fidelities in experiment. With the dramatical progress on manipulating hybrid photon–atom systems [50, 68,69,70], these gates can be used in many other areas in quantum computation and quantum information processing.

2 Fredkin gate on a hybrid photon–atom system with Faraday rotation

2.1 Interaction between a circularly polarized light and atom–cavity system

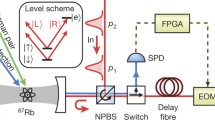
The solid-state system discussed here is an atom confined in a single-sided cavity, as shown in Fig. 1. The cavity is one side wall partially reflective and the other side wall perfectly reflective. The atom has a three-level internal state structure, i.e., two degenerated ground states \(|0\rangle \) and \(|1\rangle \) and an excited state \(|e\rangle \). Under the Jaynes–Cummings model, the Hamiltonian of the atom–cavity system can be expressed as:

$$\begin{aligned} H=\frac{{\hbar }\omega _{0}\sigma _{z}}{2}+\hbar \omega _{c}\, a^{+}a+i{\hbar } g(a\sigma _{+}-a^{+}\sigma _{-}), \end{aligned}$$
(1)

where \(\sigma _{+}\), \(\sigma _{-}\), and \(\sigma _{z}\) are raising, lowering, and inversion operators of the atom, respectively. \(\omega _{0}\) is the frequency difference between the ground state (\(|0\rangle \) or \(|1\rangle \)) and the excited state \(|e\rangle \). \(a^{+}\) and a are the creation and annihilation operators of the cavity field with frequency \(\omega _{c}\), respectively. g is the coupling strength between the trapped atom and the cavity field.

Ignoring the Langevin noise that has a trivial contribution to the dynamics, one can obtain the reflection coefficient by solving the Heisenberg-Langevin equations of motion for the internal cavity field and the atomic operator in the interaction picture [71]:

$$\begin{aligned} \frac{\hbox {d}a}{\hbox {d}t}= & {} -\left[ i(\omega _{c}-\omega _{p})+\frac{\kappa }{2}\right] \, a(t)-g\sigma _{-}(t)-\sqrt{\kappa }\, a_\mathrm{in}(t), \nonumber \\ \frac{\hbox {d}\sigma _{-}}{\hbox {d}t}= & {} -\left[ i(\omega _{0}-\omega _{p})+\frac{\gamma }{2}\right] \, \sigma _{-}(t)-g\sigma _{z}(t)\, a(t)+\sqrt{\gamma }\sigma _{z}(t)b_\mathrm{in}(t), \nonumber \\ a_\mathrm{out}(t)= & {} a_\mathrm{in}(t)+\sqrt{\kappa }\, a(t), \end{aligned}$$
(2)

where \(a_\mathrm{in}\), the cavity input operator, obeys the commutation relation \([a_\mathrm{in}(t), a_\mathrm{in}^{+}(t')] =\delta (t-t')\). \(\gamma \) and \(\kappa \) are the decay rate of the trapped atom and the cavity damping rate, respectively. \(b_\mathrm{in}(t)\) is the vacuum input field felt by the confined atom, which satisfies the commutation relation \([b_\mathrm{in}(t), b_\mathrm{in}^{+}(t')] =\delta (t-t')\). Here, by making \(\kappa \) sufficiently large, we have a weak excitation by the single-photon pulse on the atom initially prepared in the ground state, i.e., keeping \(\langle \sigma _{z}\rangle =-1\), and the reflection coefficient of the circularly polarized light after interacting with atom–cavity system is [72]

$$\begin{aligned} r(\omega _{p})=\frac{\left[ i(\omega _{c}-\omega _{p})-\frac{\kappa }{2}\right] \left[ i(\omega _{0} -\omega _{p}) +\frac{\gamma }{2}\right] +g^{2}}{\left[ i(\omega _{c}-\omega _{p})+\frac{\kappa }{2}\right] \left[ i(\omega _{0}-\omega _{p})+\frac{\gamma }{2}\right] +g^{2}}. \end{aligned}$$
(3)

Considering the case of \(g=0\) (the atom is uncoupled to the cavity), one can obtain the formula for an empty cavity,

$$\begin{aligned} r_{0}(\omega _{p})=\frac{i(\omega _{c}-\omega _{p})-\frac{\kappa }{2}}{i(\omega _{c} -\omega _{p})+\frac{\kappa }{2}}. \end{aligned}$$
(4)
Fig. 1
figure 1

a Schematic diagram of an atom confined in a single-sided optical cavity. The left wall of the cavity is partially reflective, and the right one is perfectly reflective. b The \(\Lambda \)-type level configuration of the atom. The lower levels \(|0\rangle \) and \(|1\rangle \) are Zeeman sublevels of the ground state, and the upper level \(|e\rangle \) is the excited one. L (R) represents the left (right) circularly polarized photon

Full size image

If the atom is initially prepared in the state \(|0\rangle \), the coupling of the cavity mode \(a_{_{L}}\) and the left-circularly polarized single-photon pulse \(|L\rangle \) will drive the only possible transition \(|0\rangle \leftrightarrow |e\rangle \). The output pulse can be expressed as \(|\Psi _\mathrm{out}\rangle _{L}=r(\omega _{p})|L\rangle =\mathrm{e}^{i\phi }|L\rangle \), where the phase shift \(\phi \) is determined by the parameter values in Eq. (3). However, for an incident right-circularly polarized photon \(|R\rangle \), it will only sense a bare cavity. So, the output pulse is \(|\Psi _\mathrm{out}\rangle _{R}=r_{_{0}}(\omega _{p})|R\rangle =\mathrm{e}^{i\phi _{_{0}}}|R\rangle \), in which the corresponding phase shift \(\phi _{0}\) is different from \(\phi \). Similarly, assuming that the atom is initially prepared in the state \(|1\rangle \), the right-circularly polarized photon \(|R\rangle \) will drive the transition \(|1\rangle \leftrightarrow |e\rangle \), while the photon in state \(|L\rangle \) can only sense a bare cavity. If the parameters of the atom–cavity system are adjusted to \(\omega _{p}=\omega _{c}-\kappa /2\) and \(\omega _{0}=\omega _{c}\), we can obtain

$$\begin{aligned} r(\omega _{p})=\frac{(i-1)\left( i+\frac{\gamma }{\kappa }\right) +4\left( \frac{g}{\kappa }\right) ^{2}}{(i +1)\left( i+\frac{\gamma }{\kappa }\right) +4\left( \frac{g}{\kappa }\right) ^{2}}, \quad r_{0}(\omega _{p})=i. \end{aligned}$$
(5)

Here, as the single-sided optical microcavity is a low-Q cavity, we can set \(g=\frac{\kappa }{2}\). Under the limitation \(\gamma \ll \kappa \), phase shifts \(\phi =\pi \) and \(\phi _{_{0}}=\pi /2\) can be achieved. Therefore, the evolution of the input states under the interaction of the photon and the atom can be described as follows:

$$\begin{aligned}&|R\rangle |0\rangle \rightarrow i|R\rangle |0\rangle , \qquad |R\rangle |1\rangle \rightarrow -|R\rangle |1\rangle , \nonumber \\&|L\rangle |0\rangle \rightarrow -|L\rangle |0\rangle , \qquad |L\rangle |1\rangle \rightarrow i|L\rangle |1\rangle . \end{aligned}$$
(6)

Assisted by the photonic Faraday rotation mentioned above, several meaningful works have been realized, such as controlled teleportation protocols [73] in low-Q cavities, entanglement concentration [74,75,76,77], and the construction of a CNOT gate in a quantum-dot system [78]. Here, based on the photonic Faraday rotation, we construct a Fredkin gate and a SWAP gate on the hybrid photon–atom system.

2.2 Fredkin gate on a three-qubit hybrid system by Faraday rotation

A Fredkin gate is used to exchange the states of the two target qubits only if the control qubit (the flying photon p) is in the state \(|L\rangle \). The flying photon p and the two stationary atoms 1 and 2 in single-sided cavities are prepared in random superposition states \(|\psi \rangle _{p}=\alpha _{c}|R\rangle +\beta _{c}|L\rangle \) and \(|\varphi \rangle _{i}=\alpha _{i}|0\rangle _{i}+\beta _{i}|1\rangle _{i}\) (\(i=1, 2\)), respectively, where the unknown coefficients obey \(|\alpha _{c}|^{2}+|\beta _{c}|^{2}=|\alpha _{i}|^{2}+|\beta _{i}|^{2}=1\) . Motivated by the Faraday rotation introduced above, we could construct a Fredkin gate with the steps shown in Fig. 2. The corresponding processes are described in detail as follows.

First, the injecting photon travels through \(\hbox {PBS}_{1}\), which transmits the photon in the state \(|R\rangle \) and reflects the photon in the state \(|L\rangle \). In detail, the photon is split by \(\hbox {PBS}_{1}\) into two wave-packets: The part in the state \(|L\rangle \) is input into the cavities and interacts with the atoms, while the part in the state \(|R\rangle \) transmits through \(\hbox {PBS}_{1}\) directly and nothing changes. After the photon passes through \(\hbox {PBS}_{1}\), the state of the entire system composed of a photon and two atoms is changed from \(|\Psi _{0}\rangle \) to \(|\Psi _{1}\rangle \). Here,

$$\begin{aligned} |\Psi _{0}\rangle= & {} (\alpha _{c}|R\rangle +\beta _{c}|L\rangle )(\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2}), \nonumber \\ |\Psi _{1}\rangle= & {} \alpha _{c}|R\rangle (\alpha _{1}|0\rangle _{1}+\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2} +\beta _{2}|1\rangle _{2})+\beta _{c}|L\rangle (\alpha _{1}|0\rangle _{1}\nonumber \\&+\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2}). \end{aligned}$$
(7)
Fig. 2
figure 2

Scheme for realizing a Fredkin gate on the hybrid photon–atom system in a deterministic way. \(\hbox {HWP}_{i}\) (\(i=1, 2\)) is a half-wave plate, and \(\hbox {QWP}_{j}\) (\(j=1, 2\)) is a quarter-wave plate to implement the conversion of the photons polarization. \(\hbox {PBS}_{i}\) (\(i=1, 2, \ldots , 6\)) represents a polarizing beam splitter which transmits the right-circularly polarized photon \(|R\rangle \) and reflects the left-circularly polarized photon \(|L\rangle \). \(P_{\pi }\) stands for a phase shifter that contributes a \(\pi \) phase shift to the photon. \(\hbox {TR}_{i}\) (\(i=1, 2\)) is an optical element, which can be quickly switched to reflect or transmit a photon as we need. \(\hbox {BS}_{i}\) (\(i=1, 2\)) is a 50:50 beam splitter, DL is a time-delay device, M is a mirror, and \(\hbox {C}_{k}\) (\(k=1, 2\)) is a circulator

Full size image

Second, the photon in the state \(|L\rangle \) travels through a half-wave plate (\(\hbox {HWP}_{1}\)), where it suffers a Hadamard (\(H_{p}\)) transformation upon its polarization state:

$$\begin{aligned} |R\rangle \rightarrow \frac{1}{\sqrt{2}}(|R\rangle +|L\rangle ), \quad |L\rangle \rightarrow \frac{1}{\sqrt{2}}(|R\rangle -|L\rangle ). \end{aligned}$$
(8)

After the photon goes through \(\hbox {PBS}_{2}\), the components in the states \(|R\rangle \) and \(|L\rangle \) are split into paths 1 and 2, respectively, and the state of the photon–atom system goes into

$$\begin{aligned} |\Psi _{2}\rangle= & {} \alpha _{c}|R\rangle (\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2})\nonumber \\&+\frac{\beta _{c}|R\rangle }{\sqrt{2}}(\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2})\nonumber \\&-\frac{\beta _{c}|L\rangle }{\sqrt{2}}(\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2}).\;\;\;\;\;\; \end{aligned}$$
(9)

Third, in sequence, the photon in the polarization state \(|L\rangle \) is injected into cavities 1 and 2 and interacts with atoms 1 and 2 twice, respectively, while the photon in the polarization state \(|R\rangle \) in path 1 does not interact with the cavities. Then, the two parts of the photon will interfere at \(\hbox {PBS}_{4}\) and pass through \(\hbox {HWP}_{2}\), which transforms the state of the complicated system into

$$\begin{aligned} |\Psi _{3}\rangle= & {} \alpha _{c}|R\rangle (\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2})\nonumber \\&+\beta _{c}|R\rangle (\alpha _{1}\beta _{2}|0\rangle _{1}|1\rangle _{2} +\alpha _{2}\beta _{1}|1\rangle _{1}|0\rangle _{2})\nonumber \\&+\beta _{c}|L\rangle (\alpha _{1}\alpha _{2}|0\rangle _{1}|0\rangle _{2} +\beta _{1}\beta _{2}|1\rangle _{1}|1\rangle _{2}). \end{aligned}$$
(10)

After that, making use of a \(\pi /2\) microwave pulse or optical pulse, we perform a Hadamard operation upon atoms 1 and 2, whose action is given by the transformations \(|0\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )\) and \(|1\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )\). Subsequently, the photon in path 3 is split by \(\hbox {PBS}_{5}\) into two parts: The component in the state \(|R\rangle \) is reflected by \(\hbox {TR}_{1}\) into path 4 and transmits through \(\hbox {PBS}_{2}\) to interact with atoms confined in cavities 1 and 2 twice, respectively, and then, this part goes through \(\hbox {PBS}_{3}\) and \(\hbox {QWP}_{1}\), while the component in the state \(|L\rangle \) does not change. Next, we also need perform a Hadamard operation upon atoms 1 and 2, respectively. After the two parts interfere with each other at \(\hbox {BS}_{1}\), the state of the system changes to be

$$\begin{aligned} |\Psi _{4}\rangle= & {} \alpha _{c}|R\rangle (\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2})\nonumber \\&-\frac{\beta _{c}|L\rangle ^{5}}{\sqrt{2}}(\alpha _{2}|0\rangle _{1} -\beta _{2}|1\rangle _{1})(\alpha _{1}|0\rangle _{2}-\beta _{1}|1\rangle _{2})\nonumber \\&+\frac{\beta _{c}|L\rangle ^{6}}{\sqrt{2}}(\alpha _{2}|0\rangle _{1} +\beta _{2}|1\rangle _{1})(\alpha _{1}|0\rangle _{2}+\beta _{1}|1\rangle _{2}). \end{aligned}$$
(11)

Fourth, the photon in path 5 passes through \(\hbox {QWP}_{2}\), \(\hbox {TR}_{1}\), and \(\hbox {PBS}_{2}\) to interact with atoms in cavities 1 and 2 twice, respectively. Subsequently, it travels through \(\hbox {PBS}_{3}\), \(\hbox {QWP}_{1}\), \(\hbox {TR}_{2}\), and \(P_{\pi }\) to interfere with the photon in path 6 at \(\hbox {BS}_{2}\). Then, the photons in paths 8 and 9 gather at \(\hbox {PBS}_{6}\). Finally, at the output port, the resulting state of the hybrid system is given by

$$\begin{aligned} |\Psi _{5}\rangle= & {} \alpha _{c}|R\rangle (\alpha _{1}|0\rangle _{1} +\beta _{1}|1\rangle _{1})(\alpha _{2}|0\rangle _{2}+\beta _{2}|1\rangle _{2})\nonumber \\&+\beta _{c}|L\rangle (\alpha _{2}|0\rangle _{1} +\beta _{2}|1\rangle _{1})(\alpha _{1}|0\rangle _{2}+\beta _{1}|1\rangle _{2}). \end{aligned}$$
(12)

Compared to the initial state of the photon–atom system, we can find that the quantum protocol displayed in Fig. 2 can be used to implement a Fredkin gate on a three-qubit hybrid system with the success probability of 100% in theory, which exchanges the states of the two target atomic qubits only if the control photonic qubit is in the polarization state \(|L\rangle \).

3 SWAP gate on a two-qubit photon–atom system by Faraday rotation

In this section, we present the protocol for a SWAP gate, and its schematic setup is shown in Fig. 3. As we know, a SWAP gate on a hybrid photon–atom system can accomplish the operations as follows:

$$\begin{aligned}&|R\rangle _{1}|0\rangle _{2}\rightarrow |R\rangle _{1}|0\rangle _{2},\qquad |R\rangle _{1}|1\rangle _{2}\rightarrow |L\rangle _{1}|0\rangle _{2},\nonumber \\&|L\rangle _{1}|0\rangle _{2}\rightarrow |R\rangle _{1}|1\rangle _{2},\qquad |L\rangle _{1}|1\rangle _{2}\rightarrow |L\rangle _{1}|1\rangle _{2}. \end{aligned}$$
(13)

The subscripts 1 and 2 stand for the flying qubit encoded on the polarization states of a photon and the stationary qubit encoded on the states of an atom, respectively.

Fig. 3
figure 3

Compact quantum circuit for a deterministic SWAP gate on a hybrid photon–atom system

Full size image

Now, let us discuss how to construct a SWAP gate on a hybrid photon–atom system. Assuming that the initial state of the system containing the flying photonic qubit and the stationary atomic qubit is prepared in

$$\begin{aligned} |\Psi _{0}\rangle =(\alpha |R\rangle +\beta |L\rangle )(\gamma |0\rangle +\delta |1\rangle ), \end{aligned}$$
(14)

where the coefficients satisfy \(|\alpha |^{2}+|\beta |^{2}=|\gamma |^{2}+|\delta |^{2}=1\). In order to describe the principle of our SWAP gate on a hybrid photon–atom system explicitly, we specify the evolution of the system as follows.

The incident single photon gains a Hadamard operation by passing through a half-wave plate (\(\hbox {HWP}_{1}\)), then it transmits through \(\hbox {PBS}_{1}\) and is split into two wave-packets. The component in the polarization state \(|R\rangle \) travels in path 1 to interact with the stationary atom confined in the single-sided cavity twice, while nothing occurs to the component in the polarization state \(|L\rangle \). The two parts interfere at \(\hbox {PBS}_{2}\) and passes through \(\hbox {HWP}_{2}\). After the photon goes through \(\hbox {PBS}_{3}\), the state of the system evolves into

$$\begin{aligned} |\Psi _{1}\rangle= & {} \frac{\alpha }{2}(|R\rangle +|L\rangle )_{1}(-\gamma |0\rangle +\delta |1\rangle )_{2} +\frac{\beta }{2}(|R\rangle +|L\rangle )_{1}(-\gamma |0\rangle +\delta |1\rangle )_{2}\nonumber \\&+\frac{\alpha }{2}(|R\rangle -|L\rangle )_{1}(\gamma |0\rangle +\delta |1\rangle )_{2} -\frac{\beta }{2}(|R\rangle -|L\rangle )_{1}(\gamma |0\rangle +\delta |1\rangle )_{2}. \end{aligned}$$
(15)

Meanwhile, we need preform a Hadamard operation on the atom trapped in the single-sided microcavity. After the photon passes through \(\hbox {PBS}_{3}\), the part in the state \(|R\rangle \) travels in path 2 to interact with the stationary atomic qubit twice, while the part in the state \(|L\rangle \) does not change. Then, we need perform a Hadamard operation upon the atom again. In such way, the state of the whole system is given by

$$\begin{aligned} |\Psi _{2}\rangle =-\alpha \delta |R\rangle |0\rangle +\beta \gamma |R\rangle |1\rangle -\alpha \gamma |L\rangle |0\rangle +\beta \delta |L\rangle |1\rangle . \end{aligned}$$
(16)

Subsequently, the two parts interfere at \(\hbox {PBS}_{4}\) and go through \(\hbox {HWP}_{3}\). After the photon passes through \(\hbox {PBS}_{5}\), the part in the state \(|R\rangle \) travels in path 3 to interact with the stationary atom twice, while the part in the state \(|L\rangle \) does not change. Finally, they gather at \(\hbox {PBS}_{6}\) and pass through \(\hbox {HWP}_{4}\). After the above interaction, the state of the system takes the form

$$\begin{aligned} |\Psi _{3}\rangle =(\alpha |0\rangle +\beta |1\rangle )(\gamma |R\rangle +\delta |L\rangle ). \end{aligned}$$
(17)

From the objective state \(|\Psi _{3}\rangle \) in Eq. (17), one can realize that the states of the two qubits are exchanged. That is, the quantum circuit shown in Fig. 3 can be used to construct a SWAP gate on a hybrid two-qubit system in a deterministic way.

4 Discussion and summary

Let us analyze and discuss the experimental feasibility of our compact quantum gates. To qualify the performance of the Fredkin gate and SWAP gate, we define the fidelity as \(F=|\langle \Psi _{r}|\Psi _{i}\rangle |^{2}\). Here, \(|\Psi _{r}\rangle \) is the final state of the hybrid photon–atom system after the realistic operation, and \(|\Psi _{i}\rangle \) is the target state of an ideal photon–atom system. These two gates are based on the input–output process of the photon–atom system, which indicates that the reflection coefficient in Eq. (3) determines the fidelities of our protocols. Considering the realistic condition for hybrid photon–atom systems, we calculate the fidelities of our gates, as depicted in Fig. 4. For our work, in the weak coupling condition (e.g., \(g/\kappa =0.4\)), if \(\gamma /\kappa =0.05\), the fidelity of our Fredkin gate is \(F_{F}=82.8\%\) and that of our SWAP gate is \(F_{S}=74.6\%\); when \(\gamma /\kappa =0.1\), \(F_{F}=71.8\%\), and \(F_{S}=57.1\%\). In the strong coupling condition (e.g., \(g/\kappa =2.4\)), when \(\gamma /\kappa =0.05\), \(F_{F}=98.2\%\) and \(F_{S}=97.5\%\); when \(\gamma /\kappa =0.1\), \(F_{F}=96.6\%\) and \(F_{S}=95.1\%\). Note that, in the ideal condition \(\gamma \ll \kappa \), the fidelities of our gates will be close to \(100\%\).

Fig. 4
figure 4

The fidelities of the Fredkin gate and SWAP gate as a function of the parameter \(\gamma /\kappa \) and the coupling strength \(g/\kappa \). a The fidelity of the Fredkin gate \(F_{F}\). b The fidelity of the SWAP gate \(F_{S}\). The solid (black), dashed (red), dotted (green), and dashed-dotted (blue) lines correspond to \(g=2.4\kappa \), \(g=1.0\kappa \), \(g=0.75\kappa \), and \(g=0.4\kappa \), respectively

Full size image

Recently, great progress has been made in the atom–cavity system. For example, in 2008, Dayan et al. [79] reported that strong interactions between single atoms and photons can be achieved by using a microscopic optical resonator. In their experiment, individual Cs atoms are transited through the evanescent field of the resonator, which is monolithically fabricated from \(\text {SiO}_{2}\) on a Si chip. The effective coupling strength between the atom and cavity is \(g/2\pi \approx 70\) MHz, and the rate of decay for the cavity field is \(\kappa /2\pi =(165\pm 15)\) MHz. The free-space decay rate of the atom’s excited state is \(\gamma /2\pi =2.6\) MHz. In fact, the parameters mentioned above are appropriate to the “bad cavity” limit, in which \(\kappa \gg g\gg \gamma \). Moreover, other conditions for their system are \(\omega _{0}=\omega _{c}\), \(\omega _{p}=\omega _{c}-\frac{\kappa }{2}\), and \(g=\frac{\kappa }{2}\), which satisfy our requirements in this paper. With the parameters in their system, the practical fidelities of our Fredkin gate and SWAP gate are 92.7 and \(89.4\%\), respectively, which indicates that our schemes for these two compact quantum gates are feasible in experiment.

In the past decade, many schemes have been proposed for constructing quantum gates based on hybrid systems [5, 7, 16, 51, 57, 61, 80,81,82,83]. For example, in 2014, by exploiting the strong resonant microwave coupling between adjacent Rydberg states, Pritchard et al. [84] proposed a hybrid quantum gate between an atom and a microwave photon in a superconducting coplanar waveguide cavity. Meanwhile, Reiserer et al. [50] experimentally implemented a quantum CNOT gate that a flip of the photon is controlled by an atom confined in a Fabry–Perot cavity. In 2016, Wang et al. [85] presented two deterministic schemes for a CNOT gate and a Toffoli gate on hybrid photon–atom quantum system assisted by bad cavities. In our scheme, since photons are easily controllable flying qubits, the control qubit of our gates is encoded on the photon, which allows for the transmission of quantum information over large distance at room temperature. Due to its stability and long-coherence time, the atom is chosen as the target qubit. The schemes we propose for constructing the two-qubit SWAP gate and three-qubit Fredkin gate on the hybrid photon–atom systems have some interesting features. (1) The quantum circuits are compact, especially the scheme for the Fredkin gate. Different from the work in which a Fredkin gate can be decomposed into five specific gates, i.e., two CNOT gates and three controlled-\(\sqrt{\text{ NOT }}\) gates, the complexity of our scheme for quantum gates beats its synthesis procedure. (2) The protocols for these two quantum gates can run with high fidelities not only in the strong coupling but also in the weak coupling regimes, which means that they are practicable with current cavity technology. (3) In our scheme, auxiliary photonic qubits and measurement are not required, which reduces not only quantum resources but also errors.

In summary, we have designed the compact quantum circuits for implementing some deterministic quantum gates on a hybrid photon–atom system, including the Fredkin gate and SWAP gate, and both the gates can be accomplished with a success probability of \(100\%\) in theory. Different from other works, the fidelities of our gates are higher with the existing experimental quantum technology. Moreover, our schemes need not satisfy the condition that the transmission for the uncoupled cavity is balanceable with the reflectance for the coupled cavity [16]. Owing to the remarkable advance on manipulating atom–cavity systems, our compact quantum gates for hybrid photon–atom systems may play an important role in quantum computation in the future.