1 Introduction

Ever since the first quantum key distribution (QKD) protocol was devised by Bennett and Brassard [1], numerous quantum cryptographic applications such as quantum teleportation (QT) [2, 3], quantum secret sharing (QSS) [4–8], and quantum secure direct communication (QSDC) [9–12] have been proposed to cover various security loopholes. Recently, quantum private comparison (QPC) has gained popularity as another interesting branch of quantum cryptography. The goal of a QPC protocol is to privately compare two parties’ undisclosed information for equality. Based on the properties of quantum mechanics, an equality comparison can be easily performed without any complex computation.

The private comparison concept was already a topic for discussion in conventional cryptography. Yao [13, 14] proposed a protocol to solve the millionaires’ problem, in which two millionaires (say Alice and Bob) are interested in knowing which of them is richer without revealing their actual wealth. On the basis of Yao’s solution to the millionaires’ problem, Boudot et al. [15] subsequently proposed a protocol to determine whether the two millionaires are equally rich. However, Lo [16] indicated that the equality function used to determine this cannot be securely evaluated in a two-party scenario. Therefore, some additional assumptions such as a semi-honest third party (TP) should be considered to successfully achieve a private comparison.

The pioneering works in QPC were first presented by Yang and Wen [17], Yang et al. [18] in 2009. Since then, many QPC schemes [19–30] have been proposed to improve both the security and the qubit efficiency. Thus far, these protocols have required a TP that is at least semi-honest to help the two parties, Alice and Bob, accomplish the comparison work. According to the definitions in [17–30], a legitimate TP should faithfully execute the protocol and preserve a record of all of the intermediate computations. He/she might try to infer the players’ secrets from the record, but will not be corrupted by any external adversary.

Summarizing the ideas in [17–30], a secure QPC protocol should consider the following three principles. First, the two players should compare their secrets block-by-block instead of bit-by-bit in each round to avoid leaking the actual content. Second, the players’ secrets should be well covered by a secret key to prevent TP from recognizing their bit values. Finally, to prevent any player from inferring the other player’s secret, TP should announce only the comparison result (i.e., identical or different), instead of other details such as the positions of different bits.

It should be noted, however, that Lo in 1997 indicated that a QPC may not be possible with a two-party scenario under the technology of that time. With the advance in quantum mechanics, especially in the development of quantum entanglement swapping [31, 32], this paper reconsiders this issue on constructing a two-party QPC using the entanglement swapping of Einstein–Podolsky–Rosen (EPR) pairs. Based on the property of entanglement swapping, each player’s secret can be congenitally encrypted using a one-time-pad key, which provides unconditional security for any outside eavesdropper. Furthermore, since the published information is the computation result of the user’s message hash codes and the measurement results by executing exclusive-OR operation, the security for any inside user relies on the one-time-pad encryption. On the other hand, because the proposed protocol adopts the one-step quantum transmission strategy, it can be immune to Trojan horse attacks [33–38] without requiring the installation of any optical filter devices.

The rest of this paper is organized as follows. Section 2 describes the proposed QPC protocol in details by using the entanglement swapping of two EPR pairs. Section 3 analyzes the security of the proposed scheme with all aspects of attacks. Finally, a brief conclusion will be given in Sect. 4.

2 The proposed two-party QPC protocol

In this section, first an observation to the entanglement swapping of two EPR pairs will be introduced. Then, based on the observed property, details of the newly proposed two-party QPC will be described in steps, in which the protocol can be done without a trusted TP.

2.1 The entanglement swapping of two EPR pairs

Entanglement swapping [31, 32] is a physical phenomenon of quantum mechanics, which allows two or more independent entangled systems to build up entanglement to each other by switching their photons. In this paper, we only interest in the result of swapping two EPR pairs. For convenience, suppose that there are two unrelated parties: Alice and Bob. Each prepares an EPR pair in one of the four Bell states \(| {\varPhi ^{+}}\rangle =\frac{1}{\sqrt{2}}({| {00}\rangle +| {11} \rangle }), \, | {{\varPhi }^{-}} \rangle =\frac{1}{\sqrt{2}}( {| {00} \rangle -| {11} \rangle }),\, | {{\varPsi }^{+}} \rangle =\frac{1}{\sqrt{2}}( {| {01} \rangle +| {10} \rangle })\), and \(| {{\varPsi }^{-}} \rangle =\frac{1}{\sqrt{2}}( {| {01} \rangle -| {10} \rangle })\), respectively. Here, Alice’s two particles of EPR pair are denoted as (\(A_{1},\, A_{2}\)), and those for Bob’s are denoted as (\(B_{1}, \,B_{2}\)). After Alice exchanges her particle (\(A_{1}\)) with Bob’s particle (\(B_{1}\)), the entanglement swapping can be done by performing the Bell measurement on the particle pairs (\(B_{1}, \,A_{2}\)) and (\(A_{1}, \,B_{2}\)). The relationship of the two initial Bell states and the two measurement outcomes after swapping is displayed in Table 1. For example, if the two initial states are \(\{{|{{\varPsi }^{+}} \rangle ,|{{\varPsi } ^{+}}\rangle }\}\), then the two measurement results of entanglement swapping will become one of the four sets \(\{ {| {{\varPhi }^{+}} \rangle ,| {{\varPhi }^{+}} \rangle }\},\, \{ {| {{\varPhi }^{-}} \rangle ,| {{\varPhi } ^{-}} \rangle }\}, \, \{ {| {{\varPsi }^{+}} \rangle ,| {{\varPsi }^{+}} \rangle }\}\), or \(\{ {| {{\varPsi }^{-}} \rangle ,| {{\varPsi }^{-}} \rangle }\}\), as depicted in Eq. (1).

$$\begin{aligned} \big | {{\varPsi }^{+}} \big \rangle _{A_1 A_2 } \otimes \big | {{\varPsi }^{+}} \big \rangle _{B_1 B_2 }&= \frac{1}{\sqrt{2}}\left( {\big | {01} \big \rangle +\big | {10} \big \rangle } \right) _{A_1 A_2 } \otimes \frac{1}{\sqrt{2}}\left( {\big | {01} \big \rangle +\big | {10} \big \rangle } \right) _{B_1 B_2 } \nonumber \\&= \frac{1}{2}\left( {\big | {0101} \big \rangle +\big | {0110} \big \rangle +\big | {1001} \big \rangle +\big | {1010} \big \rangle } \right) _{A_1 A_2 B_1 B_2} \nonumber \\&= \frac{1}{2}\left( {\big | {0101} \big \rangle +\big | {1100} \big \rangle +\big | {0011} \big \rangle +\big | {1010} \big \rangle } \right) _{B_1 A_2 A_1 B_2} \nonumber \\&= \frac{1}{4} \left[ \begin{array}{l} \left( \big | {{\varPsi }^{+}} \big \rangle + \big | {{\varPsi }^{-}} \big \rangle \right) \qquad \left( \big |{{\varPsi }^{+}} \big \rangle + \big | {{\varPsi }^{-}} \big \rangle \right) \\ + \left( \big | {{\varPhi }^{+}} \big \rangle - \big | {{\varPhi }^{-}} \big \rangle \right) \quad \left( | {{\varPhi }^{+}} \big \rangle + \big | {{\varPhi }^{-}} \big \rangle \right) \\ +\left( \big | {{\varPhi }^{+}} \big \rangle + \big | {{\varPhi }^{-}} \big \rangle \right) \quad \left( \big | {{\varPhi }^{+}} \big \rangle - \big | {{\varPhi }^{-}} \big \rangle \right) \\ +\left( \big | {{\varPsi }^{+}} \big \rangle - \big | {{\varPsi }^{-}} \big \rangle \right) \quad \left( \big | {{\varPsi }^{+}} \big \rangle - \big | {{\varPsi }^{-}} \big \rangle \right) \end{array}\right] _{B_1 A_2 A_1 B_2} \nonumber \\&= \frac{1}{2} \left( \big | {{\varPhi }^{+}}\big \rangle \big | {{\varPhi }^{+}} \rangle - \big | {{\varPhi }^{-}}\big \rangle \big | {{\varPhi }^{-}}\big \rangle + \big | {{\varPsi }^{+}}\big \rangle \big | {{\varPsi }^{+}}\big \rangle + \big | {{\varPsi } ^{-}}\big \rangle \big | {{\varPsi }^{-}}\big \rangle \right) _{B_1 A_2 A_1 B_2}\nonumber \\ \end{aligned}$$
(1)
Table 1 The comparative table of entanglement swapping two Bell states [39]
Full size table

Let the four Bell states \(| {{\varPhi }^{+}}\rangle , \, | {{\varPhi }^{-}}\rangle , \,| {{\varPsi }^{+}}\rangle \), and \(| {{\varPsi }^{-}}\rangle \) represent the two bit of classical information “00”, “01”, “10”, and “11”, respectively. Suppose \(\{IS_{1}, IS_{2}\}\) are the two-bit codes of two initial Bell states, and \(\{MR_{1}, MR_{2}\}\) are the two-bit codes of two measured Bell states after entanglement swapping. According to Table 1, a special correlation can be found that \(IS_1 \oplus MR_1 =IS_2 \oplus MR_2 \). Since the result of \(MR_i\) can be one of the four possibilities of two-bit information, it can be regarded as a one-time-pad key to encrypt its corresponding initial state \(IS_{i}\). Furthermore, if the two initial Bell states are identical, then the two measurement results after entanglement swapping will also be the same. This feature can be used in designing a QPC protocol, which will be described in the following subsection.

2.2 The proposed QPC protocol using EPR pairs

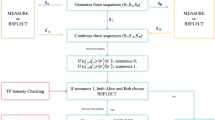
This subsection gives description of the proposed two-party QPC protocol based on EPR pairs. Suppose two parties (say Alice and Bob) want to make contrast on the equality of their document. Both parties are able to generate EPR pairs in four Bell states \(\{ {| {{\varPhi }^{+}}\rangle ,| {{\varPhi }^{-}} \rangle ,| {{\varPsi }^{+}} \rangle ,| {{\varPsi }^{-}}\rangle }\}\), and single photon in four types of qubit \(\{{| 0 \rangle ,| 1 \rangle ,| + \rangle ,| - \rangle }\}\), where \(| + \rangle =\frac{1}{\sqrt{2}}( {| 0 \rangle +| 1 \rangle })\) and \(|-\rangle =\frac{1}{\sqrt{2}}( {| 0\rangle -| 1\rangle })\). To be noted, the four Bell states can be identified by Bell measurement, and the orthogonal state \(\{ {| 0 \rangle ,| 1 \rangle }\} \quad ({\{{| + \rangle ,|-\rangle }\}})\) can be distinguished by Z-basis measurement (X-basis measurement). Alice and Bob compare the length of their private information. If their private information has the same length, then the proposed protocol can be depicted in steps as follows.

  1. Step 1.

    Alice (Bob) prepares a sequence of EPR pairs \(S_{A} (S_{B})\) according to each two bit of her secret message \( M_{A} (M_{B})\), where “00” is \(| {{\varPhi }^{+}}\rangle \),“01” is \(| {{\varPhi }^{-}}\rangle \), “10” is \(| {{\varPsi } ^{+}}\rangle \), and “11” is \(| {{\varPsi }^{-}}\rangle \). She (he) divides these EPR pairs into two sequences \(S_{A_1 } \) and \(S_{A_2 } (S_{B_1 }\) and \(S_{B_2} )\), which include the 1st and the 2nd particles of all states, respectively.

  2. Step 2.

    Alice (Bob) mixes \(S_{A_1 }\, (S_{B_1 } )\) with some decoy photons \(D_A \,(D_B )\) for each particle randomly in \(\{{| 0\rangle ,| 1 \rangle ,| + \rangle ,| - \rangle }\}\) to form a new sequence \(S_{A_1 }^{*}\, (S_{B_1 }^{*} )\) and then sends it to Bob (Alice) via a quantum channel.

  3. Step 3.

    After confirming that Bob (Alice) has received the quantum sequence \(S_{A_1 }^{*}\, (S_{B_1 }^{*} )\), Alice (Bob) announces the positions and the measurement bases of \(D_A\, (D_B )\) to Bob (Alice). Subsequently, Bob (Alice) extracts the particles in \(D_A\, (D_B )\) from \(S_{A_1 }^{*}\, (S_{B_1 }^{*})\) and performs the corresponding bases on them to obtain the measurement results \(R_{D_A }\, (R_{D_B } )\). The presence of eavesdropper can be discussed between Alice and Bob by analyzing the error rate of \(R_{D_A }\, (R_{D_B } )\). If there is no eavesdropper, then the protocol continues to the next step. Otherwise, Alice (Bob) aborts the protocol and restarts from Step 1.

  4. Step 4.

    Alice and Bob perform Bell measurement on (\(S_{B_1}^i, \,S_{A_2}^i\)) and (\(S_{A_1}^i, \,S_{B_2}^i\)) to derive two bunches of measurement results \(MR_{A}\) and \(MR_{B}\), respectively, where \(i\) represents the \(i\)th set of EPR pair. They transform the result string \(MR_{A} \,( MR_{B})\) into a binary string \(C_{A}\, (C_{B})\) of \(M\) bit length and then employ the one-way hash function [40] (i.e., \(H:\{ {0,1} \}^{N}\rightarrow \{ {0,1} \}^{M}\), where \(N\) denotes the length of the inputted data, and \(M\) denotes the length of the hash code) on their secret message (\(M_{A}\) and \(M_{B}\)) to obtain two hash codes, \(h_{A}\) and \(h_{B}\), each of \(M\) bit length (i.e., \(h_A =H({M_A})\) and \(h_B =H({M_B }))\). Finally, they compute the exclusive-OR result \(R_{A} \,(R_{B})\) of \(h_{A}\) and \(C_{A} \,(h_{B}\) and \(C_{B})\) (i.e., \(R_A =h_A \oplus C_A \) and \(R_B =h_B \oplus C_B )\).

  5. Step 5.

    Alice (Bob) sends \(R_{A}\, (R_{B})\) to Bob (Alice) via an authenticated classical channel. Later, they can compute the exclusive-OR result \(R_{C}\) of \(R_{A}\) and \(R_{B}\) (i.e., \(R_C =R_A \oplus R_B )\). If \(R_{C}\) is all bit “0”, then the compared secrets of the two parties are identical. Otherwise, Alice’s and Bob’s secret message are regarded as different. (i.e., one or more classical bits in are “1”).

In the proposed QPC protocol, even if the compared secrets fall within a range of value (e.g., wealth or bid), the measurement results after entanglement swapping will cover the secret with a one-time-pad key, which is conform to the unconditional security. More specifically, it is difficult for a malicious insider (say Alice) to acquire the other party Bob’s secret content \(M_{B}\) from \(R_B =h_B \oplus C_B,C_{A}\), and \(M_{A}\). Furthermore, the difficulty for an insider (say Alice) to retrieve the other participant Bob’s encrypted secret \(M_{B}\) is based on the security of the one-time-pad encryption. It should be noted that abiding by the protocol means the two participants must help themselves successfully accomplish the protocol. That is, they are responsible for the correct result (i.e., \(R_{A}\) and \(R_{B})\) of the protocol in Step 5.

According to [19, 23], the function \(\eta _E =\frac{q_\mathrm{s}}{q_\mathrm{t}}\) has been used to evaluate the qubit efficiency, where \(q_\mathrm{s}\) denotes the compared classical bits, and \(q_\mathrm{t}\) denotes the total generated photons without the decoy photons. Since two EPR pairs can compare two bit of secret among two parties, the qubit efficiency can be computed as 50 % (i.e., \(\eta _E =\frac{2}{4}=50\) %), which is equivalent to the most efficient scheme proposed by Tseng et al. [23]. However, the proposed QPC does not require any semi-honest TP to complete the work.

3 Security analysis

This section analyzes the security of the proposed QPC protocol. Suppose an eavesdropper Eve intends to steal the secret message of the two participants. He/she can play the role of an outside unknown adversary or an inside malicious user. Fortunately, the protocol is demonstrated to be secure against three types of quantum attack: the Trojan horse attacks, the intercept–resend attack, and the Entangle-measure attack in Sects. 3.1, 3.2, and 3.3, respectively.

3.1 Trojan horse attacks

There are two kinds of Trojan horse attack: the IPE attack [33–35] and the delay-photon attack [36, 37]. In general, the IPE attack can be prevented by installing a wavelength optical device that filters out the invisible photons. As for the delay-photon attack, the receiver can pick up a portion of the photons and split each particle by a photon number splitter (PNS). If there is an unreasonable high rate of multi-photon signal, then the presence of the delay-photon attack is detected. However, these quantum equipments would consume a great amount of transmitted photons. Therefore, in the proposed QPC protocol, all photons are sent one time only to the receiver, which can make it free from the Trojan horse attacks without any optical filter devices.

3.2 Intercept–resend attack

In the proposed QPC protocol, there are some decoy photons hidden in random positions of the transmitted photon sequences \(S_{A_1 }^{*} \) and \(S_{B_1 }^{*} \). If Eve chooses the wrong polarized basis to measure and resend these particles, she will cause an error to each decoy photon with a probability of \(\frac{1}{4}\). Hence, the probability of detecting Eve’s attack from the public discussion is \(1-\left( {\frac{3}{4}}\right) ^{n}\), where \(n\) is the total number of decoy photons. When \(n\) is large enough, the detection rate of eavesdropping check will approach to 1.

3.3 Entangle-measure attack

Eve may also try to retrieve some useful information from the transmitted photon sequence by performing the entangle-measure attack. She first prepares some ancillas \(E=\{{| {E_1} \rangle ,| {E_2}\rangle ,\ldots ,| {E_{2N}}\rangle }\}\) and then entangles them with the transmitted sequence by performing a unitary operation \(U_{E}\), in which \(U_E^\dagger U_E =U_E U_E^\dagger =I\). However, the effect of Eve’s operation on the decoy photons will cause the following possible results:

$$\begin{aligned} U_E \big | 0 \big \rangle \big | {E_i} \big \rangle&= \alpha \big | 0 \big \rangle \big | {e_{00}} \big \rangle +\beta \big | 1 \big \rangle \big | {e_{01}} \big \rangle \\ U_E \big | 1 \big \rangle \big | {E_i } \big \rangle&= \gamma \big | 0 \big \rangle \big | {e_{10}} \big \rangle +\delta \big | 1 \big \rangle \big | {e_{11}} \big \rangle \\ U_E \big | + \big \rangle \big | {E_i } \big \rangle&= \frac{1}{2}\left[ {\begin{array}{l} \big | + \big \rangle \left( {\alpha \big | {e_{00}} \big \rangle +\beta \big | {e_{01}} \big \rangle +\gamma \big | {e_{10}} \big \rangle +\delta \big | {e_{11}} \big \rangle } \right) \\ +\big | - \big \rangle \left( {\alpha \big | {e_{00}} \big \rangle -\beta \big | {e_{01}} \big \rangle +\gamma \big | {e_{10}} \big \rangle -\delta \big | {e_{11}} \big \rangle } \right) \end{array}} \right] \\ U_E \big | - \big \rangle \big | {E_i } \big \rangle&= \frac{1}{2} \left[ \begin{array}{l} \big | + \big \rangle \left( {\alpha \big | {e_{00}} \big \rangle +\beta \big | {e_{01}} \big \rangle -\gamma \big | {e_{10}} \big \rangle -\delta \big | {e_{11}} \big \rangle } \right) \\ +\big | - \big \rangle \left( {\alpha \big | {e_{00}} \big \rangle -\beta \big | {e_{01}} \big \rangle -\gamma \big | {e_{10}} \big \rangle +\delta \big | {e_{11}} \big \rangle } \right) \\ \end{array} \right] \end{aligned}$$

To be noted, \(| {E_i }\rangle \) is the initial state of Eve’s ancilla, and \(| {e_{00}}\rangle ,| {e_{01}} \rangle ,| {e_{10} } \rangle ,| {e_{11}}\rangle \) are the four distinguishable quantum states, where the relationship of the coefficients is \(| {\alpha ^2}|+| {\beta ^2 } |=| {\gamma ^2 }|+| {\delta ^2 }|=1\). Apparently, if the decoy photon is \(| 0\rangle \) or \(| 1\rangle \), Eve has to let \(\beta =\gamma =0\) to pass the eavesdropping check. On the contrary, if the decoy photon is \(| +\rangle \) or \(| - \rangle \), Eve has to let \(\alpha | {e_{00}} \rangle -\beta | {e_{01} } \rangle +\gamma | {e_{10} } \rangle -\delta | {e_{11} }\rangle =\alpha | {e_{00}}\rangle +\beta | {e_{01}}\rangle -\gamma | {e_{10} }\rangle -\delta | {e_{11}} \rangle ={\vec {0}}\) to escape from the detection, where \({\vec {0}}\) denotes a zero vector. If the above two situations are all conformed, then Eve’s attack will be successfully undetectable during the public discussion.

Nevertheless, since \(\beta =\gamma =0\) leads to the result of \(\alpha | {e_{00}}\rangle -\delta | {e_{11} }\rangle ={\vec {0}}\), it implies a contradictory relationship that \(\alpha | {e_{00}}\rangle =\delta | {e_{11} }\rangle \); thus, Eve is unable to identify \(\alpha | {e_{00}}\rangle \) from \(\delta | {e_{11} }\rangle \) in such case. Hence, she cannot obtain any useful information by measuring these ancillas. On the other hand, if Eve tries to make the ancillas distinguishable (i.e., \(\alpha | {e_{00}}\rangle \ne \delta | {e_{11}}\rangle )\), the states of the decoy photons will be disturbed and end up being detected in the public discussion.

4 Conclusion

Based on the entanglement swapping of two EPR pairs, this paper provides a way to compare the quantum secrets of two legitimate parties without any help from a TP. The proposed QPC scheme has adopted the one-step quantum transmission strategy and the decoy state photons to prevent various types of eavesdropping attacks. Since the participants’ encrypted secrets are protected by the entanglement swapping and the one-time-pad encryption, it provides unconditional security for outside attackers and inside attackers. Moreover, to extend such arbitrator-free QPC to a multiparty scenario, and then to construct more practical applications like quantum auction and quantum voting based on these QPC’s might be a promising issue in quantum cryptography.