Thermodynamic Properties of Binary In–Ni Alloys

The mixing enthalpies of liquid binary In–Ni alloys (0.85 < x _Ni < 1) at 1800 K were determined by isoperibol calorimetry. The thermodynamic properties of the In–Ni alloys were calculated for the entire composition range using the model of ideal associated solutions. The thermodynamic activities of melt components show negative deviations from the ideal behavior. The mixing enthalpies are characterized by moderate exothermic effects. The minimum mixing enthalpy of the melts is –12.0 ± 0.1 kJ/mol at x _Ni = 0.59.

Introduction

Indium is a component of semiconductor materials (for example, InSb) and a new class of lead-free solders. Research of chemical interaction between nickel and indium is of particular interest since nickel and its alloys are often used as contact materials in electronic devices.

Our objective is to study the mixing enthalpies of the melts at 0.85 < x _Ni < 1 in the In–Ni system at 1800 K as the alloys in this region have not been examined applying calorimetry by other researchers [1].

Literature Overview

We should note that the thermodynamic properties of In–Ni alloys were previously studied in both liquid and solid states. Calorimetry was also used to experimentally determine the mixing enthalpies (∆H) of liquid alloys in the indium-rich region. However, the form of digitized data is not suitable for comparison (line in Fig. 1 [1]) and thus their accuracy is questionable; this especially concerns the data differentiated to find the partial mixing enthalpies of components. The activities of indium in the In–Ni system at 1248 K were defined by effusion over a wide composition range [2]. They demonstrate moderate negative deviations from the ideal behavior. The enthalpies of forming intermetallic phases in the In–Ni system were determined by calorimetry of dissolution in liquid aluminum. They can be characterized by quite high exothermic effects [3, 4]. The paper [5] attempted to perform a backward calculation applying a semiempirical model relying on the effect of filling the d-level of the transition metal (nickel) with electrons of the p-metal (indium). According to [6], the first partial enthalpy of dissolving nickel in indium is $\Delta {\overline{H}}_{\mathrm{Ni}}^{\infty }=\hbox{--} 25$ kJ/mol at 1300–1700 K. The literature overview for the In–Ni system, including the optimized phase diagram, is presented in [7]. The thermodynamic properties of In–Ni alloys are indicative of sufficiently strong interaction between the components. The phase diagram testifies that there are In–Ni solid solutions with wide homogeneity ranges of the In_~7Ni_~3, In₃Ni₂, In_~5Ni_~6, InNi, In₉Ni₁₃, In_~4Ni_~7, InNi₂, and InNi₃ phases.

Fig. 1

Partial and integral mixing enthalpies for the binary In–Ni melts obtained at 1800 K

Experimental Procedure

Data Obtaining and Processing. The experimental procedure with the isoperibol calorimeter is described in [8]. For the experiments, we used indium (99.99%) and nickel (99.9%). The indium and nickel samples weighing 0.014–0.042 g and 0.013–0.047 g were introduced in solid state at T = 298 K into the melt, which consisted of pure nickel 1.3–1.7 g in weight at the beginning of the experiments. The alloys were examined in crucibles made of alumina being inert to all melt components.

Indium is the only component in the In–Ni system possessing noticeable volatility at operating temperatures of our calorimeter that are needed to keep the system in molten state over a wide composition range (1500–1800 K). According to [9], pressure of saturated indium vapors at 1485 K is 100 Pa, approximately corresponding to the point when its volatility can still be neglected. Evaporation of the metal from the crucible is undesired because of gradual changes in the melt composition, which can hardly be calculated accurately. When evaporates, the metal tends to deposit on cold sections of the calorimeter, gradually leading to its ageing and failure, thus requiring replacement of individual parts. Indium strongly interacts with nickel and becomes much less volatile, making it possible to increase temperature to 1800 K, needed to melt nickel, being the most refractory component.

The calorimeter was calibrated against six to seven nickel samples. To calculate the thermal effects accompanying the dissolution of the samples, the Tian equation was applied:

$$ K{\displaystyle \underset{0}{\overset{\uptau_{\infty }}{\int }}\left(T-{T}_0\right)dt=\Delta {H}_T+{n}_i\Delta {H}_{298}^T}, $$

where K is the calorimeter constant; τ_∞ is the temperature relaxation time in recording the heat exchange pattern; T – T ₀ = ∆T is the difference between the crucible with melt and isothermal calorimeter shell; t is time; ni is the amount of addition, mol; ΔH ^T₂₉₈ is the enthalpy of heating 1 mol of addition from 298 K to the experimental temperature calculated by the equation from [10].

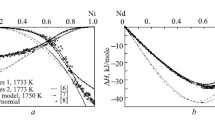
Using the partial mixing enthalpies for one component, we integrated the Gibbs–Duhem equation to calculate these parameters for the other and then determine the integral values. We combined all the data with the results reported in [1] to determine the partial and integral mixing enthalpies for the binary In–Ni melts over the entire composition range (Fig. 1). We processed the literature and experimental data applying the software that we developed with the model of ideal associated solutions (IAS). For calculation, we selected the minimum but necessary and sufficient number of associates to assess thermodynamic data within the experimental error. In the In–Ni system, they are InNi and InNi₂ associates.

Experimental Results. The integral and partial mixing enthalpies for the binary In–Ni melts with rounded amounts of the components are provided in Table 1 and Fig. 1.

Table 1 Partial and Integral Mixing Enthalpies of the In–Ni Melts at 1800 K (kJ/mol)

The partial and integral mixing enthalpies and entropies at 1300 K were fitted to polynomial dependences, which give less accurate fitting of the thermodynamic functions than the IAS model but accelerate calculation in case of multicomponent systems based on the binary In–Ni system:

$$ \begin{array}{c}\hfill \Delta H={x}_{\mathrm{Ni}}\left(1-{x}_{\mathrm{Ni}}\right){\displaystyle \sum_{i=0}^n{a}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill \Delta {\overline{H}}_{\mathrm{In}}={x}_{\mathrm{Ni}}^2{\displaystyle \sum_{i=0}^n{b}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill \Delta {\overline{H}}_{\mathrm{Ni}}={\left(1-{x}_{\mathrm{Ni}}\right)}^2{\displaystyle \sum_{i=0}^n{c}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill \Delta {S}^{\mathrm{ex}}={x}_{\mathrm{Ni}}\left(1-{x}_{\mathrm{Ni}}\right){\displaystyle \sum_{i=0}^n{d}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill \Delta {\overline{S}}_{\mathrm{In}}^{\mathrm{ex}}={x}_{\mathrm{Ni}}^2{\displaystyle \sum_{i=0}^n{e}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill \Delta {\overline{S}}_{\mathrm{Ni}}^{\mathrm{ex}}={\left(1-{x}_{\mathrm{Ni}}\right)}^2{\displaystyle \sum_{i=0}^n{f}_i{x}_{\mathrm{Ni}}^i},\hfill \\ {}\hfill {b}_i=\left(i+1\right)\left({a}_i-{a}_{i+1}\right),\hfill \\ {}\hfill {c}_i=\left(i+1\right){a}_i,\hfill \\ {}\hfill {e}_i=\left(i+1\right)\left({d}_i-{d}_{i+1}\right),\hfill \\ {}\hfill {f}_i=\left(i+1\right){d}_i.\hfill \end{array} $$

The coefficients of polynomial dependences for In–Ni at 1800 K are as follows: a _i = –28.8 and d _i = –6.1 at i = 0; a _i = –11.9 and d _i = –1.9 at i = 1; a _i = –84.6 and d _i = –35.3 at i = 2; a _i = 77.1 and d _i = 31.3 at i = 3. Hence, $\Delta {\overline{H}}_{\mathrm{Ni}}^{\infty }=\hbox{--} 28.8$, $\Delta {\overline{H}}_{\mathrm{In}}^{\infty }=\hbox{--} 48.5\pm 1.0$, and ∆H _min = –12.0 ± 0.12 kJ/mol at x _Ni = 0.59.

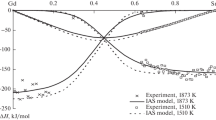
Thermodynamic Modeling. The activities of pure components and the molar fractions of associates in the binary In–Ni melts are shown in Fig. 2, and the IAS model parameters in Table 2.

Fig. 2

Activities (a _i ) of pure In and Ni and molar fractions (x _i ) of InNi and InNi₂ associates in the In–Ni melts at 1800 K obtained with the IAS model

Table 2 Enthalpies (kJ/mol at.) and Entropies (J/(mol at. · K)) of Forming Associates (L) and Intermetallics (S) in the Binary In–Ni System at Temperatures Close to Equilibrium with the Melt

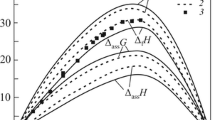
The temperature dependences of the first partial mixing enthalpies of components in the binary In–Ni melts calculated with the IAS model are provided in Fig. 3, and the excess entropies and Gibbs energies in Fig. 4 (points denote the data obtained from the indium activities determined experimentally by effusion).

Fig. 3

Temperature dependences of the first partial mixing enthalpies ($\Delta {\overline{H}}_i^{\infty }$) of components in the liquid or supercooled (dashed lines) binary In–Ni melts according to the IAS model

Fig. 4

Excess entropies and Gibbs energies of mixing for the binary In–Ni melts at 1800 K calculated with the IAS model

Discussion of Results

Figure 5 shows activities of the In–Ni melt components at 1248 K that we calculated and determined experimentally [2]. It should be noted that the indium activities [2] were defined at quite a low temperature of 1248 K. According to the generally accepted phase diagram, there are two heterogeneous ranges at 1248 K: 0.6 < < x _Ni < 0.67 and 0.75 < x _Ni < 1. Hence, some distinctions between our modeled and experimental data for these regions are not fundamental.

Fig. 5

Activities of components in the liquid or supercooled In–Ni alloys at 1248 K calculated and obtained experimentally

Figure 6 shows the enthalpies and entropies of forming the associates and intermetallics. They were optimized as parameters of the thermodynamic model of the In–Ni alloys (Table 2) and compared with the literature data (experimental or modeled) if any.

Fig. 6

Enthalpies (∆_f H) and entropies (∆_f S) of forming associates (L) and intermetallics (S) in the In–Ni system according to the IAS model versus literature ∆_f H for the intermetallics

The mixing enthalpies of In–Ni intermetallics that we calculated somewhat differ from the literature data. This is likely because we modeled only high-temperature phases, while the literature defines the properties of low-temperature phases, most of which have no equilibrium regions with the melt.

Conclusions

Isoperibol calorimetry has been used to determine the thermodynamic properties of the In–Ni system at 1800 K. Our results agree with the literature data.

We have applied the literature and our own data calculated with the IAS model to define activities of the components and molar fractions of the associates in the In–Ni system.

Our mixing enthalpies of the In–Ni intermetallics correlate with the literature, with some deviations resulting from the temperature difference.