1 Introduction

FBGs are spectral filters based on the phenomenon of Bragg reflection occurring within the optical fiber waveguide. These filters known as FBG-based sensors are quasi-distributed sensing structures and have been extensively used in the last decade for various commercial applications including security, communications, military, electric vehicles, and aeronautics (Sante 2015; Mckenzie and Karafolas 2005; Foote and Read 2000; Phing et al. 2007).

Unlike systems based on fully distributed sensing systems, FBG-based sensing systems (FBGSSs) particularly measure the temperature and strain formations and acquire information relevant to the measurands by utilizing the shift of the reflected light at a specific wavelength, i.e. Bragg wavelength. In other words, these systems depend on the principle that light is reflected back at a certain wavelength, allowing it to be transmitted at all other wavelengths in the spectrum.

FBGs are generally formed by exposing certain regions of the fiber core to ultraviolet (UV) light (Hill et al. 1993). In other words, forming the gratings through the fiber core is based on the phenomenon resulting in fluctuations of the core refractive index. In the conventional grating inscription technique, the polymer material on the fiber coating is first stripped and then the stripped fiber region is exposed to the grating pattern exploiting a UV source and phase mask providing control of FBG structural shape and optical properties of the sensing system. Consequently, the production process of the grating causes crucial limitations on the sensing performance of the system according to the parameters such as grating period, Bragg wavelength, and wavelength shift. Thus, there may be a restriction on the accurate measurement of temperature and strain formations (Foote and Read 2000; Agarwal and Mishra 2014; Maske et al. 2018; Ramalingam and Neumann 2011; Garcia et al. 2015).

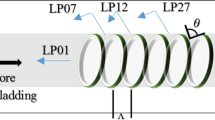
The working principle of a uniform FBG is shown in Fig. 1. As is seen in Fig. 1 when a broadband source is coupled to the single-mode fiber with an inscribed Bragg grating, incident light is reflected in the waveguide due to the alteration of the grating period, i.e. pitch of the grating (Sante 2015).

Fig. 1
figure 1

Basic configuration of a uniform fiber Bragg grating

Full size image

As the light travels through the optical fiber, there is a correlation between the reflected and continuing modes propagating in the optical fiber as a result of its interaction with the gratings. The amplitudes of these modes vary according to the position depending on the axis in the direction of movement. Taking account of the fluctuations in the core refractive index as well as in the grating period, the variations of both the strain and the temperature formations can easily be measured and analyzed (Sahidan et al. 2019; Ugale and Mishra 2010).

The Bragg wavelength, i.e. wavelength of the light reflected back along the grating length changes due to the effective refractive index of the fiber core and the grating period as in (1) (Sante 2015; Mrad and Xiao 2005; Sahidan et al. 2019; Ibrahima et al. 2017, Mihailov 2012).

$${\uplambda }_{{\text{B}}}=2{{\text{n}}}_{{\text{eff}}}\Lambda$$
(1)

where \({{\text{n}}}_{{\text{eff}}}\) is the effective refractive index of the fiber core and \(\Lambda\) is the grating period of FBG also known as the pitch of the grating.

As is understandable from (1), since the strain and temperature formations cause the changes in neff and Λ, Bragg wavelength changes with both the effective refractive index of the fiber core and the grating period of FBG, linearly (Kipriksiz and Yucel 2021).

2 Theoretical analysis of FBG-based sensing system

Both the Bragg wavelength and wavelength shift are susceptible to temperature and strain variations occurring along the optical fiber employed in the FBG-based sensing system. The ratio of wavelength shift to Bragg wavelength of the FBG varies with temperature and strain formations as given by (2) (Guan et al. 2000; Alalibo et al. 2019)

$$\frac{\Delta {\uplambda }_{{\text{B}}}}{{\uplambda }_{{\text{B}}}}=\left(1-{\uprho }_{\mathrm{\alpha }}\right)\upvarepsilon +\left(\mathrm{\alpha }+\upxi \right)\mathrm{\Delta T}$$
(2)

where \(\Delta {\uplambda }_{{\text{B}}}\) is the wavelength shift of incident light, \({\uplambda }_{{\text{B}}}\) is Bragg wavelength, \({\uprho }_{\mathrm{\alpha }}\) is the photoelastic coefficient of the silica fiber core (\({\uprho }_{\mathrm{\alpha }}\)= 0.22), \(\mathrm{\alpha }\) is the thermal expansion coefficient of the fiber core, \(\xi\) is the thermo-optical coefficient appertaining to the type and concentration of dopants used for production of the fiber core, \(\upvarepsilon\) is the strain formation, \(\mathrm{\Delta T}\) is the temperature change (Morey et al. 1989, Kersey et al. 1997; Xie et al. 2004; Majumder et al. 2008; Lai et al. 2016).

The photoelastic coefficient of the fiber core (\({\uprho }_{\mathrm{\alpha }})\) can be stated as in (3)

$${\uprho }_{\mathrm{\alpha }}=\frac{{{\text{n}}}_{{\text{eff}}}^{2}}{2}\left[{\uprho }_{12}-\upsigma ({\uprho }_{11}-{\uprho }_{12})\right]$$
(3)

where \(\upsigma\) corresponds to the Poisson’s ratio of the fiber core and the ρij are the photo elastic tensor components (Sante 2015). The photoelastic coefficient changes linearly with the square of the effective refractive index and the change in Poisson’s ratio of the fiber core.

The first term in (2), i.e. \(\left(1-{\uprho }_{\mathrm{\alpha }}\right)\) denotes the gage factor (k) and hence (2) takes the form of (4)

$$\Delta {\uplambda }_{{\text{B}}}={\uplambda }_{{\text{B}}}({\text{k}}.\upvarepsilon )+{\uplambda }_{{\text{B}}}\left(\mathrm{\alpha }+\upxi \right)\mathrm{\Delta T}$$
(4)

For silica fibers since \({\uprho }_{\mathrm{\alpha }}\) = 0.22, \({\text{k}}=1-{\uprho }_{\mathrm{\alpha }}=0.78\) and the central wavelength, i.e. Bragg wavelength is 1550 nm, typical strain sensitivity is about 1.2 pm/µ \(\upvarepsilon\) (Rao 1998).

Temperature and strain information can be obtained from the amount of wavelength shift utilizing various methods. These methods generally use the principle of compensating for one of the temperature or strain effects on the wavelength shift. Practically, the most applicable method consists of measuring temperature occurrences along the fiber gratings using an additional strain-free FBG sensor provided that both sensors are exposed to the same temperature change. If there is no strain-free area in the region to be measured, placing the reference FBG sensor in a suitable capillary tube can be used as a suitable method to compensate for the strain effects, properly (Kim et al. 2008).

When the strain effects on the Bragg wavelength are appropriately balanced, shifts in the Bragg wavelength due to the temperature variations are obtained by taking the derivative of (1) with respect to temperature, as expressed in (5) (Sante 2015).

$$\Delta {\uplambda }_{{\text{B}}}=2\left({{\text{n}}}_{{\text{eff}}}\frac{\mathrm{d\Lambda }}{{\text{dT}}}+\Lambda \frac{{{\text{dn}}}_{{\text{eff}}}}{{\text{dT}}}\right)\Delta {\text{T}}$$
(5)

It can be unambiguously seen that the increase in temperature change induces thermal elongation of the grating and changes of both the grating period, i.e. the pitch of the grating, and the core refractive index of the optical fiber.

It is possible to perform temperature analysis with FBGSSs that are integrated in a way not to be exposed to strain (Yucel et al. 2017; Garcia et al. 2015; Mrad and Xiao 2005). Therefore, using (4) and assuming that there is no external strain effect in the sensing medium, the relationship between wavelength shift and Bragg wavelength can be written as a function of the temperature variations (∆T) and the thermal expansion coefficient (\(\mathrm{\alpha })\) of the core and the thermo-optic coefficient (\(\upxi\)) as in (6) (Ferraro and Natale 2002).

$$\Delta {\uplambda }_{{\text{B}}}={\uplambda }_{{\text{B}}}\left(\mathrm{\alpha }+\upxi \right)\mathrm{\Delta T}$$
(6)

For fused silica fiber α is about 0.55 × 10–6 K−1 and \(\upxi\) takes the values changing in the range of 3 × 10−6 K−1 − 8.6 × 10−6 K−1 for the germanium-doped fused silica fiber used for FBGSS (Kreuzer 2006).

Assuming that the sum of the coefficients α and \(\upxi\) is equal to the temperature coefficient β, (4) takes the form in (7a) by ignoring the first term defining the strain effect, and β can also be written as in (7b) (Sante 2015)

$$\Delta {\uplambda }_{{\text{B}}}={\uplambda }_{{\text{B}}}.\upbeta .\mathrm{\Delta T}$$
(7a)
$$\upbeta =\frac{1}{{\text{n}}}.\frac{{\text{dn}}}{{\text{dT}}}$$
(7b)

where n denotes the refractive index of the fiber core, and ∆T is the temperature change. Temperature coefficient β describes the variation of the core refraction index (n) caused only by temperature effects occurring through the optical fiber.

The expression of \(({\text{k}}.\upvarepsilon )\) in (4) corresponds to the strain effect caused by force (\({\upvarepsilon }_{{\text{m}}}\)) and temperature (\({\upvarepsilon }_{{\text{T}}}\)), and hence \(\upvarepsilon\) can be stated by (8)

$$\upvarepsilon ={\upvarepsilon }_{{\text{m}}}+{\upvarepsilon }_{{\text{T}}}$$
(8)

where \({\upvarepsilon }_{{\text{m}}}\) and \({\upvarepsilon }_{{\text{T}}}\) are strain variations caused by the force changes mechanically and the ambient temperature, respectively. The strain (\({\upvarepsilon }_{{\text{T}}}\)) caused by the temperature change can be expressed with (9)

$${\upvarepsilon }_{{\text{T}}}=\mathrm{\alpha }.\mathrm{\Delta T}$$
(9)

where \(\mathrm{\alpha }\) is the expansion coefficient of the optical fiber core.

Substituting (6) to (9) into (2) and rearranging the equation, the ratio of the shift in Bragg wavelength to the Bragg wavelength (\({\Delta\uplambda }_{{\text{B}}}/{\uplambda }_{{\text{B}}}\)) can be obtained as given in (10).

$$\frac{\Delta {\uplambda }_{{\text{B}}}}{{\uplambda }_{{\text{B}}}}=\left(1-{\uprho }_{\mathrm{\alpha }}\right).\left({\upvarepsilon }_{{\text{m}}}+\mathrm{\alpha }.\mathrm{\Delta T}\right)+\frac{{\text{dn}}/{\text{n}}}{{\text{dT}}}.\mathrm{\Delta T}={\text{k}}.\left({\upvarepsilon }_{{\text{m}}}+\mathrm{\alpha }.\mathrm{\Delta T}\right)+\upbeta .\mathrm{\Delta T}$$
(10)

In the case of a pure temperature sensor used for the measurement system, the Bragg grating remains unstrained. In other words, the fiber is fixed only at one point in the measurement system, sufficiently apart from the Bragg grating located on the optical fiber. Hence, temperature variation can be measured accurately and reliably.

Making use of (10) and reorganizing the equation properly, the temperature sensitivity (ST) along the length of the fiber grating can be stated as in (11) (Sante 2015).

$${{\text{S}}}_{{\text{T}}}=\Delta {\uplambda }_{{\text{B}}}/\mathrm{\Delta T}={\uplambda }_{{\text{B}}}/(1/({\text{k}}.\mathrm{\alpha }+\frac{1}{{\text{n}}}.\frac{{\text{dn}}}{{\text{dT}}}))$$
(11)

As is seen from (11), the change in temperature sensitivity varies linearly with both the variations of Bragg wavelength and the wavelength shift. Therefore, this relationship can be exploited in the implementation of temperature sensing systems based on FBG.

3 Design of FBG-based sensing system

The basic configuration of an FBGSS with different parameters in Table 1 has been designed using the OptiSystem 17.1 program to analyze the effects of grating length, Bragg wavelength, wavelength shift, and reflection rate on temperature sensitivity. In other words, the OptiSystem program has been exploited to design an FBG-based sensing system, which is a suitable approach to simulate and analyze the performance of FBGs. Its schematic representation is shown in Fig. 2.

Table 1 Optical fiber and grating parameters used in FBGSS
Full size table
Fig. 2
figure 2

Basic configuration of an FBGSS

Full size image

As obviously seen in FBGSS configuration, a light source pumping light with a wavelength of 1550 nm and two uniform FBG sensing elements with grating lengths of 1 mm are utilized in the installation. Nevertheless, FBG sensing systems with the grating lengths changing in the range of 0.1–100 mm have been designed for analyzing the effects of grating length on temperature sensitivity, i.e. temperature measurement accuracy, in this study.

The optical spectrum analyzer and WDM FBG sensor interrogator employed in the configuration of FBGGSS are used to obtain wavelength reflection spectrums and wavelength-power simulations, respectively. The simulations and the plottings obtained from the FBG sensor interrogator are for various values of temperature, grating length, Bragg wavelength, and reflection rate of the FBG-based sensing systems.

The characteristics of the optical fiber and the parameters of the grating employed in the configuration of FBGSS are given in Table 1.

4 Simulation results and discussions

The simulations representing the effects of grating length, Bragg wavelength, and reflection rate on the temperature sensitivity of the FBG have been performed by exploiting the configurations of FBGSSs designed in the OptiSystem program. In this regard, using the simulation results and obtained data, the relationships between these parameters and their temperature sensitivities have been analyzed utilizing the regression method and Matlab curve-fitting tool, and the corresponding formulas expressing their dependencies have also been achieved.

4.1 Effects of grating length on temperature sensitivity

The configuration of FBGSS shown in Fig. 2 has been employed to perform simulations regarding the effects of grating lengths on the temperature sensitivity of FBG and to numerically analyze the data acquired from the simulations. Furthermore, to determine the temperature measurement accuracy, i.e. temperature sensitivity, theoretical analyses have been made based on the the simulation results for temperature values of 1 °C, 5 °C, 10 °C, 20 °C, 50 °C, and 120 °C.

Using this FBGSS setup, the wavelength reflection spectrums for grating lengths of 0.1 mm, 0.6 mm, 1 mm, 3 mm, 10 mm, and 100 mm and temperature values of 1 °C, 5 °C, 10 °C, 20 °C, 50 °C and 120 °C are obtained as shown in Fig. 3, respectively.

Fig. 3
figure 3

Wavelength reflection spectrums of FBGSS with grating lengths of a 0.1 mm, b 0.6 mm, c 1 mm, d 3 mm, e 10 mm and f 100 mm

Full size image

It is observed that the grating length decreases as the amount of the power of back-reflected light decreases since the FBG interrogator system can not perceive the Bragg wavelength accurately for the grating length below ~ 1 mm, as shown in Figs. 3a, b. The wavelength shifts can not be clearly seen or understood in the graphs shown in Figs. 3a, b. Therefore, FBGSS performs more effectively at values of the grating length higher than approximately 1 mm.

In the wavelength reflection spectrum given in Figs. 3d, e, and f, shifts in Bragg wavelength can be clearly seen and interpreted. Wavelength shifts are obtained as 280 pm, 700 pm, and 1680 pm for grating lengths of 3 mm, 10 mm and 100 mm, respectively.

For changes in grating length in the range of 0.1–100.0 mm, wavelength shifts versus both the temperature change and the variations of grating lengths are given in Table 2.

Table 2 Corresponding values of grating length, temperature change and wavelength shift
Full size table

It is inferred from Table 2 that the main reason for the change in the Bragg wavelength shift is the temperature change although there is a change in grating length. In other words, the grating lengths have no direct impact on the temperature sensitivity. As can be seen from the values given in Table 2, a temperature change of 1 °C causes a wavelength shift of approximately about 14 pm resulting in a temperature sensitivity of 14 pm/°C. Taking into consideration (1), it is observed that the grating period of the FBG has an important role in Bragg wavelength in comparison with the grating length. On the other hand, there is a linear relationship between the grating period and Bragg wavelength as opposed to the grating length, due to the fluctuations in the refractive index of the optical fiber core.

4.2 Effects of Bragg wavelength and wavelength shift on temperature sensitivity

One of the important characteristic parameters of FBGSS is the Bragg wavelength. Accurately detecting the Bragg wavelength is crucial when choosing FBG sensors to determine physical parameters such as strain and temperature. Since FBGs can be connected in series in the system designs, interference of the wavelengths reflected from the FBGs can cause measurement errors. Therefore, it is important to estimate the effect of Bragg wavelength on temperature sensitivity.

In this section the paper, in order to observe the effects of Bragg wavelength on temperature sensitivity, the FBG-based sensing system shown in Fig. 2 is used to acquired the necessary simulations for Bragg wavelengths ranging from 400 to 2000 nm and wavelength shifts in this range.

Figure 4 shows the simulation of temperature sensitivities corresponding to Bragg wavelength ranging from 400 to 2000 nm for a temperature change of 100 °C.

Fig. 4
figure 4

Temperature sensitivity versus Bragg wavelength

Full size image

Benefiting from the drawing shown in Fig. 4, the linear and quadratic formulas for the relationships between Bragg wavelength (\({\uplambda }_{{\text{B}}}\)) and temperature sensitivity (ST) are derived as in (12.a) and (12.b), respectively.

$${{\text{S}}}_{{\text{T}}}={9.1468\times {10}^{-3}.\uplambda }_{{\text{B}}}+3.5793\times {10}^{-4}$$
(12a)
$${{\text{S}}}_{{\text{T}}}=1.7204\times {10}^{-7}{{.\uplambda }_{{\text{B}}}}^{2}+8.7409\times {10}^{-3}{.\uplambda }_{{\text{B}}}+0.17527$$
(12b)

It is observed that the formula expressing temperature sensitivity given in (11) and the equations in (12a) and (12b) are compatible with each other. The correlation coefficients of the regression formulas for both (12a) and (12b) are 99.98%. The temperature sensitivity for the Bragg wavelength of 1550 nm at a temperature change of 100 °C is computed as 14.188 pm/°C and 14.137 pm/°C, respectively.

Meanwhile, when the first order derivative of (12a) is taken with respect to the Bragg wavelength, the change in temperature sensitivity according to the Bragg wavelength is calculated as approximately 9.15 × 10–3 pm/°C(nm)−1. In other words, the temperature sensitivity takes the value of ~ 9.2 pm/°C for a Bragg wavelength of 1000 nm.

As can be seen, increasing the Bragg wavelength causes a proportional increase in temperature sensitivity. However, considering nonlinear phenomena such as dispersion and attenuation losses in optical fiber waveguides, a Bragg wavelength of 1550 nm can be deemed as the optimum wavelength in both FBGSS configurations and optical fiber distributed sensing systems based on the scattering mechanisms.

A schematic diagram of an FBGSS with a Bragg wavelength of 500 nm, i.e. wavelength of the source, exploiting the WDM FBG sensor interrogator and two uniform FBG sensors with a grating lengths of 10 mm for temperature changes of 20 °C and 100 °C is indicated in Fig. 5.

Fig. 5
figure 5

FBGSS with Bragg wavelength of 500 nm

Full size image

The simulations with regard to the shifts in Bragg wavelength are attained using the configuration shown in Fig. 5 for the Bragg wavelength of 500 nm and for the parameter values of grating length and temperature change.

Using the simulation results obtained from the configuration in Fig. 5, shifts in Bragg wavelength are obtained at values ranging from 92 to 458 pm for temperature changes between 20 and 100 °C. As a result, there is a linear relationship between temperature change and wavelength shift.

Wavelength shifts due to the changes in Bragg wavelength and temperature change are obtained using the FBGSS shown in Fig. 2. For the variations of Bragg wavelength in the range of 400–2000 nm and changes in the temperature ranging from 20 to 120 °C, shifts in Bragg wavelength, i.e. wavelength shifts take the values given in Table 3.

Table 3 Parameter values of Bragg wavelength, temperature change and wavelength shift
Full size table

As is seen from Table 3, Bragg wavelength affects the temperature measurement sensitivities of FBGSS. From hence, it is determined that the FBGSS with a Bragg wavelength of 2000 nm has ~ 5.03 times more temperature sensitivity than the system with 400 nm. In other words, as the temperature change increases the wavelength shift shows a linear increase.

Figure 6 shows the simulations about the wavelength shifts for Bragg wavelengths of 2000 nm and 400 nm, respectively, at temperature change of 100 °C. For the Bragg wavelength of 2000 nm, wavelength shift takes the value of 1840 pm at 100 °C while for the 400 nm value, it takes the value of 366 pm at the same temperature change as plotted in the simulations below.

Fig. 6
figure 6

Wavelength shifts at 100 °C for Bragg wavelengths of a 2000 nm b 400 nm

Full size image

There are linear relationships between the temperature change measured where the FBGs are located along the fiber and the ratio of the shift in Bragg wavelength to the Bragg wavelength (\({\Delta\uplambda }_{{\text{B}}}/{\uplambda }_{{\text{B}}}\)) matching the equations given in (6) and (7a). As the temperature change increases, \({\Delta\uplambda }_{{\text{B}}}/{\uplambda }_{{\text{B}}}\) which represents the temperature coefficient (β) also increases linearly.

Using the interpolation method and the values given in Table 3, information on the shifts in Bragg wavelength for 1550 nm is obtained, and the simulation representing the correlation between temperature change and shift in Bragg wavelength, i.e. the wavelength shift is plotted as shown in Fig. 7.

Fig. 7
figure 7

Shift in Bragg wavelength versus temperature change

Full size image

The linear equation expressing the temperature dependence of the wavelength shift can be written by making use of the curve-fitting method as in (13).

$$\Delta {\uplambda }_{{\text{B}}}=14\times {\text{T}}+3.0115\times {10}^{-13}$$
(13)

The correlation coefficient related to the regression formula is ~ 99.99%. By taking the first order derivative of (13) according to the temperature change, the temperature sensitivity can be computed as 14 pm/°C. In other words, as seen in the plot, for a temperature of 100 °C, the shift in Bragg wavelength is 1400 pm.

4.3 Effects of reflection rate on temperature sensitivity

The reflection rate defines the power level of the reflected light from the FBG in the sensing systems. Although the reflection rate value is generally above 70%, it can decrease to the level of 0.1% depending on the design of the detection system. One of the principal aims of this research is to observe the effects of reflection rate on temperature sensitivity and compare them with other effects mentioned in the previous sections of the study. In this context, FBGSSs using two uniform FBG sensors with the reflection rates ranging from 0.99% to 0.001% have been designed in OptiSystem program. In addition, the numerical analyses have been carried out on the parameters of reflection rate, wavelength shift and reflected power of the light scattered back from FBG.

Figure 8 shows the configurations of the FBGSSs with reflection rates of 0.99 and 0.70, respectively. The reflected power values obtained for temperature changes of 20 °C and 100 °C are acquired using optical spectrum analyzers. As the reflection rate increases, the reflection power level also increases as shown in Fig. 9.

Fig. 8
figure 8

FBGSSs exploiting two uniform FBG with reflection rates of a 0.99 and b 0.70 for the same temperature changes

Full size image
Fig. 9
figure 9

Reflection rate versus reflected power of FBG

Full size image

The shifts in Bragg wavelength due to the variations of the reflection rates of FBGs for a temperature change of 100 °C are given in Table 4. The variation of the reflection rate causes little change in the Bragg wavelength shift. In other words, for variations in the reflection rate ranging from 0.001 to 0.99%, the wavelength shifts change from 1398 to 1400 pm resulting in a temperature sensitivity of ~ 14 pm/°C at 100 °C.

Table 4 Corresponding values of the parameters of RR, ∆λB and RP for ∆T = 100 °C
Full size table

As seen in Table 4, in response to the change in wavelength shift, there is a change in the reflection rate value between 0.001 and 0.99% and a change in the reflected power value between 11.1 and 42 dBm. In other words, the reflection rate increases with the reflected power of the light scattered back from the FBG, whilst the wavelength shift varies slightly.

The simulation showing the dependence of the reflected optical power (RP) of the backscattered light wave along the grating length of the FBG on the reflection rate (RR) is obtained using Table 4 and is given in Fig. 9.

The equation that best fits the relationship between reflection rate (RR) and reflected power (RP) is a third-order equation. Making use of the curve-fitting and the interpolation method, the cubic equation expressing the dependence of the reflection rate on the reflected power is given by the following equation:

$${{\text{R}}}_{{\text{R}}}=1.071\times {10}^{-4}.{{{\text{R}}}_{{\text{P}}}}^{3}-6.433\times {10}^{-3}.{{{\text{R}}}_{{\text{P}}}}^{2}+0.122.{{\text{R}}}_{{\text{P}}}-0.7074$$
(14)

where RR and RP are the reflection rate and the reflection power of the FBG, respectively.

Benefiting from the regression analysis, the correlation coefficient of the regression formula is found to be 99.60%. As can be understood from the correlation coefficient, i.e. 99.60%, the relationship between reflection rate and reflection power is in the form of a 3rd degree equation. In other words, the formula that best explains the relationship between these two parameters is in the form of a 3rd degree equation. As can be seen from the simulation in Fig. 9, although the change in reflected power is low when the reflection rate changes between 0.001 and 0.10%, the reflected power value shows a rapid increase when the reflection rate changes between 0.10 and 0.99%.

Using the data in Table 4, the plot representing the change in temperature sensitivity varying with the reflection rate at 100 °C is shown in Fig. 10. Additionally, by applying the curve-fitting and interpolation method to the data points in the simulation in Fig. 10, the equation expressing the relationship between sensitivity (ST) and reflection rate (RR) can be written as in (15).

Fig. 10
figure 10

Temperature sensitivity versus reflection rate

Full size image
$${{\text{S}}}_{{\text{T}}}=2.409.{{{\text{R}}}_{{\text{R}}}}^{5}-5.648.{{{\text{R}}}_{{\text{R}}}}^{4}+4.580.{{{{\text{R}}}_{{\text{R}}}}^{3}-1.539.{{{\text{R}}}_{{\text{R}}}}^{2}+0.2218.{\text{R}}}_{{\text{R}}}+13.98$$
(15)

As is seen from (15), the relationship that best expresses the relationship between sensitivity and reflection rate is in the form of a 5th degree polynomial. When regression analysis is applied, the correlation coefficient and temperature sensitivity are computed as approximately 0.9963%, and 14.00 pm/°C on average, respectively, in response to the change in reflection rate between 0.001 and 0.99%. Although, the reflection rates of FBG vary over a wide range, its sensitivity varies within a small range.

The sensitivity change according to the reflection rate variation in this range is computed as ~ 0.021 pm/°C(%)−1. Therefore, it seems that the effect of reflection rate on sensitivity is more decisive than the effect of Bragg wavelength on sensitivity.

The simulation showing the change between temperature sensitivity and reflected power is illustrated in Fig. 11. Using numerical methods such as regression and curve-fitting, temperature sensitivity can be obtained as a function of reflected power.

Fig. 11
figure 11

Temperature sensitivity versus reflected power

Full size image

In other words, the expression corresponding to the relationship between sensitivity (ST) and reflected power (RP) is written as in (16).

$${{\text{S}}}_{{\text{T}}}=-1.53\mathrm{ x }{10}^{-7}{{.{\text{R}}}_{{\text{P}}}}^{5}+2.18\mathrm{ x }{10}^{-5}.{{{\text{R}}}_{{\text{P}}}}^{4}-0.0012.{{{{\text{R}}}_{{\text{P}}}}^{3}+0.031.{{{\text{R}}}_{{\text{P}}}}^{2}-0.39\mathrm{ x R}}_{{\text{P}}}+15.74$$
(16)

The correlation between sensitivity and reflected power is also in the form of a 5th degree polynomial. The regression coefficient is computed to be 0.9877%. The sensitivity change depending on the variation of reflected power is found to be ~ 0.0007475 pm/°C(%)−1. Therefore, this value is much smaller than the change in temperature sensitivity obtained in response to the variation of the unit reflection rate. Briefly stated, its value is approximately 1/30 of the temperature sensitivity.

5 Conclusion

Temperature sensitivity is an important parameter for system performance in FBG-based sensing systems. In the literature, there are many studies focusing on temperature sensitivity in such systems. However, studies analyzing the effects of individual FBG design parameters on temperature sensitivity and interpreting their relationship mathematically are very limited.

In this paper, the effects of parameters such as grating length, Bragg wavelength, wavelength shift, and reflection rate on the temperature sensitivity of FBGSS have been analyzed and the mathematical formulas expressing the relationships between these parameters have been derived by using numerical methods in the Matlab and the configurations performed in the OptiSystem. It has been observed that the grating length variations have no direct impact on the temperature sensitivities. For grating lengths ranging from 0.1 to 100 mm, temperature sensitivity takes the value of about 14 pm/°C for temperature changes in the range of 1–120 °C. From the simulation results presented in this study, it has been concluded that the ratio of wavelength shift to Bragg wavelength varies with temperature changes thereby affecting the temperature sensitivity of the sensing system.

The temperature sensitivities have taken the values of 3.7 pm/°C, 4.6 pm/°C, 5.5 pm/°C, 9.2 pm/°C, 14 pm/°C, 18.4 pm/°C approximately for the Bragg wavelengths of 400 nm, 500 nm, 600 nm, 1000 nm, 1550 nm, and 2000 nm, respectively. Furthermore, the change in temperature sensitivity with Bragg wavelength has been computed to be ~ 9.15 × 10–3 pm/°C(nm)−1.

As a result of the simulation studies, it has been seen that there are significant changes in the amount of power of the light reflected from FBGs depending on the reflection rate. Since the reflection rate changes the reflected power of the light, it results in a slight increase in temperature sensitivity. For the reflection rate variations in the range of 0.001–0.99%, temperature sensitivity has taken the value of ~ 14 pm/°C at 100 °C for the reflected powers changing from 11.1 to 42 dBm. In addition, changes in temperature sensitivity depending on both reflection rate and reflected power have been computed as ~ 0.021 pm/°C(%)−1 and ~ 0.0007475 pm/°C(%)−1, respectively.

Finally, it has been observed in this study that the temperature measurement sensitivity can be changed depending on the FBG parameters such as grating length, Bragg wavelength, wavelength shift, and reflection rate. Moreover, significant enhancements in the amount of reflected power can be achieved by changing the reflection rate and properly designing the FBG-based sensing systems. For this reason, the characteristic properties of optical fiber and the parameters of the sensing system have an important role in FBGSS applications. In particular, measuring the temperature formations occurring in the systems exploited in aircraft, rail systems, electric vehicles, unmanned aerial and land vehicles and so forth structures with high accuracy significantly reduces the potential for system errors and accidents. Therefore, FBG-based sensing systems provide precise and reliable data acquisition, helping the structures they are integrated to operate at optimum levels. In this context, this research paper will provide significant benefits to researchers and shed light on investigations in the field.