1 Introduction

In the past few decades, there has been an increasing interest in the propagation of laser beams through turbulent environments due to its wide range of applications including laser communications, remote sensing, laser radar, laser weapons, and tracking. Numerous studies have been conducted to examine various properties of laser beams in turbulent environments (Cai 2006; Belafhal et al. 2011; Korotkova et al. 2012; Boufalah et al. 2016; Ez-Zariy et al. 2016; Khannous et al. 2016; Wu et al. 2016; Saad et al. 2017; Liu et al. 2018; Yaalou et al. 2019; Chang et al. 2020; Hricha et al. 2021; Nossir et al. 2021; Boufalah et al. 2022). Simultaneously, the field of ultra-short pulse technology has also made significant progress and has gained the attention of many researchers (Pan 2007; Zou and Hu 2016; Liu et al. 2017; Duan et al. 2020; Jo et al. 2021, 2022; Zhu et al. 2021; Benzehoua et al. 2021a, 2021b). Spectral changes in laser beams, as they move through different turbulent and optical systems have been investigated, which has opened up new possibilities in areas such as optical communication, information encoding and transmission, and lattice spectroscopy (Yadav et al. 2007, 2008; Han 2009). These spectral changes can be caused by various factors, including correlated sources (Wolf 1987), lightwave focusing (Gbur et al. 2001), scattering from spatially random media (Wolf et al. 1989; Wang et al. 2017), turbulence (Ji 2008; Tang and Zhao 2014; Benzehoua and Belafhal 2023a, b), and aperture propagation (Pu et al. 1999; Pan et al. 2007; Benzehoua and Belafhal 2023a, b). The spectral changes of laser beams can be categorized during propagation into two types: spectral shift and spectral switches. The first type occurs when the frequency of the spectrum shifts to either lower or higher frequencies during propagation, while spectral switches refer to the phenomenon where the spectrum switches from one frequency to another. However, the second type has been both theoretically predicted (Liu and Lü, 2004) and experimentally verified (Kandpal and Vaishy 2002) in optical imaging systems. Many studies have been conducted to explore the spectral changes of laser beams as they travel through different media and optical systems. For instance, Zou et al. investigated the spectral anomalies of a diffracted chirped pulsed super-Gaussian beam (Zou and Hu 2016), while Liu et al. studied the spectral and coherence properties of a Gaussian Schell-model pulsed beam in a turbulent atmosphere (Liu et al. 2016). Jo et al. examined the spectral properties of a chirped Gaussian pulsed beam that propagated through a slant turbulent atmosphere path (Jo et al. 2021), and Duan et al. studied the impact of biological tissue and spatial correlation on the spectral changes of a Gaussian-Schell model vortex beam (Duan et al. 2020). In the context of oceanic turbulence, Ding et al. examined the impact of turbulence kinetic energy dissipation rate and other factors on the spectral changes of partially coherent Gaussian Schell-model pulsed beams in two dimensions (Ding et al. 2018). Recently, Jo et al. studied the impact of oceanic turbulence on the spectral changes of a diffracted chirped Gaussian pulsed beam, aiming to understand the distortion effects of oceanic turbulence on the beam’s intensity and shape (Jo et al. 2022).

The present paper provides analytic formulae to describe the spectral characteristics of the pulsed HhChG beam as it propagates through a turbulent atmosphere, for both truncated and non-truncated diffracted laser. The effects of this later and turbulence parameters on the beam's evolution are then illustrated graphically, and the conclusion is finally presented.

2 Field distribution of pulsed HhChG beam

For the propagation of a pulsed beam in a turbulent atmospheric, we can first deal with the propagation of its Fourier monochromatic part, then perform the inverse Fourier transform to obtain the propagation equation of the pulsed beam in the space–time domain.

In the Cartesian coordinates system, the initial electrical field of the pulsed HhChG beam in space–time domain in the source plane (z = 0), can be expressed as (Saad et al. 2022)

$$E_{N,l} \left( {x_{01} ,y_{01} ,t} \right) = E_{N,l} \left( {x_{01} ,t} \right).E_{N,l} \left( {y_{01} ,t} \right),$$
(1)

where \(E_{N,l} \left( {x_{0} ,t} \right)\) and \(E_{N,l} \left( {y_{0} ,t} \right)\) are given by

$$E_{N,l} \left( {s,t} \right) = A_{0} \left( {\frac{{x_{01}^{{}} }}{{w_{0} }}} \right)^{l} \cosh^{N} \left( {x_{01} \Omega } \right)e^{{\left( { - x_{01}^{2} /w_{0}^{2} } \right)}} \,\left( {\frac{{y_{01}^{{}} }}{{w_{0} }}} \right)^{l} \cosh^{N} \left( {y_{01} \Omega } \right)e^{{\left( { - y_{01}^{2} /w_{0}^{2} } \right)}} \,A\left( t \right),$$
(2)

with \(A_{0}\) is being amplification factor, \(s = \left( {x_{01} ,y_{01} } \right)\) represents the coordinates on the source plane with \(\left( {x_{01} ,y_{01} } \right)\), N and l are beam order and hollowness parameters, respectively, \(w_{0}\) is the waist radius of the Gaussian part, \(\Omega\) is the argument of cosh function, and \(A\left( t \right)\) is the temporal envelop of the initial pulsed beam.

By using the following identity (Abramowitz and Stegun 1970)

$$\exp \left( { - \frac{{x^{2} }}{{w_{0}^{2} }}} \right)\cosh^{N} \left( {\Omega x} \right) = \frac{1}{{2^{N} }}\sum\limits_{m = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\exp \left( {a_{m}^{2} } \right)\exp \left\{ { - \left( {\frac{x}{{w_{0} }} - a_{m} } \right)^{2} } \right\}} ,$$
(3)

where

$$a_{m} = \left( {m - \frac{N}{2}} \right)\sqrt \delta ,\quad a_{n} = \left( {n - \frac{N}{2}} \right)\sqrt \delta \;{\text{and}}\quad \delta = w_{0}^{2} \Omega^{2} ,$$
(4)

Equation (1) can be written as

$$\begin{aligned} E_{N,l} \left( {x_{01} ,y_{01} ,t} \right) = & \frac{1}{{2^{2N} }}\left( {\frac{{x_{01} }}{{w_{0} }}} \right)^{l} \left( {\frac{{y_{01} }}{{w_{0} }}} \right)^{l} \sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \\ & \quad \times exp\left( { - \frac{{x_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{m} }}{{w_{0} }}x_{01} } \right)\,exp\left( { - \frac{{y_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{n} }}{{w_{0} }}y_{01} } \right)A\left( t \right). \\ \end{aligned}$$
(5)

In the following, we assume that the incident pulsed beam has a Gaussian form (Agrawal 1999)

$$A\left( t \right) = e^{{ - t^{2} /T^{2} }} e^{{ - i\omega_{0} t}} ,$$
(6)

where T is the pulse duration, and \(\omega_{0}\) is the central frequency.

Performing the Fourier transform on Eq. (5), we obtain the field expressed, in the space-frequency domain, as

$$E_{N,l} \left( {x_{01} ,y_{01} ,\omega } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {E_{N,l} \left( {x_{01} ,y_{01} ,t} \right)e^{ - i\omega t} } dt\, = E_{N,l} (x,y,z = 0)A(\omega ),$$
(7)

where \(A(\omega )\) is the original Fourier spectrum of the pulsed beam and is given by

$$A(\omega ) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {f(t){\text{e}}^{i\omega t} } dt.$$
(8)

On substituting from Eq. (6) into Eq. (8), the integral calculation yields

$$S^{\left( 0 \right)} \left( \omega \right) = \left| {A\left( \omega \right)} \right|^{2} = \left| {\frac{T}{\sqrt 2 }\exp \left( {\frac{{ - T^{2} \left( {\omega - \omega_{0} } \right)^{2} }}{4}} \right)} \right|^{2} ,$$
(9)

where \(S^{\left( 0 \right)} \left( \omega \right)\) is the original power spectrum of the incident beam.

The cross-spectral density function of the pulsed HhChG beam at the input plane is given by

$$\begin{aligned} W_{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} ,0,\omega } \right) = & E\left( {x_{01} ,y_{01} ,0,\omega } \right)\,E^{*} \left( {x_{02} ,y_{02} ,0,\omega } \right) \\ & = S^{\left( 0 \right)} \left( \omega \right)\left( {\frac{{x_{01} x_{02} }}{{w_{0}^{2} }}} \right)^{l} \left( {\frac{{y_{01} y_{02} }}{{w_{0}^{2} }}} \right)^{l} \sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \\ & \quad \times exp\left( { - \frac{{x_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{m} }}{{w_{0} }}x_{01} } \right)\,exp\left( { - \frac{{x_{02}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{{m^{\prime}}} }}{{w_{0} }}x_{02} } \right)exp\left( { - \frac{{y_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{n} }}{{w_{0} }}y_{01} } \right)exp\left( { - \frac{{y_{02}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{{n^{\prime}}} }}{{w_{0} }}y_{02} } \right), \\ \end{aligned}$$
(10)

where \({\mathbf{r}}_{1} = \left( {x_{01} ,y_{01} } \right)\) and \({\mathbf{r}}_{{\mathbf{2}}} = \left( {x_{02} ,y_{02} } \right)\) are two arbitrary position vectors in the source plane.

In the following paragraph, we will study the propagation of the pulsed HhChG beam through the turbulent atmosphere using the generalized Huygens-Fresnel diffraction integral to investigate their propagation features.

2.1 The analytical formula for a non-truncated pulsed beam

In this Section, we will explore the details and complexities of a non-truncated pulsed beam to derive an analytical formula that describes its characteristics. Based on the extended Huygens-Fresnel integral formula, the cross-spectral density function of pulsed HhChG beam propagating through the turbulent atmosphere can be presented as (Andrews and Phillips 2005)

$$\begin{aligned} W_{N,l} \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} ,z,\omega } \right) =\, & S^{\left( 0 \right)} \left( \omega \right)\left( {\frac{k}{2\pi z}} \right)^{2} \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {d^{2} {\mathbf{r}}_{{\mathbf{1}}} d^{2} {\mathbf{r}}_{{\mathbf{2}}} } } W_{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} ,0,\omega } \right) \\ & \quad \times \exp \left[ { - \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{1}}} } \right)^{2} + \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{2}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)^{2} } \right]\,\left\langle {\exp \left[ {\psi^{ * } \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{1}}} } \right) + \psi \left( {{\mathbf{r}}_{{\mathbf{2}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} , \\ \end{aligned}$$
(11)

where \({{\varvec{\uprho}}}_{{\mathbf{1}}}\) and \({{\varvec{\uprho}}}_{{\mathbf{2}}}\) are two position vectors at the receiver plane, \(k = \frac{\omega }{c}\) is the wave number, with c is the speed of the source radiation in vacuum and \(\left\langle \cdot \right\rangle\) is the ensemble average over the turbulent media. This average describes the influence of the turbulence on the propagation of laser beam and it can be expressed as

$$\left\langle {\exp \left[ {\psi^{ * } \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{1}}} } \right) + \psi \left( {{\mathbf{r}}_{{\mathbf{2}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} \approx \exp \left\{ { - \frac{1}{{\rho_{0}^{2} }}\left[ {\left( {{\mathbf{r}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)^{2} + \left( {{\mathbf{r}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {{\varvec{\uprho}}}_{{\mathbf{2}}} } \right) + \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)^{2} } \right]} \right\},$$
(12)

where \(\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}\) is the coherence length of a spherical wave spreading in the turbulent atmosphere medium, with \(C_{n}^{\,2}\) is the structure constant of the refractive index, which characterizes the local strength of the turbulent atmosphere.

By letting \({{\varvec{\uprho}}}_{{\mathbf{1}}} = {{\varvec{\uprho}}}_{2} = {{\varvec{\uprho}}}\) and inserting Eqs. (10) and (12) into Eq. (11), the following result is obtained

$$\begin{aligned} W_{N,l} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) =\, & S^{\left( 0 \right)} \left( \omega \right)\frac{{k^{2} }}{{4\pi^{2} z^{2} 2^{4N} w_{0}^{2l} }}\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {dx_{01} dy_{01} dx_{02} dy_{02} x_{01}^{l} x_{02}^{l} } } } } y_{01}^{l} y_{02}^{l} \\ & \quad \times exp\left( { - \alpha_{x} x_{01}^{2} + 2\left( {\gamma_{1 \cdot x} + \frac{{x_{02}^{{}} }}{{\rho_{0}^{2} }}} \right)x_{01} } \right)\exp \left[ { - \left( {\frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}}} \right)x_{02}^{2} + 2\left( {\frac{{a_{{m^{\prime}}} }}{{w_{0} }} - \frac{ikx}{{2z}}} \right)x_{02} } \right] \\ & \quad \times exp\left( { - \alpha_{y} x_{01}^{2} + 2\left( {\gamma_{1 \cdot y} + \frac{{y_{02}^{{}} }}{{\rho_{0}^{2} }}} \right)y_{01} } \right)\exp \left[ { - \left( {\frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}}} \right)y_{02}^{2} + 2\left( {\frac{{a_{{n^{\prime}}} }}{{w_{0} }} - \frac{iky}{{2z}}} \right)y_{02} } \right], \\ \end{aligned}$$
(13)

where

$$\alpha_{1} = - \frac{ik}{{2z}} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }},$$
(14)
$$\gamma_{1,x} = \frac{{a_{m} }}{{w_{0} }} + \frac{ikx}{{2z}},$$
(15)

and

$$\gamma_{1,y} = \frac{{a_{n} }}{{w_{0} }} + \frac{iky}{{2z}}.$$
(16)

Applying the following formulae (Abramowitz and Stegun 1970; Erdelyi et al. 1954; Belafhal et al. 2020)

$$H_{n} \left( {x + y} \right) = \frac{1}{{2^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} }}\sum\limits_{k = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)H_{k} \left( {\sqrt 2 x} \right)} H_{n - k} \left( {\sqrt 2 y} \right),$$
(17)
$$H_{n} \left( x \right) = \sum\limits_{k = 0}^{{\left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right]}} {\left( { - 1} \right)^{k} \frac{n!}{{k!\left( {n - 2k} \right)!}}\left( {2x} \right)^{n - 2k} } ,$$
(18)
$$\int\limits_{ - \infty }^{ + \infty } {x^{l} \exp \left( { - px^{2} + 2qx} \right)} dx = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{l} H_{l} \left( \frac{iq}{p} \right),$$
(19)

and

$$\int\limits_{ - \infty }^{ + \infty } {x^{l} \exp \left( { - px^{2} + 2qx} \right)H_{m} \left( {\alpha x} \right)\,dx} = \sqrt {\frac{\pi }{p}} \frac{{\exp \left( {{{q^{2} } \mathord{\left/ {\vphantom {{q^{2} } p}} \right. \kern-0pt} p}} \right)}}{{2^{l} }}\sum\limits_{k = 0}^{{\left[ {{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right)\left( {\frac{\alpha }{i\sqrt p }} \right)^{m + l - 2k} ,$$
(20)

and after skipping a lot of tedious calculations, we can deduce the analytical expression of the intensity spectral pulsed HhChG beam in the turbulent atmosphere as

$$S_{N,l}^{{}} \left( {{{\varvec{\uprho}}},z,\omega } \right) = W_{N,l}^{{}} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = S^{\left( 0 \right)} \left( \omega \right)M_{N,l} \left( {{{\varvec{\uprho}}},z,\omega } \right),$$
(21)

where

$$\begin{aligned} M_{N,l}^{{}} \left( {{{\varvec{\uprho}}},z,\omega } \right) = & \frac{{k^{2} }}{{4z^{2} 2^{4N} w_{0}^{2l} }}\frac{1}{{\alpha_{1} \alpha_{2} }}\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \\ & \quad \times \exp \left( {\frac{{\gamma_{1 \cdot x}^{2} }}{{\alpha_{1} }} + \frac{{\gamma_{2 \cdot x}^{2} }}{{\alpha_{2} }}} \right)\,\left( {\frac{1}{{2i\sqrt {\alpha_{1} } }}} \right)^{l} \,\sum\limits_{h = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ h \\ \end{array} } \right)H_{l - h} } \left( {\frac{{i\sqrt 2 \gamma_{1 \cdot x} }}{{\sqrt {\alpha_{1} } }}} \right)\sum\limits_{\mu = 0}^{{\left[ {h/2} \right]}} {\frac{{\left( { - 1} \right)^{\mu } h!}}{{\mu !\left( {h - 2\mu } \right)!}}} \left( {\frac{\sqrt 2 }{{\rho_{0}^{2} \sqrt {\alpha_{1} \alpha_{2} } }}} \right)^{h + l - 2\mu } \\ & \quad \times H_{h + l - 2\mu } \left( {\frac{{i\gamma_{2 \cdot x} }}{{\sqrt {\alpha_{2} } }}} \right)\exp \left( {\frac{{\gamma_{2 \cdot y}^{2} }}{{\alpha_{1} }} + \frac{{\gamma_{2 \cdot y}^{2} }}{{\alpha_{2} }}} \right)\,\left( {\frac{1}{{2i\sqrt {\alpha_{1} } }}} \right)^{l} \,\sum\limits_{{h^{\prime} = 0}}^{l} {\left( {\begin{array}{*{20}c} l \\ {h^{\prime}} \\ \end{array} } \right)H_{{l - h^{\prime}}} } \left( {\frac{{i\sqrt 2 \gamma_{1 \cdot y} }}{{\sqrt {\alpha_{1} } }}} \right)\sum\limits_{{\mu^{\prime} = 0}}^{{\left[ {h^{\prime}/2} \right]}} {\frac{{\left( { - 1} \right)^{{\mu^{\prime}}} h^{\prime}!}}{{\sigma !\left( {h^{\prime} - 2\mu^{\prime}} \right)!}}} \\ & \quad \times \left( {\frac{\sqrt 2 }{{\rho_{0}^{2} \sqrt {\alpha_{1} \alpha_{2} } }}} \right)^{{h^{\prime} + l - 2\mu^{\prime}}} H_{{h^{\prime} + l - 2\sigma }} \left( {\frac{{i\gamma_{2 \cdot y} }}{{\sqrt {\alpha_{2} } }}} \right), \\ \end{aligned}$$
(22)

with

$$\alpha_{2} = \frac{ik}{{2z}} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{1}{{\rho_{0}^{4} \alpha_{1} }},$$
(23)
$$\gamma_{2,x} = \frac{{a_{{m^{\prime}}} }}{{w_{0} }} - \frac{ikx}{{2z}} + \frac{{\gamma_{1,x} }}{{\rho_{0}^{2} \alpha_{1} }},$$
(24)

and

$$\gamma_{2,y} = \frac{{a_{{n^{\prime}}} }}{{w_{0} }} - \frac{iky}{{2z}} + \frac{{\gamma_{1,y} }}{{\rho_{0}^{2} \alpha_{1} }}.$$
(25)

In the following, we will derive the analytical formulae for a truncated HhChG beam propagating through a turbulent atmosphere.

2.2 The analytical formula for a truncated pulsed beam

We will study, in this Section, our pulsed beam truncated to develop an analytical formula that describes its behavior. Using the extended Huygens–Fresnel principle (Andrews and Phillips 2005), we can express the cross-spectral density function of pulsed HhChG beam diffracted through atmospheric turbulence as follows

$$\begin{aligned} W_{N,l} \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} ,z,\omega } \right) = & \left( {\frac{k}{2\pi z}} \right)^{2} S^{\left( 0 \right)} \left( \omega \right)\int\limits_{ - h}^{ + h} {\int\limits_{ - h}^{ + h} {d^{2} {\mathbf{r}}_{{\mathbf{1}}} d^{2} {\mathbf{r}}_{{\mathbf{2}}} } } W_{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} ,0} \right) \\ & \quad \times \exp \left[ { - \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{1}}} } \right)^{2} + \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{2}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)^{2} } \right]\left\langle {\exp \left[ {\psi^{ * } \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{1}}} } \right) + \psi \left( {{\mathbf{r}}_{{\mathbf{2}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} . \\ \end{aligned}$$
(26)

By letting \({{\varvec{\uprho}}}_{{\mathbf{1}}} = {{\varvec{\uprho}}}_{2} = {{\varvec{\uprho}}}\) and inserting Eqs. (10) and (12) into Eq. (26), one obtains

$$\begin{aligned} W_{N,l}^{{}} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = & \frac{{k^{2} }}{{4\pi^{2} z^{2} 2^{4N} w_{0}^{2l} }}S^{\left( 0 \right)} \left( \omega \right)\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \\ & \quad \times \int\limits_{ - h}^{ + h} {\,\int\limits_{ - h}^{ + h} {f\left( {x_{02} ,y_{02} } \right)g\left( {x_{02} ,y_{02} } \right)} } dx_{02} \,dy_{02} {\kern 1pt} , \\ \end{aligned}$$
(27)

where

$$f\left( {x_{02} ,y_{02} ,x,y} \right){\kern 1pt} {\kern 1pt} = x_{02}^{l} \,y_{02}^{l} \times \exp \left( { - \alpha_{1}^{*} x_{02}^{2} + 2\sigma_{x} x_{02} } \right)\exp \left( { - \alpha_{1}^{*} y_{02}^{2} + 2\sigma_{y} y_{02} } \right),$$
(28)

and

$$\begin{aligned} g\left( {x_{02} ,y_{02} ,x,y} \right){\kern 1pt} = & \int\limits_{ - h}^{ + h} {\,\int\limits_{ - h}^{ + h} {x_{01}^{l} y_{01}^{{_{l} }} \,\exp \left[ { - \alpha_{1} \,x_{01}^{2} + 2\left( {\gamma_{1,x} + \frac{{x_{02} }}{{\rho_{0}^{2} }}} \right)x_{01} } \right]} } \\ & \quad \times \exp \left[ { - \alpha_{1} \,y_{01}^{2} + 2\left( {\gamma_{1,x} + \frac{{x_{02} }}{{\rho_{0}^{2} }}} \right)y_{01} } \right]dx_{01} \,dy_{01} . \\ \end{aligned}$$
(29)

The parameters \(\alpha_{1}\), \(\gamma_{1,x}\) and \(\gamma_{1,y}\) are defined by Eqs. (14–16), and \(\alpha_{1}^{*}\) is the complex conjugate.

The others parameters are expressed as

$$\sigma_{x} = \frac{{a_{{m^{\prime}}} }}{{w_{0} }} - \frac{ikx}{{2z}},$$
(30)

and

$$\sigma_{y} = \frac{{a_{{n^{\prime}}} }}{{w_{0} }} - \frac{iky}{{2z}}.$$
(31)

Using the definition of cosh function and the variable separation property, Eq. (29) can be rewritten as

$$g\left( {x_{02} ,y_{02} ,x,y} \right){\kern 1pt} {\kern 1pt} = g_{m} \left( {x_{02} ,x} \right){\kern 1pt} {\kern 1pt} g_{m} \left( {y_{02} ,y} \right){\kern 1pt} ,$$
(32)

where

$$g_{m} \left( {s_{02} ,s} \right){\kern 1pt} = \left( {g_{m}^{ + } \left( {s_{02} ,s} \right) + \left( { - 1} \right)^{l} g_{m}^{ - } \left( {s_{02} ,s} \right)} \right),$$
(33)

with

$$g_{m}^{ \pm } \left( {s_{02} ,s} \right){\kern 1pt} = \int\limits_{0}^{ + h} {s_{01}^{l} \,\exp \left[ { - \alpha_{1} \,s_{01}^{2} \pm 2\left( {\gamma_{1,x} + \frac{{s_{02} }}{{\rho_{0}^{2} }}} \right)s_{01} } \right]} ds_{01} ,$$
(34)

and \(s = (x_{02} \,\,or\,\,y_{02} ).\)

By invoking the integral formula (see Appendix A)

$$\begin{aligned} \int\limits_{0}^{ + h} {x^{l} e^{{ - px^{2} + 2qx}} } dx = & \frac{{e^{{\frac{{q^{2} }}{p}}} }}{{p^{{\frac{l + 1}{2}}} }}\sum\limits_{r = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ r \\ \end{array} } \right)} \left( {\frac{q}{\sqrt p }} \right)^{l - r} \\ & \quad \times \left\{ {\left( { - 1} \right)^{r} \frac{{\left( {\frac{{q^{2} }}{p}} \right)^{{\frac{r + 1}{2}}} }}{r + 1}{}_{1}F_{1} \left( {\frac{r + 1}{2};\frac{r + 3}{2}; - \frac{{q^{2} }}{p}} \right) + \frac{{\left[ {p\left( {h - \frac{q}{p}} \right)^{2} } \right]^{{\frac{r + 1}{2}}} }}{r + 1}{}_{1}F_{1} \left( {\frac{r + 1}{2};\frac{r + 3}{2}; - p\left( {h - \frac{q}{p}} \right)^{2} } \right)} \right\}, \\ \end{aligned}$$
(35)

where \({}_{1}F_{1} \left( \cdot \right)\) is the Kummer function, Eq. (34) can be written in the below form

$$\begin{aligned} g_{m}^{ \pm } \left( {s_{02} ,s} \right) = & \frac{{e^{{\frac{{q_{ \pm }^{2} \left( {s_{02} ,s} \right)}}{{\alpha_{1} }}}} }}{{\alpha_{1}^{{\frac{l + 1}{2}}} }}\sum\limits_{r = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ r \\ \end{array} } \right)} \left( {\frac{{q_{ \pm } \left( {s_{02} ,s} \right)}}{{\sqrt {\alpha_{1} } }}} \right)^{l - r} \\ \quad \times \left\{ {\left( { - 1} \right)^{r} \frac{{\left( {\frac{{q_{ \pm }^{2} \left( {s_{02} ,s} \right)}}{{\alpha_{1} }}} \right)^{{\frac{r + 1}{2}}} }}{r + 1}{}_{1}F_{1} \left( {\frac{r + 1}{2};\frac{r + 3}{2}; - \frac{{q_{ \pm }^{2} \left( {s_{02} ,s} \right)}}{{\alpha_{1} }}} \right) + \frac{{\left[ {\alpha_{1} \left( {h - \frac{{q_{ \pm } \left( {s_{02} ,s} \right)}}{{\alpha_{1} }}} \right)^{2} } \right]^{{\frac{r + 1}{2}}} }}{r + 1}{}_{1}F_{1} \left( {\frac{r + 1}{2};\frac{r + 3}{2}; - \alpha_{1} \left( {h - \frac{{q_{ \pm } \left( {s_{02} ,s} \right)}}{{\alpha_{1} }}} \right)^{2} } \right)} \right\}, \\ \end{aligned}$$
(36)

where

$$q_{ \pm } \left( {s_{02} ,s} \right) = \pm \left( {\gamma_{1,x} + \frac{{s_{02} }}{{\rho_{0}^{2} }}} \right).$$
(37)

Substituting from Eqs. (32), (33) and (36) into Eq. (27) leads to

$$\begin{aligned} W_{N,l} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = & \frac{{k^{2} }}{{4\pi^{2} z^{2} 2^{4N} w_{0}^{2l} }}S^{\left( 0 \right)} \left( \omega \right)\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \,\int\limits_{ - h}^{ + h} {\,\int\limits_{ - h}^{ + h} {dx_{02} dy_{02} f\left( {x_{02} ,y_{02} ,x,y} \right)} } \\ & \quad \times \left\{ {\left[ {g_{m}^{ + } \left( {x_{02} ,x} \right) + \left( { - 1} \right)^{l} g_{m}^{ - } \left( {x_{02} ,x} \right){\kern 1pt} } \right]\left[ {g_{m}^{ + } \left( {y_{02} ,y} \right) + \left( { - 1} \right)^{l} g_{m}^{ - } \left( {y_{02} ,y} \right)} \right]} \right\}. \\ \end{aligned}$$
(38)

This formula can be evaluated by using the separation of variables method and an integration process. For that, we recall the expanding form of the hypergemeric function and the well-known binomial formula (Gradshteyn et al. 2007)

$${}_{1}F_{1} \left( {a;b;x} \right) = \sum\limits_{j = 0}^{\infty } {\frac{{(a)_{j} }}{{\left( b \right)_{j} }}\frac{{x^{j} }}{j!}} ,$$
(39)

and

$$\left( {u{\kern 1pt} + {\kern 1pt} v{\kern 1pt} } \right)^{m} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{m} {C_{l}^{m} } u^{l} v^{m - l} ,$$
(40)

then the cross spectral density reads

$$W_{N,l} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = \frac{{k^{2} }}{{4\pi^{2} z^{2} 2^{4N} w_{0}^{2l} }}S^{\left( 0 \right)} \left( \omega \right)\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \,G(x)G(y),$$
(41)

where

$$G(s) = \left( { - 1} \right)^{l} G^{ + } \left( s \right) + G^{ - } \left( s \right),$$
(42)

with

$$G^{ \pm } \left( s \right){\kern 1pt} = \int\limits_{ - h}^{ + h} {ds_{02} f\left( {s_{02} ,s} \right)} g_{m}^{ \pm } \left( {s_{02} ,s} \right).$$
(43)

By using a second time of the integral formula of Eq. (35), and after tedious algebraic calculations, Eq. (43) yields

$$\begin{aligned} G^{ \pm } \left( s \right){\kern 1pt} = & \frac{{e^{{\frac{{\left( {\gamma_{1,s} } \right)^{2} }}{{\alpha_{1} }}}} }}{{\alpha_{1}^{{\frac{l + 1}{2}}} }}\sum\limits_{r = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ r \\ \end{array} } \right)} \left( { \pm \frac{1}{{\sqrt {\alpha_{1} } }}} \right)^{l - r} \sum\limits_{{t_{1} }}^{l - r} {\left( {\begin{array}{*{20}c} {l - r} \\ {t_{1} } \\ \end{array} } \right)} \left( {\gamma_{1,s} } \right)^{{l - r - t_{1} }} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{l - r} \\ & \quad \times \left[ {\left( { - 1} \right)^{r} \frac{{\left( {\frac{1}{{\sqrt {\alpha_{1} } }}} \right)^{r + 1} }}{{\left( {r + 1} \right)}}} \right.\sum\limits_{{t_{2} = 0}}^{r + 1} {\left( {\begin{array}{*{20}c} {r + 1} \\ {t_{2} } \\ \end{array} } \right)} \left( {\gamma_{1,s} } \right)^{{r + 1 - t_{2} }} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{{t_{2} }} \,\sum\limits_{{t_{3} = 0}}^{\infty } {\frac{{\left( {\frac{r + 1}{2}} \right)_{{t_{3} }} }}{{\left( {\frac{r + 2}{2}} \right)_{{t_{3} }} }}\frac{{\left( { - \frac{1}{{\alpha_{1} }}} \right)^{{t_{3} }} }}{{t_{3} !}}} \sum\limits_{{t_{4} = 0}}^{{2t_{3} }} {\left( {\begin{array}{*{20}c} {2t_{3} } \\ {t_{4} } \\ \end{array} } \right)} \left( {\gamma_{1,s} } \right)^{{2t_{3} - t_{4} }} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{{t_{4} }} T\left( s \right){\kern 1pt} \\ & \quad + \frac{{\left( {\sqrt {\alpha_{1} } } \right)^{r + 1} }}{r + 1}\sum\limits_{{t_{5} = 0}}^{r + 1} {\left( {\begin{array}{*{20}c} {r + 1} \\ {t_{5} } \\ \end{array} } \right)} \left( {h \mp \frac{{\gamma_{1,s} }}{{\alpha_{1} }}} \right)^{{r + 1 - t_{5} }} \left( { \mp \frac{1}{{\alpha_{1} \rho_{0}^{2} }}} \right)^{{_{{t_{5} }} }} \times \left. {\sum\limits_{{t_{6} = 0}}^{\infty } {\frac{{\left( {\frac{r + 1}{2}} \right)_{{t_{6} }} }}{{\left( {\frac{r + 2}{2}} \right)_{{t_{6} }} }}\frac{{\left( { - \alpha_{1} } \right)^{{t_{6} }} }}{{t_{6} !}}} \sum\limits_{{t_{7} = 0}}^{{2t_{6} }} {\left( {\begin{array}{*{20}c} {2t_{6} } \\ {t_{7} } \\ \end{array} } \right)} \left( {h \mp \frac{{\gamma_{1,s} }}{{\alpha_{1} }}} \right)^{{2t_{6} - t_{7} }} \left( { \mp \frac{1}{{ \alpha_{1} \rho_{0}^{2} }}} \right)^{{t_{7} }} R\left( s \right){\kern 1pt} } \right], \\ \end{aligned}$$
(44)

where

$$T\left( s \right){\kern 1pt} = \left( {T^{ + } \left( s \right) + \left( { - 1} \right)^{{l + t_{1} + t_{2} + t_{4} }} T^{ - } \left( s \right)} \right),$$
(45)

and

$$R\left( s \right){\kern 1pt} = \left( {R_{{}}^{ + } \left( s \right) + \left( { - 1} \right)^{{l + t_{1} + t_{5} + t_{7} }} R_{{}}^{ - } \left( s \right)} \right).$$
(46)

By using the integral formula of Eq. (35), and after tedious algebraic calculations, \(T_{{}}^{ \pm } \left( s \right){\kern 1pt}\) and \(R_{{}}^{ \pm } \left( s \right){\kern 1pt}\) become

$$\begin{aligned} T^{ + } \left( s \right){\kern 1pt} = & \frac{{e^{{\frac{{J_{1, \pm }^{2} \left( s \right)}}{\eta }}} }}{{\eta^{{\frac{{l + t_{1} + t_{2} + t_{4} + 1}}{2}}} }}\sum\limits_{{v_{1} = 0}}^{{l + t_{1} + t_{2} + t_{4} }} {\left( {\begin{array}{*{20}c} {l + t_{1} + t_{2} + t_{4} } \\ {v_{1} } \\ \end{array} } \right)} \left( {\frac{{J_{1, \pm } \left( s \right)}}{\sqrt \eta }} \right)^{{v_{1} }} \\ & \quad \times \left[ {\left( { - 1} \right)^{{v_{1} }} \frac{{\left( {\frac{{J_{1, \pm }^{2} \left( s \right)}}{\eta }} \right)^{{\frac{{v_{1} + 1}}{2}}} }}{{v_{1} + 1}}{}_{1}F_{1} \left( {\frac{{v_{1} + 1}}{2};\frac{{v_{1} + 3}}{2}; - \frac{{J_{1, \pm }^{2} \left( s \right)}}{\eta }} \right) + \frac{{\left[ {\eta \left( {h - \frac{{J_{1, \pm } \left( s \right)}}{\eta }} \right)^{2} } \right]^{{\frac{{v_{1} + 1}}{2}}} }}{{v_{1} + 1}}{}_{1}F_{1} \left( {\frac{{v_{1} + 1}}{2};\frac{{v_{1} + 3}}{2};\eta \left( {h - \frac{{J_{1, \pm } \left( s \right)}}{\eta }} \right)^{2} } \right)} \right], \\ \end{aligned}$$
(47)

and

$$\begin{aligned} R^{ + } \left( s \right){\kern 1pt} = & \frac{{e^{{\frac{{J_{2, \pm }^{2} \left( s \right)}}{\eta }}} }}{{\eta^{{\frac{{l + t_{1} + t_{5} + t_{7} + 1}}{2}}} }}\sum\limits_{{v_{2} = 0}}^{{l + t_{1} + t_{5} + t_{7} }} {\left( {\begin{array}{*{20}c} {l + t_{1} + t_{5} + t_{7} } \\ {v_{2} } \\ \end{array} } \right)} \left( {\frac{{J_{2, \pm } \left( s \right)}}{\sqrt \eta }} \right)^{{v_{1} }} \\ & \quad \times \left\{ {\left( { - 1} \right)^{{v_{1} }} \frac{{\left( {\frac{{J_{2, \pm }^{2} \left( s \right)}}{\eta }} \right)^{{\frac{{v_{2} + 1}}{2}}} }}{{v_{2} + 1}}{}_{1}F_{1} \left( {\frac{{v_{2} + 1}}{2};\frac{{v_{2} + 3}}{2}; - \frac{{J_{2, \pm }^{2} \left( s \right)}}{\eta }} \right) + \frac{{\left[ {\eta \left( {h - \frac{{J_{2, \pm } \left( s \right)}}{\eta }} \right)^{2} } \right]^{{\frac{{v_{2} + 1}}{2}}} }}{{v_{2} + 1}}{}_{1}F_{1} \left( {\frac{{v_{2} + 1}}{2};\frac{{v_{2} + 3}}{2};\eta \left( {h - \frac{{J_{2, \pm } \left( s \right)}}{\eta }} \right)^{2} } \right)} \right\}. \\ \end{aligned}$$
(48)

The parameters in Eqs. (47) and (48) are expressed as

$$J_{ \pm } \left( s \right) = \pm \left( {\frac{{\sigma_{s} }}{2} - \frac{{\gamma_{1,s} }}{{\alpha \rho_{0}^{2} }}} \right),$$
(49)

and

$$\eta = \alpha * - \frac{1}{{\alpha \rho_{0}^{4} }}.$$
(50)

Finally, the spectrum of a diffracted pulsed HhChG beam traveling an atmospheric turbulence is given by

$$S_{N,l} \left( {{{\varvec{\uprho}}},z,\omega } \right) = W_{N,l} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = S^{\left( 0 \right)} \left( \omega \right)M_{N,l} \left( {{{\varvec{\uprho}}},z,\omega } \right),$$
(51)

where

$$\begin{aligned} M_{N,l} \left( {{{\varvec{\uprho}}},z,\omega } \right) = & \frac{{k^{2} }}{{4\pi^{2} z^{2} 2^{4N} w_{0}^{2l} }}S^{\left( 0 \right)} \left( \omega \right)\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} } \\ & \quad \times \left\{ {\left[ {\left( { - 1} \right)^{l} G^{ + } \left( x \right) + G^{ - } \left( x \right)} \right] \times \left[ {\left( { - 1} \right)^{l} G^{ + } \left( y \right) + G^{ - } \left( y \right)} \right]} \right\}. \\ \end{aligned}$$
(52)

If l = 0 and N = 1 in this equation, one can derive the expression for the spectral intensity of diffracted pulsed Cosh-Gaussian beams propagating through atmospheric turbulence, which is consistent with the well-known expression given by Zhang et al. (Zhang et al. 2007).

Based on Eqs. (21) and (51), one can see that the spectral intensity of pulsed HhChG beam propagating through atmospheric turbulence is a product of the original spectrum \(S^{\left( 0 \right)} \left( \omega \right)\) and spectral modifier \(M_{N,l}^{{}} \left( {{{\varvec{\uprho}}},z,\omega } \right)\). The first part \(S^{\left( 0 \right)} \left( \omega \right)\) depends on the pulse duration T and the central frequency \(\omega_{0}\). The second part \(M_{N,l}^{{}} \left( {{{\varvec{\uprho}}},z,\omega } \right)\) depends on the radial coordinate, beam parameters and atmospheric parameters including the structure constant of the refraction index.

3 Numerical simulations and discussions

In this Section, the influence of atmospheric turbulence on the spectral intensity of a non-truncated pulsed HhChG beam is shown through numerical calculations using Eq. (21). The normalized on-axis and off-axis spectral intensities of the resulting beam after propagation through atmospheric turbulence are discussed by using the relative spectral shift. This later is given by \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} = {{\left( {\omega_{\max } - \omega_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{\max } - \omega_{0} } \right)} {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}\), where \(\omega_{\max }\) is the frequency related to the maximum spectral intensity. For \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} > 0\), the spectral intensity is blue-shifted and for \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} < 0\), the spectral intensity is red-shifted. For simplicity, the normalized original spectrum is taken as \(S^{00} (\omega ) = S^{\left( 0 \right)} \left( \omega \right)/S^{\left( 0 \right)} \left( {\omega_{0} } \right)\), the normalized spectral intensity is \(S_{N,l}^{{}} (\omega ) = S_{N,l} \left( {{{\varvec{\uprho}}},z,\omega } \right)/S_{N,l} ({{\varvec{\uprho}}},z,\omega_{\max } )\) and the normalized spectral modifier is given by \(M_{N,l} (\omega_{0} ) = M_{N,l} \left( {{{\varvec{\uprho}}},z,\omega_{0} } \right)/M_{(N,l)\max } ({{\varvec{\uprho}}},z,\omega_{0} )\) where \(M_{(N,l)\max }^{{}} ({{\varvec{\uprho}}},z,\omega_{0} )\) is the maximum value of \(M_{N,l} ({{\varvec{\uprho}}},z,\omega_{0} )\) at the observation point \(({{\varvec{\uprho}}},z)\). The study focuses on investigating the effects of atmospheric turbulence on the spectral modifier of a pulsed HhChG beam during propagation. The calculation parameters are set as \(\Omega = 10\,{\text{m}}^{ - 1}\), \(\lambda = 0.8\,\mu {\text{m}}\), \(w_{0} = 2\;{\text{cm}}\), \(\omega_{0} = 2\pi c/\lambda\), l = 1 and N = 2.

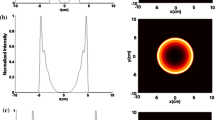
As a starting point in this study, we depict in Fig. 1 the cross line \((y = 0)\) and corresponding contour graphs of the normalized spectral modifier of a pulsed HhChG beam propagating in turbulence atmospheric for \(C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}\) at different receiver planes (z = 1, 3, 6 and 8 km). One can clearly see that the spectral modifier profile will take a bright central core like the flat-top Gaussian profile as the HhChG beam propagates through turbulence, as shown as in Fig. 1.

Fig. 1
figure 1

The normalized spectral modifier of a pulsed HhChG beam in atmospheric turbulence with several propagation distances z

Full size image

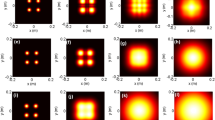
Figure 2 displays the influence of the turbulent atmosphere on the propagation properties of the considered beam at the transverse plane for three values of the structure constant of the refractive index (\(C_{n}^{2} = 5 \times 10^{ - 16} {\text{m}}^{ - 2/3}\), \(C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{ - 2/3}\) and \(C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}\)). It can be observed that the resulting beam takes on a distinct shape characterized by four individual petal-like lobes over short propagation distances (0 < z < 6 km).

Fig. 2
figure 2

Evolution of the normalized spectral modifier of a pulsed HhChG beam in different turbulence with several propagation distances. The structure constants corresponding are: a \(5 \times 10^{ - 16} {\text{m}}^{ - 2/3}\), b \(1 \times 10^{ - 15} {\text{m}}^{ - 2/3}\), and c \(1 \times 10^{ - 14} {\text{m}}^{ - 2/3}\)

Full size image

Under weak atmospheric turbulence (as depicted in Fig. 2a), the optical path surface of the beam gradually resembles that of a rhombic crystal shape, particularly at longer propagation distances (z = 8 km). However, under strong atmospheric turbulence (as seen in Fig. 2b andc), the four lobes evolve into a central bright spot surrounded by square or round, wide dimmer rings. This evolution in the shape of the beam can have significant implications for its practical applications in fields such as remote sensing or free-space optical communication.

In Fig. 3, we can observe the impact of the Gaussian waist parameter on the evolution of the normalized spectral modifier of a pulsed HhChG beam as it propagates through stronger atmospheric turbulence (\(C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}\)) at the plane z = 1 km with \(\Omega = 100\,{\text{m}}^{ - 1}\). As the value of the Gaussian waist parameter \(w_{0}\) increases, we can see that the pulsed HhChG beam gradually transforms from a Gaussian beam-like shape into a dark hollow beam. Furthermore, the dark and deep hollow area of the pulsed HhChG beam becomes wider as the value of \(w_{0}\) increases.

Fig. 3
figure 3

Evolution of the normalized spectral modifier of a pulsed HhChG beam propagating in a turbulence atmosphere with three several waist widths at a propagation distance \(z = 1\;{\text{km}}\)

Full size image

Figure 4 illustrates how the evolution of the normalized spectral modifier of a pulsed HhChG beam is influenced by the decentered and hollowness parameters as it propagates through stronger atmospheric turbulence at the plane z = 1 km. Specifically, we observe that the pulsed HhChG beam gradually transforms from a Gaussian beam-like shape into a dark hollow beam as the value of the arguments of the cosh function Ω increases and the hollowness parameter l decreases. Additionally, the dark and deep hollow area of the pulsed HhChG beam widens as the value of the arguments of the cosh function increases.

Fig. 4
figure 4

Normalized spectral modifier of a pulsed HhChG beam propagating in a turbulent atmosphere medium with z = 1 km, \(C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}\) and for different values of: a the order of the beam l and b the arguments of the cosh function

Full size image

Below, we present the impact of atmospheric turbulence and pulse duration on the spectral intensity of the pulsed HhChG beam. The calculation parameters are: \(C_{n}^{2} = 3 \times 10^{ - 14} {\text{m}}^{ - 2/3}\), \(z = 4\,km,\)\(T = 3fs,\)\(y = 0,\) \(\Omega = 10\,m^{ - 1}\), \(\lambda = 0.8\,\mu m\), \(w_{0} = 2cm\), \(\omega_{0} = 2\pi c/\lambda\), l = 1 and N = 2.

Figure 5 depicts the normalized on-axis and off-axis spectra intensity of the pulsed HhChG beam for various values of the structure constant of the refractive index. The circles indicate the normalized original spectrum \(S^{00} \left( \omega \right)\). From the results presented in Fig. 5a, it is evident that the on-axis spectral intensity of the pulsed HhChG beam is blue-shifted. Furthermore, it appears that the degree of blue-shift decreases slightly with the value of the refractive index structure constant. For example, for \(C_{n}^{2} = 1 \times 10^{ - 14} m^{ - 2/3}\), we have (\(\delta \omega /\omega_{0}\) = 0.0585), \(C_{n}^{2} = 1 \times 10^{ - 15} m^{ - 2/3}\) (\(\delta \omega /\omega_{0}\) = 0.0686) and \(C_{n}^{2} = 1 \times 10^{ - 16} m^{ - 2/3}\)(\(\delta \omega /\omega_{0}\) = 0.0953). However, as shown in Fig. 5b, the off-axis \((x = 0.15m)\) spectral intensity exhibits a blue shift and the blue shift becomes redshift with a decreasing refractive index structure constant \(C_{n}^{2} .\) This indicates that both the on-axis and off-axis spectra tend to approach the original spectrum when the milieu becomes very turbulent (\(C_{n}^{2} = 1 \times 10^{ - 14} m^{ - 2/3}\)).

Fig. 5
figure 5

Normalized spectral intensity of pulsed HhChG beam propagating in atmospheric turbulence for several values of structure constant of the refractive index: a on-axis (0) and b off axis \((x = 0.15\;{\text{m}})\)

Full size image

In Fig. 6, the normalized on-axis and off-axis spectra intensity of the pulsed HhChG beam is shown for different values of the pulse duration T.

Fig. 6
figure 6

Normalized spectral intensity of pulsed HhChG beam propagating in atmospheric turbulence for different values of pulse duration: a on-axis (0) and b off axis \((x = 0.6\;{\text{m}}).\)

Full size image

The original normalized spectrum is indicated by circles. As seen in Fig. 6a, it is clear that the on-axis spectral intensity of the pulsed HhChG beam is blue-shifted. Additionally, it is apparent that the amount of blue-shift decreases as the pulse duration increases.

On the other hand, from the results in Fig. 6b, it is apparent that the off-axis spectral intensity is red-shifted for all values of pulse duration. The amount of red-shift increases as the value of pulse duration decreases. This indicates that both the on-axis and off-axis spectra tend to approach the original spectrum for T = 8 fs. This means that the redshift is more pronounced for shorter pulse durations.

4 Conclusion

This chapter focuses on the analytical formulae for diffracted pulsed Hollow higher-order Cosh-Gaussian beams propagating through a turbulent atmosphere. The formulas are derived using the Fourier transform and the extended Huygens-Fresnel method. Numerical examples are provided to illustrate the behavior of the spectral intensity of the beam as the initial beam parameters and the atmospheric turbulence structure constant change. The results show that the on-axis spectrum is blue-shifted and red-shifted as the transverse distance increases. The effect of the medium and beam parameters on spectral shifts at different observation positions is explained. Our results can be useful in various fields of Mathematical Physics, particularly in optical communications and remote sensing. The theoretical treatments of this field are complicated, especially for truncated beams, and we have developed various theories for evaluating finite and infinite integrals with different weights that involve the product of special functions and orthogonal polynomials.