1 Introduction

Due to the continual increase of human activities like the study of the oceans, marine life, search for minerals and other resources in the ocean bed, the necessity for robust and reliable underwater wireless communication systems has been continuously increasing in the past few decades (Naik et al. 2022). Acoustic wave, radio-frequency and optical communication are three different wireless communication techniques that have been employed for communicating information in underwater environments. In comparison with RF and acoustic communication systems, optical wireless communication systems provide high bandwidth and secure point-to-point transmission over short to moderate distances (up to about hundred’s of meters) (Kaushal and Kaddoum 2016; Naik and Chung 2022).

When light propagates in the underwater medium, factors such as attenuation (brought about by absorption and scattering), turbulence, and pointing error (misalignment between transmitter and receiver) can induce errors in the bit stream being transmitted (Zeng et al. 2017; Uppalapati et al. 2020; Singh et al. 2022; Malathy et al. 2020). Statistical models like the log-normal and gamma-gamma distribution have been employed to estimate the effect of the channel on the transmission of the optical wireless communication system in weak turbulence and moderate to strong turbulence regimes, respectively (Jamali et al. 2018). A low complexity and accurate hyperbolic tangent log-normal (HTLN) distribution has been proposed in literature as an alternative to the log-normal distribution for quantifying the effect of weak turbulence (Ramavath et al. 2020). The primary purpose of introducing the HTLN distribution is that it allows the computation of analytical closed-form expressions quantifying the average bit error rate (BER) and ergodic channel capacity (ECC) performance, which are impossible to derive using the log normal distribution function (Ramavath et al. 2020; Naik et al. 2021). In addition to underwater turbulence, beam attenuation as well as pointing errors influence the UVWOC system. Beam attenuation is a deterministic quantity obtained using the Beer–Lambert’s law. Beam attenuation occurs due to the absorption and scattering of incident beam (Mobley et al. 1993). The dependence of average BER on transmitter-receiver misalignment (pointing errors) has been determined by employing the Rayleigh displacement pointing error model (Sandalidis et al. 2008).

In most literature, turbulence is assumed as being homogeneous throughout the link, which is valid only for the horizontal underwater wireless optical communication (UWOC) connections (links which operate at the same depth below water) (Huang et al. 2018; Jiang et al. 2020). In the case of UVWOC links, turbulence will vary according to the depth of the ocean. Hence, the channel model obtained using the horizontal UWOC link not suitable to obtain the performance of UVWOC link. UVWOC channel model using turbulence alone has been evaluated by considering the depth dependency of temperature and salinity in the ocean in Elamassie and Uysal (2020). In this paper, we have also employed these parameters to obtain accurate closed-form expressions for several performance parameters associated with the UVWOC channel.

It is a well-known fact that the performance of a communication system can be improved by using diversity techniques (Ramavath et al. 2020; Singh et al. 2022). Hence, we have used maximum ratio combining (MRC), selection combining (SC) and majority logic combining (MLC) as diversity techniques to enhance the UVWOC system’s BER performance, Outage Probability (OP) and Ergodic Channel Capacity (ECC) (Liu et al. 2015; Ramavath et al. 2018, 2020). The corresponding improvement in performance has been quantified by using analytical expressions derived in the paper.

The contributions made by this research paper are enumerated below:

  • A unified probability density function (PDF) of UVWOC channel perturbed by weak turbulence using HTLN distribution function, attenuation losses using Beer–Lambert’s law and pointing errors obtained using the Rayleigh displacement error has been derived.

  • Closed-form expressions quantifying the average BER, outage probability (OP) and ergodic channel capacity (ECC) of UVWOC channel for a SISO link have been derived.

  • Analytical average BER expressions have been evaluated for receiver diversity schemes, such as MLC, MRC and SC.

  • Closed-form expressions quantifying the ECC and OP for SC receive diversity schemes have been determined.

  • Numerical results obtained using the closed-form expressions are corroborated with the Monte-Carlo simulations.

The remainder of the paper is organized as follows. The system model and individual channel models have been presented in Sect. 2. The average BER analysis of UVWOC SISO link and UVWOC links with different receive diversity schemes are described in Sect. 3. Outage probability (OP) analysis is presented in Sect. 4 and ergodic channel capacity (ECC) has been determined in Sect. 5. A discussion of the relevance of the results obtained in this paper is presented in Sect. 6. The paper has been concluded in Sect. 7.

2 System and channel models

In this section, the system and channel models of a UVWOC link employing on-off keying (OOK) modulation have been described.

2.1 System model

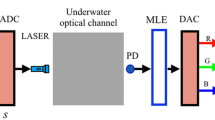
We have considered a system model as shown in Fig. 1. The source is placed at the surface of the sea and the detector is placed at vertical distance d in sea from the source. We have considered k independent and non identical turbulence layers. These layers are formed due to temperature and salinity variation with respect to depth of sea between source and destination. The vertical link distance is \(d=\sum _{K=1}^{k} d_K\), here \(d_{1}, d_{2},\ldots , d_{k}\) are thickness of each non-identical layer formed due to temperature and salinity variations with respect to depth of sea. The received signal at detector is given by Ramavath et al. (2020),

$$\begin{aligned} Y=\eta I \sqrt{P_{t} T_{b}}s+n \end{aligned}$$
(1)

where \(T_b\) is bit duration, \(\eta\) is responsivity of photo-detector, \(s \in [0,1]\) represents transmitted bits, n is a realization (sample value) of an additive white Gaussian noise process with zero mean and variance \(\sigma ^2\). In Eq. (1) ‘I’ is total fading coefficient (Farid and Hranilovic 2007) and is represented as the product of the fading coefficients due to attenuation, turbulence and pointing errors, \(i.e.,~I=I_a\times I_t\times I_p\), here, \(I_a,~I_t,\) and \(I_p\) represents the fading coefficients due to attenuation, turbulence and pointing errors, respectively.

Fig. 1
figure 1

Underwater vertical wireless optical communication system

Full size image

2.2 Channel model

2.2.1 Attenuation channel model

The fading coefficient due to attenuation in case of underwater medium is given by Beer–Lambert’s law (Ramavath et al. 2020),

$$\begin{aligned} I_a=\exp \left( -dC(\lambda ) \right) \end{aligned}$$
(2)

where \(C(\lambda )\) is wavelength \((\lambda )\) dependent extinction coefficient and d is the vertical link distance between source and detector.

2.2.2 Vertical link turbulence channel model

The total fading coefficient due to vertical turbulence is \(I_{t}=\prod _{K=1}^{k} I_{t_{K}}\), here \(I_{t_1}, I_{t_2} \ldots I_{t_k}\) are fading coefficients of each non-identical layer formed due to temperature and salinity variations with respect to depth of ocean (Elamassie and Uysal 2020). Each individual layer exhibits weak underwater turbulence, corresponding irradiance fluctuation realized using the log-normal distribution function. The PDF of log-normal distribution for K th layer is given by Jamali et al. (2018),

$$\begin{aligned} f_{I_{t_K}}\left( I_{t_K}\right) =\frac{1}{2I_{t_K} \sqrt{2 \pi \sigma _{x_{K}}^{2}}} \exp \left( -\frac{\left( \ln \left( I_{t_K}\right) -2 \mu _{x_{K}}\right) ^{2}}{8 \sigma _{x_{K}}^{2}}\right) \end{aligned}$$
(3)

where \(\mu _{x_{K}}\) and \(\sigma _{x_{K}}^{2}\) are mean and variance of log-amplitude coefficient \(X_{K}=0.5 \ln \left( I_{t_K}\right)\) of \(K^{th}\) layer, respectively. \(I_{t_1},I_{t_2}, \ldots I_{t_k}\) are independent log-normally distributed random variables. Their parameters (\(\mu _{x_K}\), \(\sigma _{x_{K}}^{2}\)) vary from layer to layer. Under these conditions, it has been shown that the PDF of overall fading coefficient due to turbulence \(I_t\) is given by Elamassie and Uysal (2020),

$$\begin{aligned} f_{I_{t}}\left( I_{t}\right) =\frac{1}{2I_{t} \sqrt{2 \pi \sigma _{{t}}^{2}}} \exp \left( -\frac{\left( \ln \left( I_{t}\right) -2 \mu _{{t}}\right) ^{2}}{8 \sigma _{{t}}^{2}}\right) \end{aligned}$$
(4)

where total mean and variance are \(\mu _{t}=\sum _{K=1}^{k} \mu _{x_{K}}\) and \(\sigma _{t}^{2}=\sum _{K=1}^{k} \sigma _{x_{K}}^{2}\), respectively. The PDF of log-normal distribution in Eq. (4) is replaced by HTLN for ease of mathematical analysis and obtaining closed-form expressions. The equivalence between these two distributions has been established in Ramavath et al. (2020), Ramavath et al. (2020).

$$\begin{aligned} f_{I_t}(I_t)=\frac{b \exp \left( 2 a\right) I_t^{b-1}}{\left( 1+I_t^{b} \exp \left( 2 a\right) \right) ^{2}} \end{aligned}$$
(5)

where a and b are scaling and shaping parameters of the HTLN distribution, respectively.

2.2.3 Pointing error channel model

Another factor contributing to fading due to source and detector misalignment is pointing error. This happens as a result of turbulence, ocean currents and waves moving the source or detector. The fading coefficient due to pointing errors is given as Farid and Hranilovic (2007),

$$\begin{aligned} I_{p} \approx A_{0} \exp \left( -\frac{2 R^{2}}{\omega _{z e q}^{2}}\right) , \quad R \ge 0 \end{aligned}$$
(6)

where R denotes the Rayleigh random displacement variable and is given as \(R=\sqrt{R_{x}^{2}+R_{y}^{2}}\), \(R_x\) and \(R_y\) denote the displacement along horizontal and elevation axes respectively, \(A_0\) is the fraction of the collected power at \(R=0\) and \(\omega _{Z e q}\) is the equivalent beam width. They are respectively defined by \(A_{0}=[{\text {erf}}(v)]^{2}\) and \(\omega _{z e q}=\omega _{z} \sqrt{\sqrt{\pi } {\text {erf}}(v) / 2 v \exp \left( -v^{2}\right) }\), \(v=\sqrt{\pi / 2}\left( D_{R} / 2 \omega _{z}\right)\) is the ratio between aperture diameter \(\left( D_R\right)\) and beam width \(\left( \omega _{z} \approx \omega _{0} \sqrt{1+\left( \lambda d / \pi \omega _{0}^{2}\right) ^{2}}\right)\), and \(\omega _0\) represents the spot size of Gaussian beam wave (Farid and Hranilovic 2007). The PDF associated with the pointing errors \(I_p\) is given as Farid and Hranilovic (2007),

$$\begin{aligned} f_{I_{p}}\left( I_{p}\right) =\frac{\xi ^{2}}{A_{0}^{\xi ^{2}}} I_{p}^{\xi ^{2}-1}, \quad 0 \le I_{p} \le A_{0} \end{aligned}$$
(7)

where \(\xi =w_{\mathrm {Zeq}} / 2 \sigma _{\mathrm {s}}\) defines the ratio between the equivalent beam radius and the pointing error displacement standard deviation.

2.2.4 Combined channel model

UVWOC channel fading coefficient in the presence of weak underwater turbulence, beam attenuation and pointing errors is \(I=I_t\times I_a\times I_p\), corresponding resultant PDF is obtained as Farid and Hranilovic (2007),

$$\begin{aligned} f_{I}(I) = \frac{\xi ^{2}}{(A_{0}I_{a})^{\xi ^{2}}}I^{\xi ^{2}-1}\int \limits _{\frac{I}{I_aA_0}}^{\infty }I_{t}^{-\xi ^{2}}f_{I_{t}}(I_{t}) dI_{t} \end{aligned}$$
(8)

Substituting Eq. (5) in (8) and then integrated using (Adamchik and Marichev 1990), we get

$$\begin{aligned} f_{I}(I) = \frac{\xi ^{2} \exp (2 a)}{(A_{0}I_{a})^b} I^{b-1} G_{1+b, 1+b}^{1+b, 1}\left( \frac{\exp (2a) I^b}{(A_0 I_a)^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{b} \\ \frac{i-b+\xi ^2-1}{b},0\end{array}\right) \end{aligned}$$
(9)

where i ranges from \(1,2,\ldots ,b\).

3 Average bit error rate

Average BER is a primary metric used to quantify the efficacy of communication systems (both wired and wireless) in preserving the integrity of information transfer. In this paper, we have employed OOK modulation scheme for establishing the UVWOC link. The performance of this link with a single receiver (SISO) as well as with multiple receivers suitably combined to obtain various receive diversity schemes (SC, MRC and MLC) has been analyzed and quantified.

3.1 SISO UVWOC link

The average BER of SISO system employing OOK modulation in case of a vertical link is given by Ramavath et al. (2020)

$$\begin{aligned} P_{S I S O}=\int _{0}^{\infty } Q\left( \eta I \sqrt{\frac{P_{t} T_{b}}{4 \sigma ^{2}}}\right) f_{I}(I) d I \end{aligned}$$
(10)

where \(Q(\cdot )\) is Q-function. Substituting Eq. (9) in (10), using relation \({Q(x)}=\frac{1}{2} {\text {erfc}}\left( \frac{x}{\sqrt{2}}\right)\), we get

$$\begin{aligned} P_{S I S O}=\frac{{\mathscr {W}} \xi ^2}{2 \sqrt{\pi }}\int _{0}^{\infty } I^{b-1} G_{1+b, 1+b}^{1+b, 1}\left( {\mathscr {W}} I^b \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{b} \\ \frac{i-b+\xi ^2-1}{b},0\end{array}\right) G_{1,2}^{2,0}\left( {\mathscr {S}} I^2 \bigg \vert \begin{array}{l}1 \\ 0,\frac{1}{2}\end{array}\right) d I \end{aligned}$$
(11)

where \({\mathscr {W}}=\frac{\exp (2a)}{(A_0 I_a)^b}\) and \({\mathscr {S}}=\frac{\eta ^2 P_t T_b}{8 \sigma ^2}\). Integrating Eq. (11) using change of variable method and the obtained expression is given as,

$$\begin{aligned} P_{S I S O}= {\mathscr {K}} G_{2+4b, 2+3b}^{2+2b,2+2b}\left( \frac{{\mathscr {W}}^2 b^b }{ {\mathscr {S}}^b} \bigg \vert \begin{array}{l } -\frac{1}{ 2} , 0 ,\frac{2i-b}{ 2b} ,\frac{2i-b-1}{ 2b}, \frac{i-b+\xi ^2}{ 2b},\frac{i+\xi ^2}{ 2b} \\ \frac{i-b+\xi ^2-1}{ 2b},\frac{i-1+\xi ^2}{ 2b},0,\frac{1}{ 2},\frac{2i-b-2}{ 2b} \end{array}\right) \end{aligned}$$
(12)

where \(i=1,2,\ldots ,b\) and \({\mathscr {K}}=\frac{{\mathscr {W}}\xi ^2 b^{{b}{ 2}-1} {\mathscr {S}}^{-\frac{b}{ 2}}}{ 2 \sqrt{\pi } (2 \pi )^{b+1 }{ 2}}\).

3.2 UVWOC link with selection combining

The average BER of SC receive diversity scheme considering N detectors and single source in case of OOK modulation is given by Tsiftsis et al. (2009)

$$\begin{aligned} P_{SC}=\int _{0}^{\infty } Q\left( I_{SC} \sqrt{{\mathscr {L}}}\right) f_{I_{SC}}(I_{SC}) d I \end{aligned}$$
(13)

where \({\mathscr {L}}=\frac{\eta ^2 P_t T_b}{8 N \sigma ^2}\) and \(I_{SC}=\max (I_1, I_2, \ldots ,I_N)\), \(I_1,I_2,\ldots . I_N\) are modeled as independent identical random variables associated with the corresponding diversity channel, \(f_{I_{SC}}(I_{SC})\) is PDF of \(I_{SC}\). Expanding Q-function and integrating using the integration by parts method to Eq. (13), we get

$$\begin{aligned} P_{SC}=\int _{0}^{\infty } {\sqrt{\frac{{\mathscr {L}}}{\pi }} \exp (-{\mathscr {L}} I_{SC}^2)F_{I_{SC}}(I_{SC}) d I} \end{aligned}$$
(14)

where \(F_{I_{SC}}(I_{SC})\) is cumulative distribution function (CDF) of \(I_{SC}\). The CDF of ‘N’ independent identical distribution random variables \(I_1,I_2,\ldots ,I_N\) is \(F_{I_{SC}}(I_{SC})=[{F_{I}(I_{SC})}]^N\), here \(F_{I}(I_{SC})=\int _{0}^{I_{SC}} f_{I}(I) d I\) (Ramavath et al. 2020). By using Eq. (9) and integrated, we get

$$\begin{aligned} F_{I}(I_{SC})=\frac{{\mathscr {W}} \xi ^2 I_{SC}^b }{ b } G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} I_{SC}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b},-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b} \end{array}\right) \end{aligned}$$
(15)

By utilizing Eqs. (15) in (14) we get,

$$\begin{aligned} P_{SC}= & {} \int _{0}^{\infty } \sqrt{\frac{{\mathscr {L}}}{ \pi } }\exp (-{\mathscr {L}} I_{SC}^2) \left( \frac{ {\mathscr {W}}\xi ^2 I_{SC}^b }{ b }\right) ^N \nonumber \\&\times \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} I_{SC}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b},-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b}\end{array}\right) \right) ^N d I \end{aligned}$$
(16)

Solutions to Eq. (16) does not exist. In order to obtain the closed-form expressions, we have used Gauss–Laguerre quadrature for ‘M’ sample points (Concus et al. 1963). Obtained average BER expression is given as,

$$\begin{aligned} P_{SC}= & {} \frac{1}{ 2 \sqrt{\pi }} \left( \frac{{\mathscr {W}} \xi ^2 }{ b }\right) ^N \sum _{j=1}^{M} H_{j} {{\left( \frac{t_j}{{\mathscr {L}}}\right) }^{b N }{ 2}}\nonumber \\&\times \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} {\left( \frac{t_j}{ {\mathscr {L}}}\right) }^{\frac{b}{2}} \bigg \vert \begin{array}{l } \frac{i-b}{ b},-1,\frac{i-b+\xi ^2}{ b} \\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b} \end{array}\right) \right) ^N d I \end{aligned}$$
(17)

where \(t_j\) and \(H_j\) are abcissae and weight coefficients for the Gauss–Laguerre quadrature respectively.

3.3 UVWOC link with maximum ratio combining (MRC)

The average BER of MRC receive diversity scheme considering ‘N’ detectors and single source by employing OOK modulation is given by Tsiftsis et al. (2009)

$$\begin{aligned} P_{MRC}= & {} \frac{1}{12} \prod _{n=1}^{N} \int _{0}^{\infty } f_{I_{n}}\left( I_{n}\right) e^{-\frac{{\mathscr {P}}}{2} I_{n}^{2}} d I_{n} \nonumber \\&+\frac{1}{4} \prod _{n=1}^{N} \int _{0}^{\infty } f_{I_{n}}\left( I_{n}\right) e^{-\frac{2 {\mathscr {P}}}{3 } I_{n}^{2}} d I_{n} \end{aligned}$$
(18)

where \({\mathscr {P}}=\frac{\eta ^2 P_t T_b}{4 N \sigma ^2}\) and \(f_{I_{1}}(I_1), f_{I_{2}}(I_2),\ldots ,f_{I_{N}}(I_N)\) are PDFs of independent identical random variables \(I_1,I_2,\ldots ,I_N\) respectively. In case of ‘N’ independent and identical random variables their PDFs are equal. Hence \(f_{I_{1}}(I_1) =f_{I_{2}}(I_2)=,\ldots ,=f_{I_{N}}(I_N)\). Substituting Eq. (9) in (18) we get,

$$\begin{aligned} P_{MRC}= & {} \prod _{n=1}^{N} \int _{0}^{\infty } {\mathscr {W}} \xi ^2 I_n^{b-1} G_{1+b, 1+b}^{1+b, 1}\left( {\mathscr {W}} I_n^{b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) \nonumber \\&\times \left[ \frac{1}{12} G_{0,1}^{1,0}\left( \frac{{\mathscr {P}} I_n^2}{2} \bigg \vert \begin{array}{l} -\\ 0\end{array}\right) +\frac{1}{4} G_{0,1}^{1,0}\left( \frac{2{\mathscr {P}}I_n^2}{3} \bigg \vert \begin{array}{l} - \\ 0\end{array}\right) \right] d I_{n} \end{aligned}$$
(19)

Integrating Eq. (19), we get

$$\begin{aligned} P_{MRC}= & {} \frac{1}{12} \prod _{n=1}^{N} {\mathscr {J}} {\left( \frac{{\mathscr {P}}}{2}\right) }^{-\frac{b}{2}} G_{2+3b, 2+2b}^{2+2b,2+b}\left( \frac{{\mathscr {W}}^2 {(2b)}^b}{{\mathscr {P}}^b} \bigg \vert \begin{array}{l} a_1 \\ b_1 \end{array}\right) \nonumber \\&+\frac{1}{4} \prod _{n=1}^{N} {\mathscr {J}} {\left( \frac{2 {\mathscr {P}}}{3}\right) }^{-\frac{b}{2}} G_{2+3b, 2+2b}^{2+2b,2+b}\left( \frac{{\mathscr {W}}^2 {(3 b)}^b}{(2 {\mathscr {P}})^b} \bigg \vert \begin{array}{l} a_1\\ b_1\end{array}\right) \end{aligned}$$
(20)

where \({\mathscr {J}}=\frac{{\mathscr {W}} \xi ^2 b^{\frac{b-1}{2}}}{(2\pi )^{\frac{b+1}{2}}}\), \(a_1=\left[ -\frac{1}{2},0,\frac{2i-b}{2 b},\frac{i-b+\xi ^2}{ b},\frac{i+\xi ^2}{ b}\right]\) and \(b_1= \left[ \frac{i-b+\xi ^2-1}{ b},\frac{i+\xi ^2-1}{ b},0,\frac{1}{2}\right] .\)

3.4 UVWOC link with majority logic combining (MLC)

The average BER of MLC receive diversity scheme employing OOK modulation with ‘N’ detectors at the receiver and a single source is given by Ramavath et al. (2020),

$$\begin{aligned} P_{\mathrm {MLC}}=\sum _{i=\left\lfloor \frac{N+1}{2}\right\rfloor }^{N}\left( \begin{array}{c} N \\ i \end{array}\right) P_{\mathrm {SISO}}^{i}\left( 1-P_{\mathrm {SISO}}\right) ^{N-i} \end{aligned}$$
(21)

where \(\lfloor \cdot \rfloor\) is floor operator and \(P_{SISO}\) is average BER of SISO system obtained from Eq. (12).

4 Outage probability

In this section, we derive closed-form expressions for the OP of SISO and SC receive diversity schemes.

4.1 Outage probability of UVWOC link employing single input single output (SISO) scheme

The OP is the probability that instantaneous received signal to noise ratio (SNR) \(\gamma\) will fall below the predefined threshold SNR \(\left( \gamma _{th}\right)\). The OP of a SISO system considering OOK modulation in case of UVWOC link is given by Yu et al. (2019)

$$\begin{aligned} P_{ {o,SISO }}=P\left( \gamma \le \gamma _{th}\right) \end{aligned}$$
(22)

where \(\gamma =\frac{\eta ^2 P_t T_b I^2}{ \sigma ^2}\). Equation (22) can be written as

$$\begin{aligned} P_{ {o,SISO }}=P\left( \gamma \le \gamma _{th}\right) =P\left( I \le \sqrt{\frac{\gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2 }}\right) = \int _{0}^{\sqrt{\frac{\gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2}}} f_I(I) dI \end{aligned}$$
(23)

By substituting Eq. (9) in (23) we get

$$\begin{aligned} P_{o,SISO}= \int _{0}^{\sqrt{\frac{\gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2}}} \xi ^{2} {\mathscr {W}} I^{b-1} G_{1+b, 1+b}^{1+b, 1}\left( { {\mathscr {W}} I^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) dI \end{aligned}$$
(24)

Integrating Eq. (24), obtained expression is given as,

$$\begin{aligned} P_{o,SISO}=\frac{\xi ^2 {\mathscr {W}} }{b} \left( \frac{\gamma _{th} \sigma ^2}{P_t T_b \eta ^2}\right) ^\frac{b}{2}G_{1+2b, 1+2b}^{1+b, 1+b}\left( {\mathscr {W}} \left( \frac{\gamma _{th} \sigma ^2}{P_t T_b \eta ^2}\right) ^\frac{b}{2} \bigg \vert \begin{array}{l} \frac{i-b}{ b},-1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b}\end{array}\right) \end{aligned}$$
(25)

4.2 Outage probability of UVWOC link employing selection combining scheme

The OP of SC receive diversity scheme considering ‘N’ detectors with Selection Combining and a single transmitting source is given by

$$\begin{aligned} P_{ {o,SC }}=P\left( \gamma _{SC} \le \gamma _{th}\right) =P\left( I_{SC} \le \sqrt{ \frac{N \gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2 }}\right) = \int _{0}^{\sqrt{\frac{ N \gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2}}} f_{I_{SC}}(I_{SC}) dI_{SC} \end{aligned}$$
(26)

where \(I_{SC}\) is the response of the SC combiner and \(\gamma _{SC}=\frac{\eta ^2 P_t T_b}{N \sigma ^2}\) is the instantaneous received SNR of SC scheme. The pdf of SC scheme in terms of CDF is given by Ramavath et al. (2020)

$$\begin{aligned} f_{I_{SC}}(I_{SC})=N\left( F_{I}\left( I_{SC}\right) \right) ^{N-1} f_{I}\left( I_{SC}\right) \end{aligned}$$
(27)

By substituting Eqs. (15) and (9) in (27) we get

$$\begin{aligned} f_{I_{SC}}(I_{SC}) \; = & {} {\mathscr {A}}_{1} I_{SC}^{ b N-1} \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} I_{SC}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b} ,-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b} \end{array}\right) \right) ^{N-1}\nonumber \\&\times G_{1+b, 1+b}^{1+b, 1}\left( {{\mathscr {W}} I_{SC}^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) \end{aligned}$$
(28)

where \({\mathscr {A}}_{1}=\frac{N (W \xi ^2)^{N} }{ {b}^{N-1} }\). By replacing Eq. (28) in (26) and integrating later using Gauss–Legendre quadrature for ‘M’ sample points we get

$$\begin{aligned} P_{ {o,SC }}= & {} \frac{{\mathscr {A}}_{1} {\mathscr {A}}_{2}}{ 2} \sum _{j=1}^{M} H_j t_{j}^{ b N-1} \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} t_{j}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b},-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b} \end{array}\right) \right) ^{N-1} \nonumber \\&\times G_{1+b, 1+b}^{1+b, 1}\left( { {\mathscr {W}} t_{j}^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) \end{aligned}$$
(29)

where \({\mathscr {A}}_{2}=\sqrt{\frac{N \gamma _{th} \sigma ^2 }{ P_t T_b \eta ^2}}\), \(t_j=\frac{{\mathscr {A}}_{2} }{ 2}(1+H_j)\), \(H_j\) is abscissa and \(t_j\) is weight coefficient for the Gauss–Legendre quadrature.

5 Ergodic channel capacity

In this section, we derive novel closed-form expressions for the ECC of UVWOC links with SISO and SC based receive diversity scheme.

5.1 Ergodic channel capacity of UVWOC link employing single input single output scheme

The ECC of the SISO system in case of vertical link for OOK modulation is given by Elamassie and Uysal (2020)

$$\begin{aligned} {C_{SISO}}= \int _{0}^{\infty } 0.5\log _{2}\left( 1+ \frac{e \gamma }{ 2\pi }\right) f_{\gamma }(\gamma ) d \gamma \end{aligned}$$
(30)

where ‘e’ is exponential constant. By using change of variable technique \(\gamma =\frac{\eta ^2 P_t T_b I^2}{ \sigma ^2}\) and using relation \(\log _{2}(1+x)= {1.44}~G_{2,2}^{1,2}\left( x \bigg \vert \begin{array}{l}1,1 \\ 1,0\end{array} \right)\) in Eq. (30) we get

$$\begin{aligned} {C_{SISO}}= \int _{0}^{\infty } 0.72 {\mathscr {W}} \xi ^{2} I^{b-1} G_{2,2}^{1,2}\left( \frac{e P_t T_b I^2 }{ 2\pi \sigma ^2} \bigg \vert \begin{array}{l}1,1 \\ 1,0\end{array} \right) G_{1+b, 1+b}^{1+b, 1}\left( {\mathscr {W}} I^b \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) dI \end{aligned}$$
(31)

By integrating Eq. (31), obtained ECC expression is given as,

$$\begin{aligned} {C_{SISO}}= \frac{0.72 {\mathscr {W}} (\xi ^{2} \eta ^2 e P_t T_b)^{- \frac{b }{ 2}} }{ b \sigma ^2 (2\pi )^{-\frac{b}{ 2}+b} } G_{2+4b, 2+4b}^{2+4b, 2+b}\left( {\mathscr {W}} ^2 {\left( \frac{\eta ^2 e P_t T_b }{ \sigma ^22 \pi }\right) }^{-b} \bigg \vert \begin{array}{l} -\frac{1 }{ 2}, 0, \frac{2i-b-2}{ 2b},\frac{2i-b}{ 2b}, \frac{i-b+\xi ^2}{ 2b}, \frac{i+\xi ^2}{ 2b}\\ \frac{i-b+\xi ^2-1}{ 2b}, \frac{i-1+\xi ^2}{ 2b}, 0, \frac{1}{2}, \frac{2i-b-2}{ 2b}, \frac{2i-b-2}{ 2b} \end{array}\right) dI. \end{aligned}$$
(32)

5.2 Ergodic channel capacity of UVWOC link employing selection combining

The ECC of SC based receive diversity scheme considering ‘N’ detectors at the receiver and a single source at the transmitter is given by

$$\begin{aligned} {C_{SC}}= 0.5\int _{0}^{\infty } \log _{2}\left( 1+ \frac{e \gamma _{SC} }{ 2\pi }\right) f_{\gamma _{SC}}(\gamma _{SC}) d \gamma \end{aligned}$$
(33)

By using change of variable technique \(\gamma _{SC}= \frac{\eta ^2 P_t T_b I_{SC}^2}{ N \sigma ^2}\), \(\log _{2}(1+x)= {1.44} ~G_{2,2}^{1,2}\left( x \bigg \vert \begin{array}{l}1,1 \\ 1,0\end{array} \right)\) and substituting Eq. (28) in (33) we get

$$\begin{aligned} {C_{SC}}= & {} \int _{0}^{\infty } 0.72 A_1 I_{SC}^{bN-1} G_{2,2}^{1,2}\left( \frac{e P_t T_b I_{SC}^2 }{ N 2\pi \sigma ^2} \bigg \vert \begin{array}{l}1,1 \\ 1,0\end{array}\right) G_{1+b, 1+b}^{1+b, 1}\left( {{\mathscr {W}} I_{SC}^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) \nonumber \\&\times \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} I_{SC}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b} ,-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b}\end{array}\right) \right) ^{N-1} dI_{SC} \end{aligned}$$
(34)

By applying Gauss–Laguerre quadrature for ‘M’ sample points (Concus et al. 1963) to Eq. (34) we get

$$\begin{aligned} {C_{SC}}= & {} 0.72 A_1 \sum _{j=1}^{M} H_k t_{j}^{bN-0.5} \exp ({t_j}) G_{2,2}^{1,2}\left( \frac{e P_t T_b t_{j}^2 }{ N 2\pi \sigma ^2} \bigg \vert \begin{array}{l}1,1 \\ 1,0\end{array} \right) \nonumber \\&\times \left( G_{1+2b, 1+2b}^{1+b,1+b}\left( {\mathscr {W}} t_{j}^b \bigg \vert \begin{array}{l } \frac{i-b}{ b},-1,\frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0,\frac{i-b-1}{ b}\end{array}\right) \right) ^{N-1} \nonumber \\&\times G_{1+b, 1+b}^{1+b, 1}\left( {{\mathscr {W}} t_{j}^b} \bigg \vert \begin{array}{l} -1, \frac{i-b+\xi ^2}{ b}\\ \frac{i-b+\xi ^2-1}{ b},0\end{array}\right) dI_{SC} \end{aligned}$$
(35)

where \(t_j\) and \(H_j\) are abcissae and weight coefficients for the Gauss–Laguerre quadrature respectively.

6 Results and discussion

The system parameters that are used in simulation and numerical analysis are \(\eta =0.8~\mathrm {A/W}\), \(\lambda =530~\mathrm {nm}\), \(D_R=5~\mathrm {cm}\), \(\omega _0=1~\mathrm {cm}\) and \(\sigma ^2=2.82\times 10^{-13}\) (Ramavath et al. 2020). In this paper, we have considered a UVWOC link with transmitter–receiver separation with one, two, three and four non-identical layers where each layer has a thickness of \(30~\mathrm {m}\). The critical parameters of the multi-layer UVWOC links (log amplitude variance and corresponding HTLN parameters) are presented in Table 1. This data has been drawn from the pacific ocean at high latitudes (Elamassie et al. 2018; Elamassie and Uysal 2020). The values of extinction coefficient for different types of ocean water are given as \(C(\lambda =530~\mathrm {nm})=0.056~\mathrm {m}^{-1}, ~0.151~\mathrm {m}^{-1}\) and \(0.301~\mathrm {m}^{-1}\) for pure sea water, clear ocean water and coastal water respectively (Elamassie et al. 2019; Levidala et al. 2021; Kumar et al. 2022). Analytic computations and simulations have been carried out at data rates of \(R_b= 0.5~\mathrm {Gbps},~1~\mathrm {Gbps}\) and \(10~\mathrm {Gbps}\) (\(R_b=1/T_b\)). The pointing errors induced by variation of the displacement standard deviations \(\sigma _s\) and corresponding \(A_0\) and \(\xi\) values considered for simulation are shown in Table 2.

Table 1 Log-amplitude variation with respect to number of non-identical layers and corresponding HTLN distribution parameters
Full size table
Table 2 Pointing error parameters for UVWOC link
Full size table

In Fig. 2, we have presented the average BER for a two non-identical layer UVWOC link disturbed by different pointing errors for pure seawater obtained at \(0.5~\mathrm {Gbps}\) data rate. The SISO UVWOC system affected by very strong pointing errors attains an average BER of \(3\times 10^{-2}\) at \(50~\mathrm {dB}\) transmit power. This value of average BER performance is achieved by SISO UVWOC system under strong, moderate, weak and very weak pointing errors at a transmit power of \(33~\mathrm {dB},~23~\mathrm {dB},~16~\mathrm {dB}\) and \(13.5~\mathrm {dB}\), respectively. From Fig. 2, it is observed that an increase in \(\sigma _s\) causes an deterioration in the average BER performance.

Fig. 2
figure 2

Average BER performance for different pointing errors using SISO UVWOC link

Full size image
Fig. 3
figure 3

Average BER performance for different number of layers in the UVWOC SISO vertical link

Full size image

Figure 3 shows the average BER performance of UVWOC link when the number of non-identical layers is varied from one to four. In all cases, the operating data rate is assumed to be \(R_b=0.5~\mathrm {Gbps}\). Pointing errors are assumed to belong to the very weak class and the medium is assumed to be pure seawater. As has been discussed earlier, each layer has a thickness of \(30~\mathrm {m}\). From figure, it is observed that links consisting of one, two, three and four non-identical vertical layers attain an average BER of \(1\times 10^{-3}\) at \(4.5~\mathrm {dB},~25~\mathrm {dB},~44~\mathrm {dB}\) and \(62.5~\mathrm {dB}\) transmit power, respectively.

In Fig. 4, we have presented the average BER for a single layer UVWOC operating at \(R_b=0.5~\mathrm {Gbps}\) data rate for different types of ocean water operting under very weak pointing error condition. From this figure, it is observed that when we operate in coastal water the average BER performance deteriorates to values much inferior to the values obtained while operating in deep ocean. This may attributed to the higher values of turbidity associated with the ocean water near the coast.

Fig. 4
figure 4

Average BER performance UVWOC SISO link (with fixed pointing error) for different ocean water types

Full size image

Figure 5 represents the average BER performance of SISO UVWOC link for varying data rates for a two non-identical layers operated for pure seawater medium. The average BER is obtained for data rates \(R_b= 0.5~\mathrm {Gbps},~1~\mathrm {Gbps}\) and \(10~\mathrm {Gbps}\). It is observed that as data rate increases, the average BER increases. To achieve average BER \(=10^{-3}\), at a data rate of \(0.5~\mathrm {Gbps}\), the required transmitter power is estimated to be equal to \(25~\mathrm {dB}\) (by both calculations and Monte-Carlo simulations). When the data rate is increased to \(1~\mathrm {Gbps}\), the required transmitter power is estimated to be \(28~\mathrm {dB}\). For a data rate of \(10~\mathrm {Gbps}\), the required transmitted power is estimated to be \(38~\mathrm {dB}\).

Fig. 5
figure 5

Average BER performance for different data rates in the UVWOC SISO vertical link proposed in this paper

Full size image
Table 3 Average BER values for different UVWOC schemes
Full size table

Figure 6 shows the average BER performance of a two layers employing various receive diversity schemes for the case a UVWOC link operating in pure seawater. Computation and simulation results have been obtained under two pointing error scenarios. In the first case, very weak pointing error conditions \((\sigma _s=1\times 10^{-2}~\mathrm {m})\) have been assumed and in the second case, very strong pointing error conditions \((\sigma _s=5\times 10^{-2}~\mathrm {m})\) have been assumed. It can be observed from this plot the performance of the MRC scheme is superior to other receive diversity schemes. The computed values of average BER (assuming the transmitted power to be \(P_t= 25~\mathrm {dB}\)) are shown in Table 3.

Fig. 6
figure 6

Average BER performance of a UVWOC link employing SISO, MLC, SC and MRC receive diversity schemes

Full size image

In Fig. 7, we have presented the Outage Probability (OP) of the SISO UVWOC system operating over a link comprising of two non-identical layers for different values of pointing errors. The data rate \(R_b=0.5~\mathrm {Gbps}\) and the medium is assumed to be pure seawater medium and the threshold SNR is assumed to be \(5~\mathrm {dB}\) threshold SNR. It is observed that as \(\sigma _s\) increases, there is a degradation of the OP performance.

Fig. 7
figure 7

Outage probability performance of a SISO UVWOC vertical link for different values of pointing error

Full size image
Fig. 8
figure 8

Outage probability performance of a SISO UVWOC link for different number of layers

Full size image

Figure 8 shows the OP performance of varying vertical layers from one to four for very weak pointing errors, pure seawater medium operated at \(R_b=0.5~\mathrm {Gbps}\) data rate. One, two, three and four non-identical vertical layered UVWOC system attain an OP of \(1\times 10^{-3}\) at \(3.5~\mathrm {dB},~32~\mathrm {dB},~37~\mathrm {dB}\) and \(63~\mathrm {dB}\) respectively.

Table 4 Power transmitted at outage probability \(=10^{-2}\) for SISO and SC UVWOC links
Full size table

Figure 9 depicts the OP associated with SISO and SC receive diversity schemes for SNR thresholds \(\gamma _{th}=5~\mathrm {dB}\) and \(20~\mathrm {dB}\) for a two non-identical layers operated at \(R_b=0.5~\mathrm {Gbps}\) data rate under the influence of very weak pointing errors for pure seawater medium. It is observed that an increase in number of detectors ‘N’ will improve the performance by a reduction in the OP and an increase in SNR threshold will result in a deterioration of the OP performance. The required values of transmitted power at OP \(1\times 10^{-2}\) for SISO and SC schemes are shown in Table 4. We observe that there is a reduction in the transmit power requirement with increase in the order of diversity reception.

Fig. 9
figure 9

Outage probability performance of SISO and SC receive diversity schemes

Full size image
Fig. 10
figure 10

Ergodic channel capacity of SISO system for different pointing errors

Full size image
Fig. 11
figure 11

Ergodic channel capacity performance for different number of vertical layers in the SISO UVWOC link

Full size image
Fig. 12
figure 12

Ergodic channel capacity of SISO and SC receive diversity schemes

Full size image

In Fig. 10, we present the ECC of SISO system by varying the impact of pointing errors for a two non-identical vertical layers at \(R_b=0.5~\mathrm {Gbps}\) and pure sea water medium. It is observed that ECC of SISO system decreases as the standard deviation of pointing error \(\sigma _s\) is increased.

Figure 11 represents the SISO UVWOC link’s ECC performance for the different vertical layers. We have considered very weak pointing errors and pure sea water medium at \(R_b=0.5~\mathrm {Gbps}\). We observed a decrease in ECC performance as the number of vertical layers increased. For transmitted power \(50~\mathrm {dB}\), ECC values are \(10.96~\mathrm {bps/Hz}\), \(8.92~\mathrm {bps/Hz}\), \(5.66~\mathrm {bps/Hz}\) and \(3.11~\mathrm {bps/Hz}\) respectively for one, two, three and four vertical layers.

In Fig. 12, we present the ECC of SISO system and SC receive diversity schemes for \(N=2,~3,~4\) under the influence of a very strong pointing error at \(R_b=0.5~\mathrm {Gbps}\) by considering pure sea water medium. It is observed that as a number of detector increases, ECC increases. For transmitted power \(15~\mathrm {dB}\), the ECC values are shown in Table 5. We observe that the ECC increases with the diversity order.

Table 5 Ergodic channel capacity of SISO and SC receive diversity UVWOC link
Full size table

7 Conclusion

In this paper, we have investigated the performance of a UVWOC link employing OOK modulation for weak underwater turbulence under the influence of pointing errors and attenuation losses. We have derived closed-form expressions for the average BER, OP and ECC considering various types of link configurations (SISO and receive diversity schemes). The average BER supported by the link has been determined for different data rates, various types of ocean waters, varying number of vertical layers and differing degrees of pointing error. From the results obtained in the paper, we have concluded that the performance of the MRC scheme is superior to other receive diversity schemes when examined in terms of improvement in average BER. Further, closed-form expressions for the OP and ECC have been derived for SISO and SC schemes. The OP has been analyzed for different SNR thresholds and pointing errors. We conclude that there is an reduction in the transmit power requirement as the number of detectors is increased. The plots obtained by computation using the analytic closed-form expressions derived by us and the plots obtained using Monte-Carlo simulation are very closely matched (coincident in most cases). We feel that this is a testimony to the accuracy of the process followed to obtain the Monte-Carlo simulation results.