1 Introduction

In recent years, the evaluation properties of laser beam propagation in turbulent atmosphere were aroused extensive attention and become more and more important because of their large applications in optical communication, remote sensing and imaging system (Andrews et al. 2001; Noriega-Manez and Gutiérrez-Vega 2007; Korotkova and Gbur 2007). We know that when the wave propagates through the atmosphere, both the amplitude and the phase of the electric field caused by random changes of the refractive index. In past years, many papers have been devoted to study the propagation of some laser beams in atmospheric turbulence, such as the propagation characteristics of truncated Bessel–Gauss (Cang and Zhang 2010), Bessel-modulated Gaussian (Belafhal et al. 2011), Laguerre–Gaussian (Wang et al. 2010), Li’s flat topped (Kinani et al. 2011), Cosh-Gaussian (Chu 2007), Hermite-cosine Gaussian (Eyyuboğlu 2005), truncated modified Bessel modulated Gaussian with quadrature radial dependence (Hennani et al. 2013), and Hollow Gaussian vortex beam (Zhou et al. 2012). Recently, the propagation properties of Li’flattened Gaussian (Khannous et al. 2014), Controllable hollow flat-topped (Liu et al. 2015), and Hypergeometric Gaussian beam (Khannous et al. 2015) in a turbulent atmosphere optical system have also been investigated. More recently, the effects of the turbulent atmosphere on the on-axis average intensity of Pearcey–Gaussian (Boufalah et al. 2016), flat-topped vortex (Liu et al. 2016), Hollow-Gaussian (Khannous et al. 2016), and conical Hollow beam (Yuan et al. 2016) were also studied.

On the other hand, in Saad et al. (2016), the generation of the GSBB of an arbitrary order by CFH has been given. This beams family can be created by illuminating a CFH with a LGB. However, to the best of our knowledge, the propagation properties of the GSBB in a turbulent atmosphere have not been studied elsewhere.

Our aim here is to study the propagation characteristics of GSBB through a turbulent atmosphere. The rest of this paper is arranged as follows: In Sect. 2, we present the field distribution of the GSBB. In Sect. 3, an analytical expression of the average intensity of the GSBB is developed based on the extended Huygens-Fresnel integral formula in the paraxial approximation and by the Rytov method. An approximate analytical axial average intensity distribution is derived in Sect. 4. Some numerical simulations are performed and discussed in Sect. 5. We conclude our work in the final section.

2 Distribution field of the GSBB

In this section, we assume that the filed distribution of an arbitrary order for the GSBB by using CFH is given by (Saad et al. 2016)

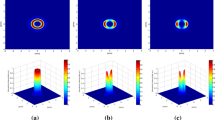
$$\begin{aligned} E_{ \pm m} \left( {r_{ \pm m} ,\theta_{ \pm m} ,z_{0} } \right) & = \left( { \mp i} \right)\left( { \mp 1} \right)^{mp} At_{ \pm m} \left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right)^{1/2} \left( {\frac{{\sqrt 2 z_{0} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)}}} \right)^{l + 1/2} \\ & \quad \times \exp \left( { - i\left( {l \mp mp} \right)\left( {\theta_{ \pm m} + \frac{\pi }{2}} \right)} \right)\exp \left[ { - ik\left( {z_{0} + \frac{{r^{2} }}{{2z_{0} }} - \frac{{c_{m}^{2} z_{0} }}{2}} \right)} \right]\, \\ & \quad \times \exp \left( { - \frac{{z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)L_{n}^{l} \left( {2\frac{{z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)\,J_{{l + \left| {mp} \right|}} \left( {kc_{m} r_{ \pm m} } \right), \\ \end{aligned}$$
(1)

where \(r_{ \pm m} ,\,\,\theta_{ \pm m} \,\,{\text{and}}\,\,z_{0}\) are the cylindrical coordinates, c m  = mα/k, with α is the parameter axicon defined as α = k(n 0 − 1)γ, n 0 is its refractive index, γ is the axicon base angle, k = 2π/λ is the wave number, λ is wavelength, ω 0 is the beam waist radius, \(L_{n}^{l} \left( \cdot \right)\) is the generalized Laguerre polynomial with mode indices n and l and \(J_{{l + \left| {mp} \right|}} \left( \cdot \right)\) is the spiraling Bessel function of the first kind of order l + |mp|. Figure 1 presents the transverse intensity in 3D of the GSBB at distance z = z 0 from the source plane for two values of topological charge of the helical axicon p = 1 and 3. For each value of p, three illustrations are plotted for different values of l = 1, 3 and 5. From the plots of this figure, it can be seen that when the beam order l increasing, the dark spot also increases and the vortex radius decreases. It also observed that the center dark region becomes greater for large values of the topological charge p. Furthermore, the number of the peaks of the vortex radius and its maximum intensity are also adjusted withpchanging (see Fig. 1A, B).

Fig. 1
figure 1

Transverse intensity distribution of the GSBB with m = 1, n = 1, γ = 1.35°, \(n_{0} = 1.48 ,\) \(\omega_{0} = 10\,{\text{mm}}\) and \(z_{0} = 450\,{\text{mm}}\) for A p = 1, and B p = 3 at (a) l = 1, (b) l = 3 and (c) l = 5

Full size image

3 Average intensity of the GSBB in a turbulent atmosphere

The propagation of the GSBB in a turbulent atmosphere can be studied based on the extended Huygens–Fresnel formula in the paraxial approximation and on the Rytov method as follows (Andrews and Philips 1998)

$$E\left( {\vec{\rho },L,t} \right) = - \frac{ik}{2\pi L}\exp (ikL)\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {E\left( {\vec{r}_{1} ,z_{0} } \right)} } \exp \left[ {\frac{ik}{2L}\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} + \psi \left( {\vec{r}_{1} ,\vec{\rho }} \right) - i2\pi ft} \right]d\vec{r}_{1} ,$$
(2)

where L is the propagation distance, a is the radius of the aperture, \(\psi \left( {\vec{r}_{1} ,\vec{\rho }} \right)\) is the solution to the Rytov method that represents the random part of the complex phase of a spherical wave propagating from the source plane to the output plane \(\vec{r}_{1} = \left( {r_{1} ,\theta_{1} } \right),\,\vec{\rho } = \left( {\rho ,\phi } \right)\), f is the frequency and t denotes the time. Here, \(E\left( {\vec{r}_{1} ,z_{0} } \right)\) and \(E\left( {\vec{\rho },L,t} \right)\) are the electric fields component of the GSBB situated at a distance z = z 0 from the source plane and the observation plane at L = z − z 0. Figure 2 shows a schematic diagram to illustrate the propagation of the GSBB in a turbulent atmosphere optical system.

Fig. 2
figure 2

A schematic illustration of the GSBB propagating in a turbulent atmosphere optical system

Full size image

By substituting Eqs. (1) into (2), the average intensity at the output plane can be written as

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },L} \right)} \right\rangle & = \left\langle {E\left( {\vec{\rho },L,t} \right)\,E^{ * } \left( {\vec{\rho },L,t} \right)} \right\rangle = \frac{{k^{2} }}{{4\pi^{2} L^{2} }}\int\limits_{0}^{a} {\,\int\limits_{0}^{a} {\,\int\limits_{0}^{2\pi } {\,\int\limits_{0}^{2\pi } {E\left( {\vec{r}_{1} ,z_{0} } \right)E^{ * } \left( {\vec{r}_{2} ,z_{0} } \right)} } } } \\ & \quad \times \exp \left\{ {\frac{ik}{2L}\left[ {\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} + \left( {\vec{r}_{2} - \vec{\rho }} \right)^{2} } \right]} \right\}\,\left\langle {\exp \left[ {\psi \left( {\vec{r}_{1} ,\vec{\rho }} \right) + \psi^{ * } \left( {\vec{r}_{2} ,\vec{\rho }} \right)} \right]} \right\rangle \,d\vec{r}_{1} d\vec{r}_{2} , \\ \end{aligned}$$
(3)

where * and 〈〉 denote the complex conjugate and the ensemble average over the medium statistics, respectively. The ensemble average term in last equation is expressed as follows (Andrews and Philips 1998)

$$\left\langle {\exp \left[ {\psi \left( {\vec{r}_{1} ,\vec{\rho }} \right) + \psi^{ * } \left( {\vec{r}_{2} ,\vec{\rho }} \right)} \right]} \right\rangle = \exp \left[ { - 0.5D_{\psi } \left( {\vec{r}_{1} - \vec{r}_{2} } \right)} \right] = \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {\vec{r}_{1} - \vec{r}_{2} } \right)^{2} } \right],$$
(4)

with D ψ is the phase structure function of the random complex in the Rytov representation and ρ 0 = (0.545C 2 n k 2 L)−3/5 is the coherence length of a spherical wave propagating in the turbulent medium. \(C_{n}^{2}\) being the refractive index structure constant whose value can indicate the turbulent strength.

Substituting Eqs. (1) and (4) into Eq. (3), and using the following notations r ±m  = r, θ ±m  = θ and \(\,{\text{t}}_{{ \pm {\text{m}}}} = t,\) then, Eq. (3) can be expressed in the following form

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },L} \right)} \right\rangle & = \frac{{A^{2} t^{2} }}{{\lambda^{2} L^{2} }}\int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)} } } } \,\,\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right) \\ & \quad \times \exp \left[ {i\frac{k}{2L}\left( {r_{1}^{2} - r_{2}^{2} } \right)} \right]\exp \left[ {i\frac{k}{{2z_{0} }}\left( { - r_{1}^{2} + r_{2}^{2} } \right)} \right] \\ & \quad \times J_{{l + \left| {mp} \right|}} \left( {kc_{m} \,r_{1} } \right)J_{{l + \left| {mp} \right|}} \left( {\,kc_{m} \,r_{2} } \right)\exp \left\{ { - i\,\left( {l \mp mp} \right)\left[ {\left( {\theta_{1} - \theta_{2} } \right)} \right]} \right\} \\ & \quad \times \exp \left\{ {i\frac{k}{L}\left( { - r_{1} \rho \cos \left( {\theta_{1} - \phi } \right) + r_{2} \rho \cos \left( {\theta_{2} - \phi } \right)} \right)} \right\} \\ & \quad \times \exp \left( { - \frac{{r_{1}^{2} + r_{2}^{2} }}{{\rho_{0}^{2} }}} \right)\,\exp \left( {\frac{{2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)}}{{\rho_{0}^{2} }}} \right)\,r_{1} r_{2} dr_{1} dr_{2} d\theta_{1} d\theta_{2} , \\ \end{aligned}$$
(5)

where

$$C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right) = \left( {\frac{{2z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)^{l + 1/2} \,\exp \left( { - \frac{{2z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)\left[ {L_{n}^{l} \left( {2\frac{{z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)} \right]^{2} .$$
(6)

From the last equation, the function \(C_{n}^{l + 1/2}\) (z 0; ω 0/c m ) denotes the Laguerre–Gaussian-doughnut type, defining the longitudinal profile of the GSBB.

4 Axial average intensity distribution of the GSBB in a turbulent atmosphere

In this section, we will evaluate the analytical expression of the axial intensity distribution of the considered beams family as given in Eq. (5). To calculate the on-axis average intensity, we will use the following expression of the hard aperture truncated function into a finite sum of complex Gaussian functions (Wen and Breazeale 1988)

$$H\left( r \right) = \sum\limits_{k = 1}^{N} {A_{k} } \exp \left( { - \frac{{B_{k} }}{{a^{2} }}r^{2} } \right),$$
(7)

where A k and B k denote the expression and the Gaussian coefficients, respectively, and N represents the number of the expansion terms and generally is equal to ten. For the propagation on the axis, we take ρ = 0, then substituting Eqs. (7) into (5), one obtains

$$\begin{aligned} \left\langle {I\left( {0,L} \right)} \right\rangle & = \frac{{A^{2} t^{2} }}{{\lambda^{2} L^{2} }}\sum\limits_{k = 1}^{N} {A_{k} \sum\limits_{s = 1}^{N} {A_{s} } } \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)} } } } \,\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right) \\ & \quad \times J_{{l + \left| {mp} \right|}} \left( {kc_{m} \,r_{1} } \right)\exp \left[ {\left( {\frac{ik}{2L} - \frac{ik}{{2z_{0} }} - \frac{1}{{\rho_{0}^{2} }} - \frac{{B_{k} }}{{a^{2} }}} \right)r_{1}^{2} } \right] \\ & \quad \times J_{{l + \left| {mp} \right|}} \left( {kc_{m} \,r_{2} } \right)\exp \left[ {\left( { - \frac{ik}{2L} + \frac{ik}{{2z_{0} }} - \frac{1}{{\rho_{0}^{2} }} - \frac{{B_{s} }}{{a^{2} }}} \right)r_{2}^{2} } \right] \\ & \quad \times \exp \left\{ { - i\,\left( {l + \left| {mp} \right|} \right)\left[ {\left( {\theta_{1} - \theta_{2} } \right)} \right]} \right\}\exp \left( {\frac{{2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)}}{{\rho_{0}^{2} }}} \right)\,r_{1} r_{2} dr_{1} dr_{2} d\theta_{1} d\theta_{2} . \\ \end{aligned}$$
(8)

To solve the finite integral in the above equation, we use the following integral formulae

$$\int\limits_{0}^{2\pi } {\exp \left[ { - im\theta_{1} + x\,\,\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} = 2\pi \exp \left( { - im\theta_{2} } \right)I_{m} \left( x \right),$$
(9)

where I m (·) is the m-order modified Bessel function. Then, we can express Eq. (8) as follows

$$\begin{aligned} \left\langle {I\left( {0,L} \right)} \right\rangle & = \frac{{4\pi^{2} A^{2} t^{2} }}{{\lambda^{2} L^{2} }}C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right) \\ & \quad \times \sum\limits_{k = 1}^{N} {A_{k} \sum\limits_{s = 1}^{N} {A_{s} } } \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {J_{{l + \left| {mp} \right|}} \left( {kc_{m} \,r_{1} } \right)\exp \left( { - \delta_{1} r_{1}^{2} } \right)} } \\ & \quad \times J_{{l + \left| {mp} \right|}} \left( {kc_{m} \,r_{2} } \right)\exp \left( { - \delta_{2} r_{2}^{2} } \right)I_{{l + \left| {mp} \right|}} \left( {\frac{{2r_{1} r_{2} }}{{\rho_{0}^{2} }}} \right)\,r_{1} r_{2} dr_{1} dr_{2} , \\ \end{aligned}$$
(10)

where

$$\delta_{1} = - \frac{ik}{2L} + \frac{ik}{{2z_{0} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{k} }}{{a^{2} }},$$
(11a)

and

$$\delta_{2} = \frac{ik}{2L} - \frac{ik}{{2z_{0} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{s} }}{{a^{2} }}.$$
(11b)

Recalling the following integral formula (Gradshteyn and Ryzhik 1994)

$$\int\limits_{0}^{\infty } {xe^{{ - \mu \,x^{2} }} } I_{v} \left( {\beta x} \right)J_{\nu } \left( {\gamma x} \right)dx = \frac{1}{2\mu }\exp \left( {\frac{{\beta^{2} - \gamma^{2} }}{4\mu }} \right)J_{\nu } \left( {\frac{\beta \gamma }{2\mu }} \right),$$
(12)

with \(\left[ {\mu > 0,\text{Re} \,\,\,\nu > - 1} \right],\) and utilizing the following relation (Gradshteyn and Ryzhik 1994)

$$I_{m} \left( z \right) = i^{ - m} J_{m} \left( {iz} \right),$$
(13)

and after some calculations, Eq. (10) can be simplify as

$$\begin{aligned} \left\langle {I\left( {0,L} \right)} \right\rangle = & \frac{{4\pi^{2} A^{2} t^{2} }}{{\lambda^{2} L^{2} }}C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right)\sum\limits_{k = 1}^{N} {\sum\limits_{s = 1}^{N} {A_{k} A_{s} \frac{1}{{2\delta_{2} }}\exp \left( { - \frac{{k^{2} c_{m}^{2} }}{{4\delta_{2} }}} \right)\,i^{{_{{_{{l + \left| {mp} \right|}} }} }} } } \\ & \quad \times \int\limits_{0}^{\infty } {\exp \left( { - \beta_{1} r_{1}^{2} } \right)} J_{{l + \left| {mp} \right|}} \left( {kc_{m} r_{1} } \right)I_{{l + \left| {mp} \right|}} \left( { - i\beta_{2} r_{1} } \right)r_{1} dr_{1} , \\ \end{aligned}$$
(14)

where

$$\beta_{1} = \delta_{1} - \frac{1}{{\rho_{0}^{4} \delta_{2} }},$$
(15a)

and

$$\beta_{2} = \frac{{kc_{m} }}{{\rho_{0}^{2} \delta_{2} }}.$$
(15b)

Using the integral formula and the relation given in Eqs. (12) and (13) again, and after some manipulations, we find the analytical expression of the axial intensity distribution of the GSBB as follows

$$\begin{aligned} \left\langle {I\left( {0,L} \right)} \right\rangle = & \frac{{4\pi^{2} A^{2} t^{2} }}{{\lambda^{2} L^{2} }}C_{n}^{l + 1/2} \left( {z_{0} ;{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right)\sum\limits_{k = 1}^{N} {\sum\limits_{s = 1}^{N} {A_{k} } } A_{s} \left( { - 1} \right)^{{l + \left| {mp} \right|}} \\ & \quad \times \frac{1}{{4\beta_{1} \delta_{2} }}\exp \left( { - \frac{{k^{2} c_{m}^{2} }}{{4\delta_{2} }} - \frac{{\beta_{2}^{2} + k^{2} c_{m}^{2} }}{{4\beta_{1} }}} \right)I_{{l + \left| {mp} \right|}} \left( { - \frac{{\beta_{2} kc_{m} }}{{2\beta_{1} }}} \right). \\ \end{aligned}$$
(16)

Finally, by the insertion of Eq. (6), Eq. (16) can be expressed in the following form

$$\begin{aligned} \left\langle {I\left( {0,L} \right)} \right\rangle = \frac{{4\pi^{2} A^{2} t^{2} }}{{\lambda^{2} L^{2} }}\left( {\frac{{\omega_{0} kc_{m} }}{\sqrt 2 }} \right)\,\left( {\frac{{2z_{0}^{2} }}{{\left( {{{w_{0} } \mathord{\left/ {\vphantom {{w_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)^{l + 1/2} \,\exp \left( { - \frac{{2z_{0}^{2} }}{{\left( {{{\omega_{0} } \mathord{\left/ {\vphantom {{\omega_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)\left[ {L_{n}^{l} \left( {2\frac{{z_{0}^{2} }}{{\left( {{{w_{0} } \mathord{\left/ {\vphantom {{w_{0} } {c_{m} }}} \right. \kern-0pt} {c_{m} }}} \right)^{2} }}} \right)} \right]^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{k = 1}^{N} {\sum\limits_{s = 1}^{N} {A_{k} } } A_{s} \left( { - 1} \right)^{{l + \left| {mp} \right|}} \frac{1}{{4\beta_{1} \delta_{2} }}\exp \left( { - \frac{{k^{2} c_{m}^{2} }}{{4\delta_{2} }} - \frac{{\beta_{2}^{2} + k^{2} c_{m}^{2} }}{{4\beta_{1} }}} \right)I_{{l + \left| {mp} \right|}} \left( { - \frac{{\beta_{2} kc_{m} }}{{2\beta_{1} }}} \right). \hfill \\ \end{aligned}$$
(17)

This last equation represents the main analytical result in this paper, which characterizes the analytical expression of the on-axis average intensity of the GSBB after propagating in a turbulent atmosphere.

5 Numerical simulations and discussion

In order to illustrate the effect of the turbulent atmosphere on the on-axis average intensity of the GSBB, some numerical simulations are performed in this paper using the above analytical result established in Eq. (17). In our numerical analysis, the following parameters are used: m = 1, a = 0.05 m, \(z_{0} = 2\;{\text{m,}}\) \(\omega_{0} = 0.05\,{\text{m}}\) and the axicon parameters are n 0  = 1.48 and \(\gamma = 1. 3 5^{ \circ } .\)

Figure 3A, B show the variation of the on-axis average intensity with propagation distance L of the GSBB for two topological charge orders of the helical axicon p = 1 and 3, at three values of \(l = 1,\,\,3\,\,{\text{and}}\,\,5,\) in each of which several curves are plotted for three values of the turbulent strength \(C_{n}^{2} = 1 \times 10^{ - 15} ,\;5 \times 10^{ - 15} \;{\text{and}}\;1 \times 10^{ - 14} \;{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\) and \(\lambda = 1060\,{\text{nm}} .\)

Fig. 3
figure 3

Plots of the on-axis average intensity versus propagation distance L of the GSBB with \(\lambda = 1060\,{\text{nm}}\) and three values of C 2 n for A p = 1 at (a) l = 1, (b) l = 3, and (c) l = 5; B p = 3 at (a) l = 1, (b) l = 3, and (c) l = 5

Full size image

We illustrate in Fig. 3A(a), the variation of the on-axis average intensity with propagation distance L of the GSBB when p = l = 1. One can note that, for each value of the turbulent strength, the average intensity first increases and reaches at maximum value, then it decreases with increasing the propagation distance L. Figure 3A(b) and (c) are similar to that in Fig. 3A(a), but here for l = 3 and 5, respectively. From these plots, it’s shown that, when l increases, the axial intensity is equal to zero within the first several hundred meters of the near field. As can be seen that the axial average intensity decreases with increasing l [see Fig. 3A(b) and (c)]. We illustrate also in Fig. 3B the variation of on-axis average intensity with propagation distance L of the GSBB for p = 3. From these plots, it can be seen that, the variation of the average intensity is more similar that in Fig. 3A but in these illustrations, the axial intensity distribution decreases with p increasing. However, from Fig. 3, we can clearly see that the axial intensity distribution keeps a similar shape profile for all turbulent strengths. We also observe that, the on-axis average intensity increases with increasing the turbulent strength \(C_{n}^{2}\) but it decreases when the topological charge increases. Furthermore, it’s shown that the axial intensity disappears and the propagation is shorter when the atmosphere is very turbulent and the topological charge is smaller.

Figure 4A, B display the on-axis average intensity of the GSBB through a turbulent atmosphere for two values of p = 1 and 3, respectively at three values of l = 1, 3 and 5.

Fig. 4
figure 4

Plots of the on-axis average intensity versus propagation distance L of the GSBB with \(C_{n}^{2} = 1 \times 10^{ - 14} \,{\text{m}}^{ - 2/3}\) and three values of λ for A p = 1 at (a) l = 1, (b) l = 3, and (c) l = 5; B p = 3 at (a) l = 1, (b) l = 3, and (c) l = 5

Full size image

For each value of l, three curves are plotted for different wavelength values λ = 632.8, 810 and 1060 nm and the turbulent strength is \(C_{n}^{2} = 1 \times 10^{ - 14} \,{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\). From Fig. 4A(a), it can be seen that when p = l are equal to one, the axial average intensity decreases with increasing the wavelength λ.

Form Figs. 4A(b)–(c), we can note that, when l (=3 and 5), respectively, the obtained results are similar to that in Fig. 4A(a) but in this plot the axial average intensity and its maximum decreases with l increasing. In Fig. 4B, for p is equal to three, one can also note that the curves are more similar to that in Fig. 4A, but in this figure the axial intensity of the GSBB decreases as p increasing. However, from Fig. 4, it’s shown that the axial intensity decreases with λ and p become larger. Furthermore, it’s also observed from the plots that, the axial intensity of the GSBB vanishes rapidly and the propagation of the beam becomes shorter when the wavelength and the topological charge are smaller.

In Fig. 5, we illustrate the on-axis average intensity of the GSBB versus the propagation distance L for \(\lambda = 1060\,{\text{nm}}\), \(C_{n}^{2} = 1 \times 10^{ - 14} \,{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\) and \(a = 0.05\,{\text{m}}\) with two values of p = 1 and 3, at three values of l = 1, 3 and 5. For each value of l, three curves of ω 0 = 0.05, 0.06 and 0.08 m are plotted.

Fig. 5
figure 5

Plots of the on-axis average intensity versus propagation distance L of the GSBB with λ = 1060 nm and three values of ω 0 for A p = 1 at (a) l = 1, (b) l = 3 and (c) l = 5; B p = 3 at (a) l = 1, (b) l = 3 and (c) l = 5

Full size image

Figure 5A shows that the variation of the axial intensity of the GSBB when p is equal to one and different values of l and ω 0. We can see from these plots that the on-axis average intensity decreases when increasing ω 0 and l, respectively.

Figure 5B also illustrates the variation of the axial intensity when the value of p is equal to three. One can observe that the obtained result is more similar to that in Fig. 5A but the axial intensity decreases with p becomes larger. However, it’s also observed from the plots that the propagation of the considered beam becomes shorter when the waist beam and the topological charge are smaller.

6 Conclusion

The propagation characteristics of the GSBB, created by illuminating a CFH with a LGB after through a turbulent atmosphere, are investigated in this paper. Analytical expression for the average intensity of the GSBB propagating in atmospheric turbulence is obtained by using the extended Huygens–Fresnel integral formula in the paraxial approximation, by means of the Rytov method and with the help of the expression of a hard aperture function into a finite sum of complex Gaussian functions. The obtained results of the variation of the axial intensity distribution in the longitudinal direction have been performed with detailed numerical calculations. The influences of some factors as the topological charge, the wavelength, the turbulent strength and the beam waist are illustrated in this investigation.