1 Introduction

Using titanium alloys in additive technologies has a long and successful history. But in layer-by-layer selective laser melting (SLM) and 3D laser cladding of titanium incontrollable growth of grains occurs quite frequently, that worsens the quality of the items. Microscopic structural patterns such as grain boundaries, dislocations, and voids bring additional uncertainty and have significant effects on macroscopic material properties. Attempts to solve this problem demand a lot of time to find optimal regimes and a great consumption of expensive powders and machine time of the SLM installation. So modeling thermal and kinetic processes is of interest, for these simulations may reduce experimental costs and material production time by avoiding trials and errors.

During SLM and 3D laser cladding the process of accelerated redistribution of alloying elements (AE) takes place in the melting pool under the laser influence (LI). AE may be part of the titanium matrix from the start (as in the Ti6Al4V alloy), or be added into the powder composition (as reinforced TiC is being brought into titanium) for hardening. After high-speed solidification a broad spectrum of heterogeneous solid solutions can be obtained, and the spectrum often differs from the equilibrium phase diagram (EPD) for TiC system. It is the most interesting property of making the titanium matrix composites (TMC) through the SLM due to high cooling velocities possibility of AE retention in the titanium matrix. Depth of the melting bath after the LI varies from hundreds of micrometers for the SLM in a powder layer to several mm for the 3D laser cladding that depends on the volume of the melted powder and the LI parameters. Mainly structural state of the phases and their combination after the SLM will subsequently determine mechanical properties of the solidified layers. The properties will also depend on: the AE quantity brought into the matrix, the grade of mutual solubility of the alloying and alloyed elements in both solid and liquid phases, the AE diffuse mobility in these phases and on the liquid–solid phase boundary, the ways of crossing this boundary, velocity of its movement during the melt crystallization (i.e. from laser cooling rate), the ways of diffusion in the solid phase and so on. The TiC or TiBx precipitation strengthened Ti-base matrix is extremely accompanied by high susceptibility to cracking during laser layerwise melting and post-process thermal residual stresses (Shishkovsky and Scherbakov 2016; Shishkovsky et al. 2016). In our opinion, additional heating during of the SLM process can activate transient liquid phase (TLP) bonding, also known as an attractive alternate technique for joining the difficult-to-clad nickel superalloys and other structural alloys (Ghoneim and Ojo 2011; Li and Agyakwa 2010; Illingworth et al. 2005). In the TLP approach an interlayer material contains melting-point depressing solute and is sandwiched between two layers melts at the high temperature and rapidly attains equilibrium through liquid phase dissolution of the base-material into the molten interlayer alloy.

The theoretical model of the TiC redistribution in the titanium matrix during the SLM can clarify the mechanism of these processes and facilitate the optimization of the SLM regimes. Evidently, of the greatest interest is the process of accelerated crystallization of the alloyed melt, for the finite state of the material after the SLM is crucial. At the same time we assume, that in the melting bath the AE redistribution has already happened and all the phases that have not dissolved during the LI (major particles of the carbide phase, the phases with higher melting temperatures—T m (TiC) = 3140 °C in comparison with T m (Ti) = 1668 °C) are being incorporated in the solid phase right in the same state they had in the melt. And the first studies (Poate et al. 1983; Change and Mazumder 1985) have shown that the LI time of ~0.1 to 1 ms is enough for effective intermixing of the AE in the liquid pool due to existence of convective flows in them, because typical convective velocities are about ~1 to 10 m/s. Dynamics of the melt and the AE migration near the boundary have already been analyzed in many researches (Ghoneim and Ojo 2011; Li and Agyakwa 2010; Illingworth et al. 2005; Rukalin et al. 1988; Gladush and Smurov 2011). The problem of diffuse redistribution of the AE (carbon) in the solid phase under LI without fusion has also been solved before (Shishkovskii et al. 1991). Conjugation of the thermal and the diffusion problems with the equation of mechanical equilibrium (Shishkovskii 1991) has revealed the importance of carbon diffusion in the type of stress (and also the residual ones) distribution under the LI.

Within the framework of the aforesaid, this research attempts to formulate the model of thermo-kinetic and diffusion processes of the AE redistribution on the final stage of the SLM process with additional heating of powder volume in the chamber of synthesis, e.g. during the accelerated cooling of the melted bath, as well as the processes at the crystallization boundary and in the titanium matrix during its cooling. The approaches of the TLP technique and the AE laser diffusion (Ghoneim and Ojo 2011; Li and Agyakwa 2010; Illingworth et al. 2005; Shishkovskii et al. 1991; Shishkovskii 1991; Shishkovsky 2010) are going to be the starting point for the presented aim.

2 Modeling of physical process

For certainty we will assume the alloy material to be binary (the Ti–C system) and the AE to be carbon, for alloying with this element is a widely known case with sufficient data of experimental analysis. It is also reasonable to take for the finite cooling stage that as initial data we have the temperatures of the melted bath zone by the ending of LI—T(x i , t), while the quantity of undissolved TiC is equal to its initial quantity in the powder mixture. But if the TiC has submicron or/and nano size (~40 to 60 nm, cubic) and its quantity in the powder mixture is <5 to 15 mass%, calling the system a solid solution of carbon in a titanium matrix seems more reasonable (Shishkovsky and Scherbakov 2016). The scheme of the layerwise SLM process for the TMC based on Ti–TiB (for Ti–TiC it was similar) system is described in details in the study (Shishkovsky et al. 2016). Below for simulation we will use one of optimal regimes for the layerwise SLM (Shishkovsky and Scherbakov 2016) which is being realized with the LI power 100 W, scan velocity of 0.12 m/s, beam diameter—70 μm, layer thickness H ~ 0.2 mm. The additional heating of the powder volume and substrate up to 200 °C in the synthesis chamber increases the heat affected zone under the melted pool and efficiency of diffusion processes and decreases the susceptibility to cracking (Shishkovsky and Scherbakov 2016; Shishkovsky et al. 2016).

2.1 The thermal problem

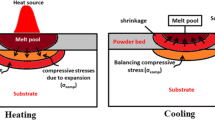
Let the thermal flow fall on the semi-infinite surface of the powder and be absorbed by the volume (Fig. 1). We also take the absorbed energy as leading to heating of the surface but no more than the titanium boiling temperature—T b . Than the heat loss due to convection and radiation may be neglected in comparison with the value of absorbed laser power density—Q. After heating the surface up to the melting temperature—T m the melted bath is being fabricated and the boundary between the liquid and solid phases moves into the depth of the material, while the external melted surface remains flat and fixed. Moreover, after the melt temperature is achieved, the nature of LI absorption changes from volume to surface heating source (Ghoneim and Ojo 2011; Li and Agyakwa 2010). At the first approximation, we will consider that thermal transfer is realized by means of heat-conduction process only. The latent heat of phase transformation is being absorbed and/or released—L m —on the melting front moving into depth depending of temperature changing.

Fig. 1
figure 1

The scheme of physical processes and the TLP approach

Full size image

We studied the laser scanning happening strictly in the given direction on the surface of powdered mixture with constant velocity—V, laser beam diameter—d b and the LI power—P. The model was formulated mathematically on a two-dimensional semi-infinite space. Moreover positive direction of Ox axis complied with the direction of the laser scanning movement (Fig. 1).

$$c\rho \frac{\partial T}{\partial t} = \lambda \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + Q_{1} \pm \rho L_{m} \frac{\partial s}{\partial t},$$
(1)

Initial and boundary conditions were following:

$$\begin{aligned} & \left. {\frac{\partial T}{\partial z}} \right|_{z = 0} = \{ 0\,if\,T < T_{m} \quad or\quad Q_{m} \,if\,T \ge T_{m} \} ,\quad T(t,x = + \infty ) = T_{0} , \\ & \left. {\frac{\partial T}{\partial x}} \right|_{x \to \pm \infty } = 0,\quad T(0,x,z) = T_{0} \\ \end{aligned}$$
(2)

where T 0—initial titanium temperature was equal 200 °C account of additional thermal heating of SLM process chamber, s(t, z, x)—depth and shape of isotherm with Tm (=1668 °C), L m —latent heat of melting, c—thermal capacity, λ—heat conductivity, ρ—density. For simplification of the formal part of the model we have taken that ρ, c and λ of the powder mixture do not change with heating during whole SLM process. Under heating (second volume part in Eq. 1) the latent heat absorption is being observed (minus sign), and under cooling the L m is being released (plus sign). Obviously, during the cooling process laser source is absent (Q 1 = Q m  = 0).

As it was noted above, according to the experimental data given in Shishkovsky (2002), for porous systems which are of the greatest interest, the heat release from the LI occurs in the volume, decreasing with increase of distance from the surface (i.e. in the positive direction to Ox axis) by the exponential law.

$$Q_{1} (t,x,z) = Q_{m} \exp \left( { - 4\left( {\frac{x - Vt}{{d_{L} }}} \right)^{2} } \right)\exp \left( { - \frac{z}{{\alpha_{L} }}} \right),$$
(3)

where α L —coefficient of volume absorption, Q m is maximum power density of the LI in the center which is determined by equation:

$$Q_{m} = \frac{4P}{{\pi \alpha_{L} d_{L}^{2} }}.$$
(4)

We will connect the system of coordinates with the centre of the LI beam by introducing a new variable parameter p = x − Vt. After combining (1, 3–4) we get:

$$\begin{aligned} c\rho \frac{\partial T}{\partial t} - c\rho V\frac{\partial T}{\partial p} & = \lambda \left( {\frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{{\partial^{2} T}}{{\partial p^{2} }}} \right) \\ & \quad + Q_{m} \exp \left( { - \left( {2\frac{p}{{d_{L} }}} \right)^{2} } \right)\exp \left( { - \frac{z}{{\alpha_{L} }}} \right) \pm \rho L\frac{\partial s}{\partial t}. \\ \end{aligned}$$
(5)

Now we insert the dimensionless variables in (5):

figure a

And then transform Eq. (5) to the following form:

$$\frac{\partial \theta }{\partial \tau } - V\frac{\partial \theta }{\partial \xi } = \frac{{\partial^{2} \theta }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \theta }}{{\partial \varsigma^{2} }} + q_{m} \exp \left( { - \left( {2\frac{\xi }{{d_{b} }}} \right)^{2} } \right)\exp \left( { - \frac{\varsigma }{{\alpha_{l} }}} \right) \pm \frac{{L_{m} }}{c}\frac{\partial s}{\partial \tau }$$
(6)

With initial and boundary conditions:

$$\begin{aligned} &\left. {\frac{\partial \theta}{\partial \varsigma}} \right|_{\varsigma = 0} = 0\quad if\,T < T_{m} \,of\,q_{m} \exp \left({- \left({2\frac{\xi}{{d_{b}}}} \right)^{2}} \right)\quad if\,T \ge T_{m},\quad \theta \left({\tau,\xi, + \infty} \right) = \theta_{0}, \hfill \\ &\left. {\frac{\partial \theta}{\partial \xi}} \right|_{\xi \to \pm \infty} = 0,\quad \theta (0,\xi,\varsigma) = \theta_{0}. \hfill \\ \end{aligned}$$
(7)

The equation set of (6–7) was solved by using different schemes known as the alternating direction approach using the sweep method. One of the main parts of the analysis of the proposed model is to examine the problem of interdependence between the LI scan velocity and the melted pool depth of the single layer passage in the powder mixture immediately behind the laser beam movement. From a practical point of view, it is of importance to calculate the melted bath volume (depth and width) when carrying out the SLM. Example of such simulation is presented in Fig. 2.

Fig. 2
figure 2

Simulated temperature distribution in Ti + 15 wt% TiC powder mixture

Full size image

The shape of the T m isotherm—s(t, z, x) could be determined by a method of successive approximations from solution of transcendental equation (Rukalin et al. 1988; Gladush and Smurov 2011). For instance, its first approximation on stage of the heating (1) can be presented next:

$$s(\zeta ,0) = s(t,0)\frac{{\zeta - t_{1} }}{{t - t_{1} }},\quad t_{2} \le t.$$
(8)

where t 1—a moment melting beginning on surface, t 2 = Δt.

2.2 Kinetic of crystallization process

Process of high speed crystallization of the melt and kinetic of the front movement for phase transformation was analyzed in detail in the literature (Chrisian 1975). If a process of rapid transformation of first order is interpreted classically i.e. realized by means of thermo-fluctuating or atomic transitions on the boundary cross-section of phases for a new atom arrangement so the velocity of new solid phase growing (melt solidification)—u is described as:

$$\frac{\partial r}{\partial t} = a\nu \exp \left( { - \frac{U}{kT(t)}} \right)\left[ {1 - \exp \left( { - \frac{\Delta F}{kT(t)}} \right)} \right],$$
(9)

whereν—characteristic Debye frequency, U—the activation energy of the atom transition through the interphase boundary section, ΔF—changing of specific free energy at appearance of new phase nucleus (usually it is limited by volume ΔF v  = L m  × [T m  − T(t)]/T(t) and surface ΔF s  = ϕσ × n 2/3 parts of the thermodynamic potential, where a—lattice parameter).

However, if the cooling speed is very high so the atoms mobility becomes insufficient to realize their rearrangement from the chaotic layout in liquids into the well-ordered one in crystals (Shishkovsky 2010). Therefore the material structure is getting amorphous. In paper (Shishkovsky 2010) the analytical solution of Fokker–Planck kinetic equation for distribution function of the particles number (DFPN)—Z(n, t) was proposed and was shown that crystallization behavior under high-speed cooling is characterized by cluster approach with number of particles in cluster from some dozens up to some 100s depending of the cooling speed v T  = ∂T/∂t and thermodynamical properties of material. At present study we will use solution (Shishkovsky 2010) for the DFPN—Z(n, t):

$$Z(\alpha ,\beta ,n) = \sqrt {\frac{n}{\alpha }} \times \int\limits_{0}^{\infty } {d\xi Z_{in} \left( {\xi^{2} e^{\beta } /4} \right)\exp \left( { - \frac{{4n + \xi^{2} }}{4\alpha }} \right) \times I_{1} \left( {\xi \frac{\sqrt n }{\alpha }} \right),}$$
(10)

where I 1—is modified Bessel function of the I order, α and β—are the task parameters:

$$\begin{aligned} & \alpha (t) = \nu \exp ( - \beta (t)) \times \int\limits_{0}^{t} {\exp \left( {\beta (\tau ) - \frac{U}{kT(\tau )}} \right)} d\tau , \\ & \beta (t) = - \frac{\Delta h\nu }{{kT_{{ .^{\prime } }} }} \times \int\limits_{0}^{t} {\frac{{T_{{ .^{\prime } }} - T(\tau )}}{T(\tau )}\exp \left( { - \frac{U}{kT(\tau )}} \right)} d\tau . \\ \end{aligned}$$
(11)

Then the relative volume of the new crystalline phase can be defined as:

$$\frac{\Delta V}{V} = 1 - \exp (\beta (t)),$$
(12)

and the average number of particles in crystalline grain can also be found explicitly

$$\langle n\rangle = \frac{3\alpha (t)}{2} \times \left[ {\alpha (t) - 1 - \frac{1}{\alpha (t)}\ln \left( {1 - \frac{\alpha (t)}{3}} \right)} \right].$$
(13)

In (Shishkovsky 2010) the asymptotical character of α and β under t → ∞ was studied only for the simplest cooling laws (linear and/or exponential equations). Here is, knowledge of thermal transfer solution (1–2) allows determining the crystalline grain size (13) and the relative volume of the new crystalline phase (12) to estimate exactly. Figure 3 shows just one option of such simulation.

Fig. 3
figure 3

Estimated velocity of grain size growth u(t) (right) and T(t) (left) after the SLM on the solidification stage. T m (Ti) = 1668 °C

Full size image

It is important to remark that the above proposed approach is traditional for the phase transformations of the first order and significantly different from widespread deterministic phase-field and stochastic cellular automaton methods which are usually applied to simulate dendrite growth during laser solidification (Yin and Felicelli 2010; Krivilyov and Mesarovic 2016; Natsume et al. 2003) and based on the Ginsburg–Landau approach for phase transformation of second order.

2.3 TLP diffusion bonding with moving boundary

Knowledge of thermal fields T(t, z, x) in liquid and solid phases, velocities of movement of phase transition front (L → S) s(t, z, x), volume and crystallizing phase size—allows providing a mathematically adequate description of carbon diffusion redistributions process under high speed cooling from the melted bath in the SLM process. It is necessary to take into account that on the moving boundary L → S phases stepwise change of the AE concentration occurs: k e  = C S /C L , where k e —is equilibrium segregation coefficient (eutectic factor), C S —the AE concentration defined by the EPD (Fig. 4) on solidus line, C L —on liquidus line (Shishkovsky and Scherbakov 2016; Aziz 1982, 1988). In conditions close to equilibrium, the concentration of soluble atoms in the solid state can not exceed maximum solubility in the solid phase, so presence of concentration additives, more equilibrium after the LI in the laser affected zone points to dominate significance of kinetic effects on the interface boundary (9, 12–13). Phase transformation is accompanied not only by reducing the specific free system energy ΔF (L→S), the latent heat release, but also with reducing of atom’s volume in the concentration space (Poate et al. 1983; Shishkovsky 2010). This process is to be distinguished from usual diffusion and is described by specific set of equations (Poate et al. 1983; Aziz 1982, 1988), for instance: in the Hillert model (works for high-speed velocities of phase transition of front movement, but does not work for low velocities), Baker and Cahn thermodynamic approach (Aziz 1982), Wood model (is based on kinetic equations suggesting more “thick” boundary zone), Jeckson and Aziz kinetic models (Aziz 1988). Let us indicate the main conclusions of this models without going into detail. For incremental moving of the phase transition front the kinetic factor dependency from front movement velocity (L → S) is to be represented as:

$$k(v) = k_{e} + (1 - k_{e} ) \times \exp \left( { - \frac{{v_{D} }}{u}} \right),$$
(14a)

where v D  = D L /a[~1 to 30 m/s (Aziz 1988), D L —diffusion coefficient for the AE in liquid phase, a—size the transformation zone (~comparable with lattice parameter). In the model of continuous front movement (L → S):

$$k(v) = \frac{{u/v_{D} + k_{e} }}{{u/v{}_{D} + 1}}.$$
(14b)
Fig. 4
figure 4

Equilibrium phase diagram in Ti–C system with percentage of the TiC nano particle additive by Shishkovsky and Scherbakov (2016)

Full size image

In Baker and Cahn model (Aziz 1982):

$$k(v) = \frac{{u/v_{D} + \ln (k_{e} )}}{{u/v{}_{D} + 1/k_{e} \times \ln (k_{e} )\exp ( - u/v_{D} )}}.$$
(14c)

Below the TPL approach was used and we have taken the laser melted region (Fig. 1), where axes are accorded to thermal task in the Sect. 2.1. According to previous models (Ghoneim and Ojo 2011; Li and Agyakwa 2010; Illingworth et al. 2005), the one-dimensional diffusion-controlled, two-phase and moving interface problem is considered. For the change of molar volume—m of the solute in the matrix phases to be further taken into account, the governing equations are given in terms of mass fraction by:

$$\begin{aligned} & \frac{\partial \rho (z,t)m(z,t)}{\partial t} = \frac{\partial }{\partial z}\left( {D_{l} (T)\frac{\partial \rho (z,t)m(z,t)}{\partial z}} \right),\quad 0 < z < s(t) \\ & \frac{\partial \rho (z,t)m(z,t)}{\partial t} = \frac{\partial }{\partial z}\left( {D_{s} (T)\frac{\partial \rho (z,t)m(z,t)}{\partial z}} \right),\quad s(t) < z < H \\ & \left. {D_{l} (T)\frac{\partial \rho (z,t)m(z,t)}{\partial z}} \right|_{{z = s(t)^{ - } }} + \,\left. {D_{s} (T)\frac{\partial \rho (z,t)m(z,t)}{\partial z}} \right|_{{z = s(t)^{ + } }} \\ & \quad = \left[ {\rho_{l} (z,t)m_{l} (z,t) - \rho_{s} (z,t)m_{s} (z,t)} \right]\frac{\partial s(t)}{\partial t},\quad z = s(t) \\ \end{aligned}$$
(15)

They are subject to the following boundary conditions:

$$\begin{aligned} & \frac{\partial \rho (z,t)m(z,t)}{\partial z} = 0,\quad z = 0 \\ & \frac{\partial \rho (z,t)m(z,t)}{\partial z} = 0,\quad z = H \\ \end{aligned}$$
(16a)

And the initial conditions can be given according the EPD for Ti–C system (Fig. 4) as carbon concentration in the liquid phase—C L (t, z, x) and in the solid phase—C S (t, z, x):

$$\begin{aligned} & \rho (z,0)m(z,0) = \rho_{l0} m_{l0} ,\quad 0 \le z \le s(0) \\ & \rho (z,0)m(z,0) = \rho_{s0} m_{s0} ,\quad s(0) \le z \le H \\ \end{aligned}$$
(16b)

Equations (15, 16) describe redistribution of carbon in the zones close to interface of both solid and liquid phases (i = L, S) and at the boundary itself. The numerical model was implemented and optimized the in efficient code in the C programming language (Illingworth et al. 2005). The code is freely available to download from the Materials Algorithm Project web-site: http://www.msm.cam.ac.uk/MAP. In future, we are planning to use another difference (C S  − C L ) in (15) on the front of the phase transition may be represented as C L  × [k(u) − 1], where k(u) was determined at (14a–14c). Choosing a special type of k(u) allows realizing different situations at the (L → S) front, when the borderline (1) retains the AE in the melt and leads to its excess on the surface, (2) forms an equilibrium redistribution (3) leads to precipitation of the AE into the second phase.

For depending on stoichiometry of titanium carbide TiC 1−y (y = 0…0.5) the value of carbon diffusion coefficient is to be represented as Dk = 0.48 × e0.92y × exp(−39,500/T) (Van Loo and Bastin 1989). So under temperature of Ti melting diffusion coefficient of carbon in titanium will be DC ~ 4.8 × 10−5 cm2/s and carbon in TiC will be DTiC ~ 7.2 × 10−10 cm2/s. For Ti–TiC mixture with 15 vol% TiC—the carbon concentration with near 30% a.i (see Fig. 4). Estimated time of the LI for the layer thickness H ~ 0.2 mm will be 1.67 ms. In Fig. 5, the half width of the liquid layer is plotted as a function of time for a Ti–C interlayer between pure Ti plates. The behavior of the TLP predicted by the theoretical model (15–16) is in accordance with our qualitative understanding of the process.

Fig. 5
figure 5

Predicted evolution of liquid layer half-width versus interlayer joining time in frameworks of the TLP approach for Ti/Ti–C system

Full size image

As it has been mentioned before, part of submicron and nano-size titanium carbides will fully dissolve in the melt during the LI time, and the other part will decrease in size and release part of its carbon into the melt. Figure 6 show the SEM micrographs of the SLM process in Ti–TiC powder mixture (Shishkovsky and Scherbakov 2016). The microstructure takes into account the free residual and coagulated TiC particles and solidified Ti based dendrite microstructure. Then, after crossing the phases interface, titanium carbides not yet dissolved are going to be “pressed” into the solid phase, changing the shape of its surfaces (t, z, x) and making additional channels for carbon diffusing from liquid to solid phase.

Fig. 6
figure 6

Scan electron microscopy of the 3D part after the SLM of Ti + nano TiC multilayer system on Ar in the bottom layers ~0.2 mm from the substrate

Full size image

3 Conclusion

At the present paper, the continuous theoretical model describing the behaviors of Ti + TiC porous powdered mixture at high-speed laser cooling, observing a separate monolayer after the SLM process was proposed on the base of earlier known approaches. Numerical simulation allows simultaneously describing liquid to solid-state solute diffusion with randomly distributed multiple TiC particles and their laser melting in the titanium based matrix. The model estimates that complete melting of the TiC nano particles can occur during the SLM, depending on the composition of the materials mixed and process variables. These include TiC size, temperature distribution and kinetic parameters.

The possibility to control the multilayer structure by changing the powder composition can expand the range of the functional 3D part’s application for the TMC reinforced by the TiC in aerospace and automotive industries.