1 Introduction

High harmonic generation (HHG) is a highly nonlinear and non-perturbative optical process that occurs when an intense femtosecond laser pulse interacts with a rare gas. Many characteristics of the high-harmonic radiation make it an ideal way for generating bright, coherent, ultrashort pulses that allow time-resolved studies on an unprecedentedly short time scale. Moreover, HHG provides an important tool for probing the ultrafast electronic dynamics in atoms (Kienberger et al. 2002; Uiberacker et al. 2007; Li et al. 2015; He et al. 2015) and tomographic imaging of molecular orbitals (Itatani et al. 2004; Lein 2007; Zhu et al. 2012; Zhai et al. 2016), etc. The HHG process can be well depicted in terms of the semiclassical three-step model (Corkum 1993; Zhu et al. 2015): tunnel ionization, acceleration, and recombination of the electrons in the intense laser field. According to the three-step process, a linearly polarized light simply defines an axis. By contrast, a circularly polarized light defines an orientation of space and is thus a unique probe of chiral matter. In previous works, High harmonics are generated in rare gases using linearly polarized laser field, yielding linearly polarized extreme ultraviolet (XUV) pulse, parallel to the driving fields polarization (Paul et al. 2001; Lan et al. 2007; Luo et al. 2012; Cao et al. 2006, 2007; Zhang et al. 2008). However, there are many difficulties to extending this scheme from linear polarization to circular polarization (Goulielmakis et al. 2008; Zhu et al. 2012).

Recently, circularly polarized radiation in the extreme ultraviolet (EUV) and soft X-ray spectral regions has proven to be very useful for investigating chirality-sensitive light-matter interaction, such as chiral recognition via photoelectron dichroism (Hergenhahn et al. 2004; Böwering et al. 2001; Powis and Chem 2000), study of ultrafast chiral-specific dynamics in molecules (Ferré et al. 2014; Travnikova et al. 2010), and time-resolved imaging of magnetic structures (Radu et al. 2011; Qin et al. 2016; Boeglin et al. 2010; Eisebitt et al. 2004; Fischer et al. 1999; López-Flores et al. 2012). By using three-step model, it is shown that the recollision is not possible with single circular pulses (Zuo and Bandrauk 1995), but achieved automatically with bichromatic circular pulses (Bandrauk and Lu 2003; Reich and Madsen 2016; Mauger et al. 2016). An elegant solution has been proposed to generate individual high harmonic with circular polarization, which relies on a counter-rotating bicircular field with the frequency ratio of 1:2 (800 + 400nm) (Milošević et al. 2000; Milošević and Becker 2000; Eichmann et al. 1995; Long et al. 1995). By invoking the conservation laws, a symmetry analysis shows that the allowed harmonics \(3q+1\) are right-circularly polarized (RCP), whereas the \(3q+2\) harmonics are left-circularly polarized (LCP), and the 3q harmonics are forbidden (Eichmann et al. 1995; Long et al. 1995; Fleischer et al. 2014; Kfir et al. 2014; Alon et al. 1998; Mauger et al. 2014; Milošević 2015). However, the intensities of the LCP and RCP components of HHG are nearly equal. By synthesizing the LCP and RCP components, attosecond pulses with linear rather than circular polarization are generated. To overcome this problem, schemes based on a Ne atom with the 2p initial state are proposed to generate elliptically polarized attosecond pulse trains (Milošević 2015) and even isolated attosecond pulses (Medi et al. 2015), but the ellipticity is less than 0.4. Besides the polarization, the intensity is also an important aspect of the attosecond pulses in many applications, e.g. studies of chiral molecules using photoelectron circular dichroism, and ultrafast molecular decay dynamics (Zhou et al. 2016).

In this paper, we theoretically demonstrate a scheme for efficient generation of highly elliptically polarized attosecond pulses. We use a counter-rotating bicircular field with the frequency ratio of 1:3 (800 + 267nm) and 1:4 (1600 + 400nm). By resolving the time-dependent Schrödinger equation, it is shown that the HHG yield increases with increasing the frequency ratio of bicircular fields. By synthesizing a series of high harmonics, attosecond pulses with ellipticity of 0.54 (800 + 267nm) and 0.79 (1600 + 400nm) can be generated, respectively. These values are much higher than the ellipticity of 0.3 with the frequency ratio of 1:2. The analysis shows that the high ellipticity mainly originates from the symmetry of the electric field. Moreover, the frequency ratio dependence of the HHG yield is also investigated. We show that the intensity of the HHG is increased by more than one order of magnitude with increasing frequency ratio.

This paper is organized as follows. In the Sect. 2, we show the method and the parameters of the laser field used in our work. In the Sect. 3, we present the results and discussions, which are divided into three subsections. First, the generation of the high harmonics and attosecond pulses for each of the frequency ratios is investigated. Then, we explain why the ellipticity is increased with a higher frequency ratio, and elaborate on the different behavior of the harmonics below and above the ionization potential. Thereafter, we investigate the scaling law of the HHG yield. Finally, the conclusion is shown in Sect. 4.

2 Theoretical model

In our simulation, the time-dependent Schrödinger equation (TDSE) is applied to calculate HHG. We solve the TDSE in the length gauge (atomic units are used throughout unless stated otherwise) (Wang et al. 2016):

$$\begin{aligned} i\frac{\partial }{\partial t}\psi (r,t)= [\widehat{T}+V(r)+r\cdot E(t)]\psi (r,t) \end{aligned}$$
(1)

the model potential is taken from (Barth and Lein 2014; Zhu et al. 2016):

$$\begin{aligned} V(r)= -\frac{Z(r)}{\sqrt{r^{2}+a}} \end{aligned}$$
(2)

where \(Z(r)=1+e^{-r^{2}}\) and \(a=2.882\) are chosen to obtain the ionization potential of model Ne atom \(I_{p}=0.79a.u.\) for 2p orbital. The laser electric field is

$$\begin{aligned} E(t)&= E_{ir}f(t)(\cos [\omega _{1}t]+(1/\sqrt{\beta }) \cos [\omega _{2}t+\phi ])\widehat{x}\nonumber \\&+E_{ir}f(t)(\sin [\omega _{1}t] -(1/\sqrt{\beta })\sin [\omega _{2}t+\phi ])\widehat{y} \end{aligned}$$
(3)

where \(E_{ir}\) is the amplitude. \(\alpha =\omega _{2}/\omega _{1}\) and \(\beta\) are the frequency ratio and the intensity ratio of the two color fields, respectively. \(\phi\) is the relative phase between the two driving colors. The \(\omega _{1}\) field rotates counterclockwise. The \(\omega _{2}\) field rotates clockwise. In the following discussion, the intensity of the laser is taken to be \(1\times 10^{14}\,W/cm^{2}\). The duration of the laser pulse is 9 optical cycles with the trapezoidal envelope (2 cycle rising and falling edges and 5 cycle plateau). \(\beta\) is set to be 1, and \(\phi\) is set to be 0. Equation (1) is solved numerically by using the split-operator method, and the generated harmonics are calculated by the time-dependent dipole acceleration a(t), which is given by

$$\begin{aligned} a(t)= \frac{d^{2}\langle r\rangle }{dt^{2}} = -\langle \psi (t)|[H(t),[H(t),r]]|\psi (t)\rangle \end{aligned}$$
(4)

where H and \(\psi\) are the Hamiltonian and the electron wave function, respectively. The harmonic spectrum is then obtained by Fourier transforming the dipole acceleration a(t):

$$\begin{aligned} a_{q}= |\frac{1}{T}\int _{0}^{T}a(t)exp(-iq\omega t)|^{2} \end{aligned}$$
(5)

where T and \(\omega\) are the duration and the fundamental frequency of the driving pulse, respectively. And q corresponds to the harmonic order. To describe the polarization properties of the HHG, we extract the left-rotating and right-rotating components of the emitted harmonics. The ellipticity \(\varepsilon\) can be defined as

$$\begin{aligned} \varepsilon = \frac{A_{r}-A_{l}}{A_{r}+A_{l}} \end{aligned}$$
(6)

where \(A_{l}\) and \(A_{r}\) are the amplitude of the left and right polarized components of the HHG field.

3 Results and discussions

Figure 1 shows the spectra of HHG in a bicircular field with different frequency ratios. The left-circularly-polarized (LCP) and right-circularly-polarized (RCP) components are marked by black and red curves. The spectrum of HHG in the case of 800 + 400 nm (\(\alpha =2\)) is shown in Fig. 1a. One can see that the LCP component is lower than the RCP component below 20 eV. From 20 to 50 eV, the LCP component is higher than the RCP component. Beyond 50 eV the relative intensity of LCP and RCP components becomes comparable. The cutoff energy of both LCP and RCP components is around 50 eV. For comparison, Fig. 1b shows the spectrum of HHG in the case of 800 + 267 nm (\(\alpha =3\)). The result shows that the intensities of both LCP and RCP components are higher and the cutoff energy is around 40 eV. We next take a comparison of the spectra of HHG in the case of 1600 + 800 nm (\(\alpha =2\)) and 1600 + 400 nm (\(\alpha =4\)) which are shown in Fig. 1c , d. One can see that the cutoff energy increases to 150 and 80 eV, respectively. Moreover, the intensity of the HHG in the case of \(\alpha =4\) is more than one order of magnitude higher than that in the case of \(\alpha =2\).

Fig. 1
figure 1

(Color online) High harmonic spectra in the a 800 + 400 nm, b 800 + 267 nm, c 1600 + 800 nm and d 1600 + 800 nm bicircular field. Black (dash) and red (solid) curves show the LCP and RCP components of the high harmonics

Full size image

In order to get a more intuitive insight into the results, we analyze the sub-cycle dynamics of the emission process by using the Gabor transform (GT) (Chirilă et al. 2010) of the time-dependent acceleration dipoles a(t). The spectrograms in Fig. 2 show the time-frequency intensity (the first row) and ellipticity (the second row). Only HHG in one optical cycle is shown. The dashed lines mark the ionization energy Ip. The results for the case of 800 + 400 nm (\(\alpha =2\)) are shown in Fig. 2a. One can see three different regions: (1) below 20 eV the ellipticity is positive; (2) from 20 to 40 eV, the ellipticity is negative; (3) beyond 40 eV the ellipticity slowly turns to positive. Moreover, three pulses can be seen in one optical cycle. In the case of 800 + 267 nm (\(\alpha =3\)) shown in Fig. 2b, the ellipticity can also be divided into three regions, but the intensity of the HHG is higher. We next take a comparison of the case of 1600 + 800 nm (\(\alpha =2\)) and 1600 + 400 nm (\(\alpha =4\)), which are shown in Fig. 2c, d. One can see that the ellipticity and the intensity of the emission in the case of \(\alpha =4\) are obviously higher in the region from 20 to 45 eV.

Fig. 2
figure 2

(Color online) Time-resolved HHG intensity and ellipticity from the a 800 + 400 nm, b 800 + 267 nm, c 1600 + 800 nm, and d 1600 + 400 nm bicircular field. The horizontal dashed lines mark Ip

Full size image

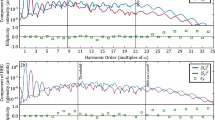
For quantitative analysis, we show the average intensity and ellipticity of the emissions in Fig. 3. The average intensity and ellipticity are obtained from the time integration of the data in Fig.2. The first row shows the average intensity of the spectrum versus the photon energy. The second row shows the average ellipticity of the spectrum versus the photon energy. By comparing the case of 800 + 400 nm (\(\alpha =2\)) and 800 + 267 nm (\(\alpha =3\)), one can see that the intensity of HHG in the case of \(\alpha =3\) is increased by about 3-times and the corresponding ellipticity is increased from 0.30 to 0.54. The ellipticity in the case of \(\alpha =3\) keeps high in the region from 20 to 40 eV. By comparing the case of 1600 + 800 nm (\(\alpha =2\)) and 1600 + 400 nm (\(\alpha =4\)), one can see that the intensity of HHG in the case of \(\alpha =4\) is increased by about 30-times and the corresponding ellipticity is increased from 0.32 to 0.79. The ellipticity in the case of \(\alpha =4\) keeps high in the region from 20 to 45 eV.

Fig. 3
figure 3

(Color online) The average HHG intensity and ellipticity of the spectra shown in Fig. 2

Full size image

By synthesizing high harmonics from 20 to 40 eV, elliptically polarized attosecond pulse trains can be generated. We show the results for the bicircular fields with different frequency ratios in Fig. 4. One can see that the intensity of the attosecond pulses is increased in a bicircular field with higher frequency ratio. To obtain the polarization of the attosecond pulses, we show the electric-vector of the attosecond pulses in Fig. 5. In the case of \(\alpha =2\), \(\alpha =3\) and \(\alpha =4\), the electric fields of the attosecond pulses show the threefold, fourfold and fivefold star-like structure, respectively, which have the same symmetry as the driving fields. Every petal of the star-like structure is elliptical, corresponding to one pulse of the attosecond pulses train.

Fig. 4
figure 4

(Color online) Temporal profiles of the attosecond pulses by synthesizing high harmonics from 20 to 40 eV

Full size image
Fig. 5
figure 5

(Color online) Electric vector of the attosecond pulses shown in Fig. 4. The red line marks one petal of the star-like structure

Full size image

Why is the ellipticity of HHG increased in the case of \(\alpha =3\) and \(\alpha =4\) (800 + 267 nm and 1600 + 400 nm)? As is known, the ellipticity of the laser field is defined as:

$$\begin{aligned} \varepsilon = \frac{A_{r}-A_{l}}{A_{r}+A_{l}}\sim \frac{\sqrt{P +2\sin \Delta \varphi }-\sqrt{P-2\sin \Delta \varphi }}{\sqrt{P+2\sin \Delta \varphi }+\sqrt{P-2\sin \Delta \varphi }} \sim \frac{2\sin \Delta \varphi }{P} \end{aligned}$$
(7)

where \(A_{l}\) and \(A_{r}\) are the amplitudes of the left and right polarized components of the laser field. The symmetry parameter is \(P=A_{x}/A_{y}+A_{y}/A_{x}\), where \(A_{x}\) and \(A_{y}\) are the amplitudes of the x and y polarized components of the laser field and the relative phase is \(\Delta \varphi =\varphi _{y}-\varphi _{x}\). From the classical view, the symmetry of the radiation field depends on the symmetry of the driving field. Figure 6 shows the Lissajous curves of the electric field. A star-like driving field will generate a star-like radiation (which can be seen in Fig. 5). As is denoted in Fig. 6, the symmetry parameter P of the driving fields is approximately 3.0 (\(\alpha =2\)), 2.3 (\(\alpha =3\)) and 2.2 (\(\alpha =4\)). According to Eq. (7), the ellipticity is proportional to 1 / P. Therefore, the ellipticity of HHG field is higher in the case of \(\alpha =3\) and \(\alpha =4\). From the quantum view, the spin expectation values (equivalent to the ellipticity) of the driving fields can be defined as \(=(n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2})/(n_{1}+n_{2})\), where \(n_{i}=I_{i}/\omega _{i}\) (\(i=1,2\)) are the number of photons and \(\varepsilon _{i}=\pm 1\)(\(i=1,2\)) are the spin values of the two driving colors, respectively (Fleischer et al. 2014). Then, \(\varepsilon (\alpha =2)=0.33\), \(\varepsilon (\alpha =3)=0.50\) and \(\varepsilon (\alpha =4)=0.60\) are obtained. It is worth noting that the spin angular momentum is the only sort of angular momentum present in HHG process. The conservation of angular momentum requires that the angular momentum keeps the same during the HHG process. Thats why the ellipticity of HHG field is higher in the case of \(\alpha =3\) and \(\alpha =4\).

Fig. 6
figure 6

(Color online) The Lissajous curves of the electric field amplitude. The red line marks one petal of the electron field

Full size image

The above results in Fig. 2 show different behavior of the harmonics below and above the ionization potential. To explain these results, we show the HHG obtained by the \(2p{+}\) and \(2p{-}\) initial state separately in Fig. 7 (Note that 2p orbital is the coherent superposition of \(2p{+}\) and \(2p{-}\) orbital). The LCP components and RCP components of HHG are marked by black and red curves. We first discuss the spectra of HHG in the case of 800 + 400 nm (\(\alpha =2\)). In the region below the ionization potential, the RCP components are higher than the LCP component of HHG in all initial states. To explain the behavior of the harmonics below ionization potential, we consider the perturbation theory, according to which the probability of the multi-photon process is proportional to \(I^{n}\). For a specific harmonic, the number of the absorbed photons is small for photons with high frequency. It is more probable to absorb a photon with high frequency. In our case, the driving field with high frequency is RCP. Therefore, the RCP component is higher than the LCP component of HHG below the ionization energy. In the region above the ionization potential (20–40 eV), for the \(2p{+}\) initial state, the LCP components of HHG are higher (see Fig. 7a). While for the \(2p{-}\) initial state, the RCP components of HHG are higher (Fig. 7c). This is a direct analogue result of Fano-Bethe propensity rules (Fano 1985). According to the semi-classical model, one can easily get that the initial transverse momentum for the returning electrons should be positive. This indicates that it is more probable for electrons in the \(2p{+}\) initial state to recombine with the parent ion than that in the \(2p{-}\) initial state (Milošević and Becker 2000). That is why the LCP component is higher than the RCP component of HHG above the ionization potential (20–40 eV). Similar results can be seen in Fig. 7b, d for the case of 800 + 267 nm (\(\alpha =3\)). The difference is that the intensity of both components of HHG are higher in the case of \(\alpha =3\).

Fig. 7
figure 7

(Color online) High harmonic spectra for Ne with the \(2p{+}\) initial state (a–b), and \(2p{-}\) initial state (c–d). =2 for (a), (c) and =3 for (b), (d). Black (dash) and red (solid) curves show the LCP and RCP components of the high harmonics

Full size image

Besides the ellipticity, we also investigate the frequency ratio dependence of the HHG yield in the bicircular field. To get a quantitative result, the HHG yield is calculated by averaging harmonics from 20 to 40 eV. The fundamental field is kept to 800 nm, and the frequency ratio is changed from 1.5 to 4. For a frequency ratio higher than 4, the cutoff energy will be close to 20 eV (\(\approx\)ionization energy). Therefore, the frequency ratios higher than 4 are not considered. In the bicircular case, a reasonable equivalent frequency can be defined as \(\varpi =(1+\alpha )/2 \omega _{1}\) (Yuan and Bandrauk 2015; Mauger et al. 2016). As can be seen in Fig. 8, the HHG yield follows a scaling of \(\varpi ^{3.7}\). It is increased by more than one order of magnitude in the bicircular fields with higher frequency ratios.

Fig. 8
figure 8

(Color online) Frequency scaling of HHG yield in the counter-rotating bicircular fields

Full size image

To obtain a deep insight into the scaling of the HHG yield, we analyze the electron trajectories by using the classical three-step model (Corkum 1993; Zhu et al. 2015). It is worth noting that the classical analogy of the average HHG yield is the average probability of the electrons recombined with the parent ion for individual harmonic. It can be expressed as:

$$\begin{aligned} HHG_{yield}\propto \overline{re}\propto \frac{P_{ion}\times P_{re}}{m_{HHG}}/\tau ^{3} \end{aligned}$$
(8)

where \(P_{ion}\) is the ionization rate, \(P_{re}\) is the classical recombination rate and \(m_{HHG}\) is the number of harmonics below the cutoff energy, \(\tau\) is traveling time of the electrons. The scaling of \(\tau ^{-3}\) is due to the spreading of the electron wave packet. We first consider the classical recombination rate (Lan et al. 2009). Due to the spreading of the electron wave packet, only the trajectories traveling less than one optical cycle are considered. Figure 9a shows the classical recombination rate of the electrons by accumulating all the returning trajectories weighted by the initial transverse momentum (Ma et al. 2016). The result shows that the classical recombination rate follows a scaling of \(\varpi ^{-4.6}\). We next study the ionization rate by TDSE. As can be seen in Fig. 9b, the ionization rate in our case follows a scaling of \(\varpi ^{1.3}\).

Fig. 9
figure 9

(Color online) Frequency scaling of the a recombination rate and b ionization rate in the counter-rotating bicircular fields

Full size image

Then, we calculated the traveling time of the classical electron trajectories by considering the acceleration process. Figure 10a show the average traveling time by accumulating all the possible returning trajectories. As shown in Fig. 10a, the average traveling time follows a scaling of \(\varpi ^{-1.5}\). Thereafter, we consider the number of harmonics below the cutoff energy. As shown in Fig. 10b, the cutoff energy follows a scaling of \(\varpi ^{-1.2}\) in our case. Moreover, the selection rule for the harmonics is \(\varOmega _{\pm }/\omega _{1}=(1+\alpha )n\pm 1\), where ± corresponds to the LCP and RCP components (Milošević 2015). Consequently, mHHG follows a scaling of \(\varpi ^{-1.2}\times \frac{2}{(1+\alpha )\omega _{1}}=\varpi ^{-2.2}\). In summary, the average probability of the electrons recombined with the parent ion follows a scaling of :

$$\begin{aligned} \overline{re}\propto \frac{P_{ion}\times P_{re}}{m_{HHG}}/\tau ^{3} = \frac{\varpi ^{1.3\times \varpi ^{-4.6}}}{\varpi ^{-2.2}}/(\varpi ^{-1.5})^{3} = \varpi ^{3.4} \end{aligned}$$
(9)

The result \(\varpi ^{3.4}\) is approximately equal to \(\varpi ^{3.7}\). Unlike the linearly case, the increasing HHG yield with bicircular fields primarily originates from two factors: (1) the weaker spreading of the electron wake packet (2) the decreasing number of high harmonics below the cutoff energy.

Fig. 10
figure 10

(Color online) a Average traveling time of the electron trajectories from ionization to recombination. b Frequency dependence of the harmonic cutoff energy in the counter-rotating bicircular fields

Full size image

We also simulate the HHG in the case where the intensity ratio of the two fields is not unity. On the one hand, we fix the intensity ratio to be 2:1, and change the frequency ratio from 1.5 to 4. We get similar results as Figs. 3 and 8. On the other hand, we change the intensity ratio from 1:2 to 2:1, and fix the frequency ratio to be 1:2. The ellipticity of the high harmonics increases for an increasing intensity ratio, but the high harmonic intensity becomes lower (Milošević 2015).

4 Conclusion

In conclusion, we theoretically demonstrate a scheme for efficiently generating attosecond pulses with high ellipticity by using a counter-rotating bicircular filed with frequency ratio of 1:3 (800 + 267 nm) and 1:4 (1600 + 400 nm). It is shown that efficient attosecond pulses with high ellipticity 0.54 (800 + 267 nm) and 0.79 (1600 + 400 nm) can be generated. The highly elliptically polarized emission mainly results from the symmetry of the driving fields. In addition, the HHG yield follows a scaling of \(\varpi ^{3.7}\) and is increased more than one order of magnitude with increasing frequency ratio. By performing the classical electron trajectories analysis, it is found that the scaling of \(\varpi ^{3.7}\) mainly results from the increasing average probability of the electrons recombined with the parent ion.