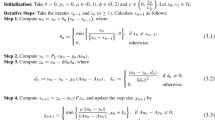1 Introduction

Let C be a closed and convex nonempty subset in a real Hilbert space \({\mathscr{H}}\) with inner product 〈⋅,⋅〉 and induced norm ∥⋅∥. Let us first review some nonlinear mappings in convex analysis. For any \( x,y\in {\mathscr{H}} \), the mapping \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is said to be (i) L-Lipschitz continuous with L > 0 if ∥Mx − My∥≤ L∥x − y∥ (if L = 1, then M is called nonexpansive); (ii) γ-inverse strongly monotone (or γ-cocoercive) if there exists γ > 0 such that 〈Mx − My, x − y〉≥ γ∥Mx − My∥2; (iii) α-strongly monotone if there exists α > 0 such that 〈Mx − My, x − y〉≥ α∥x − y∥2; (iv) monotone if 〈Mx − My, x − y〉≥ 0; (v) pseudomonotone if 〈Mx, y − x〉≥ 0⇒〈My, y − x〉≥ 0; (vi) sequentially weakly continuous if for each sequence \(\left \{x_{n}\right \}\) converges weakly to x implies \(\left \{M x_{n}\right \}\) converges weakly to Mx. Through the above definitions, it is easy to see that (iii) ⇒ (iv) ⇒ (v). The main purpose of this paper is to devote several efficient numerical methods for solving the bilevel variational inequality problem (shortly, BVIP) involving a pseudomonotone mapping in real Hilbert spaces. Let \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) and \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) be two single-valued mappings. Recall that the variational inequality problem (VIP) for the mapping M on C is described as follows:

$$ \text{find } y^{*} \in C \text { such that }\left\langle M y^{*}, z-y^{*}\right\rangle \geq 0,\quad \forall z \in C .{\kern102pt} (\text{VIP}) $$

We denote Ω the set of all solutions of the (VIP). Recall that the (BVIP) is formed as follows:

$$ \text{find } x^{\dag} \in \varOmega \text { such that }\left\langle S x^{\dag}, y-x^{\dag}\right\rangle \geq 0,\quad \forall y \in \varOmega . {\kern92pt} (\text{BVIP}) $$

Since the bilevel variational inequality problems include a number of problems, such as, quasi-variational inequality problems, complementary problems, and so on. It is therefore necessary to develop some fast and efficient numerical approaches to solve the bilevel variational inequalities. Some recent work on solution methods for (BVIP) can be found in [1,2,3,4]. There are also a number of methods dealing with approximation solution of (VIP); see, e.g., [5,6,7,8]. The simplest of these algorithms is the projected-gradient method, which, starting from any x0 ∈ C, iteratively updates xn+ 1 according to the formula

$$ x_{n+1}=P_{C}\left( x_{n}-\vartheta Mx_{n}\right) , $$
(1.1)

where M is a nonlinear mapping, 𝜗 is a positive fixed step size and PC denotes the metric projection onto C (see definition in Section 2). The projected-gradient method is based on the observation that x‡∈ C is a solution of (VIP) if and only if

$$ x^{\dag}=P_{C}\left( x^{\dag}-\vartheta Mx^{\dag}\right) . $$
(1.2)

This projected-gradient method (1.1) can be easily implemented because it only needs to calculate the function value and the projection onto C once in each iteration. However, the projected-gradient method requires a restrictive hypothesis on M for the convergence, that is, M is strongly monotone and Lipschitz continuous. To relax the strong assumptions required by the projected-gradient method and thus broaden the class of the problems that we can solve, the extragradient method was proposed. Because of (1.2), x‡∈ C is a solution of (VIP) if and only if

$$ x^{\dag}=P_{C}\left( x^{\dag}-\vartheta M\left( P_{C}\left( x^{\dag}-\vartheta Mx^{\dag}\right)\right)\right) . $$

The basic idea of this method is to update xn+ 1 according to the double projection formula

$$ x_{n+1}=P_{C}(x_{n}-\vartheta M(P_{C}(x_{n}-\vartheta Mx_{n}))) . $$

The extragradient method (EGM) was first proposed by Korpelevich [9], as shown below. Taking the initial value x0 ∈ C, we generate a succession \(\left \{x_{n}\right \}\) such that

$$ \left\{\begin{aligned} &y_{n}=P_{C}(x_{n}-\vartheta Mx_{n}) , \\ &x_{n+1}=P_{C}(x_{n}-\vartheta My_{n}) . \end{aligned}\right. {\kern192pt}({\text{EGM}}) $$

It is known that the convergence of the extragradient method is proved under the following hypothesis: Ω≠∅, mapping M is L-Lipschitz continuous monotone and fixed step size 𝜗 ∈ (0,1/L). However, we note that the (EGM) needs to perform two projection calculations on the feasible set C in each iteration, which may seriously affect the computational performance, especially when C is a general closed convex set. To overcome this disadvantage, Censor, Gibali and Reich [10] introduced the subgradient extragradient method (SEGM), which can be seen as a modification of the (EGM). They replaced the second projection onto C with a projection onto a half-space. More precisely, their algorithm is expressed as follows:

$$ \left\{\begin{aligned} &y_{n}=P_{C}(x_{n}-\vartheta M x_{n}) , \\ &T_{n}=\left\{z \in \mathscr{H} \mid \langle x_{n}-\vartheta M x_{n}-y_{n}, z-y_{n}\rangle \leq 0\right\} , \\ &x_{n+1}=P_{T_{n}}(x_{n}-\vartheta M y_{n}) , \end{aligned}\right. {\kern88pt}(\text{SEGM}) $$

where mapping M is L-Lipschitz continuous monotone and fixed step size 𝜗 is in (0,1/L). They confirmed that the (SEGM) is weakly convergent in a Hilbert space. It is worth noting that the projection onto a half-space Tn can be calculated by an explicit formula. This greatly improves the computational performance of the (EGM).

Recently, Dong, Jiang and Gibali [11] proposed a modified subgradient extragradient method (MSEGM) for solving the (VIP) by improving the step size in the second step of the (SEGM). This method was inspired by the subgradient extragradient method and the projection and contraction method [12, 13]. Their primary example demonstrates the numerical performance and advantages of this new method compared with some existing approaches. Indeed, the (MSEGM) is of the form:

$$ \left\{\begin{aligned} &y_{n}=P_{C}(x_{n}-\vartheta_{n} M x_{n}) ,\\ &T_{n}=\left\{z \in \mathscr{H} \mid \langle x_{n}-\vartheta_{n} M x_{n}-y_{n}, z-y_{n}\rangle \leq 0\right\} ,\\ &x_{n+1}=P_{T_{n}}(x_{n}-\theta \vartheta_{n} \chi_{n} M y_{n}) , \end{aligned}\right. {\kern75pt}(\text{MSEGM}) $$

where 𝜃 ∈ (0,2) and

$$ \chi_{n}:= \frac{\langle x_{n}-y_{n}, c_{n}\rangle}{\|c_{n}\|^{2}} , \quad c_{n}:=x_{n}-y_{n}-\vartheta_{n}(M x_{n}-M y_{n}) , $$
(1.3)

and \(\vartheta _{n}:=\delta \zeta ^{m_{n}} (\delta >0,\zeta \in (0,1))\) and mn is the smallest nonnegative integer such that

$$ \vartheta_{n}\|M x_{n}-M y_{n}\| \leq \phi\|x_{n}-y_{n}\| ,\quad \phi\in(0,1) . $$

They proved that the iterative sequence formed by the (MSEGM) converges weakly to a solution of the (VIP) under some approximate conditions. Note that the (MSEGM) uses an Armijo-type line search rule to update the step size in each iteration, so it does not require the prior knowledge of the Lipschitz constant of the mapping.

Next, we introduce a problem related to the (BVIP). Yamada [14] studied the problem of finding a solution of the variational inequality problem over the fixed point set of nonexpansive mappings. More precisely, this problem is stated as follows:

$$ \text {find } x^{\dag} \in \text{Fix}(T) \text { such that }\left\langle S x^{\dag}, y-x^{\dag}\right\rangle \geq 0 , \quad \forall y \in \text{Fix}(T) , $$
(1.4)

where \(T: C \rightarrow C\) is a nonexpansive mapping, and \( \text {Fix}(T) = \{x\in {\mathscr{H}}: Tx = x\} \) represents its fixed point set. Yamada introduced the hybrid steepest descent method for solving problem (1.4), which read as follows:

$$ x_{n+1} = T x_{n}-\delta_{n+1}\vartheta S(T x_{n}) , $$
(1.5)

where mapping S is γ-inverse strongly monotone and L-Lipschitz continuous, fixed step size 𝜗 is in \(\left (0, {2 \gamma }/{L^{2}}\right )\) and \(\left \{\delta _{n}\right \}\) is a suitable sequence that satisfies some conditions. He proved that the iterative sequence \(\left \{x_{n}\right \}\) formed by (1.5) converges to a solution of problem (1.4) in norm. Recently, many scholars have used this method to solve various optimization problems, such as split feasibility problems and variational inequalities; see, e.g., [4, 15, 16]. Let δ > 0. By setting Tx = PC(x − δMx), we see that x ∈Fix(T) iff x ∈Ω. Thus, the (BVIP) becomes problem (1.4) and we can use iterative algorithm (1.5) to solve the (BVIP). However, the convergence of the hybrid steepest descent method requires that mapping M is inversely strong monotone, and this strict assumption may affect the efficiency of the used algorithm. Furthermore, it can be seen from the iterative algorithm (1.5) that the constants L and γ of the mapping S must be known.

Recently, Thong and Hieu [17] combined the modified subgradient extragradient method (MSEGM) with the hybrid steepest descent method (1.5), and introduced a strongly convergent modified subgradient extragradient method for solving bilevel pseudomonotone variational inequality problems in real Hilbert spaces. Their algorithm is illustrated as follows:

$$ \left\{\begin{aligned} &y_{n}=P_{C}(x_{n}-\vartheta M x_{n}) ,\\ &T_{n}=\left\{x \in \mathscr{H} \mid \langle x_{n}-\vartheta M x_{n}-y_{n}, x-y_{n}\rangle \leq 0\right\} ,\\ &z_{n}=P_{T_{n}}(x_{n}-\theta \vartheta \chi_{n} M y_{n}) ,\\ &x_{n+1}=z_{n}-\varphi_{n} \gamma S z_{n} , \end{aligned}\right. $$
(1.6)

where mapping M is LM-Lipschitz continuous pseudomonotone on \({\mathscr{H}}\), sequentially weakly continuous on C, mapping S is LS-Lipschitz continuous and α-strongly monotone on \({\mathscr{H}}\), {χn} is defined in (1.3), the fixed step size 𝜗 is in (0,1/LM), 𝜃 ∈ (0,2), \( \gamma \in \left (0,2\alpha /{L_{S}^{2}}\right ) \) and \(\left \{\varphi _{n}\right \}\) is a real sequence in (0,1) that satisfies \(\lim _{n \rightarrow \infty } \varphi _{n}=0\) and \( {\sum }_{n=1}^{\infty } \varphi _{n}=\infty \). Then, the sequence {xn} devised by (1.6) converges to the unique solution of the (BVIP) in norm. Moreover, their numerical experiments showed that the new algorithm has a better performance than the related one. It should be mentioned that Algorithm (1.6) uses a fixed step size and thus the Lipschitz constant of mapping M must be known.

In recent years, the development of fast iterative algorithms has attracted enormous interest, in particular, the inertial technology, which is based on discrete versions of a second-order dissipative dynamic system. Many researchers have constructed various fast iterative algorithms by using the inertial technology; see, e.g., [18,19,20,21] and the references therein. One of the common features of these algorithms is that the next iteration depends on the combination of the previous two iterations. Note that this minor change greatly improves the performance of the algorithms. Recently, Dong et al. [22] introduced an inertial projection and contraction method (VIP) to solve the monotone (IPCM). For any initial points \( x_{0},x_{1}\in {\mathscr{H}} \), the iterative sequence {xn+ 1} is devised as follows:

$$ \left\{\begin{aligned} &u_{n}=x_{n}+\tau_{n}(x_{n}-x_{n-1}) ,\\ &y_{n}=P_{C}(u_{n}-\vartheta M u_{n}) ,\\ &x_{n+1}=u_{n}-\theta \chi_{n} c_{n} , \end{aligned}\right. {\kern186pt}(\text{IPCM}) $$

where 𝜃 ∈ (0,2), 𝜗 > 0 and

$$ \chi_{n}:= \frac{\langle u_{n}-y_{n}, c_{n}\rangle}{\|c_{n}\|^{2}} , \quad c_{n}:=u_{n}-y_{n}-\vartheta (M u_{n}-M y_{n}) . $$

They proved that the (IPCM) achieves the weak convergence in a Hilbert space under appropriate assumptions. Moreover, the stated Algorithm (IPCM) shown the advantages and efficiency over other algorithms through some computational tests.

Motivated and inspired by the above work, in this paper, we introduce two new self-adaptive iterative algorithms for solving bilevel pseudomonotone variational inequality problems in real Hilbert spaces. Our algorithms do not require the prior knowledge of the Lipschitz constant of the potential mapping, and only need to calculate one projection on the feasible set in each iteration. Under certain suitable conditions, we prove that the iterative sequences generated by our algorithms converge strongly to a solution of (BVIP). Based on this, we derive two new strongly convergent methods to solve pseudomonotone (VIP). Finally, some computational tests are presented to support the theoretical results of our new iterative schemes.

The present paper is built up as follows. Some essential definitions and technical lemmas, that need to be used, are given in the next section. Section 3 describes the algorithms and analyzes their convergence. In Section 4, some numerical examples are presented to illustrate the behavior of our algorithms and compare them with the related one. In Section 5, we apply the derived methods to solve optimal control problems. Finally, a brief summary is given in Section 6, the last section.

2 Preliminaries

Let C be a closed and convex nonempty subset of a real Hilbert space \({\mathscr{H}}\). The weak convergence and strong convergence of \(\left \{x_{n}\right \}_{n=1}^{\infty }\) to x are represented by \(x_{n} \rightharpoonup x\) and \(x_{n} \rightarrow x\), respectively. For each \(x, y \in {\mathscr{H}}\), we have

$$ \|x+y\|^{2} \leq\|x\|^{2}+2\langle y, x+y\rangle . $$
(2.1)

For every point \(x \in {\mathscr{H}}\), there exists a unique nearest point in C, denoted by PC(x), such that \(P_{C}(x):= \arg \min \limits \{\|x-y\|, y \in C\}\). PC is called the metric projection of \({\mathscr{H}}\) onto C. It is known that PC(x) has the following basic properties:

$$ \begin{array}{@{}rcl@{}} \|P_{C} (x)-P_{C} (y)\|^{2} &\leq&\langle P_{C} (x)-P_{C} (y), x-y\rangle, \forall x \in \mathscr{H}, y \in \mathscr{H} . \end{array} $$
(2.2)
$$ \begin{array}{@{}rcl@{}} \langle x-P_{C} (x), y-P_{C} (x)\rangle &\leq& 0 , \forall x \in \mathscr{H}, y \in C . \end{array} $$
(2.3)

We give some explicit formulas to calculate projections on special feasible sets.

  1. (i)

    The projection of x onto a half-space Hu, v = {x : 〈u, x〉≤ v} is given by

    $$ P_{H_{u, v}}(x)=x-\max\Big\{\frac{\langle u, x\rangle-v}{\|u\|^{2}}, 0\Big\} u . $$
  2. (ii)

    The projection of x onto a box Box[a, b] = {x : a ≤ x ≤ b} is given by

    $$ P_{\text{Box}[a, b]}(x)_{i}=\min \left\{ b_{i}, \max \left\{x_{i}, a_{i}\right\}\right\} . $$
  3. (iii)

    The projection of x onto a ball B[p, q] = {x : ∥x − p∥≤ q} is given by

    $$ P_{B[p, q]}(x)=p+\frac{q}{\max \{\|x-p\|, q\}}(x-p) . $$

The following lemmas play important roles in our proofs.

Lemma 2.1 ([23])

Let C be a closed and convex nonempty subset of a real Hilbert space \({\mathscr{H}}\) and let \(M: {C} \rightarrow {\mathscr{H}}\) be a continuous and pseudomonotone mapping. Then, x‡ is a solution of the (VIP) if and only if \( \left \langle M x, x-x^{\dag }\right \rangle \geq 0, \forall x \in C \).

Lemma 2.2 ([14])

Suppose that mapping \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is LS-Lipschitz continuous and α-strongly monotone with 0 < α ≤ LS. Define the mapping \(T^{\gamma }: {\mathscr{H}} \rightarrow {\mathscr{H}}\) by \( T^{\gamma } x=(I-\varphi \gamma S)(T x), \forall x \in {\mathscr{H}} \), where \(T: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is a nonexpansive mapping, γ > 0 and φ ∈ (0,1]. Then, Tγ is a contraction provided that \(\gamma <\frac {2 \alpha }{{L_{S}^{2}}}\), that is,

$$ \|T^{\gamma} x-T^{\gamma} y\| \leq(1-\varphi \chi)\|x-y\|, \quad \forall x, y \in \mathscr{H} , $$

where \(\chi =1-\sqrt {1-\gamma \left (2 \alpha -\gamma {L_{S}^{2}}\right )} \in (0,1)\).

Lemma 2.3 ([24])

Let \(\left \{p_{n}\right \}\) be a positive sequence, \(\left \{q_{n}\right \}\) be a sequence of real numbers, and \(\left \{\sigma _{n}\right \}\) be a sequence in (0,1) such that \({\sum }_{n=1}^{\infty } \sigma _{n}=\infty \). Suppose that

$$ p_{n+1} \leq\left( 1-\sigma_{n}\right) p_{n}+\sigma_{n} q_{n}, \quad \forall n \geq 1 . $$

If \(\limsup _{k \rightarrow \infty } q_{n_{k}} \leq 0\) for every subsequence \(\{p_{n_{k}}\}\) of {pn} satisfying \(\lim \inf _{k \rightarrow \infty }\)\((p_{n_{k}+1}-p_{n_{k}}) \geq ~0\), then \(\lim _{n \rightarrow \infty } p_{n}=0\).

3 Main results

In this section, we introduce two new self-adaptive iterative methods for solving the (1) and analyze their convergence. The algorithms are inspired by the inertial method, the hybrid steepest descent method (1.5), the modified subgradient extragradient algorithm (1.6) and the inertial projection and contraction method (1). Furthermore, our iterative schemes embed an Armijo-type step size criterion so that they can work without the prior knowledge of the Lipschitz constant of the involved mapping. Before starting to state the main results, we assume that our algorithms satisfy the following assumptions.

  1. (C1)

    The feasible set C is a nonempty, closed and convex subset of \( {\mathscr{H}} \).

  2. (C2)

    The solution set of the (VIP) is nonempty, that is, Ω≠∅.

  3. (C3)

    The mapping \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is LM-Lipschitz continuous and pseudomonotone on \({\mathscr{H}}\), and sequentially weakly continuous on C.

  4. (C4)

    The mapping \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is LS-Lipschitz continuous and α-strongly monotone on \({\mathscr{H}}\) such that α ≤ LS.

  5. (C5)

    Suppose that the positive sequence {εn} satisfies \(\lim _{n \rightarrow \infty } \frac {\varepsilon _{n}}{\varphi _{n}}=0\), where {φn}⊂ (0,1) such that \(\lim _{n \rightarrow \infty } \varphi _{n}=0\) and \({\sum }_{n=1}^{\infty } \varphi _{n}=\infty \).

3.1 The modified inertial subgradient extragradient algorithm

In this subsection, we propose a new self-adaptive iterative scheme that performs only one projection onto the feasible set. Now, we state the suggested Algorithm 3.1 as follows.

Remark 3.1

We make the following observations for Algorithm 3.1.

  1. (i)

    It follows from (3.1) and Assumption (C5) that

    $$ \underset{n \rightarrow \infty}{\lim} \frac{\tau_{n}}{\varphi_{n}}\|x_{n}-x_{n-1}\|=0 . $$

    Indeed, we obtain τn∥xn − xn− 1∥≤ εn,∀n, which together with \(\lim _{n \rightarrow \infty } \frac {\varepsilon _{n}}{\varphi _{n}}=0\) yields

    $$ \underset{n \rightarrow \infty}{\lim} \frac{\tau_{n}}{\varphi_{n}}\|x_{n}-x_{n-1}\| \leq \underset{n \rightarrow \infty}{\lim} \frac{\varepsilon_{n}}{\varphi_{n}}=0 . $$
  2. (ii)

    It is worth noting that the definition of χn in our Algorithm 3.1 is different from that in (IPCM). Combining (3.2) and (3.3), one sees that

    $$ \begin{array}{@{}rcl@{}} \frac{\langle u_{n}-y_{n}, c_{n}\rangle}{\|c_{n}\|^{2}} &=&\frac{\|u_{n}-y_{n}\|^{2}-\vartheta_{n}\langle M u_{n}-M y_{n}, u_{n}-y_{n}\rangle}{\|c_{n}\|^{2}} \\ & \geq&\frac{\|u_{n}-y_{n}\|^{2}-\vartheta_{n}\|M u_{n}-M y_{n}\|\|u_{n}-y_{n}\|}{\|c_{n}\|^{2}} \\ & \geq&\frac{(1-\phi)\|u_{n}-y_{n}\|^{2}}{\|c_{n}\|^{2}} . \end{array} $$
  3. (iii)

    It is well known that if \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is L-Lipschitz continuous and α-strongly monotone on \({\mathscr{H}}\) and if Ω is a nonempty, closed and convex subset of \({\mathscr{H}}\), then the (BVIP) has a unique solution (see, e.g., [25]).

figure a

Next, we give some lemmas, which are very useful to prove the convergence of our algorithms.

Lemma 3.4

Suppose that Assumptions (C1)–(C3) hold. The Armijo-like search rule (3.2) is well defined and

$$ \min \left\{\delta, \frac{\phi \zeta}{L_{M}}\right\} \leq \vartheta_{n} \leq \delta . $$

Proof

Since M is LM-Lipschitz continuous, one has

$$ \|M u_{n}-M(P_{C}(u_{n}-\vartheta M u_{n}))\| \leq L_{M}\|u_{n}-P_{C}(u_{n}-\vartheta M u_{n})\| , $$

which is equivalent to

$$ \frac{\phi}{L_{M}}\|M u_{n}-M(P_{C}(u_{n}-\vartheta M u_{n}))\| \leq \phi\|u_{n}-P_{C}(u_{n}-\vartheta M u_{n})\| . $$

This implies that (3.2) holds for all \(\vartheta \leq \frac {\phi }{L_{M}}\). Thus, 𝜗n is well defined. It is easy to see that 𝜗n ≤ δ. If 𝜗n = δ, then this lemma is proved; otherwise, if 𝜗n < δ, by the search rule (3.2), we know that \(\frac {\vartheta _{n}}{\zeta }>\vartheta _{n}\) must violate inequality (3.2), that is,

$$ \frac{\vartheta_{n}}{\zeta}\left\|M u_{n}-M\left( P_{C}\left( u_{n}-\frac{\vartheta_{n}}{\zeta} M u_{n}\right)\right)\right\|>\phi\left\|u_{n}-P_{C}\left( u_{n}-\frac{\vartheta_{n}}{\zeta} M u_{n}\right)\right\| , $$

which, combining with the fact that the mapping M is LM-Lipschitz continuous, gets \(\vartheta _{n}>\frac {\phi \zeta }{L_{M}}\). This completes the proof of Lemma 3.4. □

Lemma 3.5

If yn = un or cn = 0 in Algorithm 3.1, then yn ∈Ω.

Proof

From the fact that mapping M is LM-Lipschitz continuous and (3.2), we get

$$ \begin{array}{@{}rcl@{}} \|c_{n}\| &=&\|u_{n}-y_{n}-\vartheta_{n}(M u_{n}-M y_{n})\| \\ & \geq&\|u_{n}-y_{n}\|-\vartheta_{n}\|M u_{n}-M y_{n}\| \\ & \geq& (1-\phi)\|u_{n}-y_{n}\| . \end{array} $$

It can be easily proved that ∥cn∥≤ (1 + ϕ)∥un − yn∥. Therefore,

$$ (1-\phi)\|u_{n}-y_{n}\| \leq\|c_{n}\| \leq(1+\phi)\|u_{n}-y_{n}\| , $$

and thus un = yn iff cn = 0. Hence, if un = yn or cn = 0, then we obtain yn = PC(yn − 𝜗nMyn). In view of (1.2), we get yn ∈Ω. That is the desired conclusion. □

Lemma 3.6

Suppose that Assumptions (C1)–(C3) hold. Let \(\left \{z_{n}\right \}\), {yn} and {un} be three sequences created by Algorithm 3.1. Then, for all x‡∈Ω,

$$ \|z_{n}-x^{\dag}\|^{2} \leq\|u_{n}-x^{\dag}\|^{2}-\|u_{n}-z_{n}-\theta \chi_{n} c_{n}\|^{2}-\theta(2-\theta) \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n}-y_{n}\|^{2} . $$

Proof

From x‡∈Ω⊂ C ⊂ Tn and the property of projection (2.2), we get

$$ \begin{array}{@{}rcl@{}} 2\|z_{n}-x^{\dag}\|^{2} &\leq &2\left\langle z_{n}-x^{\dag}, u_{n}-\theta \vartheta_{n} \chi_{n} M y_{n}-x^{\dag}\right\rangle \\ &=& \|z_{n}-x^{\dag}\|^{2}+\|u_{n}-\theta \vartheta_{n} \chi_{n} M y_{n}-x^{\dag}\|^{2}- \|z_{n}-u_{n}+\theta \vartheta_{n} \chi_{n} M y_{n}\|^{2} \\ &=& \|z_{n}-x^{\dag}\|^{2}+\|u_{n}-x^{\dag}\|^{2}+ \theta^{2} {\vartheta_{n}^{2}} {\chi_{n}^{2}}\|M y_{n}\|^{2} -2\left\langle u_{n}-x^{\dag}, \theta \vartheta_{n} \chi_{n} M y_{n}\right\rangle \\ &&-\|z_{n}-u_{n}\|^{2}- \theta^{2} {\vartheta_{n}^{2}} {\chi_{n}^{2}}\|M y_{n}\|^{2}-2\langle z_{n}-u_{n}, \theta \vartheta_{n} \chi_{n} M y_{n}\rangle \\ &=& \|z_{n}-x^{\dag}\|^{2}+\|u_{n}-x^{\dag}\|^{2}-\|z_{n}-u_{n}\|^{2}-2\left\langle z_{n}-x^{\dag}, \theta \vartheta_{n} \chi_{n} M y_{n}\right\rangle , \end{array} $$

which implies that

$$ \|z_{n}-x^{\dag}\|^{2} \leq\|u_{n}-x^{\dag}\|^{2}-\|z_{n}-u_{n}\|^{2}-2 \theta \vartheta_{n} \chi_{n}\left\langle z_{n}-x^{\dag}, M y_{n}\right\rangle . $$
(3.4)

Combining the pseudomonotonicity of mapping M, yn ∈ C and x‡∈Ω, we can show from Lemma 2.1 that \(\left \langle M y_{n}, y_{n}-x^{\dag }\right \rangle \geq 0\), which means that \(\left \langle M y_{n}, z_{n}-x^{\dag }\right \rangle \geq \left \langle M y_{n}, z_{n}-y_{n}\right \rangle \). Hence,

$$ -2 \theta \vartheta_{n} \chi_{n}\left\langle M y_{n}, z_{n}-x^{\dag}\right\rangle \leq-2 \theta \vartheta_{n} \chi_{n}\langle M y_{n}, z_{n}-y_{n}\rangle . $$
(3.5)

Since zn ∈ Tn, one obtains 〈un − 𝜗nMun − yn,zn − yn〉≤ 0. This shows that

$$ \langle u_{n}-y_{n}-\vartheta_{n}(M u_{n}-M y_{n}), z_{n}-y_{n}\rangle \leq \vartheta_{n}\langle M y_{n}, z_{n}-y_{n}\rangle . $$
(3.6)

Using (3.5), (3.6) and the definition of cn, we obtain

$$ \begin{array}{@{}rcl@{}} -2 \theta \vartheta_{n} \chi_{n}\left\langle M y_{n}, z_{n}-x^{\dag}\right\rangle &\leq&-2 \theta \chi_{n}\langle c_{n}, z_{n}-y_{n}\rangle\\ &=&-2 \theta \chi_{n}\langle c_{n}, u_{n}-y_{n}\rangle +2 \theta \chi_{n}\langle c_{n}, u_{n}-z_{n}\rangle . \end{array} $$
(3.7)

Now, we estimate − 2𝜃χn〈cn,un − yn〉 and 2𝜃χn〈cn,un − zn〉. From the definitions of χn and cn and (3.2), we have

$$ \begin{array}{@{}rcl@{}} \langle c_{n}, u_{n}-y_{n}\rangle &=&\|u_{n}-y_{n}\|^{2}-\vartheta_{n}\langle M u_{n}-M y_{n}, u_{n}-y_{n}\rangle \\ & \geq&\|u_{n}-y_{n}\|^{2}-\vartheta_{n}\|M u_{n}-M y_{n}\|\|u_{n}-y_{n}\| \\ & \geq&\|u_{n}-y_{n}\|^{2}-\phi\|u_{n}-y_{n}\|^{2} \\ &=&\chi_{n}\|c_{n}\|^{2} , \end{array} $$

which indicates that

$$ -2 \theta \chi_{n}\langle c_{n}, u_{n}-y_{n}\rangle \leq-2 \theta {\chi_{n}^{2}}\|c_{n}\|^{2} . $$
(3.8)

According to the basic inequality 2ab = a2 + b2 − (a − b)2, we have

$$ 2 \theta \chi_{n}\langle c_{n}, u_{n}-z_{n}\rangle=\|u_{n}-z_{n}\|^{2} +\theta^{2} {\chi_{n}^{2}}\|c_{n}\|^{2}-\|u_{n}-z_{n}-\theta \chi_{n} c_{n}\|^{2} . $$
(3.9)

It follows from Lemma 3.5 that ∥cn∥≤ (1 + ϕ)∥un − yn∥, which combining the definition of χn yields that

$$ {\chi_{n}^{2}}\|c_{n}\|^{2}=(1-\phi)^{2} \frac{\|u_{n}-y_{n}\|^{4}}{\|c_{n}\|^{2}} \geq \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n}-y_{n}\|^{2} . $$
(3.10)

Combining (3.4), (3.7), (3.8), (3.9) and (3.10), we conclude that

$$ \|z_{n}-x^{\dag}\|^{2} \leq\|u_{n}-x^{\dag}\|^{2}-\|u_{n}-z_{n}-\theta \chi_{n} c_{n}\|^{2}-\theta(2-\theta) \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n}-y_{n}\|^{2} . $$

This completes the proof. □

Lemma 3.7

[26, Lemma 3.3] Suppose that Assumptions (C1)–(C3) hold. Let {un} and {yn} be two sequences formulated by Algorithm 3.1. If there exists a subsequence \(\{u_{n_{k}}\}\) of {un} converges weakly to \(z \in {\mathscr{H}}\) and \(\lim _{k \rightarrow \infty }\|u_{n_{k}}-y_{n_{k}}\|=0\), then z ∈Ω.

Now, we are in a position to prove the convergence of the suggested Algorithm 3.1.

Theorem 3.1

Suppose that Assumptions (C1)–(C5) hold. Then, the sequence \(\left \{x_{n}\right \}\) defined by Algorithm 3.1 converges to the unique solution of the (BVIP) in norm.

Proof

We divide the proof into four statements.

Claim 1 The sequence \(\left \{x_{n}\right \}\) is bounded. Indeed, thanks to Lemma 3.6 and 𝜃 ∈ (0,2), one has

$$ \|z_{n}-x^{\dag}\| \leq\|u_{n}-x^{\dag}\|, \quad \forall n \ge 1 . $$
(3.11)

From the definition of un, one sees that

$$ \begin{array}{@{}rcl@{}} \|u_{n}-x^{\dag}\| & \leq&\|x_{n}-x^{\dag}\|+\tau_{n}\|x_{n}-x_{n-1}\| \\ &=&\|x_{n}-x^{\dag}\|+\varphi_{n} \cdot \frac{\tau_{n}}{\varphi_{n}}\|x_{n}-x_{n-1}\| . \end{array} $$
(3.12)

It follows from Remark 3.1 (i) that \(\frac {\tau _{n}}{\varphi _{n}}\|x_{n}-x_{n-1}\| \rightarrow 0\) as \( n\rightarrow \infty \). Thus, there is a constant Q1 > 0 such that

$$ \frac{\tau_{n}}{\varphi_{n}}\|x_{n}-x_{n-1}\| \leq Q_{1}, \quad \forall n \geq 1 . $$
(3.13)

Combining (3.11), (3.12) and (3.13), one obtains

$$ \|z_{n}-x^{\dag}\| \leq\|u_{n}-x^{\dag}\| \leq\|x_{n}-x^{\dag}\|+\varphi_{n} Q_{1},\quad \forall n \geq 1 . $$
(3.14)

Using the definition of xn+ 1, Lemma 2.2 and (3.14), one concludes

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\| &=&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}-\varphi_{n} \gamma S x^{\dag}\| \\ & \leq&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}\|+\varphi_{n} \gamma\|S x^{\dag}\| \\ & \leq&(1-\varphi_{n} \chi)\|z_{n}-x^{\dag}\|+\varphi_{n} \gamma\|S x^{\dag}\| \\ & \leq&(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|+\varphi_{n}\chi \cdot\frac{Q_{1}}{\chi}+\varphi_{n} \chi \cdot \frac{\gamma}{\chi}\|S x^{\dag}\| \\ & \leq& \max \left\{\|x_{n}-x^{\dag}\|, \frac{Q_{1}+\gamma\|S x^{\dag}\|}{\chi}\right\} \\ & \leq& {\cdots} \leq \max \left\{\|x_{1}-x^{\dag}\|, \frac{Q_{1}+\gamma\|S x^{\dag}\|}{\chi}\right\} , \end{array} $$
(3.15)

where \(\chi =1-\sqrt {1-\gamma \left (2 \alpha -\gamma {L_{S}^{2}}\right )} \in (0,1) \). This shows that \(\left \{x_{n}\right \}\) is bounded. We assert that \(\left \{u_{n}\right \}\), \(\left \{y_{n}\right \}\), \(\left \{z_{n}\right \}\) and \(\left \{Sz_{n}\right \}\) are also bounded sequences.

Claim 2

$$ \begin{array}{@{}rcl@{}} &&\theta(2-\theta) \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n}-y_{n}\|^{2}+\|u_{n}-z_{n}-\theta \chi_{n} c_{n}\|^{2}\\ &&\leq \|x_{n}-x^{\dag}\|^{2}-\|x_{n+1}-x^{\dag}\|^{2}+\varphi_{n} Q_{4} \end{array} $$

for some Q4 > 0. Indeed, it follows from (3.14) that

$$ \begin{array}{@{}rcl@{}} \|u_{n}-x^{\dag}\|^{2} & \leq&\left( \|x_{n}-x^{\dag}\|+\varphi_{n} Q_{1}\right)^{2} \\ &=&\|x_{n}-x^{\dag}\|^{2}+\varphi_{n}\left( 2 Q_{1}\|x_{n}-x^{\dag}\|+\varphi_{n} {Q_{1}^{2}}\right) \\ & \leq&\|x_{n}-x^{\dag}\|^{2}+\varphi_{n} Q_{2} \end{array} $$
(3.16)

for some Q2 > 0. From (2.1), (3.16), Lemmas 2.2 and 3.6, we obtain

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\|^{2} &=&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}-\varphi_{n} \gamma S x^{\dag}\| \\ & \leq&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}\|^{2}-2 \varphi_{n} \gamma\left\langle S x^{\dag}, x_{n+1}-x^{\dag}\right\rangle \\ & \leq&(1-\varphi_{n} \chi)^{2}\|z_{n}-x^{\dag}\|^{2}+2 \varphi_{n} \gamma\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle \\ & \leq&\|z_{n}-x^{\dag}\|^{2}+\varphi_{n} Q_{3} \\ &\leq& \|x_{n}-x^{\dag}\|^{2}+\varphi_{n} Q_{4}-\|u_{n}-z_{n}-\theta \chi_{n} c_{n}\|^{2}-\theta(2-\theta) \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n}-y_{n}\|^{2} , \end{array} $$
(3.17)

where Q4 := Q2 + Q3. The desired result can be achieved by a simple conversion.

Claim 3

$$ \|x_{n+1}-x^{\dag}\|^{2} \leq(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+\varphi_{n} \chi\left[\frac{2\gamma}{\chi}\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle+\frac{3Q\tau_{n}}{\varphi_{n} \chi}\|x_{n}-x_{n-1}\|\right] $$

for some Q > 0. Indeed, we have

$$ \begin{array}{@{}rcl@{}} \|u_{n}-x^{\dag}\|^{2} &=&\|x_{n}+\tau_{n}(x_{n}-x_{n-1})-x^{\dag}\|^{2} \\ &=&\|x_{n}-x^{\dag}\|^{2}+2 \tau_{n}\left\langle x_{n}-x^{\dag}, x_{n}-x_{n-1}\right\rangle+{\tau_{n}^{2}}\|x_{n}-x_{n-1}\|^{2} \\ &\leq&\|x_{n}-x^{\dag}\|^{2}+2 \tau_{n}\|x_{n}-x^{\dag}\|\|x_{n}-x_{n-1}\|+{\tau_{n}^{2}}\|x_{n}-x_{n-1}\|^{2} . \end{array} $$
(3.18)

Using (2.1), (3.1) and (3.11), one has

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\|^{2} &=&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}-\varphi_{n} \gamma S x^{\dag}\|^{2} \\ & \leq&\|(I-\varphi_{n} \gamma S) z_{n}-(I-\varphi_{n} \gamma S) x^{\dag}\|^{2}-2 \varphi_{n} \gamma\left\langle S x^{\dag}, x_{n+1}-x^{\dag}\right\rangle \\ & \leq&(1-\varphi_{n} \chi)^{2}\|z_{n}-x^{\dag}\|^{2}+2 \varphi_{n} \gamma\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle \\ &\leq&(1-\varphi_{n} \chi)\|u_{n}-x^{\dag}\|^{2}+2 \varphi_{n} \gamma\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle . \end{array} $$
(3.19)

Substituting (3.18) into (3.19), we obtain

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\|^{2} &\leq &(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+2 \varphi_{n} \gamma\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle\\ & & + \tau_{n}\|x_{n}-x_{n-1}\|\left( 2\|x_{n}-x^{\dag}\|+\tau\|x_{n}-x_{n-1}\|\right)\\ &\leq &(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+\varphi_{n} \chi\left[\frac{2\gamma}{\chi}\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle+\frac{3Q\tau_{n}}{\varphi_{n} \chi}\|x_{n}-x_{n-1}\|\right] , \end{array} $$

where \(Q:=\sup _{n \in \mathbb {N}}\left \{\|x_{n}-x^{\dag }\|, \tau \|x_{n}-x_{n-1}\|\right \}>0\) and χ ∈ (0,1) is defined in Claim 2.

Claim 4 The sequence \(\left \{\|x_{n}-x^{\dag }\|^{2}\right \}\) converges to zero. From Lemma 2.3 and Remark 3.1 (i), it remains to show that \(\lim \sup _{k \rightarrow \infty }\left \langle S x^{\dag }, x^{\dag }-x_{n_{k}+1}\right \rangle \leq 0\) for every subsequence \(\left \{\|x_{n_{k}}-x^{\dag }\|\right \}\) of \(\left \{\|x_{n}-x^{\dag }\|\right \}\) satisfying

$$ \underset{k \rightarrow \infty}{\liminf} \left( \|x_{n_{k}+1}-x^{\dag}\|-\|x_{n_{k}}-x^{\dag}\|\right) \geq 0 . $$

For this purpose, we assume that \(\left \{\|x_{n_{k}}-x^{\dag }\|\right \}\) is a subsequence of \(\left \{\|x_{n}-x^{\dag }\|\right \}\) such that \(\liminf _{k \rightarrow \infty }\left (\|x_{n_{k}+1}-x^{\dag }\|-\|x_{n_{k}}-x^{\dag }\|\right ) \geq 0 \). Then,

$$ \begin{array}{@{}rcl@{}} &&\underset{k \rightarrow \infty}{\liminf} \left( \|x_{n_{k}+1}-x^{\dag}\|^{2}-\|x_{n_{k}}-x^{\dag}\|^{2}\right) \\ &=&\underset{k \rightarrow \infty}{\liminf} \left[\left( \|x_{n_{k}+1}-x^{\dag}\|-\|x_{n_{k}}-x^{\dag}\|\right)\left( \|x_{n_{k}+1}-x^{\dag}\|+\|x_{n_{k}}-x^{\dag}\|\right)\right] \geq 0 . \end{array} $$

It follows from Claim 2 and Assumption (C5) that

$$ \begin{array}{@{}rcl@{}} &&\theta(2-\theta) \frac{(1-\phi)^{2}}{(1+\phi)^{2}}\|u_{n_{k}}-y_{n_{k}}\|^{2}+\|u_{n_{k}}-z_{n_{k}}-\theta \chi_{n_{k}} c_{n_{k}}\|^{2}\\ & \leq& \underset{k \rightarrow \infty}{\limsup} \left[\|x_{n_{k}}-x^{\dag}\|^{2}-\|x_{n_{k}+1}-x^{\dag}\|^{2}+\varphi_{n_{k}} Q_{4}\right] \\ & \leq& \underset{k \rightarrow \infty}{\limsup} \left[\|x_{n_{k}}-x^{\dag}\|^{2}-\|x_{n_{k}+1}-x^{\dag}\|^{2}\right] +\underset{k \rightarrow \infty}{\limsup} \varphi_{n_{k}} Q_{4} \\ &=&-\underset{k \rightarrow \infty}{\liminf} \left[\|x_{n_{k}+1}-x^{\dag}\|^{2}-\|x_{n_{k}}-x^{\dag}\|^{2}\right] \\ & \leq& 0 , \end{array} $$

which indicates that

$$ \underset{k \rightarrow \infty}{\lim} \|y_{n_{k}}-u_{n_{k}}\|=0 \text{and} \underset{k \rightarrow \infty}{\lim} \|u_{n_{k}}-z_{n_{k}}-\theta \chi_{n_{k}} c_{n_{k}}\|=0 . $$
(3.20)

From \(\|c_{n_{k}}\| \geq (1-\phi )\|u_{n_{k}}-y_{n_{k}}\|\) and the definition of \( \chi _{n_{k}} \), we have

$$ \begin{array}{@{}rcl@{}} \|u_{n_{k}}-z_{n_{k}}\| & \leq&\|u_{n_{k}}-z_{n_{k}}-\theta \chi_{n_{k}} c_{n_{k}}\|+\theta \chi_{n_{k}}\|c_{n_{k}}\| \\ &=&\|u_{n_{k}}-z_{n_{k}}-\theta \chi_{n_{k}} c_{n_{k}}\|+\theta(1-\phi) \frac{\|u_{n_{k}}-y_{n_{k}}\|^{2}}{\|c_{n_{k}}\|}\\ &\leq& \|u_{n_{k}}-z_{n_{k}}-\theta \chi_{n_{k}} c_{n_{k}}\|+ \theta\|u_{n_{k}}-y_{n_{k}}\| . \end{array} $$
(3.21)

Combining (3.20) and (3.21), we get

$$ \underset{k \rightarrow \infty}{\lim} \|z_{n_{k}}-u_{n_{k}}\|=0 . $$
(3.22)

Moreover, we have

$$ \|x_{n_{k}+1}-z_{n_{k}}\|=\varphi_{n_{k}}\gamma\|S z_{n_{k}}\| \rightarrow 0 , \text{ as } n\rightarrow \infty , $$
(3.23)

and

$$ \|x_{n_{k}}-u_{n_{k}}\|=\varphi_{n_{k}} \cdot \frac{\tau_{n_{k}}}{\varphi_{n_{k}}}\|x_{n_{k}}-x_{n_{k}-1}\| \rightarrow 0 , \text{ as } n\rightarrow \infty . $$
(3.24)

From (3.22), (3.23) and (3.24), we obtain

$$ \|x_{n_{k}+1}-x_{n_{k}}\| \leq\|x_{n_{k}+1}-z_{n_{k}}\|+\|z_{n_{k}}-u_{n_{k}}\|+\|u_{n_{k}}-x_{n_{k}}\| \rightarrow 0 , \text{ as } n\rightarrow \infty . $$
(3.25)

Since \(\{x_{n_{k}}\}\) is bounded, it follows that there exists a subsequence \(\left \{x_{n_{k_{j}}}\right \}\) of \(\left \{x_{n_{k}}\right \},\) which converges weakly to some \(z \in {\mathscr{H}}\), such that

$$ \underset{k \rightarrow \infty}{\limsup} \left\langle S x^{\dag}, x^{\dag}-x_{n_{k}}\right\rangle=\underset{j \rightarrow \infty}{\lim} \left\langle S x^{\dag}, x^{\dag}-x_{n_{k_{j}}}\right\rangle=\left\langle S x^{\dag}, x^{\dag}-z\right\rangle . $$
(3.26)

By using (3.24), we get that \(u_{n_{k}} \rightharpoonup z\). This together with \(\lim _{k \rightarrow \infty }\|u_{n_{k}}-y_{n_{k}}\|=0\) and Lemma 3.7 concludes that z ∈Ω. From (3.26) and x‡ is the unique solution of the (BVIP), we get

$$ \underset{k \rightarrow \infty}{\limsup} \left\langle S x^{\dag}, x^{\dag}-x_{n_{k}}\right\rangle=\left\langle S x^{\dag}, x^{\dag}-z\right\rangle \leq 0 . $$
(3.27)

Using (3.25) and (3.27), we obtain

$$ \underset{k \rightarrow \infty}{\limsup} \left\langle S x^{\dag}, x^{\dag}-x_{n_{k}+1}\right\rangle =\underset{k \rightarrow \infty}{\limsup} \left\langle S x^{\dag}, x^{\dag}-x_{n_{k}}\right\rangle\leq 0 . $$
(3.28)

Therefore, combining (3.28), Remark 3.1 (i) and Claim 3, in the light of Lemma 2.3, we conclude that \(\lim _{n \rightarrow \infty }\|x_{n}-x^{\dag }\|=0\), i.e., \( x_{n} \rightarrow x^{\dag } \). We have thus proved the theorem. □

Now, we give a special case of Algorithm 3.1. Set S(x) = x − f(x) in Theorem 3.1, where mapping \(f: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is a ρ-contraction. It can be easily verified that mapping \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is (1 + ρ)-Lipschitz continuous and (1 − ρ)-strongly monotone. In this situation, by picking γ = 1, we get a new modified inertial subgradient extragradient algorithm for solving (VIP). More specifically, we get the following results.

Corollary 3.1

Suppose that mapping \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is LM-Lipschitz continuous pseudomonotone on \({\mathscr{H}}\) and sequentially weakly continuous on C, and mapping \(f:~{\mathscr{H}} \rightarrow {\mathscr{H}}\) is a ρ-contraction with \(\rho \in [0, \sqrt {5}-2)\). Take τ > 0, δ > 0, ζ ∈ (0,1), ϕ ∈ (0,1) and 𝜃 ∈ (0,2). Assume that the positive sequence {𝜖n} satisfies \(\lim _{n \rightarrow \infty } \frac {\epsilon _{n}}{\varphi _{n}}=0\), where {φn}⊂ (0,1) such that \(\lim _{n \rightarrow \infty } \varphi _{n}=0\) and \({\sum }_{n=1}^{\infty } \varphi _{n}=\infty \). Let \(x_{0},x_{1} \in {\mathscr{H}}\) be two arbitrary initial points and iterative sequence \(\left \{x_{n}\right \}\) be generated by the following

$$ \left\{\begin{aligned} &u_{n}=x_{n}+\tau_{n}(x_{n}-x_{n-1}) ,\\ &y_{n}=P_{C}(u_{n}-\vartheta_{n} M u_{n}) , \\ &T_{n}:=\left\{x \in \mathscr{H} \mid \langle u_{n}-\vartheta_{n} M u_{n}-y_{n}, x-y_{n}\rangle \leq 0\right\} ,\\ &z_{n}=P_{T_{n}}(u_{n}-\theta \vartheta_{n} \chi_{n} M y_{n}) , \\ &x_{n+1}=(1-\varphi_{n}) z_{n}+\varphi_{n} f(z_{n}) , \end{aligned}\right. $$
(3.29)

where \( \left \{\tau _{n} \right \}\), {𝜗n} and {χn} are defined in (3.1), (3.2) and (3.3), respectively. Then the iterative sequence \(\left \{x_{n}\right \}\) formed by (3.29) converges to x‡∈Ω in norm, where \(x^{\dag }=P_{\varOmega } \left (f\left (x^{\dag }\right )\right )\).

Remark 3.2

Our Corollary 3.1 improves and generalizes some recent results in the literature [11, 17, 27] based on the following observations. (1) Our Algorithm (3.29) is strongly convergent while the algorithm (MSEGM) introduced by Dong et al. [11] only obtains weak convergence in an infinite-dimensional Hilbert space. (2) The Algorithm (40) suggested by Thong and Hieu in [17] is a fixed step algorithm, but the proposed iterative scheme (3.29) is self-adaptive, i.e., it means that our algorithm can work without knowing the prior information of the Lipschitz constant of the mapping. (3) When the inertial parameter τn = 0 in (3.29), then the stated Algorithm (3.29) is similar to Thong and Gibali’s Algorithm 3.2 [27]. Notice that the mapping contained in our Algorithm (3.29) is pseudomonotone, whereas the corresponding mappings in Dong et al.’s Algorithm (MSEGM) and Thong and Gibali’s Algorithm 3.2 [27] are monotone.

3.2 The new modified inertial projection and contraction algorithm

In this subsection, we introduce a new modified inertial projection and contraction algorithm for solving (BVIP). The iterative procedure only involves the calculation of one projection, and it can work without the prior information of the Lipschitz constant of the mapping. The new Algorithm 3.2 is stated as follows.

figure b

The following lemma plays a vital role in the convergence analysis of the algorithm.

Lemma 3.8

Suppose that Assumptions (C1)–(C3) hold. Let \(\left \{z_{n}\right \}\), {yn} and {un} be three sequences generated by Algorithm 3.2. Then, for all x‡∈Ω,

$$ \|z_{n}-x^{\dag}\|^{2} \leq\|u_{n}-x^{\dag}\|^{2}-\frac{2-\theta}{\theta}\|u_{n}-z_{n}\|^{2} , $$

and

$$ \|u_{n}-y_{n}\|^{2} \leq \left[\frac{1+\phi}{(1-\phi) \theta}\right]^{2} \|u_{n}-z_{n}\|^{2} . $$

Proof

By using of the definition of zn, one sees that

$$ \begin{array}{@{}rcl@{}} \|z_{n}-x^{\dag}\|^{2} &=&\|u_{n}-\theta \chi_{n} c_{n}-x^{\dag}\|^{2} \\ &=&\|u_{n}-x^{\dag}\|^{2}-2 \theta \chi_{n}\left\langle u_{n}-x^{\dag}, c_{n}\right\rangle+\theta^{2} {\chi_{n}^{2}}\|c_{n}\|^{2} . \end{array} $$
(3.30)

Combining (3.2) and (3.3), one obtains

$$ \begin{array}{@{}rcl@{}} \left\langle u_{n}-x^{\dag}, c_{n}\right\rangle&=&\langle u_{n}-y_{n}, c_{n}\rangle+\left\langle y_{n}-x^{\dag}, c_{n}\right\rangle \\ &=& \|u_{n}-y_{n}\|^{2}-\vartheta_{n}\langle u_{n}-y_{n}, M u_{n}-M y_{n}\rangle +\left\langle y_{n}-x^{\dag}, c_{n}\right\rangle \\ &\geq&\|u_{n}-y_{n}\|^{2}-\vartheta_{n}\|u_{n}-y_{n}\|\|M u_{n}-M y_{n}\| +\left\langle y_{n}-x^{\dag}, c_{n}\right\rangle \\ &\geq&(1-\phi)\|u_{n}-y_{n}\|^{2}+\left\langle y_{n}-x^{\dag}, u_{n}-y_{n}-\vartheta_{n}\left( M u_{n}-M y_{n}\right)\right\rangle . \end{array} $$
(3.31)

From \(y_{n}=P_{C}\left (u_{n}-\vartheta _{n} M u_{n}\right )\) and the property of projection (2.3), one has

$$ \left\langle u_{n}-y_{n}-\vartheta_{n} M u_{n}, y_{n}-x^{\dag}\right\rangle \geq 0 . $$
(3.32)

Using x‡∈Ω and yn ∈ C, one gets \( \left \langle M x^{\dag }, y_{n}-x^{\dag }\right \rangle \geq 0 \). With the aid of the pseudomonotonicity of M, one obtains

$$ \left\langle M y_{n}, y_{n}-x^{\dag}\right\rangle \geq 0 . $$
(3.33)

It follows from (3.3) that (1 − ϕ)∥un − yn∥2 = χn∥cn∥2. This together with (3.31), (3.32) and (3.33) implies that

$$ \left\langle u_{n}-x^{\dag}, c_{n}\right\rangle \geq(1-\phi)\|u_{n}-y_{n}\|^{2}=\chi_{n}\|c_{n}\|^{2} . $$
(3.34)

Combining the definition of zn, (3.30) and (3.34), one concludes that

$$ \begin{array}{@{}rcl@{}} \|z_{n}-x^{\dag}\|^{2} & \leq&\|u_{n}-x^{\dag}\|^{2}-2 \theta {\chi_{n}^{2}}\|c_{n}\|^{2}+\theta^{2} {\chi_{n}^{2}}\|c_{n}\|^{2} \\ &=&\|u_{n}-x^{\dag}\|^{2}-\frac{2-\theta}{\theta}\|\theta \chi_{n} c_{n}\|^{2} \\ &=&\|u_{n}-x^{\dag}\|^{2}-\frac{2-\theta}{\theta}\|u_{n}-z_{n}\|^{2} . \end{array} $$

On the other hand, by using of the definition of zn and (3.3), one sees that

$$ \begin{array}{@{}rcl@{}} \|u_{n}-y_{n}\|^{2} &=&\frac{\chi_{n}}{1-\phi}\|c_{n}\|^{2}=\frac{1}{\chi_{n}(1-\phi)}\|\chi_{n} c_{n}\|^{2} \\ &=&\frac{1}{\chi_{n}(1-\phi) \theta^{2}}\|u_{n}-z_{n}\|^{2} . \end{array} $$
(3.35)

From ∥cn∥≤ (1 + ϕ)∥un − yn∥ and the definition of χn, one obtains

$$ \chi_{n}=(1-\phi) \frac{\|u_{n}-y_{n}\|^{2}}{\|c_{n}\|^{2}} \geq \frac{1-\phi}{(1+\phi)^{2}} . $$
(3.36)

It implies from (3.35) and (3.36) that

$$ \|u_{n}-y_{n}\|^{2} \leq \left[\frac{1+\phi}{(1-\phi) \theta}\right]^{2} \|u_{n}-z_{n}\|^{2} . $$

This completes the proof of Lemma 3.8. □

Theorem 3.2

Suppose that Assumptions (C1)–(C5) hold. Then the sequence \(\left \{x_{n}\right \}\) formed by Algorithm 3.2 converges to the unique solution of the (BVIP) in norm.

Proof

The proof of the theorem is very similar to the proof of Theorem 3.1, we will simplify some derivation steps.

Claim 1 The sequence \(\left \{x_{n}\right \}\) is bounded. Indeed, thanks to Lemma 3.8, we have

$$ \|z_{n}-x^{\dag}\| \leq\|u_{n}-x^{\dag}\|, \quad \forall n \ge 1 . $$
(3.37)

From (3.12), (3.13) and (3.37), we obtain

$$ \|z_{n}-x^{\dag}\| \leq\|u_{n}-x^{\dag}\| \leq\|x_{n}-x^{\dag}\|+\varphi_{n} Q_{1},\quad \forall n \geq 1 . $$
(3.38)

Using (3.15) and (3.38), we get

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\| & \leq&(1-\varphi_{n} \chi)\|z_{n}-x^{\dag}\|+\varphi_{n} \gamma\|S x^{\dag}\| \\ & \leq& \max \left\{\|x_{n}-x^{\dag}\|, \frac{Q_{1}+\gamma\|S x^{\dag}\|}{\chi}\right\} \\ & \leq& {\cdots} \leq \max \left\{\|x_{1}-x^{\dag}\|, \frac{Q_{1}+\gamma\|S x^{\dag}\|}{\chi}\right\} . \end{array} $$

Thus, sequence \(\left \{x_{n}\right \}\) is bounded. Hence, we assert \(\left \{u_{n}\right \}\), \(\left \{y_{n}\right \}\), \(\left \{z_{n}\right \}\) and \(\left \{Sz_{n}\right \}\) are also bounded sequences.

Claim 2

$$ \frac{2-\theta}{\theta}\|u_{n}-z_{n}\|^{2} \leq \|x_{n}-x^{\dag}\|^{2}-\|x_{n+1}-x^{\dag}\|^{2}+\varphi_{n} Q_{4} . $$

From (3.16), (3.17) and Lemma 3.8, we can immediately get

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\|^{2} & \leq&\|z_{n}-x^{\dag}\|^{2}+\varphi_{n} Q_{3}\\ &\leq& \|x_{n}-x^{\dag}\|^{2}+\varphi_{n} Q_{4}-\frac{2-\theta}{\theta}\|u_{n}-z_{n}\|^{2} , \end{array} $$

where Q4 is defined in the Claim 2 of Theorem 3.1.

Claim 3

$$ \|x_{n+1}-x^{\dag}\|^{2} \leq(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+\varphi_{n} \chi\left[\frac{2\gamma}{\chi}\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle+\frac{3Q\tau_{n}}{\varphi_{n} \chi}\|x_{n}-x_{n-1}\|\right] . $$

Combining (3.18), (3.19), (3.37), one obtains

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\dag}\|^{2} &\leq& (1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+2 \varphi_{n} \gamma\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle\\ &&+ \tau_{n}\|x_{n}-x_{n-1}\|(2\|x_{n}-x^{\dag}\|+\tau\|x_{n}-x_{n-1}\|)\\ &\leq&(1-\varphi_{n} \chi)\|x_{n}-x^{\dag}\|^{2}+\varphi_{n} \chi\left[\frac{2\gamma}{\chi}\left\langle S x^{\dag}, x^{\dag}-x_{n+1}\right\rangle+\frac{3Q\tau_{n}}{\varphi_{n} \chi}\|x_{n}-x_{n-1}\|\right] , \end{array} $$

where \(Q:=\sup _{n \in \mathbb {N}}\left \{\|x_{n}-x^{\dag }\|, \tau \|x_{n}-x_{n-1}\|\right \}>0\).

Claim 4 \(\left \{\|x_{n}-x^{\dag }\|^{2}\right \}\) converges to zero. As proved in Claim 4 of Theorem 3.1, from Claim 2 and 𝜃 ∈ (0,2), one has

$$ \frac{2-\theta}{\theta}\|u_{n_{k}}-z_{n_{k}}\|^{2} \leq \underset{k \rightarrow \infty}{\limsup} \left[\|x_{n_{k}}-x^{\dag}\|^{2}-\|x_{n_{k}+1}-x^{\dag}\|^{2}+\varphi_{n_{k}} Q_{4}\right] \leq 0 . $$

Thus, we get \( \lim _{k \rightarrow \infty }\|z_{n_{k}}-u_{n_{k}}\|=0 \). This together with Lemma 3.8 gives that \( \lim _{k \rightarrow \infty }\|y_{n_{k}}-u_{n_{k}}\|=0 \). The rest of the proof can refer to the Claim 4 of Theorem 3.1. We leave it to readers to verify. The proof of the theorem is now complete. □

By setting S(x) = x − f(x) in Theorem 3.2 and choosing γ = 1, we have the following result.

Corollary 3.2

Suppose that mapping \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) is LM-Lipschitz continuous pseudomonotone on \({\mathscr{H}}\) and sequentially weakly continuous on C, and mapping \(f:~{\mathscr{H}} \rightarrow {\mathscr{H}}\) is ρ-contraction with \(\rho \in [0, \sqrt {5}-2)\). Take τ > 0, δ > 0, ζ ∈ (0,1), ϕ ∈ (0,1) and 𝜃 ∈ (0,2). Assume that the positive sequence {εn} satisfies \(\lim _{n \rightarrow \infty } \frac {\varepsilon _{n}}{\varphi _{n}}=0\), where {φn}⊂ (0,1) such that \(\lim _{n \rightarrow \infty } \varphi _{n}=0\) and \({\sum }_{n=1}^{\infty } \varphi _{n}=\infty \). Let \(x_{0},x_{1} \in {\mathscr{H}}\) be two arbitrary initial points and iterative sequence \(\left \{x_{n}\right \}\) be created by the following

$$ \left\{\begin{aligned} &u_{n}=x_{n}+\tau_{n}(x_{n}-x_{n-1}) ,\\ &y_{n}=P_{C}(u_{n}-\vartheta_{n} M u_{n}) , \\ &z_{n}=u_{n}-\theta \chi_{n} c_{n} , \\ &x_{n+1}=(1-\varphi_{n}) z_{n}+\varphi_{n} f(z_{n}) , \end{aligned}\right. $$
(3.39)

where {τn}, {𝜗n} and {χn} are defined in (3.1), (3.2) and (3.3), respectively. Then the iterative sequence \(\left \{x_{n}\right \}\) generated by (3.39) converges to x‡∈Ω in norm, where \(x^{\dag }=P_{\varOmega } \left (f\left (x^{\dag }\right )\right )\).

Remark 3.3

Compared with some recent approaches presented in [22, 28,29,30], the stated Algorithm (3.39) has the following advantages. (i) If the inertial parameter τn = 0 in Algorithm (3.39), then it is similar to the viscosity projection-type algorithm 3.2 proposed by Gibali, Thong and Tuan [28]. (ii) Note that the suggested Algorithm (3.39) can update the step size adaptively by applying the Armijo-type step size criterion, while Algorithm 1 introduced by Thong, Vinh and Cho [29] and Algorithm 4.12 proposed by Gibali and Shehu [30] are both fixed step size iterative schemes. (iii) Our Algorithm (3.39) obtains strong convergence in an infinite-dimensional Hilbert space, whereas the Algorithm (IPCM) of Dong et al. [22] can only achieve weak convergence. (iv) The methods offered in [22, 28,29,30] are used to solve monotone variational inequality problems, while the recommended Algorithm (3.39) can solve pseudomonotone variational inequalities. It is known that the class of pseudomonotone mappings covers the class of monotone mappings, and thus our algorithm is more applicable. Therefore, the stated Corollary 3.2 develops and summarizes some recent results in the literature.

4 Numerical examples

In this section, we implement some examples that appear in finite- and infinite- dimensional spaces to show the numerical performance of the proposed Algorithms 3.1 and 3.2, and also to compare them with the Algorithm (1.6) suggested by Thong and Hieu [17]. We use the FOM Solver [31] to effectively calculate the projections onto C and Tn. All the programs are implemented in Matlab 2018a on a personal computer. In our experiments, we consider only variational inequalities governed by pseudomonotone operators which are not monotone.

Example 1

Let an operator \(M: \mathbb {R}^{m} \rightarrow \mathbb {R}^{m} (m=5,10,30,50)\) be given by

$$ M (x)=\frac{1}{\|x\|^{2}+1} \arg\underset{y \in \mathbb{R}^{m}}{\min} \left\{\frac{\|y\|^{4}}{4}+\frac{1}{2}\|x-y\|^{2}\right\} . $$

We emphasize that the operator M is not monotone. However, the operator M is Lipschitz continuous pseudomonotone (see [32]). The mapping S is defined by \( S(x)=\frac {1}{2}x \). It can be easily verified that mapping S is \( \frac {1}{2} \)-Lipschitz continuous and \( \frac {1}{2} \)-strongly monotone. In this example, we choose the feasible set is a box constraint C = [1,3]m. Moreover, we estimate that LM ≈ 1.4 by using Matlab. Our parameters are set as follows. In all the algorithms, we set 𝜃 = 1.5, \( \varphi _{n}=\frac {0.1}{n+1} \) and \(\gamma =\frac {\alpha }{{L_{S}^{2}}}\). Take τ = {0.1,0.8}, \( \varepsilon _{n}=\frac {1}{(n+1)^{2}} \), δ = ζ = 0.9, ϕ = 0.6 in our Algorithms 3.1 and 3.2. For Algorithm (1.6), we choose the fixed step size \( \vartheta =\frac {0.5}{L_{M}} \). Since we do not know the exact solution to this problem, we use Dn = ∥xn − xn− 1∥ to study the numerical behavior of all the algorithms. Take initial values x0 = x1 are randomly generated by rand(m,1) in Matlab. The maximum iteration 50 as a common stopping criterion. For the four different dimensions of the operator M, the numerical results of all the algorithms are presented in Fig. 1.

Fig. 1
figure 1

Numerical results of all the algorithms in Example 1

Full size image

Example 2

Consider a mapping \(S: \mathbb {R}^{5} \rightarrow \mathbb {R}^{5}\) of the form S(x) = Bx + q, where \( B\in \mathbb {R}^{5\times 5}\) is a positive-definite and symmetric matrix and \( q\in \mathbb {R}^{5}\) with their entries generated randomly in (− 2,2). It is clear that S is LS-Lipschitz continuous and α-strongly monotone with \(L_{S}={\max \limits } \{\operatorname {eig}(B)\}\) and \(\alpha ={\min \limits } \{\operatorname {eig}(B)\}\), where eig(B) represents all eigenvalues of B. Taking the feasible set \( C=\{x\in \mathbb {R}^{5}:1\leq x_{i}\leq 3,i=1,2,\ldots ,5 \} \), we consider the following quadratic fractional programming problem

$$ \underset{x\in C}{\min} f(x)=\frac{x^{\mathsf{T}} Q x+a^{\mathsf{T}} x+a_{0}}{b^{\mathsf{T}} x+b_{0}} , $$

with

$$ Q=\left[\begin{array}{ccccc} 5 & -1 & 2 & 0 & 2 \\ -1 & 6 & -1 & 3 & 0 \\ 2 & -1 & 3 & 0 & 1 \\ 0 & 3 & 0 & 5 & 0 \\ 2 & 0 & 1 & 0 & 4 \end{array}\right], a=\left[\begin{array}{c} 1 \\ 2 \\ -1 \\ -2\\ 1 \end{array}\right], b=\left[\begin{array}{c} 1 \\ 0 \\ -1 \\ 0\\ 1 \end{array}\right], a_{0}=-2, b_{0}=20 . $$

By a straightforward computation, we get

$$ M(x):=\nabla f(x)=\frac{\left( b^{\mathsf{T}} x+b_{0}\right)(2 Q x+a)-b\left( x^{\mathsf{T}} Q x+a^{\mathsf{T}} x+a_{0}\right)}{\left( b^{\mathsf{T}} x+b_{0}\right)^{2}} . $$

The operator M is Lipschitz continuous on C with the constant \( L=\max \limits \{\|\nabla M(x)\|:x\in C\} \), see [33]. We get that LM ≈ 149 by using Matlab. It is not sure that whether M is monotone or not? However, M is pseudomontone because f is pseudo-convex. The exact solution of the problem is x∗ = (1,1,1,1,1)T. In this example, the Lipschitz constant is very large. If the parameters are selected as in Example 1, our algorithms will oscillate due to the large step size. Therefore, we adjust the parameters of the Armijo-type criterion in Algorithms 3.1 and 3.2 to δ = 0.003, ζ = 0.9 and ϕ = 0.1. Our other parameters are the same as in Example 1. The maximum iteration of 500 as the stopping criterion. Figure 2 shows the numerical performance of Dn = ∥xn − x‡∥ of all the algorithms under four different initial values x0 = x1, which are randomly created by k×rand(5,1) in Matlab.

Fig. 2
figure 2

Numerical results of all the algorithms in Example 2

Full size image

Example 3

Finally, we focus on an example that appears in an infinite-dimensional Hilbert space \({\mathscr{H}}=L^{2}[0,1]\) with inner product \(\langle x, y\rangle ={{\int \limits }_{0}^{1}} x(t) y(t) \mathrm {d} t\) and induced norm \(\|x\|=\left ({{\int \limits }_{0}^{1}} |x(t)|^{2} \mathrm {d} t\right )^{1/2}\) for all \( x,y\in {\mathscr{H}} \). Let r, R be two positive real numbers such that R/(k + 1) < r/k < r < R for some k > 1. Take the feasible set \(C=\{x \in {\mathscr{H}}:\|x\| \leq r\}\) and the operator \(M: {\mathscr{H}} \rightarrow {\mathscr{H}}\) given by

$$ M(x)=(R-\|x\|) x, \quad \forall x \in \mathscr{H} . $$

Note that M is not monotone. Taking a particular pair \(\left (\tilde {x},\tilde {y}\right )=(\tilde {x}, k\tilde {x})\), one picks \(\tilde {x} \in C\) to satisfy \(R /(k+1)<\|\tilde {x}\|<r / k\). One can see that \(k\|\tilde {x}\| \in C \). By a simple operation, one gets

$$ \langle M(\tilde{x})-M(\tilde{y}), \tilde{x}-\tilde{y}\rangle=(1-k)^{2}\|\tilde{x}\|^{2}(R-(1+k)\|\tilde{x}\|)<0 . $$

Hence, the operator M is not monotone on C. Next one shows that M is pseudomonotone. Indeed, one assumes that 〈M(x),y − x〉≥ 0 for all x, y ∈ C, that is, 〈(R −∥x∥)x, y − x〉≥ 0. From ∥x∥ < R, one gets that 〈x, y − x〉≥ 0. Therefore,

$$ \begin{array}{@{}rcl@{}} \langle M(y), y-x\rangle &=&\langle(R-\|y\|) y, y-x\rangle \\ & \geq&(R-\|y\|)(\langle y, y-x\rangle-\langle x, y-x\rangle) \\ &=&(R-\|y\|)\|y-x\|^{2} \geq 0 . \end{array} $$

Let \(S: {\mathscr{H}} \rightarrow {\mathscr{H}}\) be an operator defined by \((S x)(t)=\frac {1}{2} x(t), t \in [0,1]\). It is easy to see that S is \( \frac {1}{2} \)-strongly monotone and \( \frac {1}{2} \)-Lipschitz continuous. For the experiment, we take R = 1.5, r = 1, k = 1.1. We know that the solution to the problem is x‡(t) = 0. Our parameters are the same as in Example 1. The maximum iteration of 50 as the stopping criterion. Figure 3 displays the numerical behavior of Dn = ∥xn(t) − x‡(t)∥ generated by all the algorithms with four starting points x0(t) = x1(t).

Fig. 3
figure 3

Numerical results of all the algorithms in Example 3

Full size image

Remark 4.4

We have the following observations for Examples 1–3.

  • From Figs. 1, 2, and 3, we can see that the proposed Algorithms 3.1 and 3.2 are more efficient and faster than the Algorithm (1.6) introduced by Thong and Hieu [17] under the appropriate parameters, and these results are independent of the selection of initial values and the size of dimensions. Moreover, our presented algorithms can work adaptively, while the fixed step iterative Algorithm (1.6) depends on the prior information of the Lipschitz constant of the involved mapping, which makes it invalid when the Lipschitz constant is unknown (see Examples 4–6). Therefore, the iterative schemes suggested in this paper are preferable in practical applications.

  • From Example 3, it should be emphasized that the proposed Algorithms 3.1 and 3.2 can achieve higher accuracy than the Algorithm (1.6) under the same stopping criterion. However, they need to spend more running time in an infinite-dimensional space to achieve the same error accuracy, because they use an Armijo-type rule to automatically update the step size and this update criterion requires that the value of operator M to be calculated multiple times in each iteration. It will be interesting to embed a new simple step size used recently in [3, 4, 19, 26] into the algorithms proposed in this paper, and this is also one of our future research topics.

5 Applications to optimal control problems

In this section, we use the derived algorithms (3.29) and (3.39) to solve the variational inequality that occurs in the optimal control problem. Assume that \(L_{2}\left ([0, T], \mathbb {R}^{m}\right )\) represents the square-integrable Hilbert space with inner product \(\langle p, q\rangle ={{\int \limits }_{0}^{T}}\langle p(t), q(t)\rangle \mathrm {d} t\) and norm \(\|p\|_{2}=\sqrt {\langle p, p\rangle }\). The optimal control problem is described as follows:

$$ p^{*}(t) \in \operatorname{Argmin}\{g(p) \mid p \in V\},\quad t\in [0, T] , $$
(5.1)

where V represents a set of feasible controls composed of m piecewise continuous functions. Its form is expressed as follows:

$$ V=\left\{p(t) \in L_{2}\left( [0, T], \mathbb{R}^{m}\right): p_{i}(t) \in\left[p_{i}^{-}, p_{i}^{+}\right], i=1,2, \ldots, m\right\} . $$
(5.2)

In particular, the control p(t) may be a piecewise constant function (bang-bang type). The terminal objective function has the form

$$ g(p)={\varPhi}(x(T)) , $$
(5.3)

where Φ is a convex and differentiable defined on the attainability set.

Assume that the trajectory x(t) ∈ L2([0,T]) satisfies the constraints of the linear differential equation system:

$$ \frac{\mathrm{d}}{\mathrm{d} t} x(t)=Q(t) x(t)+W(t) p(t), 0 \leq t \leq T, x(0)=x_{0} , $$
(5.4)

where \(Q(t) \in \mathbb {R}^{n \times n}\), \(W(t) \in \mathbb {R}^{n \times m}\) are given continuous matrices for every t ∈ [0,T]. By the solution of problem (5.1)–(5.4), we mean a control p∗(t) and a corresponding (optimal) trajectory x∗(t) such that its terminal value x∗(T) minimizes objective function (5.3). From the Pontryagin maximum principle, there exists a function s∗∈ L2([0,T]) such that the triple \(\left (x^{*}, s^{*}, p^{*}\right )\) solves for a.e. t ∈ [0,T] the system

$$ \begin{array}{@{}rcl@{}} &&\frac{\mathrm{d}}{\mathrm{d} t} x^{*}(t)=Q(t) x^{*}(t)+W(t) p^{*}(t), x^{*}(0)=x_{0} , \end{array} $$
(5.5)
$$ \begin{array}{@{}rcl@{}} &&\frac{\mathrm{d}}{\mathrm{d} t} s^{*}(t)=-Q(t)^{\mathsf{T}} s^{*}(t), s^{*}(T)=\nabla {\varPhi}\left( x^{*}(T)\right) , \end{array} $$
(5.6)
$$ \begin{array}{@{}rcl@{}} &&0 \in W(t)^{\mathsf{T}} s^{*}(t)+N_{V}\left( p^{*}(t)\right) , \end{array} $$
(5.7)

where NV(p) is the normal cone to V at p defined by

$$ N_{V}(p):=\left\{\begin{array}{ll} \emptyset, & \text { if } p \notin V ; \\ \{\iota \in \mathscr{H}:\langle \iota, q-p\rangle \leq 0, \forall q \in V\}, & \text { if } p \in V . \end{array}\right. $$

Denoting Gp(t) := W(t)Ts(t), Khoroshilova [34] showed that Gp is the gradient of the objective function g. Therefore, system (5.5)–(5.7) is reduced to the variational inequality problem

$$ \left\langle G p^{*}, q-p^{*}\right\rangle \geq 0 , \quad \forall q \in V . $$
(5.8)

Recently, there are many approaches to solve the optimal control problem, see, for example, [34,35,36,37]. Note that our algorithms (3.29) and (3.39) guarantee strong convergence and do not require the prior information of the Lipschitz constant of the mapping. Furthermore, the addition of inertial terms makes them converge faster.

For the convenience of numerical computation, we discretize the continuous functions. Take the mesh size h := T/N, where N is a natural number. We identify any discretized control \(p^{N}:=\left (p_{0}, p_{1}, \ldots , p_{N-1}\right )\) with its piecewise constant extension:

$$ p^{N}(t)=p_{i} , \forall t \in\left[t_{i}, t_{i+1}\right), t_{i}=ih , i=0,1, \ldots, N . $$

Moreover, we identify the discretized state \(x^{N}:=\left (x_{0}, x_{1}, \ldots , x_{N}\right )\) and co-state \(s^{N}:=\left (s_{0}, s_{1}, \ldots , s_{N}\right )\). They have the form of piecewise linear interpolation:

$$ x^{N}(t)=x_{i}+\frac{t-t_{i}}{h}\left( x_{i+1}-x_{i}\right), \forall t \in\left[t_{i}, t_{i+1}\right), i=0,1, \ldots, N-1 , $$

and

$$ s^{N}(t)=s_{i}+\frac{t_{i}-t}{h}\left( s_{i-1}-s_{i}\right), \forall t \in\left( t_{i-1}, t_{i}\right], i=N, N-1, \ldots, 1 . $$

We consider the classical Euler discretization method to solve the systems of ODEs (5.5) and (5.6). Thus, the Euler discretization of the original system (5.1)–(5.4) is given by

$$ \begin{aligned} \text{minimize} & {\varPhi}_{N}\left( x^{N}, p^{N}\right) \\ \text{subject to} & x_{i+1}^{N}={x_{i}^{N}}+h\left[Q\left( t_{i}\right) {x_{i}^{N}}+W\left( t_{i}\right) {p_{i}^{N}}\right], x^{N}(0)=x_{0} , \\ & {s_{i}^{N}}=s_{i+1}^{N}+h Q\left( t_{i}\right)^{\mathsf{T}} s_{i+1}^{N}, s(N)=\nabla {\varPhi}(x_{N}) , \\ & {p_{i}^{N}} \in V . \end{aligned} $$

It is well known that the Euler discretization has the error estimate O(h) [38]. This indicates that the difference between the discretized solution pN(t) and the original solution p∗(t) is proportional to the mesh size h. That is, there exists a constant K > 0 such that \(\left \|p^{N}-p^{*}\right \| \leq K h\).

Now, we provide some numerical examples to confirm the theoretical results of the derived algorithms (3.29) and (3.39). Our parameters are set as follows:

$$ N=100,\tau=10^{-2}, \varepsilon_{n}=\frac{10^{-4}}{(n+1)^{2}}, \delta=\zeta=0.5, \phi=0.4, \theta=1.5, \varphi_{n}=\frac{10^{-4}}{n+1}, f(x)=0.1x . $$

The initial controls p0(t) = p1(t) are randomly generated in [− 1,1], and the stopping criterion is \(\left \|p_{n+1}-p_{n}\right \| \leq 10^{-4} \).

Example 4 (Control of a harmonic oscillator, see [39])

$$ \begin{aligned} \text{minimize} &x_{2}(3 \pi)\\ \text{subject to} & \dot{x}_{1}(t)=x_{2}(t) , \\ & \dot{x}_{2}(t) =-x_{1}(t)+p(t), \forall t \in[0,3 \pi] , \\ & x(0) =0 , \\ & p(t) \in[-1,1] . \end{aligned} $$

The exact optimal control of Example 4 is known:

$$ p^{*}(t)=\left\{\begin{aligned} 1, \quad & \text { if } t \in[0, \pi / 2) \cup(3 \pi / 2,5 \pi / 2) ; \\ -1, \quad & \text { if } t \in(\pi / 2,3 \pi / 2) \cup(5 \pi / 2,3 \pi] . \end{aligned}\right. $$

Algorithms (3.29) and (3.39) obtained an approximate solution after 107 and 109 iterations, respectively. They take 0.070847 s and 0.043855 s, respectively. Figure 4 shows the approximate optimal control and the corresponding trajectories of Algorithm (3.29).

Fig. 4
figure 4

Numerical results of Algorithm (3.29) in Example 4

Full size image

We now consider examples in which the terminal function is not linear.

Example 5 (Rocket car [35])

$$ \begin{aligned} \text{minimize} & \frac{1}{2}\left( \left( x_{1}(5)\right)^{2}+\left( x_{2}(5)\right)^{2}\right) , \\ \text{subject to} & \dot{x}_{1}(t)=x_{2}(t) , \\ & \dot{x}_{2}(t)=p(t), \forall t \in[0,5] , \\ & x_{1}(0)=6, x_{2}(0)=1 , \\ & p(t) \in[-1,1] . \end{aligned} $$

The exact optimal control of Example 5 is

$$ p^{*}=\left\{\begin{aligned} 1, \quad& \text { if } t \in(3.517, 5] ; \\ -1, \quad& \text { if } t \in(0, 3.517] . \end{aligned}\right. $$

After 256 iterations, Algorithm (3.29) takes 0.14696 s to obtain an approximate solution. Moreover, Algorithm (3.39) takes 0.28532 s to achieve an approximate solution after 352 iterations. The approximate optimal control and the corresponding trajectories of Algorithm (3.39) are plotted in Fig. 5.

Fig. 5
figure 5

Numerical results of Algorithm (3.39) in Example 5

Full size image

Example 6 (See [40])

$$ \begin{aligned} \text{minimize} & -x_{1}(2)+\left( x_{2}(2)\right)^{2} , \\ \text{subject to} & \dot{x}_{1}(t)=x_{2}(t) , \\ & \dot{x}_{2}(t)=p(t), \forall t \in[0,2] , \\ & x_{1}(0)=0, x_{2}(0)=0 , \\ & p(t) \in[-1,1] . \end{aligned} $$

The exact optimal control of Example 6 is

$$ p^{*}(t)=\left\{\begin{aligned} 1, \quad& \text { if } t \in[0,1.2) ; \\ -1, \quad& \text { if } t \in(1.2,2] . \end{aligned}\right. $$

Algorithm (3.29) takes 0.098119 s to obtain an approximate solution after 256 iterations. In addition, Algorithm (3.39) takes 0.17002 s to reach an approximate solution after 346 iterations. Figure 6 gives the approximate optimal control and the corresponding trajectories of Algorithm (3.29).

Fig. 6
figure 6

Numerical results of Algorithm (3.29) in Example 6

Full size image

To compare the execution efficiency of the suggested algorithms (3.29) and (3.39), we show the error estimates ∥pn+ 1 − pn∥ of the proposed algorithms for Examples 4–6 in Fig. 7.

Fig. 7
figure 7

Error estimates of the proposed algorithms in Examples 4–6

Full size image

Finally, we compare the proposed iterative schemes (3.29) and (3.39) with some strongly convergent algorithms in the literature. Four algorithms used to compare here are the Algorithm (3.39) (shortly, TLQ Alg. (3.39)) proposed by Tan, Liu and Qin [4], the Algorithm 3.2 (THR Alg. 3.2) suggested by Thong, Hieu and Rassias [26], the Algorithm 3.2 (TG Alg. 3.2) introduced by Thong and Gibali [27] and the Algorithm 3.2 (GTT Alg. 3.2) presented by Gibali, Thong and Tuan [28]. The parameters are N = 100, f(x) = 0.1x, \( \varphi _{n}=\frac {10^{-4}}{n+1} \) for all the algorithms; δ = 1, ζ = 0.5, ϕ = 0.4, 𝜃 = 1.5 for TG Alg. 3.2, GTT Alg. 3.2 and the suggested algorithms (3.29) and (3.39); τ = 10− 2 and \( \epsilon _{n}=\frac {10^{-4}}{(n+1)^{2}} \) for TLQ Alg. (3.39), THR Alg. 3.2 and the stated algorithms (3.29) and (3.39); μ = 0.1 and λ1 = 0.4 for TLQ Alg. (3.39) and THR Alg. 3.2. The initial controls p0(t) = p1(t) are randomly generated in [− 1,1]. The stopping criterion is \(\left \|p_{n+1}-p_{n}\right \| \leq 10^{-4} \) or reaching the maximum of 1000 iterations. Table 1 compares the number of iterations and execution time required for all the algorithms to reach the stopping criterion under Examples 4–6.

Table 1 Comparison of the number of iterations and execution time of all the algorithms in Examples 4–6
Full size table

Remark 5.5

From Examples 4–6, we have the following observations.

  1. (i)

    From Figs. 4, 5, and 6, it can be seen that the derived algorithms (3.29) and (3.39) work well when the terminal function is linear or nonlinear. However, it is noticed from Fig. 7 that they perform better when the terminal function is linear than when it is nonlinear, that is, they require fewer iterations under the same stopping criterion and have a more stable behavior.

  2. (ii)

    As shown in Table 1, the proposed iterative schemes (3.29) and (3.39) have better performance than some known results in the literature, i.e., they need fewer iterations and execution time under the same stopping condition, and these results are independent of the form of the terminal function. Thus, our suggested algorithms are efficient and robust.

  3. (iii)

    It is noted that the presented algorithms use an Armijo-type step size criterion, which makes them work without knowing the prior knowledge of the Lipschitz constants of the mapping involved. Indeed, in practical applications, the prior information of the Lipschitz constant is not easy to obtain, and the fixed step size algorithms suggested in [10, 17, 29, 30] will fail in this case. Therefore, several self-adaptive methods proposed in this paper are more useful in reality.

6 Conclusions

In this paper, we proposed two new iterative methods for solving bilevel variational inequality problems in a real Hilbert space when the involved mapping is pseudomonotone and Lipschitz continuous but the Lipschitz constant is unknown. The advantage of the suggested algorithms is that only one projection onto the feasible set needs to be performed. Strong convergence theorems of the stated iterative schemes were proved without the prior knowledge of the Lipschitz constant of the involved mapping. Several numerical experiments were performed to demonstrate the efficiency of the proposed algorithms over the related one. Finally, the derived methods were applied to solve optimal control problems and compared them with existing algorithms.