Signal transmission and energy consumption in excitatory–inhibitory cortical neuronal network

Abstract

Stochastic resonance and energy consumption are significant for information processing and transmission in the neural system. In this paper, we constructed an excitatory–inhibitory cortical neuronal network to investigate the response of the system to weak signals and the corresponding energy consumption. The findings indicate that the excitability of neurons modulates the performance of signal response. Furthermore, the performance of signal response exhibits a bell-shaped dependence on ion channel noise, which is a typical manifestation of the stochastic resonance phenomenon. Stochastic resonance also exists in the network with increasing noise at different excitatory coupling strengths and inhibitory coupling strengths. Furthermore, it is found that the neuronal system obtains optimal transmission of the weak signal at a lower energy consumption. It illustrates that there is a certain economy and efficiency in the signal transmission. At weak inhibitory coupling strength, an optimal excitatory coupling strength exists to allow the neuronal network to make the optimal transmission of the weak signal. However, the phenomenon of double resonant peaks occurs at strong inhibitory coupling strength, which is due to the balance of excitatory and inhibitory synaptic currents. Finally, we demonstrated the robustness of the results to network topology and initial conditions. The results of this paper may contribute to the understanding of signal transmission and its energy consumption in cortical networks.

1 Introduction

Stochastic resonance (SR) is a phenomenon that improves the response of a nonlinear system to the weak signal by adding a random perturbation [1,2,3,4,5], and this random perturbation generally refers to noise. A number of biological experiments have demonstrated the widespread existence of SR in the neural system. For example, the mechanoreceptors of crayfish [6], the cricket cercal sensory system [7], and the human proprioceptive system [8]. Moreover, SR is extensively investigated theoretically in individual neurons and neural networks [9,10,11].

These numerous studies have shown that there are many types of noise that can induce SR, such as Gaussian white noise [10, 12,13,14], color noise [15,16,17], ion channel noise [9, 18], etc. In particular, ion channel noise is the main source of noise in neuronal systems. It is an internal source of noise due to the random opening and closing of individual ion channels [18, 19], random permeability, and differences in ion concentrations inside and outside the cell. Therefore, it is relevant to consider ion channel noise in the investigation of SR in the neural system. Researchers studied ion channel noise-induced SR phenomena in various network topologies. Ozer et al. demonstrated in a small-world network [20] and feedforward network [21] that the existence of optimal intensity of ion channel noise makes the optimization of signal transmission for neuronal networks. Yilmaz et al. showed that the best temporal coherence in a scale-free Hodgkin-Huxley (H-H) neuronal network is obtained with a certain degree of intrinsic noise [22].

With the deepening of the study, some experimental studies have revealed that SR can also be generated in cortical networks. Funke et al. discovered a similar phenomenon to SR by adding weak, sub-threshold, and peri-threshold visual stimuli to the cat primary visual cortex and superimposing noise with variable jitter amplitude [23]. Van der Groen and Wenderoth demonstrated that cortical networks that process visual stimuli can exhibit the SR phenomenon [24]. It is shown that SR has an important impact on the transmission of weak signal and information processing in the neural system. There are two major kinds of neurons in the mammalian cerebral cortex, the excitatory pyramidal neurons and the inhibitory interneurons [25, 26]. Moreover, the ratio of excitatory neurons to inhibitory neurons was found to be 4:1 in the visual cortex of rats [27]. Yu et al. constructed a cortical network based on this [28]. They demonstrated that time delay and electrical-chemical synapses have an important role in SR and determine the capacity of the neural system to enhance information transmission. Enlightened by this, We constructed an excitatory-inhibitory cortical neuronal network using the H-H neuron as the basic unit in this paper.

The normal operation of the brain is inextricably connected to energy. It is known that the human brain accounts for only 2% of body weight but consumes 20% of human metabolic energy [29]. Furthermore, the energy required for the processing and transmission of information accounts for a large portion of the energy consumption of the brain [30]. Currently, there are three methods used to study the energy of neuronal systems. The methods used to calculate energy consumption are the ion counting method [31,32,33] and the equivalent circuit method [34,35,36]. The Hamilton energy function based on Helmholtz’s theorem is mainly used to study the energy storage, conversion and energy balance of the system [37]. The ion counting method limits the accurate assessment of the metabolic cost of ionic currents in action potential conduction along the axon [38]. Therefore the equivalent circuit method is more accurate compared to the ion counting method, so the energy consumption has been calculated using the equivalent circuit method in this paper. The consumption of energy during information transmission in the neural system has been studied in recent years based on this method. For example, it is reported that information processing capacity and energy efficiency can be maximized by regulating the number of active ion channels [39]. Yu et al. showed that neuronal systems can obtain reliable logic operations with low energy consumption in logical stochastic resonance [40, 41]. SR is related to information transmission [23, 24], thus it is significant to research its energy consumption.

Despite the extensive studies on SR in the neural system, so far as we know that energy consumption during the transmission of weak signals by the neural system has not been considered. Therefore, in this paper, the response performance and energy consumption of a single H–H neuron and an excitatory-inhibitory cortical neuronal network to the weak signal are investigated by using the equivalent circuit method.

The paper is organized as follows: in Sect. 2, mathematical models of the single neuron and the excitatory-inhibitory cortical neuronal network are introduced, and equations for energy consumption are derived by the equivalent circuit method. In Sects. 3.1 and 3.2, the SR and energy consumption of the single neuron and neuronal network are discussed, respectively. In Sect. 3.3, we verify the robustness of the results. Finally, a summary of the results is given in Sect. 4.

2 Model and methods

In this paper, the classical H-H model [42] is used to investigate the capability of neurons to respond weak signals and the energy consumption of neuronal action potentials.

2.1 Single neuron

The dynamics of the membrane potential of a neuron can be described as follows:

$$ C_{m} \frac{{{\text{d}}V}}{{{\text{d}}t}} = - i_{{{\text{Na}}}} - i_{{\text{K}}} - i_{{\text{L}}} + I_{0} + I_{{{\text{ext}}}} , $$

(1)

where

$$ \left\{ \begin{gathered} i_{{{\text{Na}}}} = g_{{{\text{Na}}}} m^{3} h(V - E{}_{{{\text{Na}}}}), \hfill \\ i_{{\text{K}}} = g_{{\text{K}}} n^{4} (V - E_{{\text{K}}} ), \hfill \\ i_{{\text{L}}} = g_{{\text{L}}} (V - E_{{\text{L}}} ), \hfill \\ \end{gathered} \right. $$

(2)

where C_m = 1 µF/cm² is the neuronal cell membrane capacitance, V denotes the membrane potential of the neuron. i_Na, i_K, and i_L are sodium ion current, potassium ion current, and leakage current, respectively. g_Na = 120 mS/cm², g_K = 36 mS/cm² and g_L = 0.3 mS/cm² are the maximum values of the conductance of each ion channel. E_Na = 50 mV, E_K = − 77 mV, E_L = − 54.4 mV are the Nernst potentials for i_Na, i_K, and i_L. To consider the effect of ion channel noise on neuronal dynamics, the Langevin equation with the addition of ion channel noise to the three gating variables, n, m, and h, is given as follows [43]:

$$ \frac{{{\text{d}}X}}{{{\text{d}}t}} = \alpha_{X} (1 - X) - \beta_{X} X + \xi_{X} (t),(X = n,m,h) $$

(3)

Where α_X (t) and β_X (t) are rate functions of the gating variables, described as follows:

$$ \left\{ \begin{gathered} \alpha_{n} = \frac{0.01(V + 55)}{{1 - \exp [ - (V + 55)/10]}},\beta_{n} = 0.125\exp [ - (V + 65)/80], \hfill \\ \alpha_{m} = \frac{0.1(V + 40)}{{1 - \exp [ - (V + 40)/10]}},\beta_{m} = 4\exp [ - (V + 65)/18], \hfill \\ \alpha_{h} = 0.07\exp [ - (V + 65)/20],\beta_{h} = \frac{1}{1 + \exp [ - (V + 35)/10]}. \hfill \\ \end{gathered} \right. $$

(4)

In Eq. (3), ξ_X (t) is independent Gaussian white noise with zero means, and its statistical characteristics are described as follows:

$$ \left\{ \begin{gathered} \left\langle {\xi_{n} (t)\xi_{n} (t^{\prime})} \right\rangle = \frac{2}{{N_{K} }}\frac{{\alpha_{n} \beta_{n} }}{{(\alpha_{n} + \beta_{n} )}}\delta (t - t^{\prime}), \hfill \\ \left\langle {\xi_{m} (t)\xi_{m} (t^{\prime})} \right\rangle = \frac{2}{{N_{Na} }}\frac{{\alpha_{m} \beta_{m} }}{{(\alpha_{m} + \beta_{m} )}}\delta (t - t^{\prime}), \hfill \\ \left\langle {\xi_{h} (t)\xi_{h} (t^{\prime})} \right\rangle = \frac{2}{{N_{Na} }}\frac{{\alpha_{h} \beta_{h} }}{{(\alpha_{h} + \beta_{h} )}}\delta (t - t^{\prime}), \hfill \\ \end{gathered} \right. $$

(5)

where N_K = ρ_KS and N_Na = ρ_NaS indicate the number of potassium and sodium ion channels, respectively, and the number of ion channels affects the level of ion channel noise. When the ion channel density is homogenous with ρ_K = 18 µm⁻² and ρ_Na = 60 µm⁻², the number of ion channels depends on the total cell membrane area S [19]. The larger S, the greater N_K and N_Na, and therefore the smaller the ion channel noise intensity.

In Eq. (1), the I₀ refers to the bias current, which regulates the level of excitability in the neuron [44]. I_ext = Acos(ωt) is the external input weak signal, where the amplitude A = 1.03 µA/cm² and the angular frequency ω = 0.3 rad/ms. The sub-threshold (resting state) and supra-threshold (firing state) states in the amplitude-period parameter plane are illustrated in Fig. 1, so the weak signal we apply to the neuron is sub-threshold. In this section, the Euler algorithm is used, the time step is set as 0.01 ms, and the initial values of (V, n, m, h) are set as (0.0, 0.0, 0.0, 0.0).

Fig. 1

The parameter plane of signal amplitude A and angular frequency ω. The yellow and green regions indicate the firing and resting states, respectively. Our parameters ensure that the weak signal applied to neurons is sub-threshold

The response of a neuron to an input weak signal is evaluated by calculating the Fourier coefficient Q [45], defined as follows:

$$ \left\{ \begin{gathered} Q = \sqrt {Q_{\sin }^{2} + Q_{\cos }^{2} } , \hfill \\ Q_{\sin } = \frac{1}{T}\int_{{T_{0} }}^{{T_{0} + T}} {} 2V(t)\sin (\omega t){\text{d}}t{,} \hfill \\ Q_{{{\text{cos}}}} = \frac{1}{T}\int_{{T_{0} }}^{{T_{0} + T}} {} 2V(t)\cos (\omega t){\text{d}}t{,} \hfill \\ \end{gathered} \right. $$

(6)

T₀ = 50 ms is set to eliminate the effect of model initialization on the simulation calculation, T = 2nπ/ω indicates the total duration of the calculation, and the number of the period n = 500 is set in the numerical simulation of a single neuron. The results are obtained by averaging 40 independent runs. It is well known that information transmission during neuronal firing primarily relies on large spikes rather than sub-threshold oscillations, so we are primary interested in the frequency of the spikes [46]. Therefore, we set the threshold V_S = 0 mV, if V < V_S, then replace V with the fixed point V_f = − 1 mV; otherwise, V remains the same [47]. The larger Q indicates the higher level of synchronization between neuronal output activity and weak signal, resulting in a better response of neurons to the weak signal.

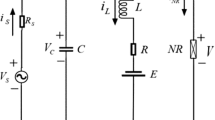
In this paper, the equivalent circuit method is used to calculate the metabolic energy of neuronal action potentials [34, 48, 49]. Considering the H-H neuron model as an electronic circuit, circuit elements include membrane capacitance, maximum variable conductance of sodium, potassium, and leakage ions, and the corresponding Nernst potentials of the ions as batteries. The equivalent circuit of the H-H neuron is shown in Fig. 2. The total energy consumption by the circuit at a given moment is [34]:

$$ H(t) = \frac{1}{2}CV^{2} + H_{{{\text{Na}}}} + H_{{\text{K}}} + H_{{\text{L}}} , $$

(7)

the first term on the right is the electrical energy accumulated in the membrane capacitance, and the other three terms are the energy consumption of each battery. It is known that the rate of the electrical energy supplied by the battery to the circuit is equal to the battery potential multiplied by the current through the battery. Thus, the total energy consumption rate is the derivative of Eq. (7) for time:

$$ P = \frac{{{\text{d}}H}}{{{\text{d}}t}} = C_{m} \frac{{{\text{d}}V}}{{{\text{d}}t}}V + i_{{{\text{Na}}}} E_{{{\text{Na}}}} + i_{{\text{K}}} E_{{\text{K}}} + i_{{\text{L}}} E_{{\text{L}}} . $$

(8)

Fig. 2

The equivalent circuit diagram of the H-H model

Substituting Eq. (1) into Eq. (8), we obtain:

$$ P = V(I_{0} + I_{{{\text{ext}}}} ) - i_{{{\text{Na}}}} (V - E_{{{\text{Na}}}} ) - i_{{\text{K}}} (V - E_{{\text{K}}} ) - i_{{\text{L}}} (V - E_{{\text{L}}} ), $$

(9)

the first term on the right side of Eq. (9) represents the electrical energy provided to the neuron by the external input, and the other three terms represent the energy consumed per second by the ion pump. Thus, the average energy consumption E_c of a neuron when it is working can be expressed as:

$$ E_{c} = \frac{1}{T}\int_{{T_{{0}} }}^{{T_{{0}} + T}} {i_{{{\text{Na}}}} (V - E_{{{\text{Na}}}} )} + i_{{\text{K}}} (V - E_{{\text{K}}} ) + i_{{\text{L}}} (V - E_{{\text{L}}} ){\text{d}}t. $$

(10)

The phenomenon of SR is important for the transmission of information [28], and the response of neurons to weak signals is also the transmission of signals. To investigate the energy efficiency of the signal transmission process, the energy efficiency η is defined as the ratio of Q to Ec:

$$ \eta = \frac{Q}{{E_{c} }}. $$

(11)

2.2 Excitatory–inhibitory cortical neuronal network

To further investigate the collective behavior of the neuronal system, and considering the experimentally observed small-world nature of cortical connectivity [50,51,52]. So an excitatory-inhibitory cortical neuronal network consisting of the same H-H neurons and implemented on the Watts-Strogatz (WS) small-world model is used. The network is composed of N = 60 identical neurons with a 4:1 ratio of excitatory to inhibitory neurons [27]. The rewiring probability is denoted by P. The degree of each node is denoted by K. Unless otherwise specified, P = 0.4, K = 12 [53]. The dynamical equations of the network are expressed as follows:

$$ C_{m} \frac{{{\text{d}}V_{i} }}{{{\text{d}}t}} = - i_{{{\text{Na,}}i}} - i_{{{\text{K,}}i}} - i_{{{\text{L,}}i}} + I_{0} + I_{{{\text{ext,}}i}} + I_{{{\text{syn,}}i}} , $$

(12)

$$ \frac{{{\text{d}}X_{i} }}{{{\text{d}}t}} = \alpha_{{X_{i} }} (1 - X_{i} ) - \beta_{{X_{i} }} X_{i} + \xi_{{X_{i} }} (t),(X_{i} = n_{i} ,m_{i} ,h_{i} ), $$

(13)

where V_i is the membrane potential of neuron i. I_ext,i = Acos(ωt) is the weak signal applied to neuron i. We apply the weak signal to each neuron. I_syn,i is the synaptic current received by neuron i. Neurons are coupled to each other by excitatory or inhibitory chemical synapses, so I_syn,i consists of the excitatory synaptic current I_synE,i and the inhibitory synaptic current I_synI,i:

$$ \begin{aligned} I_{{{\text{syn}},i}} = & I_{{{\text{syn}}E,i}} + I_{{{\text{syn}}I,i}} \\ = & g_{E} (V_{{{\text{rev}}E}} - V_{i} )\sum\limits_{j = 1}^{0.8N} {A_{ij} } \frac{1}{{1 + \exp [ - \lambda (V_{j} - \theta_{s} )]}} + g_{I} (V_{{{\text{rev}}I}} - V_{i} )\sum\limits_{j = 0.8N + 1}^{N} {A_{ij} } \frac{1}{{1 + \exp [ - \lambda (V_{j} - \theta_{s} )]}}, \\ \end{aligned} $$

(14)

g_E and g_I are excitatory coupling strength and inhibitory coupling strength, respectively. For excitatory coupling, the synaptic reversal potential is set to V_revE = 0 mV; for inhibitory coupling, the synaptic reversal potential is set to V_revI = − 80 mV. A_ij denotes the connection matrix. If neuron i is connected to neuron j, then A_ij = 1, otherwise A_ij = 0. Other parameters are set as λ = 30, θ_s = 0. In the network, we randomly and uniformly assign distinct initial conditions to each neuron from a predefined region in the four-dimensional state space (V, n, m, h).

To describe the transmission of weak signals in the network, the average Fourier coefficient $\left\langle Q \right\rangle$ is calculated as the average of each value of Q_i as follow:

$$ \left\langle Q \right\rangle = \frac{1}{N}\sum\limits_{i = 1}^{N} {Q_{i} } , $$

(15)

where

$$ \left\{ \begin{gathered} Q_{i} = \sqrt {Q_{\sin ,i}^{2} + Q_{\cos ,i}^{2} } , \hfill \\ Q_{\sin ,i} = \frac{1}{T}\int_{{T_{0} }}^{{T_{0} + T}} {2V_{i} (t)\sin (\omega t){\text{d}}t} {,} \hfill \\ Q_{{{\text{cos,}}i}} = \frac{1}{T}\int_{{T_{0} }}^{{T_{0} + T}} {2V_{i} (t)\cos (\omega t){\text{d}}t} {,} \hfill \\ \end{gathered} \right. $$

(16)

the number of the period n = 500 is set in the numerical simulation of the network. The average energy consumption $\left\langle {E_{c} } \right\rangle$ of the neurons in the network is the average of the energy consumption E_cⁱ of each neuron as follow:

$$ \left\langle {E_{c} } \right\rangle = \frac{1}{N}\sum\limits_{i = 1}^{N} {E_{c}^{i} } . $$

(17)

The average energy efficiency $\left\langle \eta \right\rangle$ in a network is defined as the ratio of $\left\langle Q \right\rangle$ to $\left\langle {E_{c} } \right\rangle$ as follows:

$$ \left\langle \eta \right\rangle = \frac{\left\langle Q \right\rangle }{{\left\langle {E_{c} } \right\rangle }} $$

(18)

We measure the mean firing rate $\left\langle r \right\rangle$ of neurons in the network:

$$ \left\langle r \right\rangle = \frac{1}{NT}\left( {\sum\limits_{i = 1}^{N} {n_{spike,i} } } \right), $$

(19)

where nspike is the number of spikes occurring in time length T.

In order to systematically measure the coherence and degree of regularity of neuronal firing, a statistic is introduced, the coefficient of variation CV [54],

$$ CV = \frac{1}{N}\sum\limits_{i = 1}^{N} {CV_{i} } , $$

(20)

where

$$ CV_{i} = \frac{{\sqrt {\left\langle {ISI_{i}^{2} } \right\rangle - \left\langle {ISI_{i} } \right\rangle^{2} } }}{{\left\langle {ISI_{i} } \right\rangle }},\left\langle {ISI_{i} } \right\rangle = \frac{1}{M}\sum\limits_{k = 1}^{M} {(t_{i,k} - t_{i,k - 1} )} ,\left\langle {ISI_{i}^{2} } \right\rangle = \frac{1}{M}\sum\limits_{k = 1}^{M} {(t_{i,k} - t_{i,k - 1} )^{2} } , $$

(21)

where ISI_i represents the inter-spike interval of each neuron and M is the number of ISI. The lower the value of CV, the more regular the firing of neurons.

In addition, a synchronization factor SF that can measure the collective synchronous dynamical behavior of neurons in the network is introduced with the following expression [55]:

$$ SF = \frac{{\overline{{F^{2} }} - \overline{F}^{2} }}{{\frac{1}{N}\sum\limits_{i = 1}^{N} {(\overline{{V_{i}^{2} }} - \overline{{V_{i} }}^{2} )} }},F = \frac{1}{N}\sum\limits_{i = 1}^{N} {V_{i} ,} $$

(22)

the average symbol in this equation represents the average of physical quantities over time, and SF close to 1 means the network is completely synchronized.

3 Numerical results and discussion

3.1 Single neuron response to the weak signal and energy consumption

The effect of ion channel noise on the response of a single neuron to the weak signal is investigated in Fig. 3a. It is found that Q exhibits a bell-shaped dependence on with S, there is an optimal S to enable the best response to the weak signal. Furthermore, the temporal evolution of the membrane potential of a neuron and the corresponding energy consumption rate are plotted in Fig. 3b-d for different S. To facilitate comparison, the weak signal is marked with the red line. When S = 1 µm² (Fig. 3b), the noise intensity is large enough to induce the neuron to firing in the absence of weak signal. It can lead to a destruction of the correlation between the neuronal firing activity and the weak signal. In Fig. 3c, a reduction in noise intensity results in the neuron’s optimal response to the weak signal, at which the weak signal is enhanced. As S increases further (Fig. 3d), the neuron still responds to the weak signal, but the response becomes worse because the noise is reduced and the neuron firing rate decreases. Furthermore, it can be observed that the ion pump energy consumption rate changes with the neuronal action potential, and its peak and oscillation frequency strictly relate to neuronal firing.

Fig. 3

a The dependence of Q on S. Temporal evolution of membrane potential and ion pump energy consumption at different S: b S = 1 µm²; c S = 10 µm²; d S = 100 µm². A part of the time series is shown for clear observation. There exists an optimal S such that the neuron has the best response to the weak signal. Fixed parameter: I₀ = 0 µA/cm²

To more clearly illustrate the response of a neuron to the weak signal in Fig. 3, the inter-spike interval histogram (ISIH) is further calculated for 1000 ISIs, as in Fig. 4. In this paper, the angular frequency of the weak signal added is ω = 0.3 rad/ms, so its period is about 21 ms. It is marked by a black dashed line at ISI = 21 ms in the figure. When S is small (Fig. 4a), there is a sharp peak in ISIH. However, the frequency corresponding to the sharp peak is not coherent with the frequency of the weak signal, so the Q value is small at a large noise intensity. For S = 10 µm² in Fig. 4b, the appropriate noise intensity causes the peak of ISIH to appear at the period of the weak signal. Because the time scale of the intrinsic oscillations caused by the weak signal matches the time scale of the noise-influenced neuronal dynamics [56], and therefore a better Q value can be obtained. As S increases further, ISIH exhibits a sharp peak at the weak signal period and some small sharp peaks at the harmonics of the period. The peak at S = 100 µm² is smaller than that at S = 10 µm², so the Q value is relatively reduced. It is because the noise intensity is diminished and the neurons sometimes do not firing even with the addition of the weak signal.

Fig. 4

The ISIH of the H–H neuron at different S. The ISI is divided equally into 1000 parts. a S = 1 µm²; b S = 10 µm²; c S = 100 µm². The appropriate ISI range is chosen for readability. The response of the neuron to the weak signal is optimal when S = 10 µm². Fixed parameter: I₀ = 0 µA/cm²

The dependence of Q and E_c on the S at different I₀ are investigated in Fig. 5. As shown in Fig. 5a, it can be seen that the ion channel noise-induced SR phenomenon is present in neurons at different I₀. As I₀ increases, the optimal S gradually increases. In other words, the larger I₀, the smaller the noise intensity is required for the neuron to obtain the best response to the weak signal. Furthermore, the peak of Q has a nonlinear effect with increasing I₀, i.e., increasing first and then decreasing. In Fig. 5b, E_c decreases and finally plateaus with increasing S. The reason is that the higher the noise, the higher the firing rate of the neuron and thus the more energy is consumed. The larger I₀ leads to an increase in energy consumption when subjected to the same level of noise [34, 41]. Thus the efficiency is shown in Fig. 5c, and it can be seen that noise maximizes the energy efficiency of the neuron. Comparing with Fig. 5a, the neuron still keeps the weak signal response high enough under the noise that maximizes energy efficiency. Moreover, the maximum value of Q has a nonlinear effect, while the maximum value of η is monotonic. The SR phenomenon is robust for different I₀, and the best signal transmission efficiency is obtained at I₀ = 0 µA/cm². Therefore, in the following investigation, we set the bias current to I₀ = 0 µA/cm².

Fig. 5

a-c The dependence of Q, E_c, and η on S for different I₀. It is seen that the SR phenomenon is robust for different I₀, and the neuron still keeps the weak signal response high enough under the noise that maximizes energy efficiency

3.2 Excitatory–inhibitory cortical neuronal network transmission of weak signals and energy consumption

We have studied SR and its energy consumption of a single neuron in Sect. 3.1, but the human brain consists of hundreds of billions of neurons [56]. Therefore, further research the signal transmission and its energy consumption in the network level is essential. The small-world network model has been widely used to study SR [20, 57, 58] and cortical connections have been experimentally observed to have small-world properties [50,51,52]. The network schematic is shown in Fig. 6. Therefore, we constructed an excitatory-inhibitory cortical neuronal network based on the small-world network model.

Fig. 6

Schematic examples of regular and small-world network topologies (For readability, N = 20 in the example schematic shown here). a Regular network: P = 0, K = 8. b Small-world network: P = 0.4, K = 8

First, the effects of excitatory coupling strength g_E and inhibitory coupling strength g_I in the network are investigated. In Fig. 7a, the dependence of $\left\langle Q \right\rangle$ on g_E is calculated for different g_I. The increase of g_E results in the SR phenomenon, where the existence of an optimal g_E allows the best transmission of the weak signal, and the increase of g_I decreases the peak of $\left\langle Q \right\rangle$ The $\left\langle {E_{c} } \right\rangle$ initially rises as g_E increases and stabilizes at a relatively constant level once it reaches the optimal g_E value. This is because a larger g_E leads to an increased firing rate of neurons, which in turn results in higher energy consumption. Additionally, when the energy efficiency is maximized, it corresponds to a better signal transmission performance.

Fig. 7

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on g_E for different g_I in the excitatory-inhibitory cortical neuronal network. $\left\langle Q \right\rangle$ has a bell-shaped dependence on g_E and when energy efficiency is maximized, the network corresponds to a better signal transmission performance. Fixed parameter: S = 30 µm²

The effects of g_E and g_I are further analyzed globally, as shown in Fig. 8. It can be seen that the increase of g_E can induce the SR phenomenon, but g_I cannot, which can only make $\left\langle Q \right\rangle$ gradually decrease. Furthermore, when g_I is small, the results are consistent with those shown in Fig. 7. However, there are double resonant peaks in $\left\langle Q \right\rangle$ with increasing g_E when g_I increases to a certain level. The balance between excitatory and inhibitory synaptic currents induces an energy-efficient mode in the cortical network [59,60,61,62,63,64,65].

Fig. 8

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on g_E and g_I in the excitatory-inhibitory cortical neuronal network. The figure shows that g_E induces the SR phenomenon while g_I cannot, and $\left\langle Q \right\rangle$ shows double resonant peaks at the larger g_I. Fixed parameter: S = 30 µm²

A comprehensive explanation is provided in Fig. 9. The results are obtained by averaging over 20 independent runs, where each run has different initial values and random noise, but the network topology remains the same. The robustness of the results to the network topology is demonstrated in Sect. 3.3.

Fig. 9

a The dependence of $\left\langle Q \right\rangle$ on g_E in the excitatory-inhibitory cortical neuronal network. b The dependence of $\left\langle r \right\rangle$ multiplied by 2π on g_E. b1-b4 The PDH of r (ω = 2πr) of 60 neurons in the network at g_E = 0.074 mV/cm², g_E = 0.144 mV/cm², g_E = 0.34 mV/cm², and g_E = 1.174 mV/cm². a1-a4 correspond to (b1)-(b4). The ω is divided equally into 20 parts. c The dependence of CV on g_E. d The dependence of SF on g_E. The figure shows that the network has better signal transmission performance only when the firing period of most neurons matches the period of the weak signal. Fixed parameter: S = 30 µm², g_I = 2.0 mV/cm²

When g_I = 2.0 mV/cm², there is a peak of $\left\langle Q \right\rangle$ at small and large g_E in Fig. 9a, respectively. The four points (a1)-(a4) are selected to further investigate the dynamics mechanism, corresponding to g_E of 0.074 mV/cm², 0.144 mV/cm², 0.34 mV/cm², and 1.174 mV/cm², respectively. To better correspond with the angular frequency of the signal, the $\left\langle r \right\rangle$ in the vertical axis in Fig. 9b is multiplied by 2π to convert it into mean angular frequency $\left\langle \omega \right\rangle$. Moreover, the probability distribution histogram (PDH) of the firing rate of 60 neurons in the network at the corresponding point is plotted respectively in Fig. 9b1-b4. We infer that the network should have the best signal transmission when $\left\langle \omega \right\rangle$ = 0.3 rad/ms. In contrast to our expectations, point (a1) corresponds to the first peak of $\left\langle Q \right\rangle$, but with $\left\langle \omega \right\rangle$ < 0.3 rad/ms; the $\left\langle Q \right\rangle$ at point (a2) is smaller than (a1), while $\left\langle \omega \right\rangle$ = 0.3 rad/ms. As in Fig. 9b1, most neurons have ω = 0.3 rad/ms so $\left\langle Q \right\rangle$ is high, but the ω of each neuron after overall averaging has $\left\langle \omega \right\rangle$ < 0.3 rad/ms. However, for Fig. 9b2, most neurons have ω > 0.3 rad/ms so $\left\langle Q \right\rangle$ is low and $\left\langle \omega \right\rangle$ = 0.3 rad/ms. The ω of the neuron deviates further by 0.3 rad/ms in Fig. 9b3, resulting in a decrease of $\left\langle Q \right\rangle$ to a minimum and $\left\langle \omega \right\rangle$ reaches a maximum. It is not until ω returns to 0.3 rad/ms for essentially all neurons $\left\langle Q \right\rangle$ reaches its peak again in Fig. 9b4. Therefore, the network has better signal transmission performance only if the firing period of most neurons matches the period of the weak signal.

Such a phenomenon is mainly related to the different mechanisms of action of excitatory and inhibitory synaptic currents on the network. The presence of strong inhibitory synaptic currents (large g_I) leads to increased disorder in each neuron within the network [66], resulting in a higher CV (Fig. 9c). Additionally, it also leads to reduced synchrony between neurons, indicated by a smaller SF (Fig. 9d). This collective asynchrony introduces the influence of synaptic noise [66, 67], resulting in worse signal transmission within the network, $\left\langle Q \right\rangle$ decreasing. The effect of excitatory synaptic currents is indeed opposite, they enhance the firing regularity and synchrony of the neuronal network [41]. When there is a balance between the excitatory and inhibitory components in the network, the firing of neurons becomes more orderly, resulting in a decrease in CV and an increase in SF. This enhances the signal transmission in the network. Our results indicate that the signal transmission performance in the cortical network strongly relies on the balance between excitatory and inhibitory synaptic currents.

In addition, the weak signal transmission of the network and $\left\langle {E_{c} } \right\rangle$ under the influence of ion channel noise at different g_E are plotted in Fig. 10. Regardless of the strength of g_E, ion channel noise induces the SR phenomenon in the network, and the optimal weak signal transmission can be obtained at moderate noise levels. It is just that at small g_E, the network has a poor transmission for weak signals and the corresponding $\left\langle {E_{c} } \right\rangle$ is small. Within the S range where $\left\langle Q \right\rangle$ exhibits better values, a plateau in $\left\langle {E_{c} } \right\rangle$ is observed, indicating a level of moderate energy consumption. These results suggest that information transmission in cortical networks also depends on the noise intensity and that better signal transmission is obtained at lower energy consumption.

Fig. 10

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on for different g_E in the excitatory-inhibitory cortical neuronal network. It can be seen that better $\left\langle Q \right\rangle$ can be obtained at moderate noise levels and better signal transmission can be obtained at lower energy consumption. Fixed parameter: g_I = 0.5 mV/cm²

The global contour plots of g_E and S are shown in Fig. 11. There is an island (red-shaded region) in Fig. 11a, and the presence of optimal g_E and S in this region allows the network to best transmit weak signals. Therefore, when g_I is small, the effect of g_E on weak signal transmission is similar to that of ion channel noise. In Fig. 11b, it can be seen that the region with optimal $\left\langle Q \right\rangle$ corresponds to a lower $\left\langle {E_{c} } \right\rangle$, which indicates the economy of signal transmission. The region with the best $\left\langle \eta \right\rangle$ in Fig. 11c is essentially consistent with the region with the optimal $\left\langle Q \right\rangle$ in Fig. 11a, which illustrates the efficiency of signal transmission.

Fig. 11

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on g_E and S in the excitatory-inhibitory cortical neuronal network. It can be seen that an island (red-shaded region) exists in a, which indicates high signal transmission performance. Furthermore, it corresponds to a moderate $\left\langle {E_{c} } \right\rangle$ region (yellow region) and a high $\left\langle \eta \right\rangle$ region (red-shaded region). Fixed parameter: g_I = 0.5 mV/cm²

The effect of ion channel noise at different g_I is also investigated, as shown in Fig. 12. Moreover, contour plots of g_I and S are shown in Fig. 13. It can be found that the SR phenomenon also occurs at different g_I, but the increase of g_I can gradually inhibit the transmission of the network to weak signals. Similarly, the network transmits optimally to weak signals at moderate noise intensity. The region in Fig. 13a where an optimal signal transmission (red-shaded region) corresponds to the moderate $\left\langle {E_{c} } \right\rangle$ (yellow region) in Fig. 13b. In addition, it also corresponds to the region in Fig. 13c where the $\left\langle \eta \right\rangle$ is highest (red-shaded region). It demonstrates that the economy and efficiency of signal transmission still exist. Finally, the network can improve the transmission of weak signals compared to that of a single neuron for the weak signal.

Fig. 12

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on S for different g_I in the excitatory-inhibitory cortical neuronal network. It can be seen that S can also induce SR phenomenon for different g_I and better signal transmission can be obtained at lower energy consumption. Fixed parameter: g_E = 0.5 mV/cm²

Fig. 13

a-c The dependence of $\left\langle Q \right\rangle$, $\left\langle {E_{c} } \right\rangle$, and $\left\langle \eta \right\rangle$ on g_I and S in the excitatory-inhibitory cortical neuronal network. It can be seen that the high $\left\langle Q \right\rangle$ region (red-shaded region) corresponds to the moderate $\left\langle {E_{c} } \right\rangle$ region (yellow region) and the high $\left\langle \eta \right\rangle$ region (red-shaded region). Fixed parameter: g_E = 0.5 mV/cm²

3.3 Robustness of network topology on results

In this section, to demonstrate that our results do not rely on a certain fixed network connectivity matrix, on fixed noise and initial value settings, or even on the characteristic parameters of network topology. The results of all our calculations in this section are obtained by averaging 20 independent runs, each of which changes the initial value random number, the noise random number, and the network connectivity matrix. The error bars for each curve are also plotted.

In Fig. 14, it is found that changing the connection matrix can still reproduce the previously obtained phenomena. It indicates that the phenomena and analysis we obtained are robust and not characteristic of a particular network connectivity matrix. In Figs. 15 and 16, the robustness of N, K, and P on the results are investigated for weak g_I = 0.1 mV/cm² and strong g_I = 2.0 mV/cm², respectively. In Fig. 15, it is found that changes in N and P have almost no effect on the curve of $\left\langle Q \right\rangle$ with g_E, and only the increase in K causes a decrease in g_E corresponding to the peak of the curve. This is because K affects the synaptic currents [41], and the excitatory and inhibitory synaptic currents in the network to maintain balance, so the g_E corresponding to the peak of $\left\langle Q \right\rangle$ changes. In general, however, changes in these three parameters still result in similar phenomena, which indicates that our phenomena are robust. In Fig. 16 it is shown that $\left\langle Q \right\rangle$ still appears double resonant peaks with increasing g_E by changing N, K, and P, respectively. It means that the bimodal phenomenon is not accidental but robust. Furthermore, when N and K are fixed, the bimodal phenomenon gradually decreases by increasing P.

Fig. 14

Robustness of the phenomenon. a The dependence of $\left\langle Q \right\rangle$ on g_E for different g_I in the excitatory-inhibitory cortical neuronal network (S = 30 µm²). b The dependence of $\left\langle Q \right\rangle$ on S for different g_E (g_I = 0.5 mV/cm²). c The dependence of $\left\langle Q \right\rangle$ on S for different g_I (g_E = 0.5 mV/cm²). The figure shows that by changing the connectivity matrix, the phenomena and results obtained are robust

Fig. 15

a The dependence of $\left\langle Q \right\rangle$ on g_E for different N in the excitatory-inhibitory cortical neuronal network (K = 12, P = 0.4). b The dependence of $\left\langle Q \right\rangle$ on g_E for different K of each node (N = 60, P = 0.4). c The dependence of $\left\langle Q \right\rangle$ on g_E for different P (N = 60, K = 12). At weak g_I, the phenomena and results obtained are robust to different characterization parameters of the network topology. Fixed parameter: g_I = 0.1 mV/cm²

Fig. 16

a The dependence of $\left\langle Q \right\rangle$ on g_E for different N in the excitatory-inhibitory cortical neuronal network (K = 12, P = 0.4). b The dependence of $\left\langle Q \right\rangle$ on g_E for different K of each node (N = 60, P = 0.4). c The dependence of $\left\langle Q \right\rangle$ on g_E for different P (N = 60, K = 12). At strong g_I, the double resonance peak phenomenon is robust to the characteristic parameters of different network topologies. Fixed parameter: g_I = 2.0 mV/cm²

4 Conclusions

Previous studies of SR have mostly focused on excitatory neuronal networks [11, 12, 58, 68, 69]. However, there are fewer studies of SR based on excitatory-inhibitory cortical neuronal networks. For example, Yu et al. showed that multiple input signals are transmitted independently through a feedforward neural network via SR, and that the E-I relation of local cortical circuits alters the transmission of information between adjacent cortical areas [70]. Lopes et al. investigated the response of neural networks to periodic stimuli plus noise by using a model of cortical circuits [71]. However, these studies have lacked consideration of the energy consumption of SR. Furthermore, resonance is important for the signal transmission in the neuronal system. Baysal et al. in their study of SR in single autapse-coupled neuron hypothesized that autapse can facilitate signal detection in the beta frequency band of brain rhythms [72]. They also discovered that chaotic activity can affect the information processing ability of Type-I and Type-II neurons, producing chaotic resonance [73].Therefore, in this paper, the SR phenomenon and its energy consumption in the single H–H neuron and excitatory-inhibitory cortical neuronal network are investigated.

It is found that moderate noise levels result in the optimal transmission to weak signals. Also, the network can relatively improve signal transmission performance compared to the single neuron. It can be found that changing the excitatory coupling strength can induce the SR phenomenon at weak inhibitory coupling strength. However, at strong inhibitory coupling strength, there is a double resonance peak phenomenon. This is because there is a balance between excitatory and inhibitory synaptic currents in the network. The strong inhibitory synaptic currents cause the firing of neurons in the network to become disordered and the neurons are asynchrony with each other. It leads to synaptic noise effects that cause worse signal transmission performance. The signal transmission is recovered until the excitatory synaptic currents increase to the level where the effect of strong inhibitory synaptic currents can be inhibited. In addition, it is shown that a high level of signal transmission is obtained with a low energy consumption, which shows the economy and efficiency of the signal transmission. It provides some theoretical basis for further understanding of the dependence of information processing and energy consumption in the brain. Eventually, we demonstrate the robustness of our results by changing the network topology.

In this paper, we have extended SR and its energy consumption to the excitatory-inhibitory cortical network for study, but the number of neurons in the numerical simulation is still relatively small compared to the real cerebral cortex. Therefore, in future work, the SR phenomenon and its energy consumption can continue to be studied in a large-scale network model of the cerebral cortex [74] or in real neuronal models like thermosensitive neurons [10], photosensitive neurons [75, 76], piezoelectric neuron [77], so that the work is more biologically justified.