1 Introduction

Thin dielectric elastomer membranes with compliant electrodes have been found to be highly useful in a variety of applications, such as actuators [1, 2], sensors [3, 4], energy harvesting [5, 6], soft robotics [7, 8], etc. These elastomers are primarily attractive due to their uncomplicated working mechanism, whereby the application of electric filed results in the expansion of the membrane due to the bulk incompressibility of the elastomer and Coulomb force between the electrodes. This interaction between constitutive and geometric nonlinearities leads to a complex behavior in thin dielectric membrane. In addition to dynamics, their energy efficiency and scale-production with moderate cost have made them a promising material candidate for mass production. Pores are usually introduced into the material during the preparation and manufacturing process, and their presence can have a significant impact on the dynamic performance of the structure [9,10,11]. Meanwhile, the dielectric permittivity of the dielectric elastomer membrane is relatively small, which restricts its use in broader engineering fields.

To overcome the limitations mentioned above, it has been shown that adding additives can improve the mechanical and dielectric properties. Among the suggested additives, graphene nanoplatelet (GNP) has been found to be one of the most effective one, as it great enhances the mechanical and dielectric properties without significantly increasing the weight of the structure. In regard of mechanical enhancement, the experiments conducted by Wang et al. [12] demonstrated that the tensile strength of composites was significantly increased when GNP was added. By utilizing atomic modeling techniques, Sun et al. [13] discovered a considerable enhancement in the elastic properties of GNP reinforced composites. Mahmun et al. [14] further explored the elastic properties of GNP reinforced nanocomposites with various analytical models and found that the Young’s modulus of the composites had increased significantly. Research also shown that GNP reinforced composites can significantly improve the electrical properties of the composites. Mergen et al. [15] investigated the dielectric relaxation properties and AC conductivity of nanocomposites. The results indicated that the incorporation of GNP fillers significantly increased the capacitive/charge storage capabilities of the nanocomposites. Liu et al. [16] created a composite of GNP/polyvinylidene fluoride (PVDF) and discovered that GNP significantly increased the dielectric constant of the composite because of the increased polarization. The model of Xia et al. [17] also demonstrated the enhanced dielectric properties of polymer nanocomposites reinforced with GNP.

Furthermore, to maximize the effectiveness and efficiency of graphene fillers, the concept of functionally graded graphene nanoplatelet reinforced composite (FG-GNPRC) has been proposed. Research on the analysis of FG-GNPRC materials and structures has been conducted by numerous papers. Feng et al. [18, 19] performed the investigation on the geometrically nonlinear free vibration and the nonlinear bending of FG-GNPRC beams. The research conducted by Shen et al. [20] focused on the nonlinear vibration of FG-GNPRC beams subjected to thermal environments by utilizing a two-step perturbation approach. Song et al. [21, 22] used a differential quadrature method to analyze free vibration and buckling of cracked FG-GNPRC beams resting on an elastic foundation. Li et al. [23] studied the nonlinear primary and secondary resonances of the FG-GNPRC beams based upon the third-order shear deformation theory. By the implementation of Ritz method, Song et al. [24] investigated nonlinear dynamic instability of edge-cracked FG-GNPRC beams within the framework of first-order shear deformation theory. The study conducted by Wang et al. [25] revealed that the nonlinear vibration of the FG-GNPRC plate can be actively adjusted by altering the characteristics of the electrical fields. Song et al. [26] introduced a modified nonlinear Hertz contact theory for analyzing low-velocity impact response of FG-GNPRC plate based on the first-order shear deformation plate theory and von Kármán-type nonlinear kinematics. Dong et al. [27] employed the Galerkin technique to explore the effects of various material and geometry parameters on the vibration behavior of FG cylindrical shells. Ye et al. [28] analyzed nonlinear forced vibration of FG-GNPRC metal foam cylindrical shells via the pseudo-arclength continuation technique.

Despite numerous studies focusing on examining the geometric and material characteristics of FG-GNPRC beams, plates, and shells, few investigations have centered on the nonlinear dynamic response of FG-GNPRC membrane structures, particularly with regards to the dielectric properties of the composites. The internal pores of these structures have been identified as having a crucial impact on their behavior, yet previous studies have either neglected this aspect or relied on empirical formulas to approximate their influence. Consequently, a two-step hybrid micromechanical model is presented to investigate the nonlinear dynamic response of the FG-GNPRC membrane. The objective of this methodology is to acquire a deeper insight into the structural performance of porous composite membranes.

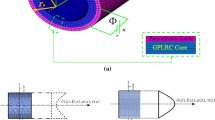
To fill research gap, this paper investigates the damped nonlinear dynamics of the dielectric membrane involving the effect of pore. The proposed structure is a GNPRC dielectric membrane, assumed to be circular with axisymmetric geometrical and physical properties, as shown in Fig. 1, with a fixed boundary condition applied around the membrane. The compliant electrodes are placed on two faces and connected to an external voltage, and a harmonic base excitation is applied transversely to the membrane. Effective medium theory (EMT), Mori–Tanaka (MT) model and rule of mixture are utilized to evaluate the effective material properties of the composite membrane. Hamilton’s principle is applied to derive the governing equations for the nonlinear damped vibration based on hyperelastic membrane theory, Neo-Hookean constitutive model and the couple dielectric theory. With the aid of Taylor series expansion (TSE) and differential quadrature (DQ) methods, the governing equations are discretized, followed by numerical solution using the incremental harmonic balance (IHB) method combined with the arc-length algorithm. A comprehensive parametric study is conducted to gain a deeper understanding of the intrinsic complexity of this dynamic system.

Fig. 1
figure 1

GNPRC membrane with electric and base excitations

Full size image

2 Determination of material properties

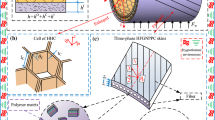
To achieve functionally graded structures, apart from uniform dispersion (profile U), four functionally graded distributions, i.e. profiles X, O, A and V, are involved in present study (as shown in Fig. 2). In Profile U, the GNP content keeps the same throughout the thickness while the concentration of GNP reinforcements linearly increases and decreases from the midplane to top and bottom surfaces of the membrane in profiles X and O, respectively. For profile A and V, the GNP content increases and decreases uniformly from the top to the bottom of the membrane, respectively. The volume fraction of the multi-layer structure in the thickness direction of the membrane is

$$ \begin{gathered} {\text{U}}:\;\varphi_{(i)} = \varphi_{{{\text{avg}}}} \hfill \\ {\text{X}}:\;\varphi_{(i)} = \frac{{Z - 2 - \left( {Z - 2\left| {Z + 1 - 2i} \right|} \right)S_{g} }}{Z - 2}\varphi_{{{\text{avg}}}} \hfill \\ {\text{O}}:\;\varphi_{(i)} = \frac{{Z - 2 + \left( {Z - 2\left| {Z + 1 - 2i} \right|} \right)S_{g} }}{Z - 2}\varphi_{{{\text{avg}}}} \hfill \\ {\text{A}}:\varphi_{(i)} = \frac{{Z - 1 + \left( {2i - Z - 1} \right)S_{g} }}{Z - 1}\varphi_{{{\text{avg}}}} \hfill \\ {\text{V}}:\varphi_{(i)} = \frac{{Z - 1 - \left( {2i - Z - 1} \right)S_{g} }}{Z - 1}\varphi_{{{\text{avg}}}} \hfill \\ \end{gathered} $$
(1)

where φ(i) denotes the GNP volume fraction of the ith layer of the composite membrane. The average volume fraction of GNP is represented by φavg. The variation of GNP components is expressed by the slope factor Sg, which is calculated as (φmax-φmin)/(φmax + φmin), where φmax and φmin are the maximum and minimum GNP concentration in the layers, respectively. The number of layers is represented by Z. It should be noted that the GNP volume fraction can be calculated using the GNP weight fraction fGNP and the densities of the GNP and matrix [29].

Fig. 2
figure 2

GNP distribution profiles a Profile U; b Profile X; c Profile O; d Profile A; e Profile V

Full size image

2.1 Hybrid micromechanical model

Considering the internal pores, GNPRC transforms from a two-phase material into a multi-phase composite, which makes it difficult to apply traditional micromechanical models to determine its material properties. To address this challenge, a two-step hybrid micromechanical model is developed in this study, and the accuracy of its prediction of mechanical and electrical properties of multiphase composite has been verified [30]. The approach involves treating both GNP and the pores as reinforcing fillers in two separate steps. The homogenization process for determining the mechanical and electrical properties of GNPRC with pores is outlined as follows: Firstly, GNP serves as the reinforcing filler while EMT is utilized to homogenize GNPRC without considering the pores. Then, in the second homogenization process, GNPRC is treated as the matrix and the pores are regarded as reinforcing fillers. This process is illustrated in Fig. 3.

Fig. 3
figure 3

Two-step method for determining effective properties of GNPRC membrane with internal pores

Full size image

The effectiveness of EMT in predicting the mechanical and electrical properties of GNPRC has been established, thereby enabling the determination of the material properties of GNPRC as a two-phase composite, without considering internal pores [17, 31], i.e.

$$ \left( {1 - \varphi_{(i)} } \right)\frac{{L_{{\text{m}}} - L_{{\text{e}}} }}{{L_{{\text{m}}} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {L_{{\text{m}}} - L_{{\text{e}}} } \right)}} + \frac{1}{3}\varphi_{(i)} \sum\limits_{k = 1}^{3} {\frac{{L_{k} - L_{{\text{e}}} }}{{L_{{\text{e}}} + S_{kk} \left( {L_{k} - L_{{\text{e}}} } \right)}}} = 0\begin{array}{*{20}c} {} & {} & {\left( {k = 1,2,3} \right)} \\ \end{array} $$
(2)

where φ and L denotes the volume fraction and moduli tensor, respectively. The subscript “m” and “e” refer to the matrix and effective medium, respectively. The kth component of the filler’s Eshelby tensor is designated by Skk. Considering the GNP reinforcement as a thin oblate spheroid, the following applies [32, 33]

$$ \begin{gathered} S_{11} = S_{22} = \frac{\alpha }{{2\left( {1 - \alpha^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\left[ {\arccos \alpha - \alpha \left( {1 - \alpha^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \hfill \\ S_{33} = 1 - 2S_{11} \hfill \\ \end{gathered} $$
(3)

where α is calculated as the ratio of tGNP (the thickness of the GNP) to DGNP (the diameter of the GNP).

For determining the electrical properties of the GNPRC, Eq. (2) can be converted into

$$ \left( {1 - \varphi_{(i)} } \right)\frac{{\sigma_{{\text{m}}}^{*} - \sigma_{{\text{e}}}^{*} }}{{\sigma_{{\text{e}}}^{*} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {\sigma_{{\text{m}}}^{*} - \sigma_{{\text{e}}}^{*} } \right)}} + \frac{1}{3}\varphi_{(i)} \sum\limits_{k = 1}^{3} {\frac{{\sigma_{k}^{*} - \sigma_{{\text{e}}}^{*} }}{{\sigma_{{\text{e}}}^{*} + S_{kk} \left( {\sigma_{k}^{*} - \sigma_{{\text{e}}}^{*} } \right)}}} = 0 $$
(4)

where \(\sigma_{m}^{ * } ,\sigma_{k}^{ * } \;{\text{and}}\;\sigma_{e}^{ * }\) are the complex conductivity of the matrix, the kth component of the fillers and the composite, respectively. The parameter σ* which denotes complex electrical conductivity can be expressed as \(\sigma^{*} = \sigma + i2\pi f_{AC} \varepsilon\), where σ and ε represent electrical conductivity and dielectric permittivity of the composites, respectively, and fAC refers to the frequency of the alternating current (AC) electrical field in Hertz.

An interphase layer is typically introduced around the reinforcing fillers to address the imperfect bonding or interaction between the filler and matrix, resulting in modifications to the electrical conductivity and dielectric permittivity of the fillers [17]

$$ \left\{ \begin{gathered} \sigma_{k}^{{\left( {\text{c}} \right)}} = \sigma_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {\sigma_{k} - \sigma_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{kk} \left( {\sigma_{k} - \sigma_{0}^{{\left( {\text{int}} \right)}} } \right) + \sigma_{0}^{{\left( {\text{int}} \right)}} }}} \right] \hfill \\ \varepsilon_{k}^{{\left( {\text{c}} \right)}} = \varepsilon_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {\varepsilon_{k} - \varepsilon_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{kk} \left( {\varepsilon_{k} - \varepsilon_{0}^{{\left( {\text{int}} \right)}} } \right) + \varepsilon_{0}^{{\left( {\text{int}} \right)}} }}} \right] \hfill \\ \end{gathered} \right.\quad \quad \left( {k = 1,2,3} \right) $$
(5)

where \(\sigma_{0}^{{\left( {\text{int}} \right)}} \;{\text{and}}\;\varepsilon_{0}^{{\left( {\text{int}} \right)}}\) denote the conductivity and dielectric permittivity of the interphase, respectively, and φint denotes the volume fraction of the surrounding interphase.

While evaluating the electrical conductivity of graphene fillers with interfacial phase, it is necessary to integrate the effect of electron tunneling. When determining the dielectric permittivity, the impact of Maxwell–Wagner–Sillars (MWS) polarization should also be considered [17, 31,32,33,34]. In order to incorporate the above effects, the conductivity and dielectric permittivity in Eq. (5) can be further modified as described in [17, 34,35,36,37].

For mechanical properties of the GNPRC, Eq. (2) can be transformed into

$$ \left( {1 - \varphi_{(i)} } \right)\frac{{E_{{\text{m}}} - E_{{\text{e}}} }}{{E_{{\text{m}}} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {E_{{\text{m}}} - E_{{\text{e}}} } \right)}} + \frac{1}{3}\varphi_{(i)} \sum\limits_{k = 1}^{3} {\frac{{E_{k} - E_{{\text{e}}} }}{{E_{{\text{e}}} + S_{kk} \left( {E_{k} - E_{{\text{e}}} } \right)}}} = 0 $$
(6)

where Em is the elastic modulus of the matrix, Ek is the elastic modulus of the reinforcing filler in the kth direction and Ee is the effective elastic modulus of the composites. Similar to electrical properties, when considering the interphase surrounding the GNP, the effective elastic modulus is altered as

$$ E_{k}^{{\left( {\text{c}} \right)}} = E_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {E_{k} - E_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{kk} \left( {E_{k} - E_{0}^{{\left( {\text{int}} \right)}} } \right) + E_{0}^{{\left( {\text{int}} \right)}} }}} \right]\begin{array}{*{20}c} {} & {} \\ \end{array} (k = 1,2,3) $$
(7)

where \(E_{0}^{{\left( {\text{int}} \right)}}\) represents the elastic modulus of the interphase surrounding GNP.

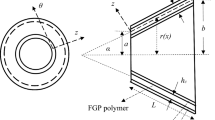
In the present study, ellipsoid-shaped hollow fillers dispersed in GNPRC are treated as pores whose presence, as reported in previous studies [10, 38], can affect the electrical and mechanical properties of the composite membrane by forming insulated networks that impact the transport of electrical carriers. In Fig. 4, the orientation of the pores in the local coordinate system is denoted by two Euler angles, ψ and ϑ. The ellipsoid pores have an aspect ratio, αp, defined as a2/a1, where a1 and a2 are respectively the half lengths of the principal axes along x1′ and x2′. n is porosity which denotes the volume fraction of the pores.

Fig. 4
figure 4

Representative volume element (RVE) of composites containing pores

Full size image

Mori–Tanaka (MT) model [39] is utilized to determine the electrical properties of the porous composites, the effective complex electrical conductivity \(\sigma_{{{\text{ep}}}}^{*}\) is expressed as

$$ \sigma_{{{\text{ep}}}}^{*} = \sigma_{{\text{e}}}^{*} + n\frac{{\int_{0}^{2\pi } {\int_{0}^{\pi } {ODF\left( {\psi ,\vartheta } \right)\left( {\sigma_{{\text{p}}}^{*} - \sigma_{{\text{e}}}^{*} } \right)G\sin \vartheta d\vartheta d\psi } } }}{{\int_{0}^{2\pi } {\int_{0}^{\pi } {ODF\left( {\psi ,\vartheta } \right)G\sin \vartheta d\vartheta d\psi } } }} $$
(8)

where \(\sigma_{{\text{p}}}^{*}\) denotes the complex electrical conductivity of pores filled with air. The orientation distribution function (ODF), which describes the distribution of ellipsoidal pores in the matrix and is equal to unity for a completely random distribution, is denoted by ODF(ψ, ϑ). The electric field concentration tensor G can be obtained through the MT model [39].

Considering the overall mechanical properties of the porous composites, the effective elastic modulus Eep can be expressed as [40]

$$ E_{{{\text{ep}}}} = E_{{\text{e}}} + n\frac{{\int_{0}^{2\pi } {\int_{0}^{\pi } {ODF\left( {\psi ,\vartheta } \right)\left( {E_{{\text{p}}} - E_{{\text{e}}} } \right)G\sin \vartheta d\vartheta d\psi } } }}{{\int_{0}^{2\pi } {\int_{0}^{\pi } {ODF\left( {\psi ,\vartheta } \right)G\sin \vartheta d\vartheta d\psi } } }} $$
(9)

where Ep denotes the elastic modulus of pores.

2.2 Rule of mixture

The rule of mixture is used to determine the Poisson’s ratio ν(i) and density γ(i) of the ith layer

$$ \left\{ \begin{gathered} \nu_{(i)} = \left( {1 - \varphi_{(i)} - \varphi_{{{\text{p}}(i)}} } \right)\nu_{{\text{m}}} + \varphi_{(i)} \nu_{{{\text{GNP}}}} + \varphi_{{{\text{p}}(i)}} \nu_{{\text{p}}} \hfill \\ \gamma_{(i)} { = }\left( {1 - \varphi_{(i)} - \varphi_{{{\text{p}}(i)}} } \right)\gamma_{{\text{m}}} + \varphi_{(i)} \gamma_{{{\text{GNP}}}} + \varphi_{{{\text{p}}(i)}} \gamma_{{\text{p}}} \hfill \\ \end{gathered} \right. $$
(10)

where subscript “m”, “GNP” and “p” represent the matrix, the GNP filler and pore, respectively.

3 Governing equations

3.1 Analytical modelling

Pre-stretch technology is often used in membrane structures to prevent pull-in between electrodes [41]. Figure 5 exhibits the three configurations of the membrane before and after pre-stretch and deformation out of the plane. The radial pre-stretch applied at the initial state causes the membrane’s radius changing from b to B, correspondingly, the point M1 moves to M2. Then the membrane undergoes the out-of-plane deformation induced by the base excitation and electrical loading, M2 further moves to M3. Using spherical coordinates, the positions of the three points are

$$ M_{1} = \left( {\rho ,\theta ,0} \right),M_{2} = \left( {r_{0} ,\theta ,0} \right),M_{3} = \left( {r,\theta ,z} \right) $$
(11)

where r denotes the radius of the projection of M3 in the planar and z denotes the distance of M3 from the xoy plane. They can be expressed as

$$ \left\{ \begin{gathered} r\left( {\rho ,t} \right){ = }r_{0} \left( \rho \right) + u\left( {\rho ,t} \right) = \eta \rho + u\left( {\rho ,t} \right) \hfill \\ z\left( {\rho ,t} \right){ = }z_{0} \left( \rho \right) + w\left( {\rho ,t} \right) = w\left( {\rho ,t} \right) \hfill \\ \end{gathered} \right. $$
(12)

where u and w respectively represent the radial and transverse displacements of the point M2 after out-of-plane deformation, and the stretching ratio η is defined as η = B/b.

Fig. 5
figure 5

Sequence of deformation for an axisymmetric circular membrane

Full size image

As depicted in Fig. 5, the three principal stretches can be written as

$$ \mu_{i} = \frac{{dS_{i} }}{{ds_{i} }}\begin{array}{*{20}c} {} & {} \\ \end{array} (i = 1,2,3) $$
(13)

where dSi and dsi are the undeformed and deformed length of an infinitesimal element in the principal direction, respectively. The subscripts “1”, “2” and “3” correspond to the meridional, circumferential, and transverse directions, respectively.

The differential is defined as \(\partial ()/\partial t = ()_{t} , \, \partial ()/\partial \rho = ()_{\rho } , \, \partial^{{2}} ()/\partial t^{{2}} = ()_{tt} , \, \partial^{{2}} ()/\partial \rho^{{2}} = ()_{\rho \rho }\). The lengths in the meridional and circumferential directions can be expressed as

$$ \left\{ \begin{gathered} \mu_{1} = \sqrt {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \hfill \\ \mu_{2} = \frac{r}{\rho } \hfill \\ \end{gathered} \right. $$
(14)

With the assumption of material incompressibility, the principal stretch μ3 is expressed as

$$ \mu_{3} = \frac{H}{h} = \frac{1}{{\mu_{1} \mu_{2} }} = \frac{\rho }{{r\sqrt {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } }} $$
(15)

where h and H are the thickness of the membrane before and after deformation, respectively.

3.2 Theoretical framework

Neo-Hookean model [42] is used to characterize the hyperelastic response of the membrane, the first strain invariant I1 is given by

$$ I_{1} = \sum\limits_{i = 1}^{3} {\mu_{i}^{2} } = \mu_{1}^{2} + \mu_{2}^{2} + \mu_{3}^{2} = \left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} + \frac{{r^{2} }}{{\rho^{2} }} + \frac{{\rho^{2} }}{{r^{2} \left[ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \right]}} $$
(16)

The mechanical behavior of the materials can be described via the strain density function [43,44,45,46], i.e.

$$ W_{1(i)} = C_{1(i)} \left( {I_{1} - 3} \right){ = }\,C_{1(i)} \left\{ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} + \frac{{r^{2} }}{{\rho^{2} }} + \frac{{\rho^{2} }}{{r^{2} \left[ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \right]}} - 3} \right\} $$
(17)

where C1(i) denotes a parameter related to the linear shear modulus of ith layer.

Assuming the material is homogeneous and isotropic, the electric displacement vector D(i) of the ith layer in the transverse direction can be expressed as

$$ {\varvec{D}}_{(i)} = \varepsilon_{r\left( i \right)} \varepsilon_{0} E_{(i)} $$
(18)

where εr(i) and ε0 are respectively the relative permittivity of the ith layer of the membrane material and the vacuum. The electric field component, E(i), within the ith layer of the membrane can be determined by the voltage, V(i), across the membrane’s electrode, i.e.

$$ E_{(i)} = \frac{{V_{(i)} }}{H} = \frac{{V_{(i)} \mu_{1} \mu_{2} }}{h} $$
(19)

Considering electrical polarization of the continuum [47], the electrostatic energy per unit volume of the ith layer resulting from the dielectric properties of the composites are expressed as

$$ W_{b(i)} = \frac{{{\varvec{D}}_{(i)}^{2} }}{{2\varepsilon_{r(i)} \varepsilon_{0} }} = \frac{{\varepsilon_{r(i)} \varepsilon_{0} E_{(i)}^{2} }}{2} $$
(20)

Then the Helmholtz free energy of the ith layer of the composites per unit volume is given by [47]

$$ W_{a(i)} = W_{1(i)} \left( {\mu_{1} + \mu_{2} + \mu_{3} } \right) + W_{b(i)} = W_{1(i)} \left( {\mu_{1} + \mu_{2} + \mu_{3} } \right) + \frac{{\varepsilon_{r(i)} \varepsilon_{0} E_{(i)}^{2} }}{2} $$
(21)

The total electrostatic energy Wb(all) of the composite membrane can be written as

$$ W_{b(all)} = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {W_{b(i)} dz} } = \frac{1}{2}\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\varepsilon_{r(i)} \varepsilon_{0} E_{(i)}^{2} dz} } $$
(22)

Equation (21) can also be derived from the composite membrane’s equivalent permittivity [48], i.e.

$$ W_{b(all)} = \frac{1}{2}\varepsilon_{0} \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\varepsilon_{(all)} E_{(i)}^{2} dz} $$
(23)

where ε(all) is the overall equivalent permittivity of the material, given as

$$ \varepsilon_{(all)} = \frac{{N_{L} }}{{\sum\limits_{i = 1}^{{N_{L} }} {\frac{1}{{\varepsilon_{r(i)} }}} }} $$
(24)

3.3 Energy integrals

To derive the governing equations, Hamilton’s principle can be employed, i.e.

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T_{e} - U_{e} + W_{e} } \right)dt} = 0 $$
(25)

where Te is the kinetic energy, Ue is the potential energy and We is the work done by the radial force fr and damping force Fr. The variational form of the three energies are expressed as [49]

$$ \begin{aligned} \delta \int_{{t_{1} }}^{{t_{2} }} {T_{e} } dt{ = } & \frac{1}{2}\delta \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{2\pi } {\int_{0}^{b} {\gamma_{(i)} \left( {r_{t}^{2} + z_{t}^{2} } \right)} } } } \rho d\rho d\theta dz} dt \\ = & 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} \left( {r_{t} \delta r_{t} + z_{t} \delta z_{t} } \right)} \rho d\rho } dzdt} } \\ = & 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} r_{t} } \rho d\rho } dzd\left( {\delta r} \right)} } + 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} z_{t} } \rho d\rho } dzd\left( {\delta z} \right)} } \\ = & \left. {r_{t} \delta r} \right|_{{t_{1} }}^{{t_{2} }} - 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} \left( {r_{tt} \delta r} \right)} \rho d\rho } dz} + \left. {z_{t} \delta z} \right|_{{t_{1} }}^{{t_{2} }} - 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} \left( {z_{tt} \delta z} \right)} \rho d\rho } dz} \\ = & - 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\gamma_{(i)} \left( {r_{tt} \delta r + z_{tt} \delta z} \right)} \rho d\rho } dz} \\ \end{aligned} $$
(26)
$$ \begin{aligned} \delta \int_{{t_{1} }}^{{t_{2} }} {U_{e} dt} { = } & \delta \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{2\pi } {\int_{0}^{b} {W_{a(i)} } } } \rho d\rho d\theta dz} dt} \\ = & 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\delta W_{a(i)} } } \rho d\rho dz} dt} \\ =\, & 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {[W_{a(i)r} } } \delta r + W_{{a(i)r_{\rho } }} \delta r_{\rho } + W_{{a(i)z_{\rho } }} \delta z_{\rho } ]\rho d\rho dz} dt} \\ =\, & 4\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {C_{1(i)} \left\{ {\frac{r\delta r}{{\rho^{2} }} - \rho^{2} \frac{{r_{\rho } \delta r_{\rho } + z_{\rho } \delta z_{\rho } }}{{r^{2} \left[ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \right]^{2} }} - \frac{{\rho^{2} \delta r}}{{r^{3} \left[ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \right]}}} \right\}} } \rho d\rho dz} dt} \\ + & 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\left\{ {2C_{1(i)} \left( {r_{\rho } \delta r_{\rho } + z_{\rho } \delta z_{\rho } } \right) + r^{2} \frac{{\varepsilon_{0} \varepsilon_{r(i)} V_{(i)}^{2} }}{{h^{2} \rho^{2} }}\left[ {\left( {r_{\rho } } \right)^{2} + \left( {z_{\rho } } \right)^{2} } \right]^{2} } \right\}} } } \rho d\rho dz} dt \\ \end{aligned} $$
(27)

and

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {W_{e} } dt = \delta f_{r} \left( {r - \rho } \right)|_{\rho = b} + 2\pi \sum\limits_{i = 1}^{{N_{L} }} {\int_{{t_{1} }}^{{t_{2} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\int_{0}^{b} {\left( { - c_{1} r_{t} \delta r - c_{2} z_{t} \delta z} \right)} } \rho d\rho dz} dt} $$
(28)

where c1 and c2 are the viscous damping coefficient.

Substituting Eq. (12) into Eqs. (26)-(28) and adding a base excitation term to the transverse motion, denoted by p(t), the governing equations for FG-GNPRC membrane can be obtained as

$$ \begin{gathered} \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {(\gamma_{(i)} u_{tt} } + c_{1} u_{t} )dz} - 2\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {C_{1(i)} \left( {\frac{1}{\rho }u_{\rho } + u_{\rho \rho } - \frac{u}{{\rho^{2} }} + \frac{{A_{2} }}{{A_{1} }}} \right)} dz} \hfill \\ + \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\frac{{\varepsilon_{0} \varepsilon_{r(i)} V_{(i)}^{2} }}{{h^{2} \rho^{2} }}\left[ {u\left( {w_{\rho } } \right)^{2} + \frac{{u^{2} }}{\rho }u_{\rho } - u\left( {u_{\rho } } \right)^{2} - u^{2} u_{\rho \rho } } \right]} dz} \hfill \\ + \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\frac{{\varepsilon_{0} \varepsilon_{r(i)} V_{(i)}^{2} }}{{h^{2} \rho^{2} }}\left\{ {\eta^{2} \left( {u - \rho^{2} u_{\rho \rho } - \rho u_{\rho } } \right) + \eta \left[ {\frac{{u^{2} }}{\rho } + \rho \left( {w_{\rho } } \right)^{2} - \rho \left( {u_{\rho } } \right)^{2} - \rho^{2} uu_{\rho \rho } } \right]} \right\}} dz} = 0 \hfill \\ \end{gathered} $$
(29)

and

$$ \begin{gathered} \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\left( {\gamma_{(i)} w_{tt} } \right.} \left. { + p + c_{2} w_{t} } \right)dz} - 2\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {C_{1(i)} \left( {\frac{1}{\rho }w_{\rho } + w_{\rho \rho } + \frac{{A_{3} }}{{A_{1} }}} \right)} dz} \hfill \\ - \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\frac{{\varepsilon_{0} \varepsilon_{r(i)} V_{(i)}^{2} }}{{h^{2} \rho^{2} }}\left( {2\eta u_{\rho } w_{\rho } + \frac{2u}{\rho }u_{\rho } w_{\rho } + 2\eta uw_{\rho \rho } - \frac{{u^{2} }}{{\rho^{2} }}w_{\rho } + \frac{{u^{2} }}{\rho }w_{\rho \rho } + \eta^{2} \rho w_{\rho \rho } + \eta^{2} w_{\rho } } \right)} dz} = 0 \hfill \\ \end{gathered} $$
(30)

where the terms A1, A2 and A3 are given in the Appendix 1.

A clamped boundary condition is supposed to be applied around the membrane, i.e.

$$ \left\{ \begin{gathered} u\left( {0,t} \right) = r\left( {0,t} \right) = 0 \hfill \\ w\left( {b,t} \right) = z\left( {b,t} \right) = 0 \hfill \\ r(b,t) = \eta b \hfill \\ u\left( {b,t} \right) = 0 \hfill \\ \end{gathered} \right. $$
(31)

For the above coupled strongly nonlinear governing equations, Eqs. (29) and (30) can be discretized directly by using the DQ method poses a challenge. To address this, TSE approach is utilized, i.e.

$$ \left\{ \begin{gathered} - \frac{{\psi_{1} }}{{\rho^{2} }}u + \frac{{\psi_{1} }}{\rho }u_{\rho } + \psi_{1} u_{\rho \rho } + \frac{{3\eta \lambda_{1} - \eta \lambda_{2} }}{{\rho^{3} }}u^{2} - \frac{{6\lambda_{1} }}{{\rho^{4} }}u^{3} - \frac{{2\eta \left( {\lambda_{1} - \lambda_{2} } \right)}}{\rho }uu_{\rho \rho } - \frac{{3\eta \lambda_{1} - \eta \lambda_{2} }}{\rho }\left( {u_{\rho } } \right)^{2} \hfill \\ + \frac{{6\lambda_{1} }}{\rho }\left( {u_{\rho } } \right)^{3} - \frac{{3\lambda_{1} + \lambda_{2} }}{{\rho^{3} }}u^{2} u_{\rho } + \frac{{3\lambda_{1} + \lambda_{2} }}{{\rho^{2} }}u^{2} u_{\rho \rho } + \frac{{3\lambda_{1} + \lambda_{2} }}{{\rho^{2} }}u\left( {u_{\rho } } \right)^{2} + \frac{\eta }{\rho }\left( {\frac{{\lambda_{1} }}{3} - \lambda_{2} } \right)\left( {w_{\rho } } \right)^{2} \hfill \\ + \frac{{\lambda_{1} - \lambda_{2} }}{{\rho^{2} }}u\left( {w_{\rho } } \right)^{2} - \frac{{8\lambda_{1} }}{3\rho }uw_{\rho } w_{\rho \rho } + \frac{{8\lambda_{1} }}{\rho }uu_{\rho } u_{\rho \rho } - \frac{{10\lambda_{1} }}{3\rho }u_{\rho } \left( {w_{\rho } } \right)^{2} + A_{4} = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\left[ {\gamma_{(i)} u_{tt} + c_{1} u_{t} } \right]} dz} \hfill \\ \frac{{\psi_{2} }}{\rho }w_{\rho } + \psi_{2} w_{\rho \rho } + \frac{{2\eta \left( {\lambda_{1} + \lambda_{2} } \right)}}{\rho }u_{\rho } w_{\rho } + \left( {\frac{{4\eta \lambda_{1} }}{3\rho } + \frac{{2\eta \lambda_{2} }}{\rho }} \right)uw_{\rho \rho } - \frac{{\left( {\lambda_{1} - \lambda_{2} } \right)}}{{\rho^{2} }}\left( {2uu_{\rho } w_{\rho } + u^{2} w_{\rho \rho } } \right) + A_{5} \hfill \\ + \frac{{\left( {\lambda_{1} - \lambda_{2} } \right)}}{{\rho^{3} }}u^{2} w_{\rho } - \frac{{\lambda_{1} }}{\rho }\left[ {6w_{\rho } \left( {u_{\rho } } \right)^{2} + \frac{8u}{3}w_{\rho } u_{\rho \rho } + \frac{8u}{3}u_{\rho } w_{\rho \rho } - \frac{2}{3}\left( {w_{\rho } } \right)^{3} } \right] = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\left[ {\gamma_{(i)} w_{tt} + p + c_{2} w_{t} } \right]} dz} \hfill \\ \end{gathered} \right. $$
(32)

where A4 and A5 in Eq. (32) are given in the Appendix 1. λ1, λ2, ψ1, and ψ2 as involved are

$$ \left\{ \begin{gathered} \lambda_{1} = \frac{6}{{\eta^{8} }}\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {C_{1(i)} } dz} \hfill \\ \lambda_{2} = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\frac{{V_{(i)}^{2} \varepsilon_{0} \varepsilon_{r(i)} }}{{h^{2} }}} dz} \hfill \\ \psi_{1} = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\left[ {2C_{1(i)} \left( {1 + \frac{3}{{\eta^{6} }}} \right) + \eta^{2} \frac{{V_{(i)}^{2} \varepsilon_{0} \varepsilon_{r(i)} }}{{h^{2} }}} \right]} dz} \hfill \\ \psi_{2} = \sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\left[ {2C_{1(i)} \left( {1 - \frac{1}{{\eta^{6} }}} \right) + \eta^{2} \frac{{V_{(i)}^{2} \varepsilon_{0} \varepsilon_{r(i)} }}{{h^{2} }}} \right]} dz} \hfill \\ \end{gathered} \right. $$
(33)

It should be mentioned that the parameter h gives rise to the nonlinearity in the system.

4 Solution

The following quantities are introduced to normalize the governing equations

$$ \begin{gathered} U = \frac{u}{h},W = \frac{w}{h},\chi = \frac{\rho }{b},\tau = \frac{t}{b}\sqrt {\frac{{C_{0} }}{{\gamma_{0} }}} ,\kappa = \frac{h}{b},\gamma_{{1_{(i)} }} = \frac{{\gamma_{(i)} }}{{\gamma_{0} }},C_{10\left( i \right)} = \frac{{C_{1(i)} }}{{C_{0} }} \hfill \\ c_{10} = \frac{{c_{1} b}}{{\sqrt {\gamma_{0} C_{0} } }},c_{20} = \frac{{c_{2} b}}{{\sqrt {\gamma_{0} C_{0} } }},P = \frac{b}{{\kappa C_{0} }}p \hfill \\ \end{gathered} $$
(34)

where γ0 and C0 represent the corresponding values of the matrix, respectively. Substituting Eq. (34)into Eq. (32) and defining \(\partial ()/\partial \tau = ()_{\tau } , \, \partial ()/\partial \chi = ()_{\chi } , \, \partial {2}()/\partial \tau^{{2}} = ()_{\tau \tau } \;{\text{and}}\; \, \partial {2}()/\partial \chi^{{2}} = ()_{\chi \chi }\), the dimensionless governing equations are obtained, i.e.

$$ \left\{ \begin{gathered} 2a_{1} \left( {1 + \frac{3}{{\eta^{6} }}} \right)\left( { - \frac{1}{{\chi^{2} }}U + \frac{1}{\chi }U_{\chi } + U_{\chi \chi } } \right) + \frac{{6a_{1} }}{{\eta^{7} }}\kappa \left[ {\frac{4}{3}W_{\chi } W_{\chi \chi } + \frac{3}{{\chi^{3} }}U^{2} + \frac{1}{3}\frac{1}{\chi }\left( {W_{\chi } } \right)^{2} } \right. \hfill \\ \left. { - \frac{2}{\chi }UU_{\chi \chi } - 4U_{\chi } U_{\chi \chi } - \frac{3}{\chi }\left( {U_{\chi } } \right)^{2} } \right] + \frac{{6a_{1} }}{{\eta^{8} }}\kappa^{2} \left[ {\frac{6}{\chi }\left( {U_{\chi } } \right)^{3} } \right. - \frac{3}{{\chi^{3} }}U^{2} U_{\chi } + \frac{3}{{\chi^{2} }}U^{2} U_{\chi \chi } \hfill \\ + \frac{3}{{\chi^{2} }}U\left( {U_{\chi } } \right)^{2} - \frac{6}{{\chi^{4} }}U^{3} + \frac{1}{{\chi^{2} }}U\left( {W_{\chi } } \right)^{2} - \frac{8}{3}\frac{1}{\chi }UW_{\chi } W_{\chi \chi } + \frac{8}{\chi }UU_{\chi } U_{\chi \chi } - \frac{10}{3}\frac{1}{\chi }U_{\chi } \left( {W_{\chi } } \right)^{2} \hfill \\ - \frac{20}{3}U_{\chi } W_{\chi } W_{\chi \chi } - \frac{10}{3}\left( {W_{\chi } } \right)^{2} U_{\chi \chi } + \left. {10\left( {U_{\chi } } \right)^{2} U_{\chi \chi } } \right] + A_{6} = a_{2} U_{\tau \tau } + c_{10} U_{\tau } \hfill \\ 2a_{1} \left( {1 - \frac{1}{{\eta^{6} }}} \right)\left( {\frac{1}{\chi }W_{\chi } + W_{\chi \chi } } \right) + \frac{{6a_{1} }}{{\eta^{7} }}\kappa \left( {\frac{2}{\chi }U_{\chi } W_{\chi } + \frac{4}{3\chi }UW_{\chi \chi } + \frac{8}{3}W_{\chi } U_{\chi \chi } + \frac{8}{3}U_{\chi } W_{\chi \chi } } \right) \hfill \\ + \frac{{6a_{1} }}{{\eta^{8} }}\kappa^{2} \left[ {\frac{1}{{\chi^{3} }}U^{2} W_{\chi } } \right. - \frac{2}{{\chi^{2} }}UU_{\chi } W_{\chi } - \frac{1}{{\chi^{2} }}U^{2} W_{\chi \chi } - \frac{6}{\chi }W_{\chi } \left( {U_{\chi } } \right)^{2} - \frac{8}{3\chi }UW_{\chi } U_{\chi \chi } \hfill \\ - \frac{20}{3}U_{\chi } W_{\chi } U_{\chi \chi } - \frac{10}{3}\left( {U_{\chi } } \right)^{2} W_{\chi \chi } - \frac{8}{3\chi }UU_{\chi } W_{\chi \chi } + \frac{2}{3\chi }\left( {W_{\chi } } \right)^{3} + \left. {2\left( {W_{\chi } } \right)^{2} W_{\chi \chi } } \right] + A_{7} = a_{2} W_{\tau \tau } + c_{20} W_{\tau } - P \hfill \\ \end{gathered} \right. $$
(35)

where a1 and a2 are

$$ \left\{ \begin{gathered} a_{1} = \frac{{\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {C_{10(i)} } dz} }}{h} \hfill \\ a_{2} = \frac{{\sum\limits_{i = 1}^{{N_{L} }} {\int_{{h_{i} }}^{{h_{i + 1} }} {\gamma_{1(i)} } dz} }}{h} \hfill \\ \end{gathered} \right. $$
(36)

The terms A6 and A7, which pertain to the dielectric properties of the composites, are given in Appendix 1.

The current study employs the DQ method to discretize the dimensionless governing equations, and the displacements and their derivatives of the membrane are defined as [50]

$$ \left\{ \begin{gathered} \left\{ {U,W} \right\} = \sum\limits_{m = 1}^{N} {l_{m} \left( \chi \right)\left\{ {U_{m} ,W_{m} } \right\}} \hfill \\ \left. {\frac{{\partial^{k} \left\{ {U,W} \right\}}}{{\partial \chi^{k} }}} \right|_{{\chi = \chi_{i} }} = \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( k \right)} \left\{ {U_{m} ,W_{m} } \right\}} \hfill \\ \end{gathered} \right. $$
(37)

where N represents the sum of discrete points along the membrane’s radius, Um and Wm represent the radial and transversal displacements at χ = χm, respectively. The Lagrange interpolation function is represented by lm(χ), and the weighting coefficient of the kth derivative is represented by \(c_{{_{im} }}^{\left( k \right)}\). Then the distribution of grid points is as follows

$$ \chi_{i} = \frac{1}{2}\left[ {1 - \cos \left( {\frac{i - 1}{{N - 1}}} \right)\pi } \right]\begin{array}{*{20}c} {} & {} \\ \end{array} (i = 1,2,3, \cdots ,N) $$
(38)

Substituting Eq. (37) into Eq. (35), the governing equations are cast as

$$ \left\{ \begin{gathered} a_{11} \left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} U_{m} } - \frac{1}{{\chi_{i}^{2} }}U_{i} + \frac{1}{{\chi_{i} }}\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } } \right) \hfill \\ - a_{44} \left[ {\frac{1}{{\chi_{i}^{3} }}U_{i}^{2} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } - \frac{1}{{\chi_{i}^{2} }}U_{i}^{2} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} U_{m} } - \frac{1}{{\chi_{i}^{2} }}U_{i} \left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } } \right)^{2} + \frac{1}{{\chi_{i}^{2} }}U_{i} \left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } } \right)^{2} } \right] \hfill \\ - a_{33} \left[ {\frac{1}{{\chi_{i}^{3} }}U_{i}^{2} - \frac{2}{{\chi_{i} }}U_{i} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} U_{m} } - \frac{1}{{\chi_{i} }}\left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } } \right)^{2} + \frac{1}{{\chi_{i} }}\left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } } \right)^{2} } \right] + A_{8} + A_{9} = a_{2} \ddot{U}_{i} + c_{10} \dot{U}_{i} \hfill \\ a_{22} \left( {\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} W_{m} } + \frac{1}{{\chi_{i} }}\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } } \right) + a_{33} \left[ {\frac{2}{{\chi_{i} }}\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } + \frac{2}{{\chi_{i} }}U_{i} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} W_{m} } } \right] \hfill \\ + a_{44} \left[ {\frac{2}{{\chi_{i}^{2} }}U_{i} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} U_{m} } \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } - \frac{{U_{i}^{2} }}{{\chi_{i}^{3} }}\sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 1 \right)} W_{m} } + \frac{1}{{\chi_{i}^{2} }}U_{i}^{2} \sum\limits_{m = 1}^{N} {c_{{_{im} }}^{\left( 2 \right)} W_{m} } } \right] + A_{10} + A_{11} = a_{2} \ddot{W}_{i} + c_{20} \dot{W}_{i} - P \hfill \\ \end{gathered} \right. $$
(39)

The coefficients related to the applied voltage in Eq. (39) become

$$ \left\{ \begin{gathered} a_{11} = 2a_{1} \left( {1 + \frac{3}{{\eta^{6} }}} \right) + b_{1} \eta^{2} \hfill \\ a_{22} = 2a_{1} \left( {1 - \frac{1}{{\eta^{6} }}} \right) + b_{1} \eta^{2} \hfill \\ a_{33} = b_{1} \kappa \eta \hfill \\ a_{44} = b_{1} \kappa^{2} \hfill \\ \end{gathered} \right. $$
(40)

A8, A9, A10 and A11 in Eq. (39) related to the radial and transversal motions are given in Appendix 1.

Correspondingly, the associated boundary conditions become

$$ \left\{ \begin{gathered} U\left( {0,\tau } \right) = U\left( {1,\tau } \right) = 0 \hfill \\ W\left( {1,\tau } \right) = 0 \hfill \\ \end{gathered} \right. $$
(41)

Equation (39) can also be written in a matrix form as

$$ \user2{M\ddot{d}} + \user2{C\dot{d}} + \left( {{\varvec{K}}_{{\text{L}}} + {\varvec{K}}_{{{\text{NL}}}} } \right){\varvec{d}} = {\varvec{P}} $$
(42)

where M and C represent matrices for mass and energy damping coefficient, respectively, KL and KNL represent linear and nonlinear stiffness matrix, respectively, depending on displacement vector \(d = \left\{ {\left\{ {U_{i} } \right\}^{T} , \, \left\{ {W_{i} } \right\}^{T} } \right\}^{T} \left( {i = {1},{ 2},{ 3}, \, \ldots ,N} \right)\), and P is the base excitation vector. The linear stiffness matrix KL is expressed as

$$ {\mathbf{K}}_{{\text{L}}} = \left( {\begin{array}{*{20}c} { - \frac{1}{{\chi^{2} }}a_{11} {\mathbf{I}} + \frac{1}{\chi }a_{11} {\mathbf{c}}^{\left( 1 \right)} + a_{11} {\mathbf{c}}^{\left( 2 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {\frac{1}{\chi }a_{22} {\mathbf{c}}^{\left( 1 \right)} + a_{22} {\mathbf{c}}^{\left( 2 \right)} } \\ \end{array} } \right) $$
(43)

The detail of the nonlinear stiffness matrix KNL is given in Appendix 2.

In present work, incremental harmonic balance (IHB) method is employed to solve the equations mentioned above. The equations involve a base excitation term, defined as P = P0cos(Ωτ), where P0 represents a generalized force vector. T = Ωτ is introduced, which allows Eq. (42) to be cast as

$$ \Omega^{2} M\ddot{d} + \Omega C\dot{d} + \left( {K_{\text{L}} + K_{{\text{NL}}} } \right)d = P_{0} \cos \left( T \right) $$
(44)

Assuming that d0Γ and Ω0 represent the displacement and frequency of a state of vibration, its adjacent state can be represented by adding an increment, i.e.

$$ d_{\Gamma } = d_{0\Gamma } + \Delta d_{\Gamma } , \, \Omega = \Omega_{0} + \Delta \Omega \, \Gamma = 1,2, \cdots ,2N $$
(45)

Upon substituting Eq. (45) into Eq. (44) and neglecting higher order infinitesimal terms, we obtain

$$ \Omega_{0}^{2} M\Delta \ddot{d} + \Omega_{0} C{\Delta }\dot{d} + \left( {K_{\text{L}} + \tilde{K}_{{\text{NL}}} } \right)\Delta d = R - \left( {2\Omega_{0} M\ddot{d}_{0} + C\dot{d}_{0} } \right)\Delta \Omega $$
(46)

where

$$ R = P_{0} \cos \left( T \right) - \left[ {\Omega_{0}^{2} M\ddot{d}_{0} + \Omega_{0} C\dot{d}_{0} + \left( {K_{\text{L}} + K_{{\text{NL}}} } \right)d_{0} } \right] $$
(47)
$$ \tilde{\varvec{K}}_{{\text{NL}}} = \left[ {\begin{array}{*{20}c} {2{\varvec{K}}_{{\text{NL}}}^{11} \left( 1 \right) + 3{\varvec{K}}_{{\text{NL}}}^{11} \left( 2 \right)} & {2{\varvec{K}}_{{\text{NL}}}^{12} \left( 1 \right) + 3{\varvec{K}}_{{\text{NL}}}^{12} \left( 2 \right)} \\ {2{\varvec{K}}_{{\text{NL}}}^{21} \left( 1 \right) + 3{\varvec{K}}_{{\text{NL}}}^{21} \left( 2 \right)} & {2{\varvec{K}}_{{\text{NL}}}^{22} \left( 1 \right) + 3{\varvec{K}}_{{\text{NL}}}^{22} \left( 2 \right)} \\ \end{array} } \right] $$
(48)
$$ {\mathbf{d}}_{0} = \left[ {d_{01} ,d_{02} , \cdots ,d_{{0\left( {2N - 1} \right)}} ,d_{{0\left( {2N} \right)}} } \right]^{T} $$
(49)

and

$$ \Delta {\varvec{d}} = \left[ {\Delta d_{1} ,\Delta d_{2} , \cdots ,\Delta d_{2N - 1} ,\Delta d_{2N} } \right]^{T} $$
(50)

Both the solution d0Γ and increment ΔdΓcan be expressed via the Fourier series expansion

$$ \begin{array}{*{20}c} {\left\{ \begin{gathered} d_{{0\Gamma }} = a_{{0\Gamma 0}} + \sum\limits_{{i = 1}}^{{N_{{\text{c}}} }} {a_{{0\Gamma i}} \cos \left( {iT} \right)} + \sum\limits_{{i = 1}}^{{N_{{\text{s}}} }} {b_{{0\Gamma i}} \sin \left( {iT} \right)} = \user2{X}_{{\text{S}}} \user2{Z}_{{0\Gamma }} \hfill \\ {\Delta }d_{\Gamma } = {\Delta }a_{{\Gamma 0}} + \sum\limits_{{i = 1}}^{{N_{{\text{c}}} }} {{\Delta }a_{{\Gamma i}} \cos \left( {iT} \right)} + \sum\limits_{{i = 1}}^{{N_{{\text{s}}} }} {{\Delta }b_{{\Gamma i}} \sin \left( {iT} \right)} = \user2{X}_{{\text{S}}} {\Delta }\user2{Z}_{\Gamma } \hfill \\ \end{gathered} \right.} & {\Gamma = 1,2, \cdots ,2N} \\ \end{array} $$
(51)

where

$$ \left\{ \begin{gathered} \user2{X}_{{\text{s}}} = \left[ {1,\cos \left( T \right),\cos \left( {2T} \right), \cdots ,\cos \left( {N_{{\text{c}}} T} \right),\sin \left( T \right),\sin \left( {2T} \right), \cdots ,\sin \left( {N_{{\text{s}}} T} \right)} \right] \hfill \\ \user2{Z}_{{0\Gamma }} = \left[ {a_{{0\Gamma 0}} ,a_{{0\Gamma 1}} ,a_{{0\Gamma 2}} , \cdots ,a_{{0\Gamma N_{{\text{c}}} }} ,b_{{0\Gamma 1}} ,b_{{0\Gamma 2}} , \cdots ,b_{{0\Gamma N_{{\text{s}}} }} } \right]^{T} \hfill \\ {\Delta }\user2{Z}_{\Gamma } = \left[ {{\Delta }a_{{\Gamma 0}} ,{\Delta }a_{{\Gamma 1}} ,{\Delta }a_{{\Gamma 2}} , \cdots ,{\Delta }a_{{\Gamma N_{{\text{c}}} }} ,{\Delta }b_{{\Gamma 1}} ,{\Delta }b_{{\Gamma 2}} , \cdots ,{\Delta }b_{{\Gamma N_{{\text{s}}} }} } \right]^{T} \hfill \\ \end{gathered} \right. $$
(52)

Assuming that the numbers of sine and cosine terms of the Fourier series in Eq. (52) are equal, i.e., Nc = Ns = a, then substituting Eq. (51) into Eqs. (49) and (50) results in

$$ {\varvec{d}}_{0} = {\varvec{SZ}}_{0} ,{\Delta }\user2{d = S}{\Delta }{\varvec{Z}} $$
(53)

where

$$ \left\{ \begin{gathered} {\varvec{S}} = diag\left[ {{\varvec{X}}_{{\text{S}}} ,{\varvec{X}}_{{\text{S}}} , \cdots ,{\varvec{X}}_{{\text{S}}} } \right]_{2N} \hfill \\ {\varvec{Z}}_{0} = \left[ {{\varvec{Z}}_{01} ,{\varvec{Z}}_{02} , \cdots ,{\varvec{Z}}_{{0\left( {2N} \right)}} } \right]^{T} \hfill \\ {\Delta }{\varvec{Z}} = \left[ {{\Delta }{\varvec{Z}}_{1} ,{\Delta }{\varvec{Z}}_{2} , \cdots ,{\Delta }{\varvec{Z}}_{2N} } \right]^{T} \hfill \\ \end{gathered} \right. $$
(54)

By substituting Eq. (53) into Eq. (46) and using the Galerkin procedure, we can derive a linear equation in terms of the increments ΔZ and ΔΩ, given by

$$ \user2{K}_{{{\text{mc}}}} \Delta \user2{Z} = \overline{\user2{R}} - \user2{R}_{{{\text{mc}}}} \Delta {\Omega } $$
(55)

where

$$ \left\{ \begin{gathered} {\varvec{K}}_{{\text{mc}}} = \int_{0}^{2\pi } {\left[ {{\varvec{S}}^{\tau } \Omega_{0}^{2} \user2{M\ddot{S}} + \Omega_{0} \user2{C\dot{S}} + \left( {{\varvec{K}}_{\text{L}} \user2{ + }\tilde{\user2{K}}_{{\text{NL}}} } \right){\varvec{S}}} \right]dT} \hfill \\ \overline{{\varvec{R}}} = \int_{0}^{2\pi } {{\varvec{S}}^{\tau } \left\{ {{\varvec{P}}0\cos \left( T \right) - \left[ {\Omega_{0}^{2} \user2{M\ddot{S}} + \Omega_{0} \user2{C\dot{S}} + \left( {{\varvec{K}}_{\text{L}} \user2{ + K}_{{\text{NL}}} } \right){\varvec{S}}} \right]{\varvec{Z}}_{0} } \right\}dT} \hfill \\ {\varvec{R}}_{{\text{mc}}} = \int_{0}^{2\pi } {{\varvec{S}}^{\tau } \left( {2\Omega_{0} \user2{M\ddot{S}} + \user2{C\dot{S}}} \right){\varvec{Z}}_{0} dT} \hfill \\ \end{gathered} \right. $$
(56)

To begin the solution process, a guessed value of Ω0 can be used to obtain both linear and nonlinear solutions. The dynamic responses of the structure can be calculated point by point by increasing the frequency Ω or a component of the coefficient vector Z0. Furthermore, the nonlinear multi-valued solution is obtained using an incremental arc-length continuation technique to improve computational efficiency [51].

5 Results and discussions

In current work, the following parameters will be adopted in the calculation unless specifically indicated [10, 17, 52]

  • The dimensions of the membrane are b = 0.008 m and h = 0.0002 m, respectively, and the radial stretching ratio is η = 1.01;

  • The amplitude of excitation is P0 = 0.1 and the damping ratio is ξ = 0.1;

  • The diameter and thickness of the GNP filler are DGNP = 8.1967 × 10–6 m and tGNP = 5 × 10–8 m, respectively;

  • The average volume fraction of GNPs is φavg = 1.6% and the slope factor is Sg = 0.2;

  • For the matrix PVDF, the density is γm = 1780 kg/m3. The elastic modulus and Poisson’s ratio are Em = 1.44 GPa and νm = 0.35. The electrical conductivity is σm = 3.5 × 10–9 S/m and the dielectric permittivity is εm = 5 × 8.85 × 10–12 F/m;

  • For the filler GNP, the density is γGNP = 2200 kg/m3. The elastic modulus and Poisson’s ratio are E1 = E2 = 1.01 TPa, E3 = 101 TPa and νGNP = 0.175. The in-plane and out-of-plane electrical conductivity are σ1 = σ2 = 8.32 × 104 S/m and σ3 = 83.2 S/m, respectively. The in-plane and out-of-plane dielectric permittivity are ε1 = ε2 = 1.3275 × 10−10 F/m and ε3 = 8.89425 × 10−11 F/m, respectively;

  • For the internal pore, the density is γp = 1.293 kg/m3. The electrical conductivity is σp = 1 × 10–15 S/m and the dielectric permittivity is εp = 8.85 × 10–12 F/m. The pore aspect ratio is αp = 0.01 and porosity is n = 0.1.

5.1 Convergence and validation study

To achieve accurate results in the discretization process employing the DQ method, a larger number of grid points is typically required. However, an increase in grid points can also result in a greater demand for computational resources. Balancing accuracy and computational efficiency, a convergence analysis is conducted to determine the minimum number of grid points needed. Table 1 tabulates the dimensionless amplitudes of the membrane for different electrical and base excitations considering different orders of Fourier series a. As observed, the effect of the order of the Fourier series is negligible, which may be attributed to the reason that the excitation frequency is selected around the frequency of the first harmonic terms, and the results converge when N = 17. Therefore, N = 17 will be used for subsequent calculation unless otherwise specified.

Table 1 Convergence study on the number of grid points
Full size table

In addition to the convergence analysis of the grid points, Table 2 presents the number of layers required to obtain the FG-GNPRC dielectric porous membrane. It can be seen that the dimensionless amplitude gradually converges as the number of layers increases. Balancing the accuracy and efficiency of the calculation, 20 layers will be used for the structural analysis.

Table 2 Dependency of the dimensionless amplitude on the number of gradient layers
Full size table

To validate the proposed model and the solution, Fig. 6 verifies the amplitude-frequency curves with the previously reported results [42] without considering dielectric properties. The material properties and structural dimensions are chosen as b = 1 m, h = 0.001 m, γ = 2200 kg·m−3 and C1 = 0.17 MPa, respectively. The results obtained by present work agree well with the ones in existing studies.

Fig. 6
figure 6

Comparison between present results and Ref [42]

Full size image

Further validation is conducted by finite element analysis (FEA) considering the internal pores. Abaqus is adopted for FEA and a total number of 8164 C3D10 elements are used for the membrane. Comparison of FEA results with the one by the present model for the nonlinear frequency response is depicted in Fig. 7. Excellent agreement is observed between the FEA and our numerical results. It is found that the membrane with relatively large porosity exhibits larger amplitude and stronger nonlinear hardening behavior.

Fig. 7
figure 7

Comparison of FEA results with the present model for the nonlinear frequency response of FG-GNPRC membrane a n = 0.1, b n = 0.3

Full size image

5.2 Parametric study

Figure 8 exhibits the variation of the dimensionless amplitude of the FG-GNPRC membrane with the slope factor Sg. It can be found that the increase of Sg engenders a gradual decrease in the susceptibility of the composite membrane’s amplitude to the influence of the applied voltage. Furthermore, the amplitude ceases to be influenced by voltage when Sg exceeds a certain value. The above observation can be attributed to the dependency of the dielectric properties of the FG-GNPRC membrane on Sg. When Sg exceeds a certain value, the presence of a percolation threshold leads to the lowest GNP concentration layer’s dielectric properties to be negligible, and thus the applied electric field becomes incapable of altering the structural behavior of the FG-GNPRC membrane. Such a phenomenon highlights the influence of Sg on the dimensionless amplitude of the FG-GNPRC membrane subjected to electro-mechanical loading, indicating the vital role of percolation in governing the dielectric behavior of the FG-GNPRC membrane.

Fig. 8
figure 8

Dependency of the dimensionless amplitude on slope factor Sg

Full size image

Figure 9 presents the effect of thickness-to-radius ratio on the dimensionless amplitude of FG-GNPRC membrane. As observed, with the application of the electrical field, the dimensionless amplitudes of FG-GNPRC membranes with different profiles exhibit a decline as κ increases, indicating a nonlinear effect of κ on the system. For example, in Fig. 9a, when the applied voltage is 20 V, for a membrane with a fixed radius of 8 mm, when κ increases from 0.02 to 0.03, the dimensionless amplitude decreases by 26.8%, while the decrease is only 7.2% as κ further increases from 0.03 to 0.04.

Fig. 9
figure 9

Dependency of the dimensionless amplitude on thickness-to-radius ratio κ for a profile O and b profile X

Full size image

Figure 10 investigates the dependency of the dimensionless amplitude on AC frequency and DC voltage. Upon observation, as the applied voltage increases, two transition regions are emerged where the amplitude is highly sensitive to the AC frequency. For the first transition, i.e., fAC = 10–3 Hz, the dielectric permittivity of the FG-GNPRC membrane increases abruptly. This is because the GNP is separated by an extremely thin dielectric layer of PVDF, which accumulates a large number of interfacial charges. As a result, many charges are trapped at the filler–polymer interface due to the effect of Maxwell–Wagner-Sillars (MWS) polarization. For the second transition, i.e., fAC = 102 Hz, the number of accumulated electrons decreases due to additional electron tunneling within the GNP interface layer at higher AC frequency. This leads to a decrease in the effect of MWS polarization. Furthermore, a comparison between Fig. 10a and b evidences that as Sg increases, the effect of MWS polarization decreases significantly. This can be elucidated by a reduction in charge accumulation within the FG-GNPRC membrane, leading to a decrease in dielectric properties.

Fig. 10
figure 10

Dependency of dimensionless amplitude on AC frequency fAC and DC voltage VDC a Sg = 0.2, b Sg = 0.4

Full size image

Figure 11 discusses the dependency of the dimensionless amplitude on the aspect ratio of pore αp and porosity n. In Fig. 11a, it can be found that the dimensionless amplitude increases with increasing n, and the trend is more pronounced for the FG-GNPRC membrane with relatively small αp of internal pore. Moreover, the observation becomes more evident after the application of the external electric field. Compared with Fig. 11a, the effect of the external electric field in Fig. 11b is relatively small. These phenomena can be explained by the dependency of the stiffness of the FG-GNPRC membrane on the attribute of pore and the stretching ratio. Pores with relatively small αp are prone to developing into microcrack patterns, which can significantly affect the mechanical robustness of the FG-GNPRC membrane due to the difference in mechanical properties and surface properties. For the FG-GNPRC membrane subjected to larger stretch, the increased stiffness of the system affects the regulation of the structural behavior by the applied voltage. Such an observation suggests that the effect of the applied voltage on structural behavior can be managed by adjusting the stretching ratio.

Fig. 11
figure 11

Dependency of dimensionless amplitude on pore aspect ratio αp and porosity n a η = 1.005, b η = 1.05

Full size image

Figure 12 shows the dependency of the dimensionless amplitude on pore aspect ratio αp and GNP diameter-to-thickness ratio DGNP/tGNP. The applied voltage is fixed as 20 V. In Fig. 12a, the dimensionless amplitude is relatively large for smaller or larger DGNP/tGNP with changing pore aspect ratio, which can be explained by the competing effects of mechanical and electrical properties on structural behavior of the FG-GNPRC membrane. When DGNP/tGNP is smaller, the mechanical properties dominate and the structural behavior is mainly related to the variation of the elastic modulus. However, as DGNP/tGNP increases, the dielectric properties of the FG-GNPRC membrane exert a substantial influence on the structural behavior, resulting in an increase in the structural amplitude. In contrast, Fig. 12b reveals a distinct phenomenon where the dimensionless amplitude of the FG-GNPRC membrane is notably reduced at DGNP/tGNP = 500 in comparison to DGNP/tGNP = 100. This once again underscores the ability to actively manipulate the effect of the applied voltage on structural behavior by altering the stretching ratio of the FG-GNPRC membrane.

Fig. 12
figure 12

Dependency of dimensionless amplitude on pore aspect ratio αp and GNP diameter-to-thickness ratio DGNP/tGNP a η = 1.005, b η = 1.05

Full size image

Figure 13 presents the variation of the frequency response of the FG-GNPRC membrane for different stretching ratios. It can be seen that the excitation frequency of the system generating the peak amplitude increases as the stretching ratio increases, while the maximum dimensionless amplitude decreases with increasing stretching ratio. Moreover, the system displays a stronger hardening behavior and wider multi-valued response region for relatively small stretching ratio. The above observation can be attributed to the fact that the natural frequency of the system increases as the stretching ratio increases. In addition, it can be observed that there exists a certain excitation frequency generating the identical amplitude for the FG-GNPRC membrane with different stretching ratios, and the identical amplitude between the membranes is larger for those with larger stretching ratios. This reflects that there exists an energy transfer mechanism between different stretched membranes.

Fig. 13
figure 13

Nonlinear frequency response of the FG-GNPRC membrane with different stretching ratios in profile O

Full size image

Figure 14 shows the frequency response of the FG-GNPRC membrane subjected to different damping ratios. Expectedly, the dimensionless amplitude decreases with the increase of the damping ratio, while the influence becomes limited when the damping ratio increases to a relatively large value. In addition, similar to the above observation, with the increase of the stretching ratio, the nonlinearity of the system becomes weaker and the multi-valued response region decreases.

Fig. 14
figure 14

Nonlinear frequency response of the FG-GNPRC membrane with different damping ratios a η = 1.01 b η = 1.11

Full size image

Figure 15 investigates the influence of different membrane thickness h and thickness-to-radius ratio κ on the frequency response of the FG-GNPRC membrane. In Fig. 15a, when there is no electrical loading, the frequency response remains consistent for different h at the same κ. However, when the external electric field is applied, the effect of DC voltage is noticeable for relatively small h, i.e., h = 0.1 mm, resulting in a stronger nonlinear response of the membrane. The above observation can be attributed to the high dependency of the Helmholtz free energy on the membrane thickness as indicated in Eqs. (19), (23) and (27). This phenomenon is more pronounced for altering only the thickness while keeping the radius b constant, as shown in Fig. 15b. When the radius of the membrane is fixed as 8 mm, and κ decreases only from 0.025 to 0.02, the frequency response becomes highly nonlinear and the structural hardening behavior is obvious.

Fig. 15
figure 15

Nonlinear frequency response of the FG-GNPRC membrane with different DC voltages and a membrane thickness h b thickness-to-radius ratio κ

Full size image

Figure 16 displays the effect of different GNP weight fraction fGNP and GNP diameter-to-thickness ratio DGNP/tGNP on the frequency response. As seen in Fig. 16a, for relatively small fGNP, i.e., fGNP = 0.5%, the frequency response is barely influenced by the electrical loading. While fGNP is relatively large, i.e., fGNP = 2.0%, the effect of the external electric field on the frequency response of the system becomes apparent. The FG-GNPRC membrane under the applied electric field shows a noticeable nonlinear frequency response and exhibits a stronger hardening behavior compared with the one without electrical loading. Similar observations can be found in Fig. 16b. For relatively small DGNP/tGNP, i.e., DGNP/tGNP = 100, there exists limited hardening behavior of the FG-GNPRC membrane. However, when DGNP/tGNP is relatively large, i.e., DGNP/tGNP = 400, the dynamic response of FG-GNPRC is significantly altered under the action of the external electric field. This can also be attributed to the dependency of the dielectric permittivity of the FG-GNPRC membrane on the percolation threshold. Below the percolation threshold, the dynamic response of the system influenced by the applied voltage is very limited, and when GNP concentration exceeds the percolation threshold, the resonance behavior of the FG-GNPRC membrane can be adjusted by varying the applied voltage.

Fig. 16
figure 16

Nonlinear frequency response of the FG-GNPRC membrane with different DC voltages and a GNP weight fraction fGNP b GNP diameter-to-thickness ratio DGNP/tGNP

Full size image

Figure 17 investigates the influence of different porosity n and pore aspect ratio αp on the frequency response of the FG-GNPRC membrane. In Fig. 17a, for the same αp, it can be clearly seen that the amplitude increases with increasing n and the applied voltage increases both the amplitude and hardening behavior, particularly for membranes with relatively large n. In Fig. 17b, it is found that pore aspect ratio αp has a significant effect on the frequency response, for relatively small αp, i.e., αp = 0.01, the system displays a stronger hardening behavior and a higher peak amplitude frequency. In addition, it is seen that the maximum dimensionless amplitude of the oscillations increases as a result of decreased αp. The above observation can be attributed to the effect of internal pore on the electrical and mechanical properties of the composite membrane. Such narrow and long pores have an obstructive effect and these pores are developed into micro-crack patterns in certain directions. Their insulating property can disrupt the formed conductive networks and block the transmission channels of the carrier. Moreover, the formation of these microcracks also reduce the stiffness of the composite membrane.

Fig. 17
figure 17

Nonlinear frequency response of the FG-GNPRC membrane with different DC voltages and a porosity n b pore aspect ratio αp

Full size image

6 Conclusion

The nonlinear dynamics of the FG-GNPRC membrane subjected to electro-mechanical loading is analyzed numerically taking into account the effects of internal pores, dimension of the membrane and other factors. The strain energy of the system is obtained by means of the hyperelastic membrane theory, Neo-Hookean constitutive model and the couple dielectric theory. The energy expressions are inserted in the Hamilton’s principle yielding a set of strongly nonlinear governing equations. The equations are discretized by combining TSE and DQ methods. IHB and arc-length continuation technique are then employed to perform a nonlinear analysis for comprehensive system parameters.

The analysis reveals that FG-GNPRC membrane with profile X exhibits the smallest dimensionless amplitude, while the largest dimensionless amplitude can be obtained for the beam with profile O. The increase of Sg reduces the effect of the applied electrical load on the structural behavior of the FG-GNPRC membrane, as does the effect of MWS polarization. Therefore, Sg needs to be controlled within 0.5 to ensure that the amplitude of the membrane can be adjusted by varying the electric field. The presence of pores affects the structural behavior and stability of the system, especially for smaller pore aspect ratio. Additionally, the effect of the applied voltage on the structural behavior can be controlled by varying the stretching ratio. The FG-GNPRC membrane with a smaller stretching ratio exhibits stronger nonlinear hardening behavior, and the energy transfer mechanism is observed by varying the stretching ratio. When h and κ are relatively small, the applied voltage has a notable influence on the system, resulting in a more pronounced nonlinear hardening behavior. Moreover, it is demonstrated that the existence of internal pores has obvious influence on the nonlinear dynamic response of the membrane. The FG-GNPRC membrane with relatively small pore aspect ratio is more affected by the external electric load, generating a higher amplitude peak and excitation frequency required for the resonance.