1 Introduction

As the primary interactive force media between the road vehicle and the ground, the tires play the fundamental role in vehicle dynamics and control research [1,2,3,4]. Vehicle braking safety, handling stability, vertical vibration and front wheel shimmy characteristics all depend on the study of tire mechanics characteristics. The design and development of the chassis control system (such as Antilock Brake System, Traction Control System, Direct Yaw Control, etc.) are based on the study of tire mechanical characteristics [5,6,7].

The study of tire mechanical properties first starts from the pure cornering condition, and then extends to the combined cornering/braking/driving conditions [4]. Compared with the pure-slip tire model, the combined-slip tire model could accurately describe the coupling relationship between longitudinal and lateral forces. Therefore, the tire model under the combined conditions have been studied extensively since the 1930’s [7]. In general, tire steady-state mechanics models can be divided into three categories: empirical models, semi-empirical models, and physical models [7]. In addition, there are some methods to obtain tire forces, such as finite-element method and Gaussian process regression [8,9,10]. The empirical model is directly obtained from tire test data, so the accuracy of the model is high. However, due to the lack of theoretical foundation, the model’s extrapolation and theoretical accuracy are poor [7]. As the most popular empirical tire model, the MF model could express the tire forces and moments accurately in combined-slip conditions [5, 6, 11], while it needs a mass of test data to identify the parameters of the model which is time-consuming and complicated in practice.

The semi-empirical model is modeled on the basis of theoretical research and experimental analysis. Thus, the semi-empirical model not only has high theoretical accuracy, good extrapolation, but also has high simulation accuracy [7]. At present, the typical semi-empirical model is the UniTire model [12,13,14,15,16]. Compared with the MF model, the UniTire model has better predictive ability, better theoretical accuracy, and fewer parameters.

The physical model is a mathematical description of the tire’s mechanical characteristics based on tire’s physical structure and deformation mechanism [7]. The model is of great significance for analyzing the physical nature of tire mechanics and studying the influence of structural parameters on the mechanical properties. Compared with empirical model and semi-empirical model, the physical model is more suitable for theoretical derivation and analytical solution in vehicle dynamics research, especially under the extreme conditions of large slip, such as drifting [7, 17]. However, there are two main problems in the current physical models. One is that the model is too complicated to be applied in actual vehicle dynamics research [18, 19]. The other is that the accuracy of the model is not high due to many simplifications in the modeling process such as Dugoff model [20,21,22,23]. As we all know, it is difficult to obtain the data of combined slip conditions, which requires expensive cost and a long test period. The predictive model can use the tire test data under pure slip conditions to predict the tire forces under combined slip conditions. Thus, it is necessary to develop a physical predictive model with high accuracy and simplified expression.

When modeling the tire combined-slip maneuvers, the allocation of the resultant shear force between the lateral and longitudinal direction has to be determined. The accuracy of the allocation would greatly affect the combined model results. In most of the combined-slip tire models available, the direction of the resultant force, or the tangent angle between the lateral and the longitudinal force, is determined by the ratio of lateral slip rate vs longitudinal slip rate [24, 25], such as COMBINATOR model [25]. To account the difference of the allocation in the adhesion region and sliding region within the contact patch, the UniTire model utilizes different allocation expression in the two regions and introduces a factor to express the transition from adhesion to sliding state. In this way, the model could express the combined-slip forces with better accuracy [12,13,14,15,16], while the exact allocation under arbitrary condition still need to be established to theoretically and exactly express the combined-slip tire mechanics. Therefore, a novel distribution principle for the combined-slip tire modelling is proposed by accounting the anisotropic tire stiffness and friction coefficient to calculate the shear forces accurately under lateral and longitudinal slip conditions.

In the paper, a physical predictive model is proposed based on the unified combine brush model which can describe the tire forces accurately under lateral and longitudinal slip conditions. Firstly, the derivation process of proposed model is introduced from pure and combined slip conditions. Then, comparison between the brush physical models based on three assumptions about the direction of resultant shear force and the proposed model is separately conducted to explain the correctness of the model in theory. Lastly, the proposed tire model is compared with COMBINATOR model, MF model and Modified Dugoff model and verified by test data under different conditions.

2 The foundation of modeling

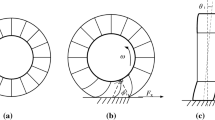
2.1 Tire coordinate system

Fig. 1
figure 1

Tire coordinate system in [10]

Full size image

The Tire Contact Process coordinate is employed to describe the longitudinal and lateral slip ratio uniformly [13], as shown in Fig. 1. The Centre of contact patch is defined as the origin of coordinate system. The coordinate axes with positive direction are shown above, and more details are described in Ref. [13]. The velocity of wheel is shown as V, and \(\gamma \) is the inclination angle, and the slip angle \(\alpha \) is angle between Xt-axis and the direction of the velocity of wheel. The figure above shows the six-component force within the contact patch , whose direction denotes positive. The main topic in the paper is calculation of shear forces under combined slip conditions, so three moments are not discussed.

2.2 The slip ratios

The slip ratios are defined as the sliding speed over the rolling speed as shown below [13].

$$\begin{aligned} \left\{ \begin{array}{lr} S_x=\dfrac{-V_{sx}}{V_r}=-\dfrac{V\cos \alpha -\Omega R_e}{\Omega R_e} &{} S_x\in (-\infty ,+\infty )\\ S_y=\dfrac{-V_{sy}}{V_r}=-\dfrac{V\sin \alpha }{\Omega R_e} &{} S_y\in (-\infty ,+\infty )\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(1)

where \(S_x\) is the longitudinal slip ratio, \(S_y\) is the lateral slip ratio, \(V_{sx}\) is the longitudinal slip velocity of tire to the road surface, \(V_{sy}\) is the lateral slip velocity to the road surface, \(V_r\) is the rolling velocity, V is the wheel velocity, \(\alpha \) is the slip angle, \(R_e\) is the effective rolling radius of tire, and \(\Omega \) is the rolling angular speed.

In practical test, the longitudinal slip ratio \(\kappa \) [13] is often used instead of Sx and its expression is:

$$\begin{aligned} \kappa =\dfrac{-V_{sx}}{V\cos \alpha }=-\dfrac{V\cos \alpha -{\Omega } R_e}{V\cos \alpha } \end{aligned}$$
(2)

2.3 The pressure distribution within tire contact patch

A parabolic distribution on vertical load over the contact patch is adopted in the work for simplifying the process of tire analytical modeling. And this distribution pattern can approximately express the pressure distribution under small load and is not suitable for pressure distribution under overload and heavy load. The distribution of the load per unit length is expressed as follows:

$$\begin{aligned} q_z=\dfrac{3F_z}{4a}\left[ 1-\left( \dfrac{x}{a}\right) ^2\right] \quad x\in (-a,a) \end{aligned}$$
(3)

where \(F_z\) is the vertical force and a is the half of the contact length 2a [6].

3 The physical model for pure slip

The proposed model gets started from pure slip conditions. The model under pure slip condition is similar to the model in Ref. [6], and the two models are different in expressions. The derivation process of pure lateral slip condition is shown as follows.

Fig. 2
figure 2

Deformation of the bristles in contact patch under pure lateral slip condition

Full size image

Figure 2 shows the deformation of bristles in contact patch under pure lateral slip condition, where ‘ABC’ is the contact line of bristles with the ground. The whole contact patch is divided into adhesion region ‘AB’ and sliding region ‘BC’, and ‘B’ is the initial sliding point. According to Fig. 2, the lateral deformation [7] of the tread elements in the adhesion region is:

$$\begin{aligned} \varDelta y=(a-x)\cdot S_y=-(a-x)\cdot \tan \alpha \end{aligned}$$
(4)

And the lateral shear stress [7] in contact patch of elastic bristles is

$$\begin{aligned} q_y=k_{ty}\cdot S_y\cdot (a-x) \quad x\in (-a,a) \end{aligned}$$
(5)

where \(k_{ty}\) is lateral stiffness of the bristles per unit length.

When the magnitude of shear stress above is equal to the maximum friction force, the coordinate of initial sliding points \(x_{t}\) meets the equation below [5]:

$$\begin{aligned} |k_{ty}\cdot S_y\cdot (a-x_t)|=\mu _y\cdot q_z \end{aligned}$$
(6)

where \(\mu _{y}\) is the lateral friction coefficient. Solving the equation above, it yields the coordinate of initial sliding points:

$$\begin{aligned} x_t=2a\dfrac{k_y |S_y|}{3\mu _y F_z}-a \quad x_t\in (-a,a) \end{aligned}$$
(7)

When \(x_t\) equals to a, the whole sliding condition is:

$$\begin{aligned} \alpha _{sl}=\arctan (\dfrac{3\mu _yF_z}{k_y}) \end{aligned}$$
(8)

where \(k_y\) is the cornering stiffness of tire and \(\alpha _{sl}\) is the slip angle where whole sliding stars.

The normalized lateral slip ratio \(\phi _{y}\) [7] is introduced to express the lateral force briefly:

$$\begin{aligned} \phi _y=\dfrac{k_y S_y}{\mu _y F_z} \quad \phi _y\in (-\infty ,+\infty ) \end{aligned}$$
(9)

If the slip angle is given, the lateral force of tire can be yield by the expression below.

$$\begin{aligned} \begin{aligned} F_y&= \left\{ \begin{array}{lr} \int _{x_t}^{a}k_{ty}S_y(a-x)dx + \int _{-a}^{x_t}\mu _yq_zdx &{} |\alpha | \le \alpha _{sl} \\ \int _{-a}^{a}\mu _yq_zdx &{} |\alpha |> \alpha _{sl}\\ \end{array} \right. \\&= \left\{ \begin{array}{ll} \mu _yF_z \cdot \phi _y \cdot (1-\frac{1}{3}|\phi _y|+\frac{1}{27}\phi _y^2) \;\quad \qquad &{} |\alpha | \le \alpha _{sl} \\ \mu _yF_z \cdot \phi _y \cdot (1-\frac{1}{3}|\phi _y|+\frac{1}{27}\phi _y^2) \; \quad &{} |\alpha | > \alpha _{sl} \end{array} \right. \end{aligned} \nonumber \\ \end{aligned}$$
(10)

The derivation process of the model under pure longitudinal slip condition is similar to the process above, so it’s not stated here. The longitudinal shear force under pure longitudinal slip condition is shown as follows:

$$\begin{aligned} F_x {=} \left\{ \begin{array}{ll} \mu _xF_z \cdot \phi _x \cdot (1-\frac{1}{3}|\phi _x|{+}\frac{1}{27}\phi _x^2) \; \quad &{} |S_x| \le S_{xsl} \\ \mu _xF_z \cdot sign(S_x) \; \quad &{} |S_x| > S_{xsl} \end{array} \right. \nonumber \\ \end{aligned}$$
(11)

where \(\phi _x\) is the normalized longitudinal slip ratio [7], and its expression is:

$$\begin{aligned} \phi _x=\dfrac{k_xS_x}{\mu _xF_z} \quad \phi _x\in (-\infty ,+\infty ) \end{aligned}$$
(12)

And \(S_{xsl}\) is the longitudinal slip ratio where whole sliding stars, and its expression is shown below:

$$\begin{aligned} S_{xsl}=3\mu _xF_z/k_x \end{aligned}$$
(13)

where \(k_x\) is the longitudinal slip stiffness of tire and \(\mu _x\) is longitudinal friction coefficient.

4 The physical model for combined slip

4.1 The derivation of the exact unified combined brush model

How to distribute accurately the longitudinal force and lateral force is a main problem in combined model. Whether the resultant force direction is assumed to be the same as that in sliding region, or adhesion region, they are not suitable when the tire is anisotropic [13]. Therefore, based on the vector distribution principle considering anisotropic tire stiffness, the exact unified combined brush model (EUCB model for short) could describe accurately the variation of the shear forces. The derivation process of combined slip condition is shown as follows.

Fig. 3
figure 3

Deformation of the bristles in contact patch under the combined conditions in [7]

Full size image

Figure 3 shows the deformation of bristles in contact patch under combined cornering and braking condition [7]. The shear stresses [7] of point \(P_t\) in X and Y directions under combined conditions is:

$$\begin{aligned} \begin{aligned} \mathbf {q}&= \begin{bmatrix} q_x \\ q_y \end{bmatrix} = \begin{bmatrix} k_{tx} \cdot \varDelta x \\ k_{ty} \cdot \varDelta y \end{bmatrix} \\&= \begin{bmatrix} k_{tx} \cdot S_x \cdot (a-x) \\ k_{ty} \cdot S_y \cdot (a-x) \end{bmatrix} \quad x\in (-\infty ,+\infty ) \end{aligned} \end{aligned}$$
(14)

The magnitude of total shear stress [7] is:

$$\begin{aligned} q=(a-x)\cdot \sqrt{(k_{tx}S_x)^2+(k_{ty}S_y)^2} \end{aligned}$$
(15)

Solving the balance equation \(q(x_t)=\mu ^a\cdot q_z(x_t)\), the coordinate of initial sliding points could be yield:

$$\begin{aligned} x_t=2a\cdot \phi /3-a \quad x_t\in (-a,a) \end{aligned}$$
(16)

where \(\phi \) is the normalized combined slip ratio with expression \(\phi =\sqrt{\phi _x^2+\phi _y^2}\) and \(\mu ^a\) is the directional friction coefficient of adhesion region, and its expression is shown below which can be obtained through the friction ellipse concept [13].

$$\begin{aligned} \mu ^a=\sqrt{ \left( \mu _x\dfrac{\phi _x}{\phi }\right) ^2+\left( \mu _y\dfrac{\phi _y}{\phi }\right) ^2} \end{aligned}$$
(17)

Integrating the magnitude of shear stress in adhesion region, the magnitude of shear force in adhesion region can be obtained:

$$\begin{aligned} F^a=\sqrt{(k_xS_x)^2+(k_yS_y)^2}\cdot (1-\phi /3)^2 \end{aligned}$$
(18)

Integrating the magnitude of shear stress in sliding region, the magnitude of shear force in the region is:

$$\begin{aligned} F^s=\mu ^sF_z \cdot \phi ^2 \cdot (1/3-2\phi /27) \end{aligned}$$
(19)

where \(\mu ^s\) is the directional friction coefficient of sliding region, and its expression can be also obtained through the friction ellipse concept.

Fig. 4
figure 4

Vector distribution relationship among normalized shear forces

Full size image

Figure 4 shows the vector distribution relationship among normalized shear forces under two assumptions, with one considering the anisotropy of tire stiffness and the other not. When the longitudinal slip stiffness of the tire is different from the cornering stiffness, the direction of shear force in sliding region and that in adhesion region are different as shown in Fig. 4b [14, 15]. Therefore, it is inaccurate that the direction of resultant shear force is assumed to be the same as the direction of shear force in sliding region or adhesion region with ignoring the anisotropy of tire stiffness as described in Fig. 4a [14, 15].

And the meaning of each symbol is explained below. The normalized resultant shear force, longitudinal force and lateral force in adhesion region can be yielded as follows:

$$\begin{aligned} \bar{F^a}=\dfrac{F^a}{\mu ^aF_z},\bar{F_x^a}=\dfrac{F_x^a}{\mu _xF_z},\bar{F_y^a}=\dfrac{F_y^a}{\mu _yF_z} \end{aligned}$$
(20)

where \(F^a\) is the absolute magnitude of its own vector \(\mathbf {F^a}\) and \(F_x^a\) , \(F_y^a\) are longitudinal and lateral forces in adhesion region. The vector \(\bar{\mathbf {F^a}}\) can be expressed as (\(\bar{F_x^a}\) ,\(\bar{F_y^a} \)).

In the same way, the normalized forces in sliding region can be obtained:

$$\begin{aligned} \bar{F^s}=\dfrac{F^s}{\mu ^sF_z},\bar{F_x^s}=\dfrac{F_x^s}{\mu _xF_z},\bar{F_y^s}=\dfrac{F_y^s}{\mu _yF_z} \end{aligned}$$
(21)

where \(F^s\) is the absolute magnitude of its own vector and \(F_x^s\),\(F_y^s\) are longitudinal and lateral forces in the region. The vector\(\bar{\mathbf {F^s}}\) can be expressed as (\(\bar{F_x^s}\) ,\(\bar{F_y^s} \)).

Combining Eqs. (20)–(21) and Fig. 4b, the following equations can be obtained obviously:

$$\begin{aligned}&\bar{F_x}=\bar{F_x^a}+\bar{F_x^s},\bar{F_y}=\bar{F_y^a}+\bar{F_y^s},\bar{\mathbf {F}}=\bar{\mathbf {F^a}}+\bar{\mathbf {F^s}} \end{aligned}$$
(22)
$$\begin{aligned}&\left\{ \begin{aligned} \bar{F^a}&=\sqrt{(\bar{F_x^a})^2+(\bar{F_y^a})^2}\\ \bar{F^s}&=\sqrt{(\bar{F_x^s})^2+(\bar{F_y^s})^2} \\ \bar{F}&=\sqrt{(\bar{F_x})^2+(\bar{F_y})^2} \end{aligned} \right. \end{aligned}$$
(23)

where \(\bar{F_x}\) , \(\bar{F_y}\) and \(\bar{F}\) are normalized longitudinal force, lateral force and resultant shear force respectively. And the vector \(\bar{\mathbf {F}}\) can be expressed as (\(\bar{F_x}\),\(\bar{F_y}\)).

From the above equations, the longitudinal and lateral forces in contact patch are:

$$\begin{aligned}&F_x=F_x^a+F_x^s=\mu _xF_z(\bar{F_x^a}+\bar{F_x^s}) \end{aligned}$$
(24)
$$\begin{aligned}&F_y=F_y^a+F_y^s=\mu _yF_z(\bar{F_y^a}+\bar{F_y^s}) \end{aligned}$$
(25)

And the directions of normalized shear forces in adhesion region and sliding region are, respectively:

$$\begin{aligned} \tan (\theta ^a)=\dfrac{\bar{F_y^a}}{\bar{F_x^a}}=\dfrac{\phi _y}{\phi _x},\quad \tan (\theta ^s)=\dfrac{\bar{F_y^s}}{\bar{F_x^s}}=\dfrac{\phi _y}{\phi _x} \cdot \dfrac{k_x}{k_y} \nonumber \\ \end{aligned}$$
(26)

And the direction of normalized shear force is:

$$\begin{aligned} \tan (\theta )=\dfrac{\bar{F_y}}{\bar{F_x}}=\dfrac{\bar{F_y^a}+\bar{F_y^s}}{\bar{F_x^a}+\bar{F_x^s}} \end{aligned}$$
(27)

Therefore, the longitudinal force and lateral force of the tire in contact patch can be obtained as follows and the expressions correspond to two conditions. One is that the contact patch is covered by sliding region entirely with \(\phi >3\), the other is that there is adhesion region in contact patch with \( 0 \le \phi \le 3\).

$$\begin{aligned} \left\{ \begin{aligned}&\left\{ \begin{array}{l} F_x=\mu _xF_z(\bar{F^a}\dfrac{\phi _x}{\phi }+ \bar{F^s}\dfrac{\phi _x \cdot k_y/k_x }{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}) \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad 0 \le \phi \le 3 \\ F_y=\mu _yF_z(\bar{F^a}\dfrac{\phi _y}{\phi }+\bar{F^s}\dfrac{\phi _y }{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}) \\ \end{array} \right. \\&\left\{ \begin{array}{ll} F_x=\mu _xF_z \dfrac{\phi _x \cdot k_y/k_x }{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}} \\ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \phi >3 \\ F_y=\mu _yF_z \dfrac{\phi _y}{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}\\ \end{array} \right. \\ \end{aligned} \right. \nonumber \\ \end{aligned}$$
(28)

where the normalized shear force in adhesion region is \( \bar{F^a}=\phi \cdot (1-\phi /3)^2\) , and the normalized shear force in sliding region is \(\bar{F^s}=\phi ^2 \cdot (1/3-2\phi /27)\).

4.2 The simulation and analysis of the exact unified combined brush model

The longitudinal force and lateral force of tire can be found through the formula (28) with given friction characteristic parameters, tire’s speed, longitudinal slip rate, slip angle and basic characteristic parameters under combined conditions.

To validate the EUCB model, the simulation results are compared with the brush physical tire model based on the arbitrary pressure distribution with three different assumptions about the direction of resultant shear force. Currently, the three direction assumptions are: the direction of resultant shear force is consistent with that in adhesion region which is \( \dfrac{F_y}{F_x}=\dfrac{k_yS_y}{k_xS_x}\) , the direction of resultant shear force is consistent with that in sliding region which is \( \dfrac{F_y}{F_x}=\dfrac{S_y}{S_x}\), and the direction of resultant shear force transitions from that in adhesion region to sliding region as the slip rate increases which is \( \dfrac{F_y}{F_x}=\dfrac{k_yS_y}{\lambda k_xS_x}\) , where \(\lambda \) is the direction factor and its expression is:

$$\begin{aligned} \lambda =1+(k_y/k_x-1)\bar{F} \end{aligned}$$
(29)

In simulation, tire speed is 80km/h , tire friction characteristic parameters are: \(\mu _x=1, \mu _y=0.7\), basic characteristic parameters of tire are: \(k_x= 90\)KN/rad, \(k_y= 40 \)KN/rad, \( F_z= 5000\)N, \(R_e=0.4\)m, \(a=12.55\)cm, where \(R_e\) is the effective radius of tire. And the brush models based on the three assumptions above are short for AAUCB, SAUCB, and DAUCB model, respectively.

Fig. 5
figure 5

Longitudinal force vs. kappa under different slip angles

Full size image
Fig. 6
figure 6

Longitudinal force comparisons between EUCB model and AAUCB model

Full size image
Fig. 7
figure 7

Longitudinal force comparisons between EUCB model and SAUCB model

Full size image
Fig. 8
figure 8

Longitudinal force comparisons between EUCB model and DAUCB model

Full size image

Figure 5 shows the longitudinal force calculated by the EUCB model at 6 slip angles. Figures 6, 7 and 8 show the comparisons of longitudinal force calculated by the EUCB model and the brush models based on the three assumptions above. It can be seen that the EUCB model and AAUCB model have similar effect on expressing longitudinal force under small longitudinal slip ratio and small slip angle, while the EUCB model and SAUCB model or DAUCB model have nearly consistent effect on describing longitudinal force under large slip conditions. The comparison results indicate the EUCB model has high accuracy on describing longitudinal force under various slip conditions.

Fig. 9
figure 9

Lateral force vs. kappa under different slip angles

Full size image
Fig. 10
figure 10

Lateral force comparisons between EUCB model and AAUCB model

Full size image
Fig. 11
figure 11

Lateral force comparisons between EUCB model and SAUCB model

Full size image
Fig. 12
figure 12

Lateral force comparisons between EUCB model and DAUCB model

Full size image

Figure 9 shows the lateral force calculated by the EUCB model at 6 slip angles. From the fig, it can be seen that the model exists ‘double peaks’ under small slip angles, and the peak value of the braking side is greater than the peak value of the driving side, which conforms to the characteristics of the double peak phenomenon [7].

Figures 10, 11 and 12 show the comparisons of lateral force calculated by the EUCB model and the brush models based on the three assumptions above. From the figures, it can be seen that the EUCB model and AAUCB model have obvious difference on describing lateral force and the difference increases as slip increases. And the EUCB model and SAUCB model or DAUCB model are nearly consistent on describing longitudinal force under large slip conditions. The comparison results show that the EUCB model could describe accurately the direction variation of shear force and express accurately the longitudinal and lateral force with anisotropic tire stiffness and friction coefficient.

4.3 The introduction of dynamic friction coefficient

Many test data indicate that the force and moment of the tire would be affected by the speed-dependent friction feature, which is particularly significant under large slip condition [26,27,28]. Therefore, the dynamic friction coefficient is introduced into the combined model. The longitudinal and lateral friction coefficients [28] are as follows.

$$\begin{aligned} \left\{ \begin{array}{l} \mu _x =\mu _{dx}+(\mu _{sx}-\mu _{dx}) \\ \qquad \ \cdot \exp \left\{ -h_x^2 \cdot \lg ^2\left[ \left| \dfrac{V_{sx}}{V_{mx}}\right| +\exp \left( -\dfrac{V_{sx}}{V_{mx}}\right) \right] \right\} \\ \mu _y=\mu _{dy}+(\mu _{sy}-\mu _{dy}) \\ \qquad \ \cdot \exp \left\{ -h_y^2 \cdot \lg ^2\left[ \left| \dfrac{V_{sy}}{V_{my}}\right| +\exp \left( -\dfrac{V_{sy}}{V_{my}}\right) \right] \right\} \end{array} \right. \end{aligned}$$
(30)

where \(\mu _{dx} , \mu _{sx}, h_x\) and \(V_{mx}\) are longitudinal parameters and \(\mu _{dy}, \mu _{sy}, h_y \)and \(V_{my}\) are lateral parameters of the friction model. When \( V_{sx}\) and \(V_{sy}\) are zeros, \(\mu _{sx}\) equals \(\mu _x\) and \(\mu _{sy}\) equals \(\mu _y\), so \(\mu _{sx}\) and \(\mu _{sy}\) are static friction coefficients [26]. When \( V_{sx}\) and \(V_{sy}\) tend to infinity, \(\mu _{dx}\) equals \(\mu _x\) and \(\mu _{dy}\) equals \(\mu _y\).

Fig. 13
figure 13

Schematic diagram of the stress distribution in contact patch with dynamic friction

Full size image

Figure 13 shows the schematic diagram of the stress distribution in contact patch with dynamic friction coefficient, and \(\mu _s\) represents the static friction coefficient and \(\mu _d\) represents the dynamic friction coefficient.

The introduction of dynamic friction coefficient mainly causes the changes of the starting slip condition and initial sliding point. For the pure lateral slip condition, the starting slip condition becomes:

$$\begin{aligned} |q_y|=\mu _{sy} \cdot q_z \end{aligned}$$
(31)

and the initial sliding point becomes:

$$\begin{aligned} x_t^{\prime }=2a\dfrac{k_y|S_y|}{3\mu _{sy}F_z}-a \qquad x_t^{\prime }\in (-a,a) \end{aligned}$$
(32)

When \(x_t^{\prime }=a\), the total sliding condition becomes:

$$\begin{aligned} |\alpha |=\alpha _{sl}^{\prime }=\arctan (3\mu _{sy}F_z/k_y) \end{aligned}$$
(33)

Then the expression of the lateral shear force is as follows:

$$\begin{aligned} F_y=\left\{ \begin{array}{l} \dfrac{\phi _y^{\prime }}{3} \cdot F_z \cdot [3\mu _{sy}(1-\dfrac{|\phi _y^{\prime }|}{3})^2 \\ +\mu _y \cdot (|\phi _{y}^{\prime }|-\dfrac{2}{9}{\phi _{y}^{\prime }}^2)] \qquad \qquad |\alpha |\le \alpha _{sl}^{\prime } \\ -\mu _{y}F_z \cdot sign(\alpha ) \ \, \qquad \qquad \quad \quad |\alpha | > \alpha _{sl}^{\prime } \end{array} \right. \end{aligned}$$
(34)

where \(\phi _y^{\prime }\) is expressed as:

$$\begin{aligned} \phi _y^{\prime }=\dfrac{\mu _y}{\mu _{sy}}\phi _y=\dfrac{k_yS_y}{\mu _{sy}F_z} \end{aligned}$$
(35)

Similarly, the longitudinal shear force under pure longitudinal slip condition becomes:

$$\begin{aligned} F_x=\left\{ \begin{array}{l} \dfrac{\phi _x^{\prime }}{3} \cdot F_z \cdot [3\mu _{sx}(1-\dfrac{|\phi _x^{\prime }|}{3})^2 \\ +\mu _x \cdot (|\phi _{x}^{\prime }|-\dfrac{2}{9}{\phi _{x}^{\prime }}^2)] \qquad \qquad |S_x| \le S_{xsl}^{\prime } \\ \mu _{x}F_z \cdot sign(S_x) \qquad \qquad \qquad \quad |S_x| > S_{xsl}^{\prime } \end{array} \right. \nonumber \\ \end{aligned}$$
(36)

where \(\phi _x^{\prime }\) is expressed as:

$$\begin{aligned} \phi _x^{\prime }=\dfrac{\mu _x}{\mu _{sx}}\phi _x=\dfrac{k_xS_x}{\mu _{sx}F_z} \end{aligned}$$
(37)

and the longitudinal slip ratio where whole sliding stars becomes \(S_{xsl}^{\prime }\), and its expression is below:

$$\begin{aligned} S_{xsl}^{\prime }=3\mu _{sx}F_z/k_x \end{aligned}$$
(38)

For the combined slip condition with considering dynamic friction coefficient, the starting slip condition becomes:

$$\begin{aligned} q(x_t^{\prime })=\mu _s \cdot q_z(x_t^{\prime }) \end{aligned}$$
(39)

Solving the equation above, the coordinate of initial sliding point is as follows:

$$\begin{aligned} x_t^{\prime }=2a \cdot \phi ^{\prime }/3-a \qquad x_t\in (-a,a) \end{aligned}$$
(40)

When \(\phi ^{\prime }\) is greater than 3, there is no adhesion region in the contact path and its expression is

$$\begin{aligned} \phi ^{\prime }=\phi \cdot \mu ^a/\mu _s \end{aligned}$$
(41)

where \(\mu _s\) is static friction coefficient, similarly, its expression can be obtained through the friction ellipse concept.

$$\begin{aligned} \mu _s=\sqrt{\left( \mu _{sx}\dfrac{\phi _x}{\phi }\right) ^2 + \left( \mu _{sy}\dfrac{\phi _y}{\phi }\right) ^2} \end{aligned}$$
(42)

From the content above, the longitudinal force and lateral force of the tire with considering the dynamic friction coefficient under combined condition become:

$$\begin{aligned} \left\{ \begin{aligned}&\left\{ \begin{array}{l} F_x=\mu _xF_z(\bar{F^a}^{\prime } \dfrac{\phi _x}{\phi }+ \bar{F^s}^{\prime }\dfrac{\phi _x \cdot k_y/k_x }{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}) \\ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad 0 \le \phi ^{\prime } \le 3 \\ F_y=\mu _yF_z(\bar{F^a}^{\prime }\dfrac{\phi _y}{\phi }+\bar{F^s}^{\prime }\dfrac{\phi _y}{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}) \\ \end{array} \right. \\&\left\{ \begin{array}{ll} F_x=\mu _xF_z \dfrac{\phi _x \cdot k_y/k_x }{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}} \\ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \phi ^{\prime } >3 \\ F_y=\mu _yF_z \dfrac{\phi _y}{\sqrt{\phi _y^2+(\phi _x \cdot k_y/k_x)^2}}\\ \end{array} \right. \\ \end{aligned} \right. \nonumber \\ \end{aligned}$$
(43)

where the normalized shear force in adhesion region is \(\bar{F^s}^{\prime }={\phi ^{\prime }}^2 \cdot (1/3-2\phi ^{\prime }/27)) \) , and the normalized shear force in sliding region is \(\bar{F^a}^{\prime }=\phi \cdot (1-\phi ^{\prime }/3)^2 \).

Fig. 14
figure 14

Tire slip test system

Full size image

5 Experiment validation

5.1 Test data used

In the section, we tested the tire of 215/60R17 specification through MTS Flat-Trac Tire Test Systems which is industry-recognized tire test system. And tires of this specification are often used in practice and made by Wanli Tire Corporation Limited. The test content is the tire force and moment characteristics on dry roads under steady-state conditions, including test data of pure cornering, pure longitudinal slip and combined-slip conditions under different loads. Figure 14 shows the tire test system used in the section.

5.2 Experiment validation for pure and combined slip conditions

Fig. 15
figure 15

Longitudinal force at pure slip condition

Full size image
Fig. 16
figure 16

Lateral force at pure slip condition

Full size image

In the section, tire test data of 215/60R17 specification are used to validate the EUCB model proposed above for pure and combined slip conditions. Firstly, the method of nonlinear least squares fitting is used to identify the parameters expressing friction characteristics, cornering stiffness and longitudinal slip stiffness from pure slip condition. Then, the characteristic parameters are brought into the proposed model with dynamic friction to predict the tire forces.

Figures 15 and 16 show the fitting results between test data and the proposed model above at three different loads under pure slip conditions. The results indicate the model could express pure lateral and longitudinal forces accurately.

Fig. 17
figure 17

Longitudinal force comparisons between EUCB model and COMBINATOR model at 5\(^{\circ }\) slip angle

Full size image
Fig. 18
figure 18

Lateral force comparisons between EUCB model and COMBINATOR model at 5\(^{\circ }\) slip angle

Full size image
Fig. 19
figure 19

Longitudinal force comparisons between EUCB model and COMBINATOR model at 2\(^{\circ }\) slip angle

Full size image
Fig. 20
figure 20

Lateral force comparisons between EUCB model and COMBINATOR model at 2\(^{\circ }\) slip angle

Full size image

Figures 17, 18, 19 and 20 indicate the compared results between EUCB model and COMBINATOR model at two slip angles and three loads. The green dashed lines denote the longitudinal and lateral forces obtained by COMBINATOR model, and the black lines denote the forces obtained by EUCB model proposed.

The results show that both models could describe tire forces well. The comparisons indicate that two models are similar at large slip condition and different obviously at small slip condition. The slip direction is viewed as the direction of resultant shear force in COMBINATOR model [24, 25]. Therefore, the similarity is because the slip direction is the same as the direction of resultant shear force at large slip condition [15]. The difference is mainly because the direction of resultant shear force of the two models are different at small slip condition. The mathematical expressions of COMBINATOR model is shown in Appendix A.

Fig. 21
figure 21

Longitudinal force comparisons between EUCB model and MF model at 5\(^{\circ }\) slip angle

Full size image
Fig. 22
figure 22

Lateral force comparisons between EUCB model and MF model at 5\(^{\circ }\) slip angle

Full size image
Fig. 23
figure 23

Longitudinal force comparisons between EUCB model and MF model at 2\(^{\circ }\) slip angle

Full size image
Fig. 24
figure 24

Lateral force comparisons between EUCB model and MF model at 2\(^{\circ }\) slip angle

Full size image

Figures 21, 22, 23 and 24 indicate the compared results between EUCB model and MF model. The red dashed lines denote forces obtained by MF model, and the black denote the forces obtained by EUCB model. The results show that MF model has better fitting effect than EUCB model on the whole. The reason is that MF empirical tire model is obtained from tire test data under pure slip and combined conditions, and EUCB model is obtained from tire test data under pure slip. The MF model has high accuracy and is suitable for tire dynamics simulation. Compared with the MF model, the EUCB model has fewer parameters, more concise expression, and lower computation load. Therefore, the EUCB model is suitable for controller design, model-based online estimation and theoretical derivation and analytical solution in vehicle dynamics research.

Combined with the relevant theoretical knowledge of tires, it can be seen that there are two main reasons that limit the accuracy of the EUCB model. One reason is inaccurate pressure distribution of contact patch. There is a big difference between this pressure distribution and the test results. The other reason is the effect of carcass elasticity on the mechanical properties of tires. When the carcass is elastic, the cornering stiffness of the tire under the combined slip conditions is affected by the longitudinal slip rate or longitudinal force, which is different from the assumption of a rigid carcass [7].

Fig. 25
figure 25

Longitudinal force comparisons between EUCB model and Modified Dugoff model at 5\(^{\circ }\) slip angle

Full size image
Fig. 26
figure 26

Lateral force comparisons between EUCB model and Modified Dugoff model at 5\(^{\circ }\) slip angle

Full size image
Fig. 27
figure 27

Longitudinal force comparisons between EUCB model and Modified Dugoff model at 2\(^{\circ }\) slip angle

Full size image
Fig. 28
figure 28

Lateral force comparisons between EUCB model and Modified Dugoff model at 2\(^{\circ }\) slip angle

Full size image

Figures 25, 26, 27 and 28 indicate the compared results between EUCB model and Modified Dugoff model. The pink dashed lines denote forces obtained by Modified Dugoff model, and the black denote the forces obtained by EUCB model. The results show that EUCB model has better fitting effect than Modified Dugoff model on the whole. And the lateral forces calculated by Modified Dugoff model have a large deviation from the test data at 2\(^{\circ }\) slip angle. This may be caused by anisotropy of tire stiffness. Combined with the previous theoretical analysis, it can be seen that the direction of resultant shear force is inconsistent with the direction of the slip velocity under the small slip condition. However, there is a proportional relationship of slip velocity in the Modified Dugoff model. The mathematical expressions of Modified Dugoff model is shown in Appendix A.

As we all known, the Modified Dugoff model is widely used in controller design and model-based online estimation. And accurate tire model is particularly important under extreme conditions of large slip. Thus, the newly proposed model can improve the performance of the vehicle’s active safety system under extreme conditions.

To further indicate the fitting accuracy of the above models, the deviations between the predicted and tested results are shown in Table 1, and \(\gamma \) is the camber angle [29].

$$\begin{aligned} \varepsilon =\sqrt{\dfrac{\sum \limits _{i=1}^{n}(y_{i,predicted}-y_{i,tested})^2}{\sum \limits _{i=1}^{n}y_{i,tested}^2}} \times 100 \% \end{aligned}$$
(44)

where \(\varepsilon \) is the deviations, n is the number of test data points, \(y_{i,predicted}\) is the predicted results, and \(y_{ i,tested} \) is the tested results. From the deviation comparisons, it can be seen that EUCB physical model has higher prediction accuracy than COMBINATOR model and Modified Dugoff model in longitudinal force and lateral force, and has lower fitting accuracy than MF empirical model, which indicates the EUCB model has acceptable fitting accuracy and good predictive effect.

Table 1 Deviation comparisons among MF model, COMBINATOR model, modified Dugoff model and EUCB model under combined condition
Full size table

6 Conclusions

An accurate and predictive tire model is very important for vehicle dynamics studies [13]. In the paper, a predictive tire model (the EUCB model) is proposed which can describe tire forces accurately under combined conditions based on pure slip test. Some conclusions are summarized as follows:

Firstly, the resultant shear force shouldn’t be the algebraic sum of the shear stress integrals in sliding and adhesion regions but the vector sum when tire slip stiffness is anisotropic. The vector distribution relationship considering anisotropic tire stiffness accurately describes the variation of shear forces from the physical mechanism.

Secondly, the proposed model is verified by test data at different angles and loads and compared with COMBINATOR model, MF model and Modified Dugoff model. The result shows the model has good accuracy even if a parabolic distribution on vertical load over the contact patch is adopted in the modelling.

Thirdly, the proposed model still needs to further improve accuracy and incorporate some uncertainty caused by unmodeled factors (such as the elasticity of carcass, etc.), and more test data need to be collected to further validate the model.

Further, in practical application, the proposed model is more suitable for the analytical solution of vehicle system, controller design and model-based online estimation than other commonly used tire models due to its simple expression and acceptable accuracy.