Modeling and simulation for wear prediction in planar mechanical systems with multiple clearance joints

Abstract

The main goal of this work is to develop a comprehensive methodology for predicting wear in planar mechanical systems with multiple clearance joints and investigating the interaction between the joint clearance, driving condition, and wear. In the process, an effective contact surface discretization method together with the Lagrangian method are used to establish the dynamic equation of the multibody system. Considering the change of the contact surface, an improved nonlinear contact force model suitable for the complicated contact conditions is utilized to evaluate the intrajoint forces, and the friction effects between the interconnecting bodies are discussed using the LuGre model. Next, the contact forces developed are integrated into the Archard model to compute the wear depth caused by the relative sliding and the geometry of the bearing is updated. Then, a crank slider mechanism with multiple clearance joints is employed to perform numerical simulations in order to demonstrate the efficiency of the dynamic procedures adopted throughout this work. The correctness of the proposed method is verified by comparing with other literature and simulation results. The results show that the wear is sensitive to different initial conditions, and the evolving contact boundary makes the dynamics of mechanical system and the joint wear prediction more complex. This study is helpful for predicting joint wear of mechanical systems with clearance and optimizing the mechanism’s design.

1 Introduction

In mechanical systems, different components are connected by elements like hinges to allow them to rotate with respect to each other. Due to the manufacturing tolerances, assembly errors, and the material deformation, the clearance in the joint is inevitable, which may lead to instability of the mechanism, deviation from the ideal trajectory, and reduction of its accuracy and reliability. There have been several reports on the effect of clearance on the dynamic characteristics of mechanisms: considering rigid [1,2,3,4] or flexible mechanical systems [5,6,7,8,9,10], planar or spatial structures [11,12,13,14,15,16], contact force models [17,18,19,20] and joint lubrication [21,22,23,24,25,26], the number of clearances [27,28,29,30,31], the position of clearances [31,32,33,34], and wear and tear [35,36,37,38,39]. The previous research on wear is mainly focused on how to embed the wear model into the dynamic equations of the multibody system, which mainly involves the calculation of contact stresses, the determination of the incremental wear amount, and the updating of geometry. However, under the complex contact conditions, the research on the coupling between joint wear and joint clearance and driving power is still limited.

In an actual mechanism, the clearance and wear in the joint are encountered simultaneously. They affect and enhance each other, which not only aggravates the energy loss between the collision bodies, but also reduces the performance of the system. Thus, it is necessary to establish a quantitative model of the material loss at interface to predict the dynamic response of the multibody system. The finite element method is one of the commonly used methods to simulate the wear process, which has high accuracy and can handle complex contact geometry problems [40]. From a computational point of view, however, this method is very time-consuming. Therefore, an alternative method is to simulate the wear process based on contact conditions and material properties, and this method can be easily integrated into the general code of dynamic equations, as proposed in the literature [41,42,43]. Considering the numerical efficiency and accuracy, the contact wear model of mechanical systems is often established using the Reye hypothesis and the Archard wear model. Based on the Reye hypothesis, Tasora et al. [41] theoretically and experimentally quantified the surface wear of revolute joints, and the overall results were very consistent with experimental tests. In addition, they observed that wear did not affect the entire surface of the journal, but mainly occurred at specific locations. Xiang et al. [42] used the improved contact force model and Archard model to quantitatively analyze the influence of contact pressure and sliding distance on wear rate under different journal motion modes. Their research is helpful to predict the joint wear of mechanical systems with clearance and optimize the mechanism in the design. Xu et al. [43] simulated the clearance revolute joint with constantly updated wear profile in a crank slider mechanism by comparing the theoretical and experimental results, confirming that wear in a revolute joint will increase the clearance and further deteriorate the dynamic performance of the multibody system. In addition, Han et al. [44] investigated the dynamic problems and wear problems of the two-dimensional space pointing mechanism using the dynamic fitting variables method and the discrete processing method. Under the tracking mode and the attitude adjustment mode, the expected service life of the two-dimensional pointing mechanism is 12591.92 h and 764.44 h. To investigate the fretting between two bodies leading to surface damage, Liu et al. [45] proposed a modified wear model that accounts for friction-induced dynamic changes. They found that the modified model can predict the wear volume of 316 steel and pure copper more accurately than the Archard model. Hou et al. [46] analyzed the effects of the material, length, angle, diameter of the finger lock, and the number of petals on the unlocking force after 500 unlocking cycles using the Archard model. The experiment results show that using Archard model can effectively calculate the finger pattern wear of locks.

It should be emphasized that, unlike the traditional wear analysis between two contact components, the wear prediction of the joint with clearance is more complicated [47]. On the one hand, in the clearance mechanical system, the contact state between two components transits between the free-flight contact, and collision [31]. When collision occurs between joint elements, the impact force produced due to the relative motion will increase the wear of the bearing profile and change its geometry [35]. Therefore, the wear of the contact elements and the dynamic characteristics of the mechanism with clearance affect each other, which should be computed under the framework of multibody system dynamics [42]. On the other hand, with the development of wear, the profile of the contact body will change, and the conformal contact may be transformed into a non-conformal contact [37, 38]. As a result, the complex and variable contact surface between two contact bodies due to wear will make it difficult to establish and solve the dynamic model of revolute joint with clearance accurately, which will aggravate the nonlinear characteristics of multibody system and make it more likely to exhibit chaotic behavior [43]. A problem worthy of consideration is how to reasonably determine the relative position between the contact components when their profiles are constantly changing due to wear, which is the premise of dynamic analysis. Therefore, it is necessary to investigate the coupling between the dynamic characteristics and wear process of multibody system with clearance and to calculate the impact force under the nonstandard contact surface using the appropriate contact force model.

The main emphasis of this work is to develop a methodology to predict the wear of multibody systems under the framework of the clearance dynamics and to discuss the interaction between the clearance size, number of clearance, and the working conditions. Based on the discretization of the profiles of the interconnecting bodies, the contact state between nonstandard contact bodies can be accurately determined, and the normal and tangential forces caused by the elastic deformation and relative motion between the contact bodies are separately computed using the improved nonlinear continuous contact force model and LuGre friction model. Because the improved model considers the physical and geometric properties of contact body and changes with deformation, it can be applied to different contact conditions. On the other hand, the influence of the unit of each physical quantity on the physical meaning of the contact force is considered, and the nonlinear index is corrected, so that the physical interpretation of the new contact force model is reasonable. Next, the wear process and the developed contact forces can be integrated into the equation of motion of the system to observe how the worn surface will affect the wear volume of the bearing profile, and further parameterize the joint wear in the mechanical system, which helps optimizing the mechanism in the design stage for prolonging its life and performance.

The remaining part of this paper is organized as follows: In Sect. 2, a new discretization method for nonstandard circle contact surface is proposed, the clearance joint model is established, and the normal and tangential contact impact models are presented. In Sect. 3, the mathematical model of a mechanical system with clearance is established based on the Lagrange equation, while the mathematical model of the multibody system considering the joint clearance and wear is developed in Sect. 4. Then, the simulation work is carried out on a crank slider mechanism with imperfect joints and the effects of different clearance joint size, location, number, and driving speed on the joint wear and the dynamic characteristics of the mechanism are studied in Sect. 5. Finally, conclusions are summed up in Sect. 6.

2 Modeling of revolute clearance joints

There are two types of contact and collision between objects: One is the forward collision based on Newton's collision law, and the other is the eccentric oblique collision, among which the eccentric oblique collision is more in line with the general collision problem [48]. Regarding the collision between two individuals, how to accurately describe the contact deformation and the resulting contact and collision force is the main content of clearance dynamics. When the wear between contacting bodies is also taken into account, the coupling between the local wear deformation between contacting bodies and the global dynamic response of the system will make this problem very complex. At this time, how to effectively capture the contact state between contact bodies will be the key to the accuracy of wear prediction.

2.1 Description of revolute joint with clearance

The journal and the bearing are basic components that form a revolute joint. According to whether their positions are consistent, the joint can be regarded as ideal or imperfect. In an ideal mechanical system, the midpoints of two components connected by a motion pair are completely coincident. When considering the gap in the revolute joint, the journal is limited to movement in the bearing boundary. According to the relative position of bearing and journal center, the movement in the clearance joint can be divided into three modes: the free-flight mode, the following or contact mode, and the impact mode [31], illustrated in Fig. 1. Figure 1a shows the free-flight mode in a revolute clearance joint, where ${\text{R}}_{{\text{J}}}$ is the radius of the journal and $R_{B}$ is the internal radius of the bearing. In this mode, there is no contact between the journal and the bearing; hence, no reaction force takes place. At the end of the free-flight mode, the contact impact occurs between the two components, and the system enters the impact mode, as shown in Fig. 1b. The resulting contact force will lead to the discontinuity of the kinematic and dynamic characteristics of the system. In Fig. 1b, e represents the eccentricity vector connecting the bearing center and the journal center, $\delta$ is the relative penetration between the two contact bodies, and $\delta = e - \left( {R_{B} - R_{J} } \right)$. When $\delta > 0$, contact collision occurs between two individuals, and the normal contact force ${\text{F}}_{{\text{n}}}$ and tangential contact force $F_{t}$ are generated. After the end of the impact mode, the motion between the two contact bodies will be changed to free-flight mode or contact mode. In terms of contact mode, the bearing and journal are always in contact and the relative penetration depth varies along the bearing wall. The transition between the three motion modes is shown in Fig. 1c, and the current system motion state can be judged by the penetration depth at the current time and the previous time. A detailed judgment method is proposed in the next section.

Fig. 1

Modes of journal motion inside the bearing in a revolute clearance joint: a Free-flight mode, b impact mode highlighting the contact deformation, c transition between motion states

2.2 New modeling methods for nonstandard contact surface

The dynamic analysis of a mechanical system with a clearance has two important components, one is the dynamic modeling of the multibody system, and the other is the selection of the contact collision force model. The former comprises contact state judgment, potential contact point search, and generalized force conversion. The traditional modeling method is to use the distance e between the journal and bearing centers to determine whether the joint elements collide, where e is the modulus of e in Fig. 1b.

It should be highlighted that when the bearing and journal have ideal circular geometries in the revolute clearance joint, it is very effective to use the center distance method to determine the contact state of the two components. This is because in this case, the contact deformation between the bearing and the journal must be located on the extension line of the centers of the clearance joint shown in Fig. 2a, where $Q_{i} Q_{j}$ and $P_{i} P_{j}$ are collinear. However, when the wear phenomenon is included in the dynamic analysis, the wear in the joint is not evenly distributed, but concentrated at some specific locations. In view of this the two contact bodies will not be able to maintain the ideal circle but will develop from a circle to a noncircular shape (such as elliptical in Fig. 2b) with the gradual accumulation of wear. The result shows that due to the change of the shape of the contact surface, when the deformation of the ideal circular contact surface is equal to or less than 0, collision between the elliptical contact surfaces may have occurred. Therefore, for noncircular shaped joints with clearance, the traditional center distance method cannot accurately capture the contact state. To address this issue, a new modeling method is proposed to establish the dynamic model of a multibody system under wear process. Assuming that the journal surface is sufficiently hard, and the wear mainly occurs on the bearing contact surface, the position of the actual contact point in the clearance joint and centerline extension line is shown in Fig. 2b. Point Q is the contact point between the bearing and the journal, while point p is at the intersection of line ${\text{P}}_{{\text{i}}} {\text{P}}_{{\text{j}}}$ with bearing profile. It can be seen from Fig. 2b that the deformation position is not on the center line of the two contact bodies, which is different from Fig. 2a.

Fig. 2

Schematic diagram of joint contact analysis

Based on the finite element discretization method, the main deformed part (bearing) in the revolute joint is discretized to establish the contact dynamic model of the system. With this approach, the profile of the bearing is divided into points, while the maximum contact depth between the contact bodies is obtained by calculating the distance between each discrete point and the geometric center of the pin. Figure 3 shows a schematic diagram of the contact of the revolute clearance joint established using the proposed discrete method. The rigid bodies b and j are connected by a real joint. $o_{j} x_{j} y_{j}$ and $o_{b} x_{b} y_{b}$ are local coordinate systems fixed to rigid bodies j and b, respectively, and ${\text{M}}xy$ is the global coordinate system. Considering that the stiffness of the pin j is higher than that of bearing b, it is assumed that the shape of body j does not change in the wear process, and the bearing profile can be discretized. The number of discrete points can be artificially controlled according to the engineering demands. As the number of discrete points increases, the bearing profile is described more accurately and the accuracy of the calculation results improves, but more computational time is required, and vice versa.

Fig. 3

Discretization of the bearing contact surface of the revolute joint with clearance

In Fig. 3, $D_{i}$ is any point on the bearing contact surface, and the position vectors of point $D_{i}$ and journal center $P_{j}$ can be expressed as:

$$ r_{b}^{D} = r_{b} + s_{b}^{D} = r_{b} + A_{b} s_{b}^{{\prime D}} ,$$

(1)

$$ \text{r} _{j}^{P} = {\mathbf{r}}_{j} + \text{s} _{j}^{P} = {\mathbf{r}}_{j} + \text{A} _{j} s_{j}^{{\prime P}} ,$$

(2)

where ${\mathbf{r}}_{b}$ and ${\mathbf{r}}_{j}$ represent the global position vectors of the mass centers of bodies b and j, $s_{P}^{{\prime D}}$ and $s_{j}^{{\prime P}}$ are the local components of points $D_{i}$ and $P_{j}$ relative to local coordinate systems $o_{b} x_{b} y_{b}$ and $o_{j} x_{j} y_{j}$. ${\text{A}}_{k} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {k = b,{\kern 1pt} {\kern 1pt} {\kern 1pt} j} \right)$ is the transformation matrix of coordinates $o_{b} x_{b} y_{b}$ and $o_{j} x_{j} y_{j}$, ${\text{A}}_{k} = \left[ {\begin{array}{*{20}c} {\cos \phi_{k} } & { - \sin \phi_{k} } \\ {\sin \phi_{k} } & {\cos \phi_{k} } \\ \end{array} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {k = b,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j} \right)$, in which $\phi_{k}$ denotes the angular position of the local coordinate system of body $k$.

In the global coordinate system, the position vector of the center point $P_{j}$ of the journal with respect to point $D_{i}$ can be expressed as:

$$ d = r_{b}^{D} - r_{j}^{P} {\kern 1pt},$$

(3)

The magnitude of the relative position vector d is evaluated as,

$$ d = \sqrt {d^{T} d} $$

(4)

Next, the relative deformation between the contacting bodies is evaluated as,

$$ \delta = d - R_{j}$$

(5)

where $R_{j}$ is the journal radius. $\delta$ can be used to judge the contact state between the bearing and the journal [31], and the change between them can be calculated by the following formula.

$$ \left\{ \begin{gathered} \delta \left( {q_{t} } \right)\delta \left( {q_{t - 1} } \right) > 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \left( {q_{t} } \right) > 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{free}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{flight}}{\kern 1pt} \hfill \\ \delta \left( {q_{t} } \right)\delta \left( {q_{t - 1} } \right) > 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \left( {q_{t} } \right) < 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{continuous}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{contact}} \hfill \\ \delta \left( {q_{t} } \right)\delta \left( {q_{t - 1} } \right) \le 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \left( {q_{t} } \right) \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{from}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{contact}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{seperation}}{\kern 1pt} \hfill \\ \delta \left( {q_{t} } \right)\delta \left( {q_{t - 1} } \right) \le 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \left( {q_{t} } \right) \le 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{from}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{seperation}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{contact}} \hfill \\ \end{gathered} \right. $$

(6)

When the contact of the two components takes place, there may be multiple discrete points on the contact area which satisfy Eq. (7). Among them, these two points corresponding to the maximum contact distance are selected as the contact points, as presented by points $C_{b}$ and $C_{j}$ in Fig. 4.

Fig. 4

Contact deformation in the revolute joint including clearance

In Fig. 4, the position vectors of the maximum contact points are expressed as:

$$\left\{ \begin{gathered} r_{b}^{C} = r_{b} + A_{i} S_{b}^{{\prime P}} + R_{b} n \hfill \\ r_{j}^{C} = r_{j} + A_{j} S_{j}^{{\prime P}} + R_{j} n \hfill \\ \end{gathered} \right.,$$

(7)

where ${\text{s}}_{b}^{P}$ is the local component of point $P_{b}$ with respect to local coordinate systems. $R_{b}$ and $R_{j}$ are separately the bearing and the journal radius. n denotes the unit normal vector.

The velocity corresponding to the maximum contact penetration is found by differentiating Eq. (7). Further, the impact velocity is projected to the normal and tangential place of the collision, and the relative velocity components, represented by $v_{n}$ and $v_{t}$, are calculated. The relative normal velocity is used to judge whether the contact body is close or separate, and the subsequent friction model uses the relative tangential velocity to determine the relative slip or viscosity between the contact bodies.

$$\left\{ \begin{gathered} \dot{r}_{b}^{C} = \dot{r}_{b} + \dot{A}_{i} S_{b}^{{\prime P}} + R_{b} \dot{n} \hfill \\ \dot{r}_{j}^{C} = \dot{r}_{j} + \dot{A}_{j} S_{j}^{{\prime P}} + R_{j} \dot{n} \hfill \\ \end{gathered} \right. $$

(8)

$$ \left\{ \begin{gathered} v_{n} = (\dot{r}_{j}^{C} - \dot{r}_{b}^{C} )^{T} n \hfill \\ v_{t} = (\dot{r}_{j}^{C} - \dot{r}_{b}^{C} )^{T} t \hfill \\ \end{gathered} \right. $$

(9)

where the dot denotes the derivative with respect to time and t is the tangential vector obtained after rotation of n by $90^{ \circ }$.

From the calculation process, it can be seen that the bearing contact surface is discretized into different points, and the penetration between two contact bodies is directly described by the distance between the contact points on the bearing and the journal. The positions of these two contact points can be directly obtained by calculating the current bearing position and the wear amount of the bearing surface. Therefore, it is no longer necessary to calculate the positions of the potential contact points separately as the traditional method, which simplifies the calculation steps.

2.3 Contact force model and friction model

The contact force model used to describe the contact and collision phenomenon is one of the most important contents in the mechanical system with clearance, and the prediction of the dynamics between the contacting bodies strongly depends on its selection [49]. Starting from Hertz contact model, various contact models have been developed to adapt to different contact conditions, such as different speed [50,51,52], contact materials [53, 54], and different contact shape [55, 56].

Due to the wear and tear, the shape of the contact surface will change with the contact collision between two components, so the contact force model for wear prediction should be suitable for conformal and non-conformal contact simultaneously [57, 58]. In view of this a modified nonlinear continuous contact force model based on the Flores model [56] and an improved Winkler elastic foundation mode [59] is utilized to evaluate the impact force developed in the clearance joint, which is suitable for complex contact conditions. The model is discussed in detail in references [42] [60], and interested readers can refer to them.

The nonlinear contact force model can be calculated by the following formulas:

$$ F_{{\text{N}}} = K_{g} \delta^{n} [1 + \frac{{8(1 - c_{r} )}}{{5c_{r} }}\frac{{\dot{\delta }}}{{\dot{\delta }^{( - )} }}]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$

(10)

$$ K_{g} = \frac{{1}}{{8}}\pi E^{ * } \sqrt {\frac{{{2}\delta \left( {{3}\left( {R_{B} - R_{J} } \right) + {2}\delta } \right)^{{2}} }}{{\left( {R_{B} - R_{J} + \delta } \right)^{{3}} }}} $$

(11)

where $c_{r}$ is the coefficient of restitution [61], $\dot{\delta }$ and $\dot{\delta }^{( - )}$ are scalars of the relative penetration velocity and initial impact velocity, respectively. The latter is calculated at the end of the free-flight mode, but remains unchanged during contact. In addition, $K_{g}$ is the composite nonlinear stiffness coefficient. From formula (11), it can be found that it is directly related to the material property, clearance size, and deformation of contact bodies [62], where $E^{ * }$ is the compound elastic modulus expressed as:

$$ \frac{{1}}{{E^{ * } }} = \frac{{{1} - \nu_{i}^{2} }}{{E_{i} }} + \frac{{{1} - \nu_{j}^{2} }}{{E_{j} }},$$

(12)

where $\nu$ and $E$ are separately Poisson’s ratio and Young’s modulus.

It should be emphasized here that in formula (10), if the units of all physical quantities are in SI units, and the nonlinear power exponent $n$ is taken as 1.5 according to the experience of metal ball collision, we can find that the unit of $F_{{\text{N}}}$ is not Newton, which is not in line with the basic physical meaning. Therefore, in order to ensure that $F_{{\text{N}}}$ has effective physical characteristics, we take the nonlinear index $n$ as 2, then formula (10) that is the improved contact force model can be written as

$$ F_{N} = \frac{1}{8}\pi E^{ * } \sqrt {\frac{{2\delta \left( {3\left( {R_{B} - R_{J} } \right) + 2\delta } \right)^{2} }}{{\left( {R_{B} - R_{J} + \delta } \right)^{3} }}} \delta ^{2} \left[ {1 + \frac{{8(1 - c_{r} )}}{{5c_{r} }}\frac{{\dot{\delta }}}{{\dot{\delta }^{{( - )}} }}} \right] $$

(13)

The improved model can be applied to wear prediction of conformal and non-conformal surface between the contact components, as well as to different recovery factors, which expands the application range and overcomes some limitations of previous models. On the other hand, the tangential contact characteristics in the clearance joint are expressed using the LuGre friction model [63,64,65,66,67] which can capture most friction characteristics in a test [68, 69]. This dynamic friction model can be expressed as:

$$ F_{{\text{T}}} = \mu F_{{\text{N}}} $$

(14)

where $F_{T}$ is the friction force and $F_{{\text{N}}}$ is the normal contact force obtained from Eq. (13). $\mu$ denotes the instantaneous coefficient of friction, which is composed of the relative tangential velocity $v_{t}$ and an inner state quantity z, and can be described as: $\mu = \sigma_{0} z + \sigma_{1} \frac{dz}{{dt}} + \sigma_{2} v_{t}$. Substituting $\mu$ into Eq. (14), the tangential force can be expressed as:

$$ F_{{\text{T}}} = (\sigma_{0} z + \sigma_{1} \mathop z\limits^{.} + \sigma_{2} v_{{\text{t}}} )F_{{\text{N}}},$$

(15)

where $\sigma_{0}$, $\sigma_{1}$, and $\sigma_{2}$ are the bristle stiffness, microscopic damping, and viscous friction coefficient, respectively. z reflects the average deflection of the bristles, which can be solved by the following first-order ordinary differential equation [70].

$$ \mathop z\limits^{.} = \frac{dz}{{dt}} = v_{t} - \frac{{\sigma_{0} \left| {v_{t} } \right|}}{{g(v_{t} )}}z{\kern 1pt} {\kern 1pt} {\kern 1pt},$$

(16)

$$ g(v_{{\text{t}}} ){ = }\mu_{{\text{k}}} + \left( {\mu_{{\text{s}}} - \mu_{{\text{k}}} } \right)e^{{ - \left| {\frac{{v_{{\text{t}}} }}{{v_{{\text{s}}} }}} \right|^{2} }} {,} $$

(17)

where $v_{{\text{s}}}$ and $v_{{\text{t}}}$ are the Stribeck velocity [71] and the tangential velocity, respectively. In addition, $\mu_{{\text{k}}}$ and $\mu_{{\text{s}}}$ are separately the dynamic friction coefficient and static friction coefficient [72].

Considering Eqs. (14)–(17), the tangential contact force can be denoted as:

$$ F_{{\text{T}}} = \left[ {\sigma_{0} z\left[ {1 - \frac{{\sigma_{1} \left| {v_{t} } \right|}}{{\mu_{{\text{k}}} + \left( {\mu_{{\text{s}}} - \mu_{{\text{k}}} } \right)e^{{ - \left| {\frac{{v_{t} }}{{v_{s} }}} \right|^{\gamma } }} }}} \right] + \left( {\sigma_{1} + \sigma_{2} } \right)v_{t} } \right]F_{{\text{N}}} $$

(18)

The specific values of the above parameters are reported in Table 1.

Table 1 LuGre friction model parameters identification

Further mathematical calculations show that the magnitude and orientation of the contact force are as follows:

$$ \left\{ \begin{gathered} Q_{C} = \overline{K}\delta^{2} [1 + \frac{{8(1 - c_{r} )}}{{5c_{r} }}\frac{{\dot{\delta }}}{{\dot{\delta }^{( - )} }}]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma = \alpha + \varepsilon \hfill \\ \varepsilon = \tan^{ - 1} \left( {\mu {\text{sign}}\left( {v_{t} } \right)} \right) \hfill \\ \end{gathered} \right., $$

(19)

where $\alpha$ is the angle between the central vector of the contact body and the horizontal axis, $\varepsilon$ is the angle between the contact force ${\text{Q}}_{C}$ and the normal direction ${\varvec{n}}$, as shown in Fig. 5. $\overline{K}$ is calculated by square adding the tangential element obtained in Eq. (14) and the normal component of the contact force in Eq. (13), which can be described as:

$$ \overline{K} = \sqrt {1 + \mu^{2} } K_{g} $$

(20)

Fig. 5

Normal and tangential contact forces in the revolute clearance joint

3 Dynamic analysis of mechanical system with clearance joint

The crank slider mechanism is composed of two bars and a slider, in which the bar 1 is the driving bar and a constant angular velocity is applied. Obviously, the joint with clearance introduces two additional degrees of freedom for the mechanical system, including the horizontal and vertical displacement of the journal center relative to the bearing center.

3.1 Dynamical model of crank slider mechanism with one clearance

In Fig. 6, Joint B is considered to be a real joint, which connects bar 2 and the slider. The general coordinates of the mechanical system are selected as follows: angle ($\varphi_{1}$) between the crank and x-axis, angle ($\varphi_{2}$) between bar 2 and $x$-axis, and the position (x) of the slider.

Fig. 6

Crank slider mechanism with one clearance

Based on the Lagrange equation, the dynamic model of this structure considering joint clearance is expressed as:

$$ \frac{d}{dt}(\frac{\partial T}{{\partial \dot{q}_{j} }}) - \frac{\partial T}{{\partial q_{j} }} + \frac{\partial U}{{\partial q_{j} }} = Q_{j} (j = x,1,2),$$

(21)

where $T$, $U$, and $Q_{j}$ represent the kinetic energy, potential energy, and generalized force of the system, respectively, and $q_{j}$ is the generalized coordinate.

The kinetic energy of this mechanism can be given by:

$$ \begin{gathered} T = \frac{1}{2}(m_{1} l_{1}^{2} + m_{2} L_{1}^{2} + I_{1} ) \cdot \dot{\varphi }_{1}^{2} + \frac{1}{2}(m_{2} l_{2}^{2} + I_{2} ) \cdot \dot{\varphi }_{2}^{2} + m_{2} L_{1} l_{2} \dot{\varphi }_{1} \dot{\varphi }_{2} \cdot \cos (\varphi_{1} - \varphi_{2} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \frac{1}{2}m_{3} \dot{x}^{2} \hfill \\ \end{gathered} $$

(22)

where $L_{1}$ and $L_{2}$ represent the length of the bars 1 and 2, while $l_{1}$ and $l_{2}$ denote the half of the length of the bars 1 and 2, respectively.

Also, the potential energy of this mechanism can be written as:

$$ U = m_{1} gl_{1} \cdot \sin \varphi_{1} + m_{2} g \cdot (L_{1} \sin \varphi_{1} + l_{2} \sin \varphi_{2} ) $$

(23)

The generalized force corresponding to the generalized coordinates $x$, $\varphi_{1}$, and $\varphi_{2}$ can be written as:

$$ \left\{ \begin{gathered} Q_{x} = - Q_{C} \cdot \sin \gamma \hfill \\ Q_{{\varphi_{1} }} = - L_{1} \cdot Q_{C} \cdot \sin (\varphi_{1} - \gamma ) \hfill \\ Q_{{\varphi_{2} }} = - L_{2} \cdot Q_{C} \cdot \sin (\varphi_{2} - \gamma ) \hfill \\ \end{gathered} \right.,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$

(24)

where $Q_{C}$ and $\gamma$ can be obtained from Eq. (19).

Because the mechanism moves at a constant angular velocity $\omega$, its motion equation can be written as: $\varphi_{1} = \omega \cdot t + \varphi_{0}$, where $\varphi_{0}$ is the position of the initial angular of the crank. Then, by substituting Eqs. (22), (23) and (24) into Eq. (21), we can obtain the second-order nonlinear differential equations with initial conditions and variable coefficients (Eq. (25)). Furthermore, the Runge–Kutta method is used to solve the differential equation through MATLAB programming.

$$ \left\{ \begin{gathered} \ddot{\varphi }_{2} = f_{1} (t,\varphi_{2} ,x,\dot{\varphi }_{2} ,\dot{x}) \hfill \\ \ddot{x} = f_{2} (t,\varphi_{2} ,x,\dot{\varphi }_{2} ,\dot{x}) \hfill \\ \end{gathered} \right. $$

(25)

The position and speed of the next step are obtained by integral Eq. (25), and then, the driving torque of the next step is calculated by substituting Eq. (21). It should be noted that the driving torque in the first step can be obtained by initial conditions.

3.2 Dynamical model of crank slider mechanism with two clearances

In Fig. 7, Joints A and B are considered to be imperfect joints, which introduces five degrees of freedom: the angle ($\varphi_{1}$) between the crank and $x$-axis, the angle ($\varphi_{2}$) between bar 2 and x-axis, x- and y-coordinates ($x_{c}$ and $y_{c}$) of the center of mass of the connecting bar, and the position (x) of the slider.

Fig. 7

Crank slider mechanism with two clearance

Like the modeling process of the crank slider mechanism with one clearance, Lagrange equation is used to establish the dynamic model of this mechanism. The kinematic energy can be expressed as

$$ T = \frac{1}{2}(m_{1} l_{1}^{2} + I_{1} ) \cdot \dot{\varphi }_{1}^{2} + \frac{1}{2}m_{2} (\dot{x}_{c}^{2} + \dot{y}_{c}^{2} ) + \frac{1}{2}I_{2} \cdot \dot{\varphi }_{2}^{2} + {\kern 1pt} \frac{1}{2}m_{3} \dot{x}^{2} $$

(26)

The potential energy can be given by

$$ U = m_{1} gl_{1} \cdot \sin \varphi_{1} + m_{2} g \cdot y_{c} $$

(27)

The generalized force corresponding to the generalized coordinates $x$, $\varphi_{1}$, $\varphi_{2}$, $x_{c}$, and $y_{c}$ can be written as:

$$ \left\{ \begin{gathered} Q_{x} = - Q_{S} \cdot \sin \gamma_{s} \hfill \\ Q_{{\varphi_{1} }} = - L_{1} \cdot Q_{C} \cdot \sin (\varphi_{1} - \gamma_{c} ) \hfill \\ Q_{{\varphi_{2} }} = - Q_{C} (L_{2} /2) \cdot \sin (\varphi_{2} - \gamma_{c} ) - Q_{S} (L_{2} /2) \cdot \sin (\varphi_{2} - \gamma_{s} ) \hfill \\ Q_{{x_{c} }} = - Q_{C} \cdot \cos \gamma_{c} + Q_{S} \cdot \cos \gamma_{s} \hfill \\ Q_{{y_{c} }} = - Q_{C} \cdot \sin \gamma_{c} + Q_{S} \cdot \sin \gamma_{s} \hfill \\ \end{gathered} \right.,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$

(28)

where $Q_{C}$ and $Q_{S}$ represent the impact forces in the c–c joint (connecting the crank and connecting bar) and c-s joint (connecting the connecting bar and slider), respectively. $\gamma_{c}$ and $\gamma_{s}$ denote the rotation angle of the bearing in the c–c joint and c–s joint relative to the journal.

Substituting Eqs. (26), (27) and (28) into Eq. (21), where the number of generalized coordinates is five, the dynamic information of this mechanism in each step can be obtained after some iterations.

4 Wear model of revolute joint with clearance

When the two parts are in contact and move relative to each other, the wear phenomenon occurs, which directly results in the gradual loss of material on the surface of these two parts [73, 74]. Most of the previous wear prediction methods are based on the Archard wear model, which is a linear wear model and relates the wear amount to the contact conditions, such as the contact pressure, sliding distance, and tribological data that reflecting the material information and the operating conditions in contact. Also, the Archard wear equation not only represents a macroscopic model, but also expresses microscopic effects between the contact bodies. In addition, this model has been successfully applied to the wear prediction of cam [75], follower [35] [36], revolute pair [37, 38, 44], and helical gear [76]. In this paper, the Archard model is employed to predict the wear of the revolute joint with clearance in the mechanical system, which can be described as:

$$ \frac{{V_{{\text{w}}} }}{s} = \frac{{kF_{{\text{N}}} }}{H} $$

(29)

where $V_{{\text{w}}}$ is the wear amount, $s$ is the relative sliding distance, $k$ is the dimensionless wear coefficient, $F_{{\text{N}}}$ represents the normal contact force, and $H$ denotes the hardness of the soft material [77, 78].

For the revolute joint with clearance, the wear depth can better reflect the influence of wear on the component shape than the wear amount. Thus, Eq. (29) can be rewritten as

$$ \frac{h}{s} = \frac{kP}{H} $$

(30)

where $h = \frac{{V_{w} }}{{A_{a} }}$ and $P = \frac{{F_{N} }}{{A_{a} }}$ are the wear depth and the contact stress, respectively. $A_{a}$ is the actual contact area. It can be observed that the wear depth is closely related to the distribution of contact stress and the relative sliding distance, which is positively proportional to the former and inversely proportional to the latter. Also, in order to apply the model to iteration, its differential form can be described as

$$ \frac{{{\text{d}}h}}{{{\text{d}}s}} = \frac{kP}{H} $$

(31)

Based on the forward finite difference method, the wear depth can be obtained, and the updated wear depth on the discrete points can be written as:

$$ h_{i} = h_{i - 1} + kP_{i} \Delta s_{i} /H $$

(32)

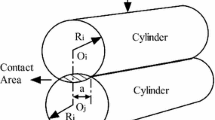
where $h_{i}$ represents the wear depth on discrete points of the bearing profile at the $ith$ cycle, $\Delta s_{i}$ denotes the incremental relative sliding distance, and $h_{i - 1}$ is the wear depth at the $i - 1st$ cycle. The contact pressure $P_{i}$ can be calculated using Hertzian contact theory where the contact between the worn bearing profile and the journal can be simulated approximately by the contact between the cylindrical surface and the cylindrical concave surface, which can be presented as:

$$ P_{i} = \sqrt {\frac{{F_{N} \cdot E^{ * } }}{{\pi R^{\prime}L}}} $$

(33)

in which $F_{N}$ is normal impact force obtained from Eq. (10) and $L$ is the contact length of the pin and bushing along the axis direction. $E^{ * }$ can be obtained from Eq. (12), and $R^{\prime}$ can be represented by:

$$ R^{\prime} = \frac{{R_{i}^{d} R_{j} }}{{R_{i}^{d} - R_{j} }},\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} d = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots ,{\kern 1pt} {\kern 1pt} n $$

(34)

where $R_{i}^{d}$ is the updated radius of the bearing corresponding to a discrete point and $R_{i}^{d} = R_{i} + h_{i}$. It can be seen that the radius of the bearing is different at different discrete points, and it changes with the amount of wear.

In addition, when the integral range is small enough, the relative sliding distance can be calculated: $\Delta s_{i} = v_{t} (t) \cdot \Delta t$, in which $v_{t} (t)$ is the tangential velocity and can be obtained from Eq. (9). When all parameters are obtained, the incremental wear depth on each discrete point can be estimated at each iteration until the desired iterations are completed.

Because the wear evaluation involves substantial mathematical and computational manipulation, this prediction process can be summarized to better model the event, which is presented in the flowchart shown in Fig. 8.

Fig. 8

Flowchart of wear prediction in the revolute joint with clearance

The steps of the wear prediction algorithm in the planar multibody framework can be summarized as:

• 1. Start simulation with given initial conditions for positions $q_{0}$ and velocities $\dot{q}_{0}$.

• 2. Define joint properties ($R_{B} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R_{J} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H$) and discretize the profile of the bearing.

• 3. Determine the contact state between the connecting components. If there is contact, determine the contact region, search the maximum contact depth, and compute the normal contact force $F_{{\text{N}}}$ and tangential friction force $F_{{\text{T}}}$. Otherwise, proceed with the dynamic equation of the system.

• 4. Compute the contact area and sliding distance, and evaluate the current and accumulated wear volume of the bearing surface.

• 5. Determine the profile of the bearing and obtain the new generalized positions and velocities of the system in the next step.

• 6. Update the time. Redistribute the contact surface of the bearing and proceed with the dynamic analysis with new positions and velocities until the simulation is completed.

5 Wear simulation of revolute clearance joint

In this section an elementary crank slider mechanism is analyzed as an example to predict joint wear in a mechanical system and to perform a parametric study to investigate the interaction between the clearance and wear in a revolute joint, as well as the driving conditions. In addition, the dynamic wear process of the crank slider mechanism with one clearance joint studied in this paper is predicted using the Adams method combined with ANSYS, in order to validate the dynamic modeling and proposed calculation method. This mechanism and the corresponding coordinate systems are shown in Figs. 6 and 7, respectively, where the former has only one clearance joint in the mechanism and the latter has two imperfect joints. Three major cases are considered, that is: (a) Case 1: Revolute joint with clearance is only between connecting bar and slider, i.e., joint B. (b) Case 2: The clearance exists for both joint A and joint B, which can be divided into three types: the same clearance size in the two joints; setting the clearance size in joint A unchanged, changing the clearance size in joint B, and in vice versa. (c) Case 3: Using the Adams method combined with ANSYS to predict the joint wear process of the mechanism in Case 1.

The dimensions and inertia properties of the crank slider mechanism are listed in Table 2, and the material properties and parameters for the dynamic simulation are provided in Table 3. It should be pointed out that during the movement of the mechanism, wear and penetration mainly occur at the contact position of the joint elements. Therefore, we only give the radial radius difference between the initial bearing and journal and the responding material, but not the specific model of the bearing and journal. On the other hand, since the developed equations of motion are numerically stiff, a variable order multi-step method is used to handle them. When there is no contact force in the pair, large steps are adopted, while when collision occurs, a smaller step size is used to capture the high frequency response of the system. In addition, in order to determine the wear between the journal and the bearing at a lower calculation cost and obtain a significant amount of wear, a larger wear coefficient is used to carry out the simulation.

Table 2 Dimensions and inertia properties for the crank slider mechanism

Table 3 Parameters in the dynamic analysis of the crank slider mechanism

5.1 Crank slider mechanism with one clearance

The mechanism of Fig. 6 consists only of a clearance joint between the connecting bar and slider. The dynamic analysis of the system is comparatively performed by changing the clearance values and driving conditions.

In this subsection, the radial clearance sizes of the joint B are set to be 0.1 mm and 0.5 mm, and the crank rotates at constant angular velocities of 2000 rpm and 1000 rpm, respectively. Figures 9, 10, 11, 12 show the results of dynamic analysis of the mechanism considering clearance and wear, in which the clearance size changes from 0.1 mm to 0.5 mm, and the crank rotates at 2000 rpm constant angular velocity.

Fig. 9

Variation of bearing surface wear for 10, 20, 30, 40 full crank rotations, for clearance size a 0.1 mm and b 0.5 mm

Fig. 10

Journal trajectory for clearance size a 0.1 mm and b 0.5 mm

Fig. 11

Wear depth accumulated for clearance size a 0.1 mm and b 0.5 mm

Fig. 12

Poincaré maps of slider for clearance size a 0.1 mm and b 0.5 mm

Figure 9 shows the bearing radius accumulated for 10, 20, 30, 40 full crank rotations, which is plotted relative to the circumferential angle. It is obvious that the wear is not uniformly distributed on the whole contact surface of the bearing, and there are significant wear on some areas. In Fig. 9a, the peaks of the bearing radius can be found at the beginning and end stages of crank rotation and about $200^{ \circ }$, which indicates that there are three obvious wear areas in the mechanism, and the clearance radius of these three positions will change greatly after wear. However, it can be observed that when the clearance size is 0.5 mm, the severely affected areas are mainly at $100^{ \circ }$ and $300^{ \circ }$, and the wear area is wider than that in Fig. 9a. On the other hand, the amount of wear increases more than 10 times as the clearance values increase, which indicates that the energy loss of the system is increasing rapidly. This is because the wear will lead to the dissipation of the system energy in the form of thermal energy. Also, these observations are supported by the fact that the contact between the bearing profile and journal is more frequent in some specific areas, as shown in Fig. 10, which leads to the increase of wear amount and the formation of severe wear areas. In Fig. 10a, only one type of motion between the contact bodies is observed, that is the follow motion mode. However, it can be observed in Fig. 10b that three types of motion occur inside the bearing: free-flight, contact, and impact modes, which may lead to more obvious and complex nonlinearity of system due to the propagation of the contact collision phenomenon between the bodies. It should be highlighted that the change of journal trajectory directly results in the change of system dynamic response. Considering the tangential motion between the bearing and the journal, the impact between the joint elements may cause the change of the contact collision position and then the change of the wear area, as shown in Fig. 9. Moreover, the accumulation of wear amount during the simulation is shown in Fig. 11, which further proves the influence of clearance size on severe wear area and wear volume, and the results are consistent with Fig. 9. Also, the Poincaré maps of the slider are plotted in Fig. 12, illustrating that when the clearance size is increased the dynamic behavior tends to be chaotic because the Poincaré maps show the unpredictability of the orbits and the sensitivity to the initial conditions.

When the driving condition is reduced from 2000 to 1000 rpm and the clearance size is kept at 0.1 mm, the dynamics of the crank slider mechanism considering wear process is shown in Fig. 13.

Fig. 13

Dynamics of the crank slider mechanism with 1000 rpm constant angular velocity: a Variation of bearing surface wear and b Poincaré maps of the slider

Comparing Fig. 13a and Figs. 9a, 12a, it can be seen that with the decrease of the driving speed the amount of wear on the contact surface of the bearing decreases gradually and the distribution of the wear area is more uniform. It can be reasonably inferred that the trajectory of the journal will be more complex, and the rebound after collision will be more frequent. Furthermore, the smaller driving condition leads to smaller acceleration amplitude, which will produce a smaller amount of wear on the contact body, as shown in Fig. 13a and b.

5.2 Crank slider mechanism with two clearance joints

The mechanism in Fig. 7 is composed of two clearance joints, the c–c joint and c–s joint described in Sect. 3.2. The dynamic response of the system is compared by changing the clearance values and driving conditions.

When the two joints have the same clearance value, the dynamic characteristics of this mechanism are shown in Figs. 14 and 15, where the dynamic parameters associated with the slider are used to observe the change.

Fig. 14

Poincaré maps with different clearance sizes: a c = 0.02 mm; b c = 0.1 mm; c c = 0.2 mm; d c = 0.5 mm

Fig. 15

Bearing radius accumulated with different clearance sizes

In Fig. 14, it is clear that with the increase of clearance size, the mechanism presents chaotic behavior. Compared with Fig. 12, which only contains one clearance in the c-s joint, it can be seen that the mechanism with multiple clearances shows higher nonlinearity and sensitivity, and the smaller clearance size will make the behavior of this mechanism challenging to predict. Also, Fig. 14 shows that the amplitude of acceleration increases gradually with the increase of clearance size, which results in higher wear of bearing radius during the movement of the mechanism, as shown in Fig. 15. The reason for this result is that the joint reaction force is closely related to the acceleration, and the amount of wear is directly proportional to the contact stress. In addition, it should be noted that the locations of severe wear areas for different gap sizes are similar, which is different from the results of single clearance joint where the main wear locations change with the increase of clearance size. The possible reason is that c–c joint is more sensitive than c-s joint and occupies a more important position in the dynamic analysis of a mechanism with clearance, which will be further verified by changing the clearance size in the subsequent part of this section. On the other hand, for different clearance size, the wear amount is different, and the larger gap size corresponds to larger wear amount. Also, it can be further observed that the wear thickness does not change significantly with the increase of gap size, because the wear thickness is determined by the contact stress and relative sliding distance at the same time. Although larger gap size will produce higher contact stress, it will also lead to increased contact frequency and shorter contact time between bearing and journal, thus reducing the relative sliding distance. Hence, the difference of wear caused by different clearance sizes is not obvious.

In order to further observe the effect of clearance values at differently positions on the dynamic characteristics of the system, two sets of application examples were employed: (1) In Fig. 16a, c and e the clearance dimension of c-s joint remains unchanged and is set at 0.1 mm, while the clearance dimension of c–c joint is taken as 0.02 mm, 0.3 mm, and 0.6 mm, respectively; (2) in Figures. 16b, d, and f, the change is opposite.

Fig. 16

Poincaré maps for different clearance sizes: (1) changing the clearance values of the c–c joint, (a) (c) (e); (2) changing the clearance values of the c-s joint (b) (d) (f)

From Fig. 16, it can be seen that for either (1) or (2), as the clearance size increases, the acceleration amplitude of the slider increases and the system shows higher nonlinearity. However, in application example (1), it is observed that changing the clearance size of the c–c joint results in higher acceleration amplitude and more obvious chaos characteristics. Therefore, it can be reasonably concluded that the c–c joint is more sensitive to the clearance size than the c-s joint. The reason for this phenomenon may be that the c–c hinge is directly connected with the crank, that is, the energy input component, and the length of the crank is shorter than that of the connecting rod. When the contact collision occurs between the contact bodies at the c–c joint, the change of local dynamic response can spread to the whole bar quickly, thus affecting the overall motion of the system. In addition, due to the direct connection between the c–c hinge and the crank, the change of the overall response of the system will lead to a change of the input energy because the crank is required to move at a constant speed, and conversely, the possible microvibration caused by the disturbance error between the two is directly reflected at the hinge. Therefore, c–c hinge is more sensitive than c-s hinge, and correspondingly, the control associated with the joint can help researchers improve the stability of the system. On the other hand, observing Fig. 17, it can be found that the wear area in application example (2) is more evenly distributed, but the wear amount of the corresponding bearing radius is less than that in application example (1), which is consistent with the change of acceleration amplitude in Fig. 16.

Fig. 17

Bearing radius accumulated for different clearance size: a changing the clearance values of the c–c joint; b changing the clearance values of the c-s joint

In Figs. 18 and 19 the wear dynamics of the crank slider mechanism under different driving conditions are observed using the wear amount of the bearing radius and the Poincaré diagram, respectively. The clearance value in both the two joints is 0.01 mm, and the selected crank speeds are 500 rpm, 1000 rpm, 1500 rpm, and 2000 rpm, respectively. Other parameters are the same as the above simulation parameters.

Fig. 18

Poincaré maps for different crank speed: a 500 rpm; b 1000 rpm; c 1500 rpm; d 2500 rpm

Fig. 19

Bearing radius accumulated for different crank speed

In Fig. 18, when the crank speed is less than 1500 rpm, the behavior of the system with clearance and wear tends to be aperiodic or even chaotic due to the nonlinear characteristics of the contact impact phenomena, while when the crank speed is increased, the dynamic behavior tends to be periodic since the Poincaré map represents the close orbit in Fig. 18d. Also, the periodic response indicates that the journal follows the bearing wall and more uniform wear regions are found on the contact body illustrated in Fig. 19. In addition, it should be emphasized that higher crank speed means that higher power is needed to drive the mechanism, which will lead to the increase of acceleration value of the slider, and further, it will produce greater wear on the contact body.

In addition, the above findings can be compared with Mukras’s [37] and Flores’ [35] results, which demonstrates to a certain extent the feasibility of the method proposed in this paper. In these studies, the authors take crank slider mechanism and four-bar linkage mechanism as examples to predict the dynamic wear process of multibody system with clearance. From the main results, it can be proved that a multibody framework is needed for wear prediction at non-ideal joints, because the contact position must be determined by dynamic analysis. Moreover, the trend from the results of Mukras and Flores is consistent with the findings of this paper. For example, the wear of the contact surface is not uniform, and the size and position of the clearance will affect the wear process, which proves the feasibility of the discrete analysis method proposed in this paper to a certain extent.

5.3 Simulation verification

In order to further verify the effectiveness of the proposed method and the correctness of the calculation results, ADAMS method combined with ANSYS is employed to verify the wear process of the crank slider mechanism with only one clearance described in Sect. 5.1. The simulation process is as follows: (1) According to the physical parameters provided in Sect. 5.1, the motion model of the crank slider mechanism with clearance is established in ADAMS; (2) the crank speed, movement time, and other initial parameters are provided as input to obtain the dynamic outputs of the crank slider mechanism after a cycle, such as contact force and rotation angle; (3) the model of the revolute joint is established in ANSYS, and the bearing’s contact pressure is obtained using the force spectrum obtained in the above step; (4) the amount of wear is calculated and the bearing profile is updated; (5) iterations of the above process are performed.

The results are presented in Figs. 20 and 21.

Fig. 20

Simulation and comparison for joint clearance, 0.1 mm. a Bearing radius after 20 full crank rotations; b bearing radius after 40 full crank rotations; c slider velocity after 40 full crank rotations; d slider acceleration after 40 full crank rotations

Fig. 21

Simulation and comparison for joint clearance, 0.5 mm. a Bearing radius after 20 full crank rotations; b bearing radius after 40 full crank rotations; c slider velocity after 40 full crank rotations; d slider acceleration after 40 full crank rotations

It can be seen from Figs. 20 and 21 that the results obtained in the software simulation are similar to those calculated by the proposed method. When the clearance is 0.1 mm, the change of bearing radius is small, and the location of main wear area is consistent, which can be confirmed from Fig. 20d. When the clearance is 0.5 mm, the location of the concentrated wear area is basically the same, but the wear amount is different in the initial stage. However, the comparison results demonstrate that the proposed method is effective in predicting the wear of multibody mechanism with clearance. In addition, it should be pointed out that in order to simplify the simulation process, the force spectrum generated after one cycle of crank operation is analyzed in ANSYS, which is an important reason for the difference of analysis results.

In conclusion, it is very important but also very complex to couple the dynamic response of a mechanical system with the prediction of clearance and joint wear. The change of initial conditions, such as clearance size, number of clearance, clearance position, and driving conditions, will lead to a significant change in the dynamic response of the system. At the same time, the motion characteristics of the system may change from periodic to quasi periodic, or even chaotic, or vice versa. Therefore, it is necessary to predict and analyze the motion of the mechanism in the design stage, so as to provide useful design parameters for the stable motion of the mechanism.

6 Conclusions

In this paper, a methodology for wear modeling and evaluation of a planar mechanical system with clearance is proposed. The method consists of two parts: dynamic analysis and wear prediction. A new contact surface discretization method is employed to establish the motion model of the mechanism under the framework of multibody dynamics with clearance, and the wear model adopted is based on the Archard equation, which relates the loss of contact material with the physical and dynamic characteristics of contact, and can be easily implemented in the computational program.

With this approach, the influence of the interaction of the clearance size, the number of clearances, clearance position, and the driving conditions on the dynamic characteristics of the crank slider mechanism is studied. From the main results obtained, it can be concluded that relatively large clearance size leads to more frequent collision between bearing and journal and more loss of contact material, but the wear area distribution becomes relatively uniform. In addition, the ‘sensitivity’ of the joints at different positions to clearance value is different. In the crank slider mechanism investigated in this work, changing the gap size of a c–c joint will make the dynamic response of the mechanism change more obviously. Also, the more the number of clearance joints, the more nonlinear the dynamics of the mechanism is, and the behavior of the system is more likely to change from periodic motion to chaotic motion. Furthermore, with the increase of input energy, the wear volume of the bearing radius increases and the behavior of the mechanism becomes more predictable.

In order to obtain more accurate dynamic output, it is important to systematically study the coupling of joint wear under complex contact conditions and the dynamics of the multi-clearance mechanism. The methodology proposed in this paper can be used to predict how the worn surface affects the dynamics of the system, and conversely, how the mechanism with clearance can bear the wear of the contact bodies without affecting the normal operation of the mechanism.

Appendices

Appendix

Notations

${\text{e}}$	Center distance vector
$\delta$	Relative penetration (m)
$\dot{\delta }$	Relative normal impact velocity in the contact (m/s)
$\dot{\delta }^{\left( - \right)}$	Initial impact velocity in the contact (m/s)
$F_{N}$	Normal contact force (N)
$F_{T}$	Tangential contact force (N)
$c_{r}$	Restitution coefficient
$K_{g}$	Composite nonlinear stiffness coefficient (N/m2)
${\text{r}}$	Global position vector
${\text{A}}$	Transformation matrix of coordinate
${\text{n}}$	Unit normal vector
${\mathbf{t}}$	Unit tangential vector
$R_{b}$	Bearing radius (m)
$R_{j}$	Journal radius (m)
E	Young’s modulus (N/m2)
$\nu$	Poisson’s ratio
$\mu$	Instantaneous friction coefficient
$v_{n}$	Relative normal velocity (m/s)
$v_{t}$	Relative tangential velocity (m/s)
$\sigma_{0}$	Bristle stiffness (N/m)
$\sigma_{1}$	Microscopic damping (Ns/m)
$\sigma_{2}$	Viscous friction coefficient
$\mu_{k}$	Kinetic friction coefficient
$\mu_{s}$	Static friction coefficient
$v_{s}$	Stribeck velocity (m/s)
$Q_{C}$	Global contact force (N)
$T$	Kinetic energy (J)
$U$	Potential energy (J)
$Q_{j}$	System generalized force (N)
$V_{w}$	Wear amount (m3)
$s$	Relative sliding distance (m)
$k$	Dimensionless wear coefficient
$H$	Hardness of the soft material (Pa)
$h$	Wear depth (m)
$A_{a}$	Contact stress (m2)
$P$	Contact stress (N/m2)