1 Introduction

Many works have studied the rotational motion of a heavy rigid body about a fixed point and subject to some torques which can be represented as perturbation and restoring torques (see, e.g., [1,2,3,4]). The perturbed motions of a rigid body, close to the Lagrange top, and related problems are studied in recent works.

Such problems can be quite strictly formulated in the framework of the rigid body motion in the Lagrange case, which can be regarded as an unperturbed motion of the body. The correction of the studied models is carried out by taking into account external and internal perturbation factors of various physical nature as well as relevant assumptions regarding the unperturbed solution.

Author of work [5] studied the dynamics of the rotating rigid body moving in atmosphere under the action of a biharmonic time-dependent restoring torque and small perturbation torques. A perturbed motion of the rigid body, similar to Lagrange gyroscope, has been considered in various works, see, e.g., [1, 5,6,7,8,9,10,11,12,13,14,15,16,17,18,19, 21,22,23]. In [1, 6], the conditions were presented for the possibility of applying the averaging procedure for the equations of motions with respect to the phase of nutation angle; the averaged system of equations was obtained. The averaging system of the equations of motion of a rigid body for a case similar to Lagrange top, in the presence of some conditions regarding nutation angle, is obtained in [6]. It is supposed that the applied perturbation torques are consider in terms of components of projections of the angular velocity vector. The generalization of this problem is considered in [7] when the perturbation torques are slowly varying in time. A perturbed rotational motion of the rigid body, close to Lagrange’s case, in the medium with linear dissipation, under the action of a torque that is slowly varying in time, was considered in [7]. In [1, 8], the perturbed fast rotations of a rigid body, close to regular precession in Lagrange’s case, were investigated for different orders of smallness of the projections of the angular momentum vector. The perturbed rotation of a rigid body, close to Lagrange’s regular precession, was studied in case where the body is acted upon by a restoring and perturbation torques slowly varying in time [9]. In paper [10], the perturbed fast rotations of a rigid body, close to regular precession, under the influence of a slowly time-varying perturbation torque and a restoring torque depending on the nutation angle, were investigated. In [11], the short overview of some results on the problem of the evolution of the rigid body rotation, close to the Lagrange’s case, is available. The rotational motion of a heavy rigid body with a fixed point under the action of the friction forces caused by the dissipative medium has been considered in [12]. The asymptotic behavior of the Lagrange gyroscope’s motion, close to regular precession, under the influence of a small perturbation torque has been investigated in [13,14,15].

In paper [16] was initiated an attempt to apply the procedure of averaging with respect to the nutation phase angle suggested earlier in [1, 6] for the motion of a rigid body, close to Lagrange gyroscope, under the action of gyro moment vector, perturbation torques and Newtonian field of force. The procedure of averaging suggested in [1, 8, 9] for investigating the fast rotation of Lagrange’s gyroscope was studied in [17] under condition of presence of a Newtonian field of force, gyro and perturbation torques.

In paper [18], the motion of a gyrostat, similar to Lagrange’s gyroscope, under the action of a gyrostatic moment vector, was investigated.

In work [19], author has considered the precession motion, close to classical Lagrange top, for the asymmetric rigid body, equipped by the strong magnet, moving on its orbit in the presence of geomagnetic field. The type of attitude motion of artificial satellite carrying a strong magnet was studied also earlier in [15]. In [20], it was indicated that the research of the dual-spin spacecraft angular motion under the action of the magnetic restoring torque is fulfilled in the generalized formulation close to the problem of motion of the Lagrange top.

Low-order resonances during the motion of the Lagrange spinning top with a small mass asymmetry were analyzed in [21].

In work [22], the effect of viscous friction on the Lyapunov stability of the rotation of a heavy rigid body about a fixed point is investigated. In [23], the author considered a problem of stationary motions of a dynamically symmetric heavy rigid body with a fixed point. It is assumed that the body is influenced by the action of the dissipative torque and the constant torque. In paper [24], the problem of the global asymptotic stabilization of a spinning top, to a uniform, steady rotation about its axis of symmetry was examined.

In [25], the method of averaging has been applied to the nonlinear system of Euler’s equations for rotational motion of a rigid body. In work [26], the problem of attitude stabilization of a rigid body with the use of restoring and dissipative torques was studied.

The author in paper [27] studied the motion of a heavy rigid body with a fixed point in Lagrange’s case with an asymmetry due to inequality of the equatorial moments of inertia. Studies [1,2,3,4, 28] reflect the classical results and analysis of various methods used in the dynamics of a heavy rigid body. The complete description of the Lagrange top can be found in studies [1,2,3,4].

Some cases of integration of the gyroscopic motion equations in a resistant medium are considered in [1, 3, 6, 7, 28].

In work [29], analytical and numerical methods are used to solve the equations of a symmetric heavy rigid body about a fixed point.

We can see from this little survey that there is significant volume of literature on the dynamics of a rigid body, moving about its center of mass under the action of perturbation torques of various physical nature. The research in this area is in connection with the problems of astronautics, the problems of the entry of flying vehicle into the atmosphere and the motion of rotating projectile and gyroscopy.

We investigate a new problem of the motion of a rigid body about a fixed point under the action of restoring and perturbation torques that are slowly varying in time. This is a more general case in comparison with works [1, 6, 7] and a particularity of this paper.

We establish the conditions of the feasibility to average with respect to the phase of the nutation angle the equations of the rigid body motion related to the Lagrange case.

We describe an averaging procedure for slow variables of a perturbed motion of a rigid body, close to the Lagrange top. In the case of the rotational motion of the body in the linear dissipative medium, the numerical integration of the averaged system of equations is conducted.

The plan of the paper is as follows. In Sect. 2, the governing equations are derived and the main assumptions are formulated. In Sect. 3, we reduce the equations of motion to the form admitting the application of the averaging method. The conditions for the possibility of averaging the equations of motion with respect to the phase of the angle of nutation are formulated. The system of equations of the perturbed Lagrange motion is represented. In Sect. 4, an actual mechanical model of the perturbations, corresponding to the rigid body’s motion in a medium with linear dissipation, is considered.

2 Statement of the problem, unperturbed motion

Let us consider the motion of a dynamically symmetric rigid body about a fixed point O, under the action of the restoring torque and perturbations depending on the slow time \( \tau = \varepsilon t \), where t is the time and \( \varepsilon \) is a small parameter characterizing the perturbation magnitude, ε ≪ 1. The equations of motion are

$$ \begin{aligned} & A\dot{p} + (C - A)\;qr = \mu (\tau)\sin \theta \cos \varphi + \varepsilon M_{1} \\ & A\dot{q} + (A - C)\;pr = - \mu (\tau)\sin \theta \sin \varphi + \varepsilon M_{2} \\ & C\dot{r} = \varepsilon M_{3};\,\,M_{i} = M_{i} (p,\,\,q,\,\,r,\,\,\psi,\,\,\theta,\,\,\varphi,\,\,\tau),\,\,\,i = 1,2,3\, \\ & \dot{\psi} = (p\sin \varphi + q\cos \varphi){\text{cosec}}\,\theta,\, \\ & \dot{\theta} = p\cos \varphi - q\sin \varphi,\,\,\,\,\,\,\dot{\varphi} = r - (p\sin \varphi + q\cos \varphi){\text{ctg}}\,\theta. \\ \end{aligned} $$
(1)

The first three dynamic equations in (1) are composed in terms of projections onto the principal axes of inertia of the body passing through the point O. Here, p, q and r are the projections of the angular velocity vector onto these axes; \( \varepsilon M_{i} \,,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3 \), are the projections of the vector of perturbation torques onto the same axes; ψ, θ and \( \varphi \) are the Euler angles; A is equatorial; and C is the axial moments of inertia of the body relative to the fixed point O, A ≠ C. We assume that the rotating body is acted upon also by a restoring torque depending on slow time \( \mu (\tau ) \) \( (0 < \mu (\tau )) \). This torque is a differentiable function.

If the perturbation torque is zero, \( M_{i} \, \equiv 0 \) and the restoring torque is time independent, \( \mu (0) = mgl \), the equations of (1) correspond to Lagrange’s case. Here, m is the mass of the body, g is the gravitational acceleration, and l is the distance from the fixed point O to the center of gravity of the body.

We have set the problem of investigating the asymptotic behavior of the solutions of system (1) for the nonzero values of small parameter ε on a sufficiently long time interval \( t\sim\varepsilon^{ - 1} \). The analysis will be carried out by method of averaging, given in [30].

The first integrals of the equations of motion for the unperturbed system (1) at parameter \( \varepsilon = 0 \) are

$$ \begin{aligned} & G_{z} = A\sin \theta \left( {p\sin \varphi + q\cos \varphi } \right) + Cr\cos \theta = c_{1} \\ & H = \frac{1}{2}\left[ {A\left( {p^{2} + q^{2} } \right) + Cr^{2} } \right] + \mu \cos \theta = c_{2} ,\,\,\,r = c_{3} \, \\ \end{aligned} $$
(2)

where \( G_{z} \) is the projection of the angular momentum vector onto vertical axis Oz; H is the body’s total energy; r is the projection of the angular velocity vector onto the axis of dynamical symmetry of the body; \( c_{i} \,\,\,(i = 1,2,3) \) are the arbitrary constants; and \( c_{2} \ge - \mu . \)

According to the results of [1, 3, 4], we can express the nutation angle θ in case of unperturbed motion as a function of the time t, of the motion integrals (2) and arbitrary phase constant β as follows:

$$ u = \cos \theta = u_{1} + (u_{2} - u_{1} )\text{sn}^{2} \left( {\alpha t + \beta } \right). $$
(3)

Here,

$$ \begin{aligned} & \alpha = \left[ {\mu \left( {u_{3} - u_{1} } \right)/\left( {2A} \right)} \right]^{1/2} ,\,\,\, \\ & \text{sn} \left( {\alpha t + \beta } \right) = \sin \,{\text{am}}\left( {\alpha t + \beta ,k} \right), \\ & k^{2} = \left( {u_{2} - u_{1} } \right)\left( {u_{3} - u_{1} } \right)^{ - 1} ,\,\,\,\,\,\,\,\,0 \le k^{2} < 1\,, \\ \end{aligned} $$
(4)

and \( u \) is the periodic function \( \alpha t + \beta \) with a period \( {{K(k)} \mathord{\left/ {\vphantom {{K(k)} \alpha }} \right. \kern-0pt} \alpha } \); \( K(k) \) is the complete elliptic integral of the first kind; sn and am are an elliptic sine and amplitude [31], respectively; k is the modulus of the elliptic functions; and \( u_{1} ,\,\,u_{2} ,\,\,u_{3} \) are the real roots of cubic polynomial

$$ Q(u) = A^{ - 2} [(2H - Cr^{2} - 2\mu u)(1 - u^{2} )A - (G_{z} - Cru)^{2} ]. $$
(5)

The relations between the roots of polynomial Q(u) and first integrals (2) can be written, according to Vieta’s theorem, in the following way:

$$ \begin{aligned} & u_{1} + u_{2} + u_{3} = \frac{H}{\mu } - \frac{{Cr^{2} }}{2\mu } + \frac{{C^{2} r^{2} }}{2A\mu };\quad u_{1} u_{2} + u_{1} u_{3} + u_{2} u_{3} = \frac{{G_{z} Cr}}{A\mu } - 1; \\ & u_{1} u_{2} u_{3} = - \frac{H}{\mu } + \frac{{Cr^{2} }}{2\mu } + \frac{{G_{z}^{2} }}{2A\mu };\quad - 1 \le u_{1} \le u_{2} \le 1 < u_{3} < + \infty. \\ \end{aligned} $$
(6)

Formulas (2), (3), (5) describe the solution of system (1) at parameter \( \,\varepsilon = 0 \) in Lagrange’s case.

In work [9], the perturbed rotations of a rigid body close to Lagrange’s regular precession are investigated in case where the body is acted upon by restoring and perturbation torques slowly varying in time. The rigid body is assumed to be spin up to a high angular velocity, and restoring and perturbation torques are assumed to be small, with a certain hierarchy of smallness for these components of torques.

3 Averaging procedure

The averaging procedure, developed earlier in [1, 6, 7], was used for averaging system (1) in the case of unsteady restoring and perturbation torques; it allows averaging over the phase of the nutation angle θ along the trajectories of angle’s changing \( \theta \left( t \right) \). The averaging method utilizes averaging the original system (1) for the perturbed case.

We reduce the equations of the motion (1) to the form allowing the application of the averaging method. We identify slow and fast variables, and here, the first integrals (2) are the slow variables for the perturbed motion (1). The fast variables are the angles of proper rotation \( \varphi \), nutation θ, and precession ψ, and we separate slow and fast variables. The frequencies of these motions have a form [32]

$$ \begin{aligned} & \omega_{\psi } = \frac{1}{2AK(k)}\left[ {\frac{{G_{z} + N}}{{1 + u_{1} }}\varPi \left( {\frac{\pi }{2},n_{1} ,k} \right) + \frac{{G_{z} - N}}{{1 - u_{1} }}\varPi \left( {\frac{\pi }{2},n_{2} ,k} \right)} \right] \\ & \omega_{\varphi } = \frac{1}{2AK(k)}\left[ {\frac{{G_{z} + N}}{{1 + u_{1} }}\varPi \left( {\frac{\pi }{2},n_{1} ,k} \right)} \right. - \left. {\frac{{G_{z} - N}}{{1 - u_{1} }}\varPi \left( {\frac{\pi }{2},n_{2} ,k} \right) + N\left( {\frac{1}{C} - \frac{1}{A}} \right)} \right] \\ & \omega_{\theta } = \frac{\pi }{K(k)}\left( {\frac{\varPi }{2A}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {u_{2} - u_{1} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,\,\,\,\,k = \left[ {\frac{{u_{2} - u_{1} }}{{u_{3} - u_{1} }}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}. \\ \end{aligned} $$
(7)

Here, \( G_{z} ,\,\,\,N \) are the projections of the angular momentum vector on the vertical and onto the axis of dynamical symmetry. \( \varPi \left( {\frac{\pi }{2},\,\,n,\,\,k} \right) \) is the complete elliptic integral of the third kind, and \( n \) is the characteristic: \( n_{1} = - \frac{{u_{2} - u_{1} }}{{1 + u_{1} }},\,\,\,n_{2} = \frac{{u_{2} - u_{1} }}{{1 - u_{1} }} \).

In [33], the frequency of nutation oscillations was found: \( 2a_{1} = 2\left( {1 + \frac{{ - 1 + 3\omega^{2} }}{8}E + \frac{\omega }{4}K} \right) \). Here, \( E \) and \( K \) are the first integrals of the full Hamilton set, \( \omega = \text{sign} (r)(1 - {{4A\mu_{0} } \mathord{\left/ {\vphantom {{4A\mu_{0} } {Cr^{2} }}} \right. \kern-0pt} {Cr^{2} }})^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \). The precession frequency is \( \upsilon = {\alpha \mathord{\left/ {\vphantom {\alpha {\Delta t}}} \right. \kern-0pt} {\Delta t}} = a_{2} - a_{1} \). The nutation and precession frequencies are \( 2a_{1} = 2.01845 \) and \( \upsilon = a_{2} - a_{1} = 0.298773 \).

Using relations (2) as the formulas for transforming the variables \( (p,\,\,q,\,\,r,\,\,\,\psi ,\,\,\theta ,\,\,\varphi ) \) to the variables \( (G_{z} ,\,\,H,\,\,r,\,\,\,\psi ,\,\,\theta ,\,\,\varphi ) \), we reduce the first three equations in (1) to

$$ \begin{aligned} & \frac{{{\text{d}}G_{z} }}{{{\text{d}}t}} = \varepsilon \left[ {\left( {M_{1} \sin \varphi + M_{2} \cos \varphi } \right)\sin \theta + M_{3} \cos \theta } \right] \\ & \frac{{{\text{d}}H}}{{{\text{d}}t}} = \varepsilon \left[ {\left( {M_{1} p + M_{2} q + M_{3} r} \right) + \frac{{{\text{d}}\mu (\tau )}}{{{\text{d}}\tau }}\cos \theta } \right] \\ & \frac{{{\text{d}}r}}{{{\text{d}}t}} = \varepsilon C^{ - 1} M_{3} ; \\ & M_{i} = M_{i} \left( {p,q,r,\psi ,\theta ,\varphi ,\tau } \right),\,\,\,i = 1,2,3.\, \\ \end{aligned} $$
(8)

Here and in the three last kinematic equations in Eq. (1), it is implied that variables p, q, r are expressed, using relations (2) as the functions of \( G_{z} ,\,\,H,\,\,\,r,\,\,\,\psi ,\,\,\theta ,\,\,\varphi \), and then substituted into appropriate expressions in (1), (8).

The dependence of the restoring torque on the slow variable \( \tau \) causes the appearance of terms containing the derivative \( {{{\text{d}}\mu \left( \tau \right)} \mathord{\left/ {\vphantom {{{\text{d}}\mu \left( \tau \right)} {{\text{d}}\tau }}} \right. \kern-0pt} {{\text{d}}\tau }} \) in the second equation of system (8).

The right-hand sides of Eq. (8) contain three fast variables \( \theta ,\,\,\,\varphi \) and ψ, which are periodic in t, and present a difficulty for the application of the averaging method (the resonance problem).

To eliminate this difficulty, we require that the right-hand sides of Eq. (8) for slow variables \( G_{z} ,\,\,H,\,\,\,r \) depend on only one fast variable, the angle of nutation \( \theta \), and are \( 2\pi \)-periodic functions of the phase of the angle \( \theta \). Then, Eq. (8) can be averaged over the phase of the nutation angle \( \theta \) and the equations of the first approximation can be obtained. A number of applied problems possess the indicated property and admit averaging over the phase of the nutation angle. It is required that the expression of the right-hand sides of (8) has the following properties of perturbation torque (see Eq. (2)):

$$ \begin{aligned} & M_{1}^{*} = M_{1} \sin \varphi + M_{2} \cos \varphi \\ & M_{2}^{*} = M_{1} p + M_{2} q,\,\,\,\,M_{3}^{*} = M_{3} \\ & M_{i}^{*} = M_{i}^{*} (G_{z} ,H,r,\tau ,\theta ),\,\,\,i = 1,2,3. \\ \end{aligned} $$
(9)

Our goal is to find the conditions for the possibility of averaging the equations of motion with respect to the phase of the nutation angle. Note that the first and the second relations (2) lead to the equalities

$$ \begin{aligned} & p\sin \varphi + q\cos \varphi = \frac{{G_{z} - Cr\cos \theta }}{A\sin \theta } \\ & p^{2} + q^{2} = \frac{{2\left[ {H - \mu (0)\cos \theta } \right] - Cr}}{A}. \\ \end{aligned} $$
(10)

The combinations of form (10) are expressed only in terms of the slow variables and the nutation angle, and they are \( 2\pi \)-periodic of the phase of the angle \( \theta \). Therefore, the combination (10) is reduced to form (9).

To be specific, the case

$$ M_{1} = pf,\,\,\,\,\,M_{2} = qf,\,\,\,\,M_{3} = \,M_{3}^{ * } $$
(11)

or the conditions

$$ M_{1} = F\sin \varphi ,\,\,\,M_{2} = F\cos \varphi ,\,\,\,M_{3} = M_{3}^{ * } $$
(12)

where the arbitrary functions \( f,\,\,\,\,F \) and \( M_{3}^{ * } \) have the form

$$ \,f = f(G_{z} ,H,r,{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ),\,\,\,\,\,F = F(G_{z} ,H,r,{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ),\,\,\,\,M_{3}^{ * } = M_{3}^{ * } (G_{z} ,H,r,{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) $$
(13)

and are \( 2\pi \)-periodic of the phase of the angle \( \theta \); then, the requirements (9) are fulfilled.

We assume the general (necessary and sufficient) conditions (9) or, in particular, the sufficient conditions (11) or (12) together with (13) are satisfied, which ensures that relations (9) are held. Then, system (8) has the following form

$$ \begin{aligned} & \dot{G}_{z} = \varepsilon F_{1} \left( {G_{z} ,H,r,\tau ,\theta } \right),\,\,\,\,\,\,\,F_{1} = M_{1}^{*} \,\sin \theta + M_{3}^{*} \cos \theta \\ & \dot{H} = \varepsilon F_{2} \left( {G_{z} ,H,r,\tau ,\theta } \right),\,\,\,\,\,\,\,F_{2} \, = M_{2}^{*} \, + M_{3}^{*} r + \frac{{{\text{d}}\mu (\tau )}}{{{\text{d}}\tau }}\cos \theta \\ & \dot{r} = \,\varepsilon F_{3} \left( {G_{z} ,H,r,\tau ,\theta } \right),\,\,\,\,\,\,\,\,\,F_{3} = C^{ - 1} M_{3}^{*}. \\ \end{aligned} $$
(14)

Here, \( F_{i} = F_{i} \left( {G_{z} ,H,r,\tau ,\theta } \right)\,,\,\,i = 1,2,3 \), are 2π-periodic functions of the phase of the angle θ.

We propose to carry out the investigation of the perturbed motion in the slow variables \( u_{i} ,\,\,\,i = 1,2,3 \), connected with \( G_{z} ,\,\,H \) and \( \,r \) by relations (6), which seem to be more convenient for analysis.

We differentiate the relations of system (6) with respect to time and transform the right-hand sides of relations (8)

$$ \begin{aligned} & \dot{u}_{1} + \dot{u}_{2} + \dot{u}_{3} = \frac{1}{\mu (0)}\left[ {\dot{H} + Cr\dot{r}\left( {\frac{C}{A} - 1} \right)} \right] \\ & \dot{u}_{1} \left( {u_{2} + u_{1} } \right) + \dot{u}_{2} \left( {u_{1} + u_{3} } \right) + \dot{u}_{3} \left( {u_{1} + u_{2} } \right) = \frac{C}{A\mu (0)}\left( {\dot{G}_{z} r + G_{z} \dot{r}} \right) \\ & \left( {\dot{u}_{1} u_{2} + u_{1} \dot{u}_{2} } \right)u_{3} + u_{1} u_{2} \dot{u}_{3} = \frac{1}{\mu (0)}\left( { - \dot{H} + Cr\dot{r} + \frac{{G_{z}^{{}} \dot{G}_{z} }}{2A\mu }} \right). \\ \end{aligned} $$
(15)

Let us obtain an algebraic system of the form

$$ \dot{u}_{i} = f_{i} (u_{1} ,\,\,\,u_{2} ,\,\,\,u_{3} ,\,\,\,G_{z} ,\,\,\,r^{2} ,\,\,\,H),\,\,\,\,i = 1,2,3. $$
(16)

As a result, we find

$$ \dot{u}_{i} = f_{i} (u_{1} ,\,\,\,u_{2} ,\,\,\,u_{3} ). $$
(17)

We denote \( H = x,\,\,\,r^{2} = y,\,\,\,G_{z}^{2} = z \).

We rewrite (6) taking into account these notations and obtain a system

$$ \begin{aligned} & \frac{1}{2\mu (0)}\left[ {2x + C\left( {\frac{C}{A} - 1} \right)y} \right] = u_{1} + u_{2} + u_{3} \\ & \frac{1}{2\mu (0)}\left[ { - 2x + Cy} \right] = u_{1} u_{2} u_{3} - \frac{1}{2A\mu (0)}z \\ & \frac{{C^{2} }}{{A^{2} \mu^{2} (0)}}yz = \left( {u_{1} u_{2} + u_{1} u_{3} + u_{2} u_{3} + 1} \right)^{2}. \\ \end{aligned} $$
(18)

After series of transformations, we obtain a quadratic equation for \( z \) \( z^{2} - 2A\mu (0)\varOmega \,z + A^{2} \mu^{2} (0)\,\varOmega^{2} = 0,\,\,\,\,\,\,\varOmega = u_{1} + u_{2} + u_{3} + u_{1} u_{2} u_{3} \), from which we find the first equation of (18).

Then, there is no need to solve cubic Eq. (5) with respect to \( u_{i} \). We consider that variables \( u_{i} ,\,\,\,i = 1,2,3, \) are different. The slow variables \( G_{z} ,\,\,\,H,\,\,\,r \) can be expressed in terms of \( u_{i} \) from relations (6) with the help of (18) in the following way:

$$ \begin{aligned} & G_{z} = \delta_{1} \delta_{3} \left( {\varOmega + \delta_{2} R} \right)^{1/2} ,\,\,\,\,\,\,\,\,\,\,r = \delta_{1} C^{ - 1} \left( {\varOmega - \delta_{2} R} \right)^{1/2} \,\, \\ & H = \frac{1}{2}\mu \left[ {\left( {u_{1} + u_{2} + u_{3} } \right)\left( {1 + AC^{ - 1} } \right) + \left( {\,\delta_{2} R - u_{1} u_{2} u_{3} } \right)\left( {1 - AC^{ - 1} } \right)} \right] \\ & R = \left[ {\left( {1 - u_{1}^{2} } \right)\left( {1 - u_{2}^{2} } \right)\left( {u_{3}^{2} - 1} \right)} \right]^{1/2} ,\,\,\,\,0 \le \left\{ {R,\varOmega } \right\},\,\,\,\,\,\delta_{1} = \left( {A\mu } \right)^{1/2} \text{sign} r \\ & \delta_{2} = \,\text{sign} \left( {G_{z}^{2} - C^{2} r^{2} } \right),\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta_{3} = \text{sign} \left( {1 + u_{1} u_{2} + u_{1} u_{3} + u_{2} u_{3} } \right). \\ \end{aligned} $$
(19)

At the initial instant, quantities \( \delta_{1} \) and \( \delta_{2} \) are determined from the initial conditions for \( G_{z} \) and r. If one or even both of the quantities \( G_{z}^{2} - C^{2} r^{2} \) and r pass through zero during the process of motion, a change of sign is possible for \( \delta_{1} \) and \( \,\delta_{2} \); to determine these signs, we can use the original system (14).

After appropriate transformations, the system of equations for the slow variables \( u_{i} ,\,\,\,i = 1,2,3 \), takes the form

$$ \begin{aligned} & \frac{{{\text{d}}u_{i} }}{{{\text{d}}t}} = \varepsilon V_{i} (u_{1} ,u_{2} ,u_{3} ,\tau ,\theta ),\,\,\,\,u_{i} (0) = u_{i}^{0} ,\,\,\,\,\,i = 1,2,3 \\ & V_{i} = V_{i1} F_{1}^{*} + V_{i2} F_{2}^{*} + V_{i3} F_{3}^{*} + V_{i4} \,\mu^{{\prime }} ,\,\,\,\,\,\,V_{ij} = V_{ij} \left( {u_{1} ,u_{2} ,u_{3} ,\tau } \right),\,\,\,\,j = 1,2,3,4 \\ & V_{11} = \frac{{G_{z} - Cru_{1} }}{A\Delta };\quad V_{12} = \frac{{u_{1}^{2} - 1}}{\Delta } \\ & V_{13} = \frac{C}{A\Delta }\left[ {Ar(1 - u_{1}^{2} ) - u_{1} (G_{z} - Cru_{1} )} \right]; \\ & V_{14} = \frac{{\left[ {A(u_{1}^{2} - 1)\left( {Cr^{2} - 2H} \right) - (G_{z} - Cru_{1} )^{2} } \right]}}{2A\mu \Delta } \\ & \mu = \mu (\tau ),\,\,\,\,\,\mu^{{\prime }} = \frac{{{\text{d}}\mu (\tau )}}{{{\text{d}}\tau }};\,\,\,\,\,\Delta = \mu \left( {u_{1} - u_{2} } \right)\left( {u_{1} - u_{3} } \right),\,\,\,\,\Delta \ne 0. \\ \end{aligned} $$
(20)

Here, instead of \( G_{z} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r \) we need to use the appropriate expressions from formulas (19). Functions \( V_{2j} ,\,\,\,V_{3j} ,\,\,j = 1,2,3,4 \) are obtained from expressions (20) for \( V_{ij} \) (at \( i = 1 \)) by the cyclic permutation of the indices for variables \( u_{i} \). Functions \( F_{i}^{*} \) are obtained by substituting expressions (19) into functions (14). The initial values of the variables \( u_{i} \) are calculated from the initial data for \( G_{z}^{0} ,\,\,\,H^{0} ,\,\,\,r^{0} \), using relations (6).

As has been mentioned, the dependence of the restoring torque on the slow time \( \tau \) leads to the appearance of an additional term \( {{\mu^{\prime} = d\mu \left( \tau \right)} \mathord{\left/ {\vphantom {{\mu^{\prime} = d\mu \left( \tau \right)} {d\tau }}} \right. \kern-0pt} {d\tau }} \) in system (20).

The procedure for averaging of Eq. (20) for the slow variables \( u_{i} \) of the first approximation is the following. We substitute the fast variable θ for the unperturbed motion, from expressions (3) into the right-hand sides of system (20). The right-hand sides of system (20) are to be the periodic functions depending on t with period \( 2K\left( k \right)/\alpha \), where k and α are defined in (4). Here, \( K(k) \) is the complete elliptic integral of the first kind. Averaging the right-hand sides of the resultant system over the phase of the nutation angle, we obtain the averaged system of first approximation in the slow time \( \tau = \varepsilon t \):

$$ \begin{aligned} & \frac{{{\text{d}}u_{i} }}{{{\text{d}}\tau }} = U_{i} \left( {u_{1} ,u_{2} ,u_{3} ,\tau } \right),\,\,\,u_{i} (0) = u_{i}^{0} ,\,\,\,i = 1,2,3 \\ & U_{i} \left( {u_{1} ,u_{2} ,u_{3} ,\tau } \right) = \frac{\alpha }{2K(k)}\int\limits_{0}^{2K/\alpha } {V_{i} \left( {u_{1} ,u_{2} ,u_{3} ,\tau ,\theta (t)} \right){\text{d}}t}. \\ \end{aligned} $$
(21)

After researching and solving system (21) for \( u_{i} \), the original slow variables \( G_{z} ,\,\,H \) and \( r \) are reconstructed by using formulas (6).

According to general theorems of the averaging method [30], slow variables \( u_{i} \) and \( G_{z} ,\,\,H,\,\,r \) are determined with an error of the order of \( \varepsilon \).

4 The test example for demonstration of advantages of solving procedure

As the test example of solving procedure, we investigate a perturbed Lagrange motion under the action of an external medium.

An external medium that slowly changes the viscous properties due to a variation in density, temperature and composition of the medium can serve as the example of the linearly dissipative perturbation torques \( \varepsilon M_{i} ,\,\,\,i = 1,2,3 \), which have the form [1, 3, 7, 28]

$$ M_{1} = - a(\tau )p,\,\,\,\,\,M_{2} = - a(\tau )q,\,\,\,\,\,M_{3} = - b(\tau )r,\quad a(\tau ),\,\,\,b(\tau ) > 0,\,\,\,\,\,\,\,\,\tau = \varepsilon t $$
(22)

where \( \,a(\tau ) \) and \( b(\tau ) \) are positive integrable functions that depend on the medium properties and the body’s shape.

We should note that torques (22) satisfy sufficient conditions (11) and (13) for the possibility of averaging over the phase of the nutation angle θ. For the given perturbations, system (14) can be written as follows:

$$ \begin{aligned} & \dot{G}_{z} = - \varepsilon \left[ {\left( {a(\tau )(p\sin \varphi + q\cos \varphi } \right)\sin \theta + b(\tau )r\cos \theta } \right] \\ & \dot{H} = - \varepsilon \left[ {a(\tau )\left( {p^{2} + q^{2} } \right) + b(\tau )r^{2} + \frac{{{\text{d}}\mu (\tau )}}{{{\text{d}}\tau }}\cos \theta } \right] \\ & \dot{r} = - \varepsilon C^{ - 1} b(\tau )r. \\ \end{aligned} $$
(23)

By integrating the third Eq. (23), we obtain (here below, \( r^{0} \) is an arbitrary initial value of the axial velocity of rotation):

$$ r = r^{0} \,\exp ( - \varepsilon C^{ - 1} \int\limits_{0}^{t} {b(\varepsilon t)dt)}. $$
(24)

Let us consider the case where

$$ \begin{aligned} & a(\tau ) = a_{0} + a_{1} \tau ,\,\,\,b(\tau ) = b_{0} + b_{1} \tau \,,\,\,\,\mu (\tau ) = \mu_{0} + \mu_{1} (\tau ), \\ & \left\{ {a_{0} ,\,\,\,a_{1} ,\,\,\,b_{0} ,\,\,\,b_{1} ,\,\,\,\mu_{0} } \right\}{\text{ = const,}}\,\,\,\,a_{0} > 0,\,\,\,b_{0} > 0,\,\,\,\mu_{0} > 0,\,\,\,a_{1} \ge 0,\,\,\,b_{1} \ge 0,\mu_{1} \ge 0. \\ \end{aligned} $$
(25)

Here, in expressions (25): \( \mu_{1} (\tau ) = \chi \tau \) or \( \mu_{1} (\tau ) = \chi \exp (\tau ) \), \( \chi = {\text{const}} \).

In accordance with the procedure in Sect. 2, we pass to the new slow variables \( u_{i} \) and we average in accord with (20). Then, we obtain the averaged system (21) in slow time \( \tau = \varepsilon t \) of form:

$$ \begin{aligned} & \frac{{{\text{d}}u_{1} }}{{{\text{d}}\tau }} = \frac{ - 1}{\Delta }\left\{ {A^{ - 1} b\left( \tau \right)r\left( {G_{z} - C\,r\,u_{1} } \right)(v - u_{1} )} \right. + \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(123) \\ & \quad + A^{ - 1} a\left( \tau \right)\left[ {A^{ - 1} \left( {G_{z} - C\,r\,u_{1} } \right)\left( {G_{z} - Crv} \right) + (u_{1}^{2} - 1)(2H - Cr^{2} - 2\mu_{0} v)} \right] - \\ & \quad - \left. {\mu^{{\prime }} \left[ {(u_{1}^{2} - 1)\left( {v + \frac{1}{2\mu }\left( {Cr^{2} - 2H} \right)} \right) - \frac{1}{2A\mu }(G_{z} - Cru_{1} )^{2} } \right]} \right\} \\ & v = u_{3} - \left( {u_{3} - u_{1} } \right)E(k)/K(k). \\ \end{aligned} $$
(26)

Symbol (123) denotes that the two unwritten relations are obtained from the written out relation (26) by cyclic permutation of indices 1, 2 and 3. However, under this permutation, the expression for v (where \( K(k),\,\,\,E(k) \) are complete elliptic integrals of the first and second kind) should remain unchanged in all three equations. Here, expressions (4) and (19) are substituted in the place of \( G_{z} ,\,\,\,H,\,\,\,r,\,\,\,k \).

We shall receive a comparison of solutions obtained by averaging method and the numerical method for the input Eq. (1).

The aim of this part is to examine the representations of the numerical solutions of the averaged systems for different values of the nutation angle \( \theta \), value of moments of inertia \( A \) and \( C \). We consider the following data (Table 1 and (27)).

Table 1 Three cases that correspond to the following initial data
Full size table

The averaged system (21) was integrated numerically for \( \tau \ge 0 \) under various initial conditions and parameters of the problem. Let us present the results of calculation for three special cases corresponding to the following initial data in Table 1.

These data correspond to a spinning top which, at the initial moment of time, have an angular velocity of rotation about the axis of dynamic symmetry equal to \( r^{0} = 1.73 \), and this body is deflected by angle \( \theta^{0} \) from the vertical. In addition, we assume that

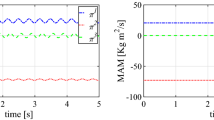
$$ C = 1,\;\mu_{0} = 0.9,\;a_{0} = 0.125,\,\,\,b_{0} = 0.1,\,\,\,a_{1} = b_{1} = 1,\,\,\,u_{2}^{0} = \cos \theta^{0}. $$
(27)

Using the values \( u_{i} \) found as result of the numerical integration, we determine the variables \( G_{z} ,\,\,\,H,\,\,\,r, \) from formulas (19). We assume that the quantity \( \mu_{1} \) increases linearly (Fig. 1) and \( \mu_{1} \) increases exponentially (Figs. 2, 3).

Fig. 1
figure 1

Plots of the first integrals and roots of the cubic polynomial in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \tau ,\,\,\,\,\chi = 0.01 \) (case 1)

Full size image
Fig. 2
figure 2

Plots of the first integrals and roots of the cubic polynomial in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \exp (\tau ),\,\,\,\chi = 0.01 \) (case 2)

Full size image
Fig. 3
figure 3

Plots of the first integrals and roots of the cubic polynomial in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \exp (\tau ),\,\,\,\chi = 0.001 \) (case 3)

Full size image

Figures 1, 2 and 3 present the graphs of functions \( u_{i} ,\,\,i = 1,2,3, \) and \( G_{z} ,\,\,\,H,\,\,\,r \) corresponding to the three cases, indicated above. The total energy of the body and angular velocity of rotation about the dynamic symmetry axis were found to decrease. The projection \( G_{z} \) of the angular momentum vector on the vertical in cases 1 and 2 monotonically decreases. In case 3, it monotonically increases, tending to zero in all three cases. The quantity \( u_{3} \) asymptotically decreases, in sufficiently rapid manner, to + 1. The quantities \( u_{1} \) and \( u_{2} \) decrease monotonically to − 1. In this case, as it follows from (3), we have \( \cos \theta \to - 1 \) if \( \theta \to \pi \). The total energy decreases monotonically asymptotically approaching the value \( H = - 0.9 \).

The numerical solution of the system of Eq. (1) and the averaged system (26) was carried out by the Runge–Kutta method of the fourth–fifth order with interpolation of the fourth degree. System (1) is integrated under the initial conditions indicated in Table 1 as well as \( p_{0} = 0,\,\,\,\,q_{0} = 0,\,\,\,\varphi_{0} = 0,\,\,\,\psi_{0} = 0 \) and \( \varepsilon = 0.1 \) to compare the results of numerical integration of system (1) with the results of solving system (26), where \( G_{z} ,\,\,\,H,\,\,\,r \) were restored using formulas (2). The values \( u_{i} ,\,\,i = 1,2,3, \) were obtained as a result of the numerical solution of the cubic polynomial (4), taking into account the values \( G_{z} ,\,\,\,H,\,\,\,r \) and parameters \( A,\,\,\,C,\,\,\mu \, \). The solution of system (1) in the first case is shown in Fig. 4, and Fig. 5 shows the comparison of the graphs obtained as a result of the solution of system (1) and system (26). In case 2, the solution of system (1) has a form similar to case 1, and also while comparing the graphs are similar to those shown in Fig. 5. The solution of system (1) in the third case is shown in Fig. 6. In Fig. 7, the plots of \( r \), \( u_{i} ,\,\,i = 1,2,3, \) obtained as a result of the solutions of system (1) and system (26) are compared.

Fig. 4
figure 4

Plots of the \( \varphi ,\,\,\psi ,\,\,\theta \) and \( r,\,\,p,\,\,q \) in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \tau ,\,\,\,\,\chi = 0.01 \) (case 1)

Full size image
Fig. 5
figure 5

Plots \( r,\,\,\,G_{z} ,\,\,\,H \) and \( u_{i} ,\,\,i = 1,2,3, \) in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \tau ,\,\,\chi = 0.01 \) (case 1)

Full size image
Fig. 6
figure 6

Plots of the \( \varphi ,\,\,\psi ,\,\,\theta \) and \( r,\,\,p,\,\,q \) in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \exp (\tau ),\,\,\chi = 0.001 \) (case 3)

Full size image
Fig. 7
figure 7

Plots of \( r \) and \( u_{i} ,\,\,i = 1,2,3, \) in Lagrange’s case where \( \mu_{1} (\tau ) = \chi \exp (\tau ),\,\,\,\chi = 0.001 \) (case 3)

Full size image

Table 2 shows the maximum difference between the values \( G_{z} ,\,\,\,H,\,\,\,r \), \( u_{i} ,\,\,i = 1,2,3, \) obtained by solving system (1) and system (26). In the third case, the error between the values is the smallest in comparison with the first and second cases. This is due to the fact that in the expression for the restoring torque, \( \chi = 0.001 \).

Table 2 Maximum errors
Full size table

5 Conclusion

We present some new qualitative and quantitative results of motion of a heavy top subject to small restoring and perturbation torques. The method of averaging is successfully applied to the nonlinear system of Euler’s equations for rotational motion.

An averaging procedure developed earlier [1, 6, 7] is used later for averaging system (1) in the case of perturbations and restoring torque depending on the slow time \( \tau \) and allowing averaging over the phase of the nutation angle \( \theta \) along the trajectories of change \( \theta (t) \). The main goal of this paper is to extend the results of the previous investigations for problem of the motion of a dynamically symmetric rigid body under the action of restoring and perturbation torques independent or dependent on the slow time. The obtained results are looked as a generalization of former works such as in [1, 6, 7] (in the absence of slow time in the perturbation and restoring torque).

We consider a perturbed motion, close to the Lagrange case, under the action of an external medium that slowly changed the viscous properties due to a variation in density, temperature and composition of the medium.

By comparing the results obtained here with the results of works [1, 6] (where \( \mu \) and \( M_{i} \) have been chosen to be independent of the slow time \( \tau \)) and, also, with the results of [7] (where \( M_{i} \) depend on the slow time only), we can emphasize their distinct mechanical content. The dependence of the restoring and perturbation torques on the slow time leads in result to the exhibiting (in the averaged system of equations of the first approximation for the slow variables) of the set of functions \( a(\tau ) \),\( \,b(\tau ) \) and \( \mu \left( \tau \right) \), depending on the slow time, which smooth out the asymptotic behavior or numerical dynamics of \( u_{i} ,\,\,i = 1,2,3 \), \( G_{z} \) and \( \,H \) at the stage of numerical integration.

Under the influence of external dissipation, the rigid body tends to the unique stable (lower) equilibrium position in more rapid manner than in cases which were considered earlier [1, 6, 7] which follows from the partial special cases at choosing the coefficients in (25)).

The correctness of calculations and the correctness of numerical results have been confirmed by close values of \( r \), obtained by numerical integration using formulae (19), which are practically identical to the exact solution (24). The numerical solution of the system of Eq. (1) and the averaged system (26) was carried out. In Figs. 5 and 7, we can see a comparison of the graphs obtained as a result of the solutions of system (1) and system (26).

In this paper, we present and analyze the input equations of motion, conduct an averaging procedure and receive the averaged equation which, being simpler that the original ones, describe the motion over the large interval of time. We establish quantitative and qualitative feat of motion and provide a description of the evolution of the body motion.

Thus, a new class of rotations of a dynamically symmetric rigid body about a fixed point has been investigated with restoring and perturbation unsteady torques being taken into account. This class is the widest among those known in the literature.

We should note that useful particular problem of the dynamics of rigid body’s rotation, close to Lagrange motion, which is of independent value for technical applications, has been solved.