Firing multistability in a locally active memristive neuron model

Abstract

The theoretical, numerical and experimental demonstrations of firing dynamics in isolated neuron are of great significance for the understanding of neural function in human brain. In this paper, a new type of locally active and non-volatile memristor with three stable pinched hysteresis loops is presented. Then, a novel locally active memristive neuron model is established by using the locally active memristor as a connecting autapse, and both firing patterns and multistability in this neuronal system are investigated. We have confirmed that, on the one hand, the constructed neuron can generate multiple firing patterns like periodic bursting, periodic spiking, chaotic bursting, chaotic spiking, stochastic bursting, transient chaotic bursting and transient stochastic bursting. On the other hand, the phenomenon of firing multistability with coexisting four kinds of firing patterns can be observed via changing its initial states. It is worth noting that the proposed neuron exhibits such firing multistability previously unobserved in single neuron model. Finally, an electric neuron is designed and implemented, which is extremely useful for the practical scientific and engineering applications. The results captured from neuron hardware experiments match well with the theoretical and numerical simulation results.

1 Introduction

Firing is one of the primary electric activities of biological neurons and plays a crucial role in neural information transmission and encoding. The neural signals encoded by neuronal action potentials are considered to be the neural bases for the realization of various advanced intelligent behaviors like learning, memory and emotion in the human brain [1,2,3]. Thus, the investigation of neuronal firing is extremely important to develop neuromorphic systems with neural functions [4,5,6,7] and artificial intelligence with emotional algorithms [8,9,10]. In the past decades, great progresses in nonlinear dynamics have inspired an increasing enthusiasm in studies on the complex dynamics in neural electrical activities. From the perspective of dynamics, firing patterns of neurons can be divided into periodic and chaotic spiking firings [11], stochastic bursting firing [12], periodic and chaotic bursting firings [13] as well as chaos firing [14]. Since British biologists Hodgkin and Huxley reproduced the pulse firing in an isolated neuron model described by dynamical equations [15], various firing patterns have been widely investigated based on theoretical and experimental neuron models. For example, Hindmarsh and Rose (HR) [16, 17] discovered the periodic spiking firing and periodic bursting firing in a two-dimension (2D) and a three-dimension (3D) nerve impulse models, respectively. In [18], the generating mechanisms of periodic bursting firing and chaotic bursting firing are revealed in a simplified HR neuron model. And Lakshmanan and his team found that the periodic and chaotic spiking, and the periodic and chaotic bursting can be observed based on the HR neuron with time delays [19]. With the rapid development in nonlinear dynamics and bio-physiology, based on single neuron, the phenomena of multiple modes and mode transition in electrical activities of neuron have been explored by considering different external environment factors. For instance, Lv and Ma [20] detected that when external electromagnetic radiation is imposed on the neuron, the bursting firings with different periodicities can be changed by changing the intensity of magnet field. Some similar research results have also been reported in [21, 22]. And [23] obtained multiple firing patterns such as periodic bursting, stochastic bursting, chaotic bursting and chaos firing in an isolated neuron exposed to external electric field. Similarly, multiple firing patterns including chaotic bursting and stochastic bursting have been verified in a sciatic nerve chronic constriction injury neuron [24]. Additionally, in [25], hidden chaos firing pattern has also been discovered in a memristive HR neuron model.

In recent years, the phenomenon of coexisting behaviors [26,27,28,29] has become a very important research topic and received extensive attention. Coexisting behavior is an intricate dynamical phenomenon that contains different kinds of stable dynamical behaviors in the same nonlinear system under different initial states [30]. Particularly, the coexistence of three or more different dynamical states under different initial conditions is called as multistability [31, 32]. Multistability means that a rich diversity of stable states exists in a nonlinear system, which reflects the characteristics of the brain itself [33, 34]. Numerous electrophysiological experiments show that multistability of firing patterns exists in the electrical activities of biological neurons [35, 36]. Such multistable behaviors may be modulated by neuromodulators, which has many potential implications for dynamic memory and information processing in a neuron [37, 38]. Recently, the phenomenon of coexisting two types of firing patterns has been observed in single neuron model. For example, in [39], the coexistence of two chaotic bursting with different topologies has been found in a modified HR neuron by imposing an external alternating current. [40] captured the coexisting phenomenon of periodic spiking firing and chaotic bursting firing in a 2D HR neuron model stimulated by bipolar pulse. In particular, Bao et al. [25] demonstrated that the coexisting behaviors of periodic spiking and hidden chaos firing can be produced in the memristive HR neuron model under two sets of different initial conditions. And the coexistence of periodic bursting firing and hidden bursting firing has been discovered in a threshold memristive neuron model [41]. Besides, the multistability with coexisting three types of periodic bursting firing patterns with different periodicities has been observed in single Morris–Lecar neuron model [42]. However, the multistability with coexisting four or more firing patterns has not been detected in isolated neuron models up to now. Therefore, it is important to explore firing multistability from single neuron models, which is helpful for better understanding of complicated dynamics of electrical activities observed in biological neurons.

It is well known that memristor [43, 44] is a natural nonlinear nano-electronic device. Due to excellent biomimetic characteristics like nano-scale, nonlinearity and memorability, memristors usually are used to imitate biological synapses [45, 46]. Local activity is considered as the origin of complexity [47, 48]. The first locally active memristor exhibiting local activity was proposed by Leon Chua in 2014 [49]. Thereafter, the mathematical and physical locally active memristive devices have attracted increasing attention from scientific and technological communities. There is evidence that the locally active memristors [50,51,52] have intense nonlinearity and complicated dynamics due to its rich equilibria stability. At present, the locally active memristor models with one or two stable pinched hysteresis loops under different initial states have been reported. For example, [49] designed the locally active memristor with one pinched hysteresis loops under different initial conditions. Jin et al. [53] presented a locally active memristor model with two stable equilibria, and using it obtained a simplest chaotic circuit. And the bistable bi-locally active memristor with two stable pinched hysteresis loops has been investigated by Chang et al. [54]. As we all know, synapses are considered as the locally active non-volatile memristors [55, 56]. Therefore, the locally active memristors can efficiently mimic the neural synapses. Motivated by these considerations, we present a new locally active and non-volatile memristor with three stable pinched hysteresis loops, which has not been reported in the previous investigation. After that, the locally active memristor is selected as a autapse to construct a novel locally active memristive neuron model based on a 2D HR neuron. Through the theoretical and numerical analysis, we determine that the locally active memristive neuron can generate multiple firing patterns and firing multistability. Moreover, hardware experiments of the locally active memristive neuron are provided to verify the effectiveness of the numerical simulation results.

The rest of this paper is organized as follows. Section 2 designs a novel locally active memristor. In Sect. 3, the locally active memristive neuron is modeled, and its firing multistability is revealed. In Sect. 4, the circuit of the locally active memristive neuron is designed, and the theoretical and numerical results are demonstrated in hardware experiments. Section 5 summarizes the paper.

2 The new locally active memristor

Generally, a memristive model with n different stable pinched hysteresis loops under different initial conditions is called n-stable memristor [52]. The value of n is determined by the number of the stable equilibrium points of the locally active memristor. Numerous investigation results [49, 50, 53, 54] show that the locally active memristor with a larger number of stable pinched hysteresis loops under different initial states exhibits more complex dynamical behaviors. Unfortunately, until now, the maximum of n is only equal to 2. In this section, a non-volatile and locally active memristor with three stable pinched hysteresis loops, namely $n=3$, will be presented. An accurate model for the locally active memristor can be derived by modifying the generic memristor model [49]. According to the theory of memristors, a voltage-controlled generic memristor can be defined as

State-dependent ohm’s law:

$$\begin{aligned} i = W(x)v \end{aligned}$$

(1)

State equation:

$$\begin{aligned} \hbox {d}x/\hbox {d}t = F(x,v) \end{aligned}$$

(2)

where W(x) is memductance, and v, i, x denote the input voltage, output current and state variable, respectively. Now, we propose a hypothetical voltage-controlled generic memristor model based on Eqs. (1) and (2), namely

$$\begin{aligned} i= & {} W(x)v = xv \end{aligned}$$

(3)

$$\begin{aligned} \hbox {d}x/\hbox {d}t= & {} F(x,v) = \alpha f(x) + \beta v \end{aligned}$$

(4)

where

$$\begin{aligned} f(x) = {\mathrm{sgn}} (x + 1) + {\mathrm{sgn}} (x - 1) - x \end{aligned}$$

(5)

$\alpha$, $\beta$ are two memristive parameters, and f(x) is the exact equation of the five-segment curve. To prove the presented mathematic model to be a non-volatile and locally active memristor, the prominent characteristics including frequency-dependent pinched hysteresis loops, non-volatile and local activity are analyzed by using the methods of theoretical analysis and numerical simulations.

2.1 Pinched hysteresis loop

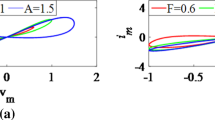
Keeping the parameters $\alpha =1$, $\beta =1$, the dynamical behaviors of the locally active memristor are explored under different signal frequencies, signal amplitudes and initial states, when a sinusoidal voltage signal $v=A\sin (2\pi Ft)$ with amplitude A and frequency F is chosen as the driving source. When the frequency $F=0.5$ and initial state $x(0)=2$ are fixed with different values of the amplitude A, and the amplitude $A=4$ and initial state $x(0)=2$ are fixed with different values of the frequency F, the frequency-dependent pinched hysteresis loops of the locally active memristor are numerically simulated and plotted in Fig. 1a, b, respectively. As can be seen from Fig.1, six pinched hysteresis loops pass through the origin in the voltage-current plane when driven by sinusoidal signal with different amplitudes and frequencies. And in Fig. 1b, as the excitation frequency increases from 0.5 to 2, the hysteresis lobe area is gradually decreased. Furthermore, it is obvious that when the frequency increases to infinity the pinched hysteresis loop will tend to a single-valued function. Evidently, the proposed mathematical model exhibits memristor peculiarities [42], which implies the model described by Eqs. (3)–(5) is a memristor device.

Fig. 1

Amplitude-/frequency-dependent pinched hysteresis loops of the locally active memristor. a$F=0.5$, $x(0)=2$ and different amplitudes. b$A=4$, $x(0)=2$ and different frequencies. (Color figure online)

Additionally, with $A=4$, $F=0.8$ unchanged, three stable pinched hysteresis loops can be obtained from the proposed locally active memristor model as shown in Fig. 2a under different initial states, and two critical points which divide three pinched hysteresis loops are −0.3521 and −1.1609, respectively. It should be pointed out that with the decreasing of the signal frequency, three distinct pinched hysteresis loops of the memristor will tend to synthesize a stable pinched hysteresis loop, as shown in Fig. 2b. Obviously, the presented memristor is a tri-stable locally active memristor, which has not been reported in the previous studies. Additionally, the memductance of the locally active memristor can be modulated by controlling voltage through it, as shown in Fig. 3 with different frequencies and initial states. Such feature is similar to the function of a biological neural synapse. Consequently, using the locally active memristor as a synapse in neuromorphic system can efficiently imitate synaptic functions.

Fig. 2

Initial state-dependent pinched hysteresis loops of the locally active memristor. a$A=4$, $F=0.8$ and different initial values. b$A=4$, $F=0.3$ and different initial values. (Color figure online)

Fig. 3

Voltage-dependent memductance of the locally active memristor. a$A=4$, $x(0)=-1$ and different frequencies. b$A=4$, $F=0.8$ and different initial states. (Color figure online)

2.2 Non-volatile memory

It is noted that not all memristors have non-volatility memories [49]. The property of non-volatile can be proved by using power-off plot (POP), that is, a curve in the F(x, 0) versus x plane. According to the non-volatile memristor theorem, the POP curve of the non-volatile memristor has two or more negative slope intersections with x-axis in the $\hbox {d}x/\hbox {d}t$ versus x plane. Here, Let $v=0$, the state equation of the locally active memristor reduces to

$$\begin{aligned} \hbox {d}x/\hbox {d}t = F(x,0) = {\mathrm{sgn}} (x + 1) + {\mathrm{sgn}} (x - 1) - x \end{aligned}$$

(6)

The dynamic route of the nonlinear dynamical function Eq. 6, namely POP, is shown in Fig. 4. In Fig. 4, when $\hbox {d}x/\hbox {d}t=0$, there are a total of five intersections with x-axis located at $Q_1(-2, 0), Q_2(-1, 0), Q_3(0, 0), Q_4(1, 0)$ and $Q_5(2, 0)$, respectively. It should be stressed that each intersection of POP with the x-axis is defined as an equilibrium point of the memristor due to $\hbox {d}x/\hbox {d}t=0$ under this case. According to the judgment method of Ref. [49], the equilibrium points $Q_1$, $Q_3$ and $Q_5$ are asymptotically stable, while the equilibrium points $Q_2$ and $Q_4$ are unstable. Thus, three stable equilibrium states exist in the non-volatile memristor under different initial state x(0), that is to say,

$$\begin{aligned} X= & {} x({Q_1}) = - 2,(x(0) < - 1) \end{aligned}$$

(7)

$$\begin{aligned} X= & {} x({Q_3}) = 0,( - 1< x(0) < 1) \end{aligned}$$

(8)

$$\begin{aligned} X= & {} x({Q_5}) = 2,(x(0) > 1) \end{aligned}$$

(9)

Fig. 4

POP of the tri-stable locally active memristor. (Color figure online)

Furthermore, the corresponding stable small-signal conductance can be calculated as

$$\begin{aligned} W(x({Q_1}))= & {} x({Q_1}) = - 2,(x(0) < - 1) \end{aligned}$$

(10)

$$\begin{aligned} W(x({Q_3}))= & {} x({Q_3}) = 0,( - 1< x(0) < 1) \end{aligned}$$

(11)

$$\begin{aligned} W(x({Q_5}))= & {} x({Q_5}) = 2,(x(0) > 1) \end{aligned}$$

(12)

Obviously, Eqs. (7)–(12) show that the state x(t) is different with initial state x(0). Therefore, the presented locally active memristor is a non-volatile memristor.

2.3 Local activity

It is noted that not all non-volatile memristors are locally active [49]. The property of local activity can be inferred by observing DC V–I plot. To measure the DC V–I loci of the locally active memristor, its equilibrium equation can be calculated by setting $\hbox {d}x/\hbox {d}t=0$, as follows

$$\begin{aligned} V = X - {\mathrm{sgn}} (X + 1) - {\mathrm{sgn}} (X - 1) \end{aligned}$$

(13)

where V denotes DC voltage, and X is a variable equilibrium state satisfying $\hbox {d}x/\hbox {d}t(\hbox {x}=\hbox {X})=0$. Then, substituting Eq. (13) into Eq. (3), the DC current I can be described by

$$\begin{aligned} I = XV = X(X - {\mathrm{sgn}} (X + 1) - {\mathrm{sgn}} (X - 1)) \end{aligned}$$

(14)

Considering Eqs. (13) and (14), the DC V–I plot of the tri-stable locally active memristor is drawn with the input DC voltage V value varying from $-1$ to 1 V and the variable X value varying within ($-2.2$, 2.2), as shown in Fig. 5. In Fig. 5, when the DC voltage $V=0$, the memristor has five different memductances which are, respectively, $W(X_1)=-2$ (the royal blue curve), $W(X_2)=-1$ (the dark yellow curve), $W(X_3)=0$ (the cyan curve), $W(X_4)=1$ (the purple curve) and $W(X_5)=2$ (the dark green curve). And when the DC voltage $V \ne 0$, five intervals of equilibrium states $X_1=(-2.2, -1.01)$, $X_2 =(-1.01, -0.9988)$, $X_3=(-0.9988, 0.9988)$ and $X_4=(0.9988, 1.002)$ and $X_5=(1.002, 2.2)$ are coincident with the corresponding five segment curves in Fig. 4, and corresponding POP curve is colored in royal blue, dark yellow, cyan, purple and dark green. It can be seen from Fig. 5 that the royal blue curve, the dark yellow curve and part of the cyan curve are negative slope, and the corresponding equilibrium state values X are ($-2.2$, $-1.01$), ($-1.01$, $-0.9988$) and ($-0.9988$, 0), respectively. Therefore, the tri-stable non-volatile memristor is locally active.

Fig. 5

DC $V-I$ loci of the tri-stable locally active memristor associated with the equilibrium state on interval $-2.2<X<2.2$. (Color figure online)

3 Dynamics of the locally active memristive neuron

3.1 Model Establishment

As it is well known, a neuron is made up of the nucleus encoding information, the dendrite collecting electrical signals, and the axon propagating electrical signals. Synapse is an important bridge for connecting the axon and the dendrite of different neurons, which plays a key role for receiving and transferring electrical signals between neurons. Based on some mathematical and biological neuron models [45, 46], the patterns in electrical activities can be modulated by the synapse current. Autapse can connect the axon and the dendrite of the same neuron by a close loop, which is a type of special synapse. As reported in [57, 58], the autapse can regulate the neuronal activity by a negative feedback autapse current. Therefore, it is significant and necessary to consider autapse as a part of a neuronal system. Numerous experiments show that the nonvolatile nature of memristors makes them an attractive candidate for the simulated autapse [56, 57]. Furthermore, the effect of electromagnetic induction current on electrical activities in neuron can be described by using memristor coupling [20,21,22, 25, 41]. Under this strategy, a reduced diagram is plotted for a new neuronal model with a memristive autaptse connection in Fig. 6. Since the memristive autapse is considered by adding memristive induction current on the neuron, a neuron model accompanying autapse current can be considered to generate complex firing patterns in biological neurons. Generally, autapse is thought as the locally active memristor, which is emulated by a locally active and non-volatile memristor considered in this paper. It should be pointed out that such locally active memristive neuron model is distinguished from the memristive neuron model in [25] and [41] due to different constructing approach. Compared with [25] and [41], we mainly focus the influence of autapse current on the firing patterns of neuron, while both [25] and [41] investigate the electromagnetic induction effects triggered by external electromagnetic radiation in biological neurons.

Fig. 6

Structure of a neuron with memristive autapse. (Color figure online)

Fig. 7

Two function curves and their intersection, where $k=0.9$, $\alpha =0.1$ and $\beta =0.42$. (Color figure online)

The 2D HR neuron model is regarded by many scholars as the idealistic one in the study of actual neuron firing. Its mathematical expression is

$$\begin{aligned} \left\{ \begin{array}{l} {\hbox {d}x/\hbox {d}t = y - a{x^3} + b{x^2} + I}\\ {\hbox {d}y/\hbox {d}t = c - d{x^2} - y} \end{array}\right. \end{aligned}$$

(15)

where x and y denote membrane potential and recovery variable of the neuron, a, b, c and d are system parameters, and I is the external current. Since the fluctuation of electrical activities in neurons can generate dynamic electromagnetic field. According to the Maxwell’s equation, the induction current following through the autapse can be occurred. When the locally active memristor in (3)–(5) is considered to emulate the autapse, a locally active memristive induction current $I_M$, namely, autapse current can be added on the neuron. As a result, a novel locally active memristive neuron model can be built. Based on Eqs. (3)–(5), a locally active memristive induction current can be described by

$$\begin{aligned} \left\{ \begin{array}{l} {{I_M} = -kW(z){V_M} = -kz{V_M}}\\ {\hbox {d}z/\hbox {d}t = \alpha ({\mathrm{sgn}} (z + 1) + {\mathrm{sgn}} (z - 1) - z) + \beta {V_M}} \end{array}\right. \end{aligned}$$

(16)

where z represents an inner state variable of the memristor synapse, k represents the coupling strength of the locally active memristor, and $V_M$ represents the membrane potential of the neuron. $W(z)=z$ is a memductance function, which stands for the synapse weight. It should be noted that the autapse current is often regarded as a negative feedback current [57, 58], namely $-I_M$. When the autapse current $-I_M$ in (16) is considered in the HR neuron model in (15), the locally active memristive neuron model can be established and written as

$$\begin{aligned} \left\{ \begin{array}{l} {\hbox {d}x/\hbox {d}t = y - a{x^3} + b{x^2} + I + kxz}\\ {\hbox {d}y/\hbox {d}t = c - d{x^2} - y}\\ {\hbox {d}z/\hbox {d}t = \alpha (\mathrm{sgn} (z + 1) + \mathrm{sgn} (z - 1) - z) + \beta x} \end{array}\right. \end{aligned}$$

(17)

where $a=1$, $b=3$, $c=1$, $d=5$, $I=0$, and $\alpha$, $\beta$ are considered as two memristor synapse parameters.

3.2 Stability analysis

By setting the left-hand side of Eq. (17) to zero, its equilibrium equation can be given by

$$\begin{aligned} \left\{ \begin{array}{l} {y = {x^3} - 3{x^2} - kxz}\\ {y = 1 - 5{x^2}}\\ {\beta x = \alpha (z - {\mathrm{sgn}} (z + 1) - {\mathrm{sgn}} (z - 1))} \end{array}\right. \end{aligned}$$

(18)

And the equilibrium points of the locally active memristive neuron can be numerically solved by solving Eq. (18), namely

$$\begin{aligned} \left\{ \begin{array}{l} {{x^*}}\\ {{y^*} = 1 - 5{{({x^*})}^2}}\\ {{z^*}} \end{array}\right. \end{aligned}$$

(19)

where the values of $x^*$ and $z^*$ are the intersection points of the two following function curves

$$\begin{aligned} \left\{ \begin{array}{l} {{f_1}(x,z) = 1 - {x^3} - 2{x^2} + kxz}\\ {{f_2}(x,z) = \alpha (\mathrm{sgn} (z + 1) + \mathrm{sgn} (z - 1) - z) + \beta x} \end{array}\right. \end{aligned}$$

(20)

The values of $x^*$ and $z^*$ can be determined through graphic analytic method. For example, when $k=0.9$, $\alpha =0.1$ and $\beta =0.42$, the two function curves given by Eq. (20) are plotted in Fig. 7, from which the only solution is gotten as $x^*=2.6143$ and $z^*=12.9801$. Correspondingly, the equilibrium point can be easily obtained from Eq. (19), namely $(x^*, y^*, z^*)=(2.6143, -33.1728, 12.9801)$. Correspondingly, the Jacobian matrix of the neuron model Eq. (17) at equilibrium point ($x^*$, $y^*$, $z^*$) can be given by

$$\begin{aligned} J= & {} \left[ \begin{array}{ccc} \frac{\partial \dot{x}}{{\partial x}} &{} {\frac{{\partial \dot{x}}}{{\partial y}}} &{} {\frac{{\partial \dot{x}}}{{\partial z}}} \\ \frac{\partial \dot{y}}{{\partial x}} &{} {\frac{{\partial \dot{y}}}{{\partial y}}} &{} {\frac{{\partial \dot{y}}}{{\partial z}}} \\ \frac{\partial \dot{z}}{{\partial x}} &{} {\frac{{\partial \dot{z}}}{{\partial y}}} &{} {\frac{{\partial \dot{z}}}{{\partial z}}} \\ \end{array}\right] \nonumber \\= & {} \left[ \begin{array}{lll} \begin{array}{l} - 3{({x^*})^2} \\ + 6{x^ *} + k{z^*} \\ \end{array} &{} 1 &{} {k{x^*}} \\ -10x^* &{} -1 &{} 0 \\ \beta &{} 0 &{} \begin{array}{l} \alpha ({10^6}(1 - {\tanh ^2}({10^6}({z^*} + 1))) \\ + {10^6}(1 - {\tanh ^2}({10^6}({z^*} - 1))) - 1) \\ \end{array}\\ \end{array}\right] \nonumber \\ \end{aligned}$$

(21)

Corresponding eigenvalues of the equilibrium point ($x^*$, $y^*$, $z^*$) can be solved by using MATLAB numerical methods. Based on the above methods, when the parameters k and $\alpha$ are fixed as 0.9 and 0.1, respectively, for different parameter $\beta$, the equilibrium points $P^*$, their corresponding eigenvalues, and the stability are given in Table 1. It can be seen from Table 1 that the potential types of $P^*$ include unstable saddle-focus with index 2, stable focus-nodes and stable saddle-nodes.

Table 1 Equilibrium points and their corresponding eigenvalues and stabilities

Fig. 8

The $\beta$-dependent dynamics with $k=0.9$, $\alpha =0.1$. a bifurcation diagram, b Lyapunov exponent spectra. (Color figure online)

Fig. 9

Numerical bifurcation diagrams for the parameter $\beta$ with $k=0.9$, $\alpha =0.1$, and four sets of different initial states. a Bifurcation diagram for $\beta$ under the initial states (0, 0, 0.1). b Bifurcation diagram for $\beta$ under the initial states (0, 0, $-0.1$). c Bifurcation diagram for $\beta$ under the initial states (0.2, $-0.1$, 0). d Bifurcation diagram for $\beta$ under the initial states ($-0.1$, 0, 0). (Color figure online)

According to the results given in Table 1, the $\beta$-parameter bifurcation diagram is depicted by Fig. 8a under the initial conditions (0, 0, $-0.1)$, where xmax is the maxima of the x variable. In Fig. 8a, when the model parameter $\beta$ increases from 0.3, the orbit of the locally active memristive neuron model begins with period-1 spiking firing pattern and evolves to period-2 spiking firing pattern at $\beta =0.34$ by forward period doubling bifurcation (FPDB) rout. Thereafter, the orbits break into chaotic bursting firing at $\beta =0.4$ until $\beta =0.46$ via crisis scenario (CS). As $\beta$ increases further, the chaotic bursting is degenerated to periodic bursting pattern via tangent bifurcation (TB) rout. Interestingly, when $\beta$ increases to 0.75, the orbit enters into hidden chaos firing pattern and finally ends at $\beta =0.96$. What follows is period-1 spiking pattern in the interval $\beta \in$(0.97, 1.1) again. It is noting that the wider chaotic band of $\beta \in$(0.4, 0.46) and $\beta \in$(0.75, 0.96) contains multiple narrow periodic windows, such as $\beta =0.44$, $\beta =0.84$, and $\beta =0.94$. The corresponding Lyapunov exponents in Fig. 8b are basically consistent with the dynamical phenomena on the bifurcation diagram in Fig. 8a. Note that the third Lyapunov exponent $L_3$ is much less than $L_2$ colored in blue and out of the picture. To systematically exhibit the complex dynamics in Eq. (17), the corresponding types of equilibrium points are superimposed on the bifurcation diagram in Fig. 8a. It can be seen from Fig. 8a that there exists a smooth transition from a unstable equilibrium point to a stable equilibrium point in $\beta \in$(0.3,1.1), which essentially leads to the emergence of firing multistability.

3.3 Multistability with coexisting multiple firings

Before exploring the firing multistability of the locally active memristive neuron, it is necessary to introduce basic definition of various firing patterns [11,12,13, 24]. Generally, firing pattern mainly includes spiking and bursting patterns. If the trajectory of a firing pattern of the neuronal system only circles around the spiking, the firing pattern is said to be spiking pattern. If the trajectory alternates between a quiescent state and repetitive spiking, the firing pattern is considered bursting pattern. The spiking patterns include periodic spiking and chaotic spiking, whereas the bursting patterns contained periodic bursting, chaotic bursting, stochastic bursting, transient stochastic bursting and transient chaotic bursting. Among them, periodic spiking containing m spikes per spiking is said to be period-m spiking ($m\in N^*$). For the chaotic spiking, except for the period-m spiking, there exist other kinds of spiking with different numbers or amplitudes of spikes. Periodic bursting containing m spikes per burst is said to be period-m bursting. For the stochastic bursting, the trajectory is stochastic transition between bursting and spiking. For the chaotic bursting, except for the period-m bursts, there exist other kinds of bursts with different numbers or amplitudes of spikes. Transient stochastic bursting is an especial behavior that the existence of stochastic bursting is on finite time. Similarly, for the transient chaotic bursting, the behavior of chaotic bursting only exists on finite time. In general, the phase trajectory of the transient firing pattern is a transient chaos attractor [33].

In our next work, the multistable dynamics of the locally active memristive neuron model is revealed in which two model parameters are kept unchanged as $k=0.9$, $\alpha =0.1$, and the model parameter $\beta$ and initial conditions $(x_0, y_0, z_0)$ are taken to be adjustable. In addition, MATLAB ODE45 algorithm is used, and the start time, the time step $\vartriangle t$ and the time length are 500, 0.01 and 4000, respectively.

Fig. 10

The time sequences of the membrane potential in the locally active memristive neuron under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.39$. a Periodic bursting firing for $(x_0, y_0, z_0)=(0, 0, 0.1)$. b Periodic spiking firing for $(x_0, y_0, z_0)=(0, 0, -0.1)$. c Chaotic bursting firing for $(x_0, y_0, z_0)={(1.5, 0.1, 0)}$. d Transient chaotic bursting firing for $(x_0, y_0, z_0)={(0.2, -0.1, 0)}$. (Color figure online)

Fig. 11

The corresponding phase plane plots under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.39$. a Periodic attractor for $(x_0, y_0, z_0)=(0, 0, 0.1)$. b Periodic attractor for $(x_0, y_0, z_0)=(0, 0, -0.1)$. c Chaotic attractor for $(x_0, y_0, z_0)={(1.5, 0.1, 0)}$. d Transient chaotic attractor for $(x_0, y_0, z_0)={(0.2, -0.1, 0)}$. (Color figure online)

Fig. 12

The time sequences of the membrane potential in the locally active memristive neuron under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.4$. a Chaotic spiking firing for $(x_0, y_0, z_0)=(0, 0, -0.1)$. b Periodic bursting firing for $(x_0, y_0, z_0)={(2, -2, -2)}$. c Chaotic bursting firing for $(x_0, y_0, z_0)={(-0.1, 0, 0)}$. d Transient chaotic bursting firing for $(x_0, y_0, z_0)={(0.2, -0.1, 0)}$. (Color figure online)

Fig. 13

The corresponding phase plane plots under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.4$. a Chaotic attractor for $(x_0, y_0, z_0)=(0, 0, -0.1)$ colored in royal blue, periodic attractor for $(x_0, y_0, z_0)={(2, -2, -2)}$ colored in purple, chaotic attractor for $(x_0, y_0, z_0)={(-0.1, 0, 0)}$ colored in olive drab. b Transient chaotic attractor for $(x_0, y_0, z_0)={(0.2, -0.1, 0)}$. (Color figure online)

Considering the model parameter $\beta$ in the range [0.32, 0.48] and four sets of different initial conditions (0, 0, 0.1), (0, 0, $-0.1$), (0.2, $-0.1$, 0) and ($-0.1$, 0, 0), four $\beta$-parameter bifurcation diagrams are depicted by Fig. 9a–d, respectively. It can be seen from Fig. 9 that the locally active memristive neuron model produces different dynamical states under different initial conditions. That is to say, diverse types of firing patterns can be observed in the locally active memristive neuron with different initial states.

According to the bifurcation plots shown in Fig. 9, when the parameter $\beta$ is selected as 0.39, and four sets of initial conditions (0, 0, 0.1), (0, 0, $-0.1$), (1.5, 0.1, 0) and (0.2, $-0.1$, 0) are used, the multistability with coexisting of periodic bursting firing pattern, period-2 spiking firing pattern, chaotic bursting firing pattern and transient chaotic bursting firing pattern can be detected in the presented locally active memristive neuron model. Correspondingly, Figs. 10 and 11 show the time sequences of membrane potential x and phase plane plots in the x–z plane, respectively. Noted that in Fig. 10d time series of membrane potential x presents a chaotic bursting firing in the time interval $t\in$(0, 1400 ms) colored in royal blue, and then it turns to periodic spiking firing colored in purple. Similarly, when the parameter $\beta$ is fixed as 0.4, with four sets of different initial values (0, 0, $-0.1$), (2, $-2$, $-2$), ($-0.1$, 0, 0) and (0.2, $-0.1$, 0), four types of firing patterns including chaotic spiking, periodic bursting, chaotic bursting and transient chaotic bursting in the locally active memristive neuron model are depicted in Figs. 12 and 13, where Fig. 12 exhibits their time sequences of the membrane potential x, and Fig. 13 shows corresponding coexisting attractors including periodic attractor, chaotic attractors with different topologies, and transient chaos attractor in the x–z plane. In Fig. 12d, time series of membrane potential x exhibits a chaotic bursting state in the time interval $t \in$(0, 1480 ms) colored in royal blue, and then it turns to periodic spiking state colored in purple. In addition, under four sets of initial states (0, 0, 0.1), (0, 0, $-1.8$), (0, 0, $-1.6$) and (0, $-1.5$, 0), four firing patterns which contain periodic bursting firing, stochastic bursting firing, transient chaotic bursting firing and transient stochastic bursting firing can be discovered when the adjustable parameter $\beta$ is chosen as 0.46. Their time sequences of the membrane potential x, and corresponding phase plane plots are shown in Figs. 14 and 15, respectively. Where in Fig. 14c, the dynamical behavior of the locally active memristive neuron begins with chaotic bursting firing pattern and evolves to periodic bursting firing pattern at $t=1400\,\hbox {ms}$. And in Fig. 14d, the neuron first generates stochastic bursting firing pattern within 2000 ms, afterwards the stochastic bursting is degenerated to periodic bursting pattern. As is clear from the above analysis, the locally active memristive neuron generates multiple firing patterns and firing multistability with coexisting four types of firing patterns. And the form of multistability of the locally active memristive neuron can be changed by choosing different model parameters.

Fig. 14

The time sequences of the membrane potential in the locally active memristive neuron under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.46$. a Periodic bursting firing for $(x_0, y_0, z_0)=(0, 0, 0.1)$. b Stochastic bursting firing for $(x_0, y_0, z_0)={(0, 0, -1.8)}$. c Transient chaotic bursting firing for $(x_0, y_0, z_0)={(0, 0, -1.6)}$. d Transient stochastic bursting firing for $(x_0, y_0, z_0)={(0, -1.5, 0)}$. (Color figure online)

Fig. 15

The corresponding phase plane plots under different initial states. $k=0.9$, $\alpha =0.1$, $\beta =0.46$. a Periodic attractor for $(x_0, y_0, z_0)=(0, 0, 0.1)$. b Chaotic attractor for $(x_0, y_0, z_0)={(0, 0, -1.8)}$. c Transient chaotic attractor for $(x_0, y_0, z_0)={(0, 0, -1.6)}$. d Transient chaotic attractor for $(x_0, y_0, z_0)={(0, -1.5, 0)}$. (Color figure online)

Fig. 16

For different $\beta$, local basins of attraction in two initial planes, where yellow, loyal blue, orange and cyan stand for different firing states. a With $\beta =0.39$, the four color regions stand for periodic spiking, chaotic bursting, periodic bursting and transient chaotic bursting, respectively. b With $\beta =0.4$, the four color regions stand for chaotic spiking, periodic bursting, transient chaotic bursting and chaotic bursting, respectively. c With $\beta =0.46$, the four color regions stand for stochastic bursting, periodic bursting, transient chaotic bursting and transient stochastic bursting, respectively. (Color figure online)

In addition, considering the aforementioned parameters and performing a measurement of initial conditions, the attraction basin defined as the domain of initial conditions can be depicted, in which different types of firing patterns are marked by different colors. When the adjustable parameter $\beta$ and the initial state $z_0$ are chosen as 0.39 and 0, as well as the measureable initial conditions $x_0$ and $y_0$ are scanned in the regions of [$-4$, 4] and [$-4$, 4], respectively, the attraction basin in the $x_0$–$y_0$ initial plane is plotted in Fig. 16a, where the yellow, royal blue, orange and cyan regions stand for periodic spiking firing pattern, chaotic bursting firing pattern, periodic bursting firing pattern and transient chaotic bursting firing pattern, respectively. When the adjustable parameter is selected as $\beta =0.4$, and the initial condition $y_0$ is fixed as 0, the attraction basin in the $x_0$–$z_0$ initial plane is drawn in Fig. 16b, where the yellow, royal blue, orange and cyan regions denote chaotic spiking firing, periodic bursting firing, transient chaotic bursting firing and chaotic bursting firing, respectively. Similarly, when $\beta =0.46$, $z_0=0.1$, the attraction basin in the $y_0$–$z_0$ initial plane is given in Fig. 16c, where the yellow, royal blue, orange and cyan regions represent stochastic bursting firing, periodic bursting firing, transient chaotic bursting firing and transient stochastic bursting firing, respectively. It is obvious that the proposed locally active memristive neuron exhibits multistability with coexisting four kinds of different firing patterns.

To better exhibit the characteristics of the proposed neuron model, a performance comparison with other memristive neuron models is given in Table 2. Obviously, the locally active memristive neuron can generate more complex firing patterns, such as stochastic bursting, transient chaotic bursting and transient stochastic bursting. More importantly, the presented locally active memristive neuron exhibits firing multistability with coexisting four firing patterns, which has never been reported in isolated neuron model.

Table 2 Comparison of different memristive neuron models

4 Circuit design and hardware experiments

From the view of practical engineering applications, it is significant and necessary to the hardware circuit realization of mathematical models [59, 60]. Generally, nonlinear dynamical equations can be physically realized by adopting commercially available analog electric elements, such as operational amplifiers, analog multipliers, capacitors and resistors [61,62,63]. Thus, the hardware circuit of the locally active memristive neuron model can be designed and implemented by employing already-existing electronic elements, which is helpful to promote the rapid development of neuromorphic circuits.

4.1 Circuit implementation

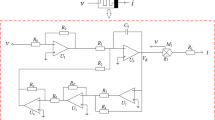
Before realizing the locally active memristive neuron circuit, based on operational amplifiers and analog multipliers, a circuit of the locally active memristor described by Eqs. (3)–(5) is designed, as plotted in Fig. 17. It can be seen from Fig. 17 that the locally active memristor circuit is composed of one capacitor C, one analog multiplier M, six operational amplifiers $U_1$–$U_6$ and eleven passive resistors, which means that the neuron circuit can be easily realized by adopting common electric components. According to the Kirchhoff’s law, the circuit equations of the locally active memristor circuit can be given as

Fig. 17

Circuit configuration of the locally active memristor emulator

Fig. 18

Circuit configuration of the locally active memristive neuron model

$$\begin{aligned} i= & {} W({v_z})v = \frac{{g{v_z}}}{{{R_L}}}v \end{aligned}$$

(22)

$$\begin{aligned} C\frac{{\hbox {d}{v_z}}}{{\hbox {d}t}}= & {} \frac{{{R_F}}}{{{R_A}}}\left( \frac{{13.5\mathrm{sgn} ({v_z} {+} e)}}{{{R_S}}} {+} \frac{{13.5\mathrm{sgn} ({v_z} {-} e)}}{{{R_S}}} -\frac{{{v_z}}}{{{R_C}}}\right) {+} \frac{v}{{{R_B}}}\nonumber \\ \end{aligned}$$

(23)

where $v_z$ represents inner state, RC is the integral time constant, v and i are the input voltage and output current of the locally active memristor, respectively. The model described by Eqs. (22) and (23) agrees with the definition of the locally active memristor in Eqs. (3)–(5). Assuming that $RC=1\,\hbox {ms}$, the resistance $R=10\,\hbox {k}\Omega$, then the C can be chosen as 100nF. Some resistances in Eqs. (22) and (23) are calculated from Eqs. (3)–(5) as $R_S=13.5\,\hbox {k}\Omega$, $R_C=1\,\hbox {k}\Omega$, $R_F/R_A=0.1\alpha$, $R_B=R/\beta$. Based on the locally active memristor circuit in Fig. 17, the circuit of the locally active memristive neuron is implemented and shown in Fig. 18. The corresponding circuit state equations are expressed by

$$\begin{aligned} \left\{ \begin{array}{l} {C\frac{{\hbox {d}{v_x}}}{{\hbox {d}t}} = \frac{{{v_y}}}{{{R_1}}} + \frac{{g{v_x}^2}}{{{R_2}}} -\frac{{{g^2}{v_x}^3}}{{{R_3}}} + \frac{{g{v_x}{v_z}}}{{{R_L}}}}\\ {C\frac{{\hbox {d}{v_y}}}{{\hbox {d}t}} = \frac{e}{{{R_S}}} - \frac{{g{v_x}^2}}{{{R_4}}} -\frac{{{v_y}}}{{{R_6}}}}\\ {C\frac{{\hbox {d}{v_z}}}{{\hbox {d}t}} = \frac{{{R_F}}}{{{R_A}}}\left( {\frac{{13.5\mathrm{sgn} ({v_z} + e)}}{{{R_S}}} + \frac{{13.5\mathrm{sgn} ({v_z} - e)}}{{{R_S}}} - \frac{{{v_z}}}{{{R_C}}}} \right) + \frac{{{v_x}}}{{{R_B}}}} \end{array}\right. \end{aligned}$$

(24)

According to Eq. (17), the resistances in Fig. 18 are derived as $R_1=10\,\hbox {k}\Omega$, $R_2=333\Omega$, $R_3=100\Omega$, $R_4=200\Omega$, $R_5=10\,\hbox {k}\Omega$ and $R_6=10\,\hbox {k}\Omega$. Moreover, the resistances of $R_L$, $R_F$, $R_A$ and $R_B$ can be determined by $R_L=gR/k$, $R_F/R_A=0.1\alpha$, $R_B=R/\beta$, where $g=0.1$ is the multiplier gain.

Fig. 19

The experimental results of three stable pinched hysteresis loops of the locally active memristor. (Color figure online)

Fig. 20

Experimentally captured coexisting firing patterns with $R_B=25.58\,\hbox {k}\Omega$. a Periodic bursting firing. b Periodic spiking firing. c Chaotic bursting firing. d Transient chaotic bursting firing. (Color figure online)

Fig. 21

Experimentally captured corresponding coexisting attractors with $R_B=25.58\,\hbox {k}\Omega$. a Periodic attractor. b Periodic attractor. c Chaotic attractor. d Transient chaotic attractor. (Color figure online)

Fig. 22

Experimentally captured coexisting firing patterns with $R_B=24.99\,\hbox {k}\Omega$. a Chaotic spiking firing. b Periodic bursting firing. c Chaotic bursting firing. d Transient chaotic bursting firing. (Color figure online)

Fig. 23

Experimentally captured coexisting firing patterns with $R_B=21.74\,\hbox {k}\Omega$. a Periodic bursting firing. b Stochastic bursting firing. c Transient chaotic attractor with transient chaotic bursting firing. d Transient chaotic attractor with transient stochastic bursting firing. (Color figure online)

4.2 Hardware experiments

Based on the circuit topology given in Fig. 18, the circuit of the locally active memristive neuron model in Eq. (18) is realized on the experimental breadboard by using electronic elements of R/metal resistors and precision potentiometers, C/ceramic capacitors, M/AD633 and U/TL082CP. In experimental measurements, the time series and phase trajectories of the membrane potential in the memristive neuron are captured by 2 channel analog oscilloscope. Firstly, the circuit of the locally active memristor is demonstrated in the hardware experiments. When the $R_A=10\,\hbox {k}\Omega$, $R_F=1\,\hbox {k}\Omega$, $R_B=10\,\hbox {k}\Omega$ and $e=0.8\,\hbox {V}$, that is, $\alpha =1$, $\beta =1$, three stable pinched hysteresis loops can be obtained from the hardware circuit of the locally active memristor, as shown in Fig. 19. Secondly, the coexisting behavior of multiple firing patterns is verified by using the neuron circuit shown in Fig. 18. When the parameters $k=0.9$, $\alpha =0.1$ and $\beta$ are set to 0.39, 0.4 and 0.46, the time series and corresponding phase trajectories were numerically simulated by MATLAB, as shown in Figs. 10, 11, 12, 13, 14 and 15. Accordingly, in the hardware experiments, the values of resistors $R_L$, $R_F$ and $R_A$ are fixed as $1.11\,\hbox {k}\Omega$, $1\,\hbox {k}\Omega$ and $100\,\hbox {k}\Omega$, respectively. When the resistance $R_B$ is set to $25.58\,\hbox {k}\Omega$ ($\beta =0.39$), the periodic bursting firing, periodic spiking firing, chaotic bursting firing and transient chaotic bursting firing can be captured by turning on and off the driven voltage source, and the corresponding time sequences and phase trajectories are shown in Figs. 20 and 21, respectively. Using the same method, when $R_B=24.99\,\hbox {k}\Omega (\beta =0.4)$, the experimental results shown in Fig. 22 are good for verifying the numerical results shown in Fig. 12. Similarly, when $R_B=21.74\,\hbox {k}\Omega (\beta =0.46)$, the numerical simulation results in Figs. 14a, b and 15c, d are verified by the experimental results in Fig. 23a–d. Obviously, the experimental results are basically consistent with the numerical simulation results. However, it should be pointed out that it is extremely difficult to determine an ideal initial value in the hardware experiments. Thus, the experimental results are slightly different from the simulation results.

5 Conclusion

In this article, we presented a novel locally active memristive neuron model based on a new locally active and non-volatile memristor with three stable pinched hysteresis loops. The dynamics of electrical activity of the locally active memristive neuron model is numerically and experimentally investigated. The results show the proposed locally active memristive neuron generates three multistable phenomena of coexisting four firing patterns, which are the phenomenon of coexistence of periodic bursting, chaotic bursting, periodic spiking and transient chaotic bursting, the phenomenon of coexistence of chaotic spiking, periodic bursting, chaotic bursting and transient chaotic bursting, and the phenomenon of coexistence of stochastic bursting, periodic bursting, transient stochastic bursting and transient chaotic bursting. The firing multistability is practically demonstrated in the hardware experiments. The phenomenon of firing multistability observed in the single neuron model is useful to understand the function of biological neuron. Moreover, the hardware circuit of the locally active memristive neuron model is implemented by using common circuit elements, which is very important to the application in the area of artificial intelligence.