On the frequency response computation of geometrically nonlinear flat structures using reduced-order finite element models

Abstract

This paper presents a general methodology to compute nonlinear frequency responses of flat structures subjected to large amplitude transverse vibrations, within a finite element context. A reduced-order model (ROM) is obtained by an expansion onto the eigenmode basis of the associated linearized problem, including transverse and in-plane modes. The coefficients of the nonlinear terms of the ROM are computed thanks to a non-intrusive method, using any existing nonlinear finite element code. The direct comparison to analytical models of beams and plates proves that a lot of coefficients can be neglected and that the in-plane motion can be condensed to the transverse motion, thus giving generic rules to simplify the ROM. Then, a continuation technique, based on an asymptotic numerical method and the harmonic balance method, is used to compute the frequency response in free (nonlinear mode computation) or harmonically forced vibrations. The whole procedure is tested on a straight beam, a clamped circular plate and a free perforated plate for which some nonlinear modes are computed, including internal resonances. The convergence with harmonic numbers and oscillators is investigated. It shows that keeping a few of them is sufficient in a range of displacements corresponding to the order of the structure’s thickness, with a complexity of the simulated nonlinear phenomena that increase very fast with the number of harmonics and oscillators.

1 Introduction

Recent advances in non-intrusive reduced-order finite element modeling of geometrically nonlinear structures offer new perspectives for nonlinear prediction in structural computation. These geometrical nonlinearities are due to large transverse displacements of thin structures which induce a non-negligible stretching in the plane of the structure known as membrane–bending coupling phenomena. They are involved in a wide range of applications, among others: micro-electromechanical systems (MEMS) developments [1,2,3], energy harvesting [4], vibroacoustics of music instruments [5, 6], dynamics of blades and rotors [7], and aerospace engineering [8]. In a finite element context, since geometrical nonlinearities couple all the displacement degrees of freedom, the computation of models with a large number of variables is found to be a tough challenge, for which strategies for model reduction have been the focus of sustained efforts since the 1980s [9, 10]. In vibration analyses, the expansion of displacements on a reduced basis of vibration eigenmodes is an efficient and well-known approach to study structural dynamics at low and middle frequencies. This article addresses the use of this kind of modal reduced-order models (ROMs) to compute the frequency response of geometrically nonlinear thin structures.

Modal ROMs are the most used technique to solve analytical models of thin structures like beams, plates and shells. Nonlinear models based on the Von Kármán assumptions [11] are well known and able to capture the membrane–bending coupling. The interested reader can refer to [12] for an overview of the most popular cases, [13, 14] for plate models, [15] for beam models and [16] that shows the similarities between beam and plate models. Since the coefficients of the ROM depend on the structure’s geometries as well as its boundary conditions, a huge literature is available for a large set of particular cases. Among others, the reader can refer to [17] for beams with doubly hinged ends, to [7] for an assembly of clamped/free boundary conditions with cyclic symmetry, to [18] for clamped circular plates, to [19] for free circular plates and to [20] for rectangular plates with several boundary conditions. In those analytical models, the in-plane inertia is usually neglected, which enables to use a mixed formulation, in which a transverse motion (described with a displacement field) is coupled to the in-plane motion described by a force unknown: an Airy stress function in the case of plates [14] and the axial force for beams [15].

To address complex geometries out of the scope of analytical models, modal ROMs can be obtained from numerical models. It can be first achieved by explicit computations, based on finite element discretization [21, 22]. p-type finite elements (high-order elements of large size) have also been applied to geometrically nonlinear vibrations of beams and plates in a family of papers [23, 24]. However, with the increasing spread of commercial finite element codes, non-intrusive methods—i.e., using the finite element code as a “black box” without modifying it—have been proposed. Two main families of methods have been introduced, both relying on static finite element computations, since the geometrical nonlinearities are concentrated in the stiffness part of the model (the internal force vector). On the one hand, one can impose static loads as linear combination of eigenmodes [25], and on the other hand, static displacement fields, also as linear combination of eigenmodes [26], can be prescribed. These methods—and particularly the second one called “STiffness Evaluation Procedure” (STEP) on which this paper focuses—have retained a large attention in the past two decades (see, e.g., the review [27]), motivated by the perspective to compute nonlinear responses of structures with arbitrary geometries. More recently, a variant of the STEP has been proposed in [28], which enables to reduce the number of static computations by using the tangent stiffness matrix. In the past few years, those reduced-order models have been validated by combining computational and experimental investigations [29, 30]. They have been applied to problems of increasing difficulty, such as fatigue life estimation of thin gauges [31], calibration of a perforated plate [32] and dynamical simulations of composite plates [27, 33], of a nine-bay panel structure [28] or of an electromechanical nanobeam [34].

In the above-cited methods, one major issue lies in the selection of the linear modal basis to perform nonlinear structural calculations. In-plane modes must be included to account for bending–membrane coupling, whereas only transverse modes constitute most of the times the modal basis in linear dynamic analysis since in-plane modes are located at higher frequencies than transverse ones. To capture these effects, several methods have been proposed. The most natural one consists in keeping in the ROM basis several in-plane modes in addition to transverse one. Since numerous in-plane modes are necessary, some authors propose to reduce the ROM size by condensing the in-plane modes into the transverse oscillators by neglecting the membrane inertia [27, 35, 36]. In the case of flat/transversely symmetric structures, it is also possible to reduce the number of computed coefficients of the ROM by observing that a lot of them are zero. This sparsity property has been mentioned in [27, 37], but no precise proof is available, to the knowledge of the authors. It is also possible to select the most relevant in-plane modes by using proper/smooth orthogonal decomposition (P/SOD) [38, 39]. These strategies are efficient but rely on the drawback of requiring the preliminary time integration of the full-scale model. Some authors propose strategies to naturally compute relevant in-plane displacement field with prescribed modal loads, with so-called implicit condensation with expansion approach [35] or dual modes strategies [33]. These methods have the drawback that the ROM coefficients are sensitive to the size of the transverse modal basis and the amplitudes of the prescribed loads [40]. A last family of method is based on the addition of a modal derivative subspace to the transverse linear basis [41]. It enables to capture efficiently the relevant in-plane displacement associated with a transverse linear mode [42]. Since the size of the subspace grows quadratically with the number of investigated eigenmodes, the concept of quadratic manifold has been proposed to minimize the number of unknowns [43]. The computation of the modal derivatives with a commercial finite elements code is based on a finite difference scheme that requires the extraction of the tangent stiffness matrix, which renders the strategy more intrusive [44]. An asymptotic expansion of a full finite element discretization proposed in [45] can lead to build a different reduction basis than the modal one which gives satisfactory results [46].

When the reduced-order model has been built, the dynamical nonlinear responses of the structures at low and middle frequencies can be investigated. Most of the early studies about modal ROMs investigate transient responses and rely on direct time integration [27, 33, 35, 39]. Conversely, it is possible to investigate the frequency response by computing the nonlinear modes of the structure, because they constitute the skeleton of the dynamics, since the harmonically forced responses lies around [47]. The so-called nonlinear normal modes—(NNMs) can be represented as frequency energy plots (or amplitude–frequency plots, also called “backbone curves” [12]) and computed by various analytical [48] or numerical [49] methods. Among these last, a method combining shooting and pseudo-arclength continuation proposed in [50] enables to compute NNMs from reduced-order finite element models: with a homemade finite element beam formulation [42, 51] or some finite element commercial codes [52], the energy is computed by injecting the result of the ROM in the full FE model.

Among the huge literature described above, the present article addresses the computation of the nonlinear frequency response of thin structures using a continuation method and finite element modal reduced-order models, obtained by the STEP. Within this subject, we focus on two main points: (i) a precise validation of the STEP using reference analytical models of flat structures (beams and plates) and (ii) the modal convergence of the ROMs, especially when internal resonance is involved. This study is restricted to flat structures since simple analytical models are available and in order to provide reference benchmarks that can be used to test algorithms, potentially adapted to more complex structures such as shells or thin structures with stiffeners. Moreover, the flat geometry gives a natural separation of in-plane and transverse modes in terms of the ROM convergence, which is especially addressed. Since in-plane modes are condensed into the transverse motion, we first analyze the convergence of the ROM in terms of in-plane modes at the coefficient level and its convergence in terms of transverse modes is studied in a second step, with frequency response computations. For the STEP validation, several topics are proposed: (a) a systematic validation of the ROM coefficients value with reference analytical models; (b) the proof of the sparsity structure of the coefficients matrices of the ROM and its consequences on the computation time saving; (c) the proof of the robustness of the STEP in terms of static prescribed displacement amplitude; (d) an heuristic rule to filter significant ROM coefficients to reduce the ROM size. We show that the STEP is perfectly validated on two reference cases (a clamped–clamped beam and a clamped circular plate) for which analytical models are known. Finally, the method is applied to a perforated plate, for which no analytical solutions are known. Convergence results are obtained, showing that very reduced ROM, composed of a few transverse oscillators coupled by cubic terms only, is efficient to compute nonlinear modes even in the case of internal resonances and vibration localization.

2 Reference analytical models of flat structures

The purpose of this section is to recall classical analytical models for flat structures, firstly to serve as a reference for the validations of the STEP proposed in the upcoming sections and secondly to systematically prove that a lot of coefficients of the modal reduced-order models are null. Here, only models relying on the von Kármán theory have been selected since they are valid for most of practical cases of 2D (plate) structures and 1D (beam) structures with immovable ends in the axial direction. In those cases, large rotation “geometrically exact” models give the same results in the same range of amplitude of vibration and are thus not necessary. Von Kármán models can be viewed as an intermediate and consistent model between linear models and full large rotation models [53, 54]. On the contrary, large rotation models have to be considered in the other cases (beams with ends free to move such as cantilever beams, see [55, 56]), out of the scope of the article.

2.1 Straight beam model

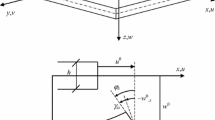
In this section, we consider a non-prestressed beam of length L of uniform rectangular cross section of area S and second moment of area I, made in an homogeneous and isotropic material of Young’s modulus E and density $\rho$. Only the bending motion is under concern, and w(x, t) and u(x, t) denote, respectively, the transverse and axial displacements at time t and abscissa x.

Following the von Kármán assumptions and with a linear elastic constitutive law, the equations of motions can be written:

$$\begin{aligned}&\rho S \ddot{w} + E I w_{,xxxx} - ES \left[ u_{,x} w_{,x} + \frac{1}{2} w_{,x}^3\right] _{,x} = p(x,t), \end{aligned}$$

(1a)

$$\begin{aligned}&\rho S \ddot{u}- ES \left( u_{,xx} + w_{,x} w_{,xx} \right) = n(x,t) . \end{aligned}$$

(1b)

where $\circ _{,x}=\partial \circ /\partial x$. All details about this formulation can be found in “Appendix A”.

To obtain a generic formulation as well as to scale the different terms in the equations, the following dimensionless parameters are introduced:

$$\begin{aligned} {\bar{w}}= & {} \frac{w}{h} , \quad {\bar{x}} = \frac{x}{L} \quad {\bar{u}}=\frac{L}{h^2}u,\nonumber \\ {\bar{t}}= & {} \frac{1}{L^2}\sqrt{\frac{EI}{\rho S}}t,\quad {\bar{p}}= \frac{L^4}{EIh} p, \end{aligned}$$

(2)

$$\begin{aligned} {\bar{n}}= & {} \frac{L^3}{ESh^2} n, \quad \varepsilon = \frac{Sh^2}{I},\quad \mu = \frac{I}{SL^2}. \end{aligned}$$

(3)

where the scaling of the transverse displacement has been chosen as the thickness h of the beam. Then, Eqs. (1a, b) are rewritten as:

$$\begin{aligned}&\ddot{w} + w_{,xxxx} - \varepsilon \left[ u_{,x} w_{,x} + \frac{1}{2} w_{,x}^3\right] _{,x} = p(x,t), \end{aligned}$$

(4a)

$$\begin{aligned}&\mu \ddot{u}- ( u_{,xx} + w_{,x} w_{,xx} ) = n(x,t) , \end{aligned}$$

(4b)

where the overbars have been dropped for simplification.

The bending and axial displacements are expanded onto a linear basis of, respectively, $N_w$ transverse modes $\varPhi _k$ and $N_u$ axial modes $\varPsi _p$:

$$\begin{aligned}&w(x,t) = \sum _{k=1}^{N_w} \varPhi _k(x) q_k(t) \quad \text {and} \nonumber \\&\quad \quad u(x,t) = \sum _{p=1}^{N_u} \varPsi _p(x) \eta _p(t) \end{aligned}$$

(5)

with time dependencies governed by unknown modal coordinates $q_k$ and $\eta _p$. The modes are chosen to satisfy the following two eigenproblems associated with the linear parts of Eqs. (4a, b):

$$\begin{aligned}&\varPhi _{k,xxxx} - \omega ^2_k \varPhi _k = 0 \end{aligned}$$

(6a)

$$\begin{aligned}&\varPsi _{p,xx} - \gamma _p^2 \varPsi _p = 0 \end{aligned}$$

(6b)

where $\omega _k$ and $\gamma _p$ are the transverse and axial dimensionless eigenfrequencies. Finally, by multiplying (4a, b), respectively, by $\varPhi _k$ and $\varPsi _p$, integrating on the length of the beam and using the orthogonality properties, the following ROM is obtained, for all $k=1,\ldots N_w$, $p=1,\ldots N_u$:

$$\begin{aligned}&\ddot{q}_k + \omega _k^2 q_k + \varepsilon \sum _{p=1}^{N_u} \sum _{i=1}^{N_w} C_{pi}^k \eta _p q_i \nonumber \\&\quad + \varepsilon \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} \sum _{l=1}^{N_w} D_{ijl}^k q_i q_j q_l = Q_k \end{aligned}$$

(7a)

$$\begin{aligned}&\mu \ddot{\eta }_p + \gamma _p^2 \eta _p - \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} G_{ij}^p q_i q_j = E_p \end{aligned}$$

(7b)

where the forcing terms $Q_k(t)$, $E_p(t)$ and the coefficients of the nonlinear terms $C_{pi}^k$, $D_{ijl}^k$ and $G_{ij}^p$ are defined in “Appendix A”. Notice that the value of those coefficients depends on the mode normalization.

The above dimensionless form of the equations shows that because of the slender geometry of the beam ($h/L\ll 1$), the axial displacement u is one order of magnitude smaller than the transverse displacement w, which leads to neglect the axial inertia because $\mu \ll 1$. In this case, if no axial external forcing is prescribed ($n(x,t)=0\Rightarrow E_p=0$), Eq. (7b) leads to write the axial modal coordinates modes as:

$$\begin{aligned} \eta _p = \frac{1}{\gamma _p^2}\sum _{i=1}^{N_w} \sum _{j=1}^{N_w} G_{ij}^p q_i q_j, \end{aligned}$$

(8)

and to condense them in the transverse equation of motion (7a) to obtain, for all $k=1,\ldots N_w$:

$$\begin{aligned} \ddot{q}_k + \omega _k^2 q_k + \varepsilon \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} \sum _{l=1}^{N_w} \varGamma _{ijl}^k q_i q_j q_l = Q_k \end{aligned}$$

(9)

with

$$\begin{aligned} \varGamma _{ijl}^k = D_{ijl}^k + \sum _{p=1}^{N_u} \frac{G_{ij}^p C_{pi}^k}{\gamma _p^2}. \end{aligned}$$

(10)

Initial problem (7a, b) has been replaced by a reduced one composed of only $N_w$ transverse equations with cubic nonlinear terms only.

2.2 Plate model

In the same way as the beam, we consider here a thin plate of thickness h with a boundary of arbitrary shape, made in an homogeneous and isotropic material of Young’s modulus E, Poisson’s ratio $\nu$ and density $\rho$. The transverse and in-plane displacements are written $w(\varvec{r},t)$ and $\varvec{u}(\varvec{r},t)$ at time t and position $\varvec{r}$. The vectors $\varvec{u}$ and $\varvec{r}$ are two-dimensional vectors of the mid-plane of the plate. The equations of motions can be written [57]:

$$\begin{aligned}&\rho h \ddot{w} + D\Delta \Delta w - {\mathrm{div}}\,(\varvec{N}\varvec{\nabla }w) = p(\varvec{r},t), \end{aligned}$$

(11a)

$$\begin{aligned}&\rho h \ddot{\varvec{u}} - {\mathbf {div}}\,\varvec{N} = \varvec{n}(\varvec{r},t). \end{aligned}$$

(11b)

where $\varvec{N}$ is the membrane forces tensor, function of $\varvec{u}$ and w, ${\mathrm{div}}\,$ and ${\mathbf {div}}\,$ are the scalar/vector divergence of a vector/tensor field, $\Delta$ is the Laplacian of a scalar field, $D=Eh^3/[12(1-\nu ^2)]$ is the bending stiffness and p, $\varvec{n}$ are transverse and in-plane external forces by unit area.

By eliminating $\varvec{N}$ between Eqs. (50) and (11a, b), one obtains a $(\varvec{u},w)$-formulation written in terms of displacement unknowns only. Then, by expanding w and $\varvec{u}$ on a linear basis of, respectively, $N_w$ transverse modes $\varPhi _k$ and $N_u$ axial modes $\varvec{\varPsi }_p$, one obtains exactly the same ROM than in the case of beams, namely Eqs. (7a, b), which has the form of a set of $N_w$ transverse and $N_u$ in-plane oscillators, coupled by quadratic and cubic terms of coefficients $C_{pi}^k$, $D_{ijl}^k$ and $G_{ij}^p$. Finally, it can also be proven that for the same reasons, the in-plane unknowns can be condensed in the transverse equations to obtain exactly the same ROM (9), composed of only $N_w$ transverse equations with cubic nonlinear terms. All details are provided in “Appendix B”.

2.3 Synthesis on analytical models for flat structures

The previous two sections have shown two main results, valid for any flat structure (beam or flat plate).

• First, in the case of a ROM written in term displacements unknowns only (the (u, w)-formulation for beams and the $(\varvec{u},w)$-formulation for plates) expanded on the linear eigenmodes basis, the form of the ROM is the one of Eqs. (7a, b), with only a few nonzero nonlinear terms:

  • quadratic terms in the transverse-$q_k$ oscillators that couple the transverse and in-plane coordinates: $C_{pi}^k \eta _p q_k$;

  • quadratic terms in the in-plane-$\eta _p$ oscillators that involve only transverse coordinates: $G_{ij}^p q_iq_j$;

  • cubic terms in the transverse-$q_k$ oscillators that couple only transverse coordinates: $D_{ijl}^k q_iq_jq_l$.

• Second, by neglecting the in-plane inertia, it is possible to condense the in-plane coordinates into the transverse oscillators, which leads to set (9), a ROM composed of $N_w$ transverse oscillators only, without additional oscillators for the in-plane motion, coupled by cubic terms only.

Another interesting result comes from the dimensionless form of the equations. For beams, if the axial inertia is neglected ($\mu \ll 1$), there is only one free parameter in the equations of motion (4a, b), which is $\varepsilon =h^2/i^2$ with $i=\sqrt{I/S}$ the radius of gyration of the beam’s cross section. If the transverse motion would have been scaled by i [${\bar{w}}=w/i$ in place of Eq. (2)], $\varepsilon$ would be equal to 1, which means that the nonlinear dynamics of any straight slender beam with a uniform cross section depends only on its boundary conditions, whatever be the geometry of the cross section and its length. For plates, an analogous result holds if w is scaled by $h/\sqrt{12(1-\nu ^2)}$. In this case, $\varepsilon =1$ in Eq. (59) and the nonlinear dynamics of any flat plate of uniform thickness depends only on the geometry of the mid-plane (circular, rectangular...) and the boundary conditions. That is why, the numerical values of the nonlinear coefficients of Tables 9 and 10 can serve as references.

3 Finite element reduced-order model

3.1 Finite element model and expansion on a linear modal basis

The general expression of a conservative nonlinear dynamical system with smooth (geometrical) nonlinearities, discretized with a finite element method, can be written in the following form:

$$\begin{aligned} \varvec{M}\ddot{\varvec{x}} + \varvec{f}_\text {i}(\varvec{x}) = \varvec{f}_\text {e} , \end{aligned}$$

(12)

where $\varvec{x}, \varvec{M}, \varvec{f}_\text {i}$ and $\varvec{f}_\text {e}$ denote, respectively, the vector of unknown displacements, the mass matrix, the internal and external force vectors. This model is obtained after any discretization of the displacement field in a finite element context. In this article, shell finite elements have been used, but the method is valid in the case of any displacement-based finite elements (beams, 3D...).

It is convenient to split the internal force vector into a linear part and a purely nonlinear part. Assuming that the equilibrium point is at $\varvec{x}=\varvec{0}$, the tangent stiffness matrix $\varvec{K}$ writes:

$$\begin{aligned} \varvec{K}=\left. \frac{\partial \varvec{f}_\text {i}}{\partial \varvec{x}}\right| _{\varvec{x}=\varvec{0}} \end{aligned}$$

(13)

so that the nonlinear internal force vector is defined by:

$$\begin{aligned} \varvec{f}_\text {nl}(\varvec{x}) = \varvec{f}_\text {i}(\varvec{x}) - \varvec{K}\varvec{x}, \end{aligned}$$

(14)

and the equations of motion are rewritten:

$$\begin{aligned} \varvec{M}\ddot{\varvec{x}} + \varvec{K}\varvec{x} + \varvec{f}_\text {nl}(\varvec{x}) = \varvec{f}_\text {e} , \end{aligned}$$

(15)

where the geometrically nonlinear part of the problem is concentrated in the nonlinear internal force vector $\varvec{f}_\text {nl}(\varvec{x})$.

The displacements are expanded on a basis of N eigenmodes $(\omega _r, \varvec{\varPhi }_r)$ of the linearized counterpart of (15):

$$\begin{aligned} \varvec{x}(t) = \sum _{r=1}^{N} \varvec{\varPhi }_r q_r(t). \end{aligned}$$

(16)

where $q_r(t)$ is the rth unknown modal coordinate. The eigenmodes are solutions of:

$$\begin{aligned} (\varvec{K}-\omega _r^2 \varvec{M})\varvec{\varPhi }_r = 0. \end{aligned}$$

(17)

By introducing Eq. (16) into Eq. (15), multiplying by $\varvec{\varPhi }_r^{{\text {T}}}$ and using the orthogonality properties, one obtains the following set of differential equations verified by the modal coordinates $q_r(t)$:

$$\begin{aligned}&\ddot{q}_r + \omega _r^2 q_r + \sum _{\alpha =1}^{N} \sum _{\beta =\alpha }^{N} a_{\alpha \beta }^r q_{\alpha } q_{\beta }\nonumber \\&\qquad + \sum _{\alpha =1}^{N} \sum _{\beta =\alpha }^{N} \sum _{\gamma =\beta }^{N} b_{\alpha \beta \gamma }^r q_{\alpha } q_{\beta } q_{\gamma } = Q_r , \end{aligned}$$

(18)

where $Q_r = \varvec{\varPhi }_r^{{\text {T}}} \varvec{f}_\text {e}/m_r$ is the modal force and $m_r=\varvec{\varPhi }_r^{{\text {T}}}\varvec{M}\varvec{\varPhi }_r$ is the rth modal mass, usually equal to 1 with a suitable normalization of the mode shapes $\varvec{\varPhi }_r$. In set (18), we have written the nonlinear force vector expansion $\varvec{\varPhi }_r^{{\text {T}}} \varvec{f}_\text {nl}$ in the form of quadratic and cubic coupling terms. It is the result of an implicit Taylor expansion of $\varvec{f}_\text {nl}(\varvec{x})$ around $\varvec{x}=\varvec{0}$, truncated to the third order in $q_r$, $r=1,\ldots N$. Depending on the formulation of the geometrical nonlinearities in the finite element discretization, this expansion can be exact (it is the case for 3D elements or for shell/plate/beam elements with a von Kármán strain/displacement nonlinear law [22, 34]) or truncated, for instance in the case of large rotation elements (such as geometrically exact beam elements for which the internal force vector include sine and cosine functions of the rotation degrees of freedom of the cross section [56, 58]). Notice that Eq. (18) is written in an upper triangular form by organizing the coupling terms such that $\alpha \le \beta \le \gamma$.

3.2 Computation of the nonlinear coefficients

In ROM (16,18), parameters $\omega _r$, $\varvec{\varPhi }_r$ and $Q_r$ are obtained by the linear modal analysis of Eq. (17), available in any finite element code. The main issue is thus to compute the coefficients $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ of the nonlinear terms. As stated in the Introduction section, several methods are available for this and we propose here to use the STiffness Evaluation Procedure (STEP) introduced in [26]. It consists in two steps.

• First, one has to prescribe a set of displacement vectors $\varvec{x}$ which are linear combination of selected linear mode shapes $\varvec{\varPhi }_r$ and computing the corresponding nonlinear force vector $\varvec{f}_\text {nl}(\varvec{x})$. This operation is available in any finite element code and is a simple evaluation of $\varvec{f}_\text {nl}(\varvec{x})$ by knowing $\varvec{x}$. It thus does not require to solve any nonlinear system, for instance with a Newton–Raphson technique.

• Second, it is shown that the unknown coefficients $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ are solutions of linear systems for which the second members are known functions of the $\varvec{f}_\text {nl}(\varvec{x})$ computed at the previous step.

To illustrate the method, we first show the computation of coefficients $a_{\alpha \alpha }^r$ and $b_{\alpha \alpha \alpha }^r$. We prescribe the following time-independent displacements to the structure:

$$\begin{aligned} \varvec{x}_1 =\pm \lambda \varvec{\varPhi }_{\alpha }\quad \Rightarrow \quad \left\{ \begin{array}{l} q_\alpha =\lambda \\ q_i=0\quad \forall i\ne \alpha \end{array}\right. \end{aligned}$$

(19)

where $\lambda$ refers to an amplitude coefficient of the mode $\varvec{\varPhi }_{\alpha }$ whose value will be addressed hereafter. The second part of the above equations comes from Eq. (16), which states that since the modes are orthogonal, imposing $\varvec{x}$ on the $\alpha$th is equivalent to setting to zero all modal coordinates but the $\alpha$th. Since $\varvec{x}_1$ is time independent, introducing Eq. (19) into Eqs. (15) and (18) leads to, for all $r=1,\ldots N$:

$$\begin{aligned} \lambda ^2 a_{\alpha \alpha }^r + \lambda ^3 b_{\alpha \alpha \alpha }^r&= \varvec{\varPhi }_r^{{\text {T}}} \varvec{f}_\text {nl}(\lambda \varvec{\varPhi }_\alpha )/m_r, \end{aligned}$$

(20a)

$$\begin{aligned} \lambda ^2 a_{\alpha \alpha }^r - \lambda ^3 b_{\alpha \alpha \alpha }^r&= \varvec{\varPhi }_r^{{\text {T}}} \varvec{f}_\text {nl}(-\lambda \varvec{\varPhi }_\alpha )/m_r. \end{aligned}$$

(20b)

As announced, the problem thus reduces to solve the above linear system which unknowns are the nonlinear coefficients $a_{\alpha \alpha }^r$ and $b_{\alpha \alpha \alpha }^r$.

On a same way, the expansion on two or three modes $(\alpha , \beta , \gamma )$ of the prescribed displacement

$$\begin{aligned} \varvec{x}_2&=\pm \lambda _{\alpha } \varvec{\varPhi }_{\alpha } \pm \lambda _{\beta } \varvec{\varPhi }_{\beta } \end{aligned}$$

(21a)

$$\begin{aligned} \varvec{x}_3&=\pm \lambda _{\alpha } \varvec{\varPhi }_{\alpha } \pm \lambda _{\beta } \varvec{\varPhi }_{\beta } \pm \lambda _{\gamma } \varvec{\varPhi }_{\gamma }, \end{aligned}$$

(21b)

leads to other linear systems enabling to compute the $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ with $\alpha \ne \beta \ne \gamma$ (see [26] for details).

In the above developments, the values of the $\lambda$ coefficients can be arbitrarily chosen, which means that for a given number of nonlinear coefficients to estimate, an infinite number of equations can be took into consideration. As Eqs. (19) and (21) show, the overdetermination comes from the amplitude as well as from the sign of the modal amplitude coefficients $\lambda$. Thus, the linear system whose unknowns are the nonlinear coefficients could be overdeterminated as well as minimal. In the first case, the overdetermined system is solved in a least square sense, as it has been done in [59, 60]. The second case needs to dispose the minimal set of prescribed loads and nonlinear static computations. It is the approach chosen in this work.

For a linear mode basis of size N, the number $N_\mathrm{c}$ of coefficients to compute is equal to:

$$\begin{aligned} N_\mathrm{c} = N\left[ \left( \left( \genfrac{}{}{0.0pt}{}{N}{2}\right) \right) + \left( \left( \genfrac{}{}{0.0pt}{}{N}{3}\right) \right) \right] = \frac{N^4}{6}+N^3+\frac{5N^2}{6}, \end{aligned}$$

(22)

where the number of combinations of size k with repetition in a given set of size n is the multiset number:

$$\begin{aligned} \left( \left( \genfrac{}{}{0.0pt}{}{n}{k}\right) \right) = \left( {\begin{array}{c}n+k-1\\ k\end{array}}\right) =\frac{(n+k-1)!}{k!\,(n-1)!}, \end{aligned}$$

where the binomial coefficient is

$$\begin{aligned} \left( {\begin{array}{c}n\\ k\end{array}}\right) =\frac{n!}{k!\,(n-k)!} \end{aligned}$$

and $\bullet !$ is the factorial of integer $\bullet$. Equation (22) shows that the computational burden increases with the power four of N. Figure 1 gives the evolution of $N_\mathrm{c}$ as a function of N. One has to notice that the number of static computations necessary to obtain the $N_\mathrm{c}$ coefficients is much less than $N_\mathrm{c}$: In Eq. (20), computing solely the two vectors $f_\text {nl}(\pm \lambda \varvec{\varPhi }_\alpha )$ leads to obtain the 2N coefficients $a_{\alpha \alpha }^r$ and $b_{\alpha \alpha \alpha }^r$ with $r=1,\ldots N$.

Fig. 1

Order of coefficients of the ROM as a function of the number N of modes in the expansion basis. ‘$\circ$’: $N_\mathrm{c}$ from Eq. (22); “$\bigtriangleup$,” “$\bigtriangledown$,” “$\triangleright$,” “$\triangleleft$”: $N'_c$ from Eq. (24), with $N=N_u+N_w$ and with, respectively, $N_u=N_w$, $N_u=2N_w$, $N_u=5N_w$ and $N_u=10N_w$

3.3 Significant coefficients for flat structures

As stated in the previous section, the number of coefficients $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ greatly increases with the number N of retained modes in the reduction basis. A question arises naturally: Does all the coefficients have the same impact on the nonlinear dynamics of the structure, or, to begin with, is there some of the coefficients that are simply zero ? To precise this idea, we compare the present finite element formulations with the analytical models of flat structures described in Sect. 2.

Since the structures under consideration are flat, the bending and in-plane motion are uncoupled at the linear stage and their modes $\varvec{\varPhi }_r$ [solutions of eigenproblem (17)] are either pure bending modes $\varvec{\varPhi }_r^{(w)}$ or pure in-plane modes $\varvec{\varPhi }_r^{(u)}$. It is then possible to separate them in the modal basis, which is now written $\{\varvec{\varPhi }_1^{(w)},\ldots \varvec{\varPhi }_{N_w}^{(w)}, \varvec{\varPhi }_1^{(u)},\ldots \varvec{\varPhi }_{N_u}^{(u)}\}$ with $N_w$ and $N_u$ the number of bending and in-plane mode, respectively. In practice and in the case of plate/shell/beam finite elements, these modes can be calculated separately in most finite element codes, by separating the degrees of freedom involved in bending and in in-plane. This approach considerably reduces the computation time of in-plane modes which are located at higher frequency than bending modes.

Table 1 Nonzero coefficients $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ of nonlinear terms for flat structures as a function of the type (bending $\varvec{\varPhi }_r^{(w)}$ or in-plane $\varvec{\varPhi }_r^{(u)}$) modes involved

Then, since the results obtained in Sect. 2 for analytical models of flat plates are valid for any flat structure with an arbitrary edge geometry, reduced-order model (7) can be identified to the one obtained with present finite element formulation (18), showing that a large number of coefficients $a_{\alpha \beta }^r$ and $b_{\alpha \beta \gamma }^r$ are in fact zero for flat structures. More precisely, it depends on the values of $\alpha$, $\beta$ and $\gamma$ that correspond to a bending mode $\varvec{\varPhi }_r^{(w)}$ or a in-plane mode $\varvec{\varPhi }_r^{(u)}$. Table 1 gathers those results.

As a consequence, we rewrite the finite element ROM of Eqs. (18) by separating the modal coordinates into bending ones and in-plane ones and keeping only nonzero nonlinear coefficients. For this, indices $i,j,k,l\in \{1,\ldots N_w\}$ will refer to bending coordinates (BC), whereas $p\in \{N_w+1,\ldots N_w+N_u\}$ will refer to in-plane coordinates (MC). One obtains:

$$\begin{aligned}&\text {BC:}\quad \underset{1,\ldots N_w}{\forall k} \quad&\ddot{q}_k + \omega _k^2 q_k +\sum _{p=N_w+1}^{N_w+N_u} \sum _{i=1}^{N_w} a_{pi}^k q_i q_p \nonumber \\&\quad&\quad + \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} b_{ijl}^k q_i q_j q_l = Q_k, \end{aligned}$$

(23a)

$$\begin{aligned}&\text {MC:}\quad \underset{N_w+1,\ldots N_w+N_u}{\forall p} \quad&\ddot{q}_p + \omega _p^2 q_p + \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} a_{ij}^p q_i q_j = Q_p, \end{aligned}$$

(23b)

which is a set of oscillators of the same form than the one obtained for analytical models (Eqs. (7)).

The number of nonzero coefficients to be computed with this approach is:

$$\begin{aligned} N_\mathrm{c}'&=N_w\left[ N_wN_u + \left( \left( \genfrac{}{}{0.0pt}{}{N_w}{3}\right) \right) \right] + N_u\left( \left( \genfrac{}{}{0.0pt}{}{N_w}{2}\right) \right) , \nonumber \\&= \frac{N_w^4}{6}+\frac{N_w^3}{2}+\frac{3N_w^2N_u}{2}+\frac{N_w^2}{3}+\frac{N_uN_w}{2}. \end{aligned}$$

(24)

In practice—it will be discussed in Sects. 4, 5 and 6—one often includes a larger number of in-plane modes than transverse ones in the modal basis, which means $N_w \ll N_u$. To illustrate this point, Fig. 1 shows $N'_c$ as a function of the number of modes in the ROM expansion basis $N=N_u+N_w$, for several values of $N_u$ as a function of $N_w$ ($N_u=iN_w$ with $i\in \{1,2,5,10\}$). To illustrate the gain in the number of coefficients to be computed, $N_\mathrm{c}$ as a function of N, from Eq. (22), is also plotted in Fig. 1. One can observe that the number $N_\mathrm{c}$ of coefficients to be computed in the present approach can be largely reduced. Moreover, for a given modal basis size $N=N_u+N_w$, the number of coefficients $N'_c$ to be computed largely decreases with the ratio $i=N_u/N_w$. In addition, as shown in “Appendix E”, the required number of static computations $N'_{\text {sc}}$ is one order of power smaller than $N'_c$:

$$\begin{aligned} N'_\text {sc} = \frac{N_w^3}{6}+\frac{N_w^2}{2}+\frac{N_w}{3}+N_uN_w. \end{aligned}$$

(25)

In practice, $N_\mathrm{c}$ can be reduced to a factor of about 1000 if $N_u=10N_w$. For instance, if 4 transverse modes and 40 in-plane modes are retained ($N_w=4$, $N_u=40$) and the total number of modes is $N=44$, the total number of coefficients is $N_\mathrm{c}$ = 711,480, which becomes $N'_c=1120$ by considering only the nonzero coefficients, with a requirement of only $N'_\text {sc}=180$ static computations.

3.4 Condensation of the in-plane coordinates

A further simplification of the finite element ROM can be obtained. In the same way than what was done for analytical models (Sect. 2), if the in-plane inertia is neglected and if no in-plane forcing is applied, the in-plane coordinates are found to be quadratically linked to the transverse oscillators by Eq. (23b), for all $p=1,\ldots N_u$:

$$\begin{aligned} q_p = -\frac{1}{\omega _p^2} \sum _{j=1}^{N_w} \sum _{l=j}^{N_w} a_{jl}^p q_j q_l. \end{aligned}$$

(26)

The above in-plane coordinates can thus be condensed in transverse oscillators (23a), to obtain the following set of equations:

$$\begin{aligned} \ddot{q}_k&+ \,\omega _k^2 q_k - \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} \sum _{l=j}^{N_w} \left( \sum _{p=N_w+1}^{N_u+N_w} \frac{a_{pi}^k a_{jl}^p}{\omega _p^2} \right) q_i q_j q_l \nonumber \\&+ \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} b_{ijl}^k q_i q_j q_l = Q_k \end{aligned}$$

(27)

which leads to:

$$\begin{aligned} \ddot{q}_k + \omega _k^2 q_k + \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} \varGamma _{ijl}^{k} q_i q_j q_l = Q_k, \end{aligned}$$

(28)

where the coefficients of the cubic terms are defined in accordance with the upper triangular form chosen for the above equation, with $l>j>i$:

$$\begin{aligned}&\varGamma _{iii}^{k} = b_{iii}^k - \sum _{p=N_w+1}^{N_u+N_w} \frac{a_{pi}^k a_{ii}^p}{\omega _p^2},&\quad \forall k,i \end{aligned}$$

(29a)

$$\begin{aligned}&\varGamma _{iij}^{k} = b_{iij}^k - \sum _{p=N_w+1}^{N_u+N_w} \frac{\big (a_{pi}^k a_{ij}^p + a_{pj}^k a_{ii}^p \big )}{\omega _p^2}&\quad \forall k,i,j>i \end{aligned}$$

(29b)

$$\begin{aligned}&\varGamma _{ijj}^{k} = b_{ijj}^k - \sum _{p=N_w+1}^{N_u+N_w} \frac{\big (a_{pi}^k a_{jj}^p + a_{pj}^k a_{ij}^p \big )}{\omega _p^2}&\quad \forall k,i,j>i \end{aligned}$$

(29c)

$$\begin{aligned}&\varGamma _{ijl}^{k} = b_{ijl}^k - \sum _{p=N_w+1}^{N_u+N_w} \frac{\big (a_{pi}^k a_{jl}^p + a_{pj}^k a_{il}^p + a_{pl}^k a_{ij}^p\big )}{\omega _p^2},&\quad \forall k,i,j>i,l>j \end{aligned}$$

(29d)

ROM (28), valid if the in-plane inertia is neglected, is the most reduced since it involves only transverse coordinates, with all the in-plane motion embedded in the cubic coupling terms. It is also the most natural since it is very similar to classical linear modal models in which one considers only transverse modes. The issue of truncation of this model remains, but has been simplified since the choice of the in-plane modes to keep in the basis has been solved by the condensation.

Table 2 Mesh, geometrical and mechanical characteristics of the finite element beam and plate test cases

Table 3 Order of appearance in the basis (#), eigenfrequencies and shapes of the first transverse and axial modes for the clamped–clamped beam. The axial mode shapes are shown with arrows showing the in-plane vector field corresponding to $\varvec{\varPhi }_p^{(u)}$, with colors related to their length

Table 4 Label, number of appearance in the basis (#), eigenfrequencies and shapes of the first transverse and in-plane modes for the clamped circular plate. The in-plane mode shapes are shown with arrows showing the in-plane vector field corresponding to $\varvec{\varPhi }_p^{(u)}$, with colors related to their length. The labels of the transverse modes are a doublet (k, n) with k the number of nodal diameters and n the number of nodal circles

4 Validation on beam and plate test cases

4.1 Definition of the two test cases

In order to test the finite element reduced-order modeling procedure of Sect. 3, two test cases have been selected, for which analytical solutions are at hand with the models of Sect. 2. Those two test cases are described in Table 2: a clamped–clamped straight beam of length L and uniform rectangular cross section of width b and thickness h and a clamped circular plate of radius R and thickness h, both made in a homogeneous and isotropic material of Young’s modulus E, Poisson’s ratio $\nu$ and density $\rho$. The numerical values of those parameters used for the computations are given in Table 2, even if they have no influence on the final results since, as stated in Sect. 2.3, they depend only on the shape of the plate (rectangular and circular in our cases) and the boundary conditions.¹ For this reason, only dimensionless results are given in the following. The open-source finite element software Code_Aster [61] has been used for all computations of the present article, with DKQ four-noded shell elements with large rotation geometrical nonlinearities (GROT_GDEP option).

The reduction basis consists of $N_u$ in-plane modes and $N_w$ bending modes, with a total of $N=N_w+N_u$ linear modes (LMs) kept in the ROM of Eq. (18). The first transverse and in-plane LMs of the two test cases, solutions of eigenproblem (17), are shown in Tables 3 and 4 . Since one of the purpose of the present study is to evaluate the effect on the ROM quality of the in-planes modes kept in the reduced basis, a more larger number of in-plane than transverse LMs is took into account, as shown in Table 5.

4.2 Numerical validation of significant coefficients

The purpose of this section is to numerically validate the results of Sect. 3.3 in which structures with a flat geometry are considered. The results presented in this paragraph were computed on the clamped beam, with a discretization consisting of 100 element in the length and 4 element in the width of a beam (see the mesh in Table 2), and maximum of modal amplitudes for the static nonlinear STEP computations fixed at

$$\begin{aligned} \lambda _r \underset{i}{\max }|[\varvec{\varPhi }_r]_i|=h/20, \end{aligned}$$

(30)

with $r = \{ \alpha , \beta , \gamma \}$ (see Sect. 3.2) and $[\varvec{\varPhi }_r]_i$ the ith displacement² component of vector $\varvec{\varPhi }_r$ In order to validate the numerical values of coefficients of nonlinear terms obtained with the STEP, they are compared to those obtained by the analytical model of Sect. 2.1 (the numerical values of some of them are given in Table 9). Since the coefficients value depend on the mode shapes normalization, the same normalization must be applied to both FE and analytical mode shapes. For this, the following dimensionless parameters are defined and applied to the FE model:

$$\begin{aligned} \bar{\varvec{x}} = \frac{\varvec{x}}{x_r} , \quad {\bar{t}} = \frac{t}{t_0} \quad \bar{\varvec{\varPhi }}_r=\upsilon _r \varvec{\varPhi }_r, \end{aligned}$$

(31)

Table 5 Modal basis of the two test cases for which the coefficients of the ROMs are computed

Table 6 Comparison of nonlinear stiffness coefficient estimations with one bending mode $\varvec{\varPhi }_1 = \varvec{\varPhi }_{1}^{(w)}$ and two axial modes $\varvec{\varPhi }_2 = \varvec{\varPhi }_{1}^{(u)}$ and $\varvec{\varPhi }_3 = \varvec{\varPhi }_{2}^{(u)}$

where $x_r$, $t_0$ are defined in the same way than for analytical models (Eq. (2)): $x_r=h$ (resp. $x_r=h^2/L$) for the components of $\varvec{x}$ related to transverse (resp. in-plane) motion; $t_0=L^2\sqrt{\rho S/EI}$. The mode shape scaling $\upsilon _r$ is chosen to obtain the same maximal amplitude for the analytical and FE mode shapes. Introducing those parameters into Eq. (16,18) leads to replace them by identical ones that now depend on scaled modal coordinate ${\bar{q}}_r$ and coefficients ${\bar{a}}_{\alpha \beta }^r$ and ${\bar{b}}_{\alpha \beta \gamma }^r$, defined by:

$$\begin{aligned}&{\bar{q}}_r = \frac{q_r}{\upsilon _r x_r},\quad {\bar{a}}_{\alpha \beta }^r = t_0^2 \frac{x_\alpha x_\beta }{x_r}\frac{\upsilon _\alpha \upsilon _\beta }{\upsilon _r} \,a_{\alpha \beta }^r ,\nonumber \\&\quad {\bar{b}}_{\alpha \beta \gamma }^r = t_0^2 \frac{x_\alpha x_\beta x_\gamma }{x_r}\frac{\upsilon _\alpha \upsilon _\beta \upsilon _\gamma }{\upsilon _r} \,b_{\alpha \beta \gamma }^r . \end{aligned}$$

(32)

The two formulations are compared by analyzing the coupling coefficients of an expansion basis composed of three modes of the beam: the first transverse mode and the first two axial modes (in Table 3: mode 1 of the first column and modes 1,2 of the second column). Table 6 gathers the results. It shows that the estimation of the coefficients from the two formulations (FE with the STEP and analytic (u, w) – formulation, see “Appendix A” for details) is equivalent. In particular, the coefficients computed by the STEP that should be nonzero according to the theory of Sect. 3.3 are accurately obtained with at least 3 identical digits. For those that should be zero, values less than $10^{-10}$ are obtained. One can notice that the analytical model shows that some coefficients $G_{ij}^p$ and $C_{pi}^k$ are zero: This is due to the chosen modes and the symmetry properties of the structure.

4.3 Sensitivity of the coefficients to the finite element discretization

Fig. 2

Convergence of the first eigenfrequencies $\omega _k$ (left) and of the cubic coefficients $D_{kkk}^{k}\equiv b_{kkk}^k$ (right) as a function of the number of FE in the length of the beam, computed by the FE model and normalized by their theoretical values obtained with the analytical (u, w) beam model of Sect. 2.1. Clamped–clamped beam FE model

In this section, we analyze the convergence of the numerical values of the coefficients computed by the STEP as a function of the FE mesh refinement. Figure 2 shows the convergence of (a) the eigenfrequencies $\omega _k$ and (b) the cubic coefficient $D_{kkk}^k\equiv b_{kkk}^k$, for $k=1\ldots 5$, computed with the FE code, as a function of the number of finite elements in the length of the beam. While the first eigenfrequencies are fastest converging toward the analytic ones, the convergence of the numerical estimations of cubic coefficients $D_{kkk}^k$ is slower. A non-monotonic convergence of the coefficients is also noticed. It could be explained by the dependency of the nonlinear coefficients to the nodal force evolution along the axial direction, governed in the case of the beam by Eq. (44b): The zeros of the internal axial force would match the number of nodes of the mesh to be correctly approximated. Those tendencies are found identical to the one noticed in [34] in the case of a beam with a Euler–Bernoulli kinematics.

4.4 Sensitivity of the coefficients to the modal displacement amplitude

Fig. 3

Sensitivity of cubic coefficient $D_{kkk}^{k}\equiv b_{kkk}^k$ to the maximal prescribed transverse displacement of mode i (left) and of quadratic coefficient $C_{pi}^i\equiv a_{pi}^i$ to the maximal prescribed axial displacement of mode p (right). Clamped–clamped beam FE model

As explained in Sect. 3.2, the computation of the coefficients $a_{ij}^k$ and $b_{ijl}^k$ depends on free parameters $\lambda _r$, $r=\alpha ,\beta ,\gamma$, which are theoretically arbitrary, but that have to be chosen in practice. From a physical point of view, $\lambda _r$ governs the amplitude of the prescribed displacements of Eqs. (19), (21), which have to be chosen with an amplitude able to activate the geometrical nonlinearities of the stiffness part of the model. In particular, if $\lambda _r$ is too small, the nonlinear part $\varvec{f}_\text {nl}(\varvec{x})$ of Eq. (15) would be negligible with respect to the linear one $\varvec{K}\varvec{x}$ and linear system (20) would be badly conditioned, the values of $a_{ij}^k$ and $b_{ijl}^k$ depending on divisions of 0 by 0.

Fig. 4

Evolution of nonlinear beam cubic coefficients $\varGamma _{iii}^i$ with regard to the number of axial modes retained in the summations of Eqs. (29a), for the first six transverse modes of the beam (1st column of Table 3, $i=1,\ldots 6$)

To verify this point, Fig. 3 shows the evolution of some typical quadratic and cubic coefficients as a function of $\lambda _r$. More precisely, measures of the amplitude of the prescribed displacement are defined as $w_\text {max},u_\text {max}=\max (\lambda _r\varvec{\varPhi }_r)$ with $\varvec{\varPhi }_r$ being, respectively, a bending mode³ or an in-plane mode, scaled by the thickness h of the structure: $w_\text {max}/h$, $u_\text {max}/h$. According to Fig. 3 (left), the coefficients $D_{iii}^i\equiv b_{iii}^i$ are merely constant on a large range of displacement. For very small transverse amplitudes ($w_\text {max}/h<10^{-4}$), the estimated coefficients present a random variation, probably due to the fact that nonlinearities are not activated enough. On the contrary, if displacements are too large ($w_\text {max}/h>100$), estimated values of nonlinear coefficients are underestimated, in a smooth tendency. This can be explained by considering that expansion (18), which includes quadratic and cubic terms only, is exact for moderate rotation models of the von Kármán type, as shown in Sect. 2. Those von Kármán models are known to be valid for moderate transverse amplitudes, of the order of the thickness h of the structure. On the contrary, the FE used for the STEP includes a large rotation formulation (the GROT_GDEP option is used in Code_Aster; see Sect. 4.1), valid for any displacement amplitude, that would activate geometrical nonlinearities of a higher order than 3, not included in the model of Eq. (18).

In the case of coefficients $C_{pi}^i\equiv b_{pi}^i$ [Fig. 3(right)], which involves both axial and bending modes, there is also an accuracy plateau that cease to exist for $u_\text {max}/h\simeq 10$. Above this critical amplitude, an erratic behavior is observed, which can probably be explained by observing that this critical amplitude is very large (ten times the thickness h of the beam), since the axial motion is physically one order of magnitude in h / L smaller than the transverse motion.

Those numerical experiments tend to show that the thickness h of the structure is the average order of magnitude of proper values of $w_\text {max}$ and $u_\text {max}$. Consistently to these results, modal displacements amplitudes will thereafter be chosen as 1 / 20 of the thickness of the investigated structures (Eq. (30)).

Fig. 5

Evolution of nonlinear plate cubic coefficients $\varGamma _{iii}^i$ with regard to number of in-plane modes retained in the summations of Eqs. (29a), for the six transverse modes of the 1st column of Table 4, $i=1,2,4,6,15,30$

4.5 Convergence of the cubic coefficients and in-plane motion condensation

As explained in Sect. 3.4, the in-plane/bending coupling inherent to the correct simulation of the geometrical nonlinearities in thin structures can be included in the cubic $\varGamma _{ijl}^k$ coefficients, which depend on the quadratic coefficients $a_{pi}^k$ and $a_{ij}^p$ associated with the in-plane modes of the expansion basis of the ROM, as defined by Eqs. (29a–d). In this section, we analyze the convergence of the numerical values of some typical $\varGamma _{ijl}^k$ with the number of in-plane modes retained in the summations of Eqs. (29a–d). The two test structures of Table 2 are considered here with the reference numerical values of the $\varGamma _{ijl}^k$ coefficients, from the analytical models of Sect. 2, given in Table 10.

Figure 4, in the case of the clamped–clamped beam, and Fig. 5, in the case of the clamped circular plate, highlight that a set of in-plane LMs are needed to converge to a nearly constant value of coefficients $\varGamma _{iii}^i$. It indicates also which of these oscillators participate in the nonlinear response of the structure. Thus, in the case of the beam, it is possible to associate a given transverse mode to a set of axial LMs, thus giving an indication of which axial modes are nonlinearly linked to a particular bending mode at large amplitude. Indeed, Fig. 4 shows that the first bending mode is mainly linked to the fourth axial mode, the second bending mode is notably associated with the second, fourth and sixth axial ones, whereas the third bending mode is linked to the second, sixth and eight axial modes. For higher orders, the convergence could be nearly reached by retaining only two axial modes in the condensation. Figure 4 also shows that the second axial mode has an effects on all cubic coefficient $\varGamma _{iii}^i$, although for some of them it could be considered as negligible. In the case of the plate, analogous results can be drawn by analyzing Fig. 5.

Since Figs. 4 and 5 show coefficients $\varGamma _{iii}^i$ computed with the STEP normalized by their analytical value (obtained by Eq. (10) and given in “Appendix D”), one can notice that the STEP has a tendency to underestimate the values of the coefficients, since the asymptotic value in Fig. 4 is slightly smaller than 1, the more and more as the order of the involved modes is increasing. It can be due to the mesh refinement, which is correct for low-order modes with a large wavelength and that brings errors for higher-order modes with a smaller wavelength.

Notice that this condensation has always the effect of decreasing the absolute value of the cubic coefficients by taking into account the contribution of in-plane modes. In the case of the beam, most of the time, more than one axial mode has a significant effect on the transverse motion, except in the case of the first bending mode. This holds true as well for the circular plate—see Fig. 5—whose modal convergence needs more in-plane modes because of the strong density of asymmetric LMs.

5 Dynamical responses of structures

5.1 Solving of the nonlinear system

A continuation method is used to compute the dynamical response of reduced-order model (28). The continuation method used in this text is the asymptotic numerical method (ANM) coupled to the harmonic balance method (HBM) [62], implemented in the software Manlab [63]. For this, the system is first rewritten in the state space. Secondly, a quadratic form is used, which considerably improve the performance of the continuation procedure. By introducing the state variable $v_k = {\dot{q}}_k$ and the product of two modal coordinates $S_{ij} = q_i q_j$, $j\ge i$, set (28) is replaced by:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \dot{q_k} = v_k \\ \displaystyle \dot{v_k} = Q_k{-} \omega _k^2 q_k {-} 2\xi _k\omega _k v_k {-}\varepsilon \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} \varGamma _{ijl}^k S_{ij} q_l \\ \displaystyle 0 = S_{ij} - q_i q_j \end{array} \right. \end{aligned}$$

(33)

with all the unknowns gathered in the following unknown vector:

$$\begin{aligned}&\varvec{u} = \big [q_1 q_2 \ldots q_{N_w} v_1 v_2 \ldots \nonumber \\&\qquad v_{N_w} S_{11}S_{12}\ldots S_{N_w N_w}\big ] \end{aligned}$$

(34)

A linear modal damping terms of factor $\xi _k$ has been added in the model.

Periodic solutions of this system are computed. Following the HBM, $\varvec{u}$ is expanded in Fourier series:

$$\begin{aligned} \varvec{u}(t) = \varvec{u}_0+\sum _{h=1}^H \big [ \varvec{u}_h^c \cos (h \varOmega t) + \varvec{u}_h^s \sin (h \varOmega t) \big ] \end{aligned}$$

(35)

where $\varOmega$ is the angular frequency of the periodic motion. Introducing the above equation into (33), one obtains an algebraic quadratic system:

$$\begin{aligned} \varvec{R}(\varvec{U},\varOmega )=0, \end{aligned}$$

(36)

where

$$\begin{aligned} \varvec{U}=\big [\varvec{u}_0\;\varvec{u}_1^c\;\varvec{u}_1^s\ldots \varvec{u}_H^c\;\varvec{u}_H^s\big ], \end{aligned}$$

(37)

is the vector of unknowns that gathers all the Fourier components of the unknowns.

In the software Manlab [63] used for the computations, system (33) is given as input. Then, the application of the HBM to write algebraic system (36) is automatic and final algebraic system (36) is solved by the ANM, which computes $\varvec{U}$ and $\varOmega$ as Taylor series of a pseudo-arclength parameter a [62]:

$$\begin{aligned} \varvec{U}= & {} \varvec{U}_0+a\varvec{U}_1+\cdots +a^n\varvec{U}_n,\nonumber \\ \varOmega= & {} \varOmega _0+a\varOmega _1+\cdots +a^n\varOmega _n \end{aligned}$$

(38)

where n is the order of the series, chosen by the user ($n=20$ in the present study). Then, $(\varvec{U}_0,\varOmega _0)$ are solutions of a nonlinear algebraic system solved by a Newton–Raphson algorithm, whereas $\varvec{U}_i$, $i=1,\ldots ,n$ are solutions of a cascade of linear systems.

In this text, two kinds of computations are done:

• the first one is the free conservative response of the investigated system, i.e., the backbone curve of a given nonlinear mode (NNM), which means the system of Eqs. (33) with $Q_k = 0$ and $\xi _k=0 \quad \forall k \in \{ 1, ..., N_w \}$. In this case, as proposed in [64], a perturbation term $-\lambda v_k$ is added to the second line of Eq. (33) at each oscillator k, where $\lambda$ is an explicit continuation parameter, which enables to add a phase condition. According to [65], it ensures that the computed solutions are those of the unperturbed and conservative system of Eqs. (28) and (33). The phase conditions used in this work consist in setting to zero the sine component of the first harmonic of $q_i$ in (35) if the ith NNM is computed. Moreover, the initial Newton–Raphson algorithm (to compute $\varvec{U}_0$ in Eq. (38)) needs to be initialized in the vicinity of a given NNM. In this work, for the ith NNM, the unknowns are initialized on the corresponding linear mode: $q_i(t)=q_0\cos \omega _i t$, ${v_i(t)=-\omega _iq_0\sin \omega _i t}$, $S_{ii}=\frac{1}{2}(1+\cos 2\omega _i t)$, $\varOmega =\omega _i$ and all the other unknowns are set to zero. The amplitude $q_0$ is chosen small with respect to the plate thickness h.

• The second one is the harmonically forced response of the system, considering consistent values of $Q_k$ and $\xi _k$.

Fig. 6

Organization of the two bases of the ROMs for the circular plate computations: eigenfrequencies of the modes as a function of there number. a First basis and b second basis

The size of algebraic system (36) increases fast with the number of harmonics and transverse oscillators retained in the basis. In practice, there is generally no simplification allowing to neglect the coupling between two oscillators, which infers that all additional variables $S_{ij}$ must be included in $\varvec{u}$. Then, the size $N_s$ of the final unknown vector $\varvec{U}$ of a system with $N_w$ oscillators is given by:

$$\begin{aligned} N_s =(2H + 1) \left( 2N_w+\frac{N_w(N_w+1)}{2}\right) . \end{aligned}$$

(39)

5.2 Modal bases of the ROMs

Since condensed model (9) is used for the computations, the expansion basis has to be selected in two steps:

• firstly, one has to select a given set of $N_w$ transverse modes to be retained in ROM (9);

• secondly, one has to select a larger set of $N_u\gg N_w$ modes used to compute the quadratic coefficients $a_{pi}^k$ and $a_{ii}^p$ necessary for the estimations of the cubic coefficients $\varGamma _{ijl}^k$ (see Eqs. (28)) with the condensation of the in-plane motion into the bending motion.

In the results presented in the next paragraphs and figures, we assume that all cubic coefficients $\varGamma _{ijl}^k$ have attained convergence with a suitable number $N_u$ of in-plane modes. Those computations are made offline before the computation of the dynamical response with Manlab.

Fig. 7

Maximum amplitude of the transverse displacement of the periodic response of the beam (left) and circular plate (right) around their first NNM. The x-axis is scaled by the first eigenfrequency $\omega _1$ of the structure. Free response in black and forced responses in color. The responses are computed at $x=L/\pi$ and with modal dampings $\xi _k = 2\%$ for the beam, and at $r = 0.5461$ and with modal dampings $\xi _k = 5\%$ for the plate. $H=10$ harmonic components are used for the computations

Fig. 8

Backbone curve of the first four NNMs of the clamped–clamped beam in a frequency energy plot. The internal resonance (IR) tongues are labeled, and the backbones of the associated NNMS are plotted in gray dashed lines as a function of their divided frequency (for a 1 : n IR, the associated NNM is plotted as a function of $\varOmega /n$)

For the beam examples, the basis composed of the first 10 bending modes has been used. For the circular plate simulations, one has to consider that asymmetric modes appear in pair in the basis (so-called companion modes). Three different bases are used, in regard to possible modal interactions between axisymmetric and companion asymmetric modes. The first modal basis is presented in Fig. 6a and is composed of the first 5 axisymmetric modes; the second one includes the two first pairs of asymmetric modes (4 modes) also shown in Fig. 6a; the third one is composed of the first 12 LMs of the circular plate, but includes only one of the companion modes associated with each asymmetric mode shape, as shown in Fig. 6b.

5.3 Nonlinear normal modes and forced responses

A useful property of NNM is that all nonlinear forced responses of the system are distributed around the computed free undamped response. This is illustrated in Fig. 7 which presents the forced responses of the clamped beam and the clamped circular plate around their first NNM.

More precisely, a point harmonic excitation at location $\varvec{\zeta }$ of amplitude F and frequency $\varOmega$ has been selected, for which the value of the modal forcing in Eqs. (28), (33) is

$$\begin{aligned} Q_k=\varPhi _k(\varvec{\zeta })P\cos (\varOmega t). \end{aligned}$$

(40)

where $\varPhi _k(\varvec{\zeta })$ is the transverse modal amplitude at location $\varvec{\zeta }$. The forced response of the beam is computed with a damping value of each LMs fixed at $\xi _k = 2\%$ and the excitation point chosen at $x=L/\pi$, such that all LMs are involved in the displacement response. For the plate, the damping values are $\xi _k = 5\%$ and the excitation point is located at $r = 0.5461$.

A tongue is noticeable on the free response of the two structures. It corresponds to 1:5 and 1:7 internal resonances, respectively, for the beam and the plate. This phenomena are not visible on the forced response, and it would appear if the dampings of the interacting LMs were reduced.

Figure 7 enables to draw generic results. As announced, the free response (also known as the NNM or the backbone curve) represents the skeleton of the dynamics since it connects all the forced responses at their resonance point. Since it is obtained in a single continuation, it appears to be an efficient way of characterizing the dynamics of the structure. In the following, the free responses of the beam and the plate are considered to analyze the behavior and the efficiency of the numerical method.

5.4 Nonlinear modes of the plane structures

Fig. 9

Backbone curve of the first four NNMs of the circular plate in a frequency energy plot. The internal resonance (IR) tongues are labeled, and the backbones of the associated NNMS are plotted in gray dashed lines as a function of their divided frequency (for a 1 : n IR, the associated NNM is plotted as a function of $\varOmega /n$)

In this section, we present an overview of the dynamical response of the clamped beam and the circular plate, through their first four NNMs, shown in Figs. 8 and 9 as frequency energy plots (FEP). In fact, NNMs are the free conservative oscillations of the structure (with $Q_k = 0$ and $\xi _k=0 \quad \forall k \in \{ 1, ..., N_w \}$ in Eqs. (33)), for which the mechanical energy ${\mathcal {H}}$ is an invariant at any given amplitude. Here, the energy can be written:

$$\begin{aligned} {\mathcal {H}} = \frac{1}{2} \sum _{k=1}^{N_w} \big (\dot{q}_k^2 + \omega _k^2 q_k^2 \big ) + {\mathcal {V}}_\text {nl} \end{aligned}$$

(41)

where ${\mathcal {V}}_\text {nl}$ denotes the nonlinear part of the energy defined in “Appendix F”. In practice, the backbone curves shown in Figs. 8 and  9 are computed with the ANM/HBM method (see Sect. 5.1) and ${\mathcal {H}}$ is computed in post-processing in the time domain, with the Fourier coefficients of $q_k$ and ${\dot{q}}_k$, by taking the mean value over one period of Eq. (41). $H = 10$ harmonic components are used for the computations. The 10 first LMs compose the reduction basis for the computation of the beam FEP (Fig. 8). For the plate FEP (Fig. 9), the first basis (Fig. 6a) is used for the axisymmetric NNMs (0,1) and (0,2), whereas the second one is used for the asymmetric ones (1,1) and (2,1).

All the NNMs show the same qualitative behavior. First, since both structures are plane, all the NNMs have a hardening behavior, which globally bends the backbone curves toward the high frequencies (indeed, the $\varGamma _{iii}^i$ coefficients are all positive; see “Appendix D”). Secondly, some internal resonances modify the topology of the backbone curve, which is described more precisely in the next section.

Fig. 10

Topology of the 1:5 internal resonance of NNM1 with NNM3 of the clamped–clamped beam. a Zoom of the FEP of Fig. 8 and b harmonics amplitude of NNM1 (H1 of LM1 in blue and H5 of LM3 in orange) and NNM3 (H1 of LM3 in gray dashed line, as a function of $\varOmega /5$)

Fig. 11

Topology of the 1:3 internal resonance of NNM2 with NNM4 of the clamped–clamped beam. a Zoom of the FEP of Fig. 8 and b harmonics amplitude of NNM2 (H1 of LM2 in blue and H5 of LM4 in orange) and NNM4 (H1 of LM4 in gray dashed line, as a function of $\varOmega /3$)

5.5 A focus on internal resonances

On the FEP of Figs. 8 and 9 , only simple internal resonances of the form 1:n with $n\in {\mathbb {N}}$ are observed. They are characterized by a strong coupling between two NNMs (the ith and the jth) when the following frequency relation is fulfilled:

$$\begin{aligned} \omega _{j\text {nl}}\simeq n \omega _{i\text {nl}}, \end{aligned}$$

(42)

where $\omega _{i\text {nl}}, \omega _{j\text {nl}}$ are the oscillation frequencies of the two involved NNMs, which are read on the x-axis of the FEP. This kind of internal resonance appears here in two distinct ways, which can be gathered in two families.

The first family gathers 1:n internal resonance that naturally appears at high energy levels because of the bending of the backbone curves. At low energy, $\omega _{i\text {nl}}$ and $\omega _{j\text {nl}}$ are close to the natural frequencies $\omega _i$ and $\omega _j$, which are far from fulfilling $\omega _j=n\omega _i$. Then, because of the bending of the backbones, the oscillations frequencies $\omega _{i\text {nl}}$, $\omega _{j\text {nl}}$ change and Eq. (42) is fulfilled at high energy. This kind of internal resonances always shows the same features, illustrated by Figs. 10 and 11:

• if an IR tongue emerges from the main backbone curve in the FEP, it is characterized in terms of frequency content by a transfer of energy between the first harmonics $q_{i1}$ (H1) of mode i and the nth harmonics $q_{jn}$ (Hn) of mode j.

• there is always a particular point on the IR tongue, close to its tip, for which Eq. (42) is an equality ($\omega _{j\text {nl}}=n \omega _{i\text {nl}}$). At this point, denoted B in Figs. 10 and 11 , the tongue of the ith NNM is connected to the backbone curve of the jth NNM. Precisely, it is the curve ${\mathcal {H}}=f(\omega _{i\text {nl}})$ that is connected to the curve ${\mathcal {H}}=f(\omega _{j\text {nl}}/n)$, shown in gray dashed line in Figs. 8, 9, 10 and 11 .

• when following the tongue from its emergence from the ith backbone (point A) to point B, a transfer of energy is observed from the first harmonics of mode i to the nth harmonics of mode j. Indeed, the latter increases while the former decreases, giving a continuous change of the dynamics between mode i oscillating at $\varOmega$ and mode j oscillating at $n\varOmega$. At point B, mode i is zero and the dynamics only involves mode j oscillating at $n\varOmega$.

• since the observed internal resonances tongues are with n odd, they naturally emerge from the main backbone without any bifurcation point.

Fig. 12

Topology of the 1:1 internal resonance of NNM2 with companion NNM3 of the circular plate. First harmonics amplitude of NNM2 and NNM3 for the two branches, the

The second family gathers the 1:1 internal resonances observed in the backbone curves of the asymmetric modes of the circular plate (modes (1,1) and (2,1) of Figs. 9 and 12), for which the natural frequencies of the companion modes are naturally tuned and fulfill Eq. (42). In this case, well documented in [19, 66], the backbone curve of one of the companion modes becomes unstable after a pitchfork bifurcation (denoted by PF in Fig. 12), appearing at very low energy. It gives rise to a new branch, for which both companion modes have nonzero energy and oscillate with a quadrature phase shift, giving rise to a traveling wave.

On the FEPs of Figs. 8 and 9 , the internal resonances are labeled as “1:n IR,” with the mode in interaction specified by “NNMj$\varOmega /n$.” For instance, the first NNM of the beam shows a 1:5 internal resonance with the third NNM.

Fig. 13

Convergence with the number of harmonic components of the free responses of the beam around its first NNM. Maximum amplitude of the transverse displacement of the periodic response computed at $x=L/\pi$ with $N_w=10$ transverse LMs. The x-axis is scaled by the first eigenfrequency $\omega _1$ of the beam

5.6 Convergence with the number of harmonic components

Figure 13 presents the free response of the beam around its first NNM with a varying number of harmonic components retained in the Fourier series expansion of Eq. (35), with a converged (see next section) number of transverse modes [$N_w=10$ in Eqs. (28), (33)] retained in the ROM basis. It shows that $H=3$ harmonics are sufficient to predict correctly the backbone curve anywhere out of the internal resonance tongue. One would have expect that $H=1$ harmonics would have been sufficient with the HBM, whereas $H=3$ is necessary here. This can be explained by the quadratic recast imposed by the HBM (see Eq. (33)), which imposes the introduction of the quadratic variables $S_{ij}$ which need at least two harmonics to accurately embed the nonlinear response.

When more harmonics are retained, the free response changes only with the apparition of the internal resonance. In this case, since it is a 1:5 internal resonance, at least $H=5$ harmonics are necessary to correctly compute it.

Fig. 14

Modal convergence with the number of transverse modes of the free responses of the beam around the a first, b second and c third NNMs of the beam. Maximum amplitude of the transverse displacement of the periodic response computed at $x=L/\pi$ with $H=10$ harmonic components. The x-axis is scaled by the first eigenfrequency $\omega _1$ of the beam

5.7 Modal convergence of NNMs

We investigate now the convergence of the computation of the free response of the first NNMs of the beam and the plate as a function of the number of modes retained in the ROM basis. For the first NNM of the clamped beam, Fig. 14a shows that a correct computation is obtained with only the first oscillator—the first LM of the clamped beam—for a range of transverse displacements w until half the thickness h. The contribution of the second LM is negligible, whereas the effect of the third LM is significant on a larger range of displacement. The convergence of the backbone curve is thus achieved with the first and third linear modes only. The internal resonances need to retain the LMs interacting with the first oscillator: Indeed, the second internal resonance involves here a LM of higher order than the third and then cannot be computed with three oscillators. The second NNM shows analogous results. The third NNM needs to take more LMs into account to limit the error in comparison with the reference solution, as shown in Fig. 14c. Adding an oscillator to the system has either a softening or an hardening effect on the response: It is associated with the sign of the nonlinear coefficients $\varGamma$ which involve the retained LMs. In particular, the LMs of lower order than the computed NNM must be retained in the basis: The softening effect of the first oscillator on the third NNM cannot be neglected.

Fig. 15

Modal convergence with the number of transverse modes of the free responses of the circular plate around some NNMs: a first axisymmetric (0,1) (NNM 1), b second axisymmetric (0,2) (NNM 6) and c first asymmetric (1,0) (NNM 2). Maximum amplitude of the transverse displacement of the periodic response computed at $r = 0.5461$ with $H=3$ or $H=10$ harmonic components. The x-axis is scaled by the first eigenfrequency $\omega _1$ of the plate

In the case of the plate, the convergence is shown in Fig. 15 for the first two axisymmetric NNMs (mode (0,1) and mode (0,2)) and the first asymmetric one (mode (1,1)), by comparing several modal basis and $H = 3$ and $H=10$ harmonic components. As for the beam case, the reduction to only one oscillator is correct on a moderate range of displacements, the responses needing to include more LMs in the basis after a certain value of the displacements. One can notice that an example of modal interaction between axisymmetric and asymmetric modes is exhibited in the case of NNM (0,2) (Fig. 15b): The internal resonance which is noticeable here needs asymmetric modes in the basis to be obtained.

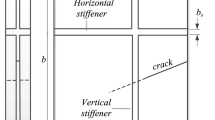
6 Nonlinear dynamics of a perforated plate

In this section, we test the proposed method on a plane structure with an original geometry, for which we want to compute the nonlinear dynamics. It has the form of a perforated rectangular plate with three rectangular holes that delineate two beams at the center, as shown in Fig. 16. The main parameters of the model are gathered in Table 7. The dimensions of this structure have been adjusted in order to obtain two linear modes (LM) which present mode shapes similar to those of the first LM of a clamped–clamped beam, respectively, with an in-phase and an out-of-phase motion between the two beams. This is verified by analyzing the modal basis of the structure, shown in Table 8, for which the 7th and 8th modes have the required shape. They are similar to the two first modes of a structure composed of two clamped–clamped beams connected by a linear spring of small stiffness. This particular structure has been selected to analyze and compute the nonlinear dynamics of those two beam-like modes and their bifurcation to a localized motion on one of the beams [67, 68].

Fig. 16

Geometry and mesh of the structure

Table 7 Parameters of the model

Table 8 Natural frequencies and shapes of the first twelve transverse LMs of the free perforated plate

Fig. 17

Evolution of the physical nonlinear coefficients $\varGamma _{iii}^i$ of the perforated plate in regard to the number of in-plane modes

Fig. 18

Scaled cubic coefficients $\varGamma _{ijl}^k$ of Eq. (43), for the clamped–clamped beam, as a function of k. (left) ROM with 4 bending modes $i,j,l,k\in \{1,\ldots 4\}$; (left) ROM with 16 bending modes $i,j,l,k\in \{1,\ldots 16\}$

6.1 Computation of the nonlinear coefficients of the ROM

Since the studied structure is a plate with a particular boundary, all the theory described in the present article can be applied. We then compute its nonlinear dynamics with the reduced-order model of Eq. (28) in which the $\varGamma _{ijl}^k$ includes the in-plane motion effect, which has been condensed thanks to Eqs. (29a–d). Only the nonzero coefficients $a_{ij}^k$ and $b_{ijl}^k$ are computed (see Table 1) with the STEP.

Figure 17 shows the convergence of the condensation of coefficients $\varGamma _{ijl}^k$ as a function of the number $N_u$ of in-plane modes retained in Eq. (29). This number has been chosen voluntarily high—1000 in-planes LMs— in order to discuss the convergence of cubic coefficients throughout the condensation. Although numerous in-plane modes are included in the modal basis, the evolution of the nonlinear cubic condensed coefficients presented in Fig. 17 seems to need more in-plane modes to converge toward a stable value. This could be explained by the high density of the platelike LMs. As for the beam and circular plate, the value of the coefficients decreases with the number of condensed in-plane LMs, which then have a softening effect on the nonlinear system. Notice that the ratio between the initial and final value of the cubic coefficients is greater than those of the beam and the plate. The low-order in-plane modes have a strong influence on the cubic coefficients related to platelike transverse modes. For the coefficients $\varGamma _{777}^7$ and $\varGamma _{888}^8$, there is a large range of in-plane LMs which does not influence the condensation.

6.2 Sorting and selection of the ROM coefficients

After those operations, the computation time of the nonlinear dynamics by the ANM/HBM is mainly sensitive to the number of nonlinear terms associated with coefficients $\varGamma _{ijl}^k$ in Eqs. (33). Among this set of cubic coefficients, many of them are still negligible. Consequently, an heuristic filtering procedure is applied. First, coefficients $\varGamma _{ijl}^k$ are scaled with Eqs. (31), (32), with $x_r=h$, $t_0=1/\omega _1$ and $v_r = 1$. Then, observing Eq. (32) naturally shows that the nonlinear coefficients are scaled by $t_0^2$, equivalent to the inverse of the square of a frequency and because $\varGamma _{ijl}^k$ depends on modes i, j, l, k, we propose to remove from system (28) all coefficients such that:

$$\begin{aligned} \frac{{\bar{\varGamma }}_{ijl}^{k}}{\sqrt{{\bar{\omega }}_i{\bar{\omega }}_j{ \bar{\omega }}_l{\bar{\omega }}_k}} < \epsilon ,\quad \text {with}\quad {\bar{\omega }}_i=\frac{\omega _i}{\omega _1}, \quad {\bar{\varGamma }}_{ijl}^k=\frac{h^2}{\omega _1^2}\varGamma _{ijl}^k. \end{aligned}$$

(43)

with the filtering criteria chosen as $\epsilon =10^{-3}$.

Fig. 19

Response of the two LMs reduced-order model. a Convergence as a function of the number of harmonics components of the modal coordinates $q_7$ and $q_8$ on the backbones of NNMs 7 and 8. b Maximal displacement of the periodic response of the center of the two beams (points $P_1$ and $P_2$ of Fig. 16)

To verify this scaling, Fig. 18 shows the application of this filtering process on the cubic coefficients of the clamped–clamped beam of Sects. 2 and 4 (see Table 10). First of all, one can observe that the scaling of Eq. (43) almost counterbalances the increasing the cubic coefficient with their order k: Coefficients $\varGamma _{kkk}^k$ are of the order of magnitude of 1 independently of k. Then, the other scaled coefficients decrease with the natural frequency distance between the involved modes i, j, l and k. With $\epsilon =10^{-3}$, a 1000 factor is kept between the higher and the smaller cubic coefficient. In this case, all beam coefficients for $i,j,l,k\in \{1,\ldots 4\}$ are kept, whereas the smallest of them are neglected for higher ranges of variation of i, j, l, k.

6.3 A two LMs reduced-order model

At first, a reduced-order model composed of the 7th and 8th oscillators only, associated with mode 7 and 8 of interest, has been selected. The two backbone curves of the corresponding NNMs are shown in Fig. 19 for an increasing number of harmonics. This plot shows the classical picture of a nonlinear localization of the motion. NNM7, of lower frequency, has a standard hardening backbone curve. On the contrary, NNM8 shows a pitchfork bifurcation that give birth to two branches on which the motion is a coupling between mode 7 and 8, which are associated with a localization of the motion on beam 1 or beam 2 (depending on the considered branch). A minimal number of three harmonic components in the harmonic balance formulation is necessary to reach convergence.

6.4 Convergence in terms of LMs

Fig. 20

Modal convergence with the number of transverse LMs retained in the basis, for NNMs 7 and 8. Displacements at the center of one of the beams

We now consider an enrichment of the 2 degrees of freedom basis of the previous section by including the first 16 transverse modes in the ROM basis. The Fig. 20 shows that this enrichment does not significantly change the geometry of the backbone curves but renders the computations tedious since more degrees of freedom are involved. It thus validates, in this case, the two LM model of the previous section.

7 Conclusion

In this paper, a complete procedure to compute the geometrically nonlinear frequency response of flat structures by using reduced finite element models has been proposed.

A study at the coefficient level has confirmed that a large part of the ROM coefficients are equal to zero, which enables to significantly reduce the computational burden of the stiffness evaluation procedure, in terms of number of coefficients to compute (and stock) and number of nonlinear static problems. The resulting reduced-order model can be further simplified by condensing the in-plane motion to the transverse one, such that only transverse modes coupled by cubic nonlinearities appear in the system. A convergence of the cubic coefficients is reached when a sufficient number of in-plane modes is retained. At this stage of the procedure, all coefficients of the ROMs of a straight beam and circular plate have been validated by a direct comparison with analytical models. It is shown that the ROM coefficient value is independent of the prescribed displacement amplitude on a large range, attesting the robustness of the method and providing some guidelines for the STEP. Moreover, an heuristic rule, to filter the significant ROM coefficients, is also provided. It is validated for flat structures and could be applied with no restriction to more complex geometries, extending the relevance of the present study.

An original coupling of the obtained nonlinear systems with a ANM-HBM following-path method allows to equally compute the forced as well as the free response of the plane structures. In accordance with previous studies, the distribution of the forced response around the free response and the backbone curve was attested with this method.

Finally, the computation of the free responses—also known as nonlinear modes—highlights many typical nonlinear phenomena as hardening behaviors and internal resonances. These latter can complexify the resolution procedure when too many oscillators and harmonics are retained in the reduced-order model, because of the computation of all modal interactions which occur between the retained oscillators. At each resonance, a very reduced model, where only one transverse oscillator is kept and with $H = 3$ harmonics, has been found sufficient to compute the backbone curves with a negligible error on an acceptable range of motion amplitude. In the case of a 1:1 internal resonance, in axisymmetric structures or linked to vibration localization, a model with only the two transverse modes involved in the internal resonance seems sufficient in a large range of amplitude.

Appendices

Appendix A: The beam (u,w) model

The beam model of Eq. (1) is here discussed. Using Hamilton principle, one obtained the classical equations of motion for the axial and transverse motion of the beam, which are:

$$\begin{aligned} \rho S \ddot{w} + EIw_{,xxxx} - \left( N w_{,x}\right) _{,x}&= p(x,t) \end{aligned}$$

(44a)

$$\begin{aligned} \rho S \ddot{u} - N_{,x}&= n(x,t). \end{aligned}$$

(44b)

where p(x, t) and n(x, t) are distributed transverse and in-plane forces per unit length and where the axial force in the beam is:

$$\begin{aligned} N=ES\left( u_{,x} + \frac{1}{2} w_{,x}^2\right) . \end{aligned}$$

(45)

Equations (45) and (44a, b) constitute the classical von Kármán model describing the transverse motion of a beam with geometrical nonlinearities [12, 15, 16]. Then, eliminating N between Eqs. (45) and (44a, b) leads to the (u, w) model of Eq. (1).

After the modal expansion of Sect. 2.1, the analytical expressions of the coefficients of nonlinear terms in Eq. (7a, b) are:

$$\begin{aligned} C_{pi}^k= & {} -\frac{\displaystyle {\int _0^1 (\varPsi _{p,x} \varPhi _{i,x})_{,x} \varPhi _{k} \,\text {d}x}}{\displaystyle {\int _0^1 \varPhi _k^2 \,\text {d}x}}, \nonumber \\ G_{ij}^p= & {} \frac{\displaystyle { \int _0^1 \varPsi _{p} \varPhi _{i,x} \varPhi _{j,xx} \,\text {d}x}}{\displaystyle { \int _0^1 \varPsi _p^2 \,\text {d}x}} \end{aligned}$$

(46a)

$$\begin{aligned} D_{ijl}^k= & {} - \frac{1}{2} \frac{\displaystyle { \int _0^1 (\varPhi _{i,x} \varPhi _{j,x} \varPhi _{l,x})_{,x} \varPhi _k\,\text {d}x}}{\displaystyle { \int _0^1 \varPhi _k^2 \,\text {d}x}}, \end{aligned}$$

(46b)

$$\begin{aligned} Q_k(t)= & {} \frac{\displaystyle { \int _0^1 \varPhi _k(x)p(x,t)\,\text {d}x}}{\displaystyle { \int _0^1 \varPhi _k^2 \text {d}x}},\nonumber \\ E_p(t)= & {} \frac{\displaystyle { \int _0^1 \varPsi _p(x)n(x,t)\,\text {d}x}}{\displaystyle { \int _0^1 \varPsi _p^2 \text {d}x}}. \end{aligned}$$

(46c)

The modes are here normalized as:

$$\begin{aligned} \int _0^1\varPhi _k^2(x)\,\text {d}x=\int _0^1\varPsi _p^2(x)\,\text {d}x=1. \end{aligned}$$

(47)

Table 9 Numerical values, computed with a trapezoidal rule, of some nonlinear coefficients of a the clamped–clamped beam model (Eqs. (46a, b)). Scaling of Eqs. (2) and mode normalization of Eqs. (47)

In the case of a clamped–clamped boundary conditions, the transverse mode shapes are solution of Eq. (6a) and can be written:

$$\begin{aligned} \varPhi _k(x)= & {} \kappa _k\left[ (\sin \beta _k-\sinh \beta _k)(\cos \beta _kx- \cosh \beta _kx)\right. \nonumber \\&\left. -(\cos \beta _k-\cosh \beta _k)(\sin \beta _kx-\sinh \beta _kx)\right] .\nonumber \\ \end{aligned}$$

(48)

with $\cos \beta _k\cosh \beta _k-1=0,\quad \omega _k=\beta _k^2$ for all $k>1$ and $\kappa _k$ is numerically computed to verify Eq. (47). The axial mode shapes are solutions of Eq. (6b) and can be written:

$$\begin{aligned} \varPsi _p(x)=\sqrt{2}\sin \gamma _px,\quad \gamma _p=p\pi . \end{aligned}$$

(49)

They naturally verify Eq. (47). The values of some of these coefficients are given in Table 9.

Appendix B: On the plate $(\varvec{u},w)$-formulation ROM

Some details about the analytical plate model of Sect. 2.2 are given here. The in-plane forces in the plate are represented by a two-dimensional tensor $\varvec{N}$, which, with the von Kármán assumptions, can be written [14]:

$$\begin{aligned} \varvec{N}= & {} A\left[ (1-\nu )\varvec{\epsilon }+\nu {\text {tr}}\varvec{\epsilon }\varvec{1}\right] ,\nonumber \\ \varvec{\epsilon }= & {} \frac{1}{2}\left( \varvec{\nabla }\varvec{u}+\varvec{\nabla }^{{\text {T}}}\varvec{u} + \varvec{\nabla }w\otimes \varvec{\nabla }w\right) \end{aligned}$$

(50)

where $\varvec{\epsilon }$ is the in-plane strain tensor, $A=Eh/(1-\nu ^2)$ is the in-plane stiffness of the plate, $\varvec{\nabla }$ denotes the vector/tensor gradients of scalar/vector fields, ${\text {tr}}$ is the trace of a tensor $\otimes$ is the tensor product of two vectors and $\varvec{1}$ is the identity tensor.

By eliminating $\varvec{N}$ between Eqs. (50) and (11a, b), one obtains the following $(\varvec{u},w)$-formulation:

$$\begin{aligned}&\rho h \ddot{w}+ D \Delta \Delta w {-} A \Big [ (1{-}\nu )\Big (\varvec{\nabla }\varvec{u}:\varvec{\nabla }\varvec{\nabla }w + \varvec{\Delta }\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad +\nu \Big ({\mathrm{div}}\,\varvec{u} \,\Delta w + \varvec{\nabla }{\mathrm{div}}\,\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad + \varvec{\nabla }w \cdot \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w + \frac{1}{2} (\varvec{\nabla }w)^2 \,\Delta w\Big ] = 0. \end{aligned}$$

(51a)

$$\begin{aligned}&\rho h \ddot{\varvec{u}} - \frac{A}{2}\Big [ (1-\nu ) \varvec{\Delta }\varvec{u} + (1+\nu ) \varvec{\nabla }{\mathrm{div}}\,\varvec{u} \nonumber \\&\quad +(1-\nu ) \Delta w \varvec{\nabla }w + (1+\nu ) \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w \Big ] = 0. \end{aligned}$$

(51b)

where  :  denotes the doubly contracted product of two tensors, $\varvec{\Delta }$ the vector Laplacian of a vector field and $\cdot$ the dot product.

With the following dimensionless variables:

$$\begin{aligned} {\bar{w}}= & {} \frac{w}{h} , \quad \bar{\varvec{r}} = \frac{\varvec{r}}{L} \quad {\bar{F}}=\frac{F}{Eh^3}, \nonumber \\ \varepsilon= & {} 12(1-\nu ^2),\quad {\bar{t}}=\frac{1}{L^2}\sqrt{\frac{D}{\rho h}}t,\quad {\bar{p}}= \frac{L^4}{Dh} p, \end{aligned}$$

(52)

$$\begin{aligned} {\tilde{\varepsilon }}= & {} \frac{Ah^2}{D}=\frac{\varepsilon }{1-\nu ^2}=12,\quad \mu = \frac{D}{AL^2},\nonumber \\ \bar{\varvec{u}}= & {} \frac{L}{h^2}\varvec{u},\quad \bar{\varvec{N}}=\frac{L^2}{Eh^3}\varvec{N}. \end{aligned}$$

(53)

where L is a characteristic dimension of the middle plane of the plate (its diameter for instance). The $(\varvec{u},w)$-formulation is then rewritten:

$$\begin{aligned}&\ddot{w} + \Delta \Delta w - {\tilde{\varepsilon }}\Big [ (1-\nu )\Big (\varvec{\nabla }\varvec{u}:\varvec{\nabla }\varvec{\nabla }w + \varvec{\Delta }\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad +\nu \Big ({\mathrm{div}}\,\varvec{u} \,\Delta w + \varvec{\nabla }{\mathrm{div}}\,\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad + \varvec{\nabla }w \cdot \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w + \frac{1}{2} (\varvec{\nabla }w)^2 \,\Delta w\Big ] = 0. \end{aligned}$$

(54a)

$$\begin{aligned}&\mu \ddot{\varvec{u}} - \Big [ (1-\nu ) \varvec{\Delta }\varvec{u} + (1+\nu ) \varvec{\nabla }{\mathrm{div}}\,\varvec{u} \nonumber \\&\quad +(1-\nu ) \Delta w \varvec{\nabla }w + (1+\nu ) \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w \Big ] = 0. \end{aligned}$$

(54b)

The bending and in-plane displacements are expanded onto a linear basis of, respectively, $N_w$ transverse modes $\varPhi _k$ and $N_u$ axial modes $\varvec{\varPsi }_p$:

$$\begin{aligned}&w(\varvec{r},t) = \sum _{k=1}^{N_w} \varPhi _k(\varvec{r}) q_k(t) \quad \text {and} \nonumber \\&\quad \varvec{u}(\varvec{r},t) = \sum _{p=N_w+1}^{N_u+N_w} \varvec{\varPsi }_p(x) \eta _p(t). \end{aligned}$$

(55)

The modes are chosen to satisfy the following two eigenproblems associated with the linear parts of Eqs. (54a, b):

$$\begin{aligned}&\Delta \Delta \varPhi _{k} - \omega ^2_k \varPhi _k = 0 \end{aligned}$$

(56a)

$$\begin{aligned}&(1-\nu )\varvec{\Delta }\varvec{\varPsi }_{p} + (1+\nu )\varvec{\nabla }{\mathrm{div}}\,\varvec{\varPsi }_{p} - \gamma _p^2 \varPsi _p = 0 \end{aligned}$$

(56b)

Table 10 Numerical values of the cubic coefficients $\varGamma _{ijl}^k$ of Eq. (9), for the clamped–clamped beam [(u, w)-formulation, Eq. (10), scaling of Eq. (2) and mode normalization of Eq. (47)] and the clamped circular plate [(w, F)-formulation of section C, Eq. (63), scaling of Eqs. (52) and mode normalization of Eqs. (65)]

where $\omega _k$ and $\gamma _p$ are the transverse and in-plane dimensionless eigenfrequencies (the frequency equation of the in-plane vibrations of a clamped circular plate has been derived in [69]). Then, by multiplying (54a, b), respectively, by $\varPhi _k$ and $\varvec{\varPsi }_p$, integrating on the mid-plane surface ${\mathcal {S}}$ and using the orthogonality properties, the ROM of Eqs. (7a, b) is obtained, with:

$$\begin{aligned} C_{pi}^k= & {} -\frac{\displaystyle {\int _{\mathcal {S}} \Big [(1-\nu )\Big (\varvec{\nabla }\varvec{\varPsi }_p:\varvec{\nabla }\varvec{\nabla }\varPhi _i + \varvec{\Delta }\varvec{\varPsi }_p\cdot \varvec{\nabla }\varPhi _i\Big )+\nu \Big ({\mathrm{div}}\,\varvec{\varPsi }_p \,\Delta \varPhi _i + \varvec{\nabla }{\mathrm{div}}\,\varvec{\varPsi }_p\cdot \varvec{\nabla }\varPhi _i\Big )\Big ]\varPhi _k\,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}, \end{aligned}$$

(57a)

$$\begin{aligned} G_{ij}^p= & {} \frac{\displaystyle {\int _{\mathcal {S}} \Big [(1-\nu ) \Delta \varPhi _i \varvec{\nabla }\varPhi _j + (1+\nu ) \varvec{\nabla }\varvec{\nabla }\varPhi _i \cdot \varvec{\nabla }\varPhi _j \Big ]\cdot \varvec{\varPsi }_p \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varvec{\varPsi }_p^2 \,\text {d}S}},\nonumber \\ \end{aligned}$$

(57b)

$$\begin{aligned} D_{ijl}^k= & {} - \frac{\displaystyle {\int _{\mathcal {S}} \Big [\varvec{\nabla }\varPhi _i \cdot \varvec{\nabla }\varvec{\nabla }\varPhi _j \cdot \varvec{\nabla }\varPhi _l + \frac{1}{2} \varvec{\nabla }\varPhi _i\cdot \varvec{\nabla }\varPhi _j \,\Delta \varPhi _l\Big ]\varPhi _k \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}.\nonumber \\ \end{aligned}$$

(57c)

The above developments are not analytically investigated in this study: They have been reported here for a sake of completeness and to precisely demonstrate the results of Sect. 2.3.

Appendix C: On the plate (w, F)-formulation ROM

In the literature dealing with analytical models of plates, the $(\varvec{u},w)$-formulation of the previous section is never used since it would lead to tedious—maybe impossible—computations in an analytical context (see Eq. (51)) and also because there are three unknown displacement fields (w and the two components of $\varvec{u}$). In most of the cases, the in-plane inertia is neglected and Eq. (11b) reduces to ${\mathbf {div}}\,\varvec{N}=\varvec{0}$, which enables the introduction of an Airy stress function $F(\varvec{r},t)$ defined by:

$$\begin{aligned} \Delta F\varvec{1} + \varvec{\nabla }\varvec{\nabla }F = \varvec{N}. \end{aligned}$$

(58)

Then, by adding a compatibility condition, one obtains the following (w, F)-formulation (all details can be found in [14]):

$$\begin{aligned} \ddot{w} + \Delta \Delta w&= \varepsilon \phi (w,F) + p(\varvec{r},t) \end{aligned}$$

(59a)

$$\begin{aligned} \Delta \Delta F&= -\frac{1}{2} \phi (w,w) \end{aligned}$$

(59b)

where the overbars have been dropped and where $\phi (\cdot ,\cdot )$ is a bilinear operator [14]. Similarly to the beam case, the transverse displacements and the force function are expanded on a linear basis of vibration modes $\varPhi _k$ and $\varUpsilon _j$:

$$\begin{aligned}&w(\varvec{r},t) = \sum _{k=1}^{N_w} \varPhi _k(\varvec{r}) q_k(t) \quad \text {and} \nonumber \\&\qquad F(\varvec{r},t) = \sum _{j=1}^{N_F} \varUpsilon _j(\varvec{r}) \eta _j(t) \end{aligned}$$

(60)

where the $q_k$ and $\eta _j$ are time-dependent modal coordinates, respectively, associated with bending and in-plane eigenmodes, which verify:

$$\begin{aligned} \Delta \Delta \varPhi _{k} - \omega ^2_k \varPhi _k&= 0, \end{aligned}$$

(61a)

$$\begin{aligned} \Delta \Delta \varUpsilon _{j} + \zeta _j^4 \varUpsilon _j&= 0. \end{aligned}$$

(61b)

After multiplying equation (59a) by a mode $\varPhi _l$, equation (59b) by a mode $\varUpsilon _m$ and integrating on the surface of the plate, the orthogonality property of the eigenmodes yields:

$$\begin{aligned}&\ddot{q}_k + \omega _k^2 q_k - \varepsilon \sum _{p=1}^{N_w} \sum _{j=1}^{N_F} E_{rj}^k q_r \eta _j = Q_k(t) \end{aligned}$$

(62a)

$$\begin{aligned}&\zeta _j^4 \eta _j = - \frac{1}{2}\sum _{p=1}^{N_w} \sum _{q=1}^{N_w} H_{pq}^j q_p q_q, \end{aligned}$$

(62b)

where nonlinear quadratic coefficients $(E_{rj}^k, H_{pq}^j)$ and modal load $Q_k$ are defined in “Appendix C”. Finally, eliminating $\eta _j(t)$ between Eqs (62a, b) leads to the same set of $N_w$ coupled transverse oscillators with cubic nonlinearities than in the case of beams, Eq. (9), with the following values of the condensed cubic coefficients:

$$\begin{aligned} \varGamma _{pqr}^k = \sum _{j=1}^{N_F} \frac{E_{rj}^kH_{pq}^j}{2\zeta _j^4}. \end{aligned}$$

(63)

Again, the above-defined nonlinear coefficients depend on the mode normalization, defined by Eq. (65).

The analytical expressions of the coefficients of nonlinear terms in Eq. (63) are:

$$\begin{aligned} E_{rj}^k= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varPhi _k L (\varPhi _r, \varUpsilon _j) \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}, \nonumber \\ H_{pq}^j= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varUpsilon _j L(\varPhi _p, \varPhi _q) \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varUpsilon _j^2 \,\text {d}S}}, \nonumber \\ Q_k (t)= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varPhi _{k} p(\varvec{r},t)\,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}. \end{aligned}$$

(64)

The modes are here normalized as:

$$\begin{aligned} \int _{\mathcal {S}} \varPhi _k^2\,\text {d}S=\int _{\mathcal {S}} \varUpsilon _p^2\,\text {d}S=1. \end{aligned}$$

(65)

Appendix D: Numerical values of beam and plate cubic ROM coefficients

The numerical values of the $\varGamma _{ijl}^k$ coefficients of Eq. (9), in the case of the clamped–clamped beam and the circular plate, are gathered in Table 10. They have been computed by the analytical models (Eq. (10) and (63)) and are identical to those computed by the STEP (Sect. 3.2).

Appendix E: Details of STEP

We develop here the details to compute only the nonzero coefficients of (23) with the method of [26]. We refer to the notations $C_{pi}^k$, $D_{ijl}^k$ and $G_{ij}^p$ of Eq. (7). Four distinct steps are necessary, by separating bending modes (BM) and in-plane modes (MM). We also consider unitary modal masses ($m_r=1\;\forall r$).

• Step 1 Imposing a displacement on a single BM, $\varvec{x}_1=\lambda \varvec{\varPhi }_\alpha$, and expanding the result on either a BM $\varvec{\varPhi }_k$ or a MM $\varvec{\varPsi }_p$ leads to:

  $$\begin{aligned} \lambda ^3 D_{\alpha \alpha \alpha }^k&= \varvec{\varPhi }_k^{{\text {T}}} \varvec{f}_\text {nl}(\lambda \varvec{\varPhi }_\alpha ), \end{aligned}$$

  (66)
  $$\begin{aligned} \lambda ^2 G_{\alpha \alpha }^p&= \varvec{\varPsi }_p^{{\text {T}}} \varvec{f}_\text {nl}(\lambda \varvec{\varPhi }_\alpha ). \end{aligned}$$

  (67)

  Consequently, only $N_w$ static computations are necessary to obtain coefficients $D_{\alpha \alpha \alpha }^k$ and $G_{\alpha \alpha }^p$.

• Step 2 Imposing displacements on two BM, $\varvec{x}_2=\lambda _\alpha \varvec{\varPhi }_\alpha \pm \lambda _\beta \varvec{\varPhi }_\beta$, with $\beta >\alpha$, and expanding the result on either a BM $\varvec{\varPhi }_k$ or a MM $\varvec{\varPsi }_p$ leads to:

  $$\begin{aligned} \lambda _\alpha ^2\lambda _\beta D^k_{\alpha \alpha \beta } + \lambda _\alpha \lambda _\beta ^2 D^k_{\alpha \beta \beta } =&\varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) \nonumber \\&- \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k - \lambda _\beta ^3 D_{\beta \beta \beta }^k, \end{aligned}$$

  (68)
  $$\begin{aligned} -\lambda _\alpha ^2\lambda _\beta D^k_{\alpha \alpha \beta } + \lambda _\alpha \lambda _\beta ^2 D^k_{\alpha \beta \beta } =&\varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha - \lambda _\beta \varvec{\varPhi }_\beta )\nonumber \\&- \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k + \lambda _\beta ^3 D_{\beta \beta \beta }^k \end{aligned}$$

  (69)
  $$\begin{aligned} \lambda _\alpha \lambda _\beta G_{\alpha \beta }^p =&\varvec{\varPsi }_p^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) \nonumber \\&- \lambda _\alpha ^2 G_{\alpha \alpha }^p + \lambda _\beta ^2 G_{\beta \beta }^p \end{aligned}$$

  (70)

  where the last part of the second members is known from the first step. At this step, since $\beta >\alpha$, $N_w(N_w-1)$ static computations are required.

• Step 3 Imposing displacements on one BM and one MM, $\varvec{x}_3=\lambda _\alpha \varvec{\varPhi }_\alpha +\lambda _\beta \varvec{\varPsi }_\beta$, and expanding the result on a BM $\varvec{\varPhi }_k$ leads to:

  $$\begin{aligned} \lambda _\alpha \lambda _\beta C_{\alpha \beta }^k = \varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) - \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k \end{aligned}$$

  (71)

  Since $\alpha =1,\ldots N_w$ and $\beta =1,\ldots N_u$, the computation of the coefficients $C_{\alpha \beta }^k$ thus requires $N_wN_u$ static computations.

• Step 4 Imposing a displacement on a three BM, $\varvec{x}_4=\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta + \lambda _\gamma \varvec{\varPhi }_\gamma$, and expanding the result on a BM $\varvec{\varPhi }_k$ leads to:

  $$\begin{aligned} \lambda _\alpha \lambda _\beta \lambda _\gamma D_{\alpha \beta \gamma }^k&= \varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta + \lambda _\gamma \varvec{\varPhi }_\gamma ) \nonumber \\&- \sum _{\begin{array}{c} i,j,l\in \{\alpha ,\beta ,\gamma \}\\ l\ge j\ge i\\ ijl\ne \alpha \beta \gamma \end{array}}\lambda _i\lambda _j\lambda _l D_{ijl}^k. \end{aligned}$$

  (72)

  This computation of the $D_{\alpha \beta \gamma }^k$ coefficients thus requires $N_w^3/6-N_w^2/2+N_w/3$ static computations.

Appendix F: Computation of the energy for the FEPs

The nonlinear part of the potential energy in Eq. (41) writes:

$$\begin{aligned} {\mathcal {V}}_{nl}&= \sum _{i=1}^{N _w}\varGamma _{iii}^i \frac{q_i^4}{4} + \sum _{i=1}^{N_w} \sum _{j>i}^{N_w} \bigg (\varGamma _{iij}^i \frac{q_i^3 q_j}{3}+\varGamma _{iij}^{j}q_{i}^2q_{j}^{2} \nonumber \\&\quad + \varGamma _{ijj}^j \frac{q_j^3 q_i}{3} \bigg ) \nonumber \\&\quad + \sum _{i=1}^{N_w} \sum _{j>i}^N \sum _{k>j}^{N_w} \bigg ( \frac{\varGamma _{ijk}^i}{2} q_i^2 q_j q_k + \frac{\varGamma _{ijk}^j}{2} q_i q_j^2 q_k \nonumber \\&\quad + \frac{\varGamma _{ijk}^k}{2} q_i q_j q_k^2 \bigg )\nonumber \\&\quad + \sum _{i=1}^{N_w} \sum _{j>i}^{N_w} \sum _{k>j}^{N_w} \sum _{l=1}^{N_w} \varGamma _{ijk}^l q_i q_j q_k q_l . \end{aligned}$$

(73)

To obtain this equation, the starting point is the general expression of a dynamical system with cubic nonlinearities:

$$\begin{aligned} \ddot{q}_k + \omega _k^2 q_k + \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} \varGamma _{ijl}^{k} q_i q_j q_l = Q_k, \end{aligned}$$

(74)

which can also be written $\ddot{\varvec{q}} + \varvec{f}(\varvec{q}) = 0$, where $\varvec{f}$ denotes the internal forces vector. It derives from a potential and can be integrated over time if and only if the following condition on the crossed derivatives is verified:

$$\begin{aligned} \frac{\partial f_i}{\partial q_j} = \frac{\partial f_j}{\partial q_i} \quad \forall i \ne j. \end{aligned}$$

(75)

According to the developments of [14], it is established for some classical boundary conditions of plates—including the clamped one—that the symmetry properties of the bilinear operator L lead to the following equality between the nonlinear coefficients of the (w, F)-formulation ROM presented in “Appendix B”:

$$\begin{aligned} H_{pq}^j = E_{pj}^q, \qquad H_{pq}^j = H_{qp}^j. \end{aligned}$$

(76)

It results after some developments to some equalities between the non-upper triangular form coefficients ${\bar{\varGamma }}_{ijl}^k, {i,j,l,k} \in [1,N_w]$, which are written:

$$\begin{aligned} {\bar{\varGamma }}_{ijl}^k {=}{} \mathbf {\bar{\varGamma }}_{jil}^k = {\bar{\varGamma }}_{kjl}^i = {\bar{\varGamma }}_{klj}^i = {\bar{\varGamma }}_{lki}^j {=} {\bar{\varGamma }}_{kli}^j = {\bar{\varGamma }}_{jki}^l = {\bar{\varGamma }}_{kji}^l, \end{aligned}$$

(77)

thus, the upper triangular form yields

$$\begin{aligned}&\varGamma _{iij}^i = 3 \varGamma _{iii}^j, \quad \varGamma _{ijj}^i = \varGamma _{iij}^j,\quad \varGamma _{ijj}^j = 3\varGamma _{jjj}^i \quad \forall j>i \nonumber \\&\varGamma _{ijl}^j = 2 \varGamma _{jjl}^i = 2\varGamma _{ijj}^l, \quad \varGamma _{ijl}^i = 2 \varGamma _{iij}^l = 2\varGamma _{iil}^j, \nonumber \\&\varGamma _{ijl}^l = 2 \varGamma _{ill}^j =2 \varGamma _{jll}^i \quad \forall l>j>i\nonumber \\&\varGamma _{ijl}^k = \varGamma _{ijk}^l = \varGamma _{ilk}^j = \varGamma _{jlk}^i \quad \forall k>l>j>i, \end{aligned}$$

(78)

which allows to verify the condition of Eq. (75). The general expression of the energy in Eq. (73) is then obtained by multiplying the equation of the kth oscillator of Eq. (74) by the modal velocity ${\dot{q}}_k$ and integrating over time.