Review of dynamic soaring: technical aspects, nonlinear modeling perspectives and future directions

Abstract

In this paper, we present a comprehensive and detailed review of dynamic soaring process, and in particular, its application to unmanned aerial vehicles (UAVs). We start by explaining the biological inspiration that comes from soaring birds and how researchers have tried to utilize the dynamic soaring phenomenon/maneuver and apply it to UAVs. We present and discuss the fundamentals of wind shear models in both the linear and nonlinear cases. Moreover, a comprehensive parametric characterization of the key performance parameters for the dynamic soaring maneuver is given. Numerical methods for nonlinear trajectory optimization are summarized and methodologies capable of generating rapid solutions suitable for real-time implementation, are presented. Additionally, the paper introduces mathematical modeling and procedure to generate the optimized dynamic soaring trajectory. Through this paper, a consolidated platform is built, which not only covers technical aspects of advancements made over the passage of time, but also identifies and discusses the existing challenges. These challenges which are encountered by UAVs curtail the potential utility of dynamic soaring. Integrating dynamic soaring with morphology and inclusion of nonlinear control theory in the flight control system are introduced as a possible future research directions that may overcome the existing limitations.

1 Introduction

1.1 Origin of dynamic soaring: biological inspiration

Birds such as albatross can fly long distances almost without flapping wings. This process can be so efficient that it allows un-powered (gliding) flight for hundreds of miles as typically done by the albatross [1] without any mechanical cost [2]. In fact, albatross are so well adapted to this maneuver that they can travel very long distances with sustained non-flapping flight [3,4,5]. They have a shoulder lock mechanism that maintains their wings outstretched with almost no effort. Sachs et al. [6] observed that an albatross needs to generate 81.0 W for flying at 70 km/h, that is the same as that generated by 0.9 L of gasoline per day. A typical voyage of an albatross spans more than 13 days [7], which implies that the energy consumed during the journey equals to 11 L of gasoline. Since this much amount of energy cannot be generated from food, this has triggered the researchers to think about the probable source for this sustained energy, which the bird utilizes.

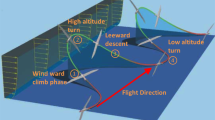
After observations, it was concluded that albatross exploits a special technique known as dynamic soaring, while flying in wind shear. Dynamic soaring extracts energy from the air through velocity gradients (typically occur near the ground due to the boundary layer) or shear layers (typically occur on the leeward side of mountains and ridges). Fig. 1 provides an illustration of an albatross executing a typical dynamic soaring periodic maneuver during forward flight. The soaring maneuver consists of four characteristic phases: (1) windward climb, (2) higher altitude turn, (3) leeward descent, and (4) lower altitude turn. The bird, at the end of the maneuver, maintains the same conditions it had when starting the maneuver cycle with approximately the same speed, altitude, angle of attack and flight path angle but with a gained distance along the desired flight direction without any input power. The length of forward distance covered by acquiring energy from atmospheric wind shear (i.e., dynamic soaring) corresponds to the amount of the work that otherwise would have been done by the bird during the forward flight.

Fig. 1

Typical trajectory of albatross executing dynamic soaring during forward flight

Fig. 2

Limitations of sUAV

1.2 Dynamic soaring applied to UAVs

Unmanned aerial systems (UAS) represent an important class of aerial vehicles with wide spread applications. Figure 2 depicts the typical range, endurance and ceiling of different class of UAS such as, high altitude long endurance (HALE), medium altitude long endurance (MALE), tactical, close range, and small (including mini, micro and nano) UAVs [8]. Among these systems, small UAVs (sUAVs) have a role in aviation industry for surveillance, communication relay and loitering dominated missions. The utility of sUAVs is, however, greatly curtailed because of low endurance. The diverse set of mission requirements necessitates sUAVs to improve their time aloft. Hence, a primary objective of today’s research is to identify methods that, not only can supply energy for long-endurance missions, but also does not affect their size because of extra weight.

Dynamic soaring has the potential to greatly enhance range and endurance [9] of small UAVs. However, it requires good knowledge of the wind field to calculate trajectories which result in energy gain. Therefore, instead of pursuing battery and engine performance, researchers find that UAVs can conserve energy by taking advantage of the wind gradients. Recently, energy extraction from wind shear has attracted attention of researchers all around the world [10,11,12]. This is because wind shear is persistently distributed in the boundary layer above the ocean’s surface as well as on land [13]. With the rapid technology development for UAVs, dynamic soaring can become a new way to extract energy from the atmosphere.

1.3 Objectives and content of this review

It can be noted that the literature is almost empty from a comprehensive review on the topic of dynamic soaring and its application to UAVs. Therefore, in this review, we try to connect the missing dots and provide the state-of-the-art background that should help scholars aiming at working on the nonlinear dynamics, optimization, modeling and/or control aspects of dynamic soaring and its application. The contribution of this review is listed below:

• (i) Consolidation of relevant work Since the concept of dynamic soaring first presented by Lord Rayleigh in 1883 [14, 15], significant work has been done in understanding soaring flight. In this paper, a consolidated platform is built, where all available information highlighting different aspects of dynamic soaring are documented. A detailed review of the major studies performed by different researchers, dating back from Lord Rayleigh [14, 16, 17] (1883) till date, are presented (refer Sect. 2). Wind shear, including its linear and nonlinear approximate modalities (refer Sect. 4), is presented as well. Moreover, optimization techniques suitable for implementing dynamic soaring (refer Sect.6) are also made part of this review. Still however, one of the most important documentations of this review is presenting the nonlinear modeling and trajectory generation of UAVs performing dynamic soaring, all in a step-by-step basis (refer Sect.5).

• (ii) Exploration of design space and parametric characterization Till today, existence of a unified design philosophy is scarce in literature. Most work refers to the implementation of dynamic soaring maneuvers for a conventional configuration, but lacks discussion on the platform versatility. This necessitates parametric studies to investigate the effect of different sizing and design parameters on dynamic soaring, such as aerodynamic and mass properties. The review covers this content in Sect. 3.

• (iii) Survey of nonlinear trajectory optimization methodologies The selection of methodology to perform nonlinear trajectory optimization is the most important question for computational and numerical studies. It is not surprising that the development of the numerical methods for optimization has closely paralleled to the exploration of space and the development of the digital computers [18]. In order to formulate optimal trajectories for dynamic soaring, trajectory optimization problem is conventionally treated as a nonlinear optimal control problem in which well-established tools are utilized to solve the problem. A large search space is therefore available in this regard, whereby which various numerical methodologies have been utilized by different researchers. This necessitates the requirement to perform a detailed study to identify optimization algorithms available for performing nonlinear trajectory optimization. We provide this study in Sect. 6.

• (iv) Existing limitations and the way forward Another contribution of this review is to identify the factors which are limiting the utility of dynamic soaring in UAVs and to propose suitable measures. The immaturities observed are categorized into two fundamental areas: (a) limitations in UAV design versatilities, and (b) limitations in existing autonomous flight control system (FCS) of soaring UAVs [19]. In Sect. 7, both the mentioned issues are individually discussed. We do propose two paths of research that the literature seems almost empty from. These proposals discuss morphing and nonlinear controllability. It is shown in Sect. 7.1 that a biologically inspired platform with morphing capability greatly enhance the energy gain from the atmosphere. Similarly, inclusion of nonlinear controllability in the autonomous flight dynamic system and its positive impact are discussed in Sect. 7.2.

1.4 Organization of the paper

This paper is organized as follows. An overview of the major work done in regard to dynamic soaring and its salient characteristics is presented in Sect. 2. Parametric studies summarizing (a) Albatross and UAV aerodynamic and mass parameters, and (b) dynamic soaring flight characteristics, are presented in Sect. 3. Different models of wind shear and their estimation techniques are defined in Sect. 4. Details pertaining to the dynamic soaring problem formulation are presented in Sect. 5, where optimal trajectories are generated, step by step, for the convenience of the reader. Section 6 explains the aspects related to trajectory optimization and optimal control. Analysis of the governing mechanisms of energy extraction from wind shear during the maneuver are presented. Section 7 presents the challenges and proposed potential solutions. Section 8 finally concludes the article.

2 Relevant studies of dynamic soaring

The significant start point of dynamic soaring can be attributed to Lord Rayleigh [14, 16, 17]. In 1883, it was proposed that a bird without working its wings cannot maintain level flight indefinitely in steady air or in a uniform horizontal wind. Whenever a bird pursues course for some time without flapping wing, it must be concluded that either the course is not horizontal (gliding flight), or the wind is not horizontal (static soaring), or the wind is not uniform (dynamic soaring).

2.1 Documentation and layout of relevant research

Initial work on dynamic soaring Initial research on dynamic soaring focused on understanding the basis of soaring flight, exhibited by soaring birds. Idraac [20, 21], Walkden [22] and Wood [17] performed experimental study on the soaring flight of albatross to determine soaring fight characteristics. Pennycuick [5, 23, 24] carried out a detailed work in this regard by performing analysis on the mechanics of gliding flight in fulmar petrel/albatross and ascertained the power requirements for horizontal flight [25]. Aerodynamics of gliding flight was further explored by Turcker and Parrot [26]. Hargrave [27], based upon analysis of sea birds flight, suggested that the soaring birds obtained a significant fraction of their flight energy from static lift. This is achieved by flying on the windward side of ocean waves. Wilson [1] proposed sweeping flight mechanism as the means, through which the birds gain energy. The bird while staying in the wave generated updraft gains the speed. This increase in speed can be traded to gain height. Once the desired height is achieved, the bird can cruise back downward to the next wave in the intended direction. Pennycuick [5] proposed that Albatross extracts energy from the wind utilizing both soaring and sweeping mechanisms. The sweeping flight is more prominent in upwind flight, while dynamic soaring dominates for downwind flight. Experimental research focused on tracking/observing soaring birds, such as Albatross, by satellite and other measurement devices (Jouventin and Weimerskirch [28], Prince et al. [29], Alerstam et al. [30], Tuck et al. [31], Weimerskirch and Wilson [32] and Nel et al. [33]), provided useful information in determining soaring flight parameters. Weimerskirch [34] identified that wandering albatross typically cruise at speed in excess of 85 km/h (24 m/s) and can attain maximum speed up to 135 km/h (38 m/s). Wakefield et al. [35] utilized GPS to track albatross flight. A linear relationship between ground speed and the component of wind speed in the direction of the flight was established. Weimerskirch and Guionnet [36] studied the impact of wind on soaring flight of albatross by installing miniature electronic devices (a heart-rate transmitter recorder, an activity recorder and a satellite transmitter). Heart rate was used as an instantaneous index of energy expenditure to measure the instantaneous effort and energy expenditure [37]. Rosen and Anders [38] performed wind tunnel testing to explore the gliding flight mechanism. It was observed that gliding speed of 6–11 m/s was achieved by the birds. During flight, the birds vary both the wingspan and wing area to maximize the performance. This provided an evidence that birds maximize the profound effects of soaring through morphing.

Soaring for manned gliders Initially, manned gliders employed static soaring technique to perform long-duration powerless flights. In this regard, first recorded gliding and possibly soaring (static) flight was made by Lilienthal in 1897 at Berlin [39]. Subsequently, simple algorithms such as the speed-to-fly rules specified by MacCready (1958) [39] for cross-country gliding were developed. These rules were used to determine when a vehicle should utilize a thermal and when to travel to maximize overall average speed based on an estimate of thermal strengths. The use of dynamic soaring by humans was initially limited to radio-controlled (RC) sailplanes because of the high flight speeds (90 m/s) acquired in close proximity to the ground. The first recorded glider flight utilizing dynamic soaring was made by Ingo Renner [40]. With this achievement of Renner, dynamic soaring for manned gliders surfaced as an area of interest.

Identification of feasible regions for dynamic soaring Geographical regions, in which dynamic soaring can be performed, also remained an area of interest throughout the literature. Since dynamic soaring is dependent on wind shear, areas were specifically identified, where wind shear gradient is normally sufficient enough to facilitate dynamic soaring. The identified areas, where wind shear occurs naturally, were low altitude boundary layer shear and high altitude metrological shear. Low altitude boundary layer shear occurs over surfaces (land or ocean) [41] and geographical obstacles [42]. Over land (hills or ridges), they arise due to friction between the moving air mass and the surface, or in proximity to other obstacles. The velocity is near zero at the surface and increases gradually over altitudes [43, 44]. Relatively, strong wind flowing over the top of the windward side sets up a wind gradient consisting of gradually decreasing wind speed with the downward slope on the leeward side. Dynamic soaring in these areas involve skewed helical maneuvers, very close to the leeward side of a geophysical formation [41]. Over sea, this type of wind, known as shear flow, frequently exists in the boundary layer above the ocean surface. Seabirds use this technique to fly hundreds of kilometers across the ocean [40]. High altitude meteorological shear, in the jet stream, occurs primarily due to temperature inversions [13]. Jet streams are bands of strong winds in the upper atmosphere that extend over thousands of kilometers, but are relatively narrow (less than 5 km). Unlike locations that are dependent on surface winds, the gradients in the jet stream are persistent and have the potential to support perpetual flight.

Dynamic soaring heuristics Wharington [45] first presented a heuristic approach (pitch and bank control) for formulating dynamic soaring trajectories for a UAV. He proposed two approaches to the closed-loop dynamic soaring problem, the first involved extensive analysis of perturbed open-loop trajectory solutions and the second involved the adoption of a simple heuristic. It is, however, noticeable that his heuristics did not provide a function to predict the speed gain per loop of maneuver [41] and heuristic control was subsequently found ineffective [46].

Determination of minimum wind shear Formulation of minimum wind shear required to perform dynamic soaring posed a challenging numerical problem because of coupled and nonlinear nature of the equations of motion. Data given by Idrac [47] refers to a wind speed of 5 m/s close to the sea surface as a value below which dynamic soaring is not performed by albatrosses. A value of 5 m/s was also quoted by Pennycuick [48], below which no observations were obtained. Similar values were ascertained by Sachs [49] who determined a minimum wind shear value $V_{W_{\min }}$ of 5 m/s at an altitude of 0.79 m.

Dynamic soaring for full-scale aircraft Sachs and Da Costa [50] performed studies to extend dynamic soaring to full-scale sailplanes. Based upon the values of wind shear conventionally found near mountain ridges, it was considered possible. Gordan [40] carried out detailed search in this regard with an aim to prove or disprove the viability of dynamic soaring for full size aircraft. He showed that full size sailplanes could extract energy from horizontal wind shears, although the utility of the energy extraction could be marginal depending on the flight conditions and type of sailplane used.

Nonlinear trajectory optimization: Generally, dynamic soaring maneuvers are three dimensional, and would involve pitch, yaw and roll. Wharington [45] attempted to derive the aerodynamic heuristics of dynamic soaring in order to design a closed-loop controller, which should be able to control an aircraft to achieve autonomous dynamic soaring. He managed to integrate a glide slope function or sink relation, updraft and horizontal wind gradient function, and bank-pitch commands. Despite this detailed analysis, the paper still maintained that the open-loop heuristics can best be described by a sinusoidal airspeed function with a vertical wind gradient. Consequently, Ariff and Go [51] proposed trajectory forming algorithm, which used the concept of Dubin’s curves expressed in the parameters of differential geometry. Dubin’s curves have been previously used for trajectory generation for cooperative guidance algorithms. Simulated studies reported that the new technique can provide identical solutions while reducing the degree of computation time by half or more.

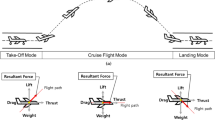
Dynamic soaring modes Dynamic soaring exhibited by soaring birds like albatross were examined by a number of researchers (Zhao [52], Barnes [53] , Richardson [54], Alerstam et al. [30], and Wakefield [35]) to formulate optimal dynamic soaring patterns for UAVs. Subsequently, three fundamental modes of dynamic soaring, such as (a) basic mode, (b) forward mode, and (c) loiter mode, were identified. These modes are graphically depicted in Fig. 3.

Fig. 3

Dynamic soaring modes (utilizing linear wind shear model)

Loiter mode is a circular hover mode with the wings banked in the same direction. In this mode, the UAV dives across the wind gradient, then climb into the wind, and then turns and dives again. A minor modification of this (as specified by Barnes [53]) is a figure-eight-shaped hover mode, in which a bird switches the direction of its banked wings on every other crossing of the shear layer. In loiter mode, glider would dive across the wind gradient, then climbs into the wind, and then turns and dives again, for powerless sustained loiter flight. In loiter mode, the final position is completely constrained as the end coordinates has to be exactly the same as the initial coordinates. This is governed by boundary constraints specified by Eq. (1):

$$\begin{aligned} x_{t_\mathrm{f}}= x_{t_0}, y_{t_\mathrm{f}}= y_{t_0}, h_{t_\mathrm{f}}= h_{t_0}, \end{aligned}$$

(1)

where $x_{t_\mathrm{f}}$, $y_{t_\mathrm{f}}$, $h_{t_\mathrm{f}}$ are the final coordinates and $x_{t_0}$, $y_{t_0}$ ,$h_{t_0}$ are the initial coordinates along the inertial east, north and altitude axis. In the basic/forward modes, the glider dives along the wind direction until it is very close to the ground, or water, to gain speed. Then, it makes a climbing turn into the wind gradient, while losing speed. At the end, it makes a further turn and dives down again to repeat the process. In the forward mode, the position after completing the maneuver is partially fixed and is governed by the constraint mentioned in Eq. (2):

$$\begin{aligned} x_{t_\mathrm{f}}\ne x_{t_0}, y_{t_\mathrm{f}}= y_{t_0}, h_{t_\mathrm{f}}= h_{t_0}+\Delta h, \end{aligned}$$

(2)

where $\Delta h$ is the altitude change during the maneuver. In the basic mode, the final position after the completion of the maneuver is totally unconstrained and is governed by Eq. (3):

$$\begin{aligned} x_{t_\mathrm{f}}\ne x_{t_0}, y_{t_\mathrm{f}}\ne y_{t_0}, h_{t_\mathrm{f}}= h_{t_0} +\Delta h. \end{aligned}$$

(3)

The basic/forward modes can be across wind, upwind, downwind or diagonal, as shown in Fig. 4. Across-wind travel mode usually consists of a series of $180^{\circ }$ turns, while heading on an average course across the wind [54]. Upwind travel mode [5, 35] can be either diagonal or directly up wind depending on the bank angles, and is more efficient than across-wind mode [55]. To soar upwind, a series of turns are executed, first right then left, after upwind climbs resulting in a series of $180^{\circ }$ turns similar to the across-wind mode. This technique is used for fast down-wind soaring if upwind climbs across the wind shear layer are replaced with downwind descents across the wind shear layer. In diagonal upwind travel mode, climb is made up across the wind shear layer headed upwind and then $90^{\circ }$ to the right. Then, a descend across the wind shear layer headed perpendicular to the wind and $90^{\circ }$ bank to the left into the wind again. Using a series of $90^{\circ }$ turns, upwind zig-zag diagonally through the air is made at an average angle of around $45^{\circ }$ relative to the wind direction. By adjusting the direction of the turns, either to the left or right after an upwind climb, any effectively upwind direction can be tracked.

Fig. 4

Travel submodes [54]

3 Design variability and parametric characterization

Dynamic soaring maneuver can be represented by several parameters: maximum altitude, peak altitude/speed attained during the soaring maneuvers, cycle time, minimum wind shear required and so on. Several authors studied the effect of these parameters on the energy gain and the minimum required wind shear [45, 56,57,58,59]. A larger parameter space is available in this regard for different UAV models. This trigger the absolute need for parametric characterization of the dynamic soaring maneuver, and to define the aerodynamic and mass properties of the soaring UAVs/birds. In this section, several design variables are identified that are most suitable for dynamic soaring maneuver [60]. Various parameters, as depicted in Table 3, are ascertained to have an insight of the soaring mechanism. Aerodynamic and mass parameters for soaring birds and UAVs utilized in literature are also collected in a tabular form for the convenience of the readers (refer Sect. 3, Tables 1 and 2).

3.1 Albatross aerodynamic and mass parameters

Since dynamic soaring flight is inspired from the flight of soaring birds (such as albatross), UAVs performing dynamic soaring maneuver were initially sized to the wandering albatross. Many researchers (Idrac [47], Berger and Gohde [61], Tucker and Parrott [26] , Wood [17], Pennycuick [5], Sachs [49], and Bonnin [62]), utilizing different techniques, gathered data to estimate albatross aerodynamic and mass parameters. These parameters, summarized in Table 1, were subsequently referred to and utilized by other researchers for performing their numerical studies and validation for optimized dynamic soaring trajectories.

Table 1 Albatross aerodynamic and mass parameters reported in different studies

3.2 UAV aerodynamic and mass parameters

For performing dynamic soaring studies, different researchers utilized different models for UAVs (both small sized and large sailplanes). Radio Controlled gliders have now achieved amazingly high speeds during dynamic soaring maneuver. The pilots of these RC gliders have worked out strength and control issues for fast flight. The acclaimed maximum speed holder (244 m/s) for RC gliders is by Spencer Lisenby [63]. In this research, a larger parameter space was explored that should be close to albatross parameters. Different parametric characteristics for a model were subsequently selected as representative of typical dynamic-soaring capable sailplane. These are generally characterized and influenced by the requirement of having high wing loading and high lift-to-drag ratio. Table 2 present details of platforms, with pertinent aerodynamic and mass parameters that have been utilized in literature for dynamic soaring.

Table 2 Aerodynamic and mass parameters of UAVs utilized for dynamic soaring

3.3 Dynamic soaring flight characteristics

Dynamic soaring flight characteristics were investigated by various researchers [5, 49] to determine the fundamentals of soaring flight. Various parameters [60] (refer Table 3), such as the peak altitude/speeds attained during the soaring maneuvers, cycle time, minimum wind shear required and so on, were subsequently ascertained to have an insight of the soaring mechanism. These parameters defined the governing conditions for the performance of dynamic soaring maneuver. Among these, the minimum wind shear is the most crucial parameter, as dynamic soaring cannot be performed without the presence of the least required wind shear. Wind strength of 5 m/s [47,48,49] at sea level conditions was identified as the minimum value below which sustained dynamic soaring is not possible. Dynamic soaring in regions such as over sea, or land is considered feasible as these regions have wind shears which satisfies this condition.

Table 3 Dynamic soaring flight parameters

4 Wind shear

Dynamic soaring involves extraction of energy from the wind shear present near the earth surface. Presence of wind shear is, therefore, fundamental in performing soaring flight. Wind shear is a difference in wind speed and direction over a relatively short distance in the atmosphere. It is an atmospheric phenomenon, which occurs on thin layers separating two regions, where the predominant airflow vector is different. In a wind gradient field, the horizontal wind speed increases with altitude before reaching the values of the free air stream. This dependence on altitude may be linear [10, 40, 68] or nonlinear [49, 58, 65, 69,70,71]. Since wind shear is a necessary condition for dynamic soaring, a well-defined model for describing wind dynamics is needed for the studies of UAV dynamic soaring flights. In order to perform estimates for wind field, two approaches are conventionally followed, (a) approximating the wind shear with some known model once the wind conditions are known, and (b) online estimation of wind shear in unknown wind conditions.

4.1 Mathematical representation of wind shear

Since stable atmospheric conditions exist near sea surface, with wind velocity gradually increasing with altitude, the mean velocity profile of actual wind gradients can, therefore, be approximated using linear or nonlinear (exponential or logarithmic) wind models, as shown in Fig. 5.

4.1.1 Linear modeling

In linear wind shear model, the wind shear slope is constant with altitude [10, 40, 68]. Linear wind model profile is the simplest model for wind estimation, in which there exists a constant vertical wind gradient as presented in Eq. 4:

$$\begin{aligned} V_\mathrm{W}=\frac{\partial V}{\partial h} h, \end{aligned}$$

(4)

where $\beta = \frac{\partial V}{\partial h}$ is the strength of wind shear. A quadratic variation of the linear wind profile as specified by Zhao [52] is presented in Eq. (5):

$$\begin{aligned} V_\mathrm{W}=\beta \left( Ah + \frac{(1-A)}{h_{tr}}h^2\right) . \end{aligned}$$

(5)

where $0<A<1$ corresponds to an exponential wind profile and $1<A<2$ corresponds to a logarithmic wind profile. At $A=1$, the wind profile becomes a linear profile. The wind shear gradient is represented in Eq. (6).

$$\begin{aligned} {\dot{V}}_\mathrm{W}=\beta {\dot{h}}. \end{aligned}$$

(6)

4.1.2 Nonlinear modeling

Wind shear velocity over sea and ridges are often represented with nonlinear exponential model [49, 58, 65, 71], as shown in Eq.(7). In this model, the wind shear speed increases in an exponential manner before reaching the value of the free air stream.

$$\begin{aligned} V_\mathrm{W}=V_{w_\mathrm{ref}}\left( \frac{h}{H_R}\right) ^p, \end{aligned}$$

(7)

where $V_\mathrm{W}$ is the wind velocity as a function of height, $V_{w_\mathrm{ref}}$ is the velocity of wind at reference altitude $H_R$ and p is the wind shear parameter to define wind strength, taking into account the properties of the surface. Also, wind shear gradient is represented by Eq. (8):

$$\begin{aligned} {\dot{V}}_\mathrm{W}=p{\dot{h}} V_{w_\mathrm{ref}} \left( \frac{h}{H_R}\right) ^{(p-1)} . \end{aligned}$$

(8)

Apart from exponential wind shear, the wind shear can also be modeled by a nonlinear logarithmic model [49, 58, 71]. This profile is commonly used in meteorological studies and is mostly applicable to measurements near the surface of the earth. The logarithmic relation between wind speed (V$_\mathrm{W}$) and height above the surface (h) is given by Eq. (9):

$$\begin{aligned} V_\mathrm{W}=V_{w_\mathrm{ref}} \left( \frac{\ln (h/h_0)}{\ln ({h_\mathrm{ref}}/h_0)}\right) , \end{aligned}$$

(9)

where $V_{w_\mathrm{ref}}$ denote reference value for wind shear strength at a reference altitude $h_\mathrm{ref}$. Also $h_0$ is the surface correctness factor that determines the distribution of the wind gradients with varying altitude, reflecting the surface properties, such as irregularity, roughness, and drag. The minimum value of the reference wind speed ($V_{W_\mathrm{ref}}$) at reference height ($h_\mathrm{ref}$), which still permits dynamic soaring, is ascertained through the optimization process. The wind shear gradient is represented by Eq. (10):

$$\begin{aligned} {\dot{V}}_\mathrm{W}=V_{w_\mathrm{ref}} \frac{1}{h\ln \left( h_\mathrm{ref}/h_0\right) }{\dot{h}}. \end{aligned}$$

(10)

Table 4 summarizes different wind shear models that have been utilized in literature to model the wind shear dynamics under many different conditions.

Fig. 5

Linear, exponential and logarithmic wind shear models. a Linear and exponential wind shear models. b Logarithmic wind shear model

Table 4 Typical wind shear models used in different studies

4.1.3 Necessary considerations for model implementation

Without loosing generality, the mathematical models (Eqs. 9 and 4), developed for representing wind dynamics, are based on certain assumptions. These are stated below:

Fig. 6

Wind shear modeling considerations

• (a) Wind shear is assumed to be steady and is distributed uniformly in the x-axis [43, 44, 68] direction. Hence, wind in the y-axis and vertical (h) directions are zero. This is graphically illustrated in Fig. 6 and mathematically represented by Eq. (11):

  $$\begin{aligned} W_y=0 , W_h=0. \end{aligned}$$

  (11)

• (b) Horizontal wind component is stationary [44], as shown in Eq. (12) and is a function of altitude only, i.e., $W_x$ = $W_x(h)$.

  $$\begin{aligned} W_x=\frac{\partial {W_x}}{\partial {x}}{\dot{x}} +\frac{\partial {W_y}}{\partial {y}}{\dot{y}}+\frac{\partial {W_h}}{\partial {h}}{\dot{h}}. \end{aligned}$$

  (12)

• (c) In a wind gradient field, the horizontal wind speed increases with altitude. Wind gradients can occur at different altitudes. They often occur near the surface of ground or water due to the friction of wind component with the surface, where the velocity is near zero at the surface and increases gradually over altitudes. This dependence on altitude may be linear [10, 40, 68] or nonlinear [49, 58, 65, 69,70,71].

• (d) The aerodynamic wind shear models utilized for dynamic soaring assume flat ocean (no waves) [54]. This assumption of a flat ocean implies that these models are most appropriate for dynamic soaring in regions without waves, such as harbors, where albatross has been observed to exploit dynamic soaring. Thus, the slope soaring effects are neglected.

• (e) Moreover, presence of vertical wind is neglected [68], which means thermal and ridge soaring are non-existent.

4.2 Online estimation of wind shear

Majority of the research on UAV energy extraction from wind shear has been done with strong assumptions on the wind shear models specified in Eqs. (4–7) [10, 49, 68,69,70,71]. This was done because at times, it is feasible to approximate wind gradient with a certain profile, given certain geographical and meteorological conditions. These wind shear models remained static throughout the flight. However, in real-world conditions, this assumption may not be valid. Wind shear follows different patterns at different geographical locations, as its speed and/or direction can change. Therefore, no constant wind shear model can be utilized for analyzing wind effects. It is, therefore, unreasonable to apriorly model the wind shear, through any of the constant empirical relationships as specified in Eqs. (4–7). Control of energy harvesting methods for UAVs, therefore, require online estimation of wind shear to simulate the UAV optimal trajectory without assuming a predefined constant wind shear. For performing dynamic soaring in unknown wind shear conditions, different methods have been proposed for wind shear estimation. The methods used values obtained from dynamic equations of motion, and those collected during the flight and estimate wind shear parameters employing estimation techniques (least square estimates [57], linear Kalman filter [72], Extended Kalman filter [19], particle filter [73], Gaussian process regression [74] and so on). Wind speed estimated through these methods was within ± 0.45 m/s of the actual value, depicts the accuracy of such techniques.

5 Flight dynamic modeling

5.1 Nonlinear equations of motion

UAV dynamics can be represented by a three dimensional (3D) point-mass model (computationally fast but considerably inaccurate) [75] or an elaborate 6-DOF model (computationally expensive but accurate) [76]. Conventionally, 3-DOF point-mass model, because of its low computational requirements, has been utilized by researchers [45, 68] for describing the system dynamics while formulating dynamic soaring maneuvers. There are mainly two types of 3-DOF model to describe a UAV flying in a spatially and temporally varying wind field, the Sach’s [6, 49, 49, 50, 67, 77, 78] equations of motion (refer Eqs.(13) and the Zhao’s [52, 68, 71] equations of motion (refer Eqs.(14)). Neglecting UAV’s rotational dynamics [79, 80], the nonlinear differential equations for both the Sachs and Zhaos models are given as follows:

$$\begin{aligned} \begin{aligned} {\dot{u}}&= -\frac{D}{{M}}[\cos \gamma \cos \psi ]+\frac{L}{{M}}[\cos \phi \sin \gamma cos\psi \\&\quad + \sin \phi \sin \psi ],\\ {\dot{v}}&= -\frac{D}{{M}}[\cos \gamma \sin \psi ]+\frac{L}{{M}}[\cos \phi \sin \gamma sin\psi \\&\quad - \sin \phi \cos \psi ],\\ {\dot{w}}&= -\frac{D}{{M}}[-\sin \gamma ] + \frac{L}{{M}}[\cos \phi \cos \gamma ]-g,\\ {\dot{x}}&= u,\quad {\dot{y}} = v, \quad {\dot{h}} = -w, \end{aligned} \end{aligned}$$

(13)

where u,v,w are the UAV velocity components along the body axis, $W_x$,$W_y$,$W_z$ are the wind velocity components along the body axis, $\gamma$ is the flight path angle, $\psi$ is the heading angle, $\phi$ is the bank angle, L is the Lift, D is the drag, M is the mass of the UAV, and x,y,h are the position vectors.

$$\begin{aligned} \begin{aligned} {\dot{V}}&= \frac{1}{{M}}[-D-{M}g\sin \gamma -{M}{\dot{V}}_\mathrm{W}\cos \gamma \sin \psi ], \\ {\dot{\psi }}&=\frac{1}{{M}V_t\cos \gamma }[L\sin \phi -{M} {\dot{V}}_\mathrm{W}\cos \psi ], \\ {\dot{\gamma }}&=\frac{1}{{M}V_t}[L\cos \phi -{M} g\cos \gamma +{M}{\dot{V}}_\mathrm{W}\sin \psi \sin \gamma ],\\ {\dot{x}}&= V\cos \gamma \sin \psi +V_\mathrm{W},\\ {\dot{y}}&= V\cos \gamma \cos \psi , \\ {\dot{h}}&=V\sin \gamma ,\\ \end{aligned} \end{aligned}$$

(14)

where V is the UAV speed. In both the models, speed of UAV is modeled in a wind relative reference frame and the position of UAV is modeled in an earth fixed frame. Detailed advantages and disadvantages of the two sets of equations of motion have been explained by Bower [81]. Zhao’s model is considered to be more intuitive by using airspeed, flight path pitch angle, and heading angle as state variables. The assumptions made in literature [19, 79, 80] to derive equations of motion (refer Eqs. (13–14)) are introduced below:

• (i) For the sake of mathematical analysis, a non-rotating, flat earth is assumed [40, 68, 82], since dynamic soaring trajectory typically occurs over a very brief period of time and over a small localized area of the Earth. Also vehicle rotation rate is considerably small as compared to the rotation rate of earth. Hence, only the body fixed and North-East-Down coordinate systems were used.

• (ii) Aircraft is considered to be a rigid body having a constant mass [10, 50]. The point-mass model equations neglecting UAV’s rotational dynamics with no thrust component are chosen sufficiently, to provide an optimal dynamic soaring flight profile for the UAV.

5.2 Optimal control formulation

Mathematical models specified in Eqs. (13) and (14) are linked through a similarity transformation, that is they are similar representation in two different axis systems. Therefore, only Eqs. (14) will be considered in this paper from now onwards. Conventionally, the flight model described by Eqs. (14), together with a wind shear profile (as specified in Eqs. (4–7)), is configured as a nonlinear system [78] with state and the control variables defined in Eqs. (15) and (16), respectively [10, 59].

$$\begin{aligned} \varvec{x}(t)= & {} [V, \,\, \psi \,\,\gamma , \,\, x, \,\, y, \,\,h]^T, \,\,\,\varvec{x}(t) \in {\mathbb {R}}^6, \end{aligned}$$

(15)

$$\begin{aligned} \varvec{u}(t)= & {} [\alpha , \,\,\phi ]^T, \,\,\, \varvec{u} \in {\mathbb {R}}^2, \end{aligned}$$

(16)

where $\alpha$ is the angle of attack and $\phi$ is wing sweep angle. Dynamic soaring flight is then formulated as a nonlinear optimal control problem to find a control sequence that optimizes a certain performance measure [83]. Performance measures, such as, but not limited to minimum cycle time, maximum altitude gain, minimum wind shear required, maximum energy gain and minimum power/thrust required, are utilized to evaluate different aspects of dynamic soaring, defined in Eqs. (17) [10, 64, 66, 68] subject to the dynamic constraints presented by equations of motion specified in Eqs. (13–14), and satisfying the path and boundary constraints.

$$\begin{aligned} \begin{aligned} J=&\,\min \,(V_{w,\mathrm{ref}}),\\ J=&\,\min \,(T_\mathrm{cyc}), \\ J=&\,\max \,(h), \\ J=&\,\max \,(\mathrm{Energy})_\mathrm{gain},\\ J=&\,\min \,(\mathrm{Thrust}) \,\,\mathrm{or} \, \, \mathrm{min}\, (\mathrm{Power}). \end{aligned} \end{aligned}$$

(17)

Different modes of dynamic soaring (i.e., basic, loiter, and forward flight modes), as discussed in Sect. 2, are implemented through boundary constraints [52]. Boundary constraints for implementing dynamic soaring basic mode are presented in Eq. (18).

$$\begin{aligned} V_{t_{f}}= V_{t_0}, \psi _{t_{f}}= \psi _{t_0}, \gamma _{t_{f}}= \gamma _{t_0}, h_{t_{f}}= h_{t_0} +\Delta h, \end{aligned}$$

(18)

where $[V_{t_{0}}, \psi _{t_{0}}, \gamma _{t_{0}}, h_{t_{0}}]$ and $[V_{t_{f}}, \psi _{t_{f}}, \gamma _{t_{f}},h_{t_{f}}]$ represents the velocity, heading angle, flight path angle, and altitude at initial and final times, respectively. $\Delta h$ represents the net change in altitude after the maneuver is completed. For the UAV, to incorporate traveling mode of dynamic soaring, the initial and final orientation along east (i.e., x-axis) direction should be the same. Thus, boundary constraint, specified in Eq. (19) [68], needs to be added in addition to those specified in Eq. (18).

$$\begin{aligned} x_{t_{f}}= x_{t_0}. \end{aligned}$$

(19)

For the loiter pattern, the final coordinates after the completion of the maneuver must be exactly the same as the coordinates at the start of the maneuver. This requires that the boundary condition specified in Eq. (20) to be included [66], along with those specified in Eqs. (18) and (19).

$$\begin{aligned} y_{t_{f}}= y_{t_0}, h_{t_{f}}= h_{t_0}. \end{aligned}$$

(20)

Path constraints [52, 53, 68] for the states and control during the dynamic soaring maneuver are represented in Estimates. (21).

$$\begin{aligned}&V_{\min }<V<V_{\max } , \psi _{\min }<\psi<\psi _{\max }, \gamma _{\max }<\gamma<\gamma _{\min }\nonumber \\&x_{\min }<x<x_{\max } , y_{\min }<y<y_{\max }, h \ge 0, \phi _{\min }<\phi <\phi _{\max }\,\,,\nonumber \\ \end{aligned}$$

(21)

Since dynamic soaring is a high maneuvering cycle, which generates high accelerations, an additional path constraint of load factor is included [52]. This constraint specified in Eq. (22) ensures that UAVs structural bounds are not violated.

$$\begin{aligned} n=\frac{L}{W} \le n_{\max }, \end{aligned}$$

(22)

where $n_{\max }$ is the maximum permissible value. The constraint of load factor put limits on the maximum velocity during the dynamic soaring cycle, as represented in Eq. (23).

$$\begin{aligned} \begin{aligned}&n=\frac{L}{W}=\frac{q_ \infty SC_L}{{M}g} =\frac{0.5 \rho V^2 cbC_L}{{M}g},\\&V_{\max }=\sqrt{\frac{n {M}g}{0.5\rho S_{\min } C_L}}, \end{aligned} \end{aligned}$$

(23)

where g is the acceleration due to gravity, $q_ \infty$ is the free stream dynamic pressure, c is the wing chord and m is the UAV mass. Normalized energy [66] is defined in Eqs. ( 24):

$$\begin{aligned} \begin{aligned}&E_T = P.E + K.E \\&E_T = {M}gh + \frac{{M}v^2}{2}\\&E_{T_(\mathrm{norm})} =gh+ \frac{v^2}{2}\\ \end{aligned} \end{aligned}$$

(24)

5.3 Analysis of energy extraction process during dynamic soaring

Since the wind relative frame is not inertial, an induced force, $F_\mathrm{dyn}$ acts on the UAV [64], which is pictorially shown in Fig. (6) and is represented by Eq. (25):

$$\begin{aligned} \begin{aligned} {\dot{V}}&= \frac{1}{{M}}[-D-{M}gsin \gamma -\varvec{F}_\mathrm{dyn}]. \end{aligned} \end{aligned}$$

(25)

This dynamic soaring force, which is due to, wind shear is given by Eq. (26).

$$\begin{aligned} \begin{aligned} \varvec{F}_\mathrm{dyn}={M}{\dot{V}}_w. \end{aligned} \end{aligned}$$

(26)

Its projection along the direction of airspeed is given by Eq. (27).

$$\begin{aligned} \begin{aligned} \varvec{F}_\mathrm{dyn}={M}{\dot{V}}_w \cos \gamma \sin \psi . \end{aligned} \end{aligned}$$

(27)

For logarithmic wind shear (governed by Eq. (10)), the gradient is given by Eq. (28).

$$\begin{aligned} {\dot{V}}_\mathrm{W}=V_{w_{ref}} \frac{1}{h\ln (h_\mathrm{ref}/h_0)}{\dot{h}}. \end{aligned}$$

(28)

But from Eqs. (14),

$$\begin{aligned} {\dot{h}}=V \sin \gamma . \end{aligned}$$

(29)

So, Eq. (27) becomes Eq. (30).

$$\begin{aligned} \begin{aligned} \varvec{F}_\mathrm{dyn}={M} V_{w_\mathrm{ref}} \frac{1}{h \ln (h_\mathrm{ref}/h_0)}\cos \gamma \sin \psi \sin \gamma , \end{aligned} \end{aligned}$$

(30)

and Eq. (25) is transformed into Eq. (31).

$$\begin{aligned} \begin{aligned} {\dot{V}}&= \frac{1}{M}\left[ -D-{M}g\sin \gamma \right. \\&\quad \left. - {M} V_{w_\mathrm{ref}} \frac{1}{h \ln (h_\mathrm{ref}/h_0)}\sin \gamma \cos \gamma \sin \psi \right] . \end{aligned} \end{aligned}$$

(31)

In order to have sustained powerless flight, for extracting energy from wind shear, the velocity added by wind shear (third term) must be greater than or at least equal to that consumed by drag (first term). This requires that Estimates. (32) must be satisfied.

$$\begin{aligned} \begin{aligned} \sin \gamma \, \cos \gamma \, \sin \psi <0. \end{aligned} \end{aligned}$$

(32)

This can be achieved through windward climb and tailwind descend. During the windward climb phase, Estimates. (33) holds.

$$ \begin{aligned} \begin{aligned}&0<\gamma< \pi /2 \Rightarrow \sin \gamma \,\, \& \,\,\cos \gamma >0, \\&\pi< \psi<2\pi \quad or\, \, -\pi< \psi<0 \Rightarrow \sin \psi<0, \\&\text {so overall}, \,\,\sin \gamma \, \cos \gamma \, \sin \psi <0. \end{aligned} \end{aligned}$$

(33)

Similarly during the decent phase, Estimates. (34) holds.

$$ \begin{aligned} \begin{aligned}&-\pi /2<\gamma< 0 \Rightarrow \sin \gamma<0, \ \& \,\cos \gamma>0,\\&0< \psi<\pi \quad or\, \, -\pi< \psi<-2\pi \Rightarrow sin\psi >0,\\&\mathrm{so}\,\, \mathrm{overall}, \,\,\sin \gamma \, \cos \gamma \, \sin \psi <0. \end{aligned} \end{aligned}$$

(34)

UAV can, therefore, extract energy from the atmosphere, during both the climb and descent phase. In case the maneuver is reversed (windward descent or tailwind climb), the UAV will lose energy. Eq. (32) necessitates that, to acquire energy from atmospheric wind shear, product of sin$\gamma$ and sin$\psi$ must be negative, that is the UAV dives downwind or climbs upwind. If the maneuver is reversed (upwind dive or downwind climb), the UAV loses energy. So, a UAV can always extract energy from wind gradient, whether the gradient of wind shear is positive or negative.

6 Nonlinear trajectory optimization

6.1 Numerical techniques

With the exception of simple problems (e.g., the infinite-horizon linear quadratic problem [84]), optimal control/ trajectory optimization problems must be solved numerically [85,86,87,88]. Numerical methods for solving optimal control problems are, in general, divided into three major methods, namely, dynamic programming, direct methods and indirect methods [89]. Each of the three methods are then subdivided into different sub-methods, which are graphically shown in Fig. 7 and explained in following subsections.

• (i) Dynamic programming Dynamic programming [90] is an optimization approach that transforms a complex problem into a sequence of simpler problems. The optimality criterion in continuous time is based on the Hamilton–Jacobi–Bellman partial differential equation [90, 91].

• (ii) Indirect methods Indirect methods [91] utilizes calculus of variation to determine the first-order optimality conditions. In this approach, the original optimal control problem is transcribed to a boundary-value problem and the optimal solution is determined by solving the system of differential equations that satisfies endpoint and interior point conditions. The indirect approach leads to a multiple-point boundary-value problem that is solved to determine candidate optimal trajectories called extremals. Each of the computed extremals is then examined to see if it is a local minimum, maximum, or a saddle point. This approach relies on the necessary conditions of optimality that can be derived from Pontryagin’s Maximum Principle [92]. The three most common indirect methods are the indirect shooting method, the indirect multiple shooting method, and indirect collocation methods.

• (iii) Direct methods In direct methods, the continuous state and/or control parameters are discretized to transform the infinite-dimensional optimization problem to a finite dimension. The finite-dimensional problem is typically solved using an optimization method, such as nonlinear programming problem (NLP) technique. They are different from indirect methods in a way that they can be applied without deriving the necessary condition of optimality. Direct methods are categorized into shooting (direct shooting [93] and direct multiple shooting [94]) and collocation methods [95]. Direct shooting methods integrate the state equations directly between the nodes, while direct collocation methods use a polynomial approximation to the integrated state equations between the nodes. Generally, the optimal control problems are solved utilizing direct collocation technique [89]. Direct collocation method is a state and control parameterization method, where the state and control are approximated using a specified functional form. The two most common forms of collocation are local collocation [96] and pseudospectral (global orthogonal) collocation [96]. Local collocation has been employed using one of two categories of discretization, that is Runge–Kutta methods and orthogonal collocation method. [97,98,99]. In pseudospectral method [42, 100], parameterization of the state and control is done using global polynomials (basis function are Chebyshev or Lagrange polynomials), and collocating the differential-algebraic equations, using nodes obtained from a Gaussian quadrature.

Fig. 7

Numerical techniques for solving optimal control

6.2 Optimization softwares and numerical solvers

Different optimal control solvers were utilized by researchers to determine the optimal trajectories for dynamic soaring in different conditions. Sachs [49, 50, 67] determined energy-neutral dynamic soaring trajectory utilizing optimal control software ALTOS (Aerospace Launch Trajectory Optimization Software) [101]) and GESOP (Graphical Environment for Simulation and OPtimization)[102]. ALTOS is an optimization tool for aerospace vehicles and is an optimal trajectory finder. This is primarily because in the presence of several local minima, the initial guess can strongly influence the outcome of the solution. In another study, Sachs [103] calculated energy-neutral trajectories for dynamic soaring utilizing two other optimization software’s namely ’BOUNDSCO’ and ’TOMP’. The first program ’BOUNDSCO’ is based upon multiple shooting methodology, whereas ’TOMP’ is based on parameter optimization technique for determining optimal control.

Zao et al. [52, 68] converted dynamic soaring optimal control problem into parameter optimization via a collocation approach, and solved numerically with the software ”Nonlinear Programming Solver” (NPSOL) [104]. NPSOL is a suite of Fortran 77 subroutines designed for solving nonlinear programming problem. NPSOL uses a Sequential Quadratic Programming (SQP) algorithm, in which the search direction is the solution of a quadratic programming sub problem. The step size at each iteration is iteratively selected to produce a sufficient decrease in an augmented Lagrangian merit function. After a successful convergence, solutions of the NPSOL program represent a local optimal solution to the nonlinear programming problem. Liu et al. [105] utilized Imperial College London Optimal Control Software (ICLOCS) to solve the optimal control problem in conjunction with Matlab®. In this, optimal control problem is transcribed to a static optimization problem by employing direct multiple shooting, or is then solved utilizing the solver Interior Point OPTimizier (IPOPT) or Matlab®solver ’fmincon’. Goa et al. [64] proposed guidance-strategy for autonomous dynamic soaring utilizing GPOPS[106]. It is a general purpose software for solving optimal control problems. It utilizes variable-order adaptive orthogonal collocation methods together with sparse nonlinear programming and is designed to work with the NLP solvers Sparse Nonlinear OPTimizer (SNOPT) (commercial) and IPOPT (open source). Similarly, Akhtar et al. [57, 75] utilized a technique known as Inverse Dynamics in Virtual Domain (IDVD) to implement dynamic soaring trajectories. Combined with Matlab®solver ’fmincon’, nonlinear programming problem was solved to determine feasible trajectories. In another study, Akhtar et al. [10] utilized another technique, which was based on the direct method of Taranenko. The direct method is a nonlinear constrained optimization method, where reference polynomials are determined by the boundary conditions. Various other useful trajectory optimization softwares that can be applied to dynamic soaring, include PSOPT (pseudo spectral optimizer) [107], PROPT [108], Sparse Optimal Control Software (SOCS)[109] and A Mathematical Programming Language (AMPL)[110]. Complete details of all such solvers utilized in literature and cited in this paper are collected in Table 5.

Table 5 Softwares and NLP solvers used in trajectory optimization of dynamic soaring maneuvers

Table 6 UAV model and flight parameters

6.3 Generation of optimal trajectories

It has been noticed that throughout the literature, the optimal trajectories for the states and controls (Figs. 4 and 5 [64], Figs. 2 and 3 [68], Figs. 1, 3 and 4 [52]) are generated without much clarity or insight for how one can generate them. Therefore, we built optimal trajectories from the governing conditions specified in the previous subsection. This is to clarify and help the readers to understand and generate these curves by themselves. The UAV platform selected for this paper consists of a conventional radio controlled (RC) aircraft model, which is commercially available. It has a standard wing-tail configuration. The geometrical and flight model parameters of the UAV utilized in this study, are defined in Table 6.

The optimal trajectories for the states and control for implementing dynamic soaring loiter mode [66] are generated utilizing GPOPS-II [106]. It is an optimal control solver, which is based upon hp-adaptive Gaussian quadrature collocation technique and utilizes NLP solver IPOPT. Dynamic soaring trajectory optimization problem was configured utilizing the nonlinear equations of motion specified in Eqs. (14), state and control vectors defined by Eqs (15) and (10b), boundary constraints specified in Eqs. (18–20), path constraints specified in Estimates. (21), and wing load factor constraint specified in Eq. (22). The performance measure utilized for the generation of the optimized soaring trajectory is given by Eq. (35).

$$\begin{aligned} \begin{aligned} J=&\,\min \,(V_{w,\mathrm{ref}}),\\ \end{aligned} \end{aligned}$$

(35)

3-D perspective view of the optimized trajectory for dynamic soaring loiter mode is depicted in Fig. 8. To start with the loiter maneuver, the UAV turns into the headwind and gain height, trading kinetic energy with potential energy. At the highest point, it takes a steep turn and dives down with tailwind. It continues to descend until it reaches the lowest point trading potential energy for kinetic (gain in the velocity), until it reaches the minimum possible height. At that point, it takes the low altitude turn and returns to the original orientation to culminate the energy-neutral maneuver cycle.

Fig. 8

Optimized 3D dynamic soaring trajectory for loiter mode

The soaring trajectories along the inertial east, north and vertical axis are depicted in Fig. 9. As evident in Fig. 9, the UAV incorporates movement along all the three axis, that is inertial east, north and vertical axis to ensure loiter maneuver. The final location after the competition of the maneuver is exactly the same as that at the start of the maneuver.

The optimized trajectories of state and control variables are depicted in Fig. 10. The trajectories for the flight path angle and heading angles satisfy the constraints imposed for windward climb (see Estimates. (33)) and tailwind descent (see Estimates. (34)). During the climb phase, the UAV follows a trajectory, which maintains a heading angle within $-\,180^{\circ }$ to $0^{\circ }$ and the flight path angle $0^{\circ }$ to $90^{\circ }$. Similarly, during descent phase, heading angle is between $-\,180^{\circ }$ to $-\,360^{\circ }$ and flight path angle between $-\,90^{\circ }$ to $0^{\circ }$. This implies that the trajectory formulated for UAV ensures that the energy is extracted from wind shear during both the climb and ascend phase. Similarly, variation in bank angle during various phases of the maneuver shows that in both the high and low altitude turns, the bank angle takes on quite large values. Similarly, the required angle of attack is low during the initial climb phase of the maneuver. As the altitude increases, the velocity decreases, and the required angle of attack increases.

Fig. 9

UAV 2D trajectories for loiter mode

Normalized energy (total, potential and kinetic) as defined in Eqs.(24) are depicted in Fig. 11. The kinetic energy is turned into potential energy as the UAV gains height. After reaching maximum altitude, the UAV takes the high altitude turn and start its downwind flight, where the potential energy is traded for the kinetic energy. The overall energy at the start and end of the maneuver remains constant which ensures an energy-neutral cycle.

Formulation of minimum required wind shear to perform dynamic soaring pose a challenging numerical problem because of coupled and nonlinear nature of the equations of motion. The results indicate that the minimum required wind shear for dynamic soaring is 10.8 m/s at reference altitude of 10 m (Fig. 12). The speed decreases during the windward climb phase of the maneuver once the UAV climbs into the head wind, going to a bare minimum at the highest point. Then, the UAV takes a turn and starts descending in the direction of the wind. It starts to gain speed until it reaches the bare minimum level near the ground. At this point, the speed becomes maximum and the UAV is ready to repeat the maneuver.

Fig. 10

State and control trajectories. a State variables of optimized trajectory. b Control variables of optimized trajectory

The logarithmic wind model in Eq. (9) is transformed into Eqs. (36) for the stated configuration.

$$\begin{aligned} \begin{aligned}&V_{w,\mathrm{ref}}=10.8 \frac{ln(h/h_0)}{ln(10/0.03)}. \end{aligned} \end{aligned}$$

(36)

This follows that minimum required wind speeds for dynamic soaring at sea level conditions is around 6 m/s. Wind shear ascertained is of the magnitude, which normally exists over conventional environments (such as over sea, hills, rural areas and so on), making dynamic soaring possible over these areas.

7 Key challenges and some proposed solutions

In spite of dynamic soaring being an active area of research for over a century, dynamic soaring as a mean of energy extraction from atmospheric wind shear has not been furnished to the fullest. Dynamic soaring for UAVs has been confined to maneuvers, with far less benefits, than those acquired by soaring birds. This curtails the potential benefits envisaged from dynamic soaring. These immaturities are embodied in many aspects, which can be broadly categorized under two areas: (a) limitations in UAV design versatility, and (b) limitation in autonomous flight control system (FCS). In this section, we shall individually discuss both the issues that have greatly limited the potential benefits of dynamic soaring for UAVs. Then, we propose potential solutions.

Fig. 11

Normalized energy

Fig. 12

Optimal trajectories for minimum required wind shear

7.1 Limitations in UAV design versatility

One principal area that warrants considerable attention is the lack of the design versatility in the UAV utilized for dynamic soaring. The forces acting on the UAV during high-speed dynamic soaring maneuver is of the order of several times of the gravity, which necessitates design to bear such high stresses. Although efforts have been made in improving the material composition, finding a balance between the UAV design and the aerodynamic efficiency, while remaining within the weight limits, is still a problem for the designer. Soaring birds, such as albatross, which are of the size of a small UAV, make changes in its geometric configuration continually during dynamic soaring. The bird, while resting on its wings with a shoulder lock, skillfully, varies wing planform and twists, all without flapping, as it performs dynamic soaring maneuver [53, 61]. Incorporating to the most befitting planform configuration by adjusting parameters, such as wing sweep, span, dihedral and so on, the bird not only reduces the aerodynamic forces acting on the body, but also maximizes the energy gain from the wind shear during agile dynamic soaring maneuvers. This results in an energy efficient flight (under reduced stresses), in which different geometrical and aerodynamic parameters such as $(L/D)_{\max }$, sink speed, turning rate, glide range, cycle time, peak velocity, and max altitude are optimized via morphing.

Fig. 13

Drag variations with velocity and altitude. a Drag variations with velocity and altitude : span morphology. b Drag variations with velocity and altitude : sweep morphology

From the study of relevant literature and the cited papers (such as, but not limited to [54, 103, 112]), it is observed that dynamic soaring maneuver has not been studied for a morphing UAV. Since soaring birds acquire optimum energy from atmosphere during the dynamic soaring maneuver under morphing condition(s), it is envisaged that a biologically inspired platform having the capability to morph, like soaring birds, can best imitate nature and, therefore, will be able to acquire the maximum energy from atmosphere under much reduced aerodynamic forces.

Recently (2018), the authors of this paper proposed the idea of performing dynamic soaring under morphing conditions [60]. In that study, the morphing UAV can dynamically modify the wing parameters through sweep variation ($0^{\circ }$ and $50^{\circ }$) and span variation (1.25 m to 1.75 m). For analysis purpose, each of the two morphologies were compared against fixed wing configurations. Results indicate 15% lesser required wind shear by the span morphology and 14% lesser required wind shear by sweep morphology in comparison with the fixed configurations. Lesser wind shear requirement indicated that the morphing UAV could perform dynamic soaring in an environment, where fixed configurations might not, because of lesser available atmospheric wind shears. Apart from this, span morphology reduced drag by 15%, lift requirement by 11% and angle of attack requirement by 20%, whereas increased the maximum velocity by 6.2%, normalized energies by 9% and improved loitering parameters (approximately 10%), in comparison with fixed span configurations. Similarly, sweep morphology exhibited 20% reduced drag, $16\%$ lesser angle of attack requirement and improved loitering performance in comparison with the fixed configurations. Figure 13 reflects how both the morphologies significantly reduced the drag encountered during the flight to exhibit improved aerodynamic performance.

The results strongly support the idea of performing dynamic soaring under morphing conditions and its potential benefits as a future direction and a proposal for solving the problem of limitation in UAVs, when compared to the soaring birds. We recommend studying the impact of different morphologies (such as variations in wing twist, wing dihedral and so on) on dynamic soaring. In line with that, parametric studies can be then performed to determine the most beneficial morphology during distant phases of the maneuver.

7.2 Limitations in existing autonomous flight control system of soaring UAVs

The flight control system developed for soaring UAVs have been confined in literature to almost only linear control theory [46, 57, 65, 105, 113]. The focus is on formulating a linear control architecture, which computes the error between the desired and reference directions, and updating the required control effort. For instance, Lawrance [46] and Akhtar [57] developed guidance and control strategy based on linear proportion integral derivative (PID) controller. Deittert et al. [65] proposed a linearized control architecture-based on linear quadratic regulator (LQR) for maintaining the nominal soaring trajectories. Liu et al.[105] proposed model predictive control (MPC) system for a soaring UAV, to harvest the energy from the atmospheric updrafts. Bird et al. [113] examined closed-loop dynamic soaring by small autonomous aircraft, based on feedforward-feedback control design, which linearizes the trajectory about an equilibrium point. The mentioned studies indicate the fact that, for the most part, all developed guidance and control strategies utilize linear control theory. The technical problem with relying only on linear control theory that it does not fully capture the system actual nonlinear dynamics. Therefore, nonlinear control theory is a reasonable, possible, useful direction to try, especially if the linear control theory work fails for any reason. As a matter of fact, there is a very recent flight mechanics and control work [114] that has proposed nonlinear controllability as a tool to capture hidden details in the flight mechanics nonlinearity. In this regard, one can see that using nonlinear controllability can lead to new control mechanisms or new under actuated control placements. Very recently (2018) the authors of this review paper proposed a new nonlinear controllability perspective study of dynamic soaring [115]. In that study, the concepts of nonlinear controllability have been utilized to study an under actuated UAV performing dynamic soaring. Results indicate that there is a significant connection between the physics of dynamic soaring and nonlinear controllability analysis. This can lead to better in-depth control studies that can utilize the nonlinear dynamics of the under actuated UAV to optimize motion planning and/or creating new control strategies. In order to help the readers following what we meant by nonlinear controllability, we present below the notion of linear and nonlinear controllability [116]. Then, we formulate the nonlinear flight dynamics model used to study dynamic soaring, in a form, where it can be helpful for the reader to apply nonlinear controllability tools analogous to the formulation in [115].

7.2.1 Controllability

Controllability is one of the indispensable problem in control theory. It is a question about the ability to steer the system from a given initial point to a given final point in a finite time.

Controllability for linear systems For linear systems, the controllability question was answered by Kalman et al. [117]. The Kalman controllability rank condition is instrumental in the modern control theory, for it is necessary, sufficient, and easy to implement. A linear time-invariant system is typically written as in Eq. (37):

$$\begin{aligned} \begin{aligned} \dot{\varvec{x}}(t)=&\varvec{A}\, \varvec{x}(t) + \varvec{B}\, \varvec{u}(t), \\ \end{aligned} \end{aligned}$$

(37)

where $\varvec{x}\in {\mathbb {R}}^{n}$ is the state vector, $\varvec{u}\in {\mathbb {R}}^{m}$ is the control input vector, $\varvec{A}\in {\mathbb {R}}^{n\times n}$ is the state matrix and $\varvec{B}\in {\mathbb {R}}^{n\times m}$ is the input matrix. A necessary and sufficient condition for the controllability of the system (37) is that the controllability matrix defined by Eq. (38):

$$\begin{aligned} \begin{aligned} \varvec{C}=\begin{bmatrix} \varvec{B},\varvec{AB},\varvec{A^2B},...,\varvec{A^{n-1}B} \end{bmatrix}, \quad \varvec{C}\in {\mathbb {R}}^{n \times nm} \end{aligned} \end{aligned}$$

(38)

has full row rank (i.e., $rank(\varvec{C}) =n)$ [117].

Controllability for nonlinear systems For nonlinear systems, linearization can be used to determine local controllability about an equilibrium point, by using Kalman criteria (Eq. 38) for the linearized system. However, linearization only offers a sufficient condition for controllability. That is, the actual nonlinear system can be controllable about the equilibrium point, even if the linearized system is not. Linearization process for a nonlinear system in particular the control-affine system in the form of Eq. (39) is introduced.

$$\begin{aligned} \dot{\varvec{x}}(t) = \varvec{f}(\varvec{x}(t)) + \sum _{j=1}^m\varvec{g}_j(\varvec{x}(t)) {u}_j(t), \end{aligned}$$

(39)

where $\varvec{x}$ is the state vector evolving on an n-dimensional Manifold ${\mathbb {M}}^n$, $\varvec{f}$ is the drift vector field (uncontrolled dynamics), $\varvec{g}_j$’s represent the control vector fields corresponding to the inputs $u_j$’s. For driftless systems ($\varvec{f}\equiv \varvec{0}$), one can generate motion along the vector $\varvec{g}_k$ by turning on the control input $u_k$ and turning off all other controls. In literature, nonlinear controllability is mostly associated with differential geometric tools, known as geometric control theory (GCT) [118]. To analyze the outright nonlinear controllability of nonlinear systems, weaker controllability notions such as accessibility and small local time controllability (STLC) are often used in the literature of GCT. In addition to these notions, which are typically used to characterize controllability from a fixed point, the concept of local controllability (LC) is used within GCT to characterize controllability along a non-stationary reference trajectory. Formal definitions of these notions are found [116], pp. 371. The first step for any nonlinear controllability research is then to have the system under study in control-affine formulation/configuration, as has been stated in all theorems and conditions in [119,120,121,122,123,124,125].

7.2.2 Control-affine formulation of dynamic soaring

For the convenience of the reader, we configure the original dynamic soaring problem in the geometric control environment. The nonlinear system dynamics (nonlinear in control) described by Eqs. (13) or (14) is transformed into the desired control-affine form (linear in control) required by geometric control environment. This is done by adding two kinematic equations relating the previous inputs (roll angle $\phi$ and angle of attack $\alpha$, equivalently the pitch angle $\theta$) to the roll and pitch rates p and q, using Euler angles formulation [126, p. 105]. The control-affine form is represented in Eqs. (40).

$$\begin{aligned} \begin{aligned} {\dot{V}}&= \frac{1}{{M}}[-D-{M}g\sin \gamma -{M}{\dot{V}}_\mathrm{W}\cos \gamma \sin \psi ], \\ {\dot{\gamma }}&=\frac{1}{{M}V}[L\cos \phi -{M} g\cos \gamma +{M}{\dot{V}}_\mathrm{W}\sin \psi \sin \gamma ],\\ {\dot{\psi }}&=\frac{1}{{M}V\cos \gamma }[L\sin \phi -{M} {\dot{V}}_\mathrm{W}\cos \psi +q\sin \phi \sec \theta ], \\ {\dot{x}}&= V\cos \gamma \sin \psi +V_\mathrm{W},\\ {\dot{y}}&= V\cos \gamma \cos \psi , \\ {\dot{h}}&=V\sin \gamma ,\\ {\dot{\phi }}&=p+q \sin \phi \tan \theta ,\\ {\dot{\theta }}&=q \cos \phi ,\\ \end{aligned} \end{aligned}$$

(40)

where $\theta$ is the pitch angle and $\gamma$ is the flight path angle. Moreover, p and q represents roll and pitch rates. Also $\alpha =\theta -\gamma$. The state variables for the transformed system is defined in Eq. (41).

$$\begin{aligned} \varvec{x}(t)= [V,\psi ,\gamma , x, y, h,\phi , \theta ]^T, \quad \varvec{x}(t) \in {\mathbb {R}}^8. \end{aligned}$$

(41)

Control variables are defined by Eq. (42).

$$\begin{aligned} \varvec{u}(t)= [p,q] , \quad \varvec{u} \in {\mathbb {R}}^2. \end{aligned}$$

(42)

That is, the UAV dynamics (40) can then be written in the control-affine form

$$\begin{aligned} \dot{\varvec{x}} = \varvec{f}(x) +\varvec{g_p}p +\varvec{g_q}q, \end{aligned}$$

(43)

where the drift vector field $f(\varvec{x})$, which includes the uncontrolled dynamics, and the two control input vector fields $\varvec{g}_p$ and $\varvec{g}_q$ associated with the two control inputs p and q are written as

$$\begin{aligned} f(\varvec{x})=\begin{bmatrix} \frac{1}{{M}}[-\frac{\rho V^2}{2} S(C_{D_o}+\frac{1}{e\cdot AR}(C_{L_\alpha }(\theta - \gamma ) - C_{L_0})^2) -{M}g\sin \gamma -m {\dot{V}}_\mathrm{W} \cos \gamma \sin \psi ] \\ \frac{1}{{M}V}[\frac{1}{2}\rho V^2 SC_{L_\alpha } ((\theta - \gamma ) -\alpha _{L=0}) \cos \phi -{M} g\cos \gamma +{M} {\dot{V}}_\mathrm{W} \sin \psi \sin \gamma ]\\ \frac{1}{{M}V\cos \gamma }[\frac{1}{2}\rho V^2 SC_{L_\alpha } ((\theta - \gamma ) -\alpha _{L=0})\sin \phi -{M} {\dot{V}}_\mathrm{W} \cos \psi ]\\ V\cos \gamma \sin \psi +V_\mathrm{W}\\ V\cos \gamma \cos \psi \\ V\sin \gamma \\ 0\\ 0 \end{bmatrix}, \end{aligned}$$

(44)

The control input fields associated with the two control inputs are expressed in Eq. (45).

$$\begin{aligned} \varvec{g}_p=\begin{bmatrix} 0\\0\\0\\0\\0\\0\\1\\0 \end{bmatrix} \varvec{g_q}=\begin{bmatrix} 0\\0\\\sin \phi \sec \theta \\0\\0\\0\\\sin \phi \tan \theta \\\cos \phi \end{bmatrix}. \end{aligned}$$

(45)

8 Conclusion

In this paper, we discussed and comprehensively summarized the dynamic soaring nonlinear phenomena, and specifically, its application to UAVs. The most important conclusions from this study are summarized below:

• (a) Consolidation of available information A detailed review of the dynamic soaring from the view of energy transformation is presented. Important studies performed by researchers, dating back from Lord Rayleigh (who first proposed the concept of dynamic soaring in 1883) up to date, are elaborated. Methods for estimating wind shear were documented, and different optimization techniques available for implementing dynamic soaring are discussed.

• (b) Exploration of design space Several design variables of the dynamic soaring maneuver are identified that are most suitable for efficient execution. Parametric characterization of the key performance parameters was performed in which parameters such as, peak altitude/speeds attained during the soaring maneuvers, cycle time, minimum wind shear required and so on, are documented. Aerodynamic and mass parameters for both the soaring birds and UAVs utilized in literature were identified.

• (c) Survey of nonlinear trajectory optimization methodologies Survey of the optimization algorithms available for performing nonlinear trajectory optimization for implementing dynamic soaring maneuver was performed. This presented a comprehensive insight into various techniques that have been utilized in literature by different researchers for dynamic soaring applications.

• (d) Problem formulation and generation of optimal trajectories A detailed explanation for how one can build a nonlinear mathematical model for the components of dynamic soaring process, was presented. Moreover, we generated, and by steps, the dynamic soaring optimized trajectory to guide the reader for how this can be achieved.

• (e) Existing limitations and a way forward This review identified some of the important challenges/obstacles faced by sUAVs when they perform dynamic soaring, which are curtailing the utility of dynamic soaring. The immaturities encountered embodied in two major areas namely: (a) limitations in design versatility of UAVs utilized for dynamic soaring, and (b) limitations in the autonomous flight control system (FCS) of the soaring UAVs. Both the mentioned issues were individually discussed. Moreover, we did propose some research directions which involved integration of two fundamental concepts of morphology, and nonlinear controllability utilizing geometric control, with dynamic soaring to solve these issues. These proposals are state of art, supported by very recent publications, and may have good potentials to open up a lot of research and investigations.

The objective of this paper is not only to present a consolidated platform, where all available information regarding dynamic soaring is available, but also identify the challenges encountered along with potential solutions and their positive impact. This study then shall serve as a good starting point and/or as a comprehensive reference/documentation, for scholars interested in extending their knowledge about the topic, and/or work on a research track that is concerned with dynamic soaring application to UAVs.