1 Introduction

Vibrational resonance (VR) is a typical nonlinear phenomenon. The classic VR theory was first proposed by Landa and McClintock [1]. When VR occurs, the response of the nonlinear system to a weak low-frequency signal can be excellently improved by a high-frequency signal. Among them, the character signal used to express the useful information is usually a weak low-frequency signal. The auxiliary signal which is often a high-frequency signal does not indicate any useful information and is only used to enhance the character signal. Specifically, the response amplitude at the driving low frequency is a nonlinear function of the amplitude or the frequency of the auxiliary signal [2,3,4,5,6,7]. In the early stage of the VR investigations, the character signal in the excitations was usually presented as a low frequency. As the research has been further developed, researchers have found that the VR not only occurs at the driving low frequency, but also at the subharmonic and superharmonic frequencies in the nonlinear framework [8,9,10]. Recently, we have proposed a re-scaled VR method [11]. Through matching the system parameters with the character signal, the re-scaled VR can occur at an arbitrary driving frequency and the weak character signal with an arbitrary frequency can be enhanced by the re-scaled VR method.

Besides the weak harmonic signal, the classic VR method can also improve the weak aperiodic signal. Chizhevsky and Giacomelli have detected the weak aperiodic signal by the aperiodic VR method in theoretical and experimental ways in the asymmetric bistable system [12]. The degree of enhancement of the weak aperiodic signal can be measured by the cross-correlation coefficient between the output series and the input aperiodic signal. In spite that all the works done in VR, to our knowledge, there is no work that has discussed the matching problem between the weak aperiodic signal and the nonlinear system parameters. This concerns the realization of the aperiodic VR and how to obtain the optimal aperiodic VR. Furthermore, this is also the main motivation of the present work.

We consider the following dimensionless system,

$$\begin{aligned} \frac{{\text {d}x(t)}}{{\text {d}t}} = ax(t) - bx(t){\left| {x(t)} \right| ^{\alpha - 1}} + s(t) + F(t), \end{aligned}$$
(1)

where \(a>0\), \(b>0\) and \(\alpha >1\), to investigate the aperiodic VR in detail. Moreover, the parameter \(\alpha \) can be an integer or a fractional number and the function s(t) is the character signal, which is a weak aperiodic signal in the bipolar binary form and is defined as

$$\begin{aligned} \begin{array}{l} s(t) = A \sum \limits _{j = - \infty }^{ + \infty } {R_j}\varGamma (t - jT) \\ \mathrm{{\Gamma (t)}} = \left\{ \begin{array}{ll} 1, &{} t \in [0,\;T] \\ 0, &{} \notin [0,\;T] \\ \end{array} \right. \\ \end{array} \end{aligned}$$
(2)

In the previous equation, A is the amplitude of the aperiodic signal. \(R_j\) is a random number generator of \(+\,1\) or \(-\,1\) with an independent Gaussian distribution. \(\varGamma (t)\) is a pulse with width T, and T is the minimal random pulse width of the aperiodic signal. The auxiliary signal F(t) is a square waveform function and is defined as

$$\begin{aligned} F(t) = B{\mathrm{sgn}} [\cos \varOmega t], \end{aligned}$$
(3)

where B is the strength of the signal. What is worth mentioning is the potential function of the system

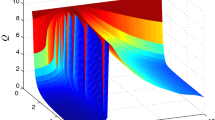
$$\begin{aligned} V(x) = -\, \frac{a}{2}{x^2} + \frac{b}{{\alpha + 1}}{\left| x \right| ^{\alpha + 1}}. \end{aligned}$$
(4)

This kind of potential is widely used in modeling many real systems. Its physical background has been described in detail in some former literatures [13,14,15]. In this paper, the nonlinear model of Eq. (1) is considered as a signal processor. When \(\alpha =3\), the potential degenerates to the classic bistable potential and the system in Eq. (1) turns to the usual double-well bistable system. There are one unstable equilibrium \(x_0=0\) and two stable equilibria \(x_{1,2}=\,\pm \, {(\frac{a}{b})^{\frac{1}{{\alpha - 1}}}}\) in Eq. (1). We show the curves of the potential function for different values of the fractional-order exponent \(\alpha \) in Fig. 1. The bistable structure of the potential is clearly displayed.

Fig. 1
figure 1

The bistable potential function of Eq. (4) for different fractional-order exponent values. The system parameters are \(a=1\) and \(b=1\)

Full size image
Fig. 2
figure 2

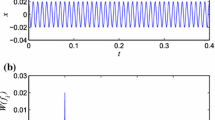
The time series of the output under different strength values of the auxiliary square waveform signal. The red thick line is the input aperiodic signal, and the blue thick line is the output of the system. a \(B=1\), b \(B=2\), c \(B=4\). Other simulation parameters are \(a=1\), \(b=1\), \(\alpha =5\), \(A=0.3\), \(T=20\) and \(\varOmega =4\)

Full size image

The rest of the paper is organized as follows. In Sect. 2, the classic aperiodic VR in Eq. (1) is presented. Effects of the fractional-order exponent \(\alpha \) and the aperiodic signal parameters on the aperiodic VR are our focus in this section. In Sect. 3, the re-scaled aperiodic VR method is proposed to realize the aperiodic VR with an arbitrary minimal random pulse width. In Sect. 4, the twice sampling aperiodic VR method is put forward to improve the weak aperiodic signal with an arbitrary minimal pulse width. The re-scaled aperiodic VR and the twice sampling VR are new methods first proposed in the aperiodic signal excited system. In Sect. 5, some further discussions on the two methods are given. Finally, we end this work with the main conclusions.

2 The classic aperiodic VR

There is no doubt that the response to the weak aperiodic signal depends on the auxiliary square waveform signal. To explain this better, we give Fig. 2 as an example, in which the response is obtained under different strength values of the auxiliary square waveform signal. As is well known, in the stochastic resonance (SR) phenomenon [16], the SR can be explained as a particle moving in the potential wells. The response of the system is the trajectory of the particle. When the particle crosses the wells synchronized with the input signal, the SR occurs and the weak input signal is improved. Moreover, a too strong or too weak noise intensity cannot make the particle trajectory go across the potential wells synchronized with the input signal. Only an appropriate dose of noise can do it. Similarly, the occurrence of VR can also be explained in a similar way. Apparently, in Fig. 2a, the auxiliary square waveform signal is too weak and it cannot induce the particle trajectory to cross the potential wells synchronized with the input aperiodic signal. Hence, the weak aperiodic signal cannot be improved. In Fig. 2c, the auxiliary square waveform signal is too strong. Although the particle trajectory crosses between the two wells, the trajectory does not synchronize with the input aperiodic signal. As a result, the weak aperiodic signal cannot be improved neither. Only in Fig. 2b, the particle trajectory crosses the potential barrier synchronized with the input aperiodic signal. As a result, the weak aperiodic signal is enhanced to a great extent. In other words, the aperiodic VR occurs in Fig. 2b. Due to the widely existence of the weak aperiodic signal in science and engineering fields, it is very important to choose the strength of the auxiliary signal to induce the occurrence of VR and improve the weak input aperiodic signal.

Further analysis is needed to quantify the occurrence of the aperiodic VR. The cross-correlation coefficient is an effective index to measure the similarity between two time series. When the cross-correlation coefficient between the output and the input aperiodic signal achieves the maximal value, the signal may be improved greatly. The cross-correlation coefficient between the output and the input of the aperiodic signal is defined by

$$\begin{aligned} {C_\mathrm{sx}} = \frac{{\mathop \sum \nolimits _{j = 1}^n [s(j) - {\bar{s}}][x(j) - {\bar{x}}]}}{{\sqrt{\mathop \sum \nolimits _{j = 1}^n {{[s(j) - {\bar{s}}]}^2}\mathop \sum \nolimits _{j = 1}^n {{[x(j) - {\bar{x}}]}^2}} }}, \end{aligned}$$
(5)

where \({\bar{s}}\) and \({\bar{x}}\) are average values of the input aperiodic signal and the output time series, respectively.

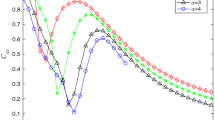
In Fig. 3, the weak input aperiodic signal is still used to obtain the \(C_\mathrm{sx}-B\) curve under different values of the fractional-order exponent \(\alpha \). All curves in this figure achieve their peaks with the increase of B. As a result, the aperiodic VR occurs and the weak aperiodic signal is improved. Another important fact in the figure is that all curves achieve their peaks at almost the same point. In particular, the peak value and the peak location are independent of the fractional-order exponent. We believe this is an important and interesting finding.

Fig. 3
figure 3

The dependence of the cross-correlation coefficient on the strength of the auxiliary square waveform signal under different values of the fractional-order exponent. The simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(T=20\) and \(\varOmega =4\)

Full size image

To make the dependence of the cross-correlation coefficient on the fractional-order exponent much clearer, a color code plot of the value of \(C_\mathrm{sx}\) in a two-dimensional plane in function of B and \(\alpha \) is illustrated in Fig. 4. The figure shows that the peak value and the peak location of the \(C_\mathrm{sx}-B\) curve are independent of the fractional-order exponent \(\alpha \) once again.

Fig. 4
figure 4

Contour plot of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the strength of the auxiliary square waveform signal B and the fractional-order exponent \(\alpha \). Different colors represent different numerical values of \(C_\mathrm{sx}\). The simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(T=20\) and \(\varOmega =4\)

Full size image
Fig. 5
figure 5

The dependence of the cross-correlation coefficient on the fractional-order exponent \(\alpha \) for different values of the amplitude of the auxiliary signal B. The simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(T=20\) and \(\varOmega =4\)

Full size image
Fig. 6
figure 6

The time series of the output for different strength values of the fractional-order exponent \(\alpha \). The red thick line is the input aperiodic signal, and the blue thick line is the output of the system. a \(\alpha =1.3\), b \(\alpha =2\), c \(\alpha =3\), d \(\alpha =7\). Other simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(T=20\), \(B=2\) and \(\varOmega =4\)

Full size image

In Fig. 5, we show the cross-correlation coefficient reaching a maximal value for different values of B, with the increase of \(\alpha \). If B is a large value, such as \(B=3\), the resonance curve is much more evident. After the peak, the cross-correlation coefficient decreases with the increase of B. If B has a little smaller value, such as \(B=2\), the cross-correlation coefficient rises rapidly and then keeps almost fixed, though slightly increasing. To explain this phenomenon, Fig. 6 shows the time series of the output for \(B=2\) and different values of \(\alpha \), where the aperiodic VR is observed. In each subplot, the output crosses the potential barrier with the input aperiodic signal synchronously. However, the amplitude of the output is different in each subplot. Obviously, with the increase of the fractional-order exponent \(\alpha \), the amplitude of the output decreases. With the aid of the information provided by Fig. 6, we can understand better the curve corresponding to \(B=2\). Specifically, for \(B=2\) in Fig. 5, with the increase of \(\alpha \), the amplitude of the output decreases, but the waveform is closer similar to the input aperiodic signal. It results that the VR always occurs for values of B above a certain critical value as shown in Fig. 5.

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of A is illustrated in Fig. 7. This allows us to investigate the effect of the weak aperiodic signal amplitude A on the cross-correlation coefficient. As it can be seen, the resonance peak corresponds to larger values of the amplitude of the aperiodic signal. Another fact in this figure is that the location of the resonance peak turns to the left with the increase of A. Moreover, for the same value of A, the value and location of the resonance peak are independent of the fractional-order exponent \(\alpha \). Similar results are shown in Figs. 3 and 4.

Fig. 7
figure 7

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of A. a \(\alpha =2\), b \(\alpha =2.5\), c \(\alpha =3\), d \(\alpha =3.5\), e \(\alpha =5\), f \(\alpha =7\). Other simulation parameters are \(a=1\), \(b=1\), \(T=20\) and \(\varOmega =4\)

Full size image

In Fig. 8, the effect of the minimal random pulse width T on the cross-correlation coefficient is investigated. The resonance peak of the cross-correlation coefficient is also larger for larger values of T. It is easy to understand that the effect of the pulse width here is similar to the effect of the low frequency in the classical VR phenomenon where a typical nonlinear system is excited by a bi-harmonic signal. Specifically, a lower-frequency weak signal can induce a stronger VR in the bi-harmonic excited nonlinear system.

Fig. 8
figure 8

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of T. a \(\alpha =2\), b \(\alpha =2.5\), c \(\alpha =3\), d \(\alpha =3.5\), e \(\alpha =5\), f \(\alpha =7\). Other simulation parameters are \(a=1\), \(b=1\), \(A=0.3\) and \(\varOmega =4\)

Full size image

To investigate the effect of the minimal random pulse width further, we plot the dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the pulse width T for different values of B in Fig. 9, where T is a control parameter. For different values of B, the cross-correlation coefficient increases with the increase of T. However, for small values of T, the cross-correlation coefficient may be also very small. This indicates that there is no aperiodic VR and the weak aperiodic signal cannot be improved by the auxiliary square waveform signal. Precisely for that reason, we propose two methods in the following sections to solve this problem. By the new methods, the aperiodic VR can occur in any value of the minimal random pulse width, leading to an improvement of the aperiodic signal with any minimal random pulse width.

3 The re-scaled aperiodic VR

For small values of T, we need to find appropriate system parameters to match the character signal. Here, we propose the re-scaled aperiodic VR method to realize it. The inspiration comes from the re-scaled SR and the re-scaled VR. The re-scaled SR is widely used in the engineering fields, such as in the subfield of fault diagnosis [17,18,19]. The re-scaled VR can be used to improve the weak harmonic signal with an arbitrary frequency [11, 20]. Herein, we introduce the re-scaled idea to deal with the bipolar binary signal with an arbitrary minimal random pulse width. The method is as follows. At first, we introduce variable substitutions,

$$\begin{aligned} \tau = \beta t,\quad x(t) = z(\tau ), \end{aligned}$$
(6)

where \(\beta \) is the scale parameter. Then, Eq. (1) becomes

$$\begin{aligned} \frac{{\text {d}z\left( \tau \right) }}{{\text {d}\tau }}= & {} \,\frac{a}{\beta }z\left( \tau \right) - \frac{b}{\beta }z\left( \tau \right) {\left| {z\left( \tau \right) } \right| ^{\alpha - 1}} + \frac{1}{\beta }s\left( \frac{\tau }{\beta }\right) \nonumber \\&+ \,\frac{1}{\beta }F\left( \frac{\tau }{\beta }\right) . \end{aligned}$$
(7)
Fig. 9
figure 9

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the pulse width T for different values of B. The simulation parameters are \(a=1\), \(b=1\), \(\alpha =3.5\), \(A=0.3\) and \(\varOmega =4\)

Full size image

Each minimal random pulse width in the re-scaled system is amplified \(\beta \) times with respect to the original system. By choosing an appropriate scale parameter \(\beta \), we can find the match condition of T with the system parameters a and b. Meanwhile, we must note that the dynamics of Eq. (7) is not equivalent to Eq. (1). This is because the amplitudes of the two signals are reduced to \(1/\beta \) of the original ones. We obtain Eq. (7) only to obtain the scale match condition. Hence, we need to amplify the signal to its \(\beta \) times strength in Eq. (7). As a result, we get Eq. (8),

$$\begin{aligned} \frac{{\text {d}z(\tau )}}{{\text {d}\tau }}= & {} \,\frac{a}{\beta }z(\tau ) - \frac{b}{\beta }z(\tau ){\left| {z(\tau )} \right| ^{\alpha - 1}} \nonumber \\&+\, s\left( \frac{\tau }{\beta }\right) + F\left( \frac{\tau }{\beta }\right) . \end{aligned}$$
(8)
Fig. 10
figure 10

Contour plot of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the strength of the auxiliary square waveform signal B and the scale parameter \(\beta \). A color code plot shows the value of \(C_\mathrm{sx}\). The simulation parameters are \(a=1\), \(b=1\), \(\alpha =3\), \(A=0.3\), \(T=0.2\) and \(\varOmega =100\pi \)

Full size image
Fig. 11
figure 11

Three waveforms of the aperiodic signal for different values of T. a \(T=0.4\), b \(T=0.2\) and c \(T=0.1\)

Full size image
Fig. 12
figure 12

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of T. a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a_1=1\), \(b_1=1\), \(\beta =100\), \(A=0.3\) and \(\varOmega =\frac{20\pi }{T}\)

Full size image

To simplify it, we let

$$\begin{aligned} {a_1} = \frac{a}{\beta },\quad {b_1} = \frac{b}{\beta }, \end{aligned}$$
(9)

so that Eq. (8) becomes

$$\begin{aligned} \frac{{\text {d}z(\tau )}}{{\text {d}\tau }}= & {} \,a_1 z(\tau ) - b_1 z(\tau ){\left| {z(\tau )} \right| ^{\alpha - 1}} + s\left( \frac{\tau }{\beta }\right) \nonumber \\&+\, F\left( \frac{\tau }{\beta }\right) . \end{aligned}$$
(10)

From above deductions, we need to realize the aperiodic VR in the equation

$$\begin{aligned} \frac{{\text {d}x(t)}}{{\text {d}t}}= & {} \,a_1 \beta x(t) - b_1 \beta x(t){\left| {x(t)} \right| ^{\alpha - 1}} \nonumber \\&+ \,\beta s(t) + \beta F(t), \end{aligned}$$
(11)

to improve the aperiodic bipolar binary signal with the arbitrary minimal random pulse width by the aperiodic VR method. In other words, if T is small, we need to find appropriate system parameters to amplify the input character and auxiliary signals according to Eq. (11). Then, the aperiodic VR occurs and the weak aperiodic signal is enhanced. Next, we will verify the validity of this method by using some examples.

In Fig. 10, we have plotted the contour plot of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the strength of the auxiliary square waveform signal B and the scale parameter \(\beta \) and fixed \(T=0.2\). As pointed out in last section, if we use the classic aperiodic VR method, there is no resonance phenomenon and the weak aperiodic signal cannot be improved. However, by using the re-scaled aperiodic VR method, the resonance appears. In other words, the weak aperiodic signal is greatly improved, which indicates the validity of the proposed method. The effect of different parameters such as B, \(\beta \), T on the cross-correlation coefficient will be discussed later in detail.

Three waveforms of the aperiodic signal for different values of T are shown in Fig. 11. They have similar wave profiles but with different values of the pulse width T.

In Fig. 12, we show that for different values of \(\alpha \) and T, the re-scaled aperiodic VR occurs. Actually, the three waveform signals shown in Fig. 11 are used as input aperiodic signals. Hence, the weak aperiodic signal can be improved by the re-scaled aperiodic VR method although the minimal random pulse width is very small, showing once again the validity of the method.

In Fig. 13, the curves of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the auxiliary square waveform signal strength B and for different values of parameter \(\beta \) are shown. The magnitude and location of the resonance peak closely depend on the scale parameter \(\beta \), because different scale parameter changes each pulse width to a different value. In other words, the aperiodic signal is stretched to a different length when a different value of \(\beta \) is chosen. For a larger value of \(\beta \), we can obtain a much stronger resonance. As a result, the weak aperiodic signal can be improved to a greater extent.

Fig. 13
figure 13

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of \(\beta \) for a fixed value of T. a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a_1=1\), \(b_1=1\), \(A=0.3\), \(T=0.2\) and \(\varOmega =100\pi \)

Full size image

In Fig. 14, we show once again the curves of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the auxiliary square waveform signal strength B. However, differently from the previous case in Fig. 13, we have fixed \(\beta \) and T in each subplot. As a result, the three curves of \(C_\mathrm{sx}-B\) in each subplot are almost identical for the same value of \(\alpha \). In other words, the dynamical behavior of the re-scaled system depends only on the parameters \(\beta \) and T. Hence, although T may be very small, we can make strong resonance to occur if we choose a large enough scale parameter \(\beta \).

Fig. 14
figure 14

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of \(\beta \) and T. a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a_1=1\), \(b_1=1\), \(A=0.3\) and \(\varOmega =20\pi /T\)

Full size image

4 The twice sampling aperiodic VR

Besides the re-scaled method, there are some other ways to improve the weak signal. The twice sampling SR method is one of them [21]. It has been successfully used in the field of fault diagnosis [22, 23]. Here, we introduce this method in the investigation of the aperiodic VR phenomenon. The method is as follows. First, we change the sampling frequency of the signal to reconstruct the signal. Specifically, if the original sampling frequency is \(f_{\mathrm{s}0}\), we let the twice sampling frequency to be \(f_\mathrm{s}\). The formula \(\gamma =f_{\mathrm{s}0}/f_\mathrm{s}\) expresses the sampling transform ratio. Through twice sampling, we get a new signal and its minimal pulse width turns to \(\gamma \) times of the original one. Then, we let the new signal to act as the new input for the nonlinear system. If the transform ratio is an appropriate value, we can make the aperiodic VR to occur. Finally, we reconstruct the output to the original sampling according to the sampling transform ratio. The new output is compared with the original signal to calculate the cross-correlation coefficient. At the peak of the cross-correlation coefficient curve, the resonance may occur showing that the weak aperiodic signal has been improved. Some examples to verify the effectiveness of the twice sampling aperiodic method are given in the following.

Fig. 15
figure 15

Contour plot of the cross-correlation coefficient \(C_\mathrm{sx}\) versus the strength of the auxiliary square waveform signal B and the scale parameter \(\gamma \). A color code plot shows the value of \(C_\mathrm{sx}\). The simulation parameters are \(a=1\), \(b=1\), \(\alpha =3\), \(A=0.3\), \(T=0.2\) and \(\varOmega =100\pi \)

Full size image
Fig. 16
figure 16

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of T. a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(\gamma =100\) and \(\varOmega =\frac{20\pi }{T}\)

Full size image

In Fig. 15, the cross-correlation coefficient versus the strength of the auxiliary square signal and the sampling transform ratio is displayed for an aperiodic signal with \(T=0.2\). On the one hand, for an appropriate value of \(\gamma \), the curve of \(C_\mathrm{sx}-B\) presents a resonance peak at which the weak aperiodic signal is improved. On the other hand, for a fixed value of B, the resonance peak on the \(C_\mathrm{sx}-B\) curve may also be induced by the sampling transform ratio \(\gamma \). In the following, we discuss in detail the effects of some important parameters on the twice sampling aperiodic VR method.

In Fig. 16, we plot the dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of T. The \(C_\mathrm{sx}-B\) curves have been plotted by the twice sampling aperiodic VR method for different values of \(\alpha \) and T, where we have used the three waveform signals of Fig. 11. These curves are almost identical to the corresponding results shown in Fig. 12. This indicates the effectiveness of the twice sampling aperiodic VR once again. Applying these two different methods, i.e., the re-scaled aperiodic VR method and the twice sampling aperiodic VR method, we have the same results. The aperiodic weak signal with an arbitrary minimal random pulse width can be improved by one of the two methods. Again in Fig. 16, it is easy to find that the resonance peak has a large value for a large T and when the corresponding B is small.

Fig. 17
figure 17

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of \(\gamma \). a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a=1\), \(b=1\), \(A=0.3\), \(T=0.2\) and \(\varOmega =100\pi \)

Full size image
Fig. 18
figure 18

The dependence of the cross-correlation coefficient \(C_\mathrm{sx}\) with respect to the strength of the auxiliary square waveform signal B for different values of \(\gamma \) and T. a \(\alpha =2.5\), b \(\alpha =3\), c \(\alpha =3.5\), d \(\alpha =5\). Other simulation parameters are \(a=1\), \(b=1\), \(A=0.3\) and \(\varOmega =\frac{20\pi }{T}\)

Full size image

In Fig. 17, the effect of the sampling transform ratio \(\gamma \) on the cross-correlation coefficient is illustrated. If we choose a large value of \(\gamma \), it means that the minimal random pulse width of the re-constructed signal is large too. As a consequence, the resonance peak also has a large value. Comparing Fig. 17 with Fig. 13, we find that the effect of the transform ratio \(\gamma \) in the twice sampling aperiodic VR method is the same as the effect of the scale parameter \(\beta \) in the re-scaled aperiodic VR method.

Fig. 19
figure 19

The time series of the output when the resonance occurs, a re-scaled aperiodic VR method, b twice sampling aperiodic VR method. The red thick line is the input aperiodic signal, and the blue thick line is the output of the system. The simulation parameters are \(a=1\), \(b=1\), \(\alpha =3\), \(A=0.3\), \(T=0.2\), \(B=2\) and \(\varOmega =100\pi \)

Full size image

In Fig. 18, although the three original signals have different minimal random pulse width, the re-constructed signals have the same waveform by choosing an appropriate transform ratio \(\gamma \). In other words, the corresponding random pulse widths are identical in the three re-constructed signals. Consequently, the \(C_\mathrm{sx}-B\) curves in each subplot are completely identical, as it can be seen by comparing Fig. 18 with Fig. 14.

To illustrate the two methods further, in Fig. 19, the time series of the signals when the resonance occurs are shown. Although the two time series are obtained by two different methods, they have the same waveform. In the two subplots, the weak aperiodic signal is improved excellently. It indicates the validity of the re-scaled aperiodic VR method and the twice sampling aperiodic VR method once again.

5 Some further discussions

The equivalent of the re-scaled VR method and the twice sampling VR method lies in the choose of the scale parameter \(\beta \) and the sampling transform ratio \(\gamma \). It can be easily understood in a mathematical viewpoint. On the one hand, in Sect. 3, we have deduced that the re-scaled VR is realized in Eq. (11). The dynamics (response amplitude to the excitations) of Eq. (11) is equivalent to that of Eq. (10). Further, when \(a_1\), \(b_1\), and \(\beta T\) in Eq. (10) equals a, b and T in Eq. (1), respectively, Eq. (10) turns to Eq. (1). Hence, the dynamics (response amplitude to the excitations) of Eq. (11) is the same as that of Eq. (1) for this case. On the other hand, according to the description in the first paragraph of Sect. 4, by twice sampling procedure, the time scale of the excitations is \(1/\gamma \) times of the original time scale. In other words, the minimal random pulse width changes to be \(\gamma T\) after the twice sampling processes. As a result, the new re-constructed signal has been changed to a slow varied one. At the same time, the system parameters in Eq. (1) are still adopted. When \(\gamma T\) (T is a small value of the signal before the twice sampling procedure) equals T (T is a large value) in Eq. (1), the response amplitude of the system to the re-constructed signal is to be calculated in Eq. (1) in fact. After the output, the time series need to be transformed to the original time scale according to the transform ratio \(\gamma \). Simultaneously, the transform here only changes the time scale but not changes the amplitude of the output. Hence, the final response amplitude is stilled determined by Eq. (1) after the twice sampling. Therefore, when \(\gamma =\beta \), \(a_1\) and \(b_1\) in Eq. (11) equal a and b in Eq. (1), the response results obtained by the re-scaled aperiodic VR method and the twice sampling aperiodic VR method are identical.

Fig. 20
figure 20

The flowcharts of the re-scaled aperiodic VR method and the twice sampling aperiodic VR method

Full size image

As we mentioned above, the results obtained by two different methods are equivalent. The main difference between them is the physical processes to achieve the same goal. In Fig. 20, we give the flowcharts of two algorithms to show the main difference apparently. When the re-scaled VR method is used, the main signal processors are the signal amplifier and the nonlinear system (with large parameters). When the twice sampling VR method is used, the main signal processors are sampling processors (with different sampling frequency) and the nonlinear system (with small parameters). However, these differences cannot be considered as their merits or demerits. Although the algorithms in the present paper are carried out by numerical simulations, it will be realized by hardware devices in most engineering occasions. The investigations of the numerical algorithms are our work of the first step. Next step, we will build the equipment based on the numerical algorithms by hardware devices. Usually, the decision as to which method to choose depends on the concrete conditions and the hardware devices one owns. Numerical study on the two algorithms is the pre-research and theoretical basis of the equipment construction in the future.

6 Conclusions

Three kinds of aperiodic VR methods are applied to improve the weak aperiodic bipolar binary signal in a typical nonlinear system. The system considered is different from the system in the former VR works. It is a nonlinear system with fractional-order deflection. Specifically, the nonlinearity in the system is an absolute value function with a fractional-order exponent.

The first kind of aperiodic VR is the classic VR phenomenon. If the minimal random pulse width of the bipolar binary signal is long enough, this kind of aperiodic VR method can improve the weak aperiodic signal excellently. Moreover, if the cross-correlation coefficient is treated as a function of the auxiliary signal strength, the resonance peak on this cross-correlation coefficient curve is independent of the fractional-order exponent. However, the magnitude of the aperiodic signal in the output depends on the fractional-order exponent closely. Further, if the minimal random pulse width of the bipolar binary signal is small, the classic aperiodic VR may not occur and the weak aperiodic signal cannot be improved.

The second kind of aperiodic VR is the re-scaled aperiodic VR that we propose in this paper to improve the bipolar binary signal whose minimal random pulse width has arbitrary length. Via a scale transformation, we transform the short minimal pulse width to a long one. Meanwhile, the system parameters of the original system are found to match the character signal. Then, the aperiodic VR occurs and leads to the improvement of the weak aperiodic signal. The scale parameter is the key parameter to realize the re-scaled aperiodic VR.

The third kind of aperiodic VR is the twice sampling aperiodic VR proposed in this paper. The twice sampling aperiodic VR can also improve the bipolar binary signal with an arbitrary minimal random pulse width. Via twice sampling, the original signal is re-constructed by an appropriate sampling transform ratio. In this step, the minimal random pulse width is changed to a long one. Then, the new signal becomes an input to the original system to induce the aperiodic VR. Finally, we transform the output to the original sampling frequency. As a result, the weak aperiodic signal can be improved to a great extent. The sampling transform ratio is the key parameter to realize the twice sampling aperiodic VR.

By three kinds of aperiodic VR methods, we can improve the aperiodic bipolar binary signal excellently. In fact, these methods can also be used to improve other kinds of aperiodic signals, e.g., linear or nonlinear frequency modulated signal, and all kinds of periodic signals. Further, when these methods are used, we must assure the system is not divergent under the excitations. Certainly, for the nonlinear model used in this paper, the response of the system will not be divergent. Moreover, if the waveform of the character signal is unknown or the signal is submerged in heavy noise, we should use other tools and the methods in this paper together to process the weak character signal. The related issues are our future work. Anyhow, our results in the present paper not only extend the works of the VR theory but also might have potential value in the signal processing field.