1 Introduction

In the past decade, research on the qualitative behavior of difference equations has been very active and fruitful and has attracted the attention of many mathematicians. This topic draws its importance from the fact that many real-life phenomena are modeled using difference equations. Examples from economy, biology, etc., can be found in [1, 8, 9, 11]. It is known that nonlinear difference equations are capable of producing a complicated behavior regardless its order. There has been a great interest in studying the global attractively, the boundedness character and the periodicity nature of nonlinear difference equations. For example, in the articles [2,3,4,5,6,7, 10, 12,13,14], closely related global convergence results were obtained which can be applied to nonlinear difference equations in proving that every solution of these equations converges to a period two solution.

In this paper, we discuss the results of Elsayed [6] for periodic solution of prime period two and three. Moreover, by using old method and new method [in [6], we study the existence of periodic solutions of some difference equation and comparison of results. The results obtained here correct and improve some known results in [6].

Now, assume that I be an interval of real numbers and let

$$\begin{aligned} f:I^{k+1}\rightarrow I \end{aligned}$$

be a continuously differentiable function. Consider the difference equation of the form

$$\begin{aligned} x_{n+1}=f(x_{n},x_{n-1},\ldots ,x_{n-k}),\, n=0,1,2,\ldots , \end{aligned}$$
(1.1)

with the initial conditions \(x_{-k},x_{-k+1},\ldots ,x_{0}\in I\).

Definition 1.1

A sequence \(\left\{ x_{n}\right\} _{n=-k}^{\infty }\) is said to be periodic with period p if \(x_{n+p}=x_{n}\) for all \(n\geqslant -k\). A sequence \( \left\{ x_{n}\right\} _{n=-k}^{\infty }\) is said to be periodic with prime period p if p is the smallest positive integer having this property.

2 Comment on [6] for periodic solution of period two and three

Elsayed [6] studied the qualitative behavior of the solutions of the difference equation

$$\begin{aligned} x_{n+1}=\alpha +\beta \frac{x_{n}}{x_{n-1}}+\gamma \frac{x_{n-1}}{x_{n}}. \end{aligned}$$
(2.1)

He investigated the periodic solution of prime period two by using a new method and proved that Eq. (2.1) has prime period two solution if

$$\begin{aligned} \alpha =\gamma -\beta \left( \frac{i^{2}+i+1}{i}\right) ,\, i\in \mathbb {R} \backslash \left\{ 0,\pm 1\right\} . \end{aligned}$$
(2.2)

Results of Elsayed are very good and important, but there exist some notes.

  • Note that, in [6], the parameters \(\alpha \) ,\(\beta \) ,\(\gamma \) and the initial conditions \(x_{-1},x_{0}\) are positive real numbers. Hence, all solution of Eq. (2.1) must be positive. So, in Theorem 3.1, 3.2 and Examples 5, 6, he studied the period two and three for Eq. (2.1) when the parameters and the initial conditions are nonzero real numbers, he does not mention that in this section.

  • For Remark 3.1 in [6], it is not difficult to obtain periodic solution of prime period two by using old method (see Theorem 3.1 in this paper).

  • Note that, if \(\alpha \) ,\(\beta \) ,\(\gamma \) ,\(x_{-1}\) and \(x_{0}\) are positive real numbers, then we have that \(i,j\in R^{+}\backslash \left\{ 1\right\} \). But, in this case, Eq. (2.1) has no prime period three solution (see Remark 3.7 in this paper).

3 Discussion and new results

Firstly, we show the steps to obtain periodic solutions of period two of a rational difference equation by using old and new methods.

Old method To obtain the conditions which insure that the rational difference equation has periodic solutions of prime period two, the most common steps are as follows:

Step 1 :

Assume that there exists a prime period two solution of Eq. (1.1)

$$\begin{aligned} \ldots ,p,q,p,q,\ldots . \end{aligned}$$

Hence, we get that

$$\begin{aligned} p= & {} f\left( q,p,q,\ldots \right) \, \, \,\left( \mathbf {a}\right) \\ q= & {} f\left( p,q,p,\ldots \right) \, \, \, \left( \mathbf {b}\right) . \end{aligned}$$
Step 2 :

From equations \(\left( \mathbf {a}\right) \) and \(\left( \mathbf { b}\right) \), we get \(p+q\) and pq.

Step 3 :

Since p and q are distinct, we assume that p and q are the two distinct roots of the quadratic equation

$$\begin{aligned} t^{2}+\left( p+q\right) t+pq=0. \end{aligned}$$

Thus, we obtain the condition

$$\begin{aligned} \left( p+q\right) ^{2}-4pq>0. \end{aligned}$$

New method To obtain the conditions which insure that the rational difference equation has periodic solutions of prime period two, the most common steps are as follows:

Step 1 :

As Step 1 in old method.

Step 2 :

We assume that \(p=iq\),\(i\ne 0,\pm 1\), and hence, equations \( \left( \mathbf {a}\right) \) and \(\left( \mathbf {b}\right) \) imply

$$\begin{aligned} p= & {} f\left( \frac{p}{i},p,\frac{p}{i},\ldots \right) \\ q= & {} f\left( iq,q,iq,\ldots \right) . \end{aligned}$$
Step 3 :

By using the fact \(p-iq=0\), we get the condition

$$\begin{aligned} f\left( \frac{p}{i},p,\frac{p}{i},\ldots \right) -i\, f\left( iq,q,iq,\ldots \right) =0. \end{aligned}$$

In the following, we state and prove useful lemma, which we intend to use later.

Lemma 3.1

Assume that \(t>0\), then

$$\begin{aligned} \frac{t^{2}+t+1}{t}>3\quad \text {for} \,\, t>0,t\ne 1. \end{aligned}$$
(3.1)

Also, if \(t<0\), then

$$\begin{aligned} \frac{t^{2}+t+1}{t}<-1\quad \text {for}\,\,t<0,t\ne -1. \end{aligned}$$
(3.2)

Proof

We define the function

$$\begin{aligned} y\left( t\right) =\frac{1}{t}\left( t^{2}+t+1\right) . \end{aligned}$$

If \(t>0\), then y attends its minimum value on \(\mathbf {\mathbb {R} }^{+}\) at \(t_{0}=1\) and \(\min _{t\in \mathbf {\mathbb {R} }^{+}}y=y\left( t_{0}\right) =3\), and hence,

$$\begin{aligned} y\left( t\right)>\min _{t\in \mathbf {\mathbb {R} }^{+}}y=3\, \, \text {for}\,t>0,\text { }t\ne 1. \end{aligned}$$

In the case where \(t<0\), we have that y attends its maximum value on \( \mathbf {\mathbb {R} }^{-}\) at \(t_{1}=-1\) and \(\max _{t\in \mathbf { \mathbb {R} }^{-}}y=y\left( t_{1}\right) =-1\) and hence,

$$\begin{aligned} y\left( t\right)<\underset{t\in \mathbf {\mathbb {R} }^{-}}{\max }y=-1 \, \, \text {for}\, t<0,\text { }t\ne -1. \end{aligned}$$

(see Fig. 1) The proof is complete. \(\square \)

In the next theorem, we study the existence of periodic solutions of Eq. (2.1) by using the old method.

Theorem 3.1

Equation (2.1) has a prime period two solution if

$$\begin{aligned} \alpha <\gamma -3\beta . \end{aligned}$$
(3.3)

Proof

By using old method, from Step 1, we obtain

$$\begin{aligned} p=\alpha +\beta \frac{q}{p}+\gamma \frac{p}{q} \, \, \, \text {and} \, \, \, q=\alpha +\beta \frac{p}{q}+\gamma \frac{q}{p}, \end{aligned}$$

and so,

$$\begin{aligned} p^{2}q= & {} \alpha pq+\beta q^{2}+\gamma p^{2} \end{aligned}$$
(3.4)
$$\begin{aligned} q^{2}p= & {} \alpha pq+\beta p^{2}+\gamma q^{2}. \end{aligned}$$
(3.5)

Subtracting these equations gives

$$\begin{aligned} \left( p-q\right) pq=\left( \gamma -\beta \right) \left( p^{2}-q^{2}\right) . \end{aligned}$$

Since p and q are distinct, we get that

$$\begin{aligned} pq=\left( \gamma -\beta \right) \left( p+q\right) . \end{aligned}$$
(3.6)

Adding (3.4) and (3.5) yields

$$\begin{aligned} pq\left( p+q\right) =2\alpha pq+\left( \gamma +\beta \right) \left( p^{2}+q^{2}\right) . \end{aligned}$$

Thus, and from (3.6), we find

$$\begin{aligned} \left( \gamma -\beta \right) \left( p+q\right) ^{2}= & {} 2\alpha \left( \gamma -\beta \right) \left( p+q\right) \\&+\left( \gamma +\beta \right) \left( \left( p+q\right) ^{2}\right. \\&\left. -\,2\left( \gamma -\beta \right) \left( p+q\right) \right) . \end{aligned}$$

This implies

$$\begin{aligned} p+q=\frac{1}{\beta }\left( \gamma -\beta \right) \left( \gamma +\beta -\alpha \right) , \end{aligned}$$

which with (3.6) gives

$$\begin{aligned} pq=\frac{1}{\beta }\left( \gamma -\beta \right) ^{2}\left( \gamma +\beta -\alpha \right) . \end{aligned}$$

From Step 3, we have \(\left( p+q\right) ^{2}>4pq\), and hence, \(\alpha <\gamma -3\beta \). Thus, Eq. (2.1) has prime period two solution if \(\alpha <\gamma -3\beta ,\) and the proof is complete. \(\square \)

Remark 3.2

If \(\alpha \), \(\beta \), \(\gamma \), \(x_{-1}\) and \(x_{0}\in \mathbb {R} ^{+}\), then Elsayed’s condition (2.2) must be take the form

$$\begin{aligned} \alpha =\gamma -\beta \left( \frac{i^{2}+i+1}{i}\right) , \, i\in \mathbf {\mathbb {R} }^{+}\mathbf {\backslash }\left\{ 1\right\} . \end{aligned}$$
(3.7)

By using Lemma 3.1, we find

$$\begin{aligned} \frac{i^{2}+i+1}{i}>3 \quad \text {for} \quad i>0,i\ne 1, \end{aligned}$$

which with (3.7) gives

$$\begin{aligned} \alpha <\gamma -3\beta . \end{aligned}$$

Then, in this case, we note that the conditions of old method and new method are the same. But, if \(\alpha \), \(\beta \), \(\gamma \), \(x_{-1}\) and \(x_{0}\in \mathbb {R}\), then we have two cases. Suppose that \(i>0\), then (2.2) implies (3.3). On the other hand, if \(i<0,\) then, by using (3.2), (2.2) implies that

$$\begin{aligned} \alpha \beta >\left( \gamma +\beta \right) \beta . \end{aligned}$$
(3.8)

(see Example 4.1). Then, the condition (2.2) yields

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha<\gamma -3\beta &{}\quad \text {for} \quad i>0,i\ne 1,\\ \alpha>\gamma +\beta \text {and } \beta >0 &{}\quad \text {for}\quad i<0, i\ne -1. \end{array} \right. \end{aligned}$$

In the following theorem, by using the new method, we study the existence of periodic solutions of equation

$$\begin{aligned} x_{n+1}=\gamma x_{n-k}+\frac{ax_{n}+bx_{n-k}}{cx_{n}-dx_{n-k}}, \end{aligned}$$
(3.9)

where k odd, \(\gamma \), a, b, c, d and the initial conditions \( x_{-k}\), \(x_{-k+1}\), \(\ldots \), \(x_{0}\) are real numbers.

Theorem 3.3

Equation (3.9) has a prime period two solution if

$$\begin{aligned} ac=b\left( c+d\right) +ad\left( \frac{i^{2}+i+1}{i}\right) , \, i\in \mathbf {\mathbb {R} \backslash }\left\{ 0,\pm 1\right\} . \end{aligned}$$
(3.10)

Proof

By using a new method, we have that

$$\begin{aligned} p=\gamma p+\frac{a+bi}{c-di} \, \, \text {and} \, \, q=\gamma q+\frac{ai+b}{ci-d}, \end{aligned}$$

and so,

$$\begin{aligned} p-iq=\gamma \left( p-iq\right) +\frac{a+bi}{c-di}-\frac{ai^{2}+bi}{ci-d}. \end{aligned}$$

Since \(p=iq\), we obtain

$$\begin{aligned} \left( a+bi\right) \left( ci-d\right) =\left( ai^{2}+bi\right) \left( c-di\right) , \end{aligned}$$

that is

$$\begin{aligned} \left( ac-bc-bd\right) i=ad\left( i^{2}+i+1\right) . \end{aligned}$$

Thus, we have that (3.10) holds and the proof is complete. \(\square \)

Remark 3.4

Zayed [14] considered the difference Eq. (3.9) and proved that Eq. (3.9) has prime period two solution, if k odd, \(\gamma \), a, b, c, d, \(x_{-k}\), \(x_{-k+1}\), \(\ldots ,x_{0}\) are positive real numbers and

$$\begin{aligned} \left( a-b\right) \left( c+d\right) >4ad. \end{aligned}$$
(3.11)

Note that, by using (3.1), if \(i>0\), then (3.10) implies (3.11). But, if \(i<0\), then, from (3.2), the condition (3.10) yields

$$\begin{aligned} ad\left( a-b\right) \left( c+d\right) <0. \end{aligned}$$
(3.12)

(see Example 4.2).

Remark 3.5

By using a new method, we obtain the new sufficient conditions which insure that solution of a class of difference equation is periodic with prime period two. Also, the new results extend a number of existing results (for example [3,4,5, 7])

Next, in [12], Moaaz investigated the periodic character of the positive solutions of equation

$$\begin{aligned} x_{n+1}=a+b\frac{x_{n-l}}{x_{n-k}}+c\frac{x_{n-l}}{x_{n-s}}. \end{aligned}$$
(3.13)

He proved that if l odd, k, s even and \(a\ne b+c\), then Eq. (3.13) has no prime period two solution. But, by using the new method, the following theorem states the sufficient conditions that Eq. (3.13) has periodic solutions of prime period two.

Theorem 3.6

Equation (3.13) has prime period two solution if \(a=b+c\).

Proof

By using a new method, we get

$$\begin{aligned} p=a+\left( b+c\right) i \, \, \text {and} \, \, q=a+\frac{b+c}{i}. \end{aligned}$$

Hence, we obtain \(p-iq=\left( 1-i\right) a+\left( i-1\right) \left( b+c\right) =0\). Since \(i\ne 1\), we have \(a=b+c\), (see Example 4.3) and the proof is complete. \(\square \)

Fig. 1
figure 1

Graph of the function \(\frac{1}{t}\left( t^{2}+t+1\right) \)

Full size image
Fig. 2
figure 2

Graph of the function \([x^{2}\left( 1-x^{2}\right) +y^{2}\left( 1-y^{2}\right) +\left( y^{2}x^{2}-1\right) ]/[y^{3}x +y+x^{3} -yx^{2}-y^{2}x-yx]\) for \(x,y \in \mathbb {R}^+\)

Full size image
Fig. 3
figure 3

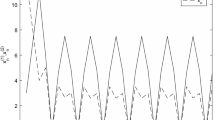
Period two solution for the Eq. (2.1) with \(\alpha =\beta =1\), \(\gamma = 5\) and initial conditions \(x_{-1} = 5.5279\), \(x_{0} = 14.4721\)

Full size image
Fig. 4
figure 4

Period two solution for the Eq. (2.1) with \(\alpha = -1\), \(\beta =2\), \(\gamma =-4\) and initial conditions \(x_{-1}=6\), \(x_{0}=-3\)

Full size image
Fig. 5
figure 5

Period two solution for the Eq. (3.9) with \(k=1\), \(\gamma =2\), \(a=3\), \(b=4\), \(c=1\), \(d=2\) and initial conditions \(x_{-1}=1\), \(x_{0}=-0.5\)

Full size image
Fig. 6
figure 6

Period two solution for the Eq. (3.13) with \(l=1\), \(k=2\), \( s=4\), \(a=2\), \(b=c=1\) and initial conditions \(x_{-4}=x_{-2}=x_{0}= 3.4015\), \(x_{-3}=x_{-1}=4.8542\)

Full size image

Finally, we discuss the results of Elsayed [6] for periodic solution of prime period three.

Remark 3.7

Elsayed proved that Eq. (2.1) has prime period three solution if

$$\begin{aligned} \alpha =\gamma \left( \frac{i^{2}\left( 1-i^{2}\right) +j^{2}\left( 1-j^{2}\right) +\left( j^{2}i^{2}-1\right) }{j^{3}-ji^{2}-j^{2}i+ji^{3}-ij+i} \right) \end{aligned}$$

and

$$\begin{aligned} \beta =\gamma \left( \frac{j^{3}i+j+i^{3}-ji^{2}-j^{2}i-ij}{ j^{3}-ji^{2}-j^{2}i+ji^{3}-ij+i}\right) . \end{aligned}$$

Thus, we find

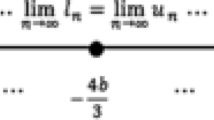
$$\begin{aligned} \alpha =\beta \left( \frac{i^{2}\left( 1-i^{2}\right) +j^{2}\left( 1-j^{2}\right) +\left( j^{2}i^{2}-1\right) }{j^{3}i+j+i^{3}-ji^{2}-j^{2}i-ij} \right) . \end{aligned}$$
(3.14)

If the parameters \(\alpha \), \(\beta \), \(\gamma \) and the initial conditions \( x_{-1},x_{0}\) are positive real numbers, then all solution of Eq. (2.1) must be positive and hence, \(i,j\in \mathbb {R} ^{+}\backslash \left\{ 1\right\} \). But, if i, j are positive, then the function

$$\begin{aligned} z\left( i,j\right):= & {} \frac{i^{2}\left( 1-i^{2}\right) +j^{2}\left( 1-j^{2}\right) +\left( j^{2}i^{2}-1\right) }{j^{3}i+j+i^{3}-ji^{2}-j^{2}i-ij}\\&<0\,\ \ \ \text {for}\quad i,j\in \mathbb {R} ^{+}. \end{aligned}$$

(see Fig. 2). Thus, \(\alpha \) or \(\beta \) is nonpositive and this is a contradiction. Therefore, Eq. (2.1) has no a prime period three. In Example 6 in [6], we note that \(i=-3,\) and hence, \(x_{0}=-\frac{35 }{3}<0\) (which contradicts the \(x_{0}\) is positive).

4 Numerical example

Example 4.1

Consider the difference Eq. (2.1). Let \(\alpha =\beta =1\) and \(\gamma =5\). It easy to see that the condition (3.3) holds, and hence, Eq. (2.1) has a prime period two solution (see Fig. 3).

On the other hand, if we take \(\alpha =-1\), \(\beta =2\) and \(\gamma =-4\), then condition (3.8) is satisfied. Thus, Eq. (2.1) has a prime period two solution (see Fig. 4).

Example 4.2

Consider the difference Eq. (3.9), if we take \(k=1\), \( \gamma =2\), \(a=3\), \(b=4\), \(c=1\) and \(d=2\). It easy to see that the condition (3.12) holds, and hence, Eq. (3.9) has a prime period two solution (see Fig. 5).

Example 4.3

Consider the difference Eq. (3.13). Assume that \(l=1\), \( k=2\), \(s=4\), \(a=2\) and \(b=c=1\), then \(a=b+c\), and hence, Eq. (3.13) has a prime period two solution (see Fig. 6).

5 Conclusions

The results of old method and new method for any difference equation are the same if every solutions are positive (Remark 3.2); otherwise, the results of new method extend and generalize results of old method (Remark 3.4). Moreover, we can simplify the conditions of new method by using Lemma 3.1 (Fig. 2). In addition, we can obtain the sufficient conditions which insure that solutions of some difference equation is periodic with prime period two by using new method, while the old method fail with these equations (Theorem 3.6).

Equation (2.1) has no a prime period three if its parameters and initial conditions are positive; otherwise, the result of Elsayed in Theorem 3.2 is correct (Remark 3.7).