1 Introduction

Finite deformation of slender structures is of interest for many problems ranging from buckling of structural frames to curling of cables and human hair, for which linear beam theories based on infinitesimal displacement cannot be used. The geometrically exact beam formulation, firstly introduced by Reissner [1, 2], takes into account large nonlinear deformations of bending, axial, and shear type; the term exact refers to the fact that the strain follows directly from geometrical considerations without approximations. The finite-element (FE) formulation introduced by Simo [3, 4] contributed to the popularity of this theory (see a more recent detailed implementation in [5]), and computational aspects arising from new formulations are still of interest [6–8]. However, the formulation proposed by Simo requires, in addition to the two degrees of freedom (dofs) corresponding to the components of the position vector, the introduction of a third dof describing the local rotation in order to enforce equilibrium. In addition to increasing the computational cost in dynamic problems, rotary dofs lead to a nonconstant mass matrix restricting time integration schemes to implicit ones [9]. The absolute nodal coordinate formulation (ANCF) [10–13] has been developed to improve these drawbacks even if it involves higher-order spatial operators.

For slender structures such as cables or rods, shear deformations can be neglected using the Euler–Bernoulli assumption of beam cross sections remaining normal to the elastic axis and plane after deformation. This leads to the formulation of extensible-elastica, for which the kinematics are often expressed in terms of trigonometric functions involving one displacement component and the rotation of the cross section of the beam [14]. If expressed in terms of both displacement components, the kinematics are mathematically represented by high-order partial differential equations (PDEs) and specifically a fourth-order spatial differential operator is involved. As consequence, in the weak formulation, the problem involves second-order derivatives for which a numerically approximated solution based on the standard Galerkin method requires the use of at least globally \({\mathcal {C}}^1\)-continuous basis functions. Conversely, when considering FE approximations based on Lagrangian polynomials which are globally \(C^0\)-continuous in the computational domain, the use of mixed formulations with auxiliary variables represents one of the most viable approaches. A similar problem arises in linear beam theory, where the curvature, proportional to the moment, is given by the second derivative of the transverse displacement. This problem is often solved by using \({\mathcal {C}}^1\)-continuous cubic Hermite basis functions with the addition of an explicit dof physically corresponding to the rotation [15]. However, this approach cannot be used for the rotation-free extensible-elastica, since second derivatives of displacements are not physically meaningful quantities. In the literature, different techniques have been used to solve the rotation-free extensible-elastica formulation. In [16], the Hu-Washizu variational principle is employed for which the rotation is numerically approximated with the aim of removing the second-order derivative. More recently, this problem has been solved by the quaternion-based method [17] and the weak-form quadrature element method [18].

Isogeometric analysis (IGA), firstly introduced by Hughes et al. [19], aims at filling the gap existing between computational mechanics for engineering applications and computational geometry, specifically computer-aided design (CAD) systems. The key feature of IGA consists in generalizing the FE method by considering an isoparametric approach for which the same basis functions used to represent the geometry are then used for the approximation of the unknown solution field of the governing PDEs. As a consequence, the representation of the computational domain is encapsulated in the numerical approximation of the governing PDEs. Since nonuniform rational B-splines (NURBS) are especially used in CAD systems, we will consider NURBS-based IGA for the approximation of the governing PDEs. A crucial property of NURBS basis functions is the possibility to increase their degree of continuity through the \(k\)-refinement procedure [20]. The smoothness of the NURBS basis functions leads in many cases to better accuracy and reduced computational cost compared to the standard FE method [19]. In addition, in vibration analysis, IGA based on smooth NURBS basis functions improves the representation of optical branches of the frequency spectrum [21, 22].

If the nonlinear response of initially curved slender structures is desired, discretization requires many elements with undesirable geometric characteristics, such as low thickness-to-length ratio, leading to erroneously increased stiffness. In this paper, we take advantage of properties of NURBS basis functions and IGA to solve the shear-free, high-order-formulation problem in the standard Galerkin framework. By employing an appropriate constitutive law, we are able to directly compare NURBS-based IGA models to analytical solutions of a certain class of beam problems, thus validating the performance of the considered computational method. The computational domain representing a beam with a single NURBS patch in particular is used. We remark that for multiple NURBS patches (typical of problems with piecewise continuous geometry), the rotation-free extensible-elastica formulation cannot be directly used, for which rigid constrains or stiff simplified elements (bending strip method [23]) between patches need to be added.

In the field of nonlinear isogeometric beams, available formulations in literature are based on elastica [20] and nonlinear Euler–Bernoulli [22–24] theories. Beam models including shear are proposed in [25, 26] for Timoshenko beams and in [27] for the third-order, shear deformation theory (TSDT). For isogeometric nonlinear plates and shells, we refer the reader to [28, 29] for Kirchhoff-Love rods, to [30–32] for Kirchhoff–Love shells, to [33, 34] for Reissner–Mindlin shells, and to [35] for modified Reissner–Mindlin shells including variable thickness.

A isogeometric method for slender beams undergoing large deformations and free of shear is proposed in [23]. With respect to this work, our formulation differs in the choice of the constitutive material model. In order to explain this difference, we recall that Irschik and Gerstmayr [36] presented an interpretation of the strain measures and stress resultants of the extensible-elastica formulation in terms of nonlinear continuum mechanics. A linear relation between the second Piola–Kirchhoff stress and the Green-Lagrange strain, as given by the Saint Venant–Kirchhoff model, results in a nonlinear relationship between stress resultants (axial force and moment) and strain (axial strain and curvature), thus introducing a nonlinear material model. The former is the formulation considered in [23]. Conversely, in this paper, we consider a linear constitutive law between Biot Stress and Biot strain resulting in a linear material model. Indeed, the axial force and moment are only a function of axial strain and curvature, respectively [36] (see [37] for a comparison with the Saint Venant–Kirchhoff model). Such linear constitutive law at the beam level is a key feature of the extensible-elastica theory [14], allowing closed-form solutions of simple nonlinear beam problems with coupled axial and transverse displacements (the term closed form refers to the fact that solutions are expressed in terms of known functions such as elliptical integrals). Closed-form solutions of known problems provide an ideal setting to evaluate the numerical performance of the IGA formulation, which we consider by using “patch tests.” Static analytical solutions for the extensible-elastica method have already been applied to buckling [14, 38], variable-length beams under concentrated/distributed forces [37, 39], and snap-through buckling [40, 41]. However, to the best of our knowledge, patch tests for initially curved extensible-elastica have not been considered yet; currently available tests differ in the constitutive laws and strain measurement [42, 43]. In the present paper, we derive a new closed-form solution for a tip-loaded curved cantilever beam using the extensible-elastica to expand available benchmark cases.

Closed-form solutions of patch tests for static beams are used to verify the convergence orders of the errors under \(h\)-refinement associated with the IGA approximations using a-priori error estimates [44, 45], including high-order PDEs [46, 47]. Despite the fact that the error estimates are derived for linear problems, the same convergence orders are often observed for nonlinear PDEs also (see, e.g., [20]). Moreover, we remark that the considered formulation is free of shear locking by design even for initially curved structures [48], but may exhibit membrane locking when beam elements possess very low aspect ratio, which is often the case in discretizing curved structures. This phenomenon is well known in FE formulations [15, 49] and has received renewed attention in the context of IGA for Timoshenko beam formulations, using different locking-free methods, namely the collocation method [25], the selective reduced integration, the reduced integration with hourglass mode control, the \(\bar{B}\) strain projection, and the discrete strain gap (DSG) method [26]. Moreover, the IGA formulation can be conveniently used for the spatial approximation of dynamic beam problems, as we illustrate by means of several numerical tests: the swinging of a pinned beam [23], the propagation of solitons (nonlinear waves) in post-buckled beams [50, 51], and snap-through buckling of a pinned beam that is axially buckled before transverse loading [41].

This paper is organized as follows. In Sect. 2, the rotation-free extensible-elastica formulation is recalled and the different terms of the weak formulation and its linearization are given; the isogeometric concept is applied to the present problem. Closed-form solutions for different static beam problems are presented and derived in Sect. 3; then, the a-priori error estimates are recalled in Sect. 4. In Sect. 5, static beam problems are solved, and convergence order is numerically estimated and compared with the a-priori error estimates. In Sect. 6, dynamic problems are solved. Conclusions follow.

2 Rotation-free extensible-elastica formulation

2.1 Strain measurement and constitutive law

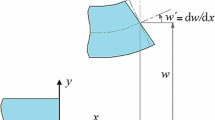
The derivation of the rotation-free extensible-elastica formulation follows from the geometrically exact beam theory including shear and is described in [5]. However, contrarily to [5], the beam formulation is provided in the global coordinate frame allowing initial deformations and is not rotated back to the local frame in order to compute strain and stress resultants [18] (Fig. 1). Indeed, the rotation to a local frame is not compatible with rotation-free formulations.

Fig. 1
figure 1

Beam kinematics: reference (dotted lines), initial (dashed lines), and current configuration (full lines)

Full size image

In the initial configuration of the beam, \(\varvec{r}_0\in {\mathbb {R}}^2\) is referred to as the position vector of a material point of the beam; \(\varvec{e}_{0,i}\), \(i=1,2\) is an orthonormal basis vector of the Euclidean space \({\mathbb {R}}^2\) such that \(\varvec{e}_{0,1}\) represents the normal direction of the cross section and \(\theta _0\in {\mathbb {R}}\) the orientation angle of the initial configuration with respect to the reference configuration. We indicate with \(s_0\in {\mathbb {R}}\) the arc-length parameter of the elastic axis of the beam (i.e., the curvilinear coordinate) and with \(l_0\) its total length. Correspondingly, \(\varvec{r}\), \(\varvec{e}_{i}\), \(\theta \), and \(s\) represent the position vector, the orthonormal basis vectors, the rotation, and the curvilinear coordinate in the current configuration of the beam, respectively. These quantities are shown in Fig. 1 and are defined as:

$$\begin{aligned} \begin{array}{l@{\quad }l} \varvec{r}_0=\left\{ r_{0,x},~ r_{0,y}\right\} ^T, &{} \varvec{r}=\left\{ r_x,~ r_y\right\} ^T,\\ \varvec{e}_{0,1}=\left\{ \cos \theta _0,~ \sin \theta _0\right\} ^T, &{} \varvec{e}_1=\left\{ \cos \theta ,~ \sin \theta \right\} ^T,\\ \varvec{e}_{0,2}=\left\{ -\sin \theta _0,~ \cos \theta _0\right\} ^T,&{} \varvec{e}_2=\left\{ -\sin \theta ,~ \cos \theta \right\} ^T. \end{array}\nonumber \\ \end{aligned}$$
(1)

where \(\varvec{r}_0=\varvec{r}_0(s_0)\), \(\varvec{r}=\varvec{r}(s)\), \(\varvec{e}_{0,i}=\varvec{e}_{0,i}(s_0)\), \(\varvec{e}_{i}=\varvec{e}_{i}(s)\), \(\theta _0=\theta _0(s_0)\), and \(\theta =\theta (s)\).

The strain relation proposed by Reissner [1] extended to global coordinates reads:

$$\begin{aligned} \begin{aligned}&\epsilon =r_x'\cos \theta +r_y'\sin \theta -\left( r_{0,x}'\cos \theta _0+r_{0,y}'\sin \theta _0\right) ,\\&\gamma =r_y'\cos \theta -r_x'\sin \theta -\left( r_{0,y}'\cos \theta _0-r_{0,x}'\sin \theta _0\right) ,\\&\kappa =\theta '-\theta _0'. \end{aligned}\nonumber \\ \end{aligned}$$
(2)

where \(\epsilon \) is the axial strain, \(\gamma \) the shear strain, and \(\kappa \) the curvature. The notation \((~)'\) denotes the derivative with respect to the initial curvilinear coordinate \(s_0\) (Lagrange formulation). The Euler–Bernoulli beam model assumes that the cross section remains planar and normal to the tangent of the elastic axis of the beam after deformation, which corresponds to assuming that the shear \(\gamma \) is identically zero. By substituting the rotations \(\theta \) and \(\theta _0\) in Eq. (2), the axial strain \(\epsilon \) and the curvature \(\kappa \) can be rewritten in terms of \(\varvec{r}_{0}\), \(\varvec{r}\), and their derivatives Footnote 1:

$$\begin{aligned} \begin{aligned}&\epsilon =\Vert \varvec{r}^{'}\Vert _2-\Vert \varvec{r}_0'\Vert _2 ,\\&\kappa =\frac{ \varvec{r}''^T \varTheta \varvec{r}^{'}}{\Vert \varvec{r}^{'}\Vert ^2_2}-\frac{ \varvec{r}_0''^T \varTheta \varvec{r}_0'}{\Vert \varvec{r}_0'\Vert ^2_2}, \end{aligned} \end{aligned}$$
(3)

where \(\Vert \varvec{r}'\Vert _2=\sqrt{r^{'2}_x+r^{'2}_y}\) is the Euclidean norm and \(\varTheta \) is a \(90^{\circ }\) rotation matrix given by:

$$\begin{aligned} \varTheta = \begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix}. \end{aligned}$$
(4)

By assuming that the strain is finite but small, even for large displacements, it is possible to describe material behavior by Hooke’s law. By using the Young modulus \(E\), the constitutive law between the force and the strain after the integration over the cross section of the beam is [1, 5, 36]:

$$\begin{aligned} \begin{Bmatrix} N_{\epsilon }\\ N_{\kappa }\\ \end{Bmatrix}= \begin{bmatrix} EA&0\\ 0&EI_z\\ \end{bmatrix} \begin{Bmatrix} \epsilon \\ \kappa \\ \end{Bmatrix}, \end{aligned}$$
(5)

where \(A\) and \(I_z\) are the area and moment of inertia of the beam, respectively; \(N_{\epsilon }\) and \(N_{\kappa }\) indicate the internal axial force and bending moment, respectively. The constitutive law Eq. (5) is equivalent in continuum mechanics to the linear relationship between the Biot’s stress and strain. For an overview of alternative constitutive laws, see [36].

2.2 The weak formulation

The weak formulation of the equilibrium equation is obtained from the principle of virtual work and is expressed in terms of the current configuration \(\varvec{r}=\varvec{r}_0+\varvec{u}\), where \(\varvec{u}=\{ u_x~u_y\}^T\) is the displacement vector, and \(\delta \varvec{u}= \delta \varvec{r}\) the virtual displacement vector; \(\varvec{f}\in {\mathbb {R}}^2\) and \(\varvec{F}\in {\mathbb {R}}^2\) are the distributed and concentrated force vectors, respectively. The distributed and concentrated moments are indicated by \(m\in {\mathbb {R}}\) and \(M\in {\mathbb {R}}\), respectively. Transverse and axial follower loads are not taken into account in our formulation, but can be derived similarly to what is done for the moment. By considering a dynamic problem, the weak formulation of the equilibrium equation is given by [5]:

$$\begin{aligned}&\text {find}~\varvec{u}\in {\mathcal {V}}~~:~~G(\varvec{r}(\varvec{u}))(\delta \varvec{u})=0\qquad \forall \, \delta \varvec{u}\in {\mathcal {V}},\nonumber \\&\quad \forall t\in (0,~t_f), \end{aligned}$$
(6)

given suitable initial conditions at the time \(t=0\), with \(t_f\) is the final time, and \({\mathcal {V}} \subset H^2(\varOmega )~(\varOmega \in (0,l_0))\) a suitable subset of the Hilbert function space \(H^2(\varOmega )\) carrying the essential boundary conditions and:

$$\begin{aligned} G(\varvec{r}(\varvec{u}))(\delta \varvec{u})= & {} \int \limits _{0}^{l_0}(N_{\epsilon }\delta \epsilon +N_{\kappa } \delta \kappa )ds_0\nonumber \\&-\int \limits _{0}^{l_0}\left( \left( \varvec{f}^T+\rho A\ddot{\varvec{u}}^T\right) \delta \varvec{u}+ m \delta \theta \right) ds_0\nonumber \\&-\left[ \varvec{F}^T \delta \varvec{u} +M \delta \theta \right] _0^{l_0}, \end{aligned}$$
(7)

for which

$$\begin{aligned} \begin{aligned}&\delta \epsilon =\varvec{R}_{\epsilon '} \delta \varvec{u}', \\&\delta \kappa = \varvec{R}_{\kappa '} \delta \varvec{u}'+\varvec{R}_{\kappa ''} \delta \varvec{u}'',\\&\delta \theta = \varvec{R}_{\theta '}\delta \varvec{u}', \end{aligned} \end{aligned}$$
(8)

where:

$$\begin{aligned} \begin{aligned}&\varvec{R}_{\epsilon '}:=\frac{\varvec{r}^{'T} }{\Vert \varvec{r}'\Vert _2},\\&\varvec{R}_{\kappa '}:=\frac{\varvec{r}''^T \varTheta \left[ \Vert \varvec{r}'\Vert ^2_2 I-2\varvec{r}'\varvec{r}'^T\right] }{\Vert \varvec{\varvec{r}}'\Vert ^4_2},\\&\varvec{R}_{\theta '}:= \varvec{R}_{\kappa ''}=\frac{\varvec{r}'^T \varTheta ^T }{\Vert \varvec{r}'\Vert ^2_2}, \end{aligned} \end{aligned}$$
(9)

with \(I\) the identity matrix and \(\varTheta \) the rotation matrix (Eq. (4)); \(\rho \) is the density, and \(\ddot{(~)}\) denotes the second derivative with respect to time. Since there are no rotation dofs in the current formulation, we do not include rotary-inertia terms in Eq. (7), thus avoiding mass matrices with possibly bad conditioning [15]. Note also that in Eq. (7), we have omitted for simplicity the explicit dependency of the unknown \(\varvec{u}\) on the time variable \(t\). The equilibrium equation (7) is nonlinear in the first argument, for which, in order to solve the problem, the Newton-Raphson scheme is used [15]. The linearization of the functional \(G(\varvec{r}(\varvec{u}))(\delta \varvec{u})\) reads:

$$\begin{aligned} DG(\varvec{r}(\varvec{u}))(\delta \varvec{u},\delta \varvec{v})= & {} \int \limits _{0}^{l_0}\left( (EA+N_{\epsilon }) \widehat{\delta \epsilon } \right. \nonumber \\&\left. +(EI_z+N_{\kappa })\widehat{\delta \kappa }-m \widehat{\delta \theta }\right) ds_0\nonumber \\&-\left[ M \hat{\delta \theta } \right] _0^{l_0} \end{aligned}$$
(10)

where:

$$\begin{aligned} \begin{aligned}&\widehat{\delta \epsilon }=(\delta \varvec{u}')^{T} G_{\epsilon '\epsilon '} \delta \varvec{v}',\\&\widehat{\delta \kappa }=(\delta \varvec{u}')^{T} G_{\kappa '\kappa '} \delta \varvec{v}' +(\delta \varvec{u}'')^{T} G_{\kappa ''\kappa '}\delta \varvec{v}'\\&\qquad +(\delta \varvec{u}')^{T} G_{\kappa '\kappa ''} \delta \varvec{v}'',\\&\widehat{\delta \theta }=(\delta \varvec{u}')^{T} G_{\theta '\theta '} \delta \varvec{v}', \end{aligned} \end{aligned}$$
(11)

and:

$$\begin{aligned} \begin{aligned}&G_{\epsilon '\epsilon '}:=\frac{ \Vert \varvec{r}'\Vert _2^2 I-\varvec{r}' \varvec{r}'^T }{\Vert \varvec{r}'\Vert ^3_2},\\&G_{\kappa '\kappa '}:=-2\frac{\left[ \varvec{r}' \varvec{r}''^T \varTheta + \varTheta ^T \varvec{r}'' \varvec{r}'^T\right] \Vert \varvec{r}'\Vert ^2_2 + \left[ \Vert \varvec{r}'\Vert ^2_2 I-4\varvec{r}' \varvec{r}'^T\right] \varvec{r}''^T \varTheta \varvec{r}' }{\Vert \varvec{r}'\Vert ^6_2},\\&G_{\theta '\theta '}:= G_{\kappa '\kappa ''} =G_{\kappa ''\kappa '} =\frac{\varTheta \left[ \Vert \varvec{r}'\Vert ^2_2 I-2\varvec{r}'\varvec{r}'^T\right] }{\Vert \varvec{\varvec{r}}'\Vert ^4_2}, \end{aligned}\nonumber \\ \end{aligned}$$
(12)

being \(\varTheta \left[ \Vert \varvec{r}'\Vert ^2_2 I-2\varvec{r}'\varvec{r}'^T\right] \) a symmetric matrix. Note that although the proposed formulation is valid for large deformations, inertia terms are independent of the deformed configuration so no inertia term appears in Eq. (10). The finite dimensional approximation of Eq. (6) reads:

$$\begin{aligned}&\text {find}~\varvec{u}_h\in {\mathcal {V}}_h~:~G(\varvec{r}_h(\varvec{u}_h))(\delta \varvec{u}_h)=0\qquad \forall \,\delta \varvec{u}_h\in {\mathcal {V}}_h,\nonumber \\&\qquad \forall t\in (0,~t_f), \end{aligned}$$
(13)

given suitable initial conditions at the time \(t=0\), and \({\mathcal {V}}_h\) is a finite dimensional subspace of \({\mathcal {V}}\), such that \({\mathcal {V}}_h\subset {\mathcal {V}}\). We remark that the spatial approximation of problem (13) by means of the standard Galerkin method requires basis functions which belong to the space \({\mathcal {V}} \subset H^2(\varOmega )\), a requirement that is satisfied when considering globally \({\mathcal {C}}^1\)-continuous functions across the mesh elements in the choice of the functions space \({\mathcal {V}}_h\subset {\mathcal {V}}\). Contrarily to classical FE methods, NURBS-based IGA can be successfully used to fulfill this requirement.

2.3 Isogeometric formulation

We consider the representation of the geometry of a curved beam by means of NURBS [19]. We say that the geometry mapping \(\varvec{r_0}\) possesses a \(p\)-degree NURBS representation when there exist \(n\in {\mathbb {N}}\) control points \(\varvec{B}_i \in {\mathbb {R}}^2\), weights \(w_i\in {\mathbb {R}}\), \(i=1,\ldots ,n\), and a set of knots \(\Xi =\{0=\xi _1 \le \ldots \le \xi _{n+p+1}=1\}\) such that:

$$\begin{aligned} \varvec{r_0}(\xi )=\sum \limits _{i=1}^{n} R_{i,p}(\xi )\varvec{B}_i, \end{aligned}$$
(14)

where \(R_{i,p}(\xi )\) is the NURBS basis defined at \(\xi \in (0,1)\) by:

$$\begin{aligned} R_{i,p}(\xi )=\frac{N_{i,p}(\xi )w_i}{\sum \limits _{j=1}^{n} N_{j,p}(\xi )w_j}, \end{aligned}$$
(15)

with \(N_{i,p}(\xi )\) the \(i\)-th B-spline basis function defined by the Cox-De Boor recursive formula [52]:

$$\begin{aligned} \begin{aligned} N_{i,0}(\xi )&= {\left\{ \begin{array}{ll} 1\quad \text {if} \quad \xi _i \le \xi < \xi _{i+1},\\ 0\quad \text {otherwise},\\ \end{array}\right. }\\ N_{i,p}(\xi )&= \frac{\xi -\xi _i}{\xi _{i+p}-\xi _{i}}N_{i,p-1}(\xi )\\&\quad + \frac{\xi _{i+p+1}-\xi }{\xi _{i+p+1}-\xi _{i+1}}N_{i+1,p-1}(\xi ), \quad \text {for}~p\ge 1 . \end{aligned} \end{aligned}$$
(16)

The use of weights \(w_i\) for \(i=1,\ldots ,n\) allows the exact representation of conical sections. The so-called knot vector \(\Xi \) defines a partition of the parameter domain \((0,~1)\) similar to the classic FE subdivision yielding the so-called mesh of the parametric domain. A nonuniform knot vector and repeated knots are the key of the NURBS flexibility, allowing locally refined, geometric descriptions and reduced continuity of the basis functions. In particular, a knot of multiplicity \(q\) such that \(1\le q\le p\) yield basis functions \({\mathcal {C}}^{p-q}\)-continuous across the knot. In the present paper, for the purposes of the proposed formulation, at least globally \({\mathcal {C}}^{p-q}\) basis functions are used with \(1\le q \le p-1\) for \(p\ge 2\).

For the sake of simplicity, the independent variable \(\xi \) is omitted in the rest of the paper. The first and second derivatives of NURBS basis functions are given by:

$$\begin{aligned}&\frac{dR_{i,p}}{d\xi }=\frac{1}{W}\left( \frac{dN_{i,p}}{d\xi }w_i-R_{i,p}\frac{dW}{d\xi }\right) ,\end{aligned}$$
(17)
$$\begin{aligned}&\frac{d^2R_{i,p}}{d\xi ^2}=\frac{1}{W}\left( \frac{d^2N_{i,p}}{d\xi ^2}w_i -2\frac{dR_{i,p}}{d\xi }\frac{dW}{d\xi }-R_{i,p}\frac{d^2W}{d\xi ^2}\right) ,\nonumber \\ \end{aligned}$$
(18)

where \(W=\sum \limits _{j=1}^{n} N_{j,p} w_j\). Derivatives of NURBS basis functions with respect to the initial curvilinear coordinate \(s_0\) are:

$$\begin{aligned} R_{i,p}'= & {} \frac{1}{\Vert \varvec{J}_0\Vert _2}\frac{dR_{i,p}}{d\xi },\end{aligned}$$
(19)
$$\begin{aligned} R_{i,p}''= & {} \frac{1}{\Vert \varvec{J}_0\Vert _2^2} \frac{d^2R_{i,p}}{d\xi ^2}-\frac{\varvec{J}_0^T \varvec{H}_0}{\Vert \varvec{J}_0\Vert _2^4}\frac{dR_{i,p}}{d\xi }, \end{aligned}$$
(20)

where \(\varvec{H}_0=\frac{d\varvec{J}_0}{d\xi }\) and the Jacobian \(\varvec{J}_0=\frac{d\varvec{r_0}}{d\xi }\) is such that:

$$\begin{aligned} s_0=\int \limits _{0}^{\xi } {\Vert \varvec{J}_0\Vert }_2 d\xi . \end{aligned}$$
(21)

The main idea of the isogeometric approach is to use the same basis functions that represent the geometry also for the approximation of the displacement field as:

$$\begin{aligned} \varvec{r}=\sum \limits _{i=1}^{n} R_{i,p}(\varvec{B}_i+\varvec{u}_i), \end{aligned}$$
(22)

where \(\varvec{u}_i\) is the discretized displacement for which in Eq. (13) we set \({\mathcal {V}}_h={\mathcal {V}}\cap \text {span}\left\{ R_{i,p},~i=1,\ldots ,n \right\} \). Note that in dynamics, the control variables \(\varvec{u}_i=\varvec{u}_i(t)\) are time dependent.

The integrals involved in the weak formulation (Eq. (7)) are evaluated in the parametric space using the change of variables given in Eq. (21), and suitable Gauss-quadrature rules (more efficient quadrature rules can be eventually used for NURBS-based IGA [53]). For dynamic beam problems, the generalized-\(\alpha \) method is employed as the time integration scheme, which can be second-order accurate and unconditionally stable in linear problems [54]. This method is implemented in the form of a predictor–multicorrector algorithm [55]. Specifically, we consider the parameters used for the method as dependent on \(\rho _{\infty }\in [0~1]\), which is the high-frequency dissipation parameter. We refer the reader to [23] for the details of the method and choice of the parameters. Moreover, it has been shown in [56] that for dynamic problems solved with the generalized-\(\alpha \) scheme, \(k\)-refinement speeds up the convergence and improves energy conservation.

3 Set of static problems and exact/closed-form solutions

We consider a set of static extensible-elastica classical problems, found in the literature, for which exact or closed-form solutions are known [14, 18, 38, 39]. In addition, we propose the closed-form solution of a clamped, initially curved, extensible-elastica subject to a transverse tip load.

3.1 Test A: straight beam under pure axial load with nonconstant Young modulus

The first problem we propose is a cantilever beam stretched by an axial force \(P\) taken as \(P=3EA\). All the properties of the beam are assumed constant except the Young modulus, which is chosen as \(E(s_0)=E/(1+0.5\sin (2\pi s_0 /l_0))\), with \(l_0\) the length of the beam. The strain equation (Eq. (3)) is pure axial and becomes linear:

$$\begin{aligned} \begin{aligned}&\epsilon = r_x'-1,\\&\kappa = 0, \end{aligned} \end{aligned}$$
(23)

and the weak form (Eq. (7)) only involves first-order derivatives. The exact solution for the displacement is:

$$\begin{aligned} \begin{aligned}&u_x(s_0)= \frac{P}{E A}\left( s_0-\frac{1}{4\pi }\left( \cos \left( \frac{2\pi s_0}{l_0}\right) -1\right) \right) ,\\&u_y(s_0)= 0. \end{aligned}\nonumber \\ \end{aligned}$$
(24)

3.2 Tests B: straight and curved beams with pure bending

We consider two similar problems where a clamped beam initially straight or curved is subjected to a moment \(M\) applied at the tip (Fig. 2). This problem is of pure bending type, and the curvature remains homogeneous along the beam [18]. In the first problem (test B\(_1\)), the initially straight beam is bent until a quarter of a circle is obtained, while for the second problem (test B\(_2\)), the initially curved beam is bent until a straight beam is obtained. The applied moment to obtain the final configuration reads:

$$\begin{aligned} M\,=\,\pm \frac{EI_z}{R_0}\,=\,\pm \frac{\pi EI_z}{2l_0}, \end{aligned}$$
(25)

where the sign \(+\) and \(-\) indicate tests B\(_1\) and B\(_2\), respectively. The strain equation (Eq. (3)) simplifies:

$$\begin{aligned} \begin{aligned}&\epsilon = 0,\\&\kappa =\frac{1}{R}-\frac{1}{R_0}, \end{aligned} \end{aligned}$$
(26)

where \(R\) and \(R_0\) are the current and initial radius of the beam, respectively. Since \(\kappa \) is a constant through the radius \(R\), the weak formulation (Eq. (7)) involves only the first-order operator. The displacement is given by:

$$\begin{aligned} \begin{aligned}&u_x(s_0)=\pm \left( \frac{2l_0}{\pi }\sin \left( \frac{\pi s_o}{2 l_0}\right) -s_0\right) ,\\&u_y(s_0)=\pm \frac{2l_0}{\pi }\cos \left( \frac{\pi s_o}{2 l_0}\right) . \end{aligned} \end{aligned}$$
(27)
Fig. 2
figure 2

Straight (test B\(_1\)) (a) and quarter circle beam (test B\(_2\)) (b); the moment \(M\) is applied to obtain a quarter circle and a straight beam, respectively

Full size image

3.3 Test C: cantilever straight beam under transverse tip load

The transverse tip load of a straight cantilever beam (Fig. 3) induces both axial and bending deformations. The force applied at the extremity is chosen as \(P=2EI_z/l_0^2\). By rewriting, the weak form in terms of \(\theta \) gives with the extensible-elastica method [39]:

$$\begin{aligned} \frac{d \theta }{ds_0}=-\sqrt{\frac{P}{EI_z}}\sqrt{ \left( \sin \theta -\sin \theta _l\right) \left( 2-\frac{P}{EA}\left( \sin \theta +\sin \theta _l\right) \right) },\nonumber \\ \end{aligned}$$
(28)

where \(\theta _l\), the angle at the tip of the beam, is determined by integration of:

$$\begin{aligned} l_0=\int _{0}^{l_0} ds_0=\int _{0}^{\theta _l} \frac{ds_0}{d\theta } d\theta . \end{aligned}$$
(29)

Similarly, the angle in the deformed (current) configuration \(\theta \) is linked to the original curvilinear coordinate \(s_0\) as:

$$\begin{aligned} s_0=\int _{0}^{s_0} ds_0=\int _{0}^{\theta } \frac{ds_0}{d\theta } d\theta . \end{aligned}$$
(30)

The displacement is given by:

$$\begin{aligned} \begin{aligned}&u_x(s_0)=\int _{0}^{\theta } \left( \cos \theta +\frac{P}{EA}\cos \theta \sin \theta \right) \frac{ds_0}{d\theta }d\theta -s_0,\\&u_y(s_0)=\int _{0}^{\theta } \left( \sin \theta +\frac{P}{EA}\sin ^2\theta \right) \frac{ds_0}{d\theta }d\theta . \end{aligned}\nonumber \\ \end{aligned}$$
(31)

Note that \(l_0\) and \(s_0\) are evaluated by means of numerical integration; alternatively, they can be expressed in terms of incomplete elliptical integrals as in [39].

Fig. 3
figure 3

Test C: cantilever straight beam under transverse tip load

Full size image

3.4 Test D: buckling of a pinned-roller beam

Beam buckling is an additional test involving axial and bending deformations (Fig. 4). The applied load is \(P=1.4P_c\) where \(P_c\) is the critical load defined as:

$$\begin{aligned} P_c=\frac{\pi ^2 EI_z}{l_0^2}. \end{aligned}$$
(32)

In order to follow the stable path from the initial configuration without adding any initial imperfections to the geometry, a second load \(P'\) (\(P'\ll P\)) is applied in the middle of the beam until \(P\le P_c\) and removed afterward. The analytical closed-form solution of this problem has been derived using again the extensible-elastica equation and can be found in [14, 38].

Fig. 4
figure 4

Test D: buckling of a pinned-roller beam

Full size image

3.5 Test E: clamped arc under a transversal tip load

A clamped, curved beam under concentrated load is used to test the formulation for curved beams with axial and bending deformations (Fig. 5). By using the same method as [14, 38] for beam buckling, or the straight beam under transverse loads [39], we derive the extensible-elastica equation for an initially curved beam. By inserting Eq. (3), expressed in terms of \(\theta \) and \(r'_x\), into Eq. (7), and by using the constitutive law (5), we obtain:

$$\begin{aligned} \frac{d \theta }{ds_0}=\sqrt{\frac{1}{R_0^2}+\frac{2P}{\textit{EI}_z} \left( \cos \theta _l\!-\!\cos \theta \right) \!+\!\frac{P^2}{\textit{EA} \textit{EI}_z}\left( \cos ^2\theta _l\!-\!\cos ^2\theta \right) }, \nonumber \\ \end{aligned}$$
(33)

where the angles \(\theta _l\) and \(\theta \) in terms of \(l_0\) and \(s_0\) are found using Eqs. (29) and (30), respectively. The displacement is given by:

$$\begin{aligned} \begin{aligned} u_x(s_0)&=\int _{0}^{s_0} r'_x ds_0-r_{0,x}\\&=\int _{0}^{\theta } \!\left( \cos \theta \!+\!\frac{P}{\textit{EA}}\cos ^2\theta \right) \frac{ds_0}{d\theta }d\theta \!-\!R_0\sin \theta _0,\\ u_y(s_0)&=\int _{0}^{s_0} r'_y ds_0-r_{0,y}\\&=\int _{0}^{\theta } \left( \sin \theta +\frac{P}{\textit{EA}}\cos \theta \sin \theta \right) \frac{ds_0}{d\theta }d\theta \\&\quad -R_0(1-\cos \theta _0). \end{aligned} \end{aligned}$$
(34)
Fig. 5
figure 5

Test E: clamped arc under a transversal tip load

Full size image

4 A-priori error estimation: convergence order

Since the exact/closed-form solutions for the considered static problems are now detailed, the efficiency of the IGA formulation can be verified by using a-priori error estimates under \(h\)-refinement [46]. We consider the convergence orders of the errors in Hilbert spaces by ensuring that numerical quadrature errors in Eqs. (29) and (30) are negligible compared to the approximation error of the Galerkin method. Similarly, we consider a sufficiently small tolerance for the convergence criterion of the Newton-Raphson method used to solve the tangent problem associated with Eq. (13).

4.1 Error norms

Convergence plots of the curve under \(h\)-refinement are obtained by comparing analytical and FE solutions. The standard error in norm \(L^2\) (\(L^2(\varOmega )\equiv H^0(\varOmega )\)), where \(\varOmega =(0,l_0)\), reads:

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{L^2(\varOmega )}=\left( \int \limits _{0}^{l_0}\left( \varvec{u}-\varvec{u}_h\right) ^2 ds_0\right) ^{1/2}. \end{aligned}$$
(35)

When considering high-order PDEs, namely of order \(2m\) with \(m\ge 1\), the Hilbert norm for \(\sigma \ge 1\) is given by:

$$\begin{aligned}&\Vert \varvec{u}-\varvec{u}_h\Vert _{H^{\sigma }(\varOmega )}\nonumber \\&\quad =\left( \Vert \varvec{u}-\varvec{u}_h\Vert _{H^{(\sigma -1)}(\varOmega )}^2+\int \limits _{0}^{l_0}\left( \frac{d^{\sigma }}{ds_0^{\sigma }}(\varvec{u}-\varvec{u}_h)\right) ^2 ds_0\right) ^{1/2}.\nonumber \\ \end{aligned}$$
(36)

4.2 A-priori error estimation

The a-priori error estimate in the norm \(H^{\sigma }\) for linear high-order elliptic PDEs provides the convergence order of the errors under \(h\)-refinement; we refer the reader to [46] for the derivation. Specifically, the error in the Hilbert norm \(H^{\sigma }\) can be estimated as:

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{H^{\sigma }(\varOmega )}^2 \le C h^{\beta }\Vert \varvec{u}\Vert _{H^r(\varOmega )}, \end{aligned}$$
(37)

if \(\varvec{u} \in {\mathcal {V}} \cap H^r(\varOmega )\), where \(h\) is the characteristic mesh size of the elements, \(C\) a constant independent of \(\varvec{u}\) and \(h\), \(\beta \) is the order of convergence defined as \(\beta =\text {min}\{\delta -\sigma ,2(\delta -m)\}\) with \(\delta =\text {min}\{r,p+1\}\) and \(p\) the NURBS degree.

We remark that the a-priori error estimates have been derived for linear problems, which is not the case of Eq. (7). However, in several instances, the convergence order of the error is often achieved also for nonlinear problems as, e.g., in [20]. Therefore, we will use the a-priori error estimate (Eq. (37)) for verification purposes.

5 Static numerical results and discussion

For all tests presented in Sect. 3, we assume that the beam has a square cross section (\(A=k_0^2\) and \(I_z=k_0^4/12\)) of thickness \(k_0=0.02\) m, length \(l_0=1\) m, and Young modulus \(E=200\) GPa. The convergence criterion for the Newton–Raphson method is defined by \(\Vert {\mathcal {R}}_j\Vert _{2}/\Vert {\mathcal {R}}_0\Vert _{2}<10^{-8}\) where \({\mathcal {R}}_j\) is the residual vector at the Newton iteration \(j\). Numerical quadrature is performed using \(p+1\) Gauss-Legendre quadrature points per element.

The geometry representing the beam in the initial configuration is \(h\)-refined starting from a straight or a quarter circle and exactly represented by globally \({\mathcal {C}}^1\)-continuous NURBS associated with the knot vector \(\Xi =\{0,0,0,1,1,1\}\). The control points and weights for both geometries are given in Table 1. Note that we arbitrarily expressed the straight beam in terms of two parameters associated with the second control point: \(\eta \) (\(0<\eta <2\)) and \(w_{\eta }\) (\(w_{\eta }>0\)), which are taken equal to \(1\) to yield a linearly geometrical map. This is the case for all tests with initially straight geometry (tests A, B\(_1\), C, and D), with the exception of test B\(_1^*\), defined from test B\(_1\), for which \(\eta \ne 1\) and/or \(w_{\eta }\ne 1\) are considered.

Table 1 Control points \(\varvec{B}=\{\varvec{B}_x~\varvec{B}_y\}^T\) and weights \(w\) of the straight (tests A, B\(_1\), B\(_1^*\), C, and D) and quarter of circle (tests B\(_2\) and E) geometries with globally \({\mathcal {C}}^1\)-continuous NURBS corresponding to the knot vector \(\Xi =\{0,0,0,1,1,1\}\)
Full size table

5.1 Convergence orders

We verify by means of numerical tests that the convergence orders of the errors under \(h\)-refinement are in agreement with expected theoretical ones. Plots of the errors versus the mesh size \(h\) are reported for each norm \(H^{\sigma }\) with \(0\le \sigma \le m\) for globally \({\mathcal {C}}^{p-q}\)-continuous NURBS basis of degree \(p\in \{2,3,4\}\), and \(1\le q \le p-1\). Theses plots are given in Figs. 6, 7, and 8 for pure axial (test A), pure bending (tests B\(_1\), B\(_2\), and B\(_1^*\)), and mixed constraints (tests C, D, and E), respectively.

Fig. 6
figure 6

Error versus mesh size \(h\) for test A in norms \(L^2\) (a) and \(H^1\) (b). NURBS basis of degree \(p\in \{2, 3, 4\}\) is represented by dotted, dashed, and full lines, respectively, and globally \({\mathcal {C}}^{p-q}\)-continuous basis functions with \(q\in \{1,2,3\}\) are represented by \(\{\circ , \times , +\}\), respectively

Full size image
Fig. 7
figure 7

Error versus mesh size \(h\) for tests B\(_1\) (a, b, c), B\(_2\) (d, e, f) and B\(_1^*\) (g, h, i) in norms \(L^2\) (a, d, g), \(H^1\) (b, e, h) and \(H^2\) (c, f, i). NURBS basis of degree \(p\in \{2,3,4\}\) is represented by dotted, dashed, and full lines, respectively, and globally \({\mathcal {C}}^{p-q}\)-continuous basis functions with \(q\in \{1,2,3\}\) are represented by \(\{\circ , \times , +\}\), respectively

Full size image
Fig. 8
figure 8

Error versus mesh size \(h\) for tests C (a, b, c), D (d, e, f) and E (g, h, i) in norms \(L^2\) (a, d, g), \(H^1\) (b, e, h) and \(H^2\) (c, f, i). NURBS basis of degree \(p\in \{2,3,4\}\) is represented by dotted, dashed, and full lines, respectively, and globally \({\mathcal {C}}^{p-q}\)-continuous basis functions with \(q\in \{1,2,3\}\) are represented by \(\{\circ , \times , +\}\), respectively

Full size image

When the mesh size \(h\) is decreased, the error decreases linearly in the log–log scale for \(h\) sufficiently small. The convergence order \(\alpha _X\) with \(X\in \{\text {A},~\text {B}_1,~\text {B}_2,~\text {B}_1^*,~\text {C},~\text {D},~\text {E}\}\) for the different tests is estimated by using the two last points of the convergence curves presented in Figs. 6, 7, and 8, and is given in Table 2. The convergence order \(\beta \) of Eq. (37) is evaluated by considering \(r\ge p+1\) since the exact/closed-form solutions of the tests under considerations are sufficiently smooth. The theoretical convergence order \(\beta \) for \(m=1\) (\(\beta _1\)) and \(m=2\) (\(\beta _2\)) is also given in Table 2 where \(2m\) is the order of the differential spatial operator in the strong form of the PDE.

Table 2 Convergence order \(\alpha \) for the different tests compared to the estimated convergence orders \(\beta _1\) or \(\beta _2\) in norm \(H^{\sigma }\), for globally \({\mathcal {C}}^{p-q}\)-continuous NURBS basis of degree \(p\)
Full size table

For the case of linear, purely axial deformations (test A), we get \(\alpha _A=\beta _1\) from Table 2, in agreement with Eq. (37) and the fact that the problem is first order and linear \((m=1)\).

For problems in pure bending (Sect. 3.2), we have shown that the exact weak form involves only first-order operators. However, this is not the case for approximated solutions since discretization leads to spurious axial terms and nonconstant curvature. For tests B\(_1\) and B\(_2\), the convergence orders are \(\alpha _{B_{1}}\simeq \alpha _{B_{2}}\simeq \beta _2\), except for curves in the norm \(L^2\) with NURBS of degree \(p=2\). Indeed, the convergence orders are higher than expected (\(\beta _2=2\)), being \(\alpha _{B_{1}}\simeq ~4\) and \(\alpha _{B_{2}}\simeq 3\) yielding a convergence order higher than the expected one. For test B\(_1^*\), the results are obtained for \(\eta =1\) and \(w_{\eta }=\frac{1}{\sqrt{2}}\) but can be extended to any case with \(\eta \ne 1\) and/or \(w_{\eta }\ne 1\). We find that \(\alpha _{B_1^*}\simeq \beta _2\) even for \(p=2\) in the \(L^2\) norm.

For the results where both axial and bending terms are activated (tests C, D, and E), we have from Table 2 that \(\alpha _{C}\simeq \alpha _{D}\simeq \alpha _{E}\simeq \beta _2\).

In passing, we emphasize that for a given NURBS basis degree \(p\) and a fixed mesh size \(h\), increasing the continuity increases the error. Indeed, for the same mesh size, smoother basis functions use fewer dofs than the basis functions with lower continuity, which have more degrees of freedom to fit the solution.

5.2 Membrane locking

The formulation considered in this paper is free of shear locking by design based on Euler–Bernoulli beam assumptions [48], but not of membrane locking. Membrane locking is attributed to the inability of the basis functions to reproduce the inextensible bending due to the appearance of spurious axial (membrane) terms that constitute the major part of the strain energy. Indeed, in Eq. (3), the axial strain \(\epsilon \) is composed of two terms of different order which are integrated using the same Gauss rule, leading, in the case of pure bending, to the inability to satisfy exactly \(\epsilon =0\). This is also the reason for which the discretized weak form cannot be simplified to a first-order problem in the case of pure bending. By defining the slenderness parameter as:

$$\begin{aligned} \lambda =\sqrt{\frac{I_z}{Al_0^2}}, \end{aligned}$$
(38)

the membrane-locking phenomenon is shown for test B\(_2\) in Fig. 9 by setting \(\lambda =k_0/\left( l_0\sqrt{12}\right) =0.001/\sqrt{12}\) (here \(k_0=0.001\)). This phenomenon does not occur for the test in Fig. 7d where \(\lambda =0.02/\sqrt{12}\). Membrane locking appears when the slenderness is small since the membrane and bending terms are proportional to \(k_0\) and \(k_0^3\), respectively. Contrarily to the Timoshenko beam [25, 26], membrane locking is present also for initially straight beams since the constant terms of \(\epsilon \) in Eq. (3) are not zero. As shown in Fig. 9, the increased NURBS degree alleviates membrane locking as it has been already observed in FE and IGA [15, 26, 49]. However, by increasing the degree \(p\), the number of dofs and the computational cost increases; we remark that for NURBS-based IGA, the dof number only moderately increases when increasing \(p\) and the smoothness of the basis function (\(k\)-refinement). Alternative methods completely free of locking are presented in [25, 26] in the framework of isogeometric Timoshenko beams.

Fig. 9
figure 9

Error versus mesh size \(h\) for test B\(_1\) in norms \(L^2\). Globally \({\mathcal {C}}^{p-1}\)-continuous NURBS basis of degree \(p\in \{2, 3, 4\}\) is represented by dotted, dashed, and full lines, respectively. The slenderness is \(\lambda =0.001/\sqrt{12}\). The simulations for which membrane locking happens are highlighted with a dashed ellipse

Full size image

Finally, even though shear-free assumptions are violated for large thickness ratio (for \(k_0\approx 1\), we have \(\lambda \approx 1/\sqrt{12}\)), we have analyzed convergence rates for such conditions. We find that the computed convergence order is reduced with respect to the one expected for linear PDEs (Eq. (37)). This phenomenon is not due to membrane locking but appears to be sensitive to the NURBS basis global continuity, and deserves further investigations.

6 Dynamic problems

We consider now three different dynamic beam problems.

6.1 Swinging of a pinned beam

An initially straight beam, pinned at one extremity, is oscillating under the action of gravity. In this example, both stiff and soft beams are considered. The oscillating period of the stiff beam is compared to that of a bar (rigid beam) pendulum of constant cross section given by [57]:

$$\begin{aligned} T_{Bar}=4\sqrt{\frac{2 I_{\theta }}{m l_0 g}}K(c), \end{aligned}$$
(39)

where \(g\) is the gravitational constant, \(I_{\theta }=ml_0^2/3\) the inertia of the beam around the rotational point, \(m\) the mass of the bar, and \(l_0\) its length; \(K(c)\) is the complete elliptic integral of the first kind where \(c=\sin (\theta _0/2)\) and \(\theta _0\) is the initial inclination of the pendulum for which the speed is null (Fig. 10a). The parameters used for the simulation are the same as in [23]: \(g=9.81\) m s\(^{-2}\), \(E=100\) MPa, \(\rho =3000\) Kg m\(^{-3}\), \(\theta _0=\pi /2\) rad, \(l_0=1\) m, and circular cross section of radius \(r=0.5\) m and \(0.001\) m for the stiff and soft beams, respectively (\(A= \pi r^2\) and \(I_z=\pi r^4/4\)). The time step used for the time discretization with the generalized-\(\alpha \) method is \(\Delta t=0.0025\) s, and the high-frequency dissipation parameter is \(\rho _{\infty }=0.5\). For the spatial discretization, as in [23], we consider NURBS basis functions of degree \(p=3\) and globally \({\mathcal {C}}^2\)-continuous across the \(n_e=10\) mesh elements. In the case of the stiff beam, the first five periods \(T_{Beam}\) are compared to Eq. (39) and results are found in excellent agreement (see Table 3).

Table 3 Period error (\(|T_{Bar}-T_{Beam}|/T_{Bar}\)) of the first five oscillations for the stiff beam (\(T_{Bar}=1.9334 s)\)
Full size table

For the case of the swinging soft beam, snapshots of the first five seconds of the simulation are shown in Fig. 10. Results are found to be similar to those in [23], even if some discrepancies arise due to the differences in the formulation.

Fig. 10
figure 10

Snapshots of the oscillating, soft beam with \(n_e=10\) and \(p=3\): a \(t\in [0.0,~0.9]\) s, b \(t\in [0.9,~1.8]\) s, c \(t\in [1.8,~2.7]\) s, d \(t\in [2.7,~3.6]\) s, e \(t\in [3.6,~4.5]\) s, and f \(t\in [4.5,~5.0]\) s. The arrows indicate swing directions

Full size image

In order to show the convergence of the results, snapshots at time \(t=1.5\) s of the soft beam are given in Fig. 11 and we find that both mesh refinement and order elevation converge to the same solution. Note that the mesh size in Fig. 10 is the same as in [23] in order to allow direct comparison, even if it is too large to be sufficiently accurate.

Fig. 11
figure 11

Snapshots of the soft beam at time \(t=1.5\) s for different meshes (\(h\)-refinement). a \(p=3\) and \(n_e=10\), \(20\), \(30\), and \(40\) from large dashes to full line, respectively. b \(n_e=20\) and \(p=2\), \(3\), \(4\), and \(5\) from large dashes to full line, respectively

Full size image

6.2 Solitons propagating in post-buckled beams

Post-buckled beams (Fig. 12a) possess a geometrically nonlinear load-displacement relationship (\(P(\Delta U)\); see Fig. 12c) and dispersion sources, such that these structures are capable of hosting solitons (nonlinear stationary waves) [50, 51]. In [51], it is shown that the phase velocity of linear waves is dispersive and may increase or decrease, depending on the buckling level, type of supports (necessary to ensure the stability), and curvature.

Fig. 12
figure 12

Schematic post-buckled beam with \(q=9\) unit cells. a Initial (dashed line) and post-buckled (solid line) configurations after applying the static load \(P_S=P(\Delta U_0)\). b Displacement control \(U_1(t)\) (Eq. (42)) resulting in a propagating compressional wave (solid line). c Nonlinear load–displacement relationship \(P(\Delta U_0)\) with elastica solution [50] (\(*\)) and results obtained by a static simulation using the present formulation (full line)

Full size image

Here we reproduce the theoretical results for solitary wave propagation in a slender beam with periodic pin supports [50]. The numerical simulation of these beam problems is obtained in two distinct steps: A static one in load control, where the beam, with a large number of unit cells (\(q\)), is buckled (Fig. 12a), and a dynamic one, in displacement control, where a pulse is sent through the buckled structure (Fig. 12b). We define the axial displacement of the support \(j\) by \(U_{j}=u_x(\xi _j)=\sum \limits _{i=1}^{n} R_{i}(\xi _j)u_{i,x}\), where \(\xi _j\) is the position of the pinned support in the knot vector. The strain \(\zeta _j\) at the support \(j\) is defined as the variation of the distance between two supports, and taken positive in compression such that:

$$\begin{aligned} \zeta _j\!=\!\frac{U_{j}-U_{j+1}}{L_0}=\frac{\Delta U_{j}}{L_0}, \qquad \! \text {for}~j=1,\ldots ,q-1,\nonumber \\ \end{aligned}$$
(40)

where \(L_0=L-\Delta U_0=L\left( 1-\zeta _0\right) \), and \(L\) is the length between two supports before buckling; \(\Delta U_0\) and \(\zeta _0\) are constant after the static buckling along the beam and are the relative displacement between two consecutive supports and strain, respectively. By modeling the structure by a series of alternating masses and nonlinear springs, and approximating locally the load-displacement by polynomial of degree two, it is shown in [50] that the homogenization of the discrete system leads to the Korteweg de Vries (KdV) equation (a canonical nonlinear PDE [58]) admitting a soliton as solution, reading:

$$\begin{aligned} \Delta \zeta =\Delta \zeta _m~\text {sech}^2\left( \Lambda ^{-1}(x-Vt)\right) , \end{aligned}$$
(41)

where \(\Delta \zeta =\zeta -\zeta _0\) is the dynamic strain wave and \(\Delta \zeta _m\) its amplitude; in addition, \(V=C_0+ \sigma \Delta \zeta _m /\left( 6 C_0\right) \) is the soliton phase velocity and \(\Lambda = \sqrt{24C_0\gamma / \left( \sigma \Delta \zeta _m \right) }\) its characteristic width, where \(C_0^2=P'(\Delta U_0) L_0^2/m\), \(\sigma =P''(\Delta U_0)L_0^3/m\), \(\gamma =C_0 L_0^2/24\), and \(m=\rho A L\). The dynamic displacement applied at the left extremity of the beam is obtained by integrating Eq. (41):

$$\begin{aligned} U_{1}(t)= & {} \Delta \zeta _m~\Lambda \left( \text {tanh}\left( \Lambda ^{-1}V \left( t - t_0 \right) \right) +1\right) \nonumber \\&+q\Delta U_0, \end{aligned}$$
(42)

where \(t_0\) is arbitrary chosen as \(t_0=5 \Lambda V^{-1}\).

In order to properly pre-buckle the structure, imperfections in the initial configuration are used instead of considering additional loads as done in Sec. 3.4. The procedure used to construct the initial geometry with imperfections reads:

  • build a straight beam with globally \({\mathcal {C}}^1\)-continuous NURBS basis of degree \(p=2\) as defined in Table 1 with \(\eta =1\) and \(l_0=qL\);

  • \(h\)-refine the knot vector to get \(q\) mesh elements of uniform length;

  • modify the \(y\) coordinates of the \(q+1\) control points such that

    $$\begin{aligned} B_{j,y}= {\left\{ \begin{array}{ll} 0 &{}\quad \text {if}~ j=\{1,~q+1\},\\ (-1)^{j} e &{}\quad \text {otherwise}, \end{array}\right. } \end{aligned}$$
    (43)

    where \(0<e\ll L_0\) is the parameter characterizing the imperfection amplitude (Fig. 13a);

  • perform order elevations and insert additional distinct knots (Fig. 13a, b) such that the NURBS basis remains globally \({\mathcal {C}}^1\)-continuous.

Fig. 13
figure 13

Four first unit cells a before and b, c after the refinement, and a, b before and c after the static buckling. Control points and knot locations are represented by \(\bullet \) and \(\varvec{\times }\), respectively. d Snapshots at time \(t=\{0.07,~0.15,~0.22\}\) s of the strain wave \(\Delta \zeta \) vs. the support number \(j\) resulting from simulation (full lines), and compared with the analytical soliton (Eq. (41)) (curves with \(\varvec{*}\))

Full size image

The applied boundary conditions are illustrated in Fig. 12a. However, since the NURBS basis functions are globally \({\mathcal {C}}^{1}\)-continuous, the control points which are not at the extremities of the beam do not lie on the geometry. For each support \(j=2,\ldots ,q-1\), the \(y\) displacement is fixed by enforcing the condition:

$$\begin{aligned} r_y(\xi _j)= & {} \sum \limits _{i=1}^{n} R_{i}(\xi _j)(B_{i,y}+u_{i,y}) =\sum \limits _{i=1}^{n} R_{i}(\xi _j)u_{i,y}\nonumber \\= & {} \varvec{C}_j \varvec{u}=0, \end{aligned}$$
(44)

where the position of the support in the knot vector is given by \(\xi _j=j/q\) and \(\varvec{C}_j\) is a vector which has for length the number of dofs, built from shape functions, and completed by zeros. In order to enforce these conditions, \(q-1\) Lagrange multipliers \(\lambda _j\) [59] are introduced, thus resulting in a coupled system of two equations:

$$\begin{aligned}&G(\varvec{r}(\varvec{u}))(\delta \varvec{u})+\sum \limits _{j=1}^{q-1}\lambda _j \varvec{C}_j \delta \varvec{u}=0, \end{aligned}$$
(45)
$$\begin{aligned}&\sum \limits _{j=1}^{q-1} \varvec{C}_j \varvec{u} \delta \lambda _j=0. \end{aligned}$$
(46)

Eq. (45) represents the virtual work (see Eq. (7)), and Eq. (46) is the variation of the force necessary to constrain the displacement of the supports along \(y\).

For the numerical simulation, the following parameters are used: number of unit cells \(q=150\), rectangular cross section of the beam width \(b_0=12\) mm and thickness \(k_0=0.4\) mm, \(L=0.06\) m, \(E=200\) GPa, and \(\rho =8000\) Kg m\(^{-3}\). The initial imperfection is \(e=0.1\) mm, the initial buckling compression \(\Delta U_0/L=0.8\) (Fig. 12c), and the amplitude of the dynamic strain wave \(\Delta \zeta _m=0.1\). Each span (unit cell) is divided into \(n_e/q=14\) mesh elements, and the degree of the NURBS basis is \(p=3\), such that these parameters give a good approximation of the analytical elastica equation [50] (see Fig. 12c). In the static part, the load is incrementally applied in \(1000\) steps, while in the dynamic part \(1000\) time steps are used with a total integration time \(t_f=qL_0V\) and \(\rho _{\infty }=0.9\). The resulting strain wave is shown in Fig. 13. While propagating, the wave preserves its shape. Moreover, the strain wave overlaps very well with the homogenized (and thus approximate) analytical equation describing solitons (Eq. (41)). This example shows that our formulation can be conveniently adapted for nonlinear wave propagation problems in initially curved slender structures undergoing large dynamic deformations.

6.3 Dynamic snap-through buckling

We consider the snap-through buckling of a transversally loaded arch, which is obtained from the buckling of an initially straight beam (see Fig. 14a, b). This problem is particularly interesting because it involves internal resonances [60] and thus is good candidate to demonstrate the robustness of the proposed methods. In particular, we are interested in the transient response of a buckled beam laterally loaded in its center by a step load, as already studied in [41], and we aim at reproducing the findings of [41]: the critical load is (1) smaller in dynamics than in statics, and (2) it decreases with extensibility (the extensibility is inversely proportional to the slenderness parameter \(\lambda \) defined in Eq. (38)). The construction of the initial geometry with the initial imperfections follows the method presented in Sect. 6.2 with a single unit cell (\(q=1\)). The beam is divided into \(n_e=150\) mesh elements, and the degree of the NURBS basis is \(p=3\) with NURBS basis functions which are \({\mathcal {C}}^2\)-continuous. The material and geometrical parameters are the same as in Sect. 6.2 except the initial length of the beam defined by \(l_0=\sqrt{I_z/A}/\lambda \). We choose \(\lambda =0.01\) and \(0.02\) to compare the influence of extensibility. The time step is \(\Delta t=0.001T\), where \(T=l_0^2\sqrt{\rho A/EI_z}\), and \(\rho _{\infty }=0.9\).

Fig. 14
figure 14

a Straight beam (large dashes) statically buckled (small dashes) and b snap-through its second (gray line) or third (black line) mode after the application of a load (\(Q\)) along the \(y\) axis at the mid-span. c Resulting load (\(Q_S\)) midpoint-displacement (\(y_m\)) curve. Points A and B are the static critical load of the second and third modes, respectively; the \((~)^+\) and \((~)^-\) give the sign of the initial angle \(\theta _0\). We set \(\theta _0=40^{\circ }\) and \(\lambda =0.01\)

Full size image

The static snapping critical load for the beam is obtained from the nonmonotonic load-displacement curve (Fig. 14c), computed using the arc-length method [61]. If the beam is perfectly symmetric and the load is applied in its center, the second mode (asymmetric) is not excited and the deformed beam “jumps” (point B in Fig. 14c) directly to the third mode (symmetric); whereas, if asymmetric imperfections are present (e.g., the load is not perfectly applied in the center), snapping occurs at point A (see Fig. 14c) with deformation given by the second mode (Fig. 14a,b). Values of the normalized critical load (\(Q_S/P_C\)) are reported in Table 4 where we can already conclude that the critical load is smaller in dynamics than in statics, in agreement with [41].

Table 4 Nondimensional static critical load \(Q_S/P_c\) (\(P_c\) defined in Eq. (32)) for snapping through the second and third bucking modes and for two different levels of beam slenderness \(\lambda \). Results are compared to [41], if available
Full size table

In Fig. 15a, the midpoint deflection history of the beam under a dynamic step load \(Q_D(t)=H(t) Q_D\) is reported, where \(H(t)\) is the Heaviside function and \(Q_D=4 P_c\) is chosen between the static critical load (\(Q_S\)) of the second and third mode (see Table 4). Both configurations of slenderness (\(\lambda \)) are considered. Although the dynamic load is smaller than the static critical load, snapping occurs directly through the third mode for the most extensible beam (\(\lambda =0.02\)) (see deformed shapes in Fig. 15d), showing that the dynamic critical load is smaller than the static one. Conversely, in the case \(\lambda =0.01\), the beam does not have enough energy to snap directly through the excited mode (mode three). The beam starts oscillating (Fig. 15b) and then snaps through the second mode (Fig. 15c). For the same load \(Q_D(t)\), since only the most extensible beam snaps directly through the third mode, dynamic critical load values become smaller and smaller for increasing values of extensibility, in agreement with [41].

Fig. 15
figure 15

Dynamic snap-through buckling of a beam with initial angle \(\theta _0=40^{\circ }\), of slenderness \(\lambda =0.01\) (gray), and \(\lambda =0.02\) (black) laterally loaded in its center by a step load (\(Q_D/P_c=4\)). a Time history of the normalized center deflection \(y_m/l_0\) and b, c, d snapshots of the deformed shape. For the less extensible case, the beam oscillates around its first mode (b) and snaps through its second buckling mode after \(t/T\approx 2\) (c), whereas for the most extensible case, the beam snaps directly to its third mode (d). Snapshots starts at time \(t/T=0\) (b, d) and \(t/T=2.2\) (c) with a time step between each snapshots of \(\Delta t/T=0.04\) (b), \(\Delta t/T=0.13\) (c), and \(\Delta t/T=0.08\) (d), and are represented in (a) by \(*\), \(\triangle \), and \(\circ \), respectively. \(l_0=\left[ 0.0289,~0.0144\right] \) m, \(P_C=\left[ 197.3921,~789.5684\right] \) N and \(T=\left[ 5.8095,~1.4524\right] \times 10^{-4}\) s for \(\lambda =\left[ 0.01,~0.02\right] \), respectively

Full size image

Although we recover the same results, the point here is to compare both methods. Indeed, in [41], the extensible-elastica concept based on the same strain kinematics and constitutive law is used, similarly to the proposed formulation. Solutions of the extensible-elastica are presented in terms of rotation and axial displacements in [41], while we report in this paper \(x\) and \(y\) displacement components. Accordingly, the main difference lies in discretization of the problem; finite differences associated with the second-order Crank-Nicolson time integration scheme are used in [41], whereas the formulation presented here considers NURBS-based IGA with the second-order generalized-\(\alpha \) scheme. Even if direct comparisons of the results are not possible, since the smoothness of the displacement field and rotation is ensured by the NURBS basis functions which are globally \({\mathcal {C}}^1\)-continuous, a small number of mesh elements and time steps are required in the present work, leading to significant gains in computational efforts.

7 Conclusions

Rotation-free extensible-elastica formulations involve fourth-order spatial derivatives of displacements not available in classical FE methods. We propose the use of IGA based on NURBS with high-degree continuous basis functions for the finite-element approximation. Owing to the linear relation between Biot stress and strain we employ, we are able to directly evaluate the performance of the discretized model by means of a-priori error estimates of FE and analytical solutions for several static benchmark problems with known analytical solution. This is to say we discretize the energy functional of the rotation-free extensible-elastica. In addition to problems available in the literature, we derive the closed-form solution based on the extensible-elastica theory for an initially curved cantilever beam subject to transverse tip load.

We remark that NURBS-based IGA formulation we investigated is advantageous to model finite deformations of initially curved slender structures which require many traditional elements to capture the nonlinear coupling of axial and transverse deformations. This leads to elements with poor aspect ratio and resulting erroneously increased stiffness. Membrane locking is typical. The high-degree, continuous basis functions used here, while also leading to a formulation prone to membrane locking, allow the use of many fewer elements to exactly represent the geometry of curved structures.

Another advantage is the reduced number of degrees of freedom for a given problem, since the formulation is rotation-free. The absence of the rotary degree of freedom is of great interest in dynamics, leading to constant mass terms which contain the computational cost and allow the simulation of complex, dynamic beam problems, as we did in the present paper.