On modified time delay hyperchaotic complex Lü system

Abstract

Time delays are often considered as sources of complex behaviors in dynamical systems. Much progress has been made in the research of time delay systems with real variables. In this article, we will focus our study on time delay complex systems. This paper investigates a modified time delay hyperchaotic complex Lü system. This system is constructed by including the constant delay to one of its states. The behaviors of our time delay system are greatly different from those of the original system without delay. By setting the parameters, we discuss the effect of delay variation on system stability. Numerically, we calculate the range of system parameters at which chaotic and hyperchaotic attractors of different order exist. We found that our system has hyperchaotic attractors of order $2,3,\ldots ,6$. However, the modified complex Lü system without delay has only hyperchaotic attractors of order 2. Different forms of modified time delay hyperchaotic complex Lü system are constructed by including the delay into different states of this system. Chaos synchronization in modified time delay hyperchaotic complex Lü system is investigated. The active control method based on Lyapunov–Krasovskii function is used to synchronize the hyperchaotic attractors. In particular, studying the time evolution of errors, we show that this technique is very effective for controlling the behavior of our system.

1 Introduction

In 1963, the work of Lorenz [1] had paved the way for identifying the important basic concept, namely Chaos. Chaos is an interesting complex nonlinear phenomenon. It is generated by determined nonlinear equations and is sensitive to the initial state values. Chaos shows potential applications in many scientific and engineering fields such as secure communications, biological systems, chemical reactions, information processing and optimization. It is well known that the appearance of time delay in many practical engineering systems is a source of instability or, in general, may induce undesired oscillations and, thus, poor performance. Systems with time delay exhibit more complex and adequate dynamic behavior than those without time delay. The primary complexity that introducing the delay adds to the system is the growth of the phase space from a finite dimension to an infinite dimension. In this connection, time delay systems described by delay differential equations (DDEs) can generate hyperchaotic attractors with large number of positive Lyapunov exponents (LEs) for suitable nonlinearities. Therefore, DDEs are used to model dynamical systems broadly in scientific and engineering areas, for instance, in population dynamics, biology, economy, neural networks, complex networks, and so on. Since the first chaotic DDE was found by Mackey and Glass [2] which is a model of blood production in patients with leukemia, several works have proposed many chaotic systems with delay [3–11].

On the other hand, the stability analysis and control design of time-delayed chaotic and hyperchaotic systems are hot topics and have been developed and thoroughly studied over the past three decades since they describe the real physical situation properly. In [12], the methodology of design and analysis of a simple first-order time-delayed chaotic system has been reported. For a class of high-order nonlinear systems with input delay, the adaptive control scheme combined with backstepping and fuzzy logic system is proposed in [13]. Ghosh [14] studied the stability and projective synchronization in multiple delay Rössler system. The authors of Ref. [15] have proposed a novel adaptive method for the control of synchrony on oscillator networks, which combines time-delayed coupling with the speed gradient method of control theory. Chaos synchronization is an interesting nonlinear phenomenon and has been intensively investigated in many years due to its potential applications in biological systems, chemical reactions, nano-oscillator, secure communications and in many other areas. So far, various types of synchronization phenomena in the chaotic and hyperchaotic DDEs have been observed, such as complete synchronization [16, 17], projective synchronization [14], projective-dual synchronization [18], adaptive modified function projective synchronization [19], generalized synchronization [20] and so on.

Since Fowler et al. [21] introduced a complex Lorenz model which is used to describe and simulate rotating fluids and detuned laser [22, 23], complex chaotic and hyperchaotic systems have attracted increasing attention. After that, Mahmoud et al. introduced and studied many chaotic and hyperchaotic complex systems, such as chaotic complex Chen and Lü systems [24], the hyperchaotic complex Lü system [25], the hyperchaotic complex Lorenz system [26] and modified hyperchaotic complex Lü system [27]. Also Mahmoud constructed a new hyperchaotic complex Lorenz [28] and a new hyperchaotic complex Chen model [29]. Interest in the complex dynamic behaviors of nonlinear systems increased due to their potential application in different fields, such as detecting changes of biological signals in different abnormalities [30], data and image encryption, studying sunspot cycles and lasers. Further, there are already some results in the literature studying the control and synchronization of complex-variable dynamical systems [31–41].

Wang et al. [42] proposed a new modified Lü system as:

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \quad \dot{y}=-xz+\beta y+w, \\ \dot{z}=xy-\gamma z, \quad \dot{w} =-\delta x, \end{array} \end{aligned}$$

(1)

where $(x,y,z,w)^\mathrm{T}\in {\mathbb {R}}^{4},\alpha ,\beta ,\gamma$ and $\delta$ are constant parameters and dots represent derivatives with respect to time. This system is hyperchaotic of order two for $\alpha =35,\beta =14,\gamma =3$ and $\delta =5.$ Based on system (1), Mahmoud et al. [27] studied the basic properties of the modified hyperchaotic complex Lü system:

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \quad \dot{y}=-xz+\beta y+w, \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z, \quad \dot{w}=\frac{-\delta }{2}\left( x+\bar{x}\right) , \end{array} \end{aligned}$$

(2)

where $x$ and $y$ are complex variables, $z$ and $w$ are real variables, overbar denotes complex conjugate variables and $\alpha ,\beta ,\gamma$ and $\delta$ are real positive constant parameters. This system is a set of 6D real first-order ordinary differential equation and has two positive LEs when $\alpha =70,\beta =15,\gamma =12$ and $\delta =5$, as an example of system parameters.

Our goal in this paper is to introduce a modified time-delayed complex Lü system by including a constant time delay into one of the states of system (2) as:

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w, \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z, \\ \dot{w}=\frac{-\delta }{2}\left( x(t-\tau )+\bar{x}(t-\tau )\right) , \end{array} \end{aligned}$$

(3)

where $x=u_{1}+iu_{2},y=u_{3}+iu_{4}$ are complex variables, $z(t)=u_{5}(t),w(t)=u_{6}(t),u_{k}(k=1,2,\ldots ,6)$ are real variables, $\tau \ge 0$ is a constant time delay, $\alpha ,\gamma ,\beta$ and $\delta$ are constant parameters and $i=\sqrt{-1}.$ The dynamics of this new system is more complicated than system (2). Because of the presence of the delay $\tau$, system (3) has infinite dimension and posses more than two positive Lyapunov exponents, while our system (2) has only two positive Lyapunov exponents. Its dynamic behaviors are greatly different from those of the original system (2), especially its simple structure can generate highly unpredictable time series. As it is cleared from system (3), the constant delay $\tau$ is added to the state $x$ to the fourth equation, so we can add it to different states of (3) to get different forms of modified delay complex Lü system.

The paper is organized in the following manner: In the next section, the stability of the fixed points are discussed. In Sect. 3, numerically the range of parameters values of the system at which chaotic and hyperchaotic attractors exist is calculated based on the calculations of LEs. The signs of LEs provide a good classification of the dynamics of our system. We can construct other modified time- delayed complex Lü systems by including the delay $\tau$ into different states of (3), in Sect. 4. LEs of these systems are calculated and their dynamics can be similarly studied as we did for (3). In Sect. 5, the active control method based on Lyapunov–Krasovskii is used to synchronize hyperchaotic attractors of (3). The last section contains our concluding remarks.

2 Basic properties of system (3)

In this section, we study the basic properties of our new system (3). Separating the real and imaginary parts of the modified time delay complex Lü system (3), we obtain the following real version:

$$\begin{aligned} \begin{array}{l} \dot{u}_{1}=\alpha (u_{3}-u_{1}+u_{3}u_{5}), \\ \dot{u}_{2}=\alpha (u_{4}-u_{2}+u_{4}u_{5}), \\ \dot{u}_{3}=-u_{1}u_{5}+\beta u_{3}+u_{6}, \\ \dot{u}_{4}=-u_{2}u_{5}+\beta u_{4}, \\ \dot{u}_{5}=u_{1}u_{3}+u_{2}u_{4}-\gamma u_{5}, \\ \dot{u}_{6}=-\delta u_{1\tau }, \end{array} \end{aligned}$$

(4)

where $u_{1\tau }\equiv u_{1}(t-\tau ).$The equilibrium points can be obtained by setting $\dot{u} _{k}=0,(k=1,2,\ldots ,6)$ and $u_{1\tau }=u_{1},$ so system (4) possesses five isolated fixed points:

$$\begin{aligned}&E_{0} =(0,0,0,0,0,0), \\&E_{1,2} =\left( 0,\pm \sqrt{\beta \gamma },0,\pm \frac{\sqrt{\beta \gamma } }{2\beta }S_{+},\frac{1}{2}S_{+},0\right) , \\ E_{3,4}&= \left( 0,\pm \sqrt{\beta \gamma },0,\pm \frac{\sqrt{\beta \gamma } }{2\beta }S_{-},\frac{1}{2}S_{-},0\right) , \end{aligned}$$

where $S_{\pm }=-1\pm \sqrt{1+4\beta }.$ So this system has only one fixed point if $\beta \le \frac{-1}{4}$ and $\gamma \ge 0$ or $\gamma \le 0.$

2.1 The stability of system (4) at $E_{0}$

Now, we will study the stability of the trivial fixed point. The linearization of system (4) at $E_{0}$ is:

$$\begin{aligned} \begin{array}{l} \dot{u}_{1}=\alpha (u_{3}-u_{1}), \\ \dot{u}_{2}=\alpha (u_{4}-u_{2}), \\ \dot{u}_{3}=\beta u_{3}+u_{6}, \\ \dot{u}_{4}=\beta u_{4}, \\ \dot{u}_{5}=-\gamma u_{5}, \\ \dot{u}_{6}=-\delta u_{1\tau }, \end{array} \end{aligned}$$

(5)

The associated characteristic equation of system (5) is:

$$\begin{aligned} \det \left( \begin{array}{cccccc} -\alpha -\lambda &{} 0 &{} \alpha &{} 0 &{} 0 &{} 0 \\ 0 &{} -\alpha -\lambda &{} 0 &{} \alpha &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta -\lambda &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} \beta -\lambda &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\gamma -\lambda &{} 0 \\ -\delta \hbox {e}^{-\lambda \tau } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \!=\!0, \end{aligned}$$

whose characteristic at $E_{0}$ is:

$$\begin{aligned}&\left( \lambda -\beta \right) \left( \lambda +\alpha \right) \left( \lambda +\gamma \right) \left( \lambda ^{3}+\left( \alpha -\beta \right) \right. \nonumber \\&\quad \left. \times \, \lambda ^{2}-\alpha \beta \lambda +\alpha \delta \hbox {e}^{-\lambda \tau }\right) =0. \end{aligned}$$

(6)

Because of the exponential in the characteristic equation, system (5) has an infinite number of eigenvalues, unlike system (2) which has only six eigenvalues [27]. We first study the distribution of the roots of Eq. (6) and find that there are two possibilities:

• (a) Under certain assumptions on the coefficients all roots have negative real parts for all delay value $\tau \ge 0.$

• (b) If the assumptions in (a) are not satisfied, then there is a critical value $\tau _{0}.$ When the delay $\tau <\tau _{0},$ the real parts of (6) are still negative; when $\tau =\tau _{0}$, there is a pair of purely imaginary roots and other roots have negative real parts; when $\tau >\tau _{0}$, there is at least one eigenvalue which has a positive real part [43].

Applying these results to the delay model (5), we show that under a set of assumptions on the parameters, the steady state of (5) is asymptotically stable. Under another set of conditions, the steady state of (5) is conditionally stable; that is, there is a critical delay value $\tau _{0}$, and the steady state is asymptotically stable when $\tau <\tau _{0},$ loses its stability when $\tau =\tau _{0},$ and becomes unstable when $\tau >\tau _{0}.$ Thus, a Hopf bifurcation occurs at the steady state when $\tau$ passes through the critical value $\tau _{0}.$ Obviously, Eq. (6) always has a negative roots for all $\tau \ge 0$ if:

$$\begin{aligned} \alpha >0,\beta <0,\gamma >0. \end{aligned}$$

Then, we need to investigate the third degree transcendental polynomial equation:

$$\begin{aligned} \lambda ^{3}+\left( \alpha -\beta \right) \lambda ^{2}-\alpha \beta \lambda +\alpha \delta \hbox {e}^{-\lambda \tau }=0, \end{aligned}$$

(7)

which can be written as:

$$\begin{aligned} \lambda ^{3}+a\lambda ^{2}+b\lambda +c+d\hbox {e}^{-\lambda \tau }=0, \end{aligned}$$

(8)

where $a=\alpha -\beta , b=-\alpha \beta , c=0,d=\alpha \delta .$ To discuss the distribution of the roots of the exponential polynomial equation (8), we need the following result which was proved by Ruan and Wei [44].

Lemma 1

Consider the exponential polynomial:

$$\begin{aligned}&\!\!\!P(\lambda ,\hbox {e}^{-\lambda \tau _{1}},\ldots ,\hbox {e}^{-\lambda \tau _{m}})\\&\quad =\lambda ^{n}+p_{1}^{(0)}\lambda ^{n-1}+\cdots +p_{n-1}^{(0)}\lambda +p_{n}^{(0)} \\&\!\!\!\qquad \,\, +\left( p_{1}^{(1)}\lambda ^{n-1}+\cdots +p_{n-1}^{(1)}\lambda +p_{n}^{(1)}\right) \hbox {e}^{-\lambda \tau _{1}}+ \cdots \\&\!\!\!\qquad \,\, +\left( p_{1}^{(m)}\lambda ^{n-1}+\cdots +p_{n-1}^{(m)}\lambda +p_{n}^{(m)}\right) \hbox {e}^{-\lambda \tau _{m}}, \end{aligned}$$

where $\tau _{j}\ge 0$ $(j=1,2,\ldots ,m)$ and $p_{k}^{(j)}$ $(j=0,1,\ldots ,m;k=1,2,\ldots ,n)$ are constants. As $(\tau _{1},\tau _{2},$ $\ldots ,\tau _{m})$ vary, the sum of the order of the zeros of $P(\lambda ,\hbox {e}^{-\lambda \tau _{1}},\ldots ,\hbox {e}^{-\lambda \tau _{m}})$ on the open right half plane can change only if a zero appears on or crosses the imaginary axis.

Clearly, $i\omega \ (\omega >0)$ is a root of Eq. (7) if and only if $i\omega$ satisfies:

$$\begin{aligned} -i\omega ^{3}-a\omega ^{2}+ib\omega +c+d\left( \cos \omega \tau -i\sin \omega \tau \right) =0. \end{aligned}$$

Separating the real and imaginary parts, we have:

$$\begin{aligned} \left\{ \begin{array}{c} c-a\omega ^{2}=-d\cos \omega \tau , \\ \omega ^{3}-b\omega =-d\sin \omega \tau . \end{array} \right. \end{aligned}$$

(9)

Adding up the squares of both equations of (9), we obtain:

$$\begin{aligned} \omega ^{6}+\left( a^{2}-2b\right) \omega ^{4}+\left( b^{2}-2ac\right) \omega ^{2}+c^{2}-d^{2}=0. \end{aligned}$$

(10)

Let $\mu =\omega ^{2}$ and denote $p=a^{2}-2b,q=b^{2}-2ac,$ and $r=c^{2}-d^{2}.$ Then, Eq. (10) becomes:

$$\begin{aligned} \mu ^{3}+p\mu ^{2}+q\mu +r=0. \end{aligned}$$

(11)

In the following, we need to seek conditions under which Eq. (11) has at least one positive root. Denote

$$\begin{aligned} h(\mu )=\mu ^{3}+p\mu ^{2}+q\mu +r. \end{aligned}$$

(12)

Therefore, applying Refs. [43, 45], we obtain the following lemma.

Lemma 2

For the polynomial equation (11), we have the following results:

• (i) If $r<0$, then Eq. (11) has at least one positive root.

• (ii) If $r\ge 0$ and $\varDelta =p^{2}-3q\le 0,$ then Eq. (11) does not have positive roots.

• (iii) If $r\ge 0$ and $\varDelta =p^{2}-3q>0,$ then Eq. (11) has positive roots if and only if $\mu _{1}^{*}=\frac{1}{3}(-p+\sqrt{\varDelta } )>0$ and $h(\mu _{1}^{*})\le 0.$

Suppose that Eq. (11) has positive roots. Without loss of generality, we assume that it has three positive roots, defined by $\mu _{1},\mu _{2}$ and $\mu _{3}$. Then, Eq. (10) has three positive roots

$$\begin{aligned} \omega _{1}=\sqrt{\mu _{1}},\quad \omega _{2}=\sqrt{\mu _{2}},\quad \omega _{3}=\sqrt{\mu _{3}}. \end{aligned}$$

From (9), we have

$$\begin{aligned} \tau _{k}^{(j)}&= \frac{1}{\omega _{k}}\left[ \arctan \left( \frac{\omega _{k}^{3}-b\omega _{k}}{c-a\omega _{k}^{2}}\right) +j\pi \right] ,\nonumber \\&k=1,2,3;\quad j=0,1,\ldots . \end{aligned}$$

(13)

Then, $\pm i\omega _{k}$ is a pair of purely imaginary roots of Eq. (7 ) with $\tau =\tau _{k}^{(j)}\ (k=1,2,3;j=0,1,\ldots ).$ Thus, we can define:

$$\begin{aligned} \tau _{0}=\tau _{k_{0}}^{(0)}=\min _{1\le k\le 3}\{\tau _{k}^{(0)}\},\quad \omega _{0}=\omega _{k_{0}}. \end{aligned}$$

Note that when $\tau =0$, Eq. (8) becomes:

$$\begin{aligned} \lambda ^{3}+a\lambda ^{2}+b\lambda +c+d=0. \end{aligned}$$

(14)

By the Routh–Hurwitz criterion, all roots of this equation have negative real parts if and only if:

$$\begin{aligned} a>0,c+d>0\text { and }ab-c-d>0. \end{aligned}$$

Lemma 3

[45] Suppose that $a>0,c+d>0,ab-c-d>0,\alpha >0,\beta <0$ and $\gamma >0.$(a) $r\ge 0$ and $\varDelta =p^{2}-3q\le 0$, then all roots of Eq. (6) have negative real parts for all $\tau \ge 0.$(b) If one of the following holds: (i) $r<0$; (ii) $r\ge 0$, $\mu _{1}= \frac{1}{3}(-p+\sqrt{\varDelta })>0$ and $h(\mu _{1})\le 0$ then all roots of Eq. (6) have negative real parts when $\tau \in [0,\tau _{0}).$

Let

$$\begin{aligned} \lambda (\tau )=\rho (\tau )+i\omega (\tau ), \end{aligned}$$

be the root of Eq. (8) satisfying:

$$\begin{aligned} \rho \left( \tau _{k}^{(j)}\right) =0,\omega \left( \tau _{k}^{(j)}\right) =\omega _{k}. \end{aligned}$$

If there is such a pair of roots lying on the imaginary axis, it is necessary to determine in which direction this root is moving with small variations on $\tau$. In order to do this, the function:

$$\begin{aligned} \varPhi \left( \lambda ,\tau \right) =\hbox {sign}\left( {\mathfrak {R}}\left\{ \frac{ \hbox {d}\lambda }{\hbox {d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }\right) , \end{aligned}$$

(15)

must be calculated. Here, only the real part matters as it is only a stability analysis. In this way, if $\varPhi \left( i\omega _{k},\tau _{k}^{(j)}\right) >0$, roots are crossing imaginary axis indicate instability. If $\varPhi \left( i\omega _{k},\tau _{k}^{(j)}\right) <0$, roots are crossing the imaginary axis from right to left, stabilizing the system. Then, we have the following transversality condition.

Lemma 4

Suppose that $\mu _{k}=\omega _{k}^{2}$ and $h^{\prime }\left( \mu _{k}\right) \ne 0$, where $h\left( \mu _{k}\right)$ is defined by (12). Then,

$$\begin{aligned} {\mathfrak {R}}\left\{ \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }\ne 0, \end{aligned}$$

and ${\mathfrak {R}}\left\{ \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }$ and $h^{\prime }\left( \mu _{k}\right)$have the same sign.

Proof

Substituting $\lambda (\tau )$ into Eq. (8) and taking the derivative with respect to $\tau$, we obtain:

$$\begin{aligned} \left( 3\lambda ^{2}+2a\lambda +b-\hbox {d}\tau \hbox {e}^{-\lambda \tau }\right) \frac{ \hbox {d}\lambda }{\hbox {d}\tau }=\lambda d\hbox {e}^{-\lambda \tau }. \end{aligned}$$

Thus,

$$\begin{aligned} \left( \frac{\hbox {d}\lambda }{\hbox {d}\tau }\right) ^{-1}=\frac{3\lambda ^{2}+2a\lambda +b }{\hbox {d}\lambda }\hbox {e}^{\lambda \tau }-\frac{\tau }{\lambda }. \end{aligned}$$

When $\lambda =i\omega _{k}$ and using Eqs. (9), we can obtain:

$$\begin{aligned}&\!\!\!\left( {\mathfrak {R}}\left\{ \frac{\hbox {d}\lambda }{\hbox {d}\tau }\right\} \right) _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }^{-1}\\&\quad \quad =\frac{1}{d^{2}}\left( 3\omega _{k}^{4}+\left( 2a^{2}-4b\right) \omega _{k}^{2}+\left( b^{2}-2ac\right) \right) \\&\quad \quad =\frac{1}{d^{2}}\left( 3\mu _{k}^{2}+\left( 2a^{2}-4b\right) \mu _{k}+\left( b^{2}-2ac\right) \right) \\&\quad \quad = \frac{1}{d^{2}}\left( 3\mu _{k}^{2}+2p\mu _{k}+q\right) \\&\quad \quad =\frac{1}{d^{2}}h^{\prime }\left( \mu _{k}\right) \ne 0. \end{aligned}$$

Thus, we have

$$\begin{aligned}&\hbox {sign}\left( {\mathfrak {R}}\left\{ \frac{\hbox {d}\lambda }{\hbox {d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }\right) \\&\quad =\hbox {sign}\left( {\mathfrak {R}}\left\{ \frac{\hbox {d}\lambda }{\hbox {d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }\right) ^{-1}\\&\quad =\frac{1}{d^{2}}h^{\prime }\left( \mu _{k}\right) \ne 0. \end{aligned}$$

So we conclude that ${\mathfrak {R}}\left\{ \frac{\hbox {d}\lambda }{\hbox {d}\tau }\right\} _{\left( i\omega _{k},\tau _{k}^{(j)}\right) }$ and $h^{\prime }\left( \mu _{k}\right)$have the same sign. $\square$

Now, we will give a numerical simulation to support our theoretical analysis. Let $\alpha =10,\beta =-4,\gamma =15,\delta =4,$ so we get $a=14,b=40,c=0,d=40,p=116,q=1{,}600$ and $r=-1{,}600.$ Obviously, $a,b,c$ and $d$ satisfy Lemma 4, where $r<0.$ Then, Eq. (11) has a unique positive real root $\mu _{1}=0.935974.$ According to (13), we obtain:

$$\begin{aligned} \tau ^{(j)}=1.27865+1.03364\pi j,\quad \ j=0,1,2,\ldots . \end{aligned}$$

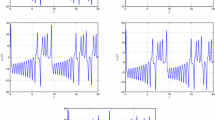
First, we choose $\tau =1<\tau _{0}$, the steady state is asymptotically stable, it can be seen in Fig. 1 that the system presents stable behavior. When $\tau =2.1>\tau _{0},$ the state of (3) becomes a periodic solution as shown in Fig. 2.

Fig. 1

Dynamic behavior of system (4): time series of ${u}_{k}{,(k=1,2,\ldots ,6).}$ The origin of system (4) is asymptotically stable with ${\alpha = 10,\beta = -4,\gamma = 15,\delta \,=\,4}$ and ${\tau =1<\tau }_{0}$, with initial values ${u}_{1}{(0)=2,}{u}_{2}{(0)=1,u}_{3}$ ${(0)=5,u}_{4}{(0)=3,u}_{5}$ ${(0)=4,u}_{6}{(0)=7:}$ a A state space in ${(t},\,{u}_{1})$ plane. b A state space in $(t,\,{u}_{2})$ plane. c A state space in $(t,\,{u}_{3})$ plane. d A state space in $(t,\,{u}_{4})$ plane. e A state space in $(t,\,{u}_{5})$ plane. f A state space in $(t,\,{u}_{6})$ plane

2.2 The stability of system (4) at $E_{1,2}$ or $E_{3,4}$

Due to the symmetry of $E_{1},E_{2},E_{3}$ and $E_{4}$, one can take the fixed point as:

$$\begin{aligned} E=(0,u_{20},0,u_{40},u_{50},0), \end{aligned}$$

in this case, we have transferred the fixed point to the origin by using the next linear transform:

$$\begin{aligned} v_{1}(t)&= u_{1}(t)-0,\quad v_{2}(t)=u_{2}(t)-u_{20}, \nonumber \\ v_{3}(t)&= u_{3}(t)-0,\quad v_{4}(t)=u_{4}(t)-u_{40}, \\ v_{5}(t)&= u_{5}(t)-u_{50},\quad v_{6}(t)=u_{6}(t)-0. \nonumber \end{aligned}$$

(16)

So system (4) becomes:

$$\begin{aligned} \dot{v}_{1}&= \alpha (v_{3}-v_{1}+u_{50}v_{3})+\alpha v_{3}v_{5}, \nonumber \\ \dot{v}_{2}&= \alpha (v_{4}-v_{2}+u_{40}v_{5}+u_{50}v_{4})\nonumber \\&+\,\alpha (u_{40}-u_{20}+v_{4}v_{5}+u_{40}u_{50}), \nonumber \\ \dot{v}_{3}&= -u_{50}v_{1}+\beta v_{3}+v_{6}-v_{5}v_{1}, \nonumber \\ \dot{v}_{4}&= -u_{50}v_{2}-u_{20}v_{5}+\beta v_{4}-v_{2}v_{5}\nonumber \\&-\,u_{20}u_{50}+\beta u_{40}, \nonumber \\ \dot{v}_{5}&= u_{40}v_{2}+u_{20}v_{4}-\gamma v_{5}+v_{1}v_{3}\nonumber \\&+\,v_{2}v_{4}+u_{20}u_{40}-\gamma u_{50}, \nonumber \\ \dot{v}_{6}&= -\delta v_{1}(t-\tau ). \end{aligned}$$

(17)

The associated characteristic equation of system (17) is:

$$\begin{aligned}&\left( \lambda ^{3}+m_{1}\lambda ^{2}+m_{2}\lambda +m_{3}\right) \nonumber \\&\quad \times \left( \lambda ^{3}+(\alpha -\beta )\lambda ^{2}+(\alpha u_{50}(1+u_{50})-\alpha \beta )\lambda \right. \nonumber \\&\quad \left. +\,\alpha \delta (1+u_{50})\hbox {e}^{-\lambda \tau }\right) =0, \end{aligned}$$

(18)

where $m_{1}=\alpha -\beta +\gamma ,m_{2}=\alpha u_{50}(1+u_{50})-\alpha \beta +\alpha \gamma -\gamma \beta +u_{20}^{2},m_{3}=\alpha u_{20}^{2}-\alpha \beta \gamma +\alpha \gamma u_{50}(1+u_{50})+\alpha u_{20}u_{40}(1+u_{50}).$Clearly, Eq. (18) has negative roots for all $\tau \ge 0$ if:

Fig. 2

Dynamic behavior of system (4): projection on ${u}_{1}-{u}_{3},{u}_{3}-{u}_{5},{u}_{6}-{u}_{5},{u}_{3}-{u}_{6}$ plane, respectively. Periodic solutions appear when $\alpha =10,\beta =-4,\gamma =15,$ $\delta =4$ and ${\tau =2.1>\tau }_{0}{:}$ a $(u_{1},{u}_{3})$ plane. b $(u_{3},{u}_{5})$ plane. c $(u_{6},{u}_{5})$ plane. d $(u_{3},{u}_{6})$ plane

Parameters	$\hbox {LE}_{1}$	$\hbox {LE}_{2}$	$\hbox {LE}_{3}$	$\hbox {LE}_{4}$	$\hbox {LE}_{5}$	$\hbox {LE}_{6}$
$\alpha =36,\beta =$ $15,\gamma =$ $12,\delta =5$ , ${\tau =1.981}$	${2.1405}$	–	–	${-}$	–	–
$\alpha =36,\beta =$ $15,\gamma =$ $12,\delta =5$,${\tau =1.97}$	${2.1133}$	${0.1791}$	–	–	–	–
$\alpha =36,\beta =$ $15,\gamma =$ $4,\delta =5$,${\tau =0.5}$	${1.4540}$	${0.5786}$	${0.1173}$	${-}$	–	–
$\alpha =36,\beta =$ $15,\gamma =$ $12,\delta =5$,${\tau =0.8}$	${1.8236}$	${1.2015}$	${0.6544}$	${0.2802}$	–	–
$\alpha =44,\beta =$ $21,\gamma =$ $4,\delta =5$,${\tau =0.5}$	${1.6958}$	${1.2505}$	${0.9293}$	${0.5818}$	${0.1673}$	–
$\alpha =36,\beta =$ $15,\gamma =$ $12,\delta =5$,${\tau =0.061}$	${1.4767}$	${1.2347}$	${1.0004}$	${0.7471}$	${0.4905}$	${0.1133}$

$$\begin{aligned} m_{1}>0,m_{3}>0,m_{1}m_{2}-m_{3}>0. \end{aligned}$$

Also, we need to further investigate the third degree transcendental polynomial equation:

$$\begin{aligned}&\lambda ^{3}+(\alpha -\beta )\lambda ^{2}+(\alpha u_{50}(1+u_{50})-\alpha \beta )\lambda \nonumber \\&\quad +\,\alpha \delta (1+u_{50})\hbox {e}^{-\lambda \tau }, \end{aligned}$$

(19)

which is the same of Eq. (8) but different coefficients. So its stability can be similarly studied.

3 Lyapunov exponents and attractors of (4)

In this section, we calculate Lyapunov exponents and attractors of system (4).According to the definition of Lyapunov exponent [46], we adopt:

$$\begin{aligned} \hbox {LE}_{k}=\underset{t\rightarrow \infty }{\lim }\frac{1}{t}\log \frac{ \left\| \delta _{k}(t)\right\| }{\left\| \delta _{k}(0)\right\| },\quad k=1,2,\ldots ,6, \end{aligned}$$

(20)

where $\delta _{k}(0)$ is the distance of two closed initial points and $\delta _{k}(t)$ is the distance of two points evolved along system equations after time $t$ from these two initial points. (In practice, we repeat the use of the Gram-Schmidt reorthonormalization (GSR) procedure on the vector frame to obtain six LEs).

Now, we will calculate some values of LEs which depicted in the following table using different values of the system parameters.

where the empty cells mean that the LEs are negative. It is obvious that there is no less than one positive LE for system (4) with different values of $\alpha ,\beta ,\gamma ,\delta$ and $\tau .$ This means that our system (4) for the choice of $\alpha ,\beta ,\gamma ,\delta$ and $\tau$ is a chaotic or hyperchaotic system [hyperchaos of order $k,(k=2,\ldots ,6)$]. The chaotic and hyperchaotic attractors of (4) using the different choice of the parameters are plotted in Fig. 3.

Fig. 3

Chaotic and hyperchaotic attractors of system (4): a Chaotic attractor when $\alpha =36, \beta =15, \gamma =12, \delta =5$ and $\tau =1.981$ ($1$ positive LE). b Hyperchaotic attractor of order $2$ when $\alpha =36, \beta =15, \gamma =12, \delta =5$ and $\tau =1.97.$ c Hyperchaotic attractor of order $3$ when $\alpha =36,\beta =15,\gamma =4,\delta =5$ and $\tau =0.5.$ d Hyperchaotic attractor of order $4$ when $\alpha =36,\beta =15,\gamma =12,\delta =5$ and $\tau =0.8.$ e Hyperchaotic attractor of order $5$ when $\alpha =44,\beta =21,\gamma =4,\delta =5$ and $\tau =0.5.$ f Hyperchaotic attractor of order $6$ when $\alpha =36,\beta =15,\gamma =12,\delta =5$ and $\tau =0.061$

Based on Lyapunov exponents $\hbox {LE}_{k}$, Eq. (20) we calculate the parameters values of system (4) at which, chaotic, hyperchaotic and fixed points attractors exist. We vary one parameter and fix the other parameters according to their values.

3.1 Fix $\alpha =36,\beta =15,\gamma =12, \delta =5$ and vary $\tau$

Using (20), we calculate $\hbox {LE}_{k}$, $(k=1,2,\ldots ,6)$ and their values are plotted versus $\tau$ in Fig. 4 using the same initial conditions as in Fig. 1. It is clear from Fig. 4 that when $\tau \in [0.06,0.101]$ system (4) has hyperchaotic attractors of order $6$, while it has hyperchaotic attractors of order $5$ for $\tau$ lying in the intervals $[0.02,0.05]$ and $[0.11,0.51].$ It has four positive LEs for $\tau$ $\in [0.52,1.17],[1.21,1.22],[2.05,2.18)$ and $[2.21,2.98]$. Solutions of system (4) are hyperchaotic attractors of order $3$ for the value of $\tau \in [1.18,1.2]\cup [1.23,1.83],$ hyperchaotic attractor of order $2$ if $\tau \in [1.841,1.971].$ The chaotic attractors of (4) exist when $\tau$ lies in the interval $[1.981,1.99].$

Fig. 4

Lyapunov exponents of (4) versus $\tau$, when $\alpha =36,\beta =15,\gamma =12,\delta =5$ and the same initial conditions as in Fig. 1. a $\tau \in (0,2].$ b $\tau \in (2,3].$

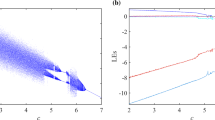
3.2 Fix $\beta =15,\gamma =12,\delta =5, \tau =0.5$ and vary $\alpha$

The values of $\hbox {LE}_{k}$, $(k=1,2,\ldots ,6)$ versus $\alpha$ are plotted in Fig. 5. From Fig. 5, one can conclude that (5) has hyperchaotic attractors of order $5$ for $\alpha \in [29.6,37.2],$ hyperchaotic attractors of order $4$ for $\alpha \in [37.3,49.5],[50.4,50.6],[51.2,51.6],[52.2,52.5],$ $[52.9,54],[55.9,56.2]$ and $[56.8,57.2],$ hyperchaotic attractors of order $3$ for $\alpha$ lying in $[25.1,25.4],$ $[29.1,29.4],[49.6,50.3],$ $[50.7,51.1],[51.7,52.1],$ $[52.6,52.8],[54.1,55.8]$ and $[57.3,70]$ and hyperchaotic attractor of order $2$ for $\alpha \in [25.5,29].$ Therefore, our system (4) does not have chaotic attractors for these values of system parameters.

Fig. 5

Lyapunov exponents of (4) versus $\alpha$, when $\beta =15,\gamma =12,\delta =5,\tau =0.5$ and the same initial conditions as in Fig. 1

3.3 Fix $\alpha =44,\gamma =12,\delta =5, \tau =0.5$ and vary $\beta$

As is shown in Fig. 6, the hyperchaotic attractors of order $6$ exist for $\beta \in [19.2,19.3]$ and $[19.6,22.6]$, while the hyperchaotic attractors of order $5$ for $\beta$ lie in the intervals $[15.2,19.1],[19.4,19.5]$ and $[22.7,22.8]$. It also has a hyperchaotic attractors of order $4$ for $\beta \in [10.8,15.1],$ hyperchaotic attractors of order $3$ for $\beta \in [3.1,3.2],[3.6,10.7]$ and $[23.2,24.3].$ The chaotic attractors of (4) are found for $\beta \in [-0.5,3]\cup [3.3,3.5].$ Attractors of our system (4) approach trivial fixed points for $\beta \in [-10,-0.5).$

Fig. 6

Lyapunov exponents of (4) versus $\beta$, when $\alpha =44,\gamma =12,\delta =5,\tau =0.5$ and the same initial conditions as in Fig. 1. a $\beta \in [-10,0).$ b $\beta \in [0,24]$

3.4 Fix $\alpha =36,\beta =15,\delta =5, \tau =0.5$ and vary $\gamma$

As we did before, we plot $\hbox {LE}_{k}$, $(k=1,2,\ldots ,6)$ in Fig.7 and we see that (4) has hyperchaotic attractors of order $5$ for $\gamma \in [13.3,22.6],$ hyperchaotic attractors of order $4$ for $\gamma \in [5.9,12.8],[13,13.2]$ and $[22.7,23.7],$ hyperchaotic attractors of order $3$ for $\gamma \in [1.7,5.8],[23.8,24.7],[40.2,40.5]$ and $[40.9,42.2]$ and hyperchaotic attractors of order $2$ for $\gamma \in [0.5,1.6],[24.8,40.1]$ and $[40.6,40.8].$ Also it has chaotic attractor for $\gamma$ takes the value in the interval $[0.1,0.4].$

Fig. 7

Lyapunov exponents of (4) versus $\gamma$, when $\alpha =36,\beta =15,\delta =5,\tau =0.5$ and the same initial conditions as in Fig. 1

3.5 Fix $\alpha =36,\beta =15,\gamma =12, \tau =0.5$ and vary $\delta$

Finally, we calculate $\hbox {LE}_{k}$, $(k=1,2,\ldots ,6)$ and their values versus $\delta$ are plotted in Fig. 8. The hyperchaotic attractors of order $5$ for $\delta$ lie in the intervals $[0.1,4.3]\cup [5.1,5.2]$, while the hyperchaotic attractors of order $4$ exist for $\delta \in [4.4,5],[5.3,7]$ and $[7.1,35].$

Fig. 8

Lyapunov exponents of (4) versus $\delta$, when $\alpha =36,\beta =15,\gamma =12,\tau =0.5$ and the same initial conditions as in Fig. 1

It is obvious that from Sects. 3.1 and 3.5, system (4) can produce chaotic and hyperchaotic attractors with large number of positive LEs. From Figs. 4, 5, 6, 7 and 8, the dynamics of (4) are studied for $\tau \in (0,3),\alpha \in (24,70],\beta \in (-10,35),\gamma \in (0,43]$ and $\delta \in (0,35]$. We note that hyperchaotic attractors (for different orders) exist for the all the parameter values of system (4). Finally, attractors that approach trivial fixed points exist only in Sect. 3.3.

4 Different forms of modified time delay hyperchaotic complex Lü systems

In this section, we propose different forms of modified time delay hyperchaotic complex Lü systems by including the $\tau$ in system variables. The LEs of these proposed systems are calculated. Their dynamics can be similarly studied as we did for system (4). These systems with their LEs are:

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w, \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z(t-\tau ), \\ \dot{w}=\frac{-\delta }{2}\left( x+\bar{x}\right) , \end{array} \end{aligned}$$

(21)

and $\hbox {LE}_{1}=1.5427,\hbox {LE}_{2}=1.2778$, $\hbox {LE}_{3}=0.9998,\hbox {LE}_{4}=0.7023$, $\hbox {LE}_{5}=0.2302,\hbox {LE}_{6}=-0.5034$, $\alpha =36,\beta =12$, $\gamma =15,\delta =5$ and $\tau =0.04.$

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w(t-\tau ), \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z, \\ \dot{w}=\frac{-\delta }{2}\left( x+\bar{x}\right) , \end{array} \end{aligned}$$

(22)

and $\hbox {LE}_{1}=1.5643,\hbox {LE}_{2}=1.2652$, $\hbox {LE}_{3}=0.9065,$ $\hbox {LE}_{4}=0.6197$, $\hbox {LE}_{5}=0.3137,\hbox {LE}_{6}=-0.2721$, $\alpha =40,\beta =12$, $\gamma =15,\delta =5$ and $\tau =0.5.$

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w(t-\tau ), \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z, \\ \dot{w}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\delta w, \end{array} \end{aligned}$$

(23)

and $\hbox {LE}_{1}=1.3503,\hbox {LE}_{2}=1.0401$, $\hbox {LE}_{3}=0.6539,$ $\hbox {LE}_{4}=0.4616$, $\hbox {LE}_{5}=0.1075,\hbox {LE}_{6}=-0.3112$, $\alpha =36,\beta =15,\gamma =10$, $\delta =3.4$ and $\tau =0.3.$

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w, \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z(t-\tau ), \\ \dot{w}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\delta w, \end{array} \end{aligned}$$

(24)

and $\hbox {LE}_{1}=1.448,\hbox {LE}_{2}=1.1742$, $\hbox {LE}_{3}=0.9556,\hbox {LE}_{4}$ $=0.7332$, $\hbox {LE}_{5}=0.4580,\hbox {LE}_{6}=0.0163$, $\alpha =36,\beta =15$, $\gamma =10,\delta =4$ and $\tau =0.05.$

$$\begin{aligned} \begin{array}{l} \dot{x}=\alpha (y-x+yz), \\ \dot{y}=-xz+\beta y+w, \\ \dot{z}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\gamma z, \\ \dot{w}=\frac{1}{2}\left( \bar{x}y+x\bar{y}\right) -\delta w(t-\tau ), \end{array} \end{aligned}$$

(25)

and $\hbox {LE}_{1}=1.2888,\hbox {LE}_{2}=0.9652$, $\hbox {LE}_{3}=0.6921,\hbox {LE}_{4}$ $=0.4418$, $\hbox {LE}_{5}=0.2469$, $\hbox {LE}_{6}=-0.3451,\ \alpha =40,\beta =13$, $\gamma =11,\delta =4$ and $\tau =0.2.$

5 Synchronization of hyperchaotic of system (3)

In this section, we will investigate the synchronization of two identical modified time delay hyperchaotic complex Lü systems via active control method. The drive and response systems for modified time delay hyperchaotic complex Lü system can be described, respectively, as:

$$\begin{aligned} \begin{array}{l} \dot{x}_{d}=\alpha (y_{d}-x_{d}+y_{d}z_{d}), \\ \dot{y}_{d}=-x_{d}z_{d}+\beta y_{d}+w_{d}, \\ \dot{z}_{d}=\frac{1}{2}\left( \bar{x}_{d}y_{d}-x_{d}\bar{y}_{d}\right) -\gamma z_{d}, \\ \dot{w}_{d}=\frac{-\delta }{2}\left( x_{d}(t-\tau )+\bar{x}_{d}(t-\tau )\right) , \end{array} \end{aligned}$$

(26)

and

$$\begin{aligned} \begin{array}{l} \dot{x}_{r}=\alpha (y_{r}-x_{r}+y_{r}z_{r})+(\theta _{1}+i\theta _{2}), \\ \dot{y}_{r}=-x_{r}z_{r}+\beta y_{r}+w_{r}+(\theta _{3}+i\theta _{4}), \\ \dot{z}_{r}=\frac{1}{2}\left( \bar{x}_{r}y_{r}-x_{r}\bar{y}_{r}\right) -\gamma z_{r}+\theta _{5}, \\ \dot{w}_{r}=\frac{-\delta }{2}\left( x_{r}(t-\tau )+\bar{x}_{r}(t-\tau )\right) +\theta _{6}, \end{array} \end{aligned}$$

(27)

where $x_{d}=u_{1d}+iu_{2d},y_{d}=u_{3d}+iu_{4d}$ are complex variables for the drive system (26), $z_{d}(t)=u_{5d}(t),w_{d}(t)=u_{6d}(t),u_{kd}(k=1,2,\ldots ,6)$ are real variables, $x_{r}=u_{1r}+iu_{2r},y_{r}=u_{3r}+iu_{4r}$ are complex variables for the response system (27), $z_{r}(t)=u_{5r}(t),w_{r}(t)=u_{6r}(t),u_{kr}(k=1,2,3,4)$ are real variables and $\theta _{l}(l=1,2,\ldots ,6)$ are the control functions to be determined.

In order to obtain the control signals, we define the errors between the drive and the response systems as:

$$\begin{aligned} e_{x}&= e_{1x}+ie_{2x}=x_{r}-x_{d},\nonumber \\ e_{y}&= e_{1y}+ie_{2y}=y_{r}-y_{d}, \nonumber \\ e_{z}&= e_{1z}=z_{r}-z_{d},\nonumber \\ e_{w}&= e_{1w}=z_{w}-z_{w}. \end{aligned}$$

(28)

So the complex error dynamical system can be written as

$$\begin{aligned} \begin{array}{l} \dot{e}_{x}=\alpha (e_{y}-e_{x}+z_{d}e_{y}+y_{r}e_{z})+(\theta _{1}+i\theta _{2}), \\ \dot{e}_{y}=-z_{d}e_{x}-x_{r}e_{z}+\beta e_{y}+e_{w}+(\theta _{3}+i\theta _{4}), \\ \dot{e}_{z}=\frac{1}{2}\left( y_{d}\bar{e}_{x}+\bar{x}_{r}e_{y}-\bar{y} _{d}e_{x}-x_{r}\bar{e}_{y}\right) -\gamma e_{z}+\theta _{5}, \\ \dot{e}_{w}=\frac{-\delta }{2}\left( e_{x}(t-\tau )+\bar{e}_{x}(t-\tau )\right) +\theta _{6}, \end{array} \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{array}{l} y_{r}z_{r}-y_{d}z_{d}=z_{d}e_{y}+y_{r}e_{z}, \\ x_{r}z_{r}-x_{d}z_{d}=z_{d}e_{x}+x_{r}e_{z}, \\ \bar{x}_{r}y_{r}-\bar{x}_{d}y_{d}=y_{d}\bar{e}_{x}+\bar{x}_{r}e_{y}, \\ x_{r}\bar{y}_{r}-x_{d}\bar{y}_{d}=\bar{y}_{d}e_{x}+x_{r}\bar{e}_{y}. \end{array} \end{aligned}$$

(30)

Separating real and imaginary parts in (29) and using (28), we have:

$$\begin{aligned} \begin{array}{l} \dot{e}_{1x}=\alpha (e_{1y}-e_{1x}+u_{5d}e_{1y}+u_{3r}e_{1z})+\theta _{1},\\ \dot{e}_{2x}=\alpha (e_{2y}-e_{2x}+u_{5d}e_{2y}+u_{4r}e_{1z})+\theta _{2},\\ \dot{e}_{1y}=-u_{5d}e_{1x}-u_{1r}e_{1z}+\beta e_{1y}+e_{1w}+\theta _{3}, \\ \dot{e}_{2y}=-u_{5d}e_{2x}-u_{2r}e_{1z}+\beta e_{2y}+\theta _{4}, \\ \dot{e}_{1z}=u_{3d}e_{1x}+u_{1r}e_{1y}+u_{4d}e_{2x}\\ \qquad \quad +\,u_{2r}e_{2y}-\gamma e_{1z}+\theta _{5}, \\ \dot{e}_{1w}=-\delta e_{1x}(t-\tau )+\theta _{6}, \end{array} \end{aligned}$$

(31)

For positive parameters $\alpha ,\beta ,\gamma$ and $\delta ,$ one can construct a positive Lyapunov–Krasovskii function as follows:

$$\begin{aligned} V&= \frac{1}{2}\left( e_{1x}^{2}+e_{2x}^{2}+e_{1y}^{2}+e_{2y}^{2}+e_{1z}^{2}+e_{1w}^{2}\right) \nonumber \\&+\int \limits _{t-\tau }^{t}e_{1x}^{2}(s)\hbox {d}s. \end{aligned}$$

(32)

Then, the time derivative of $V$ along the trajectory of the error dynamical system (31) is as follows:

$$\begin{aligned} \dot{V}&= e_{1x}\dot{e}_{1x}+e_{2x}\dot{e}_{2x}+e_{1y}\dot{e}_{1y}+e_{2y} \dot{e}_{2y}+e_{1z}\dot{e}_{1z}\nonumber \\&+\,e_{1w}\dot{e}_{1w}+e_{1x}^{2}+e_{1x}^{2}(t-\tau ) \nonumber \\&= e_{1x}(\alpha (e_{1y}-e_{1x}+u_{5d}e_{1y}+u_{3r}e_{1z})+\theta _{1}) \nonumber \\&+\,e_{2x}(\alpha (e_{2y}-e_{2x}+u_{5d}e_{2y}+u_{4r}e_{1z})+\theta _{2}) \nonumber \\&+\,e_{1y}(-u_{5d}e_{1x}\!-\!u_{1r}e_{1z}\!+\!\beta e_{1y}\!+\!e_{1w}\!+\!\theta _{3}) \\&+\,e_{2y}(-u_{5d}e_{2x}-u_{2r}e_{1z}+\beta e_{2y}+\theta _{4}) \nonumber \\&+\,e_{1z}(u_{3d}e_{1x}+u_{1r}e_{1y}+u_{4d}e_{2x}\nonumber \\&+\,u_{2r}e_{2y}-\gamma e_{1z}+\theta _{5}) \nonumber \\&+\,e_{1w}(-\delta e_{1x}(t-\tau )+\theta _{6})+e_{1x}^{2}+e_{1x}^{2}(t-\tau ).\nonumber \end{aligned}$$

(33)

If we choose the control functions $\theta _{l}(l=1,2,\ldots ,6)$ such that

$$\begin{aligned} \begin{array}{l} \theta _{1}=-\alpha e_{1y}-u_{5d}e_{1y}-u_{3r}e_{1z}-\delta e_{1x}, \\ \theta _{2}=-\alpha e_{2y}-u_{5d}e_{2y}-u_{4r}e_{1z}, \\ \theta _{3}=u_{5d}e_{1x}+u_{1r}e_{1z}-(\beta +1)e_{1y}-e_{1w}, \\ \theta _{4}=u_{5d}e_{2x}+u_{2r}e_{1z}-(\beta +1)e_{2y}, \\ \theta _{5}=-u_{3d}e_{1x}-u_{1r}e_{1y}-u_{4d}e_{2x}-u_{2r}e_{2y}, \\ \theta _{6}=-\frac{\delta ^{2}}{4}e_{1w}, \end{array} \end{aligned}$$

(34)

then (33) becomes:

$$\begin{aligned} \dot{V}&= -\left( \alpha e_{1x}^{2}+\alpha e_{2x}^{2}+e_{1y}^{2}+e_{2y}^{2}+\gamma e_{1z}^{2}\right. \nonumber \\&\left. +\left( e_{1x}(t-\tau )+ \frac{\delta }{2}e_{1w}\right) ^{2}\right) \le 0. \end{aligned}$$

(35)

Since $V$ is a positive definite function and its derivative is negative definite, then one obtains that $\lim _{t\rightarrow \infty }\left\| \varvec{e}\right\|$ $=0,$ $\varvec{e} =(e_{1x},e_{2x},e_{1y},e_{2y},e_{1z},e_{1w})^{T}.$ It follows that the states of the response system (27) and the states of the drive system (26) are ultimately completely synchronized asymptotically. Systems (27) and (26) with (34) are solved numerically for $\alpha =35,\beta =15,\gamma =12,$ $\delta =5$ and $\beta =0.5$ and the initial conditions of the drive and the response systems are $u_{1d}(0)=2,u_{2d}(0)=1,u_{3d}(0)=5,u_{4d}(0)=3,u_{5d}(0)=4,u_{6d}(0)=7$ and $u_{1r}(0)=-1,u_{2r}(0)=-2,u_{3r}(0)=5,u_{4r}(0)=2,u_{5r}(0)=1,u_{6r}(0)=4,$ respectively. The synchronization errors are plotted in Fig. 9 and demonstrate that synchronization is achieved. They converge to zero after very small values of $t$.

Fig. 9

Synchronization errors (solutions of system (31)): a $(t,\, e_1x)$ plane. b $(t,\, e_2x)$ plane. c $(t,\, e_1y )$ plane. d $(t,\, e _2y)$ plane. e $(t,\, e_1z)$ plane. f $(t, \, e_1w)$ plane

6 Conclusions

For the last few decades, delay dynamical systems have been attracting the attention of researchers of various fields including biology, physics, mathematics, economics, engineering. Many natural systems are mathematically modeled by nonlinear DDEs that contain one or more time delays. This paper deals with time delay nonlinear system where the main variables participating in the dynamics are complex. Our main goal in this paper is to introduce the modified time delay complex Lü system and study its dynamics. It is shown in Sect. 2, under certain assumptions on the coefficients, that the steady state of the modified time delay complex Lü system is asymptotically stable for all delay values $\tau$. Under another set of conditions, there is a critical delay value, and the steady state is stable when the delay is less than the critical value and unstable when the delay is greater than the critical value, see Figs. 1, 2. It is shown through numerical simulations that the system depicts chaos or hyperchaos for a certain range of the system parameters, as shown in Figs. 4, 5, 6, 7 and 8. The dynamics of modified time delay complex Lü system is rich, since it has solutions that approach to trivial fixed point, chaotic attractors and hyperchaotic attractors of order $6,5,4,3$ and $2,$ see Fig. 3. However, the modified hyperchaotic complex or real Lü systems [27, 42] have only hyperchaotic attractors of order $2$. We introduced, in Sect. 4, different forms of modified time delay complex Lü systems which can be investigated similarly as was did for system (4) in Sects. 2 and 3. The synchronization of hyperchaotic attractors of (4) is achieved using the active control based on Lyapunov–Krasovskii function and the errors approach zero for very small values of $t$, as shown in Fig. 9.