1 Introduction

Non-smooth behaviour occurs in many engineering systems. Some of such phenomena as chatter and squeal cause serious problems in industrial applications and, in general, these vibrations are undesirable because of their detrimental effects on the operation and performance of engineering systems. Numerical simulations of non-smooth systems are complicated by a necessity of an accurate detection of non-smoothness and then a robust switch from one set of equations to another. This fact makes also their mathematical description cumbersome. Moreover, the dynamical responses of such systems are complex, and different kinds of non-linear responses, including chaos, are observed (see, for example [1–4, 6, 7, 9, 12–14].

One of the engineering systems which exhibits non-smooth behaviour is a drilling rig used in the oil and gas industry for creation of the wellbore. The fundamental part of the drilling rig is a drill-string and during the system operation it experiences dangerous vibrations. A drill-string can be modelled as a non-smooth system where alternating contact and non-contact phases of the drill-bit with the rock have to be considered. The drill-string vibrations can be classified into three different modes: axial, torsional, and flexural vibrations. The coupling of these modes is essential in order to describe some important phenomena occurring during drilling [5, 8, 15].

The main objective of this research is to undertake nonlinear dynamics analysis of drilling modelled as a non-smooth system. The mathematical model describes contact and non-contact phases by different sets of ordinary differential equations, being based on the model proposed by Christoforou and Yigit [5]. Axial and torsional modes of vibrations are analysed using lumped parameters two degrees-of-freedom model where the coupling between these modes is taken into account through force generated during the bit-rock interactions, as a result of the string’s rotational movement. This model allows one to describe complex responses including stick-slip and bit-bounce.

A smoothening procedure is employed for numerical simulation of the system. Frictional effects caused by interaction of the drill bit with the formation in the torsional mode are described by a smoothened continuous function, as proposed in [17] and [11]. Moreover, to assist numerical simulations, contact and non-contact non-smoothness, associated with a split phase space, is treated by redefining the subspaces and the transition between them. Under this assumption, the equations of motion are represented by different sets that describe system behaviour in each phase subspace and also in the transition among them [11, 14, 17].

The numerical simulations are carried out to investigate the stick-slip and bit-bounce behaviours. In general, it is possible to show how different set of parameters can dramatically change the system behaviour. In essence, four different situations are discussed: normal operation, stick-slip, bit-bounce, and simultaneous stick-slip and bit-bounce. Besides, a global analysis of the system allows one to develop a general understanding of some critical operations of the considered system due to drill-string vibrations. In particular, the drill-pipe length and the rotary table frequency variations are investigated for different values of the weight-on-bit. Maximum axial amplitudes and angular velocities are monitored in order to observe system dynamics.

2 Mathematical model

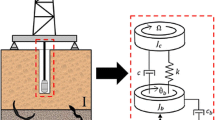
The mathematical description of the drill-string interacting with the rock considers a two degrees-of freedom system associated with axial and torsional vibrations. The model used in this work is based on the one proposed by Christoforou and Yigit [5] where the coupling between axial and torsional degrees-of-freedom are taken into account. The model aims to describe the non-smooth phenomena related to these two modes, and in particular stick-slip and bit-bounce phenomena. A lumped parameter system is used, so that the equations are simplified to ordinary differential equations. The forcing comes from the bit-rock interactions, as a result of the string’s rotational movement. The torsional forcing is caused by friction between bit and rock and the cutting torque acting on the bit. Through a coupling between the equations, the bit interactions with the rock generate the forcing in axial direction. There is a stiffness associated with the formation, relating the bit penetration into the formation and the axial force exerted.

The model treats the Bottom Hole Assembly (BHA) as a lumped mass at the bottom of the drill-string. The drill-pipe mass is considered as a lumped mass equivalent to its distributed mass. Together, the BHA mass and the equivalent drill-pipe mass make up the axial mass, m a . The axial displacement is denoted by the x variable. Figure 1 depicts a free body diagram of the system for its axial degree-of-freedom. Figure 1a shows the BHA configuration with the bit hanging just above the formation. It represents the case where the bit is just touching the formation but with no force at all. This point is considered as the origin of the axis, i.e., x=0. The x variable is positive when the bit is below x=0. Figure 1b presents the static equilibrium, with the nominal Weight-On-Bit (WOB) \(\underline{F}_{\,b}\) applied, but without any rotation of the drill-string. \(\underline{F}_{\,b}\) is called nominal WOB because during the dynamic response of the system the WOB varies. \(\underline{F}_{\,b}\) is the WOB that would exist if there are no axial vibrations present in the system, i.e., the desired WOB. The instantaneous WOB is called F b . The static displacement, \(\underline{x}\), is associated with the drill-bit penetration, when the WOB equals \(\underline{F}_{\,b}\). Figure 1c represents the dynamic situation, with the forces involved: the force that the formation exerts on the bit (instantaneous WOB, F b =k c x); the drill string elastic force; and a linear damping force.

Fig. 1
figure 1

Free body diagram of the BHA with the axial acting forces; (a) contact between the drill bit and the formation when no force is acting on the formation, (b) contact in static equilibrium; (c) dynamic equilibrium

Full size image

The formation force is modelled as being linearly related to the axial displacement, x, as shown below for the static and instantaneous cases, respectively. The formation stiffness is k c . Note that since this force is always upward, we consider it to be positive upward:

(1)
(2)

Then the equation for the axial motion is

$$ m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}(x - \underline{x}\,) + k_{c}(x - \underline{x}\,) = 0 $$
(3)

Since the two most important drilling parameters to be selected when drilling, and on which the system response will depend are the applied WOB and the applied drill-string rotation, the equation of motion is rewritten to make \(\underline{F}_{\,b}\) explicit. The equation is also manipulated in such a way that \(\underline{x}\) is not directly present, since it is only a result of the applied WOB and formation stiffness.

$$ m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = \underline{F}_{\,b}\biggl( 1 + \frac{k_{a}}{k_{c}} \biggr) - k_{c}x $$
(4)

For the sake of simplicity, the term \(\underline{F}_{\,b}( 1 + \frac{k_{a}}{k_{c}} )\), which is constant, is defined as F 0:

$$ m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = F_{0} - k_{c}x $$
(5)

The forcing in the axial direction arises as a result of the drill-bit rotation, thus being the result of the torsional-axial coupling. To include this coupling, the equation above is slightly modified. The modelling of this coupling can be quite challenging and dependent on many specific geometrical aspects of each bit. In this work, a simple coupling is employed as proposed by Christoforou and Yigit [5]. This coupling is made by considering a surface elevation on the formation that depends on the bit rotation angle ϕ. By introducing the torsional mode, Eq. (2) is valid for the case where ϕ=0, and a more general equation is introduced as follows:

$$ F_{b} = k_{c}\bigl[ x - s_{0}\sin( n_{b}\phi) \bigr] $$
(6)

where n b is an integer number. By choosing n b =3, we are representing the tri-lobe pattern common to tri-cone bits.

Introducing this change in the axial equation of motion, we obtain the following equation:

$$ m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = F_{0} - k_{c}\bigl[ x - s_{0}\sin( n_{b}\phi) \bigr] $$
(7)

The torsional degree-of-freedom is analysed by considering that torsional stiffness is provided by the drill-pipes, k t , in such a way that the BHA does not experience any torsion. The torsional inertia is composed by a combination of a lumped inertia in the tip of the string, associated with the BHA and the drill-pipes, I t . Besides, the torsional model assumes that system dissipation is represented by a linear viscous damping, c t . The applied rotation on the string, rotary table rotation, ω mr, is assumed to be constant and the rotary table angle is represented by ϕ mr. If there is no torsional vibration present, ϕ would be equal to ϕ mr. Under these assumptions, the torsional governing equation is given by

$$ I_{t}\ddot{\phi} + c_{t}\dot{\phi} + k_{t}( \phi - \phi_{\mathrm{mr}} ) = - T_{b} $$
(8)

where T b is the torque on bit. The torque acting on the drill-bit is modelled by two terms: the first one is related to the dry friction existing between the bit and the formation, while the second one is related to the torque needed to cut the rock. The equation proposed by Spanos et al. [16] is used assuming that the friction is considered to be evenly distributed on the front face of the bit. Thus, T b is modelled as follows:

$$ T_{b} = F_{b}\biggl[ \frac{2}{3}r_{h}f(\dot{\phi} ) + \varsigma\sqrt{r_{h}\delta _{c}} \biggr] $$
(9)

Here, r h is the drill-bit radius, δ c is the average cutting depth, and ς is a dimensionless parameter that characterises the force necessary to cut the rock. The average cutting depth, δ c , is obtained from the following relation:

$$ \delta_{c} = \frac{2\pi P}{\omega _{d}} $$
(10)

where P is the average rate of penetration, calculated as a function of the applied Weight-On-Bit, \(\underline{F}_{\,b}\), and the rotary table rotation, ω mr, using the following empirical relation:

$$ P = e_{1}\underline{F}_{\,b}\sqrt{\omega _{\mathrm{mr}}} + e_{2} $$
(11)

where e 1 and e 2 are constants.

The function \(f(\dot{\phi} )\) defines the dry friction and its definition uses the sign of the angular velocity.

2.1 Smoothening the governing equations

The dry friction between the formation and the drill-bit in general introduces a non-smoothness to the system in torsional mode. However, in some cases, it is possible to define a continuous function able to describe both the static and dynamic friction to represent the non-smooth shape of the dry friction. Here, a smoothened model proposed by Wiercigroch [17] and Leine [11] is employed:

(12)

In this equation, the constants μ e and μ d are the static and dynamic friction coefficients, respectively; ε and τ are dimensionless numerical constants, where ε≫1 and τ>0. These constants are responsible for the proper transition from −μ d to +μ d . If properly chosen, these constants can get the smoothened shape of the dry friction really close to that of its original non-smooth function.

Concerning the contact/non-contact non-smoothness, this non-linearity is far more complex and should be properly treated for numerical simulations purposes. Here, the same procedure used in Savi et al. [14] is employed in order to smooth the governing equations that are characterised by two different equations, representing situations with and without contact. Therefore, state space of the system may be split into two subspaces separated by a hyper-surface. The central idea to smoothen this system is to redefine the subspaces and the transition hyper-surfaces. Therefore, it is assumed that the transition has a linear variation within the transition hyper-surfaces, which is related to a thin space defined by a narrow band η around the hyper-surface of discontinuity. Under these assumptions, the system is governed by the following equations:

For the situation with contact, where x≥s 0sin(n b ϕ)+η:

$$ \left\{ \begin{array}{l} m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = F_{0} - k_{c}\bigl( x - s_{0}\sin( n_{b}\phi) \bigr) \\[6pt] I_{t}\ddot{\phi} + c_{t}\dot{\phi} + k_{t}( \phi - \phi_{\mathrm{mr}} )\\[6pt] \quad = - k_{c}( x - s_{0}\sin( n_{b}\phi) )\\[6pt] \qquad{}\times \biggl(\displaystyle\frac{2}{3}r_{h}f( \dot{\phi} ) + \varsigma\sqrt{r_{h}\delta _{c}} \biggr) \end{array}\right. $$
(13)

For the situation without contact, where x≤s 0sin(n b ϕ)−η:

$$ \left\{ \begin{array}{l} m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = F_{0} \\[3pt] I_{t}\ddot{\phi} + c_{t}\dot{\phi} + k_{t}( \phi - \phi_{\mathrm{mr}} ) = 0 \end{array}\right. $$
(14)

For the transition region, where s 0sin(n b ϕ)−η<x<s 0sin(n b ϕ)+η:

$$ \left\{ \begin{array}{l} m_{a}\ddot{x} + c_{a}\dot{x} + k_{a}x = F_{0} - \displaystyle\frac{k_{c}}{2}( x - s_{0}\sin\bigl( n_{b}\phi\bigr) + \eta) \\[12pt] I_{t}\ddot{\phi} + c_{t}\dot{\phi} + k_{t}( \phi - \phi_{\mathrm{mr}} )\\[6pt] \quad = - k_{c}\biggl( \displaystyle\frac{2}{3}r_{h}\eta f( \dot{\phi} )\\[6pt] \qquad {}+ \varsigma\sqrt{r_{h}\delta _{c}} \displaystyle\frac{( x - s_{0}\sin ( n_{b}\phi ) + \eta )}{2} \biggr) \end{array}\right. $$
(15)

For more details about this procedure, see the following references: Savi et al. [14]; Divenyi et al. [6]; Wiercigroch [17]; Leine [11].

2.2 Parameter definitions

Many of the system parameters are obtained from the drill-string and drilling fluid characteristics. Thereby, it is important to apply convenient formulations that allow these parameters to be obtained. Here, parameters are obtained in a similar way to that of Christoforou and Yigit [5]. The axial mass is given by summing up the BHA mass with the equivalent drill-pipe mass:

$$ m_{a} = m_{\mathrm{BHA}} + m_{\mathrm{ad}} + \frac{\rho \pi ( d_{e}^{2} - d_{i}^{2} )l_{\mathrm{dp}}}{12} $$
(16)

where ρ is the steel density, d e and d i are the drill pipes internal and external diameters, l dp is the drill-pipe length, and m BHA and m ad are the BHA mass and fluid added mass, respectively, and both values can be expressed by the following equations:

(17)
(18)

l BHA is the BHA length, C A is the added mass coefficient, ρ fl is the drilling fluid, and d ce and d ci are the drill collars external and internal diameters. In this model, for the sake of simplicity, the BHA is considered to be composed of drill collars alone. One should pay attention to the fact that the total depth is the sum of l BHA and l dp. The string stiffness is given by

$$ k_{a} = \frac{E\pi ( d_{e}^{2} - d_{i}^{2} )}{4l_{\mathrm{dp}}} $$
(19)

where E is the Young’s module for the steel. The torsional inertia is given by the sum of the BHA inertia and the equivalent drill pipe inertia.

$$ I_{t} = \frac{\rho \pi ( d_{\mathrm{ce}}^{4} - d_{\mathrm{ci}}^{4} )l_{\mathrm{BHA}}}{32} + \frac{1}{3}\frac{\rho \pi ( d_{e}^{4} - d_{i}^{4} )l_{\mathrm{dp}}}{32} $$
(20)

The torsional stiffness is given by

$$ k_{t} = \frac{G\pi ( d_{e}^{4} - d_{i}^{4} )}{32l_{\mathrm{dp}}} $$
(21)

and the torsional damping is expressed as follows:

$$ c_{t} = \frac{\pi \mu _{\mathrm{fl}}l_{\mathrm{BHA}}d_{\mathrm{ce}}^{3}}{2( 2r_{h} - d_{\mathrm{ce}} )} $$
(22)

The next section considers numerical simulation performed with the proposed model.

3 Numerical simulation

In this section, numerical results obtained using the proposed model are discussed. Runge–Kutta–Fehlberg method with adaptive steps is employed to perform the simulations. The appropriate values for the length of the transition region, η, are defined as discussed in [6]. Table 1 presents parameters that are used for all simulations (parameters for the rate of penetration equation, the dry friction smoothening, and the transition region). Basically, four different situations are discussed: normal operation, stick-slip, bit-bounce and simultaneous stick-slip, and bit-bounce.

Table 1 Parameters used in simulations
Full size table

3.1 Normal operation

Initially, dynamic responses for normal conditions are computed for the parameters given in Tables 2 and 3. Figure 2 presents steady state phase portraits for axial and torsional motion. It is a period-1 behaviour that is expected in regular drilling operations, without severe vibrations. Under this condition, discontinuities are not occurring, which indicates that there is no bit-bounce, meaning that the bit does not lose contact with the formation. Since the angular displacement grows with time, the torsional phase space is monitored by ϕ mr – ϕ. One can deduce that the torsional behaviour is also periodic and bounded, which means that the drilling takes place without severe torsional vibration. No occurrence of discontinuities and the fact that the angular velocity is always positive endorse the fact that there is no stick-slip present.

Fig. 2
figure 2

Normal condition behaviour: (a) phase portraits for axial and (b) torsional vibrations

Full size image
Table 2 Typical operation system parameters
Full size table
Table 3 Values of the system parameters used for calculations
Full size table

Figure 3 shows the angular displacement ϕ as a function of time. As the drill-string is continuously rotating, ϕ always increases, fluctuating around ϕ mr value. Figure 3 shows ϕ varying with time and also ϕ mr. One can realise that both curves are almost the same. A more useful way of visualising the behaviour of ϕ is through the difference between ϕ mr−ϕ against time. This way what is obtained is the angular distance between the bit and the rotary table. The figure shows how much the rotary table is ahead of the drill-bit, in rad/s.

Fig. 3
figure 3

Normal condition behaviour: (a) drill-bit and rotary table angular displacement in time; (b) difference between angular displacement of the drill-bit and rotary table

Full size image

3.2 Stick-slip

The stick-slip behaviour is now considered and a new set of parameters is given in Tables 3 and 4.

Table 4 Stick-slip system parameters
Full size table

The angular velocity amplitude increases until it reaches zero velocity (stick). Thereafter, the system behaves with stick-slip. The stick-slip can be clearly seen on the horizontal line present in dϕ/dt=0. The amplitude increase is also noticeable, both in terms of the angular velocity and in the angular displacement, associated with stick-slip. This analysis shows that the angular phase space is an adequate tool to identify the stick-slip. The axial phase space is also presented in this picture showing far more intricate steady state behaviour, since the complex torsional behaviour changes the axial behaviour effectively. Despite its complexity, this phase space does not display any discontinuity whatsoever, indicating that the bit-bounce phenomenon is not taking place (Fig. 4).

Fig. 4
figure 4

Stick-slip behaviour: phase portraits for (a) axial and (b) torsional vibrations

Full size image

Under these conditions, the drilling takes place with the stick-slip behaviour that can be easily observed in Fig. 5 that shows the time history of angular velocity dϕ/dt. Time intervals in which the angular velocity vanishes can be observed, corresponding to the stick intervals in which the drill-bit stops rotating. It is hard to compare the velocity peaks of this result with those of the previous one because many parameters are really different. Nevertheless, a qualitative comparison can be made observing the forcing frequencies (the rotary table angular velocity) in each case.

Fig. 5
figure 5

Stick-slip behaviour: time histories of (a) angular velocity and (b) relative angular displacement

Full size image

In the previous simulation, ω mr=5.236 rad/s and the peaks of dϕ/dt reach about 5.8 rad/s, which is just above the forcing frequency. In this second case, on the other hand, ω mr=3.14 rad/s and the peaks of dϕ/dt is about 7.0 rad/s, which is far above the forcing frequency. Therefore, it is possible to conclude that when stick-slip is present, the drill-bit rotation exhibits high amplitude peaks, what could explain the strong drill-bit wear usually related to this kind of response. In order to understand this phenomenon, one should observe that whether there is stick-slip or not, the average angular velocity of the bit should be, in the long term, very close to that of the rotary table. Hence, when stick-slip is present there are periods during which the drill-bit angular velocity vanishes, and this must be compensated with periods in which the drill-bit velocity is far above the one of the rotary tables; so in this way the average is maintained.

Figure 5 also presents the time history of ϕ mr−ϕ. This picture allows one to observe that an angular distance between the drill-bit and rotary table oscillates around approximately 7 rad, which corresponds to a little bit more than a complete turn. Besides, this movement amplitude varies about 1.7 rad around this average value. In the previous case, the average was around 0.11 rad, and the amplitude around 0.08 rad. This larger distance between the drill-bit and rotary table is probably not due to the stick-slip, but to the fact that the drill-string used in this case has a lower stiffness. That occurs because it is composed of smaller diameter drill-pipes and it is much longer. The larger fluctuations of ϕ mr−ϕ, on the other hand, may be related to the stick-slip. During the stick phase, the rotary table keeps on turning while the bit is standing still, and that brings both far apart.

Another interesting conclusion is that stick-slip is not easily identifiable through the analysis of the angular displacement. Therefore, to identify this behaviour it is more adequate to analyse the angular velocity or the phase space, as presented before.

3.3 Bit-Bounce

The bit-bounce behaviour is now in focus by having a new set of parameters presented in Tables 3 and 5.

Table 5 Bit-bounce system parameters
Full size table

Figure 6 shows the axial phase portrait where the behaviour is quite different from the others, since bit-bounce is observed. The system response is clearly divided in two distinct regions, highlighting the non-smoothness related to the bit-bounce. It can be clearly seen that the displacement is much greater than in the previous cases, despite the fact that the parameters have not been changed too much. The surface elevation (s 0), just like before, is 1 mm, and the displacement amplitudes now reach values on the order of 40 mm, which gives clear evidence that the contact has been lost.

Fig. 6
figure 6

Bit-bounce behaviour: phase portraits for (a) axial and (b) torsional vibrations

Full size image

By looking at the torsional phase portrait, one can see that there is no apparent stick-slip but, in a similar way to what the stick-slip did to the axial phase portrait, the bit-bounce has turned the torsional behaviour much more complex. The orbits seen fill the phase space, but the behaviour should not be confused with a chaotic motion. It is interesting to point out that, unlike what happens during the stick-slip, when the torsional mode discontinuity cannot be seen on the axial phase space, here the axial mode discontinuity can be seen on the torsional phase space.

Figure 7 shows the axial displacement and the axial velocity time histories. Compared to the first case, which had steady state vibrations, it can be observed that the responses are less smooth and having sharper peaks. However, it is not easy to realise the bit-bounce existence through these graphs. Therefore, the identification of this phenomenon requires a deeper investigation that should include acceleration analysis [10].

Fig. 7
figure 7

Bit-bounce behaviour: time histories of (a) axial displacement and (b) axial velocity

Full size image

3.4 Simultaneous stick-slip and bit-bounce

At this point, friction coefficients are altered in order to investigate a case where stick-slip and bit-bounce behaviours occur simultaneously. Tables 3 and 6 give the system parameters and μ e =0.35 and μ d =0.3 from Table 3 are replaced by μ e =0.6 and μ d =0.5 in this example.

Table 6 Simultaneous stick-slip and bit-bounce system parameters
Full size table

The axial phase portrait depicted in Fig. 8a shows the presence of the bit-bounce phenomenon. This conclusion is drawn from the existence of two distinct regions, indicating the non-smoothness characteristic of this phenomenon. Figure 8b shows the torsional phase space, where one can find points with zero velocity, which characterises the stick phases. Here, it is possible to identify both behaviours from the phase space. The stick phases are indicated by a circle around it.

Fig. 8
figure 8

Stick-slip and bit-bounce behaviours: phase portraits for (a) axial and (b) torsional vibrations

Full size image

4 Global dynamics analysis

This section presents a global analysis of the drill-string dynamics predicted by the proposed model. The idea is to promote a slow variation of some system parameter, evaluating its influence on system dynamics. The axial mode is monitored by the displacement peaks while the torsional mode is monitored by the angular velocity peaks. Therefore, we are constructing a kind of bifurcation diagram monitoring some system variable under the slow quasi-static variation of some parameter. We also indicate the occurrence of stick-slip and bit-bounce behaviours on these diagrams. Concerning the system parameter, the analysis started by considering the influence of the drill-pipe length l dp, keeping all other parameters constants. Afterward, we consider the variation of rotary table frequency, ω mr. The simulations are performed for several values of the Weight-On-Bit. This kind of analysis allows us to develop a general understanding of the system dynamics, pointing some critical conditions of the drill-string during oil exploitation.

4.1 Influence of the drill-pipe length (l dp)

Let us start the global dynamics analysis by considering the influence of the drill-pipe length l dp, varying its value and keeping all other parameters, including the BHA length, constant. The influence of the WOB is also of concern by considering different, constant values.

Tables 3 and 7 present system parameters employed in this analysis where n b =1 from Table 3 is replaced by n b =3 as a tri-cone bit is used in this example. Only the highest peak of the maximum amplitudes is presented for each l dp. Besides, we employ a procedure to identify stick-slip and/or bit-bounce for each l dp. Green circles on the horizontal axis indicate values where there is stick-slip while blue dots indicate values for which there is bit-bounce. The sensitive dependence to initial conditions and the multi-stability characteristics related to the co-existing of attractors can be evaluated by constructing two different diagrams with distinct initial conditions: one in which the initial conditions are restarted for each value of l dp (all variables take the zero value) and another one where initial conditions are not restarted and, therefore, results from previous values are used as initial conditions.

Table 7 System parameters for the analysis of drill pipe length influence
Full size table

Initially, we apply a 5000 lbf (22.24 kN) WOB. Figure 9 shows the amplitude peaks calculated for different values of the drill pipe length, l dp. Two different approaches were adopted in the calculations: in parts (a) and (b) the responses were calculated starting from the same initial conditions for each value of l dp, while in parts (c) and (d) the attractor obtained for the lower value of the drill pipe length was followed as the length increases. The peak related to the torsional resonance is identified around l dp=780 m. For values close to l dp=6000 m, there is a peak in the axial displacement amplitude and apparently the high axial amplitude increases the torsional amplitude until starting the stick-slip.

Fig. 9
figure 9

Amplitude peaks highlighting bit-bounce and stick-slip development with the increase of the drill-pipe length—\(\underline{F}_{\,b} = 5000~\mbox{lbf}\). (a, b) In these calculations, initial conditions are restarted for each value of drilling pipe length; (c, d) here the attractor obtained at the low value of drill pipe length was followed (initial conditions are not restarted)

Full size image

It should be highlighted that bit-bounce is more often present at high depths, and with great differences in their amplitudes. In some regions, we can observe that amplitude varies quickly between higher and lower values. This behaviour can be observed by enlarging some of these regions as presented in Fig. 10. These variations are related to attractors co-existence which can be identified by analysing system responses for different initial conditions. Figure 11 presents two distinct behaviours associated with both kinds of responses presented in Figs. 9 and 10 for l dp=2750 m. The parts (a) and (b) show results with all initial conditions set to be 0. On the other hand, the parts (c) and (d) present the trajectories on the phase space for the case where initial axial velocity is 0.003 m/s.

Fig. 11
figure 10

Distinct responses for different initial conditions showing the attractor coexistence at l dp=2750 m; (a, b) trajectories shown on the phase plane for zero initial conditions, (c, d) trajectories on the phase plane calculated for initial axial velocity of 0.003 m/s

Full size image
Fig. 10
figure 11

Enlargement of the axial amplitude peaks in region with bit-bounce for \(\underline{F}_{\,b} = 5000~\mbox{lbf}\)

Full size image

Figures 9(c) and 9(d) show results of axial and torsional displacement amplitudes, with continuous initial conditions for each l dp (initial conditions are not restarted). The response related to shallow depths presents bit-bounce behaviour, even though the amplitudes are not very high. Note that there is a high amplitude peak around l dp=780 m. At this depth, the torsional natural frequency (\(\sqrt{k_{t}/I_{t}}\)) is 9.4471 rad/s, what is exactly 3 times the string rotation, which is coherent with the value of n b =3. This peak is related to the torsional mode resonance, being associated with stick-slip behaviour (as identified by the green circle on the horizontal axis). Around l dp=280 m, there is another small torsional peak that is associated with a frequency 16.77 rad/s. Since this depth is related to bit-bounce behaviour, we can infer that this peak is a consequence of the non-smoothness. For values of l dp greater than 7500 m, bit-bounce behaviour starts causing angular velocity amplitude increase.

The increase of the WOB to 10,000 lbf (44.48kN) promotes changes in system dynamics. Figures 12(a) and 12(b) present results calculated for the same initial conditions for each value of the drill pipe length l dp, while Figs. 12(c) and 12(d) show the amplitudes for the attractors which was followed from the low value of l dp. Note that bit-bounce behaviours related to higher depths observed for lower weight on bit (see Figs. 9(c) and 9(d)) do not exist anymore. As can be seen from Figs. 12(a) and 12(b), bit-bounce behaviour starts a few hundred meters deeper than the previous case. In general, it is possible to observe that the increase of the WOB introduces difficulties to the occurrence of the bit-bounce behaviour.

Fig. 12
figure 12

Amplitude peaks highlighting bit-bounce and stick-slip development with the increase of the drill-pipe length—\(\underline{F}_{\,b} = 10{,}000~\mbox{lbf}\). (a, b) In these calculations initial conditions are restarted for each value of drilling pipe length; (c, d) here the attractor obtained at the low value of drill pipe length was followed (initial conditions are not restarted)

Full size image

This conclusion can be assured by increasing even more the WOB value. Figures 13 and 14 present the results for \(\underline{F}_{\,b}= 15{,}000~\mbox{lbf}\) (66.72 kN) and \(\underline{F}_{\,b}= 30{,}000~\mbox{lbf}\) (133.44 kN), respectively. It is noticeable that the increase of WOB value tends to make the bit-bounce behaviour less likely to occur.

Fig. 13
figure 13

Amplitude peaks highlighting bit-bounce and stick-slip development with the increase of the drill-pipe length—\(\underline{F}_{\,b} = 15000~\mbox{lbf}\). (a, b) In these calculations initial conditionsare restarted for each value of drilling pipe length; (c, d) here the attractor obtained at the low value of drill pipe length was followed (initial conditions are not restarted)

Full size image
Fig. 14
figure 14

Amplitude peaks highlighting bit-bounce and stick-slip development with the increase of the drill-pipe length—\(\underline{F}_{\,b}= 30000~\mbox{lbf}\). (a, b) In these calculations, initial conditions are restarted for each value of drilling pipe length; (c, d) here the attractor obtained at the low value of drill pipe length was followed (initial conditions are not restarted)

Full size image

4.2 Influence of the rotary table frequency

The forthcoming analysis deals with the influence of the rotary table frequency, ω mr, on the system dynamics. This analysis is carried out for several values of weight-on-bit. The other parameters are shown in Tables 3 and 8 where n b =1 from Table 3 is replaced by n b =3. The system response is analysed in two different ways: increasing and decreasing the frequency in a slow quasi-static way. For each forcing frequency, ω mr, the maximum amplitude of axial displacement at steady state is plotted to identify system dynamics. Initial conditions are defined from the last value of ω mr. Stick-slip and/or bit-bounce behaviours are also identified, respectively, by green circles and blue dots. This identification is on the bottom horizontal axis when frequency is increasing and on the top horizontal axis when it is decreasing.

Table 8 System parameters for the analysis of rotary table frequency influence
Full size table

Simulations for six different values of WOB are presented in Fig. 15: 5000 lbf (22.24 kN), 10,000 lbf (44.48 kN), 15,000 lbf (66.72 kN), 20,000 lbf (88.96 kN), 25,000 lbf (111.20 kN), and 30,000 lbf (133.44 kN). For all cases, it should be highlighted the differences between the increase and the decrease of frequencies. Two curves are plotted: one for the increasing frequency (black-solid) and another for the decreasing frequency (red-dashed). It is also noticeable the occurrence of several peaks that change the position during the increase and the decrease of frequency. For those, some peaks related to decreasing frequencies do not have counterpart when frequency increases. Another aspect of these curves is that there is an increase of peak values for higher frequencies.

Fig. 15
figure 15

Amplitude peaks highlighting bit-bounce and stick-slip behaviours changing forcing frequency for different WOB. Green circles indicate stick-slip and blue dots indicate bit-bounce. The lower axis is related to increasing frequency while the upper is associated with decreasing frequency. (-•-, red) Frequency increase; (-•-, black) Frequency decrease (Color figure online)

Full size image

It is important to establish the difference between black and red responses, where all red responses are associated with stick-slip phenomenon. Black-solid curves, on the other hand, are not always related to this behaviour. This indicates that the stick-slip is somehow related to the mechanism of creating these high amplitude peaks. The increase in the torque on bit, resulting from higher axial amplitudes, increases the torsional movement amplitudes and favours the appearance of the stick-slip. This explains why this behaviour is more likely to occur when starting from higher axial amplitudes as initial conditions (red-dashed curve). Besides, although the increase of the torsional amplitudes and the presence of the stick-slip do not increase the axial forcing amplitude, they change the forcing frequency. This is because the axial-torsional coupling of the driving force.

Another interesting behaviour that can be observed from these curves is the dynamical jumps. With frequency increase, the jumps occur just before amplitude peaks. On the other hand, when frequency decreases, jumps occur immediately after the red-dashed amplitude peaks. Once again, the increase of the WOB causes the bit-bounce behaviour more difficult to appear. For high values of WOB (\(\underline{F}_{\,b} = 20{,}000~\mbox{lbf}\), 25,000 lbf and 30,000 lbf), there are less occurrence of the bit-bounce behaviour and lower amplitude peaks for frequency increases (black-solid curves). During frequency decreases (red-dashed curves), there is an increase related to bit-bounce for \(\underline{F}_{\,b} = 25{,}000~\mbox{lbf}\). This region is also related to stick-slip behaviour and, therefore, it is possible to argue that the increase of the bit-bounce occurrence might be related to the stick-slip behaviour. Moreover, the stick-slip behaviour is related to the increase in WOB, which increases the torque on bit.

5 Conclusions

In this paper, we model and analyse drill-string vibrations focusing on two fundamental phenomena: stick-slip and bit-bounce. We employed a two degrees-of-freedom model to account for axial and torsional vibrations based on the model proposed by Christoforou and Yigit [5]. The coupling between both vibration modes is through contact with the formation, where the axial force is the catalyst to generate a resistive torque. The forces and torques are defined according the contact or non-contact scenarios, establishing a non-smooth system. Besides, the dry friction between the formation and the drill-bit introduces the other non-smoothness of the system.

We model the abrupt changes (non-smoothes) by adopting a smoothening procedure which is advantageous in terms of mathematical description and numerical analysis. Based on this procedure, numerical simulations are carried out showing different kinds of responses. Basically, four situations are of concern: normal operation; stick-slip; bit-bounce; simultaneous stick-slip and bit-bounce. Finally, we perform a global dynamical analysis of the system by analysing the slow quasi-static variation of some system parameter evaluating the effect on system dynamics by monitoring some system variables. The drill-pipe length and the rotary table frequency variations are considered for different values of the Weight-On-Bit.

Maximum axial amplitudes and angular velocities are monitored in order to observe system dynamics. Results allow one to identify important phenomena during drilling, highlighting some aspects of stick-slip and bit-bounce behaviours. Distinct scenarios are investigated showing the parameter variation influence in system dynamics, especially the one related to non-smooth behaviours. Therefore, it is possible to say that performed numerical simulations are capable of predicting a full range of dynamic responses including the non-smooth behaviours.