1 Introduction

Tsunami are a multifaceted threat to coastal settlements. Recent tsunami events have shocked the world, alarmed coastal residents and resulted in researchers reassessing tsunami hazard exposure. The 2004 Indian Ocean Tsunami killed over 200,000 people across 13 countries, while the more recent 2011 Tohoku Earthquake Tsunami is estimated to have killed 20,000 people and caused US$ 210,000 million worth of damage (Guha-Sapir et al. 2014). The 2004 tsunami prompted many at-risk countries to review their tsunami readiness and accelerated international research on tsunami causes and impacts (Jin and Lin 2011).

Recent tsunami events demonstrate the need for improved risk mapping and assessment to inform and train communities (Wegscheider et al. 2011; Taubenböck et al. 2009; Fraser et al. 2014). Despite scientific advancements since 2004, there are significant barriers for local authorities to carry out tsunami risk assessments and translate this information into policy and practice. Financial resources, technical capacity and competing priorities often reduce the ability of local authorities to adequately prepare for low-frequency natural hazards such as tsunami (Wood et al. 2014; Vogel et al. 2007; Løvholt et al. 2014). This paper focuses on enhancing practitioner capacity by providing a basic method for quantifying onshore tsunami inundation distance and depth in the absence of comprehensive data.

Tsunami are secondary hazards triggered by a range of geophysical events, such as submarine earthquakes or slope failures. The range in terms of size and location of their source leads to complexities in tsunami hazard mitigation. A tsunami source could be “local” resulting in limited or no warning time or far-sourced providing more time for warnings and evacuation (Byrant 2014; Jin and Lin 2011). For potentially vulnerable locations, emergency management practitioners need to consider a range of possible triggers, tsunami travel times, inundations and impacts. Tsunami risk reduction therefore requires a “whole disaster” approach that includes an understanding of the hazard characteristics and vulnerability of assets-at-risk alongside people’s awareness and willingness to prepare for and respond to future tsunami events (Cavallo and Ireland 2014).

Tsunami casualties and economic losses for coastal settlements can be reduced through activities such as land use planning, public education and evacuation planning (Scheer et al. 2012). This can only be achieved when local authorities are able to identify and map areas vulnerable to inundation and then implement tsunami risk reduction activities within these areas. Inundation identification methods use either empirical measurements from historical events, simple attenuation rules (Leonard et al. 2009) or numerical simulations of tsunami propagation (Power 2013). Limited resourcing to apply these methods can prohibit local authorities from implementing a “whole disaster” approach to tsunami risk reduction (Saunders et al. 2014).

Tsunami inundation mapping is based on the ability to calculate possible run-up and inundation distances (Imamura 2009). Despite the science of oceanic tsunami propagation being well developed, the onshore behaviour of tsunami is more complex due to the interplay of intricate variations in topography (including the ground slope and buildings), vegetation, coastal geomorphology, hydraulic roughness and entrained debris (Imamura 2009). Current basic approaches for run-up estimation are based on empirical data that when transferred and applied to “other” settings globally provide results that are potentially unreliable (Power 2013). Therefore, a sound, transparent, practical and low-cost method for calculating run-up and inundation distance is needed.

This paper aims to present a basic, conceptual tsunami run-up equation that can be locally refined where parameter calibration data are available. Section 2 of the paper outlines existing run-up prediction methods and proposes a new methodology. Section 3 compares results derived from the new method with empirical measurements from historic tsunami events. Finally, Sect. 4 discusses potential applications of the new methodology including the assumptions and limitations.

2 Tsunami run-up calculation

2.1 Current methods for estimating tsunami run-up

Camfield (1980) summarises experimental work which shows that on flatter slopes (<0.14), tsunami run-up height is equal to or less than the wave height at the shoreline. On steeper slopes, the run-up height increases as the slope increases. For the 2009 South Pacific tsunami, Reese et al. (2011) report that as the tsunami moved inland, the rate of attenuation of wave height with inland distance was a function of the topographic profile of the area and the inundation distance depended on the onshore ground slope. Their measurements showed the inundation distance relation to ground slope could be described by a negative logarithmic trend.

From a more theoretical perspective, two-dimensional shallow water equations (the depth-integrated incompressible Reynolds-averaged Navier–Stokes equations) can be solved to predict inundation extent provided sufficient computational resources and topographic and roughness information are available (Ioualalen et al. 2007; Schuiling et al. 2007; Choi et al. 2003; Titov and Synolakis 1998; Sato et al. 2003). Using such hydrodynamic models, Gayer et al. (2010) demonstrated that onshore roughness has considerable influence on run-up and inundation distances.

In many situations, there is not sufficient data (such as LiDAR-based digital elevation models), computational capacity or resources to undertake such detailed two- or three-dimensional hydrodynamic modelling and basic empirical equations or “rules-of-thumb” are applied. The simplest approximation is that a tsunami will act like a rapidly rising tide so the run-up height (vertical rise) will equal the peak height at the shoreline (Houston and Garcia 1978). According to this “bathtub” model, the peak surge height at the shore fills to a constant level inland until it intersects the ground surface giving the inland inundation distance of the tsunami. While this provides an initial estimate, the assumption cannot always be used with accuracy (Camfield 1980). Factors which influence run-up and distance include wave volume, height and velocity and lateral topographic convergence or divergence.

An offshoot of the bathtub approach are models that assume a loss in water level moving inland. A “rule-of-thumb” used for setting evacuation zones in New Zealand (Leonard et al. 2009) allows for attenuation by reducing the maximum potential run-up (doubled coastal wave height) by 1 m for every 200 m of tsunami travel inland or 1 m for every 400 m up significant rivers and 1 m for every 50 m away from rivers. Power (2013) states that the 1 for 200 ratio which is based on empirical data from the Indian Ocean Tsunami may be overly conservative.

Other models specifically incorporate onshore roughness in the form of Mannings’ n. Equation 1 predicts the inundation distance L as a function of Y s the wave height at the shore and n the surface roughness.

$$L = \, 0.06Y_{s}^{4/3} /{\mathbf{n}}^{2}$$
(1)

The original form of this equation by Bretschneider and Wybro (1977) was intended for flat-lying coastal plains, used the maximum flood height (not shoreline wave-crest level) and used a constant (not necessarily 0.06) that depended on the units of measurement. Typical values of n range from about 0.015 for very smooth terrain such as mudflats, to 0.07 for rough coastal areas such as dense brush or coarse lava formations. Hills and Mader (1997) used this equation to illustrate that a tsunami would travel four times further inland on smooth grazing land (n = 0.015) compared to typical developed land (n = 0.03). McSaveney and Rattenbury (2000) modified Eq. (1) to include a slope factor and predict onshore water depth as given in Eq. (2) where Y loss is the loss in wave height per meter of inundation distance and S 0 is the ground slope.

$$Y_{\text{loss}} = \left( {167{\mathbf{n}}^{2} /Y_{s}^{1/3} } \right) + 5\,{ \sin }\left( {S_{0} } \right)$$
(2)

The US Army Corps of Engineers (Camfield 1980) predicted wave run-up (R) using Eq. (3) where A is an experimental constant (taken as 0.5) and g is gravitational force per unit mass.

$$R/Y_{\text{s}} = \left( {1 + A} \right)\left( {1 + 2A} \right)/\left( {2A^{2} } \right)\left( {1 + \left( {8g\,{\mathbf{n}}^{2} /0.91 \, A^{2} S_{0} Y_{s}^{1/3} } \right)} \right)$$
(3)

The Fritz criteria (Liu et al. 2005) suggest an exponential decay relationship between decreasing inundation height and distance inland (Eq. 4).

$$R = 2Y_{\text{s}} { \exp }\left( { - { \ln }\left( 2 \right)/\alpha x} \right)$$
(4)

where α is the distance in metres in which the wave height drops by half and x is the distance inland (α = 2000 for land and 4000 for rivers or water bodies). However, Leonard et al. (2009) found that this approach overestimated evacuation requirements in low-gradient terrain.

While these models are relatively simple to apply, they are typically empirically based, lack a rigorous theoretical derivation and may give misleading results when conditions differ from those for which the equations were developed. Onshore tsunami behaviour is now investigated on the basis of simple hydraulic principles.

2.2 New calculations

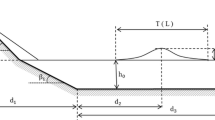
We consider an onshore tsunami from a one-dimensional perspective (shoreline slope is measured parallel to the arrival direction of the tsunami, and lateral convergence or divergence of the onshore wave is not taken into account). We assume onshore permeability can be ignored. Parameters used in the analysis are shown in Fig. 1.

Fig. 1
figure 1

Wave run-up diagram showing shoreline wave-crest levels Y s, onshore inundation distance L, run-up height R, uniform ground slope S 0, total head friction gradient S f, water depth y and the profile of wave-crest heights (dashed red line)

Full size image

Assuming flow at the crest of an onshore tsunami wave has depth-averaged velocity V and is quasi-steady (dV/dt ≪ dV 2/dx), then the Bernoulli energy equation can be written as:

$$\frac{{{\text{d}}y}}{{{\text{d}}x}} = S_{\text{f}} - S_{0} - \frac{1}{2g}\frac{{{\text{d}}(V^{2} )}}{{{\text{d}}x}}$$
(5)

where y is the flow depth, S 0 the ground slope, S f is the (always negative) friction gradient and g is gravitational force per unit mass.

For very shallow water waves (water depth is a small fraction of the wave length), the water “particles” have a velocity that is near constant throughout a vertical section, water particles move forward under a wave crest and backwards as a trough arrives and the wave velocity is given by V 2 = gy (Henderson 1966). With this assumption, Eq. (5) becomes:

$$\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{2}{3}\left( {S_{\text{f}} - S_{0} } \right)\quad {\text{under wave crest}}$$
(6)

For onshore tsunami, the height of flow resistance elements in the form of trees, houses, etc. is usually similar to or larger than the water depth and flow passes between these elements. Consequently, an appropriate flow resistance equation would be S f = −(f/d) (V 2/2 g) where f is a Darcy friction factor (constant under high Reynold’s number conditions) and d indicates the distance between the flow protrusions such as trees or houses (c.f. A pipe diameter).

A “roughness aperture” a = 2 d/f can now be defined which with V 2 = g y gives a simple flow resistance approximation: S f = −y/a. Using a typical f value of 0.05 (for fully turbulent flow in rough conduits) with a typical protrusion spacing of 2 m (e.g. distance between coconut palms or buildings) gives an indicative roughness aperture a value of around 80 m.

Thus, Eq. (6) becomes:

$$dy = - \frac{2}{3}\left( {S_{0} + \frac{y}{a}} \right)dx\quad {\text{for the wave crest}}$$
(7)

For a uniform ground slope, integrating Eq. (7) gives:

$$a\ln \left( {y + a_{{}} S_{0} } \right) = - \frac{{2_{{}} x}}{3} + {\text{const}}\quad {\text{for the wave crest}}$$
(8)

Evaluating the constant at the shoreline where y = Y s at x = 0 and rearranging gives an equation for the water depth profile:

$$y = \left( {Y_{s} + aS_{0} } \right)e^{ - 2x/3a} - aS_{0} \quad {\text{depth at wave crest}}$$
(9)

The water depth y = 0 at x = L, giving:

$$L = \frac{3a}{2}{ \ln }\left( {\frac{{Y_{s} }}{{a_{{}} S_{0} }} + 1} \right)$$
(10)

which predicts the inundation distance of an onshore tsunami given a shoreline wave-crest level Y s, uniform ground slope S 0 and a roughness aperture a. With constant ground slope, run-up height R is given by:

$$R = L \, S_{0}$$
(11)

2.3 Interpretation of derived equations

Although the proposed equations are grounded on basic physical principles, it is important to investigate their implications over a representative range of conditions. The theoretical profile of Eq. (9) predicts that water depth will decrease exponentially due to friction, as a tsunami wave moves inland with the rate of decrease depending on the roughness aperture a. The roughness aperture is a ratio of distance between protrusions to a local friction factor. The smaller the roughness aperture, the more the depth will decrease moving inland. However, a is a new parameter based on Darcy’s friction equation which is generally used for conduits. While Darcy’s f may be more appropriate for tsunami flow between onshore roughness elements (as opposed to Manning’s n which is for flow over rough surfaces), values of Darcy friction factors between buildings or tree trunks are not readily available in the literature. Taking a typical f value of 0.05 for a rough pipe and a nominal (tree or building) protrusion spacing of 2 m gives a roughness aperture parameter a value of around 80 m, and we will use this value to examine potential tsunami conditions.

Water level is determined by adding water depth to the local ground level. This is plotted in Fig. 2 which compares peak water levels predicted by Eq. (9) for a = 80 with a shoreline wave-crest level of 5 m and mild, moderate and steep onshore slopes. From Fig. 2, it can be seen that Eq. (9) predicts that where the ground is rising faster than the friction head loss, the onshore water level of a tsunami will rise above the shoreline wave-crest level.

Fig. 2
figure 2

Theoretical water level profiles (solid lines) predicted on steep, moderate and mild onshore slopes (dashed lines) using Eq. (9) for a tsunami wave with shoreline wave-crest level Y s  = 5 m, roughness aperture a = 80 m

Full size image

3 Verification of equations using measured tsunami profiles

Post-tsunami assessments are essential to prioritise relief efforts and also to validate models and understand the limitations and uncertainties of the models and the outputs they produce (Power 2013). Using such surveys, predictive equations can be evaluated with data from actual tsunami. While not as rigorous as laboratory measurements, these data describe real situations.

In July 2006, a tsunami along the South Java coastline travelled several hundred metres inland in some locations and killed over 600 people (Reese et al. 2007). Following the tsunami, Fritz et al. (2007) and Reese et al. (2007) took accurate measurements of inundation and run-up heights at locations on the South Java coast.

In September 2009, an earthquake doublet triggered a Pacific region-wide tsunami that killed over 180 people (Jaffe et al. 2010; Okal et al. 2010). It was considered the worst disaster to impact the Pacific region in the last 50 years. The tsunami reached the Samoan coastline within 15 min, highlighting the need for effective people-centred early warning systems based on simple risk assessments (Goff and Dominey-Howes 2011). Reese et al. (2011) conducted a field survey approximately 2 weeks after the event, providing raw data suitable for evaluation of onshore tsunami behaviour.

In the following sections, we compare Eq. (10) for inundation distance and Eq. (11) for run-up height with empirical data from Samoa and South Java: firstly (Sect. 3.1) assuming a uniform onshore gradient and secondly for a variable onshore gradient (Sect. 3.2), and then implications of the results are discussed and suggestions for improving the predictions are given (Sect. 4).

3.1 Uniform onshore gradient

3.1.1 Samoan Tsunami 2009

Empirical observations of the 2009 Samoan Tsunami by Reese et al. (2011) confirm that the effect of ground slope on inundation distance can be described by a logarithmic trend as predicted by Eq. (10). The proposed predictive equations are now compared with profiles of measured water depths and ground levels at sites where suitable data are available. The equations are based on flow occurring between roughness elements (rather than over a rough bed), and experimental data for wave data run-up on smooth, sloping beaches are not necessarily relevant. The equations require knowledge of shoreline wave-crest level, onshore slope and the roughness index a. In cases where the shoreline wave-crest level was not measured, this was estimated by extrapolating the line of onshore water level measurements back to the shore (and comparing this with the shoreline wave-crest level of neighbouring profiles where available). Where the inland tsunami run-up extent was not indicated, this was estimated by extrapolating the line of onshore water level measurements until it intersected the ground surface. We also initially assume a uniform ground gradient from the shoreline to the inland extent of a tsunami wave as illustrated by the green line in Fig. 1. This ground slope is taken to be the average slope between the shoreline (defined by the mean level of the sea at the time of the tsunami) and the inland location where the measured tsunami depth became zero. These assumptions are illustrated in Fig. 3 on measured profiles from the 2009 Samoa Tsunami.

Fig. 3
figure 3

Profiles measured in Samoa for the September 2009 tsunami (Reese et al. 2011) showing measured ground levels and assumed uniform ground slope (green line). Shoreline wave-crest level is assumed to be 5 m for the Ulutogia transect (top graph) and 8 m (by extrapolation of onshore levels) for the Asili transect (bottom graph)

Full size image

Equation (10) is compared with Samoan measurements of inundation distance in Fig. 4.

Fig. 4
figure 4

Inundation distance as a function of ground slope. Solid circle symbols show Samoan measurements. Hollow square symbols show distance as predicted by Eq. (10) using average shore slope, shoreline wave-crest level and a = 80 m. Labels refer to village name and survey profile. Data from Reese et al. (2011). A tabulation of the graph is provided as an online resource (online resource 1)

Full size image

Equation (11) is compared with run-up measurements at the Samoan sites of in Fig. 5.

Fig. 5
figure 5

Comparison of measured and predicted run-up at Samoan sites using Eq. (11) with a = 80 and measured average beach slope S 0

Full size image

Considering that a constant roughness aperture of 80 m is used for all sites, the proposed calculation results shown in Figs. 4 and 5 are satisfactory, particularly at the higher ground slopes.

3.1.2 South Java Tsunami 2006

The proposed equations are now applied to data measured following the 2006 South Java Tsunami. While the Samoan profile sites tend to have similar infrastructure and vegetation densities, the South Java sites display a wide variety of onshore roughness conditions, ranging from rice fields to urban infrastructure. There are no guidelines for setting values for the roughness parameter a (because the equations are new). As a first assumption, we will use the same value that was appropriate for the (more uniform) Samoan coasts. Figure 6 shows a comparison of inundation distance from water level profiles measured at Widarapayung (Cilicap), Pangandaran, Ciliang (Ciamis) and Batuhiu in South Java (Reese et al. 2007) with that predicted using Eq. (10), measured ground slopes, and a = 80 m.

Fig. 6
figure 6

Comparison of measured and predicted inundation distance for S. Java tsunami assuming constant roughness (a = 80). Numbers in brackets refer to Reese et al’s (2007) profile numbers

Full size image

Although the measured vs predicted data scatter about the 1:1 line in Fig. 6, only 20 % of the variance in observed inundation distance is explained (R 2 = 0.2). However, constant roughness is assumed. The measured inundation distance will exactly match the calculated inundation distance if the following roughness aperture values are used: Widarapayung (1) a = 66, Pangandaran (4) a = 80, Pangandaran (5) a = 132, Pangandaran (8) a = 63, Pangandaran (10) a = 90, Pananjung (12) a = 56, Batuhiu (16) a = 43. The available data and aerial photographs indicate generally higher onshore roughness in locations where lower roughness aperture values are indicated and vice versa, but care is necessary with such conclusions. As a tsunami can modify ground roughness by flattening obstructions and moving debris, the roughness at the time of the tsunami peak may not correspond to roughness observed on the ground before or after successive tsunami waves. Thus, in locations where there is “fragile” onshore roughness (such as rudimentary dwellings or easily damaged vegetation), the appropriate “a” value may need to take into account the state of onshore roughness during a tsunami.

When it comes to prediction of run-up, the calculation is also sensitive to roughness as shown in Fig. 7. In this figure, run-up is predicted assuming a constant roughness aperture value of a = 80.

Fig. 7
figure 7

Comparison of measured run-up with that predicted using Eq. (10) with a = 80 and Eq. (11)

Full size image

In Section 2.3, Fig. 2 demonstrates that the proposed equations show run-up may exceed shoreline wave-crest level on steeper slopes. The equations indicate that rather than a specific slope for which run-up will exceed the shoreline height (slope >0.14 was reported by Camfield 1980), the “crossover” slope depends on the shoreline wave-crest level and the roughness. Solving Eqs. (10) and (11) with run-up at the level of shoreline wave-crest level (R = Y s) shows that the crossover slope S c is:

$$S_{\text{c}} = 0.88Y_{\text{s}} /a$$
(12)

If the actual onshore slope exceeds S c, run-up will exceed the shoreline wave-crest level. The moderate slope example in Fig. 2 with S 0 = 0.05 has S c = 0.055. Thus, the slope is just below the crossover slope and the run-up almost reaches the shoreline wave-crest level. Reducing the onshore roughness (increasing a >80 m) would allow run-up to exceed the shoreline wave-crest level for this example.

As well as variations in roughness, another factor to consider in the evaluation of the equations above is that the onshore slopes were often not uniform. The way that Reese et al. (2011) calculated average ground slope is mathematically equivalent to dividing the measured profile run-up height by the measured inundation distance. Consequently, the above predictions of run-up and inundation distance are partially and indirectly based on knowledge of measured run-up and inundation distance which were used to determine the onshore slope S 0.

3.2 Varying onshore gradient

In many situations, the onshore land gradient is not constant as assumed in Figs. 1 and 2. The derivation of the equations assumes a uniform onshore ground slope and this is often not the case in reality. For such nonlinear gradients, it may be possible to partition an irregular slope into linear sections with the predictive equations applied to each linear section in turn. The predicted run-up height at the end of a linear section becomes the new “shoreline” height for the following section.

An extension of linearly sloped subsections could be to use every set of profiled ground coordinates. The differential form Eq. (7) can be written as

$$y_{2} =_{{}} y_{1} - \frac{2}{3}\left( {S_{0} + \frac{{y_{1} }}{a}} \right)\left( {x_{2} - x_{1} } \right)$$
(13)

An example of application of Eq. (13) is given for the village of Ulutogia in Samoa which is shown in Fig. 8. On this figure, locations at which water level measurements were taken following the 2009 Samoan Tsunami are shown by triangles. The village is very exposed to tsunami until some 100 m inland where there is a distinct change to heavy vegetation.

Fig. 8
figure 8

Triangles show locations of water level measurements in Ulutogia village, Samoa, following the 2009 tsunami. While the picture shows high-tide conditions, the shoreline is measured from the most seaward triangle

Full size image

The measured ground and tsunami water levels are shown in Fig. 9. Average ground level (Fig. 9 lower line) shows that there is a mild onshore slope that steepens moving inland. To apply Eq. (13), the calculation starts with shoreline wave-crest level y 1 = 2.53 m (i.e. shoreline wave-crest level of 4.2 m minus average ground level of 1.67 m) and calculates y 2 at a location 10 m inland (i.e. x 2 − x 1 = 10 m). The slope S 0 is the rise in average ground level over the 10-m distance, and a roughness value of a = 200 m is used for the smooth foreshore. The calculated wave level y 2 is then used as y 1 for a second application of Eq. (13) with average ground slope from 10 to 20 m and so on until the water depth at 100 m from the shore is calculated. Around this distance, the roughness changes distinctly. If a = 200 m is used past 100 m from the shore and into the trees, the tsunami level is predicted to follow the dashed line in Fig. 9 which rises as the ground rises, to a level around 7 m. Within the vegetated zone, the measured water levels are lower than indicated by the dashed line and do not rise above 5 m. As there are no guidelines for defining roughness parameter a, appropriate values were selected to match the predicted profile to measured peak depths. This was achieved by incrementally increasing the roughness beyond 100 m. The aperture a was reduced from 200 m to a = 50, 30, 20, 15 and 10 m moving from 110 to 150 m from the shore, resulting in the profile shown as the “predicted wave level” (upper solid line in Fig. 9).

Fig. 9
figure 9

Measured tsunami levels and those predicted using Eq. (13) using Y s = 2.53 m, a = 200 m (0–100 m inland) and a declining from 50 to 10 m (110 to 150 m inland)

Full size image

4 Discussion

Within this paper, we have evaluated new equations for predicting tsunami run-up and inundation using empirical data from the 2009 Samoa and 2006 South Java events. The predicted results are demonstrated to fit data measured from these events reasonably well and confirm that there will be an exponential decline in peak water depth (due to friction) as a tsunami wave moves inland. The smaller the onshore roughness aperture, the greater the decrease in peak depth as a tsunami moves inland. Where ground level rises faster than the loss of friction head, the tsunami peak water level will rise above the shoreline wave-crest level. Camfield’s (1980) criterion that run-up height does not exceed the shoreline wave-crest level for slopes less than 0.14 can now be improved by including the effect of onshore roughness. The crossover ground slope at which run-up will exceed shoreline wave-crest level can be predicted from the ratio of shoreline wave-crest level to roughness aperture (Eq. 12).

Incorporation of a roughness index enables better representation of run-up on natural shorelines. However, as evident during the 2004 Indian Ocean event, tsunami are not single waves (Liu et al. 2005) and the erosive action of multiple waves may adjust the roughness index. This is because the first waves may flatten or remove features, smoothing the topography and increasing the run-up of later waves. Conversely, tsunami waves may entrain debris which can snag as well as deposit in mounds and act to increase the roughness.

Even small-scale adjustments in topography can have a significant impact on run-up. On the Sri Lankan coast, Liu et al. (2005) noted that anthropogenic removal of a small section of a dune system significantly increased the damage and water levels during the 2004 Indian Ocean Tsunami.

For the 2009 Samoan Tsunami examples in this paper, a generic roughness aperture of 80 m was used. On less-uniform, nonlinear topographic profiles, values ranging from 10 to 200 m were found to give realistic predictions of measured tsunami depths. Because the “roughness aperture parameter” is novel, no guidelines on parameter values for different ground cover types are available. This information will become available by calibrating the equations with empirical run-up and inundation distance measurements from historic or future tsunami events, selecting a best-fit value for the roughness aperture, and then relating this to the applicable local ground cover during the tsunami.

As an initial guide, roughness aperture parameter values for different ground types are suggested in Table 1. Note that values should represent the situation during a tsunami peak when wave inrush may have already changed the prior roughness by removing light buildings and/or flattening vegetation. In addition to the roughness parameter, the proposed equations also require knowledge of shoreline wave-crest level and onshore slope. Wave height can be obtained from historic tsunami data or ocean tsunami propagation models. Where accurate survey data are not available, onshore slope could be estimated from contour maps, satellite imagery or aerial photographs (Giles 1998).

Table 1 Indication of suitable values for the roughness aperture parameter a
Full size table

Once tsunami shoreline wave-crest level, topography and roughness have been estimated, inundation distance and run-up can be calculated to delineate tsunami hazard zones. A conservative approach should be taken because of the inherent uncertainty. Factors contributing to the uncertainty include the limited data available for selecting the roughness parameter and the changes in roughness that can occur during a tsunami event.

5 Conclusions

For areas at risk, high-resolution, hydrodynamic, onshore numerical models and palaeo (ancient) tsunami measurements are appropriate for predicting tsunami inundation. For many coastal locations, palaeo-data and detailed topography and flow resistance maps are not available and computational modelling may lie beyond the resources of local authorities. Contemporary “rules-of-thumb” for predicting tsunami run-up provide a range of results with varying accuracy. Although these methods are easily applied, they are typically empirically based, lack theoretical backing and may give misleading results when local conditions differ from those for which the equations were developed. Incorporation of a roughness parameter is necessary to improve the accuracy of prediction methods.

On the basis of simple hydraulic principles using energy conservation and friction loss assumptions, this paper has shown that relatively straightforward equations for predicting tsunami maximum depth profiles and inundation distances can be derived. The equations require knowledge of shoreline wave-crest level, the onshore ground profile and an index for onshore roughness aperture. They show that where the ground level rises faster than the friction head is lost, peak tsunami water level will rise above the shoreline wave-crest level. The equations apply parallel to the arrival direction of the tsunami, and lateral convergence or divergence of the onshore wave is not taken into account. The equations are derived to improve on present "rules-of-thumb", not to replace two-dimensional or three-dimensional hydrodynamic modelling where such modelling can be justified.

Comparison of results from the proposed equations with empirical data from the 2009 Samoa and 2006 South Java Tsunami events demonstrates that the equations can satisfactorily describe observed behaviour. Given the need for tsunami risk reduction in many countries, trial application of these equations is advocated.