Abstract
In this paper I argue that English exceptive constructions introduced by except can be derived from full clauses by ellipsis. I offer a compositional analysis for this clausal exceptive construction. I propose that except introduces quantification over possible situations and the clause following it provides the restriction for this quantification. I show how the analysis developed here derives the inferences except contributes to sentences it occurs in and the restrictions on its use. I also show how this approach captures certain cases which traditional approaches to the semantics of exceptives do not, such as cases where an except-phrase contains a PP or multiple syntactic constituents. The approach I propose correctly captures the NPI licensing facts inside except-phrases. In addition, this is the first approach to the semantics of exceptives that correctly captures the contribution of modal phrases such as possibly inside except-phrases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper I discuss the syntactic and semantic properties of the English exceptive construction introduced by except. I argue that the complement of except can have a clausal structure even in cases when it appears to be phrasal. I offer novel arguments in favor of the idea first suggested by Harris (1982) that (1) canFootnote 1 be derived from (2) by ellipsis. I propose a semantic theory of except that captures the meaning it contributes to a sentence and the restrictions on its use.
-
(1)
Every girl came except Eva.
-
(2)
Every girl came, except Eva did not come.
My arguments in favor of the idea that this exceptive construction can be clausal are based on the observation that except can host syntactic elements larger than DPs, such as PPs. In (3) the preposition makes a contribution to the overall meaning of the sentence, as the contrast between (3) and (4) shows.
-
(3)
I got no presents except from my mom.
-
(4)
#I got no presents except my mom.
The ellipsis story also naturally explains the cases originally observed by Moltmann (1995) where an except-phrase contains multiple elements, as in (5).
-
(5)
Every boy danced with every girl except Eva with Bill.
I will argue that the ellipsis site inside reduced except-clauses operating on positive universal statements in examples like (1) contains negation based on NPI-licensing inside such clauses.
There are exceptives introduced by other markers in English. Two representative examples are given in (6) and (7). In this paper I will not make any claims about except for and but. I will specifically focus on the exceptives introduced by except.
-
(6)
Every girl came except for Eva.
-
(7)
Every girl came but Eva.
English exceptives are relatively well studied and there is a significant amount of literature on this topic (Keenan and Stavi 1986; Hoeksema 1987, 1990, 1995; von Fintel 1993, 1994; Moltmann 1995; Lappin 1996; Peters and Westerståhl 2006; Gajewski 2008; García Álvarez 2008; Hirsch 2016; among others). It has been established in the existing literature that when exceptives operate on universal quantifiers, as in (1), (6), and (7), they come with the inferences illustrated in (8), (9), and (10) (Keenan and Stavi 1986; Hoeksema 1987; von Fintel 1993, 1994).
-
(8)
Domain Subtraction:
Every girl who is not Eva came.
-
(9)
Containment Entailment:
Eva is a girl.
-
(10)
Negative Entailment:
Eva did not come.
Another crucial observation about exceptives that goes back to Horn (1989) is that they are not compatible with existential quantifiers, as illustrated in (11), (12), (13). Following the existing literature (Gajewski 2008; Hirsch 2016), I will refer to the puzzle of explaining this fact as the ‘Distribution puzzle’.
-
(11)
*Some girls came except Eva.
-
(12)
*Some girls came but Eva.
-
(13)
*Some girls came except for Eva.
The existing semantic theories of exceptives are based on the assumption that elements that follow exceptive markers are DPs. Those DPs are interpreted as sets (Hoeksema 1987; von Fintel 1994; Gajewski 2008; Peters and Westerståhl 2006) or atomic or plural individuals (Hirsch 2016)—semantic objects that can directly restrict domains of quantifiers quantifying over individuals. The classic theory of exceptives was developed in von Fintel’s work (1993, 1994) for exceptives introduced by but, like the one in (7). According to this proposal, in (7) but subtracts the singleton set containing Eva from the set of girls. This accounts for the domain subtraction inference. The negative inference and the containment inference are captured by adding a claim that if the subtraction does not happen, the quantificational claim is not true: it is not true that every girl came. If it is true that every girl who is not Eva came and it is not true that every girl came, then Eva is a girl and she did not come. This idea also gives us a way of dealing with the distribution puzzle (the fact that example (12) is ungrammatical): existential claims, unlike universal claims, cannot be true for a smaller domain and false for a bigger domain. Thus, by providing an exceptive phrase with access to the domain of a quantifier, the classic theory captures the inferences exceptives come with and the restrictions on their use.
In this paper I argue that this analysis cannot be extended to exceptives introduced by except. If the complement of except in (1) contains (or at least can contain) a reduced clause, as I will argue, except must relate the two clauses in (14) and (15) semantically in such a way that the inferences in (8) and (9) are captured and the restriction observed in (11) is derived. A sentence denotes a proposition and it cannot be used to restrict the domain of a quantifier quantifying over individuals.
-
(14)
Every girl came.
-
(15)
Eva did not come.
One naturally occurring idea about how (14) and (15) can be related in the relevant way is that the exceptive clause is interpreted as some sort of a counterfactual conditional.Footnote 2 The idea would be, roughly, that the meaning of (1) (or at least a part of the meaning of (1)) can be expressed by the counterfactual conditional in (16), where the exceptive clause is a part of the antecedent.
-
(16)
If (15) were false, (14) would have been true.
There are certain similarities between the meaning of the sentence with except in (1) and the meaning of the counterfactual conditional in (16). Intuitively, the part of the meaning they share is this: the fact that Eva did not come is what stands in the way of the proposition denoted by Every girl came being true in the actual world.
However, there are important differences between (1) and (16) as well. First of all, (16) does not entail that Eva is a girl. Compare (16) with (17), where Eva is replaced by the male name John. The sentence in (17) could be true in a scenario where every girl for some reason does whatever John does or goes wherever he goes.
-
(17)
If John did not come were false, Every girl came would have been true.
Moreover, the sentence in (18), where every is substituted by some, is coherent. Thus, the counterfactual paraphrase does not have anything to say about the distribution of exceptives and the fact that they are not acceptable with existential quantifiers.
-
(18)
If Eva did not come were false, Some girl came would have been true.
In this paper I propose a novel analysis for clausal exceptives that is built on the idea that the meaning of the sentence with except in (1) involves looking at possible worlds or situations that differ from what actually happened only with respect to the facts about Eva coming. What this sentence says about those situations is that every girl came in them. On my account exceptive clauses introduce quantification over possible situations and provide the restriction for this quantification. This explains the similarities in meanings between sentences with exceptives and their counterfactual paraphrases. I will call this part of the meaning except contributes Conditional Domain Subtraction, because it is responsible for the domain subtraction inference. The negative inference is contributed directly by the clause inside the exceptive.
I propose that there is also another aspect of the meaning of exceptives—what I will call Conditional Leastness. This is the principle that establishes the law-like relation between the main clause containing a quantificational expression and the clause introduced by except. In our example, Conditional Leastness is the claim that in every situation where Eva did not come, the statement Every girl came is false. The role of this meaning component is threefold. It is responsible for the containment inference (in our example, this is the inference that Eva is a girl). It is also responsible for the fact that except is not compatible with existential quantifiers. Specifically, given some additional, independently motivated assumptions about indefinites, Conditional Leastness is guaranteed to contradict Conditional Domain Subtraction if the quantifier except operates on is existential. Thus, under the assumption that contradictions that cannot be repaired by replacing open-class lexical items are perceived as ungrammatical in natural languages (Gajewski 2002), the ungrammaticality of sentences like (11) is predicted. The third role of this meaning component is that it controls the ellipsis resolution in except-clauses and ensures that the ellipsis is resolved with the right polarity.
As will be shown, the analysis proposed here can account for the cases covered by the classic theory, but also for those cases left unexplained by it, such as examples involving prepositional phrases and multiple constituents, like (3) and (5). The additional benefit of the approach presented in this paper is that it correctly captures the contribution of modal operators such as possibly inside exceptive phrases. When possibly occurs inside an except-phrase, as in (19), it does not target the containment inference (Eva has to be a girl in (19), not ‘possibly’ a girl) or the domain subtraction inference (the sentence is true if every girl other than Eva actually came, the mere possibility of every other girl coming cannot make the sentence true): it only targets the negative inference ‘It is possible that Eva did not come’.Footnote 3 The approach I propose here is the first compositional treatment of such modal operators inside except-phrases.
-
(19)
Every girl came except, possibly, Eva.
The discussion in this paper will go as follows. Section 2 lays out the classic approach to the semantics of exceptives proposed by von Fintel (1993, 1994). In Sect. 3 I show that English exceptives introduced by except cannot be analyzed in those terms. I argue that sometimes what follows except can only be understood as a remnant of a clause. In Sect. 4 I present my analysis and show how it captures the inferences contributed by except and the restrictions on its use. In Sect. 5 I show how this analysis captures the cases with PPs and multiple remnants in except-phrases. Section 6 offers a modification of my analysis that captures the cases where except-phrases contain plural, disjunctive, and quantificational remnants. In Sect. 7 I show how this modified version of the analysis captures the interaction of except and possibly. Section 8 discusses some of the limitations of the proposed approach and directions for future work.
2 The classic approach to the semantics of exceptives
An approach to the semantics of exceptives that captures the inferences they contribute and the restrictions on their use was proposed by von Fintel (1993, 1994). I will introduce von Fintel’s system by using an example with a but-exceptive, because this is the construction this analysis was designed for.
-
(20)
Every girl but Eva and Mary came.
The sentence in (20) is true only if every girl who is not Eva or Mary came. However, as von Fintel observes, it is not enough to simply subtract the set {Eva, Mary} from the domain of every girl. This does not capture the inferences that Eva and Mary are girls and that they did not come. It also does not account for the fact that (21) is not a well-formed sentence. Subtracting a set from the domain of the existential quantifier in (21) would make the sentence more informative: an existential is more informative on a smaller domain. However, but is not compatible with some.
-
(21)
*Some girl but Eva and Mary came.
According to this theory, the contribution of an exceptive is twofold. An exceptive subtracts a set from the domain of a quantifier and states that this is the minimal set that has to be subtracted in order for the quantificational claim to be true. The last claim is known in the literature as the Leastness Condition (after Gajewski 2008:75). The Leastness Condition derives both the containment entailment and the negative entailment and explains the distribution puzzle in a straightforward way. Specifically, in (20) Leastness is the claim that if either Eva or Mary are not removed from the set of girls, the universal quantificational claim is false. Since the subtraction of this set is necessary for the quantificational claim to be true, Mary and Eva have to be girls and have to be among the people who did not come.
Formally, those ideas can be implemented under the assumption that the but-phrase forms a constituent with girls as shown in (22).
-
(22)
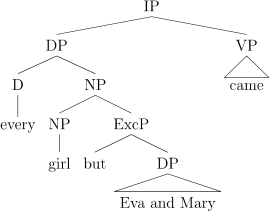
But has the semantics given in (23) below. It combines with its own sister (the set denoted by the DP immediately following it), then with a set in the restrictor of the determiner, then with the determiner and with the scopal argument of the quantificational DP. It introduces two claims (the two conjuncts in (23)). The first conjunct in (23) is the quantificational claim, where the set denoted by the sister of but is subtracted from the domain of the quantifier. The second conjunct is the Leastness Condition. It quantifies over sets. It states that if a set that does not fully contain the set denoted by the sister of but is subtracted from the domain of the quantifier, the resulting quantificational claim is not true.
-
(23)
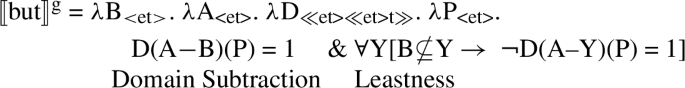
The result of interpreting the structure in (22) is given in (24). The first conjunct in (24) is the domain subtraction: this is a universal quantificational claim made on a domain that excludes Eva and Mary. The second conjunct is the Leastness Condition. An equivalent formulation of it is given in (25).
-
(24)
\([\!\![(22)]\!\!]^{\mathrm{g}}\) = 1 iff ∀x[(x is a girl & x∉{Eva, Mary}) → x came] & ∀Y[{Eva, Mary}⊈Y → ¬∀x[(x is a girl & x∉Y) → x came]]
-
(25)
∀Y[{Eva, Mary}⊈Y → ∃x[x is a girl & x∉Y & ¬ x came]]
The quantification over sets in (25) is universal. Let’s consider the set that contains every girl other than Eva. It satisfies the restrictor of the quantification over sets in (25), thus there is a girl not belonging to this set who did not come. This can only be Eva. Let’s also consider the set that contains every girl other than Mary. According to (25), there is a girl not belonging to this set who did not come. That can only be Mary. Thus, in this system, the negative entailment (the inference that Eva and Mary did not come) and the containment entailment (the inference that Eva and Mary are girls) follow from the Leastness Condition.
Von Fintel’s proposal about the meaning of but provides a unified semantic treatment for cases where but applies to universal quantifiers and for cases where it applies to negative quantifiers. The meaning predicted for the example with a negative quantifier in (26) is given in (27). Because of the second conjunct, (27) correctly captures the fact that this sentence comes with the inference that both Eva and Mary are girls who came. Let’s again consider the same two sets: the one that contains every girl who is not Eva and the one that contains every girl who is not Mary. For each of them the second conjunct in (27) requires that there is a girl who is not in this set who came. Those girls can only be Eva and Mary.
-
(26)
No girl but Eva and Mary came.
-
(27)
\([\!\![(26)]\!\!]^{\mathrm{g}}\) = 1 iff ¬∃x[(x is a girl & x∉{Eva, Mary}) & x came] & ∀Y[{Eva, Mary}⊈Y → ∃x[(x is a girl & x∉Y) & x came]]
As was noted earlier, the solution to the distribution puzzle is also in the Leastness Condition. Under the assumptions about the meaning of but that we made in (23), (21) will get the meaning given in (28).
-
(28)
\([\!\![(21)]\!\!]^{\mathrm{g}}\) =1 iff ∃x[x is a girl & x∉{Eva, Mary}& x came] & ∀Y[{Eva, Mary}⊈Y →¬∃x[x is a girl & x∉Y& x came]]
There is no model where the truth-conditions given in (28) can be satisfied. The second conjunct in (28) is Leastness. Let’s consider the empty set ∅. Since ∅ does not contain Eva or Mary, Leastness requires that (29) holds: there is no girl in the universe who came. This contradicts the first conjunct in (28) (the domain subtraction): it cannot be simultaneously true that there is a girl who is not Eva or Mary who came and that there is no girl who came at all.
-
(29)
¬∃x[x is a girl & x∉∅ & x came]
A contradiction of this kind is predicted to always arise if but is used with an existential quantifier. Consequently, under the assumption that L-analytic sentences (i.e., sentences that are contradictory or tautological due to the combination of the functional elements in them) are perceived as ungrammatical in natural languages (Gajewski 2002), this approach correctly captures the fact that (21) is ungrammatical in English.
In the next section I will argue that there are exceptive constructions that cannot be analyzed in this way.
3 Exceptive deletion exists
In the recent literature it has been observed that there are exceptive constructions where what follows an exceptive marker is a clause and not a DP. Pérez-Jiménez and Moreno-Quibén (2012) argue that Spanish exceptives can host remnants of a clausal structure. Potsdam and Polinsky (2017) argue that clausal exceptives exist in Tahitian. Soltan (2016) makes the same point about Egyptian Arabic, Potsdam (2018) about Malagasy.
In this paper, I argue that English except belongs to the same class of clausal constructions. I will start by reviewing existing arguments in favor of the idea that English except can introduce clauses. Then I will introduce novel arguments against the idea that what follows except is interpreted as a set of individuals and in favor of the idea that except can host reduced clauses.
3.1 Moltmann (1995): Except can host multiple remnants
Moltmann (1995) observes that English except can contain several constituents of different syntactic types as shown in (30).
-
(30)
Every girl danced with every boy everywhere except Eva with Bill in the kitchen.
The sentence in (30) means that Eva did not dance with Bill in the kitchen, but every pair consisting of a girl and a boy other than Eva and Bill danced in every place, even Eva and Bill danced with each other in every place other than the kitchen.
Moltmann further observes that such cases cannot be accounted for within the classic theory. One idea that we can immediately reject is that in cases like (30), an exceptive introduces several sets ({Eva}, {Bill}, {the kitchen}), these are somehow subtracted from the domains of the relevant quantifiers, and the Leastness Condition is imposed on each of the subtractions. This approach would predict that (31) and (32) below should have equivalent meanings. However, that is not the case, as was noticed by Moltmann. (31) can be true if Eva danced with Bill: this sentence says that Eva is the only exception to the generalization ‘All girls danced with all boys other than Bill and did not dance with Bill’. One way for Eva of being an exception to this generalization is to dance with Bill. (32) cannot be true in this scenario: it requires that Eva and Bill did not dance together, it states that Eva not dancing with Bill is the only thing that stands in the way of Every girl danced with every boy being true.
-
(31)
Every girl except Eva danced with every boy except Bill.
-
(32)
Every girl danced with every boy except Eva with Bill.
Moltmann (1995) argues that except introduces a clause in examples like (30), but she proposes that this is a small clause that does not denote a proposition. Instead, she suggests that in this case the clause is interpreted as a set of tuples ({< Eva, Bill, the kitchen>}). She develops a system where an exceptive operating on a universal generalized quantifier subtracts a set from every set in the denotation of this quantifier, which in this case is the polyadic quantifier formed from every girl, every boy, everywhere.
I will illustrate the work of Moltmann’s system with a simpler example (33). In set talkFootnote 4every girl denotes the set of sets of individuals containing every girl. Let’s assume that this is the set shown in (34). In (33), except subtracts {Eva, Mary} from every set in the denotation of every girl. Thus, every girl except Eva and Mary denotes the set of sets shown in (35). Then (33) is true if and only if the set came denotes is one of those sets. This accounts for the domain subtraction inference and for the negative inference: every girl who is not Eva or Mary came, and Eva and Mary did not come (they are not in the set denoted by came).
-
(33)
Every girl except Eva and Mary came.
-
(34)
〚every girl\(]\!\!]^{\mathrm{g}}\) = {{Anna, Sveta, Mary, Eva}, {Anna, Sveta, Mary, Eva, John}, {Anna, Sveta, Mary, Eva, Bill}, {Anna, Sveta, Mary, Eva, John, Bill}}
-
(35)
〚every girl except Eva and Mary\(]\!\!]^{\mathrm{g}}\) = {{Anna, Sveta}, {Anna, Sveta, John}, {Anna, Sveta, Bill}, {Anna, Sveta, John, Bill}}
In order to account for the containment inference and for the restrictions on the use of exceptives, Moltmann proposes that an exceptive also contributes the so-called Homogeneity Condition. This condition is added as a condition of definedness: except can apply only if the set introduced by it is in every set in the denotation of the quantifier. This can only hold if the quantifier is universal and every element of this set is in the restrictor set. In this case, the condition holds, because both Eva and Mary are in every set in (34). The Homogeneity Condition is not met in (36), which explains why it is not well-formed. Some girl denotes the set of sets that have at least one girl in them. This set contains, for example, the singleton sets {Eva} and {Mary}. Thus, not every set will have both Eva and Mary in it.Footnote 5
-
(36)
*Some girl except Eva and Mary came.
Those ideas are implemented in the denotation of except given in (37) below. This is a function that first composes with a set (denoted by the expression following except), then with a generalized quantifier, and then with a set of individuals (denoted by the main predicate). It returns Truth if and only if this last set can be derived from one of the sets in the denotation of the quantifier by subtracting from it the set introduced by except. The Homogeneity Condition is implemented as a presupposition. This approach differs from von Fintel’s approach in that containment is treated as a presupposition and the meaning component responsible for the negative inference is separated from it. The negative inference and the domain subtraction inference are contributed at the assertive level, both by the same meaning component.
-
(37)
\([\!\![\mathrm{except}]\!\!]^{\mathrm{g}}\) = λC<et>.λQ≪et>t>.λP<et>: ∀Z[Z∈Q → C⊆Z]. ∃Y[Y∈Q & P=Y-C]
One obvious problem with this denotation is that it is not applicable in cases with negative quantifiers, such as (38) below. The denotation of no girl is the set of sets that do not have any girls in it, as shown in (39). Removing Eva and Mary from each of these sets is not useful here. What we want to do is to add Eva and Mary to every set in (39) and state that came is one of those sets. The condition of definedness has to be formulated differently as well: the intersection of {Eva, Mary} with each of the sets in the denotation of the quantifier has to be empty. This is implemented in the denotation of except’ in (38): an exceptive in Moltmann’s system has to have two different lexical entries; in each individual case only one of the two possible denotations can result in a defined meaning because they carry different presuppositions. This ambiguity is a disadvantage of this approach.
-
(38)
No girl except Eva and Mary came.
-
(39)
〚no girl\(]\!\!]^{\mathrm{g}}\) ={∅, {John}, {Bill}, {John, Bill}}
-
(40)
〚except’\(]\!\!]^{\mathrm{g}}\) = λC<et>.λQ≪et>t>.λP<et>: ∀Z[Z∈Q → C∩Z=∅]. ∃Y[Y∈Q & P=Y∪C]
Moltmann shows how an extended version of her analysis can cover cases where the DP inside an except-phrase is quantificational, as in (41), but for reasons of space I will not discuss her analysis of such cases here.
-
(41)
Every boy except one/exactlyFootnote 6 three came.
In her system, in cases with multiple remnants like (30), the quantificational correlates of the items in an exceptive phrase form a constituent and are interpreted as quantifiers over tuples—in this specific case, over triples the first element of which is a girl, the second a boy, and the third a place. Except introduces a set of tuples ({<Eva, Bill, the kitchen>}) and basically does the same thing as in the simpler case considered above: it removes this set from every set in the denotation of the generalized quantifier and adds the Homogeneity Condition. Moltmann makes an important observation about exceptives with multiple remnants: each element inside an exceptive phrase has to have a universal quantifier as the correlate in the main clause (as shown by the ungrammatical (42) and (43)). In her system this fact is captured because the two quantificational DPs form one constituent and the resulting quantificational item must satisfy the Homogeneity Condition. Any alternative theory of except must also explain the facts in (42) and (43).
-
(42)
*Every girl danced with some boy except Eva with Bill.
-
(43)
*Some girl danced with every boy except Eva with Bill.
The observation that except can host multiple elements is an important argument in favor of the clausal syntactic theory of exceptives. However, Moltmann’s attempt to analyze clausal exceptives as introducing sets of tuples runs into a problem. Pérez-Jiménez and Moreno-Quibén (2012) point out that this proposal does not explain why with and in cannot be omitted in (30) as shown in (44).
-
(44)
*Every girl danced with every boy everywhere, except Eva Bill the kitchen.
In the next section I will show that there are cases that are problematic for any theory that treats the element following except as a set of individuals, independently of whether this set is subtracted from the domain of a quantifier or from every set in the denotation of a generalized quantifier.
3.2 English except does not introduce a set of individuals
My novel challenge to the idea that except introduces a set of individuals is based on the observation that an exceptive introduced by except can host a PP with a meaningful preposition. One such example is given in (45). It is generally assumed that PPs denote functions from individuals to truth values or, in set talk, sets of individuals. From Barcelona denotes the set of things that are from Barcelona, the set given in (46).
-
(45)
I met a student from every city in Spain except from Barcelona.
-
(46)
{x: x is from Barcelona}
Subtraction of this set from the set of cities, as required if we try to extend von Fintel’s theory of but-exceptives to except, cannot restrict the domain of the quantifier in the relevant way here, because things that are from Barcelona are not cities. Subtracting things that are from Barcelona from a set of cities in Spain is equivalent to the set of cities in Spain, as shown in (47).
-
(47)
{x: x is a city in Spain} – {x: x is from Barcelona} = {x: x is a city in Spain}
Moreover, we cannot apply the Leastness Condition to get the inferences that Barcelona is a city in Spain and that I did not meet a student from Barcelona. The Leastness Condition predicted in this case is as shown in (48) below. One of the sets satisfying the restrictor of the quantification over sets in (48) is the empty set ∅. Thus, given (48), (49) has to be true. (49) directly contradicts the quantificational claim with domain subtraction in (50). We cannot also say that except directly states that Barcelona belongs to the set of cities in Spain because except does not have access to the constituent that refers to Barcelona.
-
(48)
∀Y[{z: z is from Barcelona} ⊈ Y →¬∀x[(x is a city in Spain & x∉Y) → ∃y[y is a student from x & I met y]]]
-
(49)
¬∀x[(x is a city in Spain & x∉∅) → ∃y[y is a student from x & I met y]]
-
(50)
∀x[(x is a city in Spain & x is not from Barcelona) →∃y[y is a student from x & I met y]]
Those inferences are however still present in (45). The containment inference is tested in (51). This sentence is infelicitous because New York is not a city in Spain. The negative inference is tested in (52): due to the fact that except contributes the negative inference here, the claim with except cannot be conjoined with the claim that contradicts that inference.
-
(51)
#I met a student from every city in Spain except from New York.
-
(52)
#I met a student from Barcelona and I met a student from every city in Spain except from Barcelona.
Moltmann’s (1995) analysis runs into the same problem with this example. The Homogeneity Condition says that except can only apply if every element of the set introduced by except (the set of things that are from Barcelona) is contained in each of the sets in the denotation of the quantifier every city in Spain. The smallest set in this set of sets contains all cities in Spain and nothing else. Since things that are from Barcelona are not cities, they will not be in this set. Thus, the theory incorrectly predicts that except cannot apply in this case or that the sentence should come with the presupposition that every object from Barcelona is a city in Spain.
Another case challenging the classic phrasal syntactic analysis of exceptives is the one where an exceptive phrase contains a prepositional phrase that has no correlate (i.e., no corresponding antecedent) in the main clause. The example is given in (53) (this example is based on a structurally similar example from Spanish discussed in Pérez-Jiménez and Moreno-Quibén 2012),Footnote 7 but the argument I develop here is a new one). The contrast between (53) and (54), where the PP is substituted by a DP, tells us that the preposition from makes an important contribution to the overall meaning of the sentence.
-
(53)
I got no presents except from my mom.
-
(54)
#I got no presents except my mom.
Note that in English from my mom cannot be derived by ellipsis from the one from my mom. This is because the one is not a phrase that can be deleted in English, as shown by the contrast between (55) and (56).
-
(55)
I got two presents. The one from my mom was nice.
-
(56)
I got two presents. *From my mom was nice.
Here we could try to take the set of things that are from my mom and subtract it from the set of presents, as shown in (57). This move allows us to restrict the quantification to those presents that are not things from my mom, as shown in (58).
-
(57)
{y: y is a present} − {x: x is from my mom} = {z: z is a present & z is not from my mom}
-
(58)
¬∃x[x is a present & x is not from my mom & I got x]
However, extending the analysis von Fintel proposed for but to this case with except would also require adding the second claim: the Leastness Condition. Leastness in this case would the claim in (59): any set such that its subtraction from the domain of the quantifier makes the quantificational claim true contains the set of things from my mom as its subset.
-
(59)
∀Y[¬∃x[x is a present & x∉Y & I got x]→{x: x is from my mom} ⊆ Y]
This claim is equivalent to (60). The proof for that is given in (61).Footnote 8
-
(60)
∀x[x is from my mom → x is a present & I got x]
-
(61)
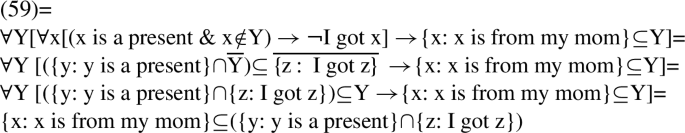
This amounts to the following claim: every object that is from my mom is a present such that I got it. The sentence in (53) does not come with this inference. It does not require that my mom gives all things only to me or that all the objects that are from my mom are gifts. Thus, this example cannot be accounted for in terms of the classic analysis.
Moltmann’s (1995) analysis runs into a similar problem with (53). Because of the Homogeneity Condition this sentence is predicted to come with the presupposition that every object that is from my mom is a present. The sentence is predicted to be true if and only if I did not get any present that is not from my mom and, crucially, I got every item that is from my mom. This is the same problematic meaning we saw above.
In this section I have considered cases where an except-phrase contains a PP that cannot be interpreted as a set of individuals restricting the domain of a quantifier. A natural alternative idea about such cases is that the PP is part of a clausal structure. There are two ways of developing this idea: (i) an exceptive containing a PP forms a conjunction-like structure with a quantificational DP and shares verbal material with it;Footnote 9 or (ii) an except-phrase contains a whole clause in it, part of which is elided. The first idea, however, is not extendable to cases with multiple syntactic elements inside an except-phrase discussed by Moltmann (1995). Cases like (30) present a challenge for this kind of approach because the three items in the except-phrase do not form one syntactic constituent (as was observed by Pérez-Jiménez and Moreno-Quibén (2012)); thus there is no available constituent that except can syntactically conjoin with a corresponding constituent in the main clause. The example in (53), where the PP does not have a corresponding element in the main clause, is also problematic for this approach, as it is not clear what this PP would be conjoined with.
In the next section I will show that in some cases the unpronounced part of an except-clause contains more material in it than the main clause of the sentence. This is an additional argument in favor of the idea that the structures of the examples I have discussed in this section are derived by ellipsis rather than via some process that results in a partially shared structure between the except-clause and the main clause.
3.3 Evidence for the polarity mismatch
In the Introduction, I suggested that (1) (repeated here as (62)) can be derived from (2) (repeated here as (63)) by ellipsis.
-
(62)
Every girl came except Eva.
-
(63)
Every girl came, except Eva did not come.
A reader can observe the polarity mismatch in (63) between the main clause and the except-clause: there is negation in the except-clause that is not present in the main clause.Footnote 10
One fact supporting the idea that ellipsis should be resolved with a polarity mismatch in this case is that many English speakersFootnote 11 find the non-elided version of (62) given in (63) acceptable. None of them accept (64), where the except-clause is positive.
-
(64)
#Every girl came, except Eva came.
Now, let’s look at the interaction of except with a negative quantifier. I propose that (65) can be derived from (66) by ellipsis. Some speakers of English find (66) acceptable. No English speaker accepts (67) where the polarity of the except-clause is negative.
-
(65)
No girl came except Eva.
-
(66)
No girl came, except Eva came.
-
(67)
#No girl came, except Eva did not come.
If a reduced except-clause operating on a universal quantifier has negation in it and a reduced except-clause operating on a negative quantifier does not, the prediction is that we should see differences between those two cases with respect to licensing of negative polarity items (NPIs). It is generally assumed (starting with Fauconnier 1975, 1978 and Ladusaw 1979) that NPIs are licensed in a downward entailing (DE) environment. It is also a well-established fact that an NPI can be licensed within a clause locally even if in the context of the entire sentence it is not in a DE environment. For instance, in (68) the global position of the NPI any vegetables in the sentence is not in a DE environment. This is because there are two negations in (68) and they cancel each other out. However, the NPI is licensed inside the syntactic constituent in brackets, which is a DE environment.
-
(68)
It’s not true that [John did not eat any vegetables].
In a similar way, if what I said about how exceptive deletion is resolved is correct, NPIs are predicted to be licensed inside reduced except-clauses providing exceptions to universal quantifiers, but not inside reduced except-clauses providing exceptions to negative quantifiers, because only in the first case is there a constituent—the sentence following except—that is a downward entailing environment because it contains negation.
This prediction is borne out, as the contrast between (69) and (70) shows. This observation does not receive discussion in existing analyses of exceptives.Footnote 12
-
(69)
John danced with everyone except with any girl from his class.
-
(70)
*John danced with no one except with any girl from his class.
On my account the contrast between (69) and (70) follows from the way the ellipsis is resolved in the two cases (shown in (71) and (72)). There is a constituent, namely the one in brackets, that is a DE environment for any girl in (71), but not in (72).
-
(71)
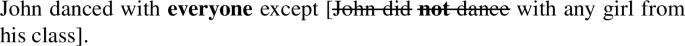
-
(72)
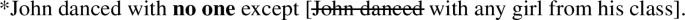
Crucially, if we consider the entire sentence (69), the NPI is not in a DE environment. Compare (73) and (74) below: the claim with the larger exception in (73) does not grant the inference that the claim with the smaller exception in (74) is true. The problem is that in (73) every quantifies over the domain that is smaller than the domain of every in (74) and every is not upward entailing on its domain.
-
(73)
John danced with everyone except with girls from his class.
-
(74)
John danced with everyone except with blond girls from his class.
Let’s consider a situation where there is a certain girl with dark hair in John’s class, say, Zahra. The claim in (74) can be true only if John danced with Zahra (he danced with everyone who is not a blond girl in his class). This is not something that follows from (73), since (73) does not impose this requirement (John danced with everyone who is not a girl in his class).
It has been argued by von Fintel (1999) that an NPI can be licensed in the scope of a Strawson DE operator. Thus, we need to establish that the NPI is not in a Strawson DE environment globally in (69) in order for the argument presented here to go through.
This notion was introduced in order to account for the NPI licensing in sentences like (75).
-
(75)
Only John ate any vegetables.
Any vegetables is not in a DE environment in (75): (76) does not entail (77). The problem is that (77) requires that John ate cucumbers, which is not something that follows from (76).
-
(76)
Only John ate vegetables.
-
(77)
Only John ate cucumbers.
However, the inference that John ate cucumbers is generally treated as a presupposition introduced by only in (77) and not as a part of its truth-conditional content (Horn 1992, 1996; Atlas 1993). The assertive content of (76) entails the assertive content of (77): from the fact that no one who is not John ate vegetables we can conclude that no one who is not John ate cucumbers. If we limit ourselves to only considering the situations where John ate cucumbers, (76) entails (77). This idea is captured by the notion of Strawson-Entailment: a sentence A Strawson-entails another sentence B if A entails B under the assumption that the presuppositions of B are satisfied. The formal definition of Strawson Downward Entailingness is given in (78).
-
(78)
Strawson Downward Entailingness (von Fintel 1999):
A function f of type <σ,τ> is Strawson-DE iff for all x,y of type σ such that x⇒y and f(x) is defined: f(y)⇒f(x)
Only is a Strawson DE operator, consequently, (76) Strawson-entails (77), which is responsible for the fact that any vegetables is licensed in (75).
However, there is no similar Strawson-entailment pattern between (73) and (74). If the quantificational claim (that John danced with everyone who is not a girl from his class) were contributed at the presuppositional level and the only assertive contribution of except were that John did not dance with any girl from his class, then we could say that (73) Strawson-entails (74): the claim that John did not dance with girls from his class entails that John did not dance with blond girls from his class. The quantificational claim, however, is not contributed at the presuppositional level. To show this, I will use the classic question test and the ‘Hey, wait a minute’ test (von Fintel 2004). The question in (79), when pronounced with neutral intonation, is understood as a question about whether John danced with everyone who is not a girl from his class.
-
(79)
Did John dance with everyone except with girls from his class?
The ‘Hey, wait a minute’ test points in the same direction. The dialog in (80) is not felicitous because the information about John dancing with everyone (with the appropriate restriction) is not contributed at the presuppositional level.
-
(80)
-
A:
John danced with everyone except with girls from his class.
-
B:
#Hey, wait a minute, I did not know John danced with everyone who is not a girl from his class.
-
A:
To conclude, the NPI in (69) is not in a downward or Strawson downward entailing environment globally. This means that the NPI has to be licensed locally.
The fact that any is not licensed inside the except-phrase in the example with the negative quantifier in (70) is expected if ellipsis has to be resolved positively. This is because the NPI is not predicted to be in a DE or Strawson DE environment globally: (81) does not entail (82). Again, if there is a dark-haired girl in John’s class, (82) can only be true if he did not dance with her. This is not something given in (81), which can be true if he did dance with her. The problem in (82) is again with the quantificational claim and its domain that gets larger in (82). The local licensing is also unavailable as ‘John danced with girls from his class’ does not entail ‘John danced with blond girls from his class’. The reasons why ellipsis has to be resolved positively in this case are discussed in Sect. 4.4.
-
(81)
John danced with no one except with girls from his class.
-
(82)
John danced with no one except with blond girls from his class.
In the semantic theory of clausal exceptives that I propose (Sect. 4), the polarity of the clause following except is restricted by the meaning of except. Ellipsis can be resolved positively or negatively in each case. However, choosing a clause with the wrong polarity leads to a meaning that is not well-formed.
If this discussion is on the right track, exceptive deletion should allow for a polarity mismatch between the antecedent and the ellipsis site. Polarity mismatches of this kind have been reported to be possible in sluicing (Kroll 2018, 2019; Rudin 2019), as shown in (83).
-
(83)
Either turn in your final paper by midnight or explain why
you didn’t turn it in by midnight. (Rudin 2019, citing an unpublished 2016 version of Kroll 2018.)
As Rudin (2019) points out, not all English speakers find this example acceptable. Examples with except, like the one in (62) (repeated below as (84)), are generally accepted by native speakers.
-
(84)
Every girl came except Eva.
I believe that what is going on in (84) is more similar to the Russian case in (85). In (85) there is a polarity mismatch between the positive antecedent and the negative elided clause. The remnant of ellipsis in (85) contains an n-word. N-words in Russian require the presence of a clause-mate negation, as the contrast between the two versions of (86) shows (see Brown 1999; Pereltsvaig 2002; among others). Somehow the presence of an n-word licenses ellipsis of a constituent containing negation. I propose that, in a similar way, the presence of except licenses ellipsis of a constituent containing negation in exceptive deletion.Footnote 13
-
(85)

-
(86)

3.4 Not just a conjunction of two clauses
The simplest hypothesis about the meaning of clausal exceptives is that the clause introduced by an exceptive and the clause containing a quantifier are simply coordinated. The idea would be that (87) is structurally similar to (88) and has the same meaning.
-
(87)
I danced with everyone except with John.
-
(88)
I danced with everyone, but I did not dance with John.
Under this hypothesis, the negative entailment is explained directly, because it is simply the contribution of the exceptive clause. It is standardly assumed that a quantifier comes with a covert domain restriction variable.Footnote 14 The sentence in (88) is not perceived as contradictory because there is a possible value for the covert domain restriction variable everyone comes with that does not include John. The same reasoning can apply to (87). This accounts for the domain subtraction inference.
The more challenging problem is the distribution puzzle. Under the assumption that an exceptive clause and a main clause are simply coordinated in clausal exceptives, one can try to explain the badness of except with some by saying that except obligatorily introduces a silent only. Thus the badness of (90) would essentially follow from the unacceptability of (89), which must be due to the pragmatic oddness of putting together the two claims: that Alex is the only person who did not help and that some people helped.
-
(89)
#Some of my friends came to help, only not Alex.
-
(90)
#Some of my friends came to help, except Alex.
One problem is that such an analysis does not explain why a sentence with except has to have a quantifier in the first place. Sentence (91), where the DP Ann is associated with only, is acceptable. However, (92) is clearly not well-formed.
-
(91)
I will talk to Mary and Ivy, only not to Ann.
-
(92)
*I will talk to Mary and Ivy except to Ann.
A more challenging problem for this idea is the containment entailment. There is a contrast between the well-formed example with only in (93) and the infelicitous example with except in (94). Example (94) is infelicitous because except requires Peter to be one of my girlfriends.
-
(93)
None of my girlfriends helped me, only Peter, who is a complete stranger (did).
-
(94)
#None of my girlfriends helped me, except Peter, who is a complete stranger.
In a similar way, (95) is well-formed because there is no containment inference here, whereas (96) requires that your computer is a textbook or a note and this is why this sentence is infelicitous.
-
(95)
You can use any textbooks or notes, only not your computer.
-
(96)
#You can use any textbooks or notes except your computer.
We can conclude from this discussion that the simple coordination analysis cannot work for exceptives because it does not capture some of their most basic properties.
4 The proposal
In this section I propose a semantic analysis for clausal exceptives introduced by except. I show how this analysis captures the facts that the classic analysis of exceptives captures, such as the inferences that exceptives come with and the restrictions on their use. The semantic theory I develop also explains why an except-clause providing an exception for a positive universal claim has to have negation in it and an except-clause providing an exception to a negative claim cannot have negation in it.
Speaking informally, I propose that the except-clause in (97) contributes three things. It states that what follows except is true: (98). This captures the negative inference. It also establishes a law-like relationship between the clause following except and the main clause: (99). They are not just two random propositions accidentally put together: because Eva did not come, it is not true that every girl came. This aspect of the meaning captures the containment inference. The third contribution of except is that nothing else stands in the way of the quantificational claim being true, as per (100). This captures the domain subtraction inference.
-
(97)
Every girl came except Eva
did not come.
-
(98)
Eva did not come.
-
(99)
In every situation where Eva did not come, the quantificational claim is not true.
-
(100)
Had Eva come while everything else remained the same, it would have been true that every girl came.
4.1 Modeling negative entailment and containment
In this work I will use situations rather than possible worlds because situations can also be restrictors for the domain of quantification (Kratzer 2007/2019; Schwarz 2009, 2012). I will assume a possibilistic situation semantics, where situations are viewed as parts of possible worlds (Kratzer 1989). However, nothing proposed here requires the use of situations as opposed to possible worlds; these ideas can be implemented in a possible world system.
Let’s assume that s0 is the actual topic situation—the situation with respect to which the entire claim is evaluated. Given the assumptions about the underlying syntactic structure of the elided except-clause in (97) I made here, we do not need to do any work to capture the inference that Eva did not come. This information is provided directly by the clause following except. The contribution of except that is responsible for the negative inference in (97) is as shown in (101).
-
(101)
¬Eva came in s0
In von Fintel’s system the negative and the containment entailments came from the Leastness Condition—the claim that if at least one of the individuals introduced by an exceptive is not subtracted from the domain of the given quantifier, the quantificational claim is not true. In order to capture the containment inference in the conditional system, we can implement a similar idea. We can say that in all possible situations where the fact about Eva not coming remains the same, the quantificational claim is not true. The formula in (102) captures this idea. As the reader can verify, (102) is equivalent to (103).
-
(102)
∀s[¬Eva came in s → ¬∀x[x is a girl in
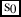 → x came in s]]
→ x came in s]]
-
(103)
∀s[¬Eva came in s→ ∃x[x is a girl in
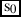 & ¬x came in s]]
& ¬x came in s]]
One crucial fact about (103) is that the extension of the predicate denoted by girl is fixed. It is evaluated with respect to the actual topic situation s0 and does not vary across possible situations (the relevant situation variable is boxed in (102) and (103)). In allowing the predicate inside the DP every girl to be evaluated with respect to a different situation than the predicate came inside the VP of the main clause I follow much of the literature (Fodor 1970; Enç 1986; Cresswell 1990; Percus 2000; Kratzer 2007/2019; Keshet 2008; Schwarz 2009, 2012).
According to (103), in every situation where Eva did not come, there is a girl of s0 who did not come. This can only hold if Eva is a girl in the topic situation. This is because there is only one way in which Eva’s not coming can guarantee that there is a girl of s0 who did not come in all possible situations: Eva is that girl who did not come.
Let’s consider a situation where Eva is not a girl in s0. (103) is not compatible with this scenario. This is because the quantification over situations in (103) is not restricted to the situations that are most similar to the actual topic situation—the quantification is simply over every possible situation where Eva did not come. Consequently, (103) is not compatible with a scenario where Eva is not a girl in s0 but, say, has a daughter who is a girl and who goes everywhere where Eva goes in s0. In this scenario, in all situations that are most similar to s0 among the ones where Eva did not come, there is a girl of s0 who did not come. However, not in every situation where Eva did not come is there a girl of s0 who did not come. This is because there is a possible situation where Eva, who is not a girl in s0, did not come, but every girl of s0 came.
I will call this claim Conditional Leastness because it plays a role similar to the role of Leastness in von Fintel’s system. Conditional Leastness is a part of the meaning contributed by an exceptive that is responsible for the containment inference. As I will show later, this meaning component also provides the solution for the distribution puzzle and is responsible for the ellipsis resolution.
I will take Conditional Leastness to be a presuppositional component of a sentence with except. Applying the classic negation test shows that this is on the right track: (104) still requires that Eva is a girl.
-
(104)
It is not true that every girl came except Eva.
A more difficult question is whether the negative inference (that Eva did not come) has to be a part of the presuppositional or the assertive content. I will assume here that this meaning component is also contributed at the presuppositional level. The reason for this is that a sentence that expresses the negative inference of a sentence with except and the sentence with except can be a part of the same discourse, as shown in (105). If at the level of meaning the negative claim was conjoined with the quantificational claim with domain subtraction, (105) would have been as bad as (106).
-
(105)
Eva did not come. Every girl came except Eva.
-
(106)
#Eva did not come. Every girl who is not Eva came and Eva did not come.
With this in mind, we can say that the sentence in (97) has a defined meaning in s0 only if (101) and (102) hold, thus capturing the negative inference and the containment inference.
4.2 Modeling domain subtraction
In this section I show how domain subtraction can be expressed in terms of quantification over possible situations. Since the quantificational claim in the main clause of (97) (every girl came) is not true in s0, I propose that we do modal displacement and evaluate it in a different possible situation. The intuition that I would like to capture here is that there is a similarity between the meaning of the example with except in (97) which we have considered so far and the conditional sentence in (107).
-
(107)
If it were not true that Eva did not come, it would have been true that every girl came.
It is standardly assumed that conditionals are interpreted as restrictors of covert or overt quantifiers over possible worlds or situations (starting from (Lewis 1975; Kratzer 1978, 1986)). It is also standardly assumed that natural language quantifiers over possible words or situations are restricted to those words or situations that minimally differ from the actual world (Stalnaker 1968; Lewis 1973a, 1973b, 1981; Kratzer 1977, 1979, 1981a, 1981b, 1989). The conditional in (107) roughly gets the truth-conditions in (108).
-
(108)
In all of the possible situations that are most similar to the actual topic situation among those where Eva came it holds that every girl came.
When we try to express the meaning of exceptives in terms of quantification over possible situations, one problem we face is how to capture the relevant notion of similarity between them. Specifically, the sentence in (107) can be true if no girl actually came at all. Let’s consider a scenario where the actual topic situation is such that Eva is the leader of all girls and they do whatever she does. In this case in the situations where Eva came that are the most similar to the actual topic situation, Eva’s coming would make every girl come, because this is what they usually do in the actual topic situation. Thus, if the actual world is such that changing Eva’s behavior can guarantee that other girls change their behavior, the sentence in (107) can be true, even if in real life it is not true that, not counting Eva, every girl came.
Our intuitions are different for the sentence with an exceptive in (97). This sentence cannot be true in the scenario described above: (97) can only be true in the actual topic situation if every girl other than Eva came. This means that exceptive constructions are less flexible than their conditional paraphrases with respect to the notion of similarity between situations. When we interpret (97), we only look at possible situations where the facts about other people coming are exactly the same as in the actual topic situation. The difference between the exceptive in (97) and the counterfactual in (107) is that in the latter case we could also look at situations where facts about other girls coming changed.
The question is how to derive the information about other individuals coming, given that the exceptive clause that is supposed to characterize the restriction on possible situations is simply Eva did not come. One fact we could use here is that according to standard assumptions about ellipsis (starting at least from Rooth 1992b), the remnant of an elided clause is marked with focus. Thus, in (97) we have access not only to the proposition denoted by Eva did not come, but also to its focus alternatives formed by replacing the focused element (namely, Eva) with other possible elements of the same semantic type (Rooth 1985, 1992a). The focus value of the sentence \(\mathit{Eva}_{F}\) did not come is given in (109) (the superscript F on the interpretation function means that the focus value is computed).
-
(109)
〚EvaF did not come〛gF = {p: ∃x[p = λs’.¬ x came in s’]} =
{λs. ¬Eva came in s, λs’. ¬Mary came in s’, λs”. ¬Sveta came in s”, λs’’’. ¬Anna came in s’’’, λs. ¬Bill came in s, λs’.¬John came in s’, etc…}
The possible situations where the facts about people other than Eva coming are the same as in s0 are picked by the function in (110).
-
(110)
λs. ∀p[(p ≠ λs’.¬Eva came in s’ & p∈〚EvaF did not come〛gF) → p(s) = p(s0)]
This is a set of situations where the propositions of the general shape ‘x did not come’ (where x is not Eva) have the same truth value as in s0. If Mary did not come in s0, then the situations we are looking at in (110) are the situations where Mary did not come. If Mary came in s0, then the situations were looking at are the situations where Mary came.
It is worth pointing out that in the situations described by the function in (110), the facts related to coming remain the same as in s0 not only for girls, but also for all other individuals. This is because the focus alternatives to Eva include John, Bill, etc. One advantage of using this strategy is that we do not need to know in advance who is a girl in order to restrict the quantification over situations in the relevant way.
The domain subtraction can now be expressed in terms of the quantification over possible situations, as shown in (111).Footnote 15
-
(111)
∃s[∀p[(p ≠ λs’. ¬Eva came in s’ & p∈〚EvaF did not come〛gF) → p(s) = p(s0)] & ∀x[x is a girl in
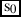 → x came in s]]
→ x came in s]]
The statement in (111) requires that every girl who is not Eva came in s0. In other words: (111) and (112) describe the same arrangement of things. This is because (111) states that there is a possible situation where everyone who is a girl in s0 came. It also says about that situation that every proposition of the form ‘x did not come’ where x is not Eva has the same truth value as in s0. Consequently, the state of affairs described in (111) obtains if every girl other than Eva came in s0, and does not obtain otherwise. Given that we know from Conditional Leastness that Eva is a girl in s0, a possible situation we are looking at in (111) is the one where Eva came.
-
(112)
∀x[(x is a girl in s0 & x is not Eva) → x came in s0]
The extension of the predicate denoted by girl is fixed again in (111): it is evaluated with respect to the actual topic situation and does not vary across possible situations. Let’s see what happens if the extension of this predicate is allowed to vary with possible situations, as shown in (113). The relevant difference between (111) and (113) is boxed: it is the situation variable.
-
(113)
∃s[∀p[(p ≠ λs’. ¬Eva came in s’ & p∈〚EvaF did not come〛gF) → p(s) = p(s0)] & ∀x[x is a girl in
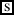 → x came in s]]
→ x came in s]]
The claim in (113) is too weak. Imagine that no individual who is a girl in s0 came in s0, but two individuals, say, John and Bill, who are boys in s0 came. The extension of the predicate girl can change across possible situations/worlds. There is a possible situation where the predicate girl denotes a set consisting of John and Bill (people who are not girls in the actual world). (113) is compatible with this scenario, but our sentence with except in (97) will not be true in it. Therefore, (113) does not correctly capture the meaning of (97). We are only interested in people who are girls in s0.
I will call this aspect of the meaning contributed by a clausal exceptive Conditional Domain Subtraction. There is a domain subtraction here: we subtract the proposition denoted by the clause following except from the domain of quantification over propositions that restricts the quantification over possible situations. Following the discussion in Sect. 3.2, I will take it to be the assertive content of a sentence with except. Thus, we can say that (97) is true in s0 if and only if (111) holds.
Note that (111), just like the domain subtraction in von Fintel’s system, by itself does not entail that Eva is a girl or that she did not come. Let’s consider (114), which is just like (111) except that the clearly female name Eva is replaced by the clearly male name John. Since John is not in the actual extension of the predicate denoted by girl, it does not matter whether he came or not in the actual topic situation s0. The state of affairs described in (114) only obtains if every girl came in s0.
-
(114)
∃s[∀p[(p≠λs’.¬John came in s’ & p∈〚JohnF did not come〛gF) → p(s)=p(s0)] & ∀x[x is a girl in s0 → x came in s]]
So far I have shown how the meaning of the specific sentence with except given in (97) can be expressed via three claims: the Negative Claim, Conditional Leastness, and Conditional Domain Subtraction. In what follows I will show how this result can be achieved in a compositional manner.
4.3 Compositional semantics
I implement the ideas discussed in the previous section in a system with indexed world/situation variables in the syntax (Percus 2000; Kratzer 2007/2019; Schwarz 2009, 2012).
A possible LF for our example (97), repeated below in (115), is shown in (116).
-
(115)
Every girl came except Eva
did not come.
-
(116)
In (116) the exceptive phrase moves from its connected position and leaves a trace s2 of type s. It is shown as rightward movement because in English, exceptive phrases introduced by except can only move rightwards.Footnote 16 Following standard assumptions, a binder for this trace 2 is merged in syntax. This binder is merged above the binder 1 that binds the situation variable inside the vP—the variable with respect to which the main predicate of the quantificational sentence is evaluated. There is another situation variable s3 inside the exceptive phrase, which is bound by the abstractor 3 at the matrix level.
With those assumptions, the denotation of the sister of Exceptive Phrase2 (ExcP2) is shown in (117).
-
(117)
λs’.λs”. ∀x[x is a girl in s’→ x came in s”]
Inside the exceptive phrase, the remnant of ellipsis is marked with focus (\(\mathit{Eva}_{F}\)). I follow Rooth (1992a) in assuming that focus is interpreted via a special operator ∼. A structure consisting of ∼ and a silent variable is merged every time there is an element marked with focus in a sentence (like ∼C5 in (116)). The value of the variable that comes with ∼ is restricted by the focus value of a clause c-commanded by the structure consisting of ∼ and the variable. This variable can be used by focus-sensitive operators such as except. This is done by providing a focus-sensitive operator with a variable that is co-indexed with the variable introduced with ∼ and assigning the focus-sensitive operator a meaning that makes reference to this silent variable.
A structure consisting of ∼ followed by a silent variable and its sister (a clause with a focused element) is interpreted via the rule given in (118). The operator ∼ does not have any effect on the at-issue content of a sentence it occurs in. Instead, it introduces the presupposition that the value of the silent variable it is accompanied by (C5 in our case) is a subset of the focus value of the clause with the focused element.
-
(118)
\([\!\![\phi (\sim \gamma )]\!\!]^{\mathrm{g}}\) = \([\!\![\phi ]\!\!]^{\mathrm{g}}\)
\([\!\![\phi (\sim \gamma )]\!\!]^{\mathrm{g}}\) is defined only if \([\!\![\gamma ]\!\!]^{\mathrm{g}}\ \subseteq \ [\!\![\phi ]\!\!]\)gF
The focus value of IP5 (the sister of ∼ with a variable) is as shown in (119).
-
(119)
\([\!\![4\ \mathrm{Eva}_{\mathrm{F}}\) did not come s4〛gF =
{λs. ¬Eva came in s, λs’. ¬Mary came in s’, λs”. ¬Sveta came in s”,
λs’’’. ¬Anna came in s’’’, λs. ¬Bill came in s, λs’.¬John came in s’, etc.}
The value of C5 has to be a subset of this set in (119). Let’s give it the value shown in (120).
-
(120)
\([\!\![\mathrm{C}_{5}]\!\!]^{\mathrm{g}}\) = g(5) =
{λs. ¬Eva came in s, λs’. ¬Mary came in s’, λs”. ¬Sveta came in s”,
λs’’’. ¬Anna came in s’’’, λs. ¬Bill came in s, λs’.¬John came in s’ }
Since ∼ does not have any effect on the at-issue content of the structure it occurs in, the sister of exceptC5 denotes the proposition shown in (121).
-
(121)
λs. ¬Eva came in s
The denotation for the focus-sensitive operator except that carries a variable Cn, where n is a numerical index, is given in (122).
-
(122)

This is a function that is looking for a proposition, a possible situation (this is the situation with respect to which the entire claim is evaluated), and then an argument of type <s<st≫ (the type of the sister of ExcP2 in the LF shown above). It introduces a presupposition and an assertive content. The presupposition is a conjunction of two claims: that the proposition this function takes as its first argument is true in the situation of evaluation, and that in every situation where it is true, the quantificational claim is not true (Conditional Leastness). The assertive content is Conditional Domain Subtraction: the function returns Truth if and only if there is a situation where all propositions in the value of the variable carried by except which are not equal to the proposition it takes at its first argument have the same truth value as in the situation of evaluation and where the quantificational claim is true.
Under these assumptions the predicted interpretation of the LF in (116) is shown in (123). As the reader can verify, the presupposition in (123) is the Negative claim conjoined with Conditional Leastness and the at-issue content is Conditional Domain Subtraction.
-
(123)
\([\!\![(116)]\!\!]^{\mathrm{g}}\)(s0)=1 iff ∃s[∀p[(p ≠ λs’. ¬Eva came in s’ & p∈g(5)) → p(s) = p(s0)] & ∀x[x is a girl in s0 → x came in s]]
\([\!\![(116)]\!\!]^{\mathrm{g}}\)(s0) is defined only if ¬Eva came in s0 & ∀s[¬Eva came in s → ¬∀x[x is a girl in s0 → x came in s]]
As was said earlier, the presence of negation in the except-clause has to be controlled by the meaning of except because it has to be there if the quantifier except operates on is universal (and the generalization is positive)Footnote 17 and not be there if the quantifier is negative. In the semantic theory I propose this is forced by Conditional Leastness. Let’s consider what happens if the ellipsis site does not contain negation, as shown in (124).
-
(124)
#Every girl came except Eva
came.
In this case the presupposition generated by the system is as shown in (125). This presupposition will not be satisfied because of the second conjunct (in bold). It is equivalent to (126). The only restriction on the universal quantification over situations in (126) is that those are the situations where Eva came. Regardless of whether Eva is a girl or not, there is a possible situation where every individual came. In that possible situation, it is not going to be the case that there is a girl in s0 who did not come. Since the requirement posed by the second conjunct of the presupposition is not satisfied, the sentence is predicted not to have a defined meaning.
-
(125)

-
(126)
∀s[Eva came in s → ∃x[x is a girl in s0 & ¬x came in s]]
It is important to point out here that the LF given in (116) does not have to be derived by the movement of the exceptive phrase. Another option is for the exceptive phrase to be based-generated in that position. In that case the insertion of the two abstractors over situation variables in the sister of the exceptive phrase is forced by the semantic type of the exceptive phrase (it is looking for an argument of type <s<st≫). Clausal exceptives that originate in a connected position (the position directly adjacent to the quantificational phrase) have to move to be interpreted.
4.4 Negative quantifiers
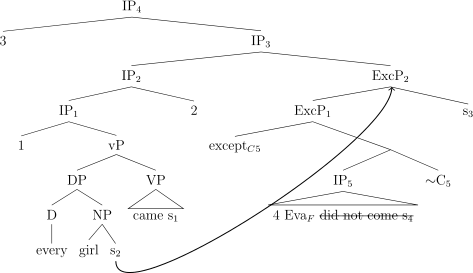
This proposal makes the correct prediction about the interaction of except with negative quantifiers. The LF for the sentence with a negative quantifier in (127) is given in (128). Following the earlier discussion, ellipsis is resolved positively. The remnant of ellipsis (Eva) is focused.
-
(127)
No girl came except EvaF
came.
-
(128)
The denotation of the sister of Exceptive Phrase2 is shown in (129).
-
(129)
λs’λs”. ¬∃x[x is a girl in s’ & x came in s”]
The value of the variable C5 has to be a subset of the focus value of IP5: this is the requirement imposed by ∼. Let’s give it the value shown in (130).
-
(130)
\([\!\![\mathrm{C}_{5}]\!\!]^{\mathrm{g}}\) = g(5) =
{λs. Eva came in s, λs’. Sveta came in s’, λs”. Mary came in s”, λs’’’. Anna came in s’’’, λs. Bill came in s, λs’. John came in s’}
Given the denotation for the except-clause in (122), the predicted interpretation for the entire sentence (127) is in (131). It again has a presuppositional component—the positive claim and Conditional Leastness—and an at-issue component—Conditional Domain Subtraction.
-
(131)
\([\!\![(128)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff ∃s[∀p[(p≠λs’. Eva came in s’ & p∈g(5)) → p(s) = p(s0)] & ¬∃x[x is a girl in s0 & x came in s]]
\([\!\![(128)]\!\!]^{\mathrm{g}}\)(s0) is defined only if Eva came in s0 & ∀s[Eva came in s → ∃x[x is a girl in s0 & x came in s]]
From the first conjunct in the presuppositional component we know that Eva came in s0. The second conjunct is Conditional Leastness. From it, we know that every possible situation in which Eva came has a girl of s0 who came in that possible situation. This can only hold if Eva is a girl in s0, so it captures the containment inference.
The sentence is predicted to be true in s0 if and only if there is a possible situation where all the facts about people other than Eva coming are the same as in s0 and where no girl of s0 came. This can only be the case if no girl other than Eva came in s0, which captures the domain subtraction inference.
Conditional Leastness is also responsible for the fact that ellipsis has to be resolved positively in this case. Let’s consider what happens if the ellipsis is resolved in the wrong way, as shown in (132).
-
(132)
#No girl came except EvaF
did not come.
The predicted presupposition cannot be satisfied in that case. This is shown in (133): the requirement posed by the second conjunct (bolded) is not satisfied because it is not the case that in every situation where Eva did not come, some girl of s0 came. There is a possible situation where no girl of s0 came at all.
-
(133)
\([\!\![(132)]\!\!]^{\mathrm{g}}\) (s0) is defined only if
¬Eva came in s0 & ∀s[¬Eva came in s → ∃x[x is a girl in s\(_{\textbf{0}}\) & x came in s]]
Crucially, one and the same denotation of except applies in cases where the quantifier is universal and in cases where it is negative.
4.5 The distribution puzzle
4.5.1 Existentials
The conditional analysis proposed here offers a solution to the distribution puzzle. However, unlike von Fintel’s original proposal, it does not derive in a straightforward way a contradiction if the denotation for except given in (122) is applied to a constituent containing an existential quantifier. An additional assumption is required in order to derive the incompatibility of exceptives with existential quantifiers. This assumption is that an existential cannot be used when it is known that the restrictor denotes a singleton set, in other words, when it is known that the conditions for the usage of a definite are met. This assumption is independently motivated; some theories explaining the incompatibility of exceptives with existentials have relied on this assumption before (Hoeksema 1995; Hirsch 2016).
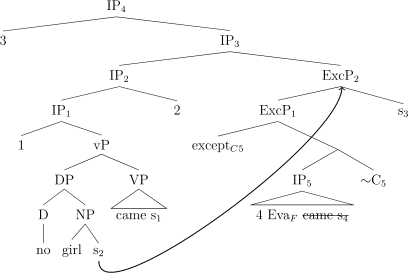
Let’s consider the ungrammatical example in (134). The LF analogous to the LFs considered above is shown in (135).
-
(134)
*Some girl came except EvaF
did not come.
-
(135)
The denotation of the sister of Exceptive Phrase2 is given in (136).
-
(136)
λs’λs”. ∃x[x is a girl in s’ & x came in s”]
The value of C5 has to be restricted by the focus value of IP5. Let’s give it the value shown in (137).
-
(137)
\([\!\![\mathrm{C}_{5}]\!\!]^{\mathrm{g}}\) = g(5) = {q:∃y[q=λs”.¬y came in s”]}
The interpretation that is predicted for this sentence is shown in (138) (the presupposition) and (139) (the assertive content).
-
(138)
\([\!\![(135)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
¬ Eva came in s0 & ∀s[¬Eva came in s → ¬∃x[x is a girl in s\(_{\textbf{0}}\) & x came in s]]
-
(139)
\([\!\![(135)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’. ¬Eva came in s’ & p∈g(5)) → p(s) = p(s0)] & ∃x[x is a girl in s0 & x came in s]]
The second conjunct of the presupposition (in bold) is Conditional Leastness. It is responsible for the fact that (134) is not a grammatical sentence of English. What we learn from it is that it is either the case that Eva is the only girl in s0 or that there are no girls in s0. The two possible outcomes come from two possible scenarios: one where Eva is a girl and one where she is not.
Let’s first consider the scenario where Eva is not a girl in s0. How can the presupposition be satisfied under this assumption? Only if there are no girls at all in s0 can it be the case that in all situations where a non-girl Eva did not come, no one who is a girl in the actual topic situation came. Imagine there is a girl, say, Sveta, in s0. Then there is a possible situation where Eva (non-girl) did not come and where Sveta came. Thus, the simple existence of a girl in s0 would make Conditional Leastness impossible to satisfy.
This possibility—that there are no girls in the actual topic situation—is, however, not compatible with the at-issue content in (139): the sentence can be true in s0 only if there is a possible situation where some girl of s0 came. This can only be the case if there are girls in s0.
Now let’s consider a scenario where Eva is a girl. Let’s also assume that there are other girls in s0, say, Sveta and Mary. Then, not in all situations where Eva did not come are there no girls of s0 who came. Let’s look at situations where Eva did not come. Among them there are possible situations where Sveta or Mary (other girls of s0) came, so the requirement posed by the second conjunct of the presupposition in (138) is not met.
If Eva is a girl in s0, there is only one way in which Eva’s not coming can absolutely guarantee that no girl of s0 came: it can be the case only if she is the only girl in s0. The assertion in (139) does not rule this out. There is a possible situation where some girl of s0 came and the facts about people other than Eva coming remain the same as in s0—namely, the situation where Eva came. In this case, the sentence can be true when the presupposition is satisfied.
Because there is a scenario under which a sentence where except operates on an existential is predicted to be defined and true, the conditional semantics for clausal exceptives requires an additional assumption in order to rule out (134). However, the assumption required here has an independent motivation. There is a well-established restriction on the use of an indefinite article (such as a and some) in a situation where the conditions for the use of a definite article are met, i.e. where there is a unique individual in the extension of the predicate denoted by the NP inside an existential DP.
The observation that indefinites come with an anti-uniqueness inference goes back to the work of Hawkins (1978, 1991) and Heim (1991). The sentence in (140) below can not be felicitously uttered if it is known that a person can only have one wife. In the same way, (141) cannot be used if it is known that the victim has only one father, and (142) is infelicitous because there is only one number in the extension of the predicate denoted by weight of our tent.
-
(140)
#Yesterday, I talked to a wife of John’s (Alonso-Ovalle et al. 2011)
-
(141)
#I interviewed a father of the victim. (Hawkins 1991)
-
(142)
#A weight of our tent is under 4 lbs. (Heim 1991)
Heim (1991) proposed to derive this anti-uniqueness inference via the principle known as Maximize Presuppositions.
-
(143)
Maximize Presuppositions: Among a set of alternatives, use the felicitous sentence with the strongest presupposition. (This formulation is from Chemla 2008.)
In a situation where an indefinite competes with another expression that presupposes that there is only one individual that satisfies the predicate in the restrictor of the determiner, namely a definite, and it is in fact known that there is only one such individual, the definite has to be used.
I propose that the reason why sentences where an exceptive operates on an existential, like the one in (134), are perceived as ungrammatical is that they receive ill-formed meanings. The use of an existential signals that the speaker does not believe there to be only one object that satisfies the restrictor of the existential. The only other way the presupposition generated by an exceptive can be satisfied is if the restrictor is empty. However, in that case, whenever the sentence is defined, it is necessarily false. This problem cannot be fixed by replacing all non-functional elements of a sentence with different lexical items: it is predicted to arise whenever an except is put together with an existential. Following Gajewski (2002), who proposed that contradictions of this kind are perceived as ungrammatical, I conclude that (134) is ungrammatical because of its meaning.Footnote 18
We run into the same issue with numeral indefinites as well. Let’s consider the ungrammatical sentence in (144). To put it informally, the analysis predicts that this sentence presupposes that in every situation where Eva did not come Two girls came is not true. Let’s imagine that there are three girls in s0. Then there is a situation where Eva did not come and the two other girls came, and thus the presupposition is not satisfied. If there are fewer than two girls overall, the presupposition is satisfied but conflicts with the at-issue meaning. The sentence is predicted to be true in s0 if and only if there is a possible situation where the truth value of every proposition of the shape ‘x did not come’, where x is not Eva, is the same as in s0, and where it is true that two girls of s0 came. If there are fewer than two girls overall in s0, this cannot hold. Only if there are exactly two girls, the sentence can be simultaneously defined and true.
-
(144)
*Two girls came except Eva
did not come.
Again, since the predicted meaning is well-formed just when the conditions for the use of a definite are met, we will have to appeal to some principle external to the theory to rule (144) out. Specifically, we will appeal to Maximize Presupposition again and say that the sentence is ruled out because the indefinite two girls cannot be used in a situation where it is known that there are exactly two girls.
We can construct an example similar to the ones in (140)–(142) illustrating that the same restriction exists for bare numerals. For example, (145) cannot be said in a scenario where it is known that the victim only has two parents.
-
(145)
#I interviewed two parents of the victim.
4.5.2 Definite descriptions
I proposed that the reason why exceptives introduced by except are not compatible with existential quantifiers is that in those cases the presupposition introduced by the exceptive can only be satisfied and compatible with the assertion if the remnant of the exceptive deletion is the only individual satisfying the restrictor of the indefinite in the topic situation. In this case the use of the existential is blocked by the principle prohibiting use of an existential when a definite can be used instead. However, definites are not valid correlates of remnants in exceptive deletion either, as illustrated in (146).
-
(146)
*The girl came except EvaF
did not come.
The meaning predicted by the proposed system for (146) is given in (147) (the presupposition) and (148) (the assertion).
-
(147)
\([\!\![(146)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
¬Eva came in s0 & ∀s[¬Eva came in s → ¬ιx[x is a girl in s0] came in s]
-
(148)
\([\!\![(146)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’. ¬Eva came in s’ & p∈{q:∃y[q = λs”.¬y came in s”]}) → p(s) = p(s0)] & ιx[x is a girl in s0] came in s]
The presupposition and the assertion are consistent with each other. From the presupposition we learn that Eva and the girl must refer to the same individual and that she did not come in s0. The sentence is predicted to be true in s0 if and only if there is a possible situation where the girl of s0 came and all the other facts regarding who came are the same as in s0.
There are several problems with (146). The first one is that the presupposition requires that Eva is the girl, but there is a general prohibition against referring to one and the same individual with a definite description and with a name in the same sentence, even if there is no c-command, as shown in (149). The restriction observed in (149), however, cannot be a general solution to the puzzle posed by (146). This is because (149) becomes grammatical if she is used instead of Eva (as shown in (150)),Footnote 19 whereas (146) does not improve in the same way, as shown in (151).
-
(149)
*Because [the girl]1 was late, Eva1 was fired.
-
(150)
Because [the girl]1 was late, she1 was fired.
-
(151)
*[The girl]1 came except her1F/she1F
did not come.
One factor contributing to the badness of (146) and (151) is that in both of these, the two clauses of the sentence do not sufficiently contrast for the ellipsis to be licensed (see Rooth 1992a; Stockwell 2018; Griffiths 2019 on the contrast requirement on ellipsis). Contrast is lacking because in each of those cases the presupposition requires that the subject of the except-clause and the subject of the main clause refer to the same individual.
There is also another issue with (146) and (151). Even though the predicted presupposition and the at-issue content are consistent with each other, there is still a problem with the meaning the system has generated. Let’s consider the resulting interpretation of (146). From the presupposition we learn that [λs.¬Eva came in s] and [λs. ¬ιx[x is a girl in s0] came in s] are equivalent. The assertive content in (148) does not depend on s0: it does not matter what the truth values of propositions of the shape ‘x did not come’ in s0 are. The sentence is predicted to be true in s0 if and only if there is a possible situation where Eva came. This only depends on whether [λs.¬Eva came in s] is a necessary truth or not. Let me for now ignore the fact that there are necessary truths (they present a more general problem for the account proposed here and will be discussed in the next section). For statements that are not necessary truths, whenever the presupposition is satisfied, the sentence is predicted to be true. Thus (146) is predicted to be a tautology in a way: there is no way for it to be false. (151) suffers from the same problem.
Again, this problem cannot be fixed by changing the non-functional elements of the sentence. I will adopt Gajewski’s (2002) idea that tautologies with this property are perceived as ungrammatical, and propose that this explains the badness of (146) and (151).
It is also the case that plural definite descriptions are not compatible with except (as shown in (152)). Adding all before the girls makes the sentence grammatical (153).
-
(152)
*The girls came except EvaF
did not come.
-
(153)
All the girls came except Eva
did not come.
I propose that the problem with (152) is in the presupposition generated by the system. As discussed, one of the contributions of except is that there is a law-like relationship between the two clauses. In (152) it would be the claim that in every situation where Eva did not come, it is not true that the girls of s0 came. Now we need to consider what happens when negation is applied to a claim containing a plural definite. One observation that have been made in the literature is that plural definite descriptions come with a homogeneity presupposition (Schwarzschild 1994; Löbner 1987, 2000; Gajewski 2005; Breheny 2005; Büring and Križ 2013; Magri 2014; Križ 2015a,b): applying negation to the claim The girls came gives us The girls (all of them) did not come. The presupposition, thus, would require that in every situation where Eva did not come, the girls of s0 (all of them) did not come. This can only hold if Eva is the only girl in s0. Then (152) is predicted to be ill-formed due to the conflict between the plural marking on the noun and the requirement that Eva is the only girl in s0 introduced by the presupposition. My tentative explanation for the fact that adding all makes the sentence grammatical is that all removes the homogeneity presupposition from the plural (Löbner 2000; Križ 2015b) and essentially makes the plural definite behave like a universal quantifier with respect to negation.
4.6 Necessary truths
The conditional analysis of clausal exceptives I have proposed here involves looking at situations where the fact about the event described by an exceptive clause is different than in the actual topic situation. One question arising at this point is what is going to happen if the exceptive clause expresses a necessary truth and there are no situations where the facts described by the exceptive clause are different than in s0. Let me illustrate the issue with example (155). Intuitively, this sentence is true.
-
(154)
4, 5, 7, 9
-
(155)
All numbers in (154) are odd except 4
is not odd.
The predicted at-issue content for this sentence is shown in (156). The sentence is predicted to be true in s0 if and only if there is a possible situation where all facts of the form ‘x is not odd’ where x is not 4 are the same as in s0 and where every number in (154) is odd. That can only be the case if there is a possible situation where 4 is odd: there is no other way for the claim All numbers in (154) in s0 are odd to become true in a possible situation.
-
(156)
\([\!\![(155)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’. ¬4 is odd in s’ & p∈{q:∃y[q = λs”.¬y is odd in s”]}) → p(s) = p(s0)] & ∀x[x is number in (154) in s0 → x is odd in s]]
The problem here is that mathematical truths, like the proposition denoted by 4 is not an odd number, are generally considered to be necessary truths; in other words, they are considered to be true in every possible situation.
What I think is going on in this case is that our language does not behave as if 4 is not an odd number is a necessary truth. Evidence for this comes from the conditional paraphrase of (155) given in (157). It is also perceived as true in the situation presented in (154). Under the assumption that mathematical facts are the same in all possible situations, we run into the same problem with the interpretation of conditional sentences. Whatever strategy we use to explain what is going on in (157), we could use to explain (155).
-
(157)
If 4 were an odd number, all numbers in (154) would have been odd.
5 Advantages of the proposed analysis
In the previous section I proposed a novel semantic analysis for except. This analysis differs from the existing analyses of exceptives in that it is based on the assumption that an exceptive marker introduces a clause and not just a DP. I have shown how this analysis captures the facts that are captured by the classic analysis: the inferences except contributes when it applies to a universal and a negative quantifier and the distributional facts. The goal of this section is to show how the proposed analysis captures the cases that are not captured in the classic system.
I will apply my analysis to the three crucial types of cases that were introduced in Sect. 3: (i) an exceptive phrase containing a prepositional phrase with a meaningful preposition; (ii) an exceptive phrase containing a prepositional phrase that has no correlate (a corresponding antecedent) in the main clause; and (iii) an exceptive containing multiple syntactic constituents.
5.1 Meaningful prepositions
In this section I show how my analysis applies to cases where an exceptive phrase contains a meaningful preposition, such as (45) (repeated below as (158)).
-
(158)
I met a student from every city in Spain except from Barcelona.
This sentence comes with the following aspects of meaning:
-
(159)
-
i.
Negative Entailment: I met no student from Barcelona.
-
ii.
Containment Entailment: Barcelona is a city in Spain.
-
iii.
Domain Subtraction: I met a student from every city in Spain that is not Barcelona.
-
i.
Capturing those inferences is challenging for theories that assume that the constituent inside an except-phrase is a set that can directly restrict the domain of a quantificational DP, because things that are from Barcelona are not cities.
I suggest that the underlying syntactic structure of (158) is as shown in (160). This structure is derived by moving the PP from Barcelona from the object DP inside the clause following except and eliding the rest of the clause.
-
(160)
I met a student from every city in Spain except [from BarcelonaF] 1
I did not meet a student T1.
Before I provide a detailed derivation of the meaning of this sentence, I will express a general idea behind it. I assume that every city in Spain takes scope over the indefinite, thus, the quantificational claim here is For every city in Spain it holds that I met a student from it. The exceptive here contributes three things, responsible for the three inferences listed above: (i) I did not meet any student from Barcelona; (ii) in every situation where that happened, the quantificational claim is not true (thus, there is a city in Spain such that I did not meet any student from it); (iii) the truth values of all other propositions of the general shape ‘I did not meet a student from x’ (where x is a place) in the topic situation are compatible with this quantificational claim.
The LF for this sentence is given in (161). Following standard assumptions, the quantificational object of the main clause (a student from every city in Spain except from Barcelona) is raised. A trace of type e (t1) bound by abstractor 1 is left in its original place. Further, the quantificational phrase inside this object (every city in Spain except from Barcelona) undergoes QR, leaving a trace of type e (t2) that is bound by abstractor 2. This is done in order to get the right scope for every city in Spain: it has to be interpreted in a position higher than the existential a student from… because a reasonable interpretation for this sentence requires there to be different students for each city. Again, I follow standard practice in assuming that the situation variable (s3) of the main predicate met is bound at LF by abstractor 3. The same abstractor binds the situation variable inside the restrictor of the indefinite (this, however, is not crucial for the analysis).
Following the assumptions I made here about exceptives, the exceptive phrase starts as a sister of the NP city in Spain. It undergoes QR, leaving a trace of type s (s4). It is bound by abstractor 4.
-
(161)
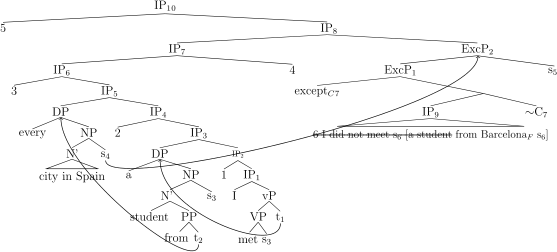
With those assumptions about the structure of the main clause, the sister of Exceptive Phrase2 gets the interpretation given in (162).
-
(162)
λs.λs’.∀x[x is a city in Spain in s→∃y[y is a student from x s’ & I met y in s’]]
For simplicity, I reconstructed the PP inside the except-clause. The remnant of ellipsis inside the clause following except is focused (\(\mathit{Barcelona}_{F}\)). The value of C7 is restricted by the focus value of IP9. The focus value of IP9 is computed by making a substitution in the position corresponding to Barcelona. Let’s give C7 the value given in (163).
-
(163)
\([\!\![\mathrm{C}_{7}]\!\!]^{\mathrm{g}}\)=g(7)=
{λs.¬∃a[a is a student from Barcelona in s & I met a in s], λs’.¬∃b[b is a student from Valencia in s’ & I met b in s’], λs”.¬∃x[x is a student from Madrid in s” & I met x in s”], λs’’’.¬∃y[y is a student from Bilbao in s’’’ & I met y in s’’’], λs.¬∃z[z is a student from Moscow in s & I met z in s], λs”.¬∃c[c is a student from New York in s” & I met c in s”] }
The predicted resulting interpretation for the entire sentence is given in (164) (the presupposition) and (165) (the assertion).
The first conjunct of the presupposition says that I met no student from Barcelona (this captures the negative inference). The second conjunct states that in every situation where I did not meet a student from Barcelona there is a thing that is a city in Spain in s0 such that I met no student from that city. This can only be the case if Barcelona is a city in Spain. This captures the containment inference.
Given the assertive content in (165), the sentence is predicted to be true in s0 if and only if there is a situation where all of the propositions in (163) other than the one denoted by I did not meet a student from Barcelona have the same truth value as in s0 and where it is true that I met a student from every city in Spain. This can only hold if I met a student from every city in Spain other than Barcelona in s0. This captures the domain subtraction inference.
-
(164)
\([\!\![(161)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
¬∃b[b is a student from Barcelona in s0 & I met b in s0] & ∀s[¬∃z[z is a student from Barcelona in s & I met z in s] → ∃x[x is a city in Spain in s0 & ¬∃y[y is a student from x in s & I met y in s]]]
-
(165)
\([\!\![(161)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p≠λs’.¬∃a[a is a student from Barcelona in s’ & I met a in s’] & p∈g(7)) → p(s) = p(s0)] & ∀x[x is a city in Spain in s0→ ∃y[y is a student from x in s & I met y in s]]
Thus, the analysis proposed here correctly captures the meaning of this sentence.
5.2 PPs with no correlates in the main clause (sprouting)
The second case I will consider is the one where the prepositional phrase inside an exceptive phrase has no correlate (a corresponding antecedent) in the main clause, such as (3) (repeated below as (166)). The preposition from makes an important contribution to the overall meaning of this sentence: if it is omitted, the sentence comes with the inference that my mom is a present. The challenge this case presents for the analysis in terms of sets of individuals is that they derive overly strong positive and containment entailments by posing the requirement that every element in the set introduced by the expression inside an except-phrase is contained in the restrictor set and that the positive inference applies to each individual in this set. The PP from my mom denotes a set that contains things that are not presents. The sentence (166) does not come with the inference that everything from my mom is a present that I got.
-
(166)
I got no presents except #(from) my mom.
I propose that (166) is derived via movement of the PP from its position inside the object DP in the except-clause and deletion of the rest of the structure, as shown in (167).
-
(167)
I got no presents except from [my mom]F 1
I got a present T1.
I will call this case sprouting, because a similar phenomenon bearing this name exists in sluicing (Chung et al. 1995). A sluicing example is given in (168).
-
(168)
I got a present, but I don’t remember from whom.
The ellipsis site in (167) contains an existential quantificational expression a present, whereas its corresponding antecedent in the main clause is a negative quantifier no presents. There is independent evidence that such a mismatch is possible in ellipsis (Sag 1976; Johnson 2001). One example of such a mismatch involving VP-ellipsis is given in (169).
-
(169)
I got no presents, but John did
get a present.
Before going into the details of the analysis of this case, let me list the meaning components of (166). The sentence comes with the set of inferences in (170). Given that the quantifier is negative, the exceptive contributes a positive inference. The containment entailment is somewhat uninformative in this case.
-
(170)
-
i.
Positive Entailment: I got a present from my mom.
-
ii.
Containment Entailment: A present from my mom is a present.
-
iii.
Domain Subtraction: I got no presents from people other than my mom.
-
i.
In what follows I will show how these inferences are naturally derived by the analysis developed here. Again, the three inferences presented above are captured by the three things contributed by except: (i) the clause following except is true (I got a present from my mom); (ii) in every situation where that happened, the quantificational claim (I got no presents) is false; (iii) the truth values of all other propositions of the general shape ‘I got a present from x’ (where x is a person) are compatible with the quantificational claim in the topic situation. I will also show how the fact that from is mandatory in (166) in order for it to be felicitous follows naturally from my proposal about how the meaning of this sentence is constructed and from what we independently know about ellipsis.
The LF for (166) is shown in (171). I adopt standard assumptions about the structure of the main clause. No presents undergoes QR and leaves a trace of type e (t1) that is bound by the abstractor 1. The situation variable of the main predicate got (s2) is bound by abstractor 2. The Exceptive Phrase starts as a sister of the predicate inside the DP (present) and undergoes extraposition, leaving a trace of type s (s3); this trace is bound by the abstractor 3. I reconstructed the PP inside the DP inside the except-clause.
-
(171)
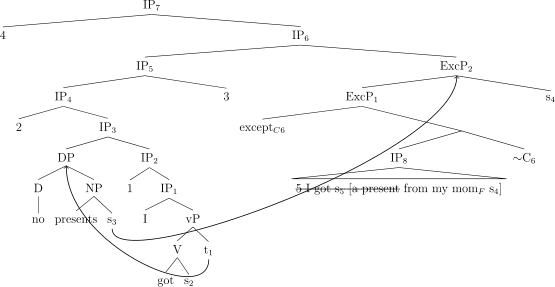
Under these assumptions, the meaning of the sister of Exceptive Phrase2 is as shown in (172).
-
(172)
λs’.λs.¬∃x[x is a present in s’ & I got x in s]
The predicted meaning is as shown in (173) (the presupposition) and (174) (the assertive content).
-
(173)
\([\!\![(171)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
∃z[z is a present from my mom in s0 & I got z in s0] & ∀s[∃x[x is a present from my mom in s0 & I got x in s] → ∃y[y is a present in s0 & I got y in s]]
-
(174)
\([\!\![(171)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.∃y[y is a present from my mom in s0 & I got y in s’ & p∈g(6)) → p(s) = p(s0)] & ¬∃z[z is a present in s0 & I got z in s]]
From the first conjunct of the presupposition in (173) we learn that I got a present from my mom in s0. This captures the positive entailment. The second conjunct says that if we look at situations where I got a present from my mom, we will find that in all of them there is a thing that is a present in s0 that I got. This is not very useful for capturing the containment inference in this case because the ellipsis site of the except-clause contains the predicate present—which is also the predicate that is in the restrictor of the quantifier no presents. It nevertheless makes an important contribution: it ensures that the ellipsis is resolved with the right polarity.Footnote 20
The assertion in (174) makes reference to the propositions in the set denoted by C6. The value of C6 is restricted by the focus value of IP8 (the sentence inside the exceptive phrase). It is given in (175): it includes the propositions denoted by I got a present from my mom, I got a present from John, I got a present from Mary, I got a present from Ann, etc. The sentence is predicted to be true in s0 if and only if there is a possible situation where the claim I got no presents is true, while all the propositions in the set denoted by C6 other than I got a present from my mom have the same truth value as in s0. This is only possible if they all are false in s0. This captures the domain subtraction inference that I did not get any present that was not from my mom.
-
(175)
\([\!\![\mathrm{C}_{6}]\!\!]^{\mathrm{g}}\) = g(6) = {q: ∃x[q = λs.∃z[z is a present from x in s0 & I got z in s]]}
The remaining issue I would like to discuss here is why (176) is infelicitous. The explanation for this fact naturally follows from the semantic theory of clausal exceptives proposed here and from what is independently known about ellipsis.
-
(176)
#I got no presents except my mom.
If ellipsis in (176) could be resolved as shown in (177), this sentence could have the LF shown in (171). In (177) the DP my mom moves from the PP inside the ellipsis site, and the rest of the structure together with the preposition is deleted. This, however, is not a possible structure because it violates a well-established constraint on ellipsis given in (178).
-
(177)
*I got no presents except my mom 1 [
I got a present from t1]
-
(178)
Chung’s generalization: A preposition can be stranded in an ellipsis site only if it has an overt correlate in the antecedent. (Chung 2005:79)
This constraint can be illustrated by the following pair of examples containing sluicing: the well-formed one in (179), where the ellipsis site contains a preposition that has a correlate in the antecedent, and the infelicitous one in (180), where the ellipsis site contains a preposition that has no correlate in the antecedent.
-
(179)
I got a present from someone but I don’t remember who
I got a present from.
-
(180)
#I got a present but I don’t remember who
I got a present from.
The idea that Chung’s generalization plays a role in ruling out (177) finds further support in the fact that (181), where the PP is present in the antecedent, is a grammatical sentence.
-
(181)
I got no presents from anyone except my mom 1 [
I got a present from t1]
Given that the possibility of the derivation in (177) is ruled out by Chung’s constraint, the two remaining options for ellipsis resolution are given in (182) and (183).
-
(182)
I got no present except
I gotmy mom.
-
(183)
I got no present except my mom
got a present.
Interpreting (182) will generate the presupposition that is responsible for the funny inference that my mom is a present that I got. It is given in (184): the second conjunct here (bolded) states that every situation where I got my mom has a thing that is a present in s0 that I got. That can only hold if my mom is a present in s0.
-
(184)
I got my mom in s0 & ∀s[I got my mom in s → ∃x[x is a present in s\(_{\textbf{0}}\) & I got x in s]]
Interpreting (183) will generate the presupposition that is impossible to satisfy. It is given in (185). The second conjunct (bolded) can only be satisfied if I am my mom. This is because it states that in every situation in which my mom got a present, I got a present. This can only hold if my mom and I are the same individual.
-
(185)
∃z[z is a present in s0 & my mom got z in s0] & ∀s[∃x[x is a present in s\(_{\textbf{0}}\) & my mom got x in s] → ∃y[y is a present in s\(_{\textbf{0}}\) & I got y in s]]
We have exhausted all possible ways of deriving the meaning of (176) and we have found no way of generating the same meaning as that of (166) (repeated below as (186)). This explains the contrast between those two sentences.
-
(186)
I got no presents except from my mom.
5.3 Exceptives with multiple remnants
In this section I consider cases where an exceptive contains multiple syntactic constituents, like the one in (30) (repeated below as (187)). Such cases are challenging for any type of a phrasal analysis because the expressions inside an except-phrase do not form a syntactic constituent. I show how the conditional system developed here accounts for the meaning of those sentences and for the restrictions on the types of quantifiers that can correspond to the elements inside the except-phrase.
-
(187)
Every girl danced with every boy everywhere except Eva with Bill in the kitchen.
I suggest that (187) is derived by moving the three phrases to the edge of the clause inside except-clause and eliding the rest of the material in the clause, as shown in (188).
-
(188)
Every girl danced with every boy everywhere except [EvaF] 1 [with BillF] 2 [in the kitchenF] 3
t1did not dance t2T3.
It is worth reminding the reader of the generalization regarding these cases from Moltmann (1995): if an exceptive phrase contains multiple syntactic elements, each of those elements has to have a corresponding universal quantifier in the main clause. This is the restriction that we observe in (42) and (43), repeated below as (189) and (190).
-
(189)
*Every girl danced with some boy except Eva with Bill.
-
(190)
*Some girl danced with every boy except Eva with Bill.
Another fact that we want to derive is that this is not a general prohibition on the presence of non-universal quantifiers in sentences where the except-phrase contains multiple remnants, as shown by the well-formed example (191), which contains an existential somewhere.Footnote 21
-
(191)
Every girl danced with every boy somewhere except Eva with Bill.
One important clarification is due here. All correlates have to be universal quantifiers in the context of the entire sentence (Moltmann 1995). For example, the sentence in (192) is grammatical, even though given standard assumptions, the NPI any boy is interpreted as an existential. However, in the context of the entire sentence under the scope of the negative quantifier the NPI gets an interpretation where it is equivalent to a universal quantifier. In (193) and (194) we observe the opposite situation. In the ungrammatical example (193) both quantifiers no girl and every boy taken in isolation are universal; however, when every boy appears under the scope of a negative quantifier its interpretation is equivalent to an existential quantifier. The same problem makes (194) ungrammatical: the lower negative quantifier no boy under the scope of another negative quantifier gets the interpretation that is equivalent to an existential quantifier.
-
(192)
No girl danced with any boy except Eva with Bill.
-
(193)
*No girl danced with every boy except Eva with Bill.
-
(194)
*No girl danced with no boy except Eva with Bill.Footnote 22
Those are the facts that a theory of clausal exceptives has to capture. In what follows I will show how the theory developed in the previous sections does that in a natural way.
5.3.1 Every…every
Sentence (195) comes with the set of inferences shown in (196).
-
(195)
Every girl danced with every boy except Eva with Bill
did not dance.
-
(196)
-
i.
Negative Entailment: Eva did not dance with Bill.
-
ii.
Containment Entailment: Eva is a girl, Bill is a boy.
-
iii.
Domain Subtraction: For every pair of individuals other than Eva-Bill it holds that every girl danced with every boy.
-
i.
Intuitively, this sentence means that Eva did not dance with Bill is the exception to the generalization Every girl danced with every boy. The analysis I developed specifies what it means for a clause to be the exception to a generalization. Being the exception in this case means that (i) Eva did not dance with Bill; (ii) in every situation where that happened the generalization is not true; and (iii) had that not happened, the generalization would have been true. Below I show how this result is derived in a compositional way.
I propose that the sentence in (195) has the LF shown in (197).
-
(197)
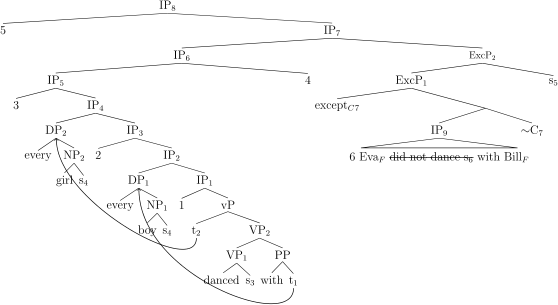
Let’s focus on the sister of Exceptive Phrase2. Following standard assumptions, I QRed both of the DPs every girl and every boy, left traces and bound them by abstractors (numerical indices 1 and 2). The situation variable s3 that comes with the verb dance is bound by abstractor 3.
There is a separate abstractor that binds situation variables inside the DPs. It is crucial here that those two variables are co-indexed and are bound by the same abstractor. If the situation variable in one of the DPs is bound by the same abstractor that binds the main predicate of the sentence, we will derive a presupposition that cannot be satisfied. I will ignore this option for now and will go over it at the end of this section. Note that this restriction only holds for situation variables inside DPs that are correlates of remnants in an except-phrase. The system makes no commitments about situation variables inside any other DPs that may be present.
I will remain agnostic here about how the except-clause gets to the sentence-final position. One option is that here as in all previous cases the except-clause originates inside a DP. It may be the case that the exceptive clause moves simultaneously from both DPs in across-the-board manner. Another possibility is that it moves from one of the DPs (and it would have to be the higher one to avoid a weak crossover violation). The third option is that the except-clause in (197) is base-generated.
What is crucial for the proposed analysis is that the except-clause is placed above both of the correlates in the main clause. For now, I will simply assume that in cases where an exceptive contains multiple remnants it has to be placed high enough to c-command both of the correlates. In the next subsection, I will show that this assumption is supported by the empirical facts.
Both of the remnants of ellipsis inside the clause following except are focused (Eva, Bill). For simplicity, I reconstructed the DPs inside the except-clause to their base positions in (197).
The predicted denotation for the sister of the exceptive phrase is in (198). Except establishes a relationship between this quantificational claim and the clause following except.
-
(198)
λs’. λs”. ∀x[x is a girl in s’ → ∀y[y is a boy in s’ → x danced with y in s”]]
The predicted meaning of this sentence is shown in (199) (the presupposition) and (200) (the assertion).
We learn from the first conjunct of the presupposition that Eva did not dance with Bill in s0. The second conjunct is Conditional Leastness: it requires that in every situation where Eva did not dance with Bill, there is a girl of s0 and a boy of s0 such that the girl did not dance with the boy. This is only possible if Eva is a girl and Bill is a boy in the topic situation s0.Footnote 23
-
(199)
\([\!\![(195)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
¬Eva danced with Bill in s0 & ∀s[¬Eva danced with Bill in s → ∃x[x is a girl in s0 & ∃y[y is a boy in s0 & ¬ x danced with y in s ]]]
The at-issue content in (200) below makes reference to the value of C7. The value of C7 has to be a subset of the focus value of the clause \(\mathit{Eva}_{F}\) did not dance with BillF. The focus value is the set of propositions formed by making a substitution in the position corresponding to one or both of the focused elements in the original proposition (thus it includes the propositions denoted by Eva did not dance with John, Mary did not dance with Bill, Mary did not dance with John, etc.). A possible value for C7 is given in (201). The sentence is predicted to be true in s0 if and only if the truth values of all propositions in C7 other than the one denoted by Eva did not dance with Bill in s0 are compatible with the claim Every girl danced with every boy. This means that the sentence is true in s0 if and only if for every pair of individuals other than Eva–Bill it holds that every girl danced with every boy in s0. This captures the domain subtraction inference.
-
(200)
\([\!\![(195)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.¬Eva danced with Bill in s’ & p∈g(7)) → p(s) = p(s0)] & ∀x[x is a girl in s0 → ∀y[y is a boy in s0 → x danced with y in s]]]
-
(201)
\([\!\![\mathrm{C}_{7}]\!\!]^{\mathrm{g}}\) = g(7) ={q: ∃x∃y[q = λs. ¬x danced with y in s]}
Thus, the predicted meaning captures all of the inferences that accompany (195).
The next issue I will address here is what happens if not all situation variables inside the correlates of the remnants in the except-clause are bound by the same abstractor. I said earlier that such a structure is ruled out because it will generate a presupposition that cannot be satisfied. The situation I have in mind is the one where the sister of the exceptive phrase has the structure shown in (202), where the situation variable that comes with the predicate girl is bound by a different abstractor than the one binding the variable that comes with boy. The exceptive phrase would combine with the constituent with the denotation given in (203). The presupposition generated by the system for such a structure will be as shown in (204).
-
(202)
[4 [3[every girl \(\mathbf{s}_{\textbf{3}}\) [2 [every boy \(\mathbf{s}_{\textbf{4}}\) [1 [t2 danced \(\mathbf{s}_{\textbf{3}}\) with t1]]]]]]]
-
(203)
λs’. λ
 . ∀x[x is a girl in
. ∀x[x is a girl in  → ∀y[y is a boy in s’ → x danced with y in
→ ∀y[y is a boy in s’ → x danced with y in  ]]
]]
-
(204)
¬Eva danced with Bill in s0 & ∀
 [¬Eva danced with Bill in
[¬Eva danced with Bill in  → ∃x[x is a girl in
→ ∃x[x is a girl in  & ∃y[y is a boy in s\(_{\textbf{0}}\) & ¬ x danced with y in
& ∃y[y is a boy in s\(_{\textbf{0}}\) & ¬ x danced with y in  ]]]
]]]
This presupposition is impossible to satisfy because of the second conjunct (bolded). It requires that Eva is a girl in every possible situation. Otherwise it could not be the case that in every situation where Eva did not dance with Bill there is an individual who is a girl in that situation who did not dance with a boy of s0. Since it is known that the predicate denoted by girl can change its extension from situation to situation, the requirements imposed by the second conjunct in (204) cannot be satisfied. Since the presupposition is not satisfied, the sentence is predicted to not have a defined meaning. However, we do not need to worry about this, because there is another LF, namely the one discussed above, that does not lead to this very strong presupposition that Eva is a girl in every possible situation.
5.3.2 The syntactic position of an exceptive with multiple remnants
In the analysis of exceptives with multiple remnants I proposed in the previous section, I made the assumption that an exceptive clause containing multiple remnants has to c-command all correlates of the remnants in the main clause. In this section, I provide the empirical support for this assumption, as well as an explanation.
Normally, the subject c-commands the except-phrase associated with the object and can bind into it, as shown in (205).
-
(205)
Every girl1 danced with every boy except her1 brother.
In general, a PP can be extraposed from the main clause and placed after an exceptive with multiple remnants, as shown in (206) (in Jack’s kitchen should not be construed as a part of the exceptive).
-
(206)
Every girl danced with every boy except Eva with Bill [in Jack’s kitchen].
Now, let’s construct an example that minimally differs from (206) insofar as [in Jack’s kitchen] is replaced by [in her kitchen], where her is co-indexed with every girl. The resulting sentence given in (207) is unacceptable under the intended interpretation, where every girl binds the pronoun her. (207) is derived from the grammatical example (208) by the extraposition of the locative PP. Given that the extraposition of the PP is in itself acceptable, as was shown in (206), the absence of binding in (207) is surprising.
-
(207)
*Every girl1 danced with every boy except Eva with Bill [in her1 kitchen].
-
(208)
Every girl1 danced with every boy [in her1 kitchen] except Eva with Bill.
Under the hypothesis that the exceptive clause in (207) is higher than the subject, the unavailability of binding in (207) finds a natural explanation. If an exceptive with multiple remnants has to c-command both of the correlates (the subject and the object of the main clause in this case), then the extraposed PP [in her1 kitchen] in (207) has to be even higher than that. This means that the subject will not c-command this PP; the absence of the bound reading is predicted.
Moreover, if an exceptive contains only one remnant, as in (209), where it simply operates on the object DP, the subject can bind into an extraposed PP. In (207) the except-clause either has moved rightward to the position above the subject or was merged in that position.
-
(209)
Every girl1 danced with every boy except Bill [in her1 kitchen].
The semantic analysis developed here provides an explanation for the fact that an except-phrase with multiple remnants has to be higher than all of the correlates in examples like (195), where the remnants are proper names. However, this cannot be a general solution. Let’s first consider the predicted interpretation of (195) for the LF where the except-phrase scopes below the subject every girl, shown schematically in (210). The problem is with the component of the presupposition that establishes the law-like relationship between the except-clause and its sister. In this case it will be as shown in (211): this formula says that for every girl it holds that in every situation where Eva did not dance with Bill, there is a boy of s0 such that the girl did not dance with him. This can only hold if Eva is the only girl in s0 or there are no girls at all and, thus, the restrictor is empty and the quantification is vacuously true. If there is at least one girl who is not Eva, say Mary, then it is certainly not the case that in every situation in which Eva did not dance with Bill, Mary did not dance with some boy. The first option is, however, ruled out by a general pragmatic principle that does not allow the use of every girl when it is known that there is only one girl (Partee 1986:371). This principle is illustrated in (212): the sentence implies that there is more than one satellite of Earth. The second option would make the sentence tautological: given that every girl is the quantifier with the maximal scope here, any claim about every girl is going to be vacuously true if the restrictor is empty. Thus, whenever the sentence is defined (only in cases when there are no girls), it is predicted to be true. Since this LF does not result in a well-formed meaning, the except-phrase has to scope above both correlates.
-
(210)
[4 [every girl s4 1 [[except Eva with Bill
did not dance]s4] 3[2 [t1 danced with s2 every boy s3]]]]
-
(211)
∀x[x is a girl in s0 → ∀s[¬Eva danced with Bill in s → ∃y[y is a boy in s0 & ¬x danced with y in s ]]]
-
(212)
#Every satellite of Earth is yellow.
The reason this cannot be a general explanation is that the problem with (211) described above disappears if Eva is replaced by the variable bound by the quantifier over girls, as shown in (213): every girl is such that in every situation where she did not dance with Bill, there is a boy of s0 who she did not dance with. This presupposition will be satisfied if Bill is a boy in s0; it does not require that there is only one girl.
-
(213)
∀x[x is a girl in s0 → ∀s[¬x danced with Bill in s → ∃y[y is a boy in s0 & ¬x danced with y in s ]]]
However, if we substitute Eva with a pronoun in (195), the sentence becomes ungrammatical, as shown in (214). Interestingly, the fully pronounced version (215) is acceptable for those English speakers who accept fully pronounced sentences after except in general. This tells us that the fact that (214) is ungrammatical has something to do with ellipsis. I propose that the reason ellipsis is not possible here is that the elided clause is not in a sufficient contrast with its antecedent. The except-clause will have to take scope below the subject, in order for binding to be possible. Then, the antecedent will have a trace in the position corresponding to the position of the pronoun she in the exceptive clause. The trace and the pronoun have to carry the same index in order to be bound by the same operator. Thus, the contrast requirement won’t be satisfied.
-
(214)
*Every girl1 danced with every boy except her1/she1 with Bill.
-
(215)
Every girl1 danced with every boy, except she1 did not dance with Bill.
The idea that there is a contrast requirement on this type of ellipsis seems very plausible. The same requirement is observed in gapping (Kuno 1976), as shown by the contrast between (216) and (217) . Gapping appears to be similar to exceptive deletion with multiple remnants (Moltmann 1995).
-
(216)
Mary danced with John and Eva with Bill.
-
(217)
*Mary1 danced with John and she1 with Bill.
To conclude, a reduced exceptive clause containing multiple remnants has to c-command all of the correlates in the main clause, because otherwise it either receives an ill-formed interpretation or violates the contrast requirement on ellipsis.
5.3.3 *Some…every, *The…every, *Every…some
One of the facts that any account of clausal exceptives has to capture is that if a reduced exceptive clause contains multiple remnants, each remnant has to have a universal quantifier as its associate in the main clause. There is a contrast between the ungrammatical example in (218) and the grammatical one in (219). This shows that, in general, there is no prohibition against existential quantifiers in sentences with exceptive clauses. The contrast we observe here is predicted by the proposed analysis.
-
(218)
*Some girl danced with every boy except Eva with Bill.
-
(219)
Some girl danced with every boy except with Bill.Footnote 24
Let’s assume that (218) is derived from (220).
-
(220)
*Some girl danced with every boy except Eva with Bill
did not dance.
Given our assumptions about the meaning of except, the predicted presupposition of (218) is as shown in (221) and its at-issue content is as shown in (222).
-
(221)
\([\!\![(218)]\!\!]^{\mathrm{g}}\)(s0) is defined only if:
¬Eva danced with Bill in s0 & ∀s[¬Eva danced with Bill in s → ¬∃x[x is a girl in s\(_{\textbf{0}}\) & ∀y[y is a boy in s\(_{\textbf{0}}\) → x danced with y in s]]]
-
(222)
\([\!\![(218)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.¬Eva danced with Bill in s’ & p∈{q:∃a∃b[q = λs”.¬a danced with b in s”]}) → p(s) = p(s0)] & ∃x[x is a girl in s0 & ∀y[y is a boy in s0 → x danced with y in s ]]]
The second conjunct of the presupposition in (221) (bolded) is Conditional Leastness and it plays a crucial role in ruling out (218). It is equivalent to (223).
-
(223)
∀s[¬Eva danced with Bill in s → ∀x[x is a girl in s0 → ∃y[y is a boy in s0 & ¬x danced with y in s ]]]
This presupposition requires that in every situation where Eva did not dance with Bill, everyone who is a girl in s0 is such that she did not dance with some boy of s0. That can only hold if Eva is the only girl in the topic situation or there are no girls (and Eva is not a girl).
Let me first discuss the possibility that Eva is a girl in s0. Here is why the presupposition cannot be satisfied if there are some girls other than Eva in s0. Let’s consider a scenario where there is another girl in the topic situation, say Mary. There is a possible situation where Eva did not dance with Bill, but another girl of the topic situation s0, namely Mary, danced with every boy of s0; thus the presupposition is not satisfied.
If, however, there is exactly one girl, then the presupposition given in (221) and the at-issue content in (222) are consistent with each other. Since Eva is the only girl, it is entirely possible that in every situation where she did not dance with Bill, for every girl (i.e. for Eva) there is a boy of s0 she did not dance with (Bill), and in some situation where the facts regarding dancing are the same as in s0 for all other pairs of individuals, there is a girl (Eva) who danced with every boy of s0. We have already faced this problem earlier, and I suggest that we use the same solution in this case: the interpretation in question is ruled out by a general pragmatic constraint against using an existential DP when it is known that the head noun denotes a singleton set.
The only option left is that there are no girls in the topic situation. The presupposition will be satisfied in that case: if there are no girls in s0, in every situation there is no girl of s0 who danced with every boy of s0. However, this will contradict the assertion. This is because the sentence can be true in s0 only if there is a possible situation where some girl of s0 danced with every boy of s0, which can only obtain if there are girls in s0. Whenever the sentence is defined, it is false. There is no way for it to be true. I propose that this is the reason the sentence is perceived as ungrammatical.
I appealed to the competition between definites and indefinites in order to rule out the ungrammatical some…every combination in (220). However, substituting some with the does not improve the sentence, as shown in (224).
-
(224)
*The girl danced with every boy except Eva with Bill
did not dance.
The meaning generated by the system for (224) is well-formed. The presupposition is given in (225). From the presupposition we learn that Eva did not dance with Bill and that Eva is the girl and Bill is a boy. The assertive content is given in (226). The sentence is predicted to be true in s0 if and only if there is a possible situation where the girl (Eva) danced with every boy of s0 while all the propositions of the shape ‘a did not dance with b’ (where either ‘a’ is not Eva or ‘b’ is not Bill) have the same truth value as in s0. This means that the sentence is predicted to be true in s0 if and only if the girl (Eva) danced with every boy other than Bill in s0.
-
(225)
\([\!\![(224)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
¬Eva danced with Bill in s0 & ∀s[¬Eva danced with Bill in s → ∃y[y is a boy in s0 & ¬ ιx[x is a girl in s0] danced with y in s ]]
-
(226)
\([\!\![(224)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.¬Eva danced with Bill in s’ & p∈{q:∃a∃b[q = λs”.¬a danced with b in s”]}) → p(s) = p(s0)] & ∀y[y is a boy in s0 → ιx[x is a girl in s0] danced with y in s ]]
The sentence can be defined and true in s0: it is entirely possible that the girl (Eva) did not dance with a certain boy (Bill) and danced with every other boy. Moreover, the presupposition and the assertion are independent of each other: the presupposition can be satisfied when the sentence is false. The sentence is predicted to be false in s0 if the girl (Eva) did not dance with some boy who is not Bill in s0. This is entirely compatible with Bill being a boy and Eva not dancing with him in s0—the requirements introduced by the presupposition. Thus, the situation here is different than in cases where an exceptive contains only one element and its correlate is a definite description (cf. Sect. 4.5.2). I remind the reader that sentences like The girl came except Eva are ruled out because they are predicted to be always true when they are defined.
The sentence in (224) can be ruled out because the girl and Eva are used to refer to one and the same individual in the same sentence and this is generally is not allowed. However, even if we modify (231) in such a way that it does not suffer from this problem (as shown in (227)), a definite description is still not an acceptable correlate of a remnant of exceptive deletion.
-
(227)
*[The girl]1 danced with every boy except her1/she1 with Bill
did not dance.
I propose that what rules out (227) is the constraint on ellipsis that requires that there be a contrast between the remnants of ellipsis and the correlates in the antecedent—a constraint which I have appealed to in other cases already. This idea is supported by the fact that the full version of (227) is acceptable for those English speakers who accept fully pronounced clauses after except in general, as shown in (228).
-
(228)
[The girl]1 danced with every boy, except she1 did not dance with Bill.
The next question I will discuss here is why (219) (repeated below as (229)), where the existential does not have a corresponding remnant in the except-clause, is predicted to be grammatical on the theory proposed here.
-
(229)
Some girl danced with every boy except with Bill.
This is because the ellipsis is resolved differently in this case. There are two ways it can be resolved here. The two possibilities come from the two possible positions of the second quantifier some girl. It can be below every boy, in which case the ellipsis site also has an existential, as shown in (230). Alternatively, it can also be above every boy, in which case the ellipsis site includes its trace, as shown in (231).
-
(230)
[IP 5 [ [ExcP2 exceptC7 [[IP 6
not a girl s6danced s6 with BillF]∼C7] s5] [4 [3 [every boy s4 [2 some girl s3 [1 [t1 danced s3 with t2] ] ] ] ] ] ] ]Footnote 25
-
(231)
[IP5 [some girl s5 [4 [ExcP2 exceptC7 [[IP 6
t4did not dances6 with BillF]∼C7] s5] [3 [2 [every boy s3 [1 [ t4 danced s2 with t1 ] ] ] ] ] ] ] ]
The predicted meaning of (229) based on the LF in (230), where the ellipsis site contains a girl, is given in (232) (presupposition) and (233) (assertive content).
The first conjunct of the presupposition in (232) gives us the negative inference: there is no girl who danced with Bill. The second conjunct (bolded) gives us the inference that Bill is a boy.
-
(232)
\([\!\![(230)]\!\!]^{\mathrm{g}}\)(s0) is defined only if: ¬∃a[a is a girl in s0 & a danced with Bill in s0] & ∀s[¬∃x[x is a girl in s & x danced with Bill in s] → ∃y[y is a boy in s\(_{\textbf{0}}\) & ¬∃z[z is a girl in s & z danced with y in s ]]]
The at-issue content in (233) captures the domain subtraction inference. (233) makes reference to the set of propositions denoted by C7 (the variable restricted by the focus value of the sentence under except), which is given in (234)). The sentence is predicted to be true in s0 if and only if there is a possible situation where the truth values of all propositions of the shape ‘No girl danced with x’ where x is not Bill are the same as in s0 and where the claim ‘Every boy is such that some girl danced with him’ is true. This means that the sentence is predicted to be true in s0 if and only if every boy who is not Bill is such that some girl danced with him in s0.
-
(233)
\([\!\![(230)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff:
∃s[∀p[(p ≠ λs’.¬∃z[z is a girl in s’ & z danced with Bill in s’] & p∈g(7)) → p(s) = p(s0)] & ∀y[y is a boy in s0 → ∃a[a is a girl in s & a danced with y in s]]]
-
(234)
g(7) = {q: ∃x[q = λs’.¬∃z[z is a girl in s’ & z danced with x in s’ ]]}
The overall meaning we get here can be presented as a combination of the three claims in (235). As the reader can verify, this is indeed one of the meanings that (229) can receive.
-
(235)
-
i.
Negative Entailment: No girl danced with Bill.
-
ii.
Containment Entailment: Bill is a boy.
-
iii.
Domain Subtraction: For every boy other than Bill it holds that some girl danced with him.
-
i.
The second LF given in (231) is predicted to get the meaning where some girl scopes above every boy and its exceptive phrase. The predicted meaning is shown in (236) below. The sentence is predicted to be defined only if there is a girl such that she did not dance with Bill and in every situation where she did not dance with Bill, there is a boy of s0 who she did not dance with. Thus, Bill has to be a boy in s0. The sentence is predicted to be true in s0 if and only if there is a possible situation where all facts about this same girl dancing with people other than Bill are the same as in s0, where she danced with every boy—in other words, if and only if she danced with every boy who is not Bill. This gives us the domain subtraction inference.
-
(236)
\([\!\![(231)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃x[x is a girl in s0 & [z: ¬z danced with Bill in s0 & ∀s’’’[¬z danced with Bill in s’’’ → ∃y[y is a boy in s0 & ¬ z danced with y in s’’’]] .
∃s[∀p[(p ≠ λs’.¬z danced with Bill in s’ & p∈{q: ∃a[q=λs”.¬z danced with a in s”]}) → p(s) = p(s0)] & ∀b[b is a boy in s0 → z danced with b in s ] ] (x)] ]
The overall meaning we get here can be presented as a combination of the three claims in (237). As the reader can verify, this is another meaning available to sentence (229).
-
(237)
There is some girl x such that:
-
i.
Negative Entailment: x did not dance with Bill.
-
ii.
Containment Entailment: Bill is a boy.
-
iii.
Domain Subtraction: x danced with every boy other than Bill.
-
i.
The system developed here explains the ungrammaticality of the every…some combination of correlates in (238) in exactly the same way as the ungrammaticality of the some…every example considered above.
-
(238)
*Every girl danced with some boy except Eva with Bill
did not dance.
5.3.4 No…any, *No…every
As stated above, the restriction on the possible quantifiers observed in cases where an exceptive phrase contains multiple remnants is not about the form of the individual quantifiers but about the interpretation: in the context of the entire sentence each correlate of each remnant should contribute a quantifier equivalent to a universal quantifier. This is predicted by the analysis suggested here.
The explanation for this fact lies in the part of the presupposition that I called Conditional Leastness. It states that in every situation where the clause introduced by except is true, the quantificational claim is not true. In other words, the quantificational claim is negated. If a quantifier corresponding to a remnant is existential, this negation will turn it into a universal. As a consequence of this, we will always find ourselves in a configuration where a fact about one individual (the remnant) has to guarantee something for all individuals in the restrictor of the quantifier in all situations. This is only possible if this one individual is the only element in the restrictor of the quantifier or if the restrictor is empty. In the cases involving existentials discussed above, the first option was ruled out because it is not possible to use an existential if it is known that there is only one element that satisfies the restrictor of the existential. A similar restriction exists for such natural language quantifiers as every and no. Pragmatically they cannot be used if it is known that there is only one individual that satisfies the restrictor.
Here, I illustrate how the theory of clausal exceptives proposed in this paper, together with the restriction discussed above, correctly captures the fact that (239) is grammatical and (240) is not.
-
(239)
No girl danced with any boy except Eva with Bill
danced.
-
(240)
*No girl danced with every boy except Eva with Bill
danced.
My assumption about (239) is that it means three things listed in (241).
-
(241)
-
i.
Positive Entailment: Eva danced with Bill.
-
ii.
Containment Entailment: Eva is a girl and Bill is a boy.
-
iii.
Domain Subtraction: For all other pairs of individuals it holds that no girl danced with any boy.
-
i.
The meaning predicted for (239) is given in (242) (presupposition) and (243) (assertion).
-
(242)
\([\!\![(239)]\!\!]^{\mathrm{g}}\)(s0) is defined only if:
Eva danced with Bill in s0 & ∀s[Eva danced with Bill in s → ∃x[x is a girl in s0 & ∃y[y is a boy in s0 & x danced with y in s ]]]
-
(243)
\([\!\![(239)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.Eva danced with Bill in s’ & p∈{q: ∃a∃b[q = λs”.a danced with b in s”]}) → p(s) = p(s0)] & ¬∃x[x is a girl in s0 & ∃y[y is a boy in s0 & x danced with y in s ]]]
The presupposition captures the positive inference that Eva danced with Bill and the containment inference that Eva is a girl and Bill is a boy. The at-issue content captures the domain subtraction inference. The sentence is predicted to be true in s0 if and only if in some situation where the dancing facts are the same as in s0 for all pairs of people other than Eva–Bill, no girl of s0 danced with any boy of s0. As the reader can verify, this correctly captures the meaning this sentence has.
The meaning predicted for the ungrammatical example (240) with the no…every combination is given in (244) (presupposition) and (245) (assertion).
-
(244)
\([\!\![(240)]\!\!]^{\mathrm{g}}\)(s0) is defined only if:
Eva danced with Bill in s0 & ∀s[Eva danced with Bill in s → ∃x[x is a girl in s\(_{\textbf{0}}\) & ∀y[y is a boy in s\(_{\textbf{0}}\) → x danced with y in s]]]
-
(245)
\([\!\![(240)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.Eva danced with Bill in s’ & p∈{q:∃a∃b[q = λs”.a danced with b in s”]}) → p(s) = p(s0)] & ¬∃x[x is a girl in s0 & ∀y[y is a boy in s0 → x danced with y in s]]]
The problem is again with the second conjunct of the presupposition (Conditional Leastness, bolded in (244)). It requires that every situation in which Eva danced with Bill has a girl of s0 that danced with all boys in s0. This can only hold if Eva is a girl in s0 and Bill is the only boy or there are no boys in s0. This is the only way a fact about Bill can guarantee something for all boys of s0 in all possible situations. The possibility that Bill is the only boy in s0 is ruled out by the pragmatic principle that does not allow the use of every boy when it is known that there is only one boy. The option of there being no boy in s0 is not compatible with the at-issue content. Its equivalent formulation is given in (246). The sentence can be true in s0 only if there is a possible situation where every girl of s0 did not dance with some boy of s0. This requires that there are boys in s0.Footnote 26
-
(246)
\([\!\![(240)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p ≠ λs’.Eva danced with Bill in s’ & p∈ {q:∃a∃b[q = λs”.a danced with b in s”]}) → p(s) = p(s0)]) & ∀x[x is a girl in s0 → ∃y[y is a boy in s0 & ¬x danced with y in s ] ] ]
Since (240) cannot get a well-formed meaning due to the combination of functional elements in it, it is perceived as ungrammatical.
6 Plural, disjunctive, and quantificational remnants in exceptive clauses
In all of the cases discussed so far, the remnant of ellipsis inside an except-clause was an expression referring to a single individual. This is not always the case, as evidenced by (247).
-
(247)
Every girl came except Eva and Mary
did notcome.
This sentence comes with the familiar inferences: Eva and Mary did not come (negative entailment); Eva and Mary are both girls (containment entailment); and every other girl came (domain subtraction inference).
For cases like this one what I have suggested so far is not going to be enough. The analysis has to be modified to take such cases into account. As it stands, the analysis does not correctly capture the containment inference in (247). The sentence comes with the inference that both Eva and Mary are girls. Replacing one of those names with a male name results in infelicity, as shown in (248).
-
(248)
#Every girl came except Eva and John
did not come.
According to the analysis proposed here, the containment inference is captured by Conditional Leastness—the claim that establishes a law-like relation between the clause following except and the main clause. In this case this would be the claim that in every situation where Eva and John did not come, it is not true that every girl of s0 came. This is equivalent to (249), which requires that Eva or John is a girl. Thus, this version of Conditional Leastness does not capture the fact that John has to be a girl in order for (248) to be well-formed.
-
(249)
∀s[Eva and John did not come in s →∃x[x is a girl in s0 & ¬x came in s ]]
Conditional Domain Subtraction also should change in order to capture the domain subtraction inference in (247). Conditional Domain Subtraction, recall, is the claim that there is a possible situation where all focus alternatives of the clause following except other than the original proposition have the same truth value as in s0 and where the quantificational claim is true. If the set of focus alternatives for the clause following except in (247) contains the propositions denoted by Eva did not come and Mary did not come, both of which are not equal to the proposition that Eva and Mary did not come, then we will evaluate the quantificational claim in situations where the truth value of the original proposition happens to be the same as in s0 because it depends on the value of those two propositions. This is not the desired result, because the quantificational claim is true only in a possible situation where Eva came and Mary came, given that they are girls. In order to capture the domain subtraction here we need to subtract both of the propositions in (250) from the domain of quantification over propositions that restrict the domain of quantification over possible situations. Conditional Leastness should also apply to both of those propositions.
-
(250)
{λs. ¬Eva came in s, λs’. ¬Mary came in s’}
Let’s assume that the set of focus alternatives for the exceptive clause in (247) ([Eva and Mary]F did not come) is as shown in (251).Footnote 27 Granted that we have the set of propositions in (250), the meaning of (247) can be captured via the three claims given in (252).
-
(251)
{λs. ¬Eva came in s, λs’. ¬Mary came in s’, λs”. ¬Sveta came in s”, λs’’’. ¬Anna came in s’’’, λs. ¬Bill came in s, λs’.¬John came in s’, etc.}
-
(252)
-
i.
Negative Entailment: Eva and Mary did not come in s0
-
ii.
Containment Entailment: ∀p[p∈(250) → ∀s[p(s) = 1 → ¬∀x[x is a girl in s0 → x came in s]]]
-
iii.
Domain Subtraction: ∃s[∀p[(p∈(251) & p∉(250)) → p(s) = p(s0)] & ∀x[x is a girl in s0 → x came in s]]
-
i.
Now we need to find a way of going from the proposition [Eva and Mary]F did not come to the two propositions in (250). The property that the two propositions in (250) have that the rest of the propositions in (251) do not have is that they are entailed by the proposition denoted by the original sentence Eva and Mary did not come. The denotation of except has to be modified in such a way that Conditional Leastness and Conditional Domain Subtraction make reference to propositions in the set of focus alternatives for the clause following except that are entailed by the original proposition.
The remnant of ellipsis can also be a disjunctive DP, as shown in (253).
-
(253)
Every girl came except Eva or Mary
did not come.
This sentence has the following meaning components: Eva or Mary did not come (negative entailment); Eva and Mary are both girls (containment); and every other girl came (domain subtraction). The only difference in meaning between (253) and the sentence with conjunction (247) considered above is in the negative entailment, and it is contributed directly by the clause following except. Here I will use the same strategy and try to find a way of going from [Eva or Mary]F did not come to the set of propositions in (251) (i.e., the propositions with the individuals in the position corresponding to the subject) and selecting from it the two propositions in (250).
We need to think about how to compute the focus alternatives for the clause following except in this case. The disjunctive DP Eva or Mary cannot be understood as an expression of type e (unlike the plural DP Eva and Mary). It is standardly assumed that the focus alternatives are formed through replacement of the focused element by elements of the same semantic type. In this case this means that if we compute the focus alternatives, we won’t get the set of propositions in (251).
What I would like to use here is the fact that Rooth’s system of focus interpretation has a certain flexibility in regard to the position where the focus alternatives are computed. In order to get the focus alternatives of the right shape we could compute them at the position below the position of the disjunctive DP. This is shown in (254), where a part of a possible LF corresponding to the exceptive phrase is given. A structure consisting of ∼ and a silent variable is placed below the disjunctive DP and above its trace t4. The trace is an element of type e and it is focused.Footnote 28
-
(254)
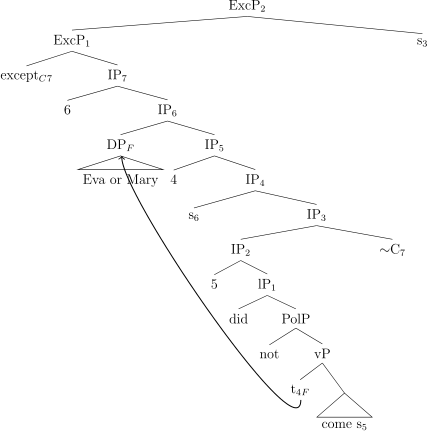
This means that the value of C7 will be the set of propositions of the general shape ‘x did not come’ where x is an individual as shown in (255). The variable on the focus sensitive operator except is co-indexed with this variable.
-
(255)
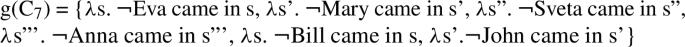
The overall meaning of the sentence in (253), where the remnant of exceptive deletion is the disjunctive DP Eva or Mary, can be expressed as a combination of the three claims in (256).
-
(256)
-
i.
Negative Entailment: Eva or Mary did not come in s0
-
ii.
Containment Entailment: ∀p[p∈{λs. ¬Eva came in s, λs’. ¬Mary came in s’} → ∀s[p(s)=1 → ¬∀x[x is a girl in s0 → x came in s]]]
-
iii.
Domain Subtraction: ∃s[∀p[(p∈g(7) & p∉{λs. ¬Eva came in s, λs’. ¬Mary came in s’}) → p(s) = p(s0)] & ∀x[x is a girl in s0 → x came in s ]]
-
i.
We again need to use the proposition that is denoted by the sister of except to select the propositions in the set {λs. ¬Eva came in s, λs’. ¬Mary came in s’}. The sister of except has the meaning given in (257). What separates those two propositions from the rest of the propositions in (255) is that they entail the proposition in (257).
-
(257)
\([\!\![\mathrm{IP}_{7}]\!\!]^{\mathrm{g}}\) = λs. Eva or Mary did not come in s
The updated version of except that captures the meaning of the examples with conjunction and disjunction is given in (258). The changes are in the second conjunct of the presupposition that is responsible for the containment inference (Conditional Leastness) and in the assertive content responsible for the domain subtraction inference. Conditional Leastness is expressed as follows: for every proposition in the restrictor set that is entailed by or entails the original proposition that except takes as its first argument it holds that in every situation where it is true, the quantificational claim is not true. The domain subtraction is captured as follows: there is a situation where all propositions in the restrictor set that are not entailed by and do not entail the original proposition have the same truth value as in the situation of evaluation, the quantificational claim is true.
-
(258)
\([\!\![\mathrm{except}_{\mathrm{Cn}}]\!\!]^{\mathrm{g}}\) = λq<st>.λs’.λM<s<st≫:
q(s’) = 1 & ∀p[(p∈g(n) & ( (q⊆p) ∨ (p⊆q) )) → ∀s[p(s) = 1→ ¬M(s’)(s) = 1]].
∃s[∀p[(p∈g(n) & q⊈p & p⊈q) → p(s) = p(s’)] & M(s’)(s) = 1]
Now let me address the question why we do not want to compute the focus alternatives higher up in this case. Let’s see what happens if the set of focus alternatives is computed by replacing Eva or Mary with elements of the same semantic type (≪et>t>). Under the assumption that proper names can undergo type-shifting to type ≪et>t> (Partee 1986), this set will include the propositions denoted by Eva did not come and Mary did not come. Those two entail the original proposition in the except-phrase (the proposition that Eva or Mary did not come). Therefore, Conditional Leastness will establish a law-like relationship between each of those two propositions and the quantificational claim, and by doing so it will give us the inference that Eva and Mary are girls. However, the set of focus alternatives will also include propositions denoted by Eva or Anna did not come and Mary or Anna did not come (where Anna refers to a girl). Those two do not entail that Eva or Mary did not come and are not entailed by this proposition. We will run into a problem with Conditional Domain Subtraction: we will have to evaluate the quantificational claim in a situation where the truth values of Eva or Anna did not come and Mary or Anna did not come are the same as in s0. Since we know from the presupposition that Eva or Mary did not come, at least one of those two propositions is true in s0. Thus, we will evaluate Every girl came in a situation where at least one of those two propositions is true. We also know from the presupposition that Eva and Mary are girls. This means that if there is at least one other girl who is not Mary or Eva in s0, the sentence is predicted to be false whenever it has a defined meaning. Therefore, we do not want to compute focus alternatives higher up in this case.
Moltmann (1995) observed that except-phrases can contain existential quantificational DPs, as illustrated in (259).
-
(259)
Every student came except three boys
didnot come.
The analysis developed above for plural remnants combined with the widely accepted idea that existentials can take a wider scope than indicated by their overt position (Fodor and Sag 1982; Farkas 1981; Reinhart 1997, among many others) can successfully handle those cases. I propose that here the existential that appears inside the except-phrase takes the widest scope in the sentence. This will allow us to capture the intuitive meaning of (276): there are three boys such that they are students who did not come, whereas every other student came. One way of implementing this is to introduce a choice function variable that applies to the predicate three boys and existentially close it at the topmost level (Reinhart 1992, 1997). Following Reinhart (1997), let’s assume that three boys in this case denotes a set of pluralities consisting of three boys. When a choice function applies to this set, it picks one of those pluralities.
A possible structure of the except-clause in this case is given in (260). In this structure f3 is a choice function variable that will be existentially closed at a higher level, and s4 is a variable over situations that will be bound by the highest abstractor over situations in the full structure. Let’s again assume that the set of focus alternatives denoted by the variable C7 contains propositions of the shape ‘x did not come’, where x is an atomic individual (in other words, g(7) is as shown in (255)). Except selects from this set the propositions that are entailed by or entail the proposition denoted by the clause following except. This proposition has the shape ‘X did not come’, where X is a specific plurality consisting of the three boys selected by the choice function; thus except selects three propositions with atomic individuals from the set of focus alternatives and establishes the law-like relationship between each of those propositions and the quantificational claim. This accounts for the inference that each of the three boys who did not come is a student. Except also states that the truth values of all propositions in the set of focus alternatives other than those three are compatible in the topic situation with the quantificational claim. With those assumptions, the predicted meaning components of (259) in s0 can be presented (quite informally) as shown in (261). This captures the intuitive meaning of the sentence.
-
(260)
[[exceptC7 ∼C7 [5 [f3 three boys s4]F
did notcomes5] ] s4]
-
(261)
\([\!\![(259)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff there is a way of choosing f such that:
-
(i)
f (〚three boys s\(_{0}]\!\!]^{\mathrm{g}}\)) did not come in s0
-
(ii)
For every proposition p in g(7) that is entailed by or entails [λs.f (〚three boys s\(_{0}]\!\!]^{\mathrm{g}}\)) did not come in s] it holds that in every situation where p is true, some student of s0 did not come.
-
(iii)
There is a possible situation where all p in g(7) that are not entailed by and do not entail [λs. f (〚three boys s\(_{0}]\!\!]^{\mathrm{g}}\) did not come in s] have the same truth value as in s0 and where it is true that every student of s0 came.
-
(i)
7 Except and possibly
The additional advantage of the approach proposed here is that it correctly captures the interaction of except and modal adverbs such as possibly. Moreover, the present approach is the first compositional treatment of modal adverbials inside exceptives. The fact that some exceptive constructions can host modal adverbials was observed by Moltmann (1995) and García Álvarez (2008).Footnote 29 An example illustrating the interaction between except and possibly is given in (262).
-
(262)
Every girl came except, possibly, Eva
did not come.
The meaning of this sentence has three components, given in (263).
-
(263)
-
i.
Negative Entailment: It is possible that Eva did not come.
-
ii.
Containment Entailment: Eva is a girl.
-
iii.
Domain Subtraction: Every other girl came.
-
i.
What is crucial here is that possibly only affects one aspect of the meaning: namely, the negative entailment (Aron Hirsch, p.c.). Eva has to be a girl and not ‘possibly’ a girl in order for the sentence to have a well-formed meaning. The sentence is true if every other girl came; a mere possibility of every other girl coming cannot make it true. Those facts are not expected if we try to extend von Fintel’s analysis of but-exceptives to except-exceptives. First of all, according to von Fintel’s approach what follows an exceptive marker is a set, and it is not clear how to put a set together with a modal operator. Second, negative entailment and containment both are inferences drawn from Leastness; they are not separated as meaning components.Footnote 30 According to the approach I propose here, the negative inference is contributed directly by the clause following except and the containment is contributed by a separate meaning component. Since those two meaning components are separated, possibly can target one of them without targeting the other one.
A possible LF for (262) is given in (264).
-
(264)
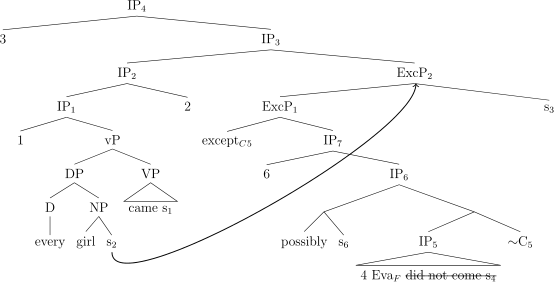
In this LF I reconstructed the subject below the position of the modal operator in the except-clause. The construction consisting of ∼ and a silent variable C5 is placed below possibly. The variable restricting the value of except is co-indexed with C5. The sister of except has the value shown in (265). The value of C5 is computed below possibly: the ∼ operator requires that its value is restricted by the focus value of the sister of ∼C5. One possible value for this variable that satisfies this condition is given in (266).
-
(265)
\([\!\![\mathrm{IP}_{7}]\!\!]^{\mathrm{g}}\) = λs.∃s’[s’ is epistemically accessible from s & ¬Eva came in s’]
-
(266)
\([\!\![\mathrm{C}_{5}]\!\!]^{\mathrm{g}}\) = g(5) =
{λs. ¬Eva came in s, λs’. ¬Sveta came in s’, λs”. ¬Mary came in s”, λs’’’. ¬Anna came in s’’’, λs. ¬Bill came in s, λs’.¬John came in s’}
Conditional Leastness and Conditional Domain Subtraction both make reference to the propositions in C5 that are entailed by or entail the original proposition in the sister of except. What are the propositions in (266) that are entailed by (265) or entail it?
The proposition denoted by Eva possibly did not come does not entail any of the propositions in (266). But there is a proposition in this set, specifically, the proposition denoted by Eva did not come (λs. ¬Eva came in s), that entails it. This is because if Eva did not come in s0, s0 must be such that the epistemic evidence available in s0 is compatible with Eva not coming. In other words: Eva did not come entails It is possible that Eva did not come.
This means that the predicted meaning for this sentence is as shown in (267) (presupposition) and (268) (assertion). The presuppositional contribution of except in this case is that the proposition denoted by the clause following except is true in s0 (Eva possibly did not come) and that for every proposition in C5 that entails or is entailed by this proposition it holds that in every situation where it is true, the quantificational claim (Every girl came) is not true. In this case there is only one proposition that satisfies this condition. This means that Conditional Leastness can be presented as shown in (267) (the bolded part). This gives us the inference that Eva is a girl (the containment entailment).
-
(267)
\([\!\![(264)]\!\!]^{\mathrm{g}}\)(s0) is defined only if
∃s’[s’ is epistemically accessible from s0 & ¬Eva came in s’] & ∀s[¬Eva came in s → ∃x[x is a girl in s\(_{\textbf{0}}\) & ¬x came in s]]
The assertive contribution of except in this case is that there is a possible situation where all propositions in C5 that are not entailed and do not entail the original proposition denoted by the clause following except have the same truth value as in s0, and where the quantificational claim is true. Since there is only one proposition that is entailed by or entails Eva possibly did not come, namely, the proposition [λs. ¬Eva came in s], the quantification over possible situations where the quantificational claim is evaluated is restricted to situations where all propositions in (266) other than [λs. ¬Eva came in s] have the same truth value as in s0. This captures the domain subtraction inference.
-
(268)
\([\!\![(264)]\!\!]^{\mathrm{g}}\)(s0) = 1 iff
∃s[∀p[(p∈g(5) & p ≠ λs’. ¬Eva came in s’) → p(s) = p(s0)] & ∀x[x is a girl in s0 → x came in s]]
The last issue I will address here is what happens if ∼C5 is not placed below possibly. In this case the presupposition that will be generated will not be satisfied. This means that the sentence will not have a defined meaning. The presupposition predicted for this case is given in (269). The problem is with the second conjunct (bold font). It is not true that in every situation where it is possible that Eva did not come, there is a girl who did not come. In some situations where it is possible that Eva did not come, every girl came even if Eva is a girl.
-
(269)
∃s’[s’ is epistemically accessible from s0 & ¬Eva came in s’] & ∀s[∃s’[s’ is epistemically accessible from s & ¬Eva came in s’] → ∃x[x is a girl in s\(_{\textbf{0}}\) & ¬x came in s]]
8 Exceptives with most and many and other open issues
In my discussion of the distribution puzzle I have focused on the interaction of exceptives with existential quantifiers. The account I suggested predicts that except should not be compatible with many, most, and few. Let’s consider a case with most given in (270). The meaning component responsible for the distribution puzzle is the one that establishes a law-like relationship between the exceptive clause and the quantificational claim. In (270), it will be as shown in (271): in every situation where Eva did not come, it is not true that most girls came (in other words: less than half or half of the girls came). In order for (270) to have a defined meaning, (271) has to hold, but it does not: it is entirely possible that there is a situation where Eva did not come but, say, all other girls came. (271) can be true only if the number of girls in s0 is not larger than two, but in this case, most girls cannot be used (see a discussion of this issue in (Hirsch 2016:145)). The analysis makes the same prediction for many and few.
-
(270)
??Most girls came except Eva
did notcome.
-
(271)
∀s[¬Eva came in s → |{x: x is a girl in s0 & x came in s}| ≤ 1/2 |{z: z is a girl in s0}| ]
García Álvarez (2008) has argued that exceptive constructions (including the ones introduced by except) are compatible with many, most, and few based on corpus data. Some of his examples are given in (272)–(274). In general, judgments about such cases are not uniform among native speakers of English. Some work in this area follows García Álvarez (2008) in assuming that these cases are grammatical (Peters and Westerståhl 2006; Nadathur and Lassiter 2018). Moltmann (1995:227) reports that most is not compatible with except. Further empirical research is required in order to establish both the acceptability of such examples and their exact interpretation.
-
(272)
Most dishwashers except very low-end models have a water-saving feature.
-
(273)
Kate is an actress who has played many roles except that of a real woman.
-
(274)
Few people except Frank Capra expected the 1946 film ‘It’s a Wonderful Life’ to become a classic piece of Americana.
García Álvarez (2008) develops an approach to the semantics of exceptives that aims to explain these data while still accounting for the fact that exceptives are not compatible with existential quantifiers, as well as for the inferences that exceptives contribute. He proposes that exceptives are always propositional semantically and that they establish a special entailment relationship between the quantificational claim and the proposition they introduce. In this respect his account has some similarity to what I have proposed here. But unlike my account, his proposal does not appeal to the notion of a possible world or situation. Another crucial difference between his approach and mine is that he treats all exceptives as syntactically phrasal. According to García Álvarez (2008), except in (275) below shares the verbal material with the quantifier most girls. Sentences that have a general shape similar to (275) are only defined if in every preferred model where Most girls came is true, Eva came is true too, if it is given that Eva is a girl.Footnote 31 This relation is called ‘preferential entailment’. The claim is that while this holds for sentences that belong to a general class of generalizations, it does not hold for existential claims like the one in (276). This sentence is not predicted to have a defined meaning because some girl came does not preferentially entail Eva came. García Álvarez (2008) does not elaborate on how the preferred models are selected. The negative inference is treated as a part of the assertive content. The assertive content of (275) is as shown in (277): it is a conjunction of the quantificational claim (Most girls came) and the statement that Eva did not come, which is constructed from the main predicate (came), the DP in the exceptive phrase (Eva), and a special unpronounced operator in the logical form of (275) that is interpreted as negation.
-
(275)
??Most girls except Eva came.
-
(276)
*Some girls except Eva came.
-
(277)
\([\!\![(275)]\!\!]^{\mathrm{g}} \) = 1 iff |{x: x is a girl & x came}| > 1/2 |{z: z is a girl}| & ¬Eva came
The biggest challenge for this kind of phrasal approach is to account for the fact that if the generalization is negative, as in (278), the inference has to be positive (that Eva came). García Álvarez (2008) proposes that the same covert operator that is interpreted as negation in (275) is here interpreted as an identity function. This is a serious disadvantage of this or any other approach that gives two different semantic treatments for positive and negative generalizations: there is no language reported so far that has two different lexical items for exceptives—one for positive generalizations and one for negative generalizations. This strongly suggests that a more plausible semantic theory of exceptive constructions has to explain their contribution in positive and negative cases in a uniform manner.
-
(278)
No girl except Eva came.
While my proposal as it stands does not predict a well-formed meaning for (275), I would like to consider possible modifications that could potentially do so. The aspect of meaning that would have to be modified is the one establishing a law-like relationship between the except-clause and the quantificational claim.
One direction would be to restrict the quantification over possible situations and select the ones that are most relevant. The problem is that I do not see what the required relevance relation would be here. Earlier in this paper I discussed the idea of restricting this quantification to situations that are most similar to the actual topic situation and rejected it. Introducing such a restriction will not help us with (270), and it would challenge the solution to the distribution puzzle. Under this approach, the example with an existential in (279) is predicted to have the truth-conditions given in (280). This can easily hold in the actual topic situation s0 if it is such that whenever Eva does not come, no girl comes, because all girls do what Eva does. For these reasons, I will not further explore this option here.
-
(279)
*Some girls came except Eva
did not come.
-
(280)
∀s[s is most similar to s0 among the situations s’ such that Eva did not come in s’ → ¬∃x[x is a girl in s0 & x came in s]]
Another line of thought would be to change the quantification over possible situations and talk about most possible situations/scenarios instead of every possible situation. The law-like relationship between the except-clause and the quantificational claim would look like this: in most possible scenarios where the except-clause is true, the quantificational claim is not true.Footnote 32
The challenge here is to find a way of counting the relevant scenarios. Let us assume that the clause following except is \(\mathit{Eva}_{F}\) did not come, as in our example with most in (270). We do not need to count all the possible situations where Eva did not come. Rather, we are interested in counting the number of unique scenarios that only differ with respect to the people who came. We can do so by using the focus alternatives of the clause following except. Let us assume for simplicity that in this case the set of focus alternatives has only three items—Eva, Mary, and Sveta—as shown in (281).Footnote 33 Let us also assume that Eva, Mary, and Sveta are the girls in s0. There are as many unique scenarios as there are subsets of this set. In this case there are 8 subsets, shown in (282), and 8 possible scenarios: zero of the propositions in (281) are true (everyone came), only the first one is true (only Eva did not come), only the second one is true (only Mary did not come), only the third one is true (only Sveta did not come), only two first propositions are true (only Eva and Mary did not come), etc.
-
(281)
Alt={λs. ¬Eva came in s, λs’. ¬Mary came in s’, λs”. ¬Sveta came in s”}
-
(282)
∅, {s. ¬Eva came in s}, {λs’. ¬Mary came in s’}, {λs”. ¬Sveta came in s”}, {s. ¬Eva came in s, s’. ¬Mary came in s’}, {s. ¬Eva came in s, s’. ¬Sveta came in s’}, {λs. ¬Mary came in s, λs’. ¬Sveta came in s’}, {s. ¬Eva came in s, s’. ¬Mary came in s’, s”. ¬Sveta came in s”}
Now we can count the number of possibilities where Eva did not come. This is the number shown in (283): the number of subsets of Alt in (281) such that in all situations where each proposition in the subset is true and the rest of the alternatives are false, Eva did not come. There are four such subsets/scenarios (they are given in (282) in bold).
-
(283)
|{m: m⊆Alt & ∀s[(∀p[p∈m → p(s) = 1] & ∀q[q∉m & q∈Alt → q(s) = 0]) → ¬Eva came in s]}|
Now we can reformulate our law-like relationship and say that in most (more than half) scenarios where the clause following except is true, the quantificational claim is false. This will hold if the quantifier is most or every, but this will not hold if the quantifier is some. Thus, under the assumption that this is the condition except imposes, we can capture the fact that except is not acceptable with existentials but is acceptable with most and every.
Most girls of s0 came is true only in one scenario out of the four where Eva did not come (this is the one where she is the only person who did not come). Thus, in most scenarios where Eva did not come, it is false that most girls of s0 came. (It is false in all scenarios where two or three girls did not come.)
Every girl of s0 came is false in all of the scenarios where Eva did not come.
However, if we count the possibilities where Some girl of s0 came is true among the four scenarios where Eva did not come, we will discover that there are three such possibilities. Thus, it is not going to be true that in most scenarios where Eva did not come, the quantificational claim Some girl of s0 came is false.
The reader can verify that adding more alternatives (including the ones where the subject is not a girl of s0) will not change this general arrangement.
The law-like relationship I proposed in this paper also captures the containment inference and ensures that the ellipsis is resolved with the right polarity. The modified version of it considered above does not do that for all cases. Let’s consider the case with every and imagine that Eva is not a girl in s0. It still holds that in most scenarios where Eva did not come, it is false that every girl of s0 came (it is true only in one case, where Eva is the only person who did not come). Thus, pursuing this modification would require introducing an additional meaning component. This could be done by stating that the reverse also holds: in most (more than half) possible scenarios where the quantificational claim is true, the clause following except is false. If Eva is not a girl, then it is not going to hold that in most possible scenarios where every girl of s0 came, Eva came. This is because if Eva is not a girl in s0, Every girl of s0 came is true in two scenarios corresponding to the first two subsets in (282); Eva came only in one of them.
Overall this is a promising modification of the approach developed in this paper that could potentially capture the judgment of some English speakers according to which except is compatible with most, many, and few, but I have to leave a proper investigation of all of its consequences for future work.
Another important question García Álvarez’s (2008) work poses for us is how to treat phrasal exceptives if such cases exist along with clausal ones, as I hypothesized here. If clausal exceptives introduce quantification over possible situations, it is natural to assume that phrasal exceptives should do that too. The idea that an exceptive forms a conjunction-like structure with a quantificational DP and constructs the relevant proposition from the main predicate that was proposed by Garcia-Alvarez seems to be promising. The biggest challenge here would be to give a unified treatment for positive and negative generalizations, as there won’t be negation in the constituent following except when the generalization is positive. I leave this issue as well for future research.Footnote 34
9 Conclusions
In this paper I have argued that the English exceptive construction introduced by except can involve ellipsis. I have empirically established some of the properties of exceptive deletion in English, in particular I proposed that this kind of ellipsis allows for a polarity mismatch between the antecedent and the ellipsis site.
I have proposed a novel conditional semantic analysis for clausal exceptives. The analysis is conditional in the sense that there is quantification over possible situations and exceptive clauses restrict the domain of this quantification. I have shown how this analysis derives the inferences that exceptives come with as well as their distribution. The conditional analysis explains the cases that the phrasal analysis cannot capture: cases where a remnant is a PP with a meaningful preposition, sprouting cases, and multiple remnant cases. I proposed that a clausal exceptive introduces an exception to a claim expressing a generalization, and I suggested a specific way of thinking about what ‘being an exception’ means. In sum, a claim X is an exception to a generalization Y if (i) X happened; (ii) in every situation where X happened Y is not true; and (iii) had X not happened, Y would have been true. An additional benefit of the approach developed here is that it provides a compositional treatment of modal operators (such as possibly) inside exceptive constructions.
Notes
I do not make a claim here that exceptives introduced by except must always be clausal.
I am grateful to Aron Hirsch (p.c.), who shared with me his observation that possibly only targets the negative inference.
Following common practice, I switch back and forth between function talk and set talk in my exposition of (Moltmann 1995).
There is one caveat here. In cases where the set introduced by except has only one individual, as in (i), and there is exactly one girl in the world, the Homogeneity Condition is met. In order to address this issue, Moltmann proposes that the Homogeneity Condition has to be satisfied “not only with respect to one particular model, but with respect to certain other models” (Moltmann 1995:242).
-
(i)
*Some girl except Eva came.
-
(i)
Not all English speakers find exactly acceptable inside except-phrases.
The observation that except can host a PP that does not have a correlate in the main clause was independently and simultaneously made by Potsdam and Polinsky (2019), who also argued that English except can be a clausal exceptive construction.
This proof is built on the general proof that von Fintel (1994) provides. The set-theoretic tautologies employed here are as follows. For any sets A, B, and C:
-
(i)
(A∩B̅)⊆C̅ = (A∩C)⊆B
-
(ii)
∀Y[A⊆Y → B⊆Y] = B⊆A
-
(i)
Stockwell and Wong (2020) also argued that except-phrases can involve ellipsis and that ellipsis is resolved with a polarity mismatch, based on the fact that except-phrases can serve as antecedents to sprouting with negation in the ellipsis site, as in John likes everyone except Ann, but I don’t know why
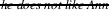 .
.Some people I consulted with did not find examples like (63) fully acceptable.
Interestingly, the exceptive construction introduced by but does not show a similar contrast: NPIs are not licensed inside but-phrases independently of whether the quantifier is universal or negative (as shown in (i) and (ii)). Another fact about but-exceptives is that they do not show traces of a clausal structure: the maximal syntactic constituent they can host is a DP (as shown in (iv)). Those facts can be taken as an argument supporting the idea that but-exceptives are not underlyingly clausal.
-
(i)
*John danced with everyone but any girl from his class.
-
(ii)
*John danced with no one but any girl from his class.
-
(iii)
I met a student from every city in Spain but Barcelona.
-
(iv)
*I met a student from every city in Spain but from Barcelona.
-
(i)
Fălăuş and Nicolae (2016) and Pasquereau (2020) argue that a covert negation can be inserted in a high projection as a last-resort rescuing mechanism only when a part of the structure has been elided. Thus, it is possible that it is not the case that the ellipsis site contains negation in (84), but rather a covert negation is inserted high in the structure inside the except-clause, which is forced by the meaning of except and is possible because ellipsis is involved. I leave this issue for future research.
This idea is based on von Fintel’s (1994) way of modeling quantifier domain restriction.
Domain subtraction is expressed as existential quantification over possible situations, which makes this analysis different from the standard analysis of bare conditionals, which are usually understood as restrictors of universal quantifiers over possible situations. The quantification can be universal if we change the restrictor and add the condition that the original proposition in the except-clause is false in the considered situations, as shown below in (i). The choice in favor of existential quantification was made rather arbitrarily here.
-
(i)
∀s[(Eva came in s & ∀p[(p ≠ λs’. ¬Eva came in s’ & p∈〚EvaF did not come〛gF) → p(s) = p(s0)]) → ∀x[x is a girl in
 → x came in s]]
→ x came in s]]
-
(i)
In this respect English except behaves like a typical connected exceptive by Hoeksema’s (1987, 1995) criteria. It can only appear in the position directly adjacent to a quantificational DP or at the end of a sentence.
-
(i)
Every girl except Eva came.
-
(ii)
Every girl came except Eva.
-
(iii)
*Except Eva every girl came.
Compare this with a free exceptive except for, which is fine in all three positions.
-
(iv)
Every girl except for Eva came.
-
(v)
Every girl came except for Eva.
-
(vi)
Except for Eva, every girl came.
It also behaves like a typical connected exceptive with plural definite descriptions:
-
(vii)
*The girls except Eva came.
-
(viii)
Except for Eva, the girls came.
-
(i)
Ellipsis is resolved positively if the generalization is negative even if the quantifier is every:
-
(i)
Every girl did not come except Eva
came.
-
(i)
The argument presented here would apply also to cases with plural indefinites, such as (i). The predicted law-like relation would be as follows: in every situation where Eva did not come, it is false that some girls of s0 came. That can only hold if Eva is the only girl in s0 or if there are no girls in s0. The second option is incompatible with the assertive content, which requires that there is a possible situation where some girls of s0 came. This means that in addition to the issues discussed in this section, there will be a conflict between the plural marking on the noun and the presupposition requiring that Eva is the only girl in s0.
-
(i)
*Some girls came except EvaF
did not come.
-
(i)
This was pointed out to me by Kyle Johnson and Keny Chatain (p.c.).
In the LF in (171) we need to pay attention to the situation variables inside the clause introduced by except. This is an IP that contains two predicates: the one denoted by the NP present from my mom and the one denoted by got. Potentially, there are two possible options for the situation variable inside the NP: it can be bound by the abstractor inside its own clause 5 or it can be bound by the highest abstractor 4 (in this case the predicate will get the transparent evaluation, i.e. it will be evaluated with respect to the topic situation s0 and not be bound by the quantifier over situations). In the LF in (171) I have chosen the latter option. The reasoning behind that choice is as follows. If both of the variables (the one on the predicate get and the one on the NP present from my mom) were bound by the same abstractor 5, then Conditional Leastness would have been as shown in (i), where the variable that has changed is boxed.
-
(i)
∀s[∃x[x is a present from my mom in
 & I got x in s] → ∃y[y is a present in s0 & I got y in s]]
& I got x in s] → ∃y[y is a present in s0 & I got y in s]]
This presupposition is very hard to satisfy. The reason for this is that something can be a present in one possible situation and not be a present in another. According to (i), every situation that has a thing that is a present from my mom in that situation is such that it has a thing that is a present in s0. This condition can only be met by a predicate that does not change its extension from situation to situation. It does not seem likely that the predicate denoted by presents has this property. However, we do not need to worry about the derivation that leads to this very strong presupposition. Nothing in the system forces the two situation variables to carry the same index. What is important is that there is an LF—the one shown in (171)—that leads to the correct interpretation.
-
(i)
I thank Kyle Johnson (p.c.) for the observation that it is only the type of the correlates of the remnants that matters.
Some speakers of English find this example grammatical under the interpretation where (194) is equivalent to (192).
Following Moltmann (1995), I assume that dance with is not a symmetric predicate. The assumption is that there is a possible situation where Eva danced with Bill, but Bill did not dance with Eva (say, he was unconscious, and she just carried him during the dance). The reason why this assumption is required is that otherwise the presupposition can be satisfied if Eva is a boy in s0 and Bill is a girl in s0.
Not all speakers of English find this sentence grammatical. For some speakers the phrasal version of the sentence is preferred (the version without with). Everyone I consulted with found the example I met a student from every city in Spain except from Barcelona acceptable. I do not know what the relevant difference between those two examples is.
For simplicity I represented the movement of the except-clause as a leftward movement in these LFs.
(246) would be compatible with there being no boys in s0 if there were no girls in s0. This is because the universal quantification is true if its restrictor is empty. However, the part of the presupposition bolded in (244) is not compatible with this scenario.
Nothing would go wrong here if the set of focus alternatives included also the propositions where the individual corresponding to the subject of the sentence denoting this proposition is plural. I make this assumption for simplicity of exposition.
Rooth (1996) discusses some cases where the focus alternatives are computed for a trace of an expression that is marked with a focus.
The prediction von Fintel’s approach makes is correct for but-exceptives: but-exceptives cannot host such modals as possibly: *Every girl came but, possibly, Eva. This is another fact that supports the idea that but-exceptives are not underlyingly clausal.
This is achieved via a reference to a specific sentence structure and a syncategorematic definition for the notions of generalization and instantiation that identify the restrictor of a quantifier by its position in the sentence structure. An advantage of the analysis in terms of possible worlds/situations proposed here is that we do not need to make a reference to a specific sentence structure to capture the containment inference; we can simply use the world/situation variable mechanism that allows the predicate inside a DP to be intensionally independent from the main predicate. Sentences with except can have different structures, and it does not seem plausible that we can give one syncategorematic definition that covers all cases (for example, sentences with one remnant can have one quantifier; sentences with multiple remnants must have multiple quantifiers).
I thank Lucas Champollion who suggested that I explore this idea.
The only reason why the number of alternatives is restricted to three is that it makes counting easier; this number corresponds to the minimal number of girls needed in order for most girls to have a defined meaning.
One idea of a unified propositional treatment of phrasal exceptives is suggested and explored in Vostrikova (2019b:404-436).
References
Alonso-Ovalle, Luis, Paula Menéndez-Benito, and Florian Schwarz. 2011. Maximize Presupposition and two types of definite competitors. In Proceedings of NELS 39, eds. Suzi Lima, Kevin Mullin, and Brian Smith. Vol. 1, 29–40. Amherst: GLSA.
Atlas, Jay. 1993. The importance of being ‘only’: Testing the neo-Gricean versus neo-entailment paradigms. Journal of Semantics 4: 301–318.
Breheny, Richard. 2005. Exhaustivity, homogeneity, and definiteness. In Proceedings of the fifth Amsterdam Colloquium, eds. Paul Dekker and Michael Franke. 59–65. Amsterdam: ILLC.
Brown, Sue. 1999. The syntax of Russian negation: a minimalist approach. Stanford: CSLI Publications.
Büring, Daniel, and Manuel Križ. 2013. It’s that and that’s it! Exhaustivity and homogeneity presuppositions in clefts (and definites). Semantics and Pragmatics 6: 1–29.
Chemla, Emmanuel. 2008. An epistemic step for anti-presuppositions. Journal of Semantics 25: 141–173.
Chung, Sandra. 2005. Sluicing and the lexicon: The point of no return. In BLS 31: General session and parasession on prosodic variation and change, eds. Rebecca T. Cover and Yuni Kim, 73–91. Berkeley: Berkeley Linguistics Society.
Chung, Sandra, William A. Ladusaw, and James McCloskey. 1995. Sluicing and logical form. Natural Language Semantics 3: 239–282.
Cresswell, Max. 1990. Entities and indices. Dordrecht: Kluwer Academic.
Enç, Mürvet. 1986. Toward a referential analysis of temporal expressions. Linguistics and Philosophy 9: 405–426.
Fălăuş, Anamaria, and Andreea C. Nicolae. 2016. Fragment answers and double negation in strict negative concord languages. In Proceedings of SALT 26, eds. Mary Moroney, Carol-Rose Little, Jacob Collard, and Dan Burgdorf, 584–600. Washington: LSA.
Farkas, Donka F. 1981. Quantifier scope and syntactic islands. In Papers from the 7th regional meeting, Chicago Linguistic Society, eds. Roberta Hendrick, Carrie Masek, and Mary Frances Miller, 59–66. Chicago: CLS.
Fauconnier, Gilles. 1975. Polarity and the scale principle. In Papers from the 11th regional meeting, Chicago Linguistic Society, eds. Robin. E. Grossman, San L. James, and Timothy J. Vance, 188–199. Chicago: CLS.
Fauconnier, Gilles. 1978. Implication reversal in a natural language. In Formal pragmatics for natural languages, eds. Franz Guenthner and S. J. Schmidt, 289–301. Dordrecht: Reidel.
von Fintel, Kai. 1993. Exceptive constructions. Natural Language Semantics 1: 123–148.
von Fintel, Kai. 1994. Restrictions on quantifiers domains, PhD dissertation, University of Massachusetts at Amherst.
von Fintel, Kai. 1999. NPI licensing, Strawson entailment, and context dependency. Journal of Semantics 16: 97–148.
von Fintel, Kai. 2004. Would you believe it? The King of France is back! In Descriptions and beyond, eds. Marga Reimer and Anne Bezuidenhout, 269–296. Oxford: Clarendon Press.
Fodor, Janet. 1970. The linguistic description of opaque contexts, PhD dissertation, MIT.
Fodor, Janet D., and Ivan A. Sag. 1982. Referential and quantificational indefinites. Linguistics and Philosophy 5(3): 355–398.
Gajewski, Jon. 2002. L-analyticity and natural language. Manuscript, University of Connecticut.
Gajewski, Jon. 2005. Neg-raising: polarity and presupposition, PhD dissertation, MIT.
Gajewski, Jon. 2008. NPI any and connected exceptive phrases. Natural Language Semantics 16: 69–110.
García Álvarez, Ivan. 2008. Generality and exception: A study in the semantics of exceptives, PhD dissertation, Stanford University.
Griffiths, James. 2019. Beyond MaxElide: An investigation of A’-movement from elided phrases. Linguistic Inquiry 3: 571–607.
Harris, Zellig. 1982. A grammar of English on mathematical principles. New York: Wiley.
Hawkins, John A. 1978. Definiteness and indefiniteness. London: Croom Helm.
Hawkins, John A. 1991. On (in)definite articles: implicatures and (un)grammaticality prediction. Journal of Linguistics 27(2): 405–442.
Heim, Irene. 1991. Artikel und Definitheit. In Semantik: Ein internationales Handbuch des zeitgenössischen Forschung, eds. Arnim von Stechow and Dieter Wunderlich, 487–535. Berlin: de Gruyter.
Hirsch, Aron. 2016. An unexceptional semantics for expressions of exception. In University of Pennsylvania working papers in linguistics, ed. Sunghye Cho. Vol. 22(1), 138–148. Philadelphia: University of Pennsylvania.
Hoeksema, Jack. 1987. The logic of exception. In Proceedings of ESCOL 4, eds. Ann Miller and Joyce Powers, 100–113. Columbus: The Ohio State University.
Hoeksema, Jack. 1995. The semantics of exception phrases. In Quantifiers, logic and languages, eds. Jaap Van der Does and Jan Van Eijk, 145–177. Stanford: CSLI Publications.
Hoeksema, Jacob. 1990. Exploring exception phrases. In Proceedings of the 7th Amsterdam Colloquium, eds. Martin Stokhof and Leen Torenvliet, 165–190. Amsterdam: ISSL.
Horn, Laurence R. 1989. A natural history of negation. Chicago: The University of Chicago Press.
Horn, Laurence R. 1992. The said and the unsaid. In Proceedings of SALT 2, eds. Chris Barker and David Dowty, 163–192. Columbus: The Ohio State University.
Horn, Laurence R. 1996. Exclusive company: only and the dynamics of vertical inference. Journal of Semantics 13: 1–40.
Johnson, Kyle. 2001. What VP ellipsis can do, what it can’t, but not why. In The handbook of contemporary syntactic theory, eds. M. Baltin and C. Collins, 439–479. Oxford: Blackwell.
Keenan, Edward, and Jonathan Stavi. 1986. A semantic characterization of natural language determiners. Linguistics and Philosophy 9: 253–326.
Keshet, Ezra. 2008. Good intensions: paving two roads to a theory of the de re/de dicto distinction, PhD dissertation, MIT.
Kratzer, Angelika. 1977. What must and can must and can mean. Linguistics and Philosophy 1(3): 337–355.
Kratzer, Angelika. 1978. Semantik der Rede: Kontexttheorie, Modalwörter, Konditionalsätze. Königstein/Taunus: Scriptor.
Kratzer, Angelika. 1979. Conditional necessity and possibility. In Semantics from different points of view, eds. Rainer Bäuerle , Urs Egli, and Arnim von Stechow, 117–147. Berlin: Springer.
Kratzer, Angelika. 1981a. Partition and revision: The semantics of counterfactuals. Journal of Philosophical Logic 10(2): 201–216.
Kratzer, Angelika. 1981b. The notional category of modality. In Words, worlds, and contexts, eds. Hans-Jürgen Eikmeyer and Hannes Rieser, 38–74. Berlin: de Gruyter.
Kratzer, Angelika. 1986. Conditionals. In Papers from the 22nd regional meeting, Chicago Linguistic Society, Vol. 2, 1–15. Chicago: CLS.
Kratzer, Angelika. 1989. An investigation of the lumps of thought. Linguistics and Philosophy 12(5): 607–653.
Kratzer, Angelika. 2007/2019. Situations in natural language semantics. In Stanford encyclopedia of philosophy, ed. N. Zalta (first published in 2007, a revised version published in 2019). Retrieved from https://plato.stanford.edu/archives/sum2019/entries/situations-semantics/.
Križ, Manuel. 2015a. Aspects of homogeneity in the semantics of natural language, PhD dissertation, University of Vienna.
Križ, Manuel. 2015b. Homogeneity, non-maximality, and all. Journal of Semantics 33(3): 493–539.
Kroll, Margaret. 2018. Polarity reversals under sluicing. In Proceedings of Sinn und Bedeutung 21(2), eds. Robert Truswell et al., 713–730. Retrieved from https://ojs.ub.uni-konstanz.de/sub/index.php/sub/article/view/163.
Kroll, Margaret. 2019. Polarity reversals under sluicing. Semantics and Pragmatics 12 (18): 1–49. https://doi.org/10.3765/sp.12.18.
Kuno, Susumu. 1976. Gapping: A functional analysis. Linguistic Inquiry 7: 300–318.
Ladusaw, Willam. 1979. Polarity sensitivity as inherent scope relations, PhD dissertation, University of Texas at Austin.
Lappin, Shalom. 1996. Generalized quantifiers, exception phrases, and logicality. Journal of Semantics 13(3): 197–220.
Lewis, David. 1973a. Counterfactuals. Cambridge: Harvard University Press.
Lewis, David. 1973b. Counterfactuals and comparative possibility. Journal of Philosophical Logic 2: 418–446.
Lewis, David. 1975. Adverbs of quantification. In Formal semantics of natural language, ed. Edward Keenan, 3–15. Cambridge: Cambridge University Press.
Lewis, David. 1981. Ordering semantics and premise semantics for counterfactuals. Journal of Philosophical Logic 10(2): 217–234. Reprinted in David Lewis, 1998, Papers in philosophical logic, 77-96. Cambridge: Cambridge University Press.
Löbner, Sebastian. 1987. The conceptual nature of natural language quantification. In Proceedings of the 87 Debrecen Symposium on Logic and Language, eds. Imre Ruzsa and Anna Szabolcsi, 81–94. Budapest: Akadémiai Kiadó.
Löbner, Sebastian. 2000. Polarity in natural language: Predication, quantification and negation in particular and characterizing sentences. Linguistics and Philosophy 23: 213–308.
Magri, Giorgio. 2014. An account for the homogeneity effects triggered by plural definites and conjunction based on double strengthening. In pragmatics, semantics and the case of scalar implicatures, ed. Salvatore Pistoia-Reda, 99–145. London: Palgrave Macmillan.
Moltmann, Friederike. 1995. Exception sentences and polyadic quantification. Linguistics and Philosophy 18(3): 223–280.
Nadathur, Prerna, and Daniel Lassiter. 2018. An experimental look at the negative implications of exceptives. In Proceedings of NELS 48, eds. Sherry Hucklebridge and Max Nelson, 201–210. Amherst: GLSA.
Partee, Barbara H. 1986. Noun phrase interpretation and type-shifting principles. In Studies in discourse representation theory and the theory of generalized quantifiers, eds. Jerome Groenendijk, Dick de Jongh, and Martin Stokhof, 115–143. Dordrecht: Foris. Reprinted in 2002.
Pasquereau, Jérémy. 2020. Polar responses to quantified utterances: Evidence from French polar response particles for scope preservation and Neg-movement. Natural Language Semantics 28: 255–306. https://doi.org/10.1007/s11050-020-09164-w.
Percus, Orin. 2000. Constraints on some other variables in syntax. Natural Language Semantics 8: 173–229.
Pereltsvaig, Asya. 2002. Monotonicity-based vs veridicality-based approaches to negative polarity: evidence from Russian. In Formal approaches to Slavic linguistics: The Philadelphia meeting, eds. Tracy H. King and Irina A. Sekerina, 328–346. Ann Arbor: Michigan Slavic Publications.
Pérez-Jiménez, Isabel, and Norberto Moreno-Quibén. 2012. On the syntax of exceptions. Evidence from Spanish. Lingua 122: 582–607.
Peters, Stanley, and Dag Westerståhl. 2006. Quantifiers in language and logic. Oxford: Oxford University Press.
Potsdam, Eric. 2018. Exceptives and ellipsis. In Proceedings of NELS 44, eds. Sherry Hucklebridge and Max Nelson, 259–269. Amherst: GLSA.
Potsdam, Eric, and Maria Polinsky. 2017. A preliminary look at exceptives in Tahitian. In Asking the right questions: Essays in honor of Sandra Chung, eds. Jason Ostrove, Ruth Kramer, and Joseph Sabbagh, 28–36.
Potsdam, Eric, and Maria Polinsky. 2019. Clausal and phrasal exceptives. Poster presented at GLOW 42, Oslo, May 2019.
Reinhart, Tanya. 1991. Elliptical conjunction: Non-quantificational QR. In The Chomskian turn, ed. Asa Kasher, 360–384. Oxford: Blackwell.
Reinhart, Tanya. 1992. Wh-in-situ: An apparent paradox. In Proceedings of the eighth Amsterdam Colloquium, eds. Paul Dekker and Martin Stokhof, 483–492. Amsterdam: ILLC.
Reinhart, Tanya. 1997. Quantifier Scope: How labor is divided between QR and choice functions. Linguistics and Philosophy 20(4): 335–397.
Rooth, Mats. 1985. Association with focus, PhD dissertation, University of Massachusetts at Amherst.
Rooth, Mats. 1992a. A theory of focus interpretation. Natural Language Semantics 1: 75–116.
Rooth, Mats. 1992b. Ellipsis redundancy and reduction redundancy. In Proceedings of the Stuttgart ellipsis workshop, eds. Steve Berman and Arild Hestvik. Stuttgart: IMS.
Rooth, Mats. 1996. Focus. In The handbook of contemporary semantic theory, ed. Shalom Lappin, 271–298. London: Blackwell.
Rudin, Deniz. 2019. Head-based syntactic identity in sluicing. Linguistic Inquiry 50(2): 253–283.
Sag, Ivan. 1976. Deletion and logical form, PhD dissertation, MIT.
Schwarz, Florian. 2009. Two types of definites in natural language, PhD dissertation, University of Massachusetts at Amherst.
Schwarz, Florian. 2012. Situation pronouns in determiner phrases. Natural Language Semantics 20: 431–475.
Schwarzschild, Roger. 1994. Plurals, presuppositions and the sources of distributivity. Natural Language Semantics 2: 201–248.
Soltan, Usama. 2016. On the syntax of exceptive constructions in Egyptian Arabic. In Perspectives on Arabic linguistics 17, eds. Stuart Davis and Usama Soltan, 35–57. Amsterdam: Benjamins.
Stalnaker, Robert. 1968. A theory of conditionals. In Studies in logical theory, ed. Nicholas Rescher, 98–112. Oxford: Blackwell.
Stockwell, Richard. 2018. Ellipsis in tautologous conditionals: the contrast condition on ellipsis. Semantics and Linguistic Theory 28: 584–603.
Stockwell, Richard, and Deborah Wong. 2020. Sprouting and the structure of except-phrases. In Proceedings of NELS 50, eds. Mariam Asatryan, Yixiao Song, and Ayana Whitmal, 169–183. Amherst: GLSA.
Vostrikova, Ekaterina. 2019a. Compositional analysis of clausal exceptives. In Proceedings of SALT 29, eds. Katherine Blake, Forrest Davis, Kaelyn Lamp, and Joseph Rhyne, 420–440. Washington: LSA.
Vostrikova, Ekaterina. 2019b. Phrasal and clausal exceptive-additive constructions crosslinguistically, PhD dissertation, University of Massachusetts at Amherst.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This project originated from my UMass Amherst dissertation. I am grateful to my advisors Seth Cable, Rajesh Bhatt, Kyle Johnson, and Barbara Partee for all of their help with this project. I am grateful to the audiences of SuSurrus and the Semantics Workshop at UMass Amherst, and to the linguistic community of UMass in general, for their comments and judgments. I would also like to thank Daniel Altshuler, Peter Alrenga, Kai von Fintel, Aron Hirsch, Sabine Iatridou, Edward Keenan, Petr Kusliy, Roumyana Pancheva, Clemens Steiner-Mayr, two anonymous reviewers, and the editors of Natural Language Semantics for their comments, which helped me to improve this work substantively. A part of this project was presented at SALT-29 (May 2019, see Vostrikova 2019a for proceedings paper) and another part at SuB-24 (September 2019). I am grateful to the audiences for their comments and suggestions. All errors are my own.
Rights and permissions
About this article
Cite this article
Vostrikova, E. Conditional analysis of clausal exceptives. Nat Lang Semantics 29, 159–227 (2021). https://doi.org/10.1007/s11050-021-09177-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11050-021-09177-z






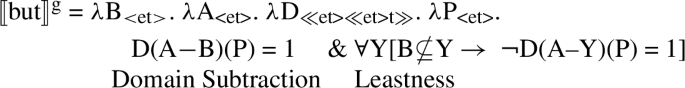
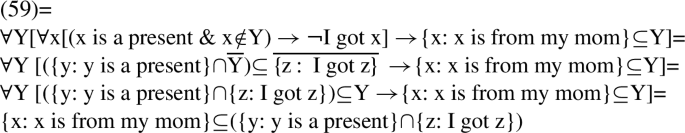
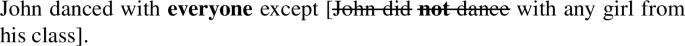
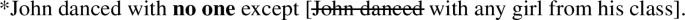


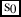 → x came in s]]
→ x came in s]]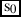 & ¬x came in s]]
& ¬x came in s]]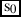 → x came in s]]
→ x came in s]] → x came in s]]
→ x came in s]]







 . ∀x[x is a girl in
. ∀x[x is a girl in  → ∀y[y is a boy in s’ → x danced with y in
→ ∀y[y is a boy in s’ → x danced with y in  ]]
]] [¬Eva danced with Bill in
[¬Eva danced with Bill in 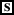 → ∃x[x is a girl in
→ ∃x[x is a girl in 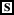 & ∃y[y is a boy in s
& ∃y[y is a boy in s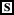 ]]]
]]]
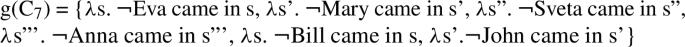

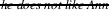 .
. → x came in s]]
→ x came in s]] & I got x in s] → ∃y[y is a present in s0 & I got y in s]]
& I got x in s] → ∃y[y is a present in s0 & I got y in s]]