1 Introduction

Control and monitoring of rail vehicles require precise knowledge of the states and parameters of different parts of the vehicle. State estimation techniques have been studied and applied in railway vehicle control, especially in active suspension systems. The active suspension control requires feedback signals, but some desired states cannot directly be measured, such as lateral displacement and angle of attack of wheelsets. State estimation can be a possibility to provide those signals by observing unmeasurable states through measurable quantities [4, 12]. Condition monitoring of railway vehicles using model-based estimation has been carried out for suspension components and wheel-rail interface monitoring; however, the conventional approaches mainly rely on signal processing and analysis [4, 13]. The model-based estimators, which are widely utilized in railway vehicle applications, mainly use fixed parameters in the state transition model. The accurate information of time-varying parameters would provide a robust estimator as the state transition model will become more accurate [17].

The dual extended Kalman filter (DEKF) was first proposed by Wan and Nelson [15, 16], combining state estimation with parameter estimation. This technique employs two extended Kalman filters (EKF), including a state filter and a parameter filter running in parallel. Therefore, this approach is suitable for a system with time-varying parameters. The DEKF approach has been used/applied in the field of road vehicles; however, it has not yet been applied to railway vehicles. For example, Wenzel et al. used the DEKF to estimate the states and parameters of a road vehicle [17]. This research utilized DEKF to estimate mass properties, including mass, the moment of inertia, and the center of gravity (COG) position, as these parameters are necessary for vehicle stability control. In their work, Wenzel et al. demonstrated the effectiveness and showed a promising possibility to use the DEKF technique in road vehicle applications [17]. Moreover, several studies in the field of road vehicles have used Dual-Kalman filter techniques to estimate operating conditions and environments, for example, road friction. Therefore, DEKF has the potential to be used in rail vehicle applications as the system contains various time-varying parameters.

In rail vehicle dynamics, various time-varying parameters such as wheel-rail contact parameters and conicity influence vehicle stability and dynamics of the system [2]. As conicity is one of the crucial parameters, Kaiser et al. performed the estimation of equivalent conicity for the railway vehicle using the constrained unscented Kalman filter (CUKF) under various contact adhesion conditions [10]. The estimation of wheelset equivalent conicity would enhance the implementation of railway vehicle condition monitoring and control. Therefore, this paper presents the dual extended Kalman filter (DEKF) for estimating the states and parameters of railway vehicle running gears. The proposed method performs the state and parameter estimation concurrently with a model derived from a half-vehicle. Moreover, this work demonstrates the online state-parameter estimator using a co-simulation environment between MATLAB/Simulink and SIMPACK (Multibody Simulation). The proposed DEKF is validated with the designated running conditions, including both straight and curved tracks.

2 Railway vehicle modeling

The model used in this paper is a high-speed railway vehicle with a maximum operating speed of 250 km/h. This vehicle is equipped with two modern running gears and has two suspension levels, including primary and secondary suspensions. It operates on the standard track gauge of 1.435 m. Moreover, each running gear consists of two solid wheelsets with S1002 wheel profiles.

2.1 Dynamic modeling

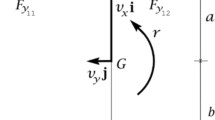
The plan and side views of a half vehicle are shown in Fig. 1. The governing equations of the system deriving from Newton’s second law of motion are formulated as Eq. (1)-(7) with respect to the yaw and lateral dynamics of wheelsets and bogie and lateral dynamics of carbody. Symbols and parameters are listed in the Appendix.

Fig. 1
figure 1

Plan view and side view of a half-railway vehicle

Full size image

Wheelsets lateral and yaw dynamics:

$$ \begin{aligned} m_{w}{\ddot{y}}_{w1}=&-\frac{2f_{22}}{v}\left ({\dot{y}}_{w1}-v\psi _{w1} \right )-\frac{2f_{23}}{v}{\dot{\psi}}_{w1}-C_{y}{\dot{y}}_{w1}-K_{y}y_{w1}+C_{y}{ \dot{y}}_{b} \\ &+K_{y}y_{b}+C_{y}l_{w}{\dot{\psi}}_{b}+K_{y}l_{w}\psi _{b}+ \frac{m_{w}v^{2}}{R_{1}} -m_{w}g\varphi _{t,1} \end{aligned} $$
(1)
$$ \begin{aligned} I_{w}{\ddot{\psi}}_{w1}=&-2f_{11}\left ( \frac{b_{0}\lambda _{eq,w1}}{r_{0}}y_{w1}+\frac{{b_{0}}^{2}}{v}{ \dot{\psi}}_{w1}-\frac{{b_{0}}^{2}}{R_{1}}\right )-K_{x}l_{b}^{2} \psi _{w1}-C_{x}l_{b}^{2}{\dot{\psi}}_{w1} \\ &+K_{x}l_{b}^{2}\psi _{b}+C_{x}l_{b}^{2}{\dot{\psi}}_{b} \end{aligned} $$
(2)
$$ \begin{aligned} m_{w}{\ddot{y}}_{w2}=&-\frac{2f_{22}}{v}\left ({\dot{y}}_{w2}-v\psi _{w2} \right )-\frac{2f_{23}}{v}{\dot{\psi}}_{w2}-C_{y}{\dot{y}}_{w2}-K_{y}y_{w2}+C_{y}{ \dot{y}}_{b} \\ &+K_{y}y_{b}-C_{y}l_{w}{\dot{\psi}}_{b}-K_{y}l_{w}\psi _{b}+ \frac{m_{w}v^{2}}{R_{2}}-mg\varphi _{t,2} \end{aligned} $$
(3)
$$ \begin{aligned} I_{w}{\ddot{\psi}}_{w2}=&-2f_{11}\left ( \frac{b_{0}\lambda _{eq,w2}}{r_{0}}y_{w2}+\frac{b_{0}^{2}}{v}{ \dot{\psi}}_{w2}-\frac{b_{0}^{2}}{R_{2}}\right )-K_{x}l_{b}^{2}\psi _{w2}-C_{x}l_{b}^{2}{ \dot{\psi}}_{w2} \\ &+K_{x}l_{b}^{2}\psi _{b}+C_{x}l_{b}^{2}{\dot{\psi}}_{b} \end{aligned} $$
(4)

Bogie lateral and yaw dynamics:

$$ \begin{aligned} m_{b}{\ddot{y}}_{b}=&C_{y}{\dot{y}}_{w1}+K_{y}y_{w1}+C_{y}{\dot{y}}_{w2}+K_{y}y_{w2}-2C_{y}{ \dot{y}}_{b}-2K_{y}y_{b}-C_{sy}{\dot{y}}_{b} \\ &-K_{sy}y_{b}+K_{sy}y_{cb}+C_{sy}{\dot{y}}_{cb}+\frac{m_{b}v^{2}}{2} \left (\frac{1}{R_{1}}+\frac{1}{R_{2}}\right ) \\ &-\frac{m_{b}g}{2}\left (\varphi _{t,1}+\varphi _{t,2}\right ) \end{aligned} $$
(5)
$$ \begin{aligned} I_{b}{\ddot{\psi}}_{b}=&C_{y}l_{w}{\dot{y}}_{w1}+K_{y}l_{w}y_{w1}-C_{y}l_{w}{ \dot{y}}_{w2}-K_{y}l_{w}y_{w2}+K_{x}l_{b}^{2}\psi _{w1}+K_{x}l_{b}^{2} \psi _{w2} \\ &+C_{x}l_{b}^{2}{\dot{\psi}}_{w1}+C_{x}l_{b}^{2}{\dot{\psi}}_{w2}-2l_{w}^{2}C_{y}{ \dot{\psi}}_{b}-2l_{w}^{2}K_{y}\psi _{b}-2l_{b}^{2}C_{x}{\dot{\psi}}_{b} \\ &-2l_{b}^{2}K_{x}\psi _{b}-C_{yaw}l_{c}^{2}{\dot{\psi}}_{b} \end{aligned} $$
(6)

Carbody lateral dynamics:

$$ m_{cb}{\ddot{y}}_{cb}=C_{sy}{\dot{y}}_{b}+K_{sy}y_{b}-C_{sy}{\dot{y}}_{cb}-K_{sy}y_{cb}+ \frac{m_{cb}v^{2}}{R}-m_{cb}g\varphi _{t} $$
(7)

In terms of track inputs, rates of curvature and cant angle are assumed to be zero. Governing equations of these track inputs are given as:

$$ \begin{aligned} {\dot{R}}^{-1}=0, \dot{\varphi _{t}}=0, \end{aligned} $$
(8)

where \(R^{-1}\) is the track curvature, and \(\varphi \) is the track cant angle. In the curve, the time delay between leading curvature and trailing curvature can be given as:

$$ R_{2}^{-1}(t)=R_{1}^{-1}\left (t+\frac{l_{w}}{v}\right ). $$
(9)

To simplify the model, the curvature and track cant angle for both wheelsets can be approximately the same due to relatively high vehicle speed and the short distance between the two wheelsets. The curvature and cant angle can be written as

$$ R_{1}^{-1}=R_{2}^{-1}=R^{-1}, $$
(10)
$$ \varphi _{1}=\varphi _{2}=\varphi _{t}. $$
(11)

2.2 Wheel-rail geometry and contact parameters

The ORE/UIC S1002 wheel and UIC60 rail profiles are chosen as wheel-rail interface in this study because of the availability of reliable profile data. These wheel and rail profiles are typically used in benchmarks for rail vehicle simulation, such as in [3] and [9]. The S1002 wheel profile is also widely used in real vehicles. The original S1002 wheel profile is shown in Fig. 2 together with the UIC60 rail profile. Dimensions of the chosen wheel profile are specified in EN 13715 standard [5] and can also be found in [2]. Figure 2 also illustrates contact pairs of S1002 wheel and UIC60 rail profiles with two rail inclinations: 1:40 (black) and 1:30 (blue).

Fig. 2
figure 2

Wheelset equivalent conicity function

Full size image

According to the mathematical model of the multibody system, time-varying parameters, including longitudinal, lateral creep coefficients and coefficient of lateral force due to spin creep (\(f_{11}\), \(f_{22}\) and \(f_{23}\)) and equivalent conicity (\(\lambda _{eq}\)), are constituted in governing equations and therefore substantially influence the dynamic behavior of the vehicle. These wheel-rail contact parameters are usually set as constant in the model-based estimation and taken into account as model uncertainties. In this paper, the equivalent conicity, as given in the following expression, is considered:

$$ \lambda _{eq}=\frac{r_{r}-r_{l}}{2\Delta y}= \frac{\Delta r_{r}-\Delta r_{l}}{2\Delta y}. $$
(12)

Equivalent conicity is a dimensionless measure of wheelset conicity defined as the change of rolling radius between the left and right wheels as a function of the wheelset lateral displacement. This parameter is unmeasurable and highly nonlinear depending on the shape of a wheel and rail, rail inclination, and track gauge. Figure 3 shows two equivalent conicity functions for rail inclinations of 1:40 (black) and 1:30 (blue), where profiles of both cases are wheel S1002 and rail UIC60 with a standard track gauge of 1.435 m.

Fig. 3
figure 3

Wheelset equivalent conicity function

Full size image

To determine the equivalent conicity, the quasi-linearization approach or harmonic linearization is one of the methods used to produce a single value of equivalent conicity in nonlinear cases. In this case, the relationship between rolling radius differences (\(\Delta{r}\)) and the amplitude of the wheelset sinusoidal motion (\(\Delta{y}\)) are considered to approximate the equivalent conicity. This method is mentioned in [8, 11] and EN 15302:2021 standard [6]. SIMPACK utilizes this method for linearization, where the wheel profile is converted into a circular arc considering equivalent linear parameters from linearization [11]. The single equivalent conicity value determined in SIMPACK is considered with the wheelset lateral movement amplitude of 3 mm. However, the equivalent conicity is dependent on relative wheelset lateral displacement as demonstrated in Fig. 3.

Therefore, in this paper, the equivalent conicity is estimated using the proposed dual extended Kalman filter with both linearized single value and lateral displacement amplitude-dependent values. The creep coefficients (\(f_{11}\), \(f_{22}\) and \(f_{23}\)) are deemed as constant with nominal values stated in the Appendix. The details of DEKF synthesis are described in the following section.

2.3 Running scenarios

The vehicle is modeled in the Multibody Simulation (MBS) software, SIMPACK. This model is developed to perform the co-simulation between SIMPACK and Simulink, where an estimator is implemented. The maximum operating speed of 250 km/h is used for the simulations. Two running cases, as described below, are chosen to perform and evaluate the performance of the estimators:

1. A test using a 3125-meter-long tangent track with linearized equivalent conicity. The lateral track irregularities input using ERRI_low power spectral density (PSD) [3] is introduced in the test to represent the real running condition. Two linearized equivalent conicity values for rail inclination of 1:40 and 1:30 are used to perform the simulation. This test exploits the quasi-linearization method [8] in SIMPACK to calculate the wheel-rail contact geometry as described in Sect. 2.2. Thus, linearized equivalent conicity is utilized in this test to investigate the ability of the estimator to quantify equivalent conicity.

2. A test with tangent and curved tracks with profiled wheelsets. The main goal of this test is to investigate the effectiveness of the synthesized estimator in identifying time-varying equivalent conicity. Hence, wheelsets with original S1002 wheel profiles are utilized in the model. In this test, the track, using UIC60 profiles with 1:40 rail cant, comprises both left- and right-hand curves with a radius of 2850 m and a maximum track cant angle of 160 mm, giving a cant deficiency of 100 mm in the circular part. In addition, 250 m transitions are located at the beginning and the end of the curves (Fig. 4). The simulations are performed with deterministic track conditions.

Fig. 4
figure 4

Track geometry for the profiled wheels test

Full size image

3 Estimator design using the dual extended Kalman filter

A dual extended Kalman filter (DEKF) has been implemented for the quantification of the time-dependent parameters. The designed estimator employs the discrete dual extended Kalman filtering (D-DEKF) technique to estimate both states and parameters simultaneously. The DEKF is a two-stage extended Kalman filter (EKF) method [14] incorporating both state and parameter estimations. Therefore, this method has the capability to estimate the time-varying parameters, especially in the wheel-rail contact of a railway vehicle.

The nonlinear system can be expressed in discrete time steps as

$$ \begin{aligned} \mathbf{x}_{k}={\mathbf{f}(\mathbf{x}}_{k-1},\mathbf{\theta}_{ \mathbf{k-1}})+\mathbf{w}_{k-1} \\ \mathbf{y}_{k}={\mathbf{h}(\mathbf{x}}_{k},\mathbf{\theta}_{ \mathbf{k}})+\mathbf{v}_{k}. \end{aligned} $$
(13)

where \(\mathbf{x}\) is the state vector, \(\mathbf{\theta}\) is the parameter vector, \(\mathbf{y}\) is the output vector, and \(\mathbf{w}\) and \(\mathbf{v}\) are process and observation noises, respectively.

Referring to the governing equations (1)–(7) and the model for track inputs, the state vector is given as

$$ \mathbf{x}= \begin{bmatrix} {\dot{y}}_{w1}&y_{w1}&{\dot{\psi}}_{w1}&\psi _{w1}&{\dot{y}}_{w2}&y_{w2}&{ \dot{\psi}}_{w2}&\psi _{w2} \\ {\dot{y}}_{b}&y_{b}&{\dot{\psi}}_{b}&\psi _{b}&{\dot{y}}_{cb}&y_{cb} & \frac{1}{R}&\varphi _{t} \end{bmatrix} ^{T}. $$
(14)

By integrating the governing equations from time \(k\) to \(k+1\) with time intervals \(\Delta t\), the extrapolated state equations for time \(k+1\) in the discrete-time domain are given as the following expressions for displacements and velocities.

Lateral dynamics:

$$ \begin{aligned} \ {\dot{y}}_{i,k}={\dot{y}}_{i,k-1}+{\ddot{y}}_{i,k-1}\ \Delta t \\ y_{i,k}=y_{i,k-1}+{\dot{y}}_{i,k-1}\Delta t \end{aligned} $$
(15)

Yaw dynamics:

$$ \begin{aligned} {\dot{\psi}}_{i,k}={\dot{\psi}}_{i,k-1}+{\ddot{\psi}}_{i,k-1}\ \Delta \mathrm{t} \\ \psi _{i,k}=\psi _{i,k-1}+{\dot{\psi}}_{i,k-1}\Delta t \end{aligned} $$
(16)

In terms of parameter estimation, the parameter vector consists of 2 variables, including the conicity of each wheelset

θ= [ λ e q , w 1 λ e q , w 2 ] T .
(17)

The lateral accelerations of two wheelsets, the yaw velocity, and the lateral acceleration of the bogie are considered as measurable quantities. Thus, the measurement vector is

y= [ y ¨ w 1 y ¨ w 2 ψ ˙ b y ¨ b ] T .
(18)

In the measurement matrix, the yaw velocity of the bogie is expressed with a track curvature relation, \({\dot{\psi}}_{b}=-vR^{-1}\). This approach makes track curvature (\({R^{-1}}\)) observable through the measurements.

The algorithm for DEKF consists of four steps running concurrently, namely parameter prediction, state prediction, state correction, and parameter correction, as shown in Fig. 5. The measurements acquired from SIMPACK simulation are given into state correction and parameter correction. Details of each step are specified below [15, 17].

Fig. 5
figure 5

Schematic representation of DEKF with measurements from SIMPACK

Full size image

Parameter prediction

$$ {\hat{\mathbf{\theta}}}_{k|k-1}=f_{\theta}({\hat{\mathbf{x}}}_{k-1},{ \hat{\mathbf{\theta}}}_{k-1}) $$
(19)
$$ \mathbf{P}_{\theta ,k|k-1}=\mathbf{P}_{\theta ,k-1}+\mathbf{Q}_{ \theta ,k}\ $$
(20)

State prediction

$$ {\hat{\mathbf{x}}}_{k|k-1}=f_{x}({\hat{\mathbf{x}}}_{k-1},{ \hat{\mathbf{\theta}}}_{k-1}) $$
(21)
$$ \mathbf{P}_{x,k|k-1}=\mathbf{F}_{x,k}\mathbf{P}_{x,k-1}\mathbf{F}_{x,k}^{T}+ \mathbf{Q}_{x,k} $$
(22)

State correction

$$ \mathbf{K}_{x,k}=\mathbf{P}_{x,k|k-1}\mathbf{H}_{x,k}^{T}\left [ \mathbf{H}_{x,k}\mathbf{P}_{x,k|k-1}\mathbf{H}_{x,k}^{T}+\mathbf{R}_{x,k} \right ]^{-1} $$
(23)
$$ {\hat{\mathbf{x}}}_{k}={\hat{\mathbf{x}}}_{k|k-1}+\mathbf{K}_{x,k} \left [\mathbf{y}_{k}-h_{x}({\hat{\mathbf{x}}}_{k|k-1},{ \hat{\mathbf{\theta}}}_{k|k-1})\right ] $$
(24)
$$ \mathbf{P}_{x,k}=\left [\mathbf{I}-\mathbf{K}_{x,k}\mathbf{H}_{x,k} \right ]\mathbf{P}_{x,k|k-1} $$
(25)

Parameter correction

$$ \mathbf{K}_{\theta ,k}=\mathbf{P}_{\theta ,k|k-1}\mathbf{H}_{\theta ,k}^{T} \left [\mathbf{H}_{\theta ,k}\mathbf{P}_{\theta ,k|k-1}\mathbf{H}_{ \theta ,k}^{T}+\mathbf{R}_{\theta ,k}\right ]^{-1} $$
(26)
$$ {\hat{\mathbf{\theta}}}_{k}={\hat{\mathbf{\theta}}}_{k|k-1}+ \mathbf{K}_{\theta ,k}\left [\mathbf{y}_{k}-h_{x}({\hat{\mathbf{x}}}_{k|k-1},{ \hat{\mathbf{\theta}}}_{k|k-1})\ \right ] $$
(27)
$$ \mathbf{P}_{\theta ,k}=\left [\mathbf{I}-\mathbf{K}_{\theta ,k} \mathbf{H}_{\theta ,k}\right ]\mathbf{P}_{\theta ,k|k-1} $$
(28)

According to the system dynamic equations, the Jacobian matrix for state equation, \(F_{x}\) at time \(k\) is calculated by:

$$ \mathbf{F}_{\mathbf{x},k}=\left . \frac{\partial f_{x}}{\partial \mathbf{x}}\right |_{{\hat{\mathbf{x}}}_{k-1},{ \hat{\mathbf{\theta}}}_{k-1}}. $$
(29)

The Jacobian matrices for state and parameter observation matrices are given as:

$$ \mathbf{H}_{\mathbf{x},k}=\left . \frac{\partial h_{x}}{\partial \mathbf{x}}\right |_{{\hat{\mathbf{x}}}_{{k}|{k-1}},{ \hat{\mathbf{\theta}}}_{{k}|{k-1}}}, $$
(30)
$$ \mathbf{H}_{\theta ,k}=\mathbf{H}_{x,k}\left . \frac{\partial f_{x}}{\partial \mathbf{\theta}}\right |_{{ \hat{\mathbf{x}}}_{k-1},{\hat{\mathbf{\theta}}}_{k-1}}. $$
(31)

As shown in Fig. 5, initial states and covariance matrices are needed in the initialization step of the proposed DEKF. The initial values of all states \(\hat{\mathbf{x}}_{0}\) are set to zero as the simulation begins on the tangent track. The covariance matrices for state and parameters, respectively, are set as

$$ P_{x,0}=diag([10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10]) $$
P θ , 0 =diag([ 1 1 ]).

The process noises of the parameter estimation are approximated as 1% of the starting values. The synthesized DEKF will be validated with the running conditions as introduced above. Co-simulation between MBS SIMPACK and Simulink will be utilized. The measurement noises (\({\mathbf{v}}_{k}\)) are added into measurements obtained from SIMPACK. All added measurement noises are assumed as white Gaussian noises, \({\mathbf{v}}_{k} \sim \mathcal{N}(0,{\mathbf{R}})\), which have zero mean with covariance \(\mathbf{R}\). The measurement noise covariance matrix is given as:

$$ \mathbf{R}_{x}=\mathbf{R}_{\theta}= \begin{bmatrix} {\sigma _{\ddot{y}_{w1}}} & 0 & 0 & 0 \\ 0 & \sigma _{\ddot{y}_{w2}} & 0 & 0 \\ 0 & 0 & \sigma _{\dot{\psi}_{b}} & 0 \\ 0 & 0 & 0 & \sigma _{\ddot{y}_{b}} \end{bmatrix} . $$
(32)

The designed estimator is implemented in MATLAB/Simulink, where measurements are obtained from SIMPACK. This setup demonstrates the possible scheme for online estimation that can be adopted in real-world applications.

4 Results

Simulations with the running conditions defined in Sect. 2.3 are performed to evaluate the performance of the designed estimator by comparing the estimation results with the SIMPACK simulation results.

4.1 Tangent track with linearized wheel/rail contact geometry

In this running condition, the equivalent conicity is linearized, as described in Sect. 2.3. Therefore, the governing equation for the parameter prediction step is given as follows:

$$ {\hat{\mathbf{\theta}}}_{k|k-1}={\hat{\mathbf{\theta}}}_{k-1}. $$
(33)

Moreover, the adaptive process noise covariance adjustment is introduced to tune the process. This is performed at the end of state correction. The adaptive estimation of \(Q_{x,k}\) using innovation (\(\mathbf{d}= \mathbf{y}_{k}-h_{x}({\hat{\mathbf{x}}}_{k|k-1},{ \hat{\mathbf{\theta}}}_{k|k-1})\)) can be given as [1]:

$$ \mathbf{Q}_{x,k}=\alpha \mathbf{Q}_{x,k-1}+(1-\alpha )(\mathbf{K}_{x,k} \mathbf{d}\mathbf{d}^{T}\mathbf{K}_{x,k}^{T}),\ $$
(34)

where \(\alpha \) denotes a forgetting factor that is the set to 0.975 in this test.

4.1.1 Equivalent conicity estimation of the linearized wheel-rail geometry with rail inclination of 1:40

According to the quasi-linearization of the wheel/rail contact geometry in SIMPACK, the constant equivalent conicity is 0.178. The starting value of equivalent conicity is set to 0.150 to evaluate the potential of the estimator in quantifying the right value. Figure 6 shows the estimation result of linearized equivalent conicity compared with the constant value from the linearized wheel-rail contact geometry in SIMPACK. The estimated equivalent conicity value almost reaches the actual value rapidly at the beginning of the estimation process. The estimated equivalent conicity then increases to get to the constant value of 0.178 within the simulation time of 45 s, which equals the traveling distance on a straight track of 3125 m. The result of the linear equivalent conicity test confirms the capability of the derived estimator to identify the constant equivalent conicity value.

Fig. 6
figure 6

Equivalent conicity estimation of wheelsets with linearized wheel/rail geometry with rail inclination of 1:40

Full size image

4.1.2 Equivalent conicity estimation of the linearized wheel-rail geometry with rail inclination of 1:30

The linearized wheel/rail contact geometry using the quasi-linearization method gives the constant equivalent conicity of 0.095. The starting value of equivalent conicity is set to 0.150, as in the previous test. Figure 7 shows the estimation result of linearized equivalent conicity. The estimated equivalent conicity value reaches the actual value at the simulation time of 8 s. The estimated equivalent conicity then increases to get to the constant value of 0.095 within the simulation time of 47.52 s. The accuracy of the results shown in Fig. 7 is less than the results in Sect. 4.1.2 because the difference between the initial value and the actual one is higher than in the previous test. The result of the linear equivalent conicity test indicates the performance of the designed estimator.

Fig. 7
figure 7

Equivalent conicity estimation of wheelsets with linearized wheel/rail geometry with rail inclination of 1:30

Full size image

4.2 Tangent and curved tracks with profiled wheelsets

In this running condition, the simulation with the original S1002 wheel profile and UIC60 rail profile is employed, as described in Sect. 2.3. Therefore, the governing equation for the parameter prediction step is given as follows [7]:

$$ {\hat{{\theta}}}_{i,k|k-1}={\hat{{\theta}}}_{i,k-1}+ \frac{d\lambda _{eq,i}}{dy_{i}}{\dot{y}}_{i,k-1}\Delta{t}. $$
(35)

This parameter prediction equation is derived to accommodate the time-varying value of the equivalent conicity. The estimation is therefore performed by setting the initial parameter values close to the actual starting values:

θ ˆ 0 = [ 0.23 0.23 ] T .

The estimated states and equivalent conicity are to be compared with the simulated results to evaluate the effectiveness of the synthesized estimator.

4.2.1 Estimation of the selected states

The lateral displacements of both wheelsets are selected to evaluate the performance of the state estimation because wheelset equivalent conicity is a function of these displacements. Moreover, the wheelset lateral displacement is difficult to measure in practice. Figure 8 shows lateral displacements estimated with the DEKF in comparison to simulated values obtained from the multibody simulation. The estimator gives accurate results, especially in tangent track and steady-state curving regions. However, transient dynamics when negotiating transition curves make the estimation results in those regions less accurate.

Fig. 8
figure 8

Simulated and estimated lateral displacements of both wheelsets under deterministic inputs

Full size image

The root mean square (RMS) errors of both states are given in Table 1. The estimates of wheelset lateral displacements indicate the reliability of state estimation by the employed DEKF estimator. The accuracy of wheelset lateral displacement estimation is also important in parameter estimation as these quantities are a part of its observation matrix \(H_{\theta}\).

Table 1 RMS errors of the selected states
Full size table

The track inputs, including track curvature and cant angle, are also considered as states in the synthesized estimator. Therefore, the estimated results of these states can reflect the performance of the state estimation of the proposed DEKF. Figures 9(a) and 9(b) illustrate the estimated track curvature and cant angle under the deterministic track feature. The maximum track curvature and cant angle are \(3.51\times 10^{-4}\text{ m}^{-1}\) and 0.10 rad, respectively, equal to the curve radius of 2850 m and 160 mm track cant. This result confirms the effectiveness of the employed estimator.

Fig. 9
figure 9

Estimated track curvature and cant angle under deterministic track input

Full size image

4.2.2 Estimation of equivalent conicity

The wheelset equivalent conicity estimates for the deterministic track feature are shown in Fig. 10. The equivalent conicity estimation has high accuracy on tangent track and steady-state curving sections. The estimation becomes less accurate in the transition curve, where transient dynamics is presented. The spike at the beginning of the transition curve is caused by the changes in process noise from the tangent track to the curved track. As the equivalent conicity function is symmetric with respect to the \(y\)-axis, the same values of both positive and negative wheelset lateral displacements give the same equivalent conicity level. Therefore, the results in Fig. 10 show the effectiveness of the synthesized DEKF and demonstrate the ability to identify time-varying wheel-rail contact parameters.

Fig. 10
figure 10

Simulated and estimated equivalent conicity of the leading (a) and trailing (b) wheelsets under deterministic conditions

Full size image

Table 2 provides a summary of the estimation errors, which are the root mean square (RMS) values of the difference between estimated and simulated values for the equivalent conicity over the entire simulated track.

Table 2 RMS errors of wheelset equivalent conicity estimation
Full size table

The equivalent conicity estimate is less accurate due to the high nonlinearity of the wheel-rail interface, especially in the curve negotiation period where wheelsets move laterally. The nonlinear conicity function affects the accuracy of the estimation, which can be seen in transition curves. Moreover, parameter estimation is more sensitive than state estimation in terms of choice of initial values and process noise covariance.

5 Discussion on applications of wheelset equivalent conicity estimation

The deployed DEKF estimator, with results shown in the preceding section, can be utilized in various real-world applications. In this section, possible applications of estimation of wheelset equivalent conicity are discussed with respect to active suspension control and vehicle condition monitoring. These applications are based on the proposed DEKF estimator that is possible to perform online/real-time estimation in operation.

5.1 Active primary suspension

The first application is aligned with vehicle control applications. One of the technological advancements in railway vehicle mechatronics is active primary suspension systems, which aim to improve curving performance. One of the control concepts is so-called active wheelset steering or actuated solid wheelset (ASW) [4]. For instance, this can be achieved by using a control strategy to steer a solid wheelset into the perfect rolling condition. In greater detail, the desired wheelset lateral displacement based on the approximation from a conical wheel profile is given as:

$$ {y^{ref}_{w}}=\frac{b_{0}r_{0}}{{\lambda}_{eq}}\cdot{\frac{1}{R}}. $$
(36)

Such a system requires the knowledge of wheelset equivalent conicity. Moreover, the control system requires wheelset lateral displacements as feedback signals. Hence, the proposed estimator, where state and parameter estimation are combined, suits the purpose well. The control scheme with the DEKF estimator for this system, as an illustration, is presented in Fig. 11. This proposed system architecture would allow the control system to adapt to a suitable steering condition in case the equivalent conicity may vary over time due to changes in the wheel-rail interface from wear.

Fig. 11
figure 11

Control scheme with DEKF estimator for active wheelset steering

Full size image

5.2 Vehicle condition monitoring

As equivalent conicity represents the characteristic of wheel-rail geometry, this parameter can be used as dynamics stability and safety measures of railway vehicles. Several studies have found the relationship between equivalent conicity and the critical speed of a vehicle, i.e., the higher equivalent conicity leads to a reduction in critical speed. However, equivalent conicity at 3 mm alone cannot represent the full characteristic of the wheel-rail geometry and its effect on vehicle behavior. According to EN 15302:2021 standard, the related nonlinearity parameter (Np) is to be used together with equivalent conicity, which can give a better understanding of wheelset-track geometry [6]. Np is given as a slope of equivalent conicity function between the lateral displacements of 2 and 4 mm. The results of time-varying equivalent conicity estimation in Sect. 4.2 can be used to estimate Np, which gives a value of \(-0.022\text{ mm}^{-1}\) where the actual value is \(-0.021\text{ mm}^{-1}\). The application of the implemented estimator is therefore foreseen to enable the real-time condition monitoring of vehicle behavior, especially in dynamic behavior and stability.

6 Conclusion

This paper demonstrates the utilization of the dual extended Kalman filter to estimate the wheelset equivalent conicity of high-speed railway vehicles. Two tests are executed, including a linearized wheel-rail contact geometry case and a profiled wheelset case. The first assignment with linearized equivalent conicity can be used to determine the feasible initial value of the equivalent conicity to avoid the divergence of the estimation of time-varying equivalent conicity. In the profiled wheelset case, the promising results with acceptable errors for the estimated equivalent conicity of both wheelsets indicate the reliability and adequate performance of the designed DEKF estimator. The nonlinearity of the wheel-rail interface properties affects the accuracy of the parameter estimation. Still, this approach has the capability to quantify the time-varying wheelset equivalent conicity. The results demonstrate the feasibility of utilizing this DEKF method in railway vehicle applications as the knowledge of time-varying parameters is not only important in achieving an effective estimator for vehicle control but also useful for vehicle condition monitoring. Two foreseen applications of the DEKF estimator are discussed, including the integration of the deployed estimator with active suspension control and application to vehicle condition monitoring.

Future works will be focused on combining creep coefficients (\(f_{11}\), \(f_{22}\), and \(f_{23}\)) into the parameter estimation as these uncertain wheel-rail contact parameters contribute to the model uncertainty and process noise of the synthesized DEKF. This would potentially improve the performance of the estimator. Furthermore, the utilization of the proposed applications will also be further studied.