1 Introduction

In the development of robotic technology, underwater manipulator has played an increasingly important role for underwater vehicles in performing deep sea tasks such as welding, sampling, maintenance and inspection of pipelines, and so forth in the field of scientific research and oceanic engineering [1, 2]. However, these tasks are carried out mostly by manned submersibles and remotely operated vehicles (ROVs) at present, both equipped with one or more robotic arms [3]. Although ROVs have been recognized to be great assets to the scientific and engineering community, limitations still exist in associated with their capabilities [4]. Firstly, ROVs and manned submersibles are normally large and heavy vehicles that need customized mother ship support, such as transportation, launch, and recovery. Secondly, the complex user interfaces and information delay require highly skilled operators continued and stressed work for hours. These two facts significantly increase the dive cost of the vehicle dives. In addition, the umbilical cable introduces additional control problems and work-space limitation for ROVs [5]. Energized by batteries, AUV complete oceanic missions through distant cruise independently for environmental inspection, topographic reconnaissance, target following, and so on [6]. Therefore, autonomous underwater vehicle (AUV) intervention is justified for light and accurate underwater tasks since an AUV cannot only operate independently but save crew and cost inputs [7].

Although valuable research findings have been obtained for vehicle-manipulator systems in space robot manipulator system and mobile manipulator system [8–10], great technology differences and difficulties still exist for autonomous under-water vehicle manipulator system (AUVMS). During manipulation period, the coupling motion of manipulator and vehicle not only abides by moment momentum conservation but is affected by hydrodynamic forces; further, more restoring forces produced by the change of gravity and buoyancy center cause the vehicle roll and pitch greatly [11]. Although more thrusters are running in this phase to keep its attitude, stable hovering underwater is nearly impossible so as to reach accurate manipulation [12]. To the best of our knowledge, only a very few research institutes have set foot in this frontier.

Since vehicle-manipulator kinematics and dynamics can describe systematic motion and mechanics behavior for design, simulation, and control, considerable efforts have been devoted to their analysis. Padois, Fourquet, and Chiron [13] developed dynamic equations of wheeled mobile manipulators by using the Lagrangian methodology to handle complex operation tasks. From et al. [14] deduced singularity-free dynamic equations for a vehicle-manipulator system by using minimal and globally valid non-Euclidean configuration coordinates. Based on the Euler–Lagrange equations of motion and decoupled natural orthogonal complement matrices, Mohan and Saha [15] proposed a recursive forward dynamics and simulations for the serial-chain robot with rigid links. On the basis of angular momentum conservation and Newton–Euler dynamics, dynamic equations for free-floating space robot system were deduced on the purpose of capturing targets while sustaining satellite in orbit mission [16]. Interactions between robot and manipulators, angular momentum distributions of the whole systems, desirable capture attitude were analyzed [17]. From controller design aspect, neural-network-based control schemes with adaptation capabilities were proposed to improve system robustness [18]. In order to overcome complicated and computational expensive difficulties of learning algorithm, Zhijun, Yipeng, and Jianxun [19] investigated mobile platform with underactuated joint by using adaptive controller with high-gain observer to reconstruct the system states; Zhang, Ye, Jiang, Zhu, Ji, and Hu [20] proposed a model-free fuzzy basis function network output feedback control strategy of space robot base with velocity reconstruction observer. Chu, Sun, and Cui [21] proposed a disturbance observer-based control scheme for free-floating space manipulator with nonlinear dynamics derived by using the virtual manipulator approach.

With regard to the underwater domain, a dynamic model of untethered underwater vehicle was proposed in [11]. In the 1990s, a Lagrangian based dynamic model of underwater vehicle manipulator system (UVMS) was firstly developed [22]. Thus, the first successful attempts at AUV intervention were successfully made under SAUVIM project support [1]. The autonomous manipulation control is more demanding and difficult since UVM is a kinematically redundant system with hydrodynamic effects and uncertain disturbance. Most AUVs have at least three active degrees of freedom (DOF); an additional manipulator with more than 3 DOF makes the combined system kinematically redundant. Therefore, motion planning is important to assign additional motion DOF. Moreover, traditional planning algorithms assumed all rigid bodies with similar dynamic characteristics, but UVMS is composed of two heterogeneous dynamic subsystems with different mass, size, and shape. Therefore, for better performance, the motion planning strategy should be worked out considering two bandwidth characteristic subsystems [23]. In the consideration with limited source of energy, Sarkar and Podder [24] developed a drag force minimization algorithm for kinematical redundancy. Enrico et al. [25] applied a task-priority framework by taking higher precision as higher priority criterion, lower priority for camera occlusion, and centering distance and height task to guarantee manipulation in sight. Ismail and Dunnigan [26] and Han and Chung [27] minimized the restoring moments according to a comparison of the task direction with that of the restoring moments by introducing the performance index. Although autonomous motion planning can optimize manipulation state and safety, an advanced control scheme with adaptive and robust nature is still essential to overcome inside and outside disturbance for precise manipulation. Sagara, Yatoh, and Shimozawa0 proposed a disturbance compensation control method for both vehicle and planar 2-link manipulator based on the resolved acceleration control method. Mohan and Kim [28] presented an indirect adaptive control method based on an extended Kalman filter (EKF) in order to overcome the disadvantages of direct adaptive control schemes. Han, Park, and Chung [29] proposed a nonlinear optimal control method with disturbance observer against parameter uncertainties, external disturbances, and actuator nonlinearities.

In comparison with Lagrangian and Kane’s dynamic equations, the Newton–Eulerian dynamics can describe system angular momentum behavior more explicitly with less complicated and time-consuming models [30]. In this paper, we deduce a UVM dynamic model on the basis of the Newton–Eulerian formalism [31] with hydrodynamic effects and restoring forces. In the autonomous manipulation process, when AUV cruises close to the target, it plans the desired trajectory for the manipulation task. An ideal trajectory should minimize self-disturbance through the presentation of desired AUV positions and manipulator joints’ angles in order to realize the manipulation and minimize energy consumption. Thus, the motion planning algorithm of this paper takes precision as the priority objective and self-disturbance minimization (including restoring forces and coupling forces produced from angular momentum conservation between vehicle and manipulator) as the second objective through primal dual optimization. In order to realize manipulation trajectory, a dynamic model-based adaptive controller has been designed in combination with kinematic and dynamic controller. We propose a disturbance observer to realize precise manipulation and stable vehicle attitude control. The resulting controller controls the motion of AUV through thrust allocation. The autonomous manipulation process is shown in Fig. 1 and is realized through manoeuvrability simulation.

Fig. 1
figure 1

Manipulation process diagram

Full size image

The rest of this study is organized as follows. In Sect. 2, we set up the dynamic model of the UVMS multibody system, and in Sect. 3, we present a genetic-based motion optimization algorithm to resolve system redundancy. An observer-based dynamic control scheme is proposed in Sect. 4. Simulation results and conclusions are given in Sects. 5 and 6, respectively.

2 Dynamic modeling of UVMS

2.1 Kinematics of UVMS

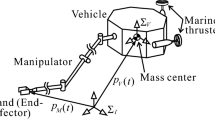
For the model of system kinematic and dynamic, the inertial frame is defined as \(\sum_{0}\), \(O_{0}\mbox{--}X_{0}Y_{0}Z_{0}\) and determines the absolute motion of each body. In Fig. 2, the coordinate systems for the UVMS is established. The frames \(\sum_{\mathrm{v}}\), \(O_{\mathrm{v}}\mbox{--}X_{\mathrm{v}}Y_{\mathrm{v}}Z_{\mathrm{v}}\) are the frames of the AUV geometrical center. The frames \(\sum_{1}\), \(O_{1}\mbox{--}X_{1}Y_{1} Z_{1}\), \(\sum_{2}\), \(O_{2}\mbox{--}X_{2}Y_{2}Z_{2}, \ldots {}\), and \(\sum_{n-1}\), \(O_{n-1} \mbox{--} X_{n-1}Y_{n-1}Z_{n-1}\) represent the frames of 1-joint, \(\ldots ,(n-1)\)-joint of the manipulator, respectively, and \(\sum_{n}\), \(O_{n}\mbox{--} X_{n}Y_{n}Z_{n}\) is the frame of the end-effector. Therefore, the transformation matrix between AUV and the inertial frame is

$${}^{0}\boldsymbol{T}_{\mathrm{v}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} c\psi c\theta & c\psi s\theta s\phi -s\psi c\phi & c\psi s\theta c\phi + s\psi s\phi & x \\ s\psi c\theta & s\psi s\theta s\phi +c\psi c\phi & s\psi s\theta c\phi - c\psi s\phi & y \\ -s\theta & c\theta s\phi & c\theta c\phi & z \\ 0 & 0 & 0 & 1 \end{array}\displaystyle \right ] , $$

where \(c(\cdot )\) represents \(\cos (\cdot )\), \(s(\cdot )\) represents \(\sin (\cdot )\), \(x, y, z, \phi , \theta \), and \(\psi \) represent the surge, lateral and vertical translations and roll, pitch, and yaw rotations of the AUV geometrical center frame \(\sum_{\mathrm{v}}\), \(O_{\mathrm{v}} \mbox{--} X_{\mathrm{v}}Y_{\mathrm{v}}Z_{\mathrm{v}}\) relative to the frame \(\sum_{0}\), \(O_{0} \mbox{--} X_{0}Y_{0}Z_{0}\). The transformation matrix between the frame of the manipulator base joint and the AUV geometrical center frame is

$${}^{\mathrm{v}}\boldsymbol{T}_{1} = \left [ \textstyle\begin{array}{c@{}c@{}c@{}c} 1 & \quad 0 & \quad 0 & \quad x_{1} \\ 0 & \quad 1 & \quad 0 & \quad y_{1} \\ 0 & \quad 0 & \quad 1 & \quad z_{1} \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{array}\displaystyle \right ] , $$

where \(x_{1}, y_{1}, z_{1}\) are the three components of the translations between the frames \(\sum_{\mathrm{v}}\), \(O_{\mathrm{v}} \mbox{--} X_{\mathrm{v}}Y_{\mathrm{v}}Z _{\mathrm{v}}\) and \(\sum_{1}\), \(O_{1} \mbox{--} X_{1}{}Y_{1}{}Z_{1}\). The transformation matrix between the \(i\mbox{th}\) and \((i+1)\mbox{th}\) joints of the manipulator is

$${}^{i }\boldsymbol{T}_{i+1} = \left [ \textstyle\begin{array}{cccc} c{\theta }_{i} & \quad -s{\theta }_{i} c{\alpha }_{i} & \quad s{\theta } _{i} s{\alpha }_{i} & \quad {a}_{i}c{\theta_{i}} \\ s{\theta }_{i} & \quad c{\theta }_{i} c{\alpha }_{i} & \quad -c{\theta } _{i} s{\alpha }_{i} & \quad {a}_{i}s{\theta_{i}} \\ 0 & \quad s{\alpha }_{i} & \quad c{\alpha }_{i} & \quad d_{i} \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{array}\displaystyle \right ] , $$

where \(d_{i}\) represents the distance on the \(z_{i}\) axis between two successive joint offsets, \(a_{i}\) represents the length of the \(i\mbox{th}\) link, \({\alpha }_{i}\) represents the angle between the \(z_{i}\)- and \(z_{i+1}\)-axes, \({\theta }_{i}\) represents the rotation of the \(i\mbox{th}\) link about the \(z_{i}\)-axis. Therefore, the transformation matrix between the end-effector and the inertial frame is

$$ {}^{n}\boldsymbol{T}_{\mathrm{end}} = {}^{n} \boldsymbol{T}_{\mathrm{v}} {}^{\mathrm{v} }\boldsymbol{T}_{1} \prod ^{n}_{i=1} {}^{i } \boldsymbol{T}_{i+1} \cdots {}^{n-1}\boldsymbol{T}_{n}, $$
(1)

where \({}^{n-1}\boldsymbol{T}_{n}\) is the transformation matrix between the end-effector and the frame \(\sum_{n}\), \(O_{n} \mbox{--} X_{n} Y_{n} Z_{n}\), and \(z_{n}\) is the translation between these two frames:

$${}^{n-1}\boldsymbol{T}_{n} = \left [ \textstyle\begin{array}{cccc} 1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 1 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 1 & \quad z_{n} \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{array}\displaystyle \right ] . $$
Fig. 2
figure 2

Coordinate frames for UVMS

Full size image

In order to make dynamic analysis based on angular momentum conservation, the forward computation of the velocity and acceleration of each link is presented through the Newton–Eulerian recursive algorithm. By the serial construction of AUV and manipulator, the angular velocity of link \((i+1)\) relative to link \(i\) is

$$ \boldsymbol{\omega }_{i+1} = \boldsymbol{\omega } _{i} + \boldsymbol{z}_{i+1} \dot{\theta}_{i+1}, $$
(2)

where \(\boldsymbol{\omega }_{i+1}\) represents the angular velocity of the \((i+1)\mbox{th}\) link, \(\boldsymbol{z}_{i}\) denotes the unit vector pointing along the \(i\mbox{th}\) joint axis, and

$$\begin{gathered} \boldsymbol{z}_{i} = {}^{0 }\boldsymbol{R}_{\mathrm{v}} {}^{\mathrm{v} }\boldsymbol{R}_{i} {[0 \quad 0 \quad 1]}^{\mathrm{T}}, \\ {}^{0}\boldsymbol{R}_{\mathrm{v}}=\left [ \textstyle\begin{array}{cccc} c\psi c\theta & \quad c\psi s\theta s\phi -s\psi c\phi & \quad c \psi s\theta c\phi +s\psi s\phi \\ s\psi c\theta & \quad s\psi s\theta s\phi +c\psi c\phi & \quad s \psi s\theta c\phi -c\psi s\phi \\ -s\theta & \quad c\theta s\phi & \quad c\theta c\phi \\ \end{array}\displaystyle \right ] , \\ {}^{i }\boldsymbol{R}_{i+1}=\left [ \textstyle\begin{array}{cccc} c{\theta }_{i} & \quad -s{\theta }_{i}{}c{\alpha }_{i} & \quad s{\theta } _{i}{}s{\alpha }_{i} \\ s{\theta }_{i} & \quad c{\theta }_{i}c{\alpha }_{i} & \quad -c{\theta }_{i}s{\alpha }_{i} \\ 0 & \quad s{\alpha }_{i} & \quad c{\alpha }_{i} \\ \end{array}\displaystyle \right ] . \end{gathered}$$

Thus, the angular velocity of the \((i+1)\mbox{th}\) link in the \(\sum_{i+1}\) frame is

$$ {}^{i+1}\boldsymbol{\omega}_{i+1} = {}^{i+1} \boldsymbol{R}_{i} \bigl({}^{i }\boldsymbol{\omega }_{i} + {}^{i }{\boldsymbol{z}}_{i} {\dot{\theta }}_{i+1} \bigr) , $$
(3)

where

$${}^{\tiny i+1}\boldsymbol{R}_{\tiny i} = \left [ \textstyle\begin{array}{cccc} c{\theta }_{i} & \quad s{\theta }_{i}{} & \quad 0 \\ -c{\alpha }_{i}{}s{\theta }_{i} & \quad c{\theta }_{i}{}c{\alpha } _{i} & \quad s{\alpha }_{i} \\ s{\theta }_{i}{}s{\alpha }_{i} & \quad -s{\theta }_{i}{}c{\alpha } _{i} & \quad c{\alpha }_{i} \\ \end{array}\displaystyle \right ] . $$

The velocity of frame \(\sum_{i+1}\) can be written in terms of \(\sum_{i}\) as follows:

$$ \boldsymbol{v}_{i+1} = \boldsymbol{v}_{i} + \boldsymbol{ \omega }_{i} \times \boldsymbol{r}_{i}. $$
(4)

Hence, (4) in the \(\sum_{i+1}\) frame is

$$ {}^{i+1}\boldsymbol{v}_{i+1} = {}^{i+1} \boldsymbol{R}_{i} {}^{i }\boldsymbol{v}_{i} + {}^{i }\boldsymbol{\omega }_{i} \times {}^{i } \boldsymbol{r}_{i}, $$
(5)

where \({}^{i }\boldsymbol{r}_{i} = [ a_{i}\ d_{i} s\alpha_{i} \ d_{i}c\alpha_{i} ] ^{\mathrm{T}} \) is a constant vector for the revolt joint. The linear velocity of the origin of link \((i+1)\) in terms of link \(i\) can be computed through recursive formula (5). If we set \({}^{i }\boldsymbol{r}_{ci} = [ a_{c}i \ d_{c}i s\alpha_{i} \ d _{ci}c\alpha_{i} ] ^{\mathrm{T}} \) to represent the constant vector of the \(i\mbox{th}\) link geometric center in \(\sum_{i}\), then \(\boldsymbol{r}_{ci}\) represents the position vector of the \(i\mbox{th}\) link geometric center relative to the inertial frame, and the velocity of the \((i+1)\mbox{th}\) link geometric center can be written in terms of \(\sum_{i}\) as follows:

$$ \boldsymbol{v}_{ci+1} = \boldsymbol{v}_{i} + \boldsymbol{ \omega }_{i}\times \boldsymbol{r} _{ci}. $$
(6)

Hence, (6) in the \(\sum_{i}\) frame is

$$ {}^{i }\boldsymbol{v}_{ci+1} = {}^{i } \boldsymbol{v}_{i} + {}^{i }\boldsymbol{\omega }_{i} \times {}^{i }\boldsymbol{r}_{ci}. $$
(7)

Therefore, we obtain the linear acceleration of the origin \(O_{i+1}\) by differentiating (1)–(7):

$$\begin{aligned} \dot{\boldsymbol{\omega }}_{i+1} & = \dot{\boldsymbol{\omega }}_{i} + \boldsymbol{z_{i}} {\ddot{\theta }} _{i+1} + \boldsymbol{\omega }_{i} \times \boldsymbol{z_{i}} {\dot{ \theta }}_{i+1}, \\ {}^{i+1}\dot{\boldsymbol{\omega }}_{i+1} &= {}^{i+1 } \boldsymbol{R}_{i} \bigl({}^{i } \dot{\boldsymbol{ \omega}}_{i} + {}^{i }\boldsymbol{z}_{i}\ddot{ \theta}_{i+1} + {}^{i }\boldsymbol{\omega }_{i} \times {}^{i }\boldsymbol{z}_{i}{\dot{\theta}}_{i+1}\bigr), \\ \dot{\boldsymbol{v}}_{i+1} &= \dot{\boldsymbol{v}}_{i} + \dot{\boldsymbol{\omega }}_{i+1} \times \boldsymbol{r}_{i+1} + \boldsymbol{\omega }_{i+1} \times (\boldsymbol{\omega }_{i+1} \times \boldsymbol{r}_{i+1}) \\ {}^{i+1}\dot{\boldsymbol{v}}_{i+1} & = {}^{i+1 } \boldsymbol{R}_{i} {}^{i }\dot{\boldsymbol{v}}_{i} + {}^{i+1}\dot{\boldsymbol{\omega }}_{i+1} \times {}^{i+1}\boldsymbol{r}_{i+1} +{}^{i+1} \boldsymbol{ \omega}_{i+1}\times \bigl({}^{i+1}\boldsymbol{\omega }_{i+1} \times {}^{i+1} \boldsymbol{r}_{i+1}\bigr), \\ \dot{\boldsymbol{v}}_{ci+1} & = \dot{\boldsymbol{v}}_{i} + \dot{\boldsymbol{\omega }}_{i+1} \times {\boldsymbol{r}}_{ci+1} + \boldsymbol{\omega }_{i+1} (\boldsymbol{\omega }_{i+1} \times \boldsymbol{r}_{ci+1}), \\ {}^{i+1}\dot{\boldsymbol{v}}_{ci+1} & = {}^{i }\dot{ \boldsymbol{v}}_{i} + {}^{i+1}\dot{\boldsymbol{\omega }}_{i+1} \times {}^{i+1}\boldsymbol{r}_{ci+1} + {}^{i+1}\boldsymbol{\omega }_{i+1}\times \bigl({}^{i+1} \boldsymbol{\omega }_{i+1} \times {}^{i+1}\boldsymbol{r}_{ci+1} \bigr). \end{aligned}$$

In what follows, we will deduce the Jacobian matrix for UVMS motion planning. The position vectors of the \(i\mbox{th}\) link at its geometrical center can also be expressed as

$$\begin{aligned} \boldsymbol{r}_{ci}& = {}^{c\mathrm{v}}\boldsymbol{T}_{\mathrm{v}} {}^{\mathrm{v}}\boldsymbol{T}_{1}\prod^{i}_{j=1}{}^{i-1} \boldsymbol{T}_{i}\boldsymbol{r}_{c\mathrm{v}}+ {}^{\mathrm{v}} \boldsymbol{T}_{1}\prod^{i}_{j=1}{}^{i-1} \boldsymbol{T}_{i}\boldsymbol{r}_{b\mathrm{v}} \\ &\quad {}+\sum_{k=1}^{i-1} \Biggl( \prod _{j=k}^{i}{}^{{j-1}} \boldsymbol{T}_{j}{}^{k }\boldsymbol{r}_{ck} + \prod_{j=k}^{i}{}^{j-1} \boldsymbol{T} _{j}{}^{k }\boldsymbol{r}_{bk} \Biggr) +{}^{i }\boldsymbol{r}_{ci}, \end{aligned}$$
(8)

where \(\boldsymbol{r}_{c\mathrm{v}}\) is the position vector of AUV at its geometrical center, \(\boldsymbol{r}_{b\mathrm{v}}\) is the position vector from AUV geometrical center to the manipulator base link, \({}^{k }\boldsymbol{r}_{bk}\) represents the position vector from the \(k\mbox{th}\) link geometric center to the \((i+1)\mbox{th}\) joint in \(\sum_{k}\). Thus, the position vector of the end-effector is

$$ \begin{aligned}[b] \boldsymbol{r}_{\mathrm{end}} &= {}^{c\mathrm {v}} \boldsymbol{T}_{\mathrm{v}} {}^{\mathrm{v}}\boldsymbol{T}_{1}\prod ^{n}_{j=1}{}^{ {i-1}} \boldsymbol{T}_{i}\boldsymbol{r}_{c\mathrm{v}}+ {}^{\mathrm{v}} \boldsymbol{T}_{1}\prod^{n}_{j=1}{}^{i-1} \boldsymbol{T}_{i}\boldsymbol{r}_{ b\mathrm {v}} \\ &\quad {}+\sum_{k=1}^{n} \Biggl( \prod _{j=k}^{n}{}^{j-1} \boldsymbol{T}_{j}{}^{k }\boldsymbol{r}_{ck} + \prod_{j=k}^{n} {}^{j-1} \boldsymbol{T}_{j}{}^{k }\boldsymbol{r}_{bk} \Biggr). \end{aligned} $$
(9)

The velocity vectors of the \(i\mbox{th}\) link at its geometrical center and the end effector are

$$ \left \{ \textstyle\begin{array} {l} \displaystyle \boldsymbol{v}_{i} = \dot{\boldsymbol{r}}_{ci} = \boldsymbol{v}_{\mathrm{v}} + \boldsymbol{ \omega }_{\mathrm{v}} \times ( \boldsymbol{r}_{ci}- \boldsymbol{r}_{c\mathrm{v}}) + \sum^{i}_{k=1} \bigl[ \boldsymbol{z}_{k}\times ( \boldsymbol{r}_{ck}- \boldsymbol{r}_{k})\bigr]\dot{\boldsymbol{\theta }}_{k} , \\ \displaystyle \boldsymbol{v}_{n} = \dot{\boldsymbol{r}}_{n} = \boldsymbol{v}_{\mathrm{v}} + \boldsymbol{\omega }_{\mathrm{v}} \times ( \boldsymbol{r}_{n}- \boldsymbol{r}_{c\mathrm{v}}) + \sum ^{n}_{i=1}\bigl[ \boldsymbol{z}_{i}\times ( \boldsymbol{r}_{n}- \boldsymbol{r}_{i})\bigr]\dot{\boldsymbol{ \theta }}_{i} , \end{array}\displaystyle \right . $$
(10)

where \(\boldsymbol{r}_{i}\) is the position vector of the \(i\mbox{th}\) joint. The angular velocity vector of the \(i\mbox{th}\) link at its geometrical centre and the end-effector are

$$ \left \{ \textstyle\begin{array}{l} \displaystyle \boldsymbol{\omega }_{i} = \boldsymbol{\omega }_{c\mathrm {v}} + \sum^{i}_{k=1} \boldsymbol{z}_{k} \dot{\boldsymbol{\theta }}_{k}, \\ \displaystyle \boldsymbol{\omega }_{e} = \boldsymbol{\omega }_{c\mathrm{v}} + \sum^{n}_{i=1} \boldsymbol{z}_{i} \dot{\boldsymbol{\theta }}_{i}. \end{array}\displaystyle \right . $$
(11)

Therefore, from (10) and (11) we obtain

$$ \left [ \textstyle\begin{array}{c} \boldsymbol{v}_{n} \\ \boldsymbol{\omega }_{n} \\ \end{array}\displaystyle \right ] = \boldsymbol{J}_{\mathrm{{v}}} \left [ \textstyle\begin{array}{c} \boldsymbol{v}_{\mathrm{v}} \\ \boldsymbol{\omega }_{\mathrm{{v}}} \\ \end{array}\displaystyle \right ] + \boldsymbol{J}_{m} \dot{\boldsymbol{\varTheta }}, $$
(12)

where \(\boldsymbol{J}_{\mathrm{v}}\) and \(\boldsymbol{J}_{m}\) are the Jacobian matrices correlated with AUV and manipulator, respectively:

$$\boldsymbol{J}_{\mathrm{v}} = \left ( \textstyle\begin{array}{ccc} \boldsymbol{E} & \quad & -( \boldsymbol{r}_{n}- \boldsymbol{r}_{c\mathrm{v}}) \\ \boldsymbol{O}& \quad & \boldsymbol{E} \\ \end{array}\displaystyle \right ) ,\qquad \boldsymbol{J}_{m} = \left [ \textstyle\begin{array}{ccc} \boldsymbol{z}_{1} \times ( \boldsymbol{r}_{n}- \boldsymbol{r}_{1}) & \quad \cdots &\quad \boldsymbol{z}_{n} \times ( \boldsymbol{r}_{n}-\boldsymbol{r}_{n-1}) \\ \boldsymbol{z}_{1} & \quad \cdots &\quad \boldsymbol{z}_{n} \end{array}\displaystyle \right ] , $$

where \(\boldsymbol{E}=\operatorname{diag}\{1,1,1\}, \boldsymbol{\varTheta }=[{\theta }_{1} {\theta }_{2} \ldots \theta _{n} ]^{\mathrm{T}}\).

2.2 Dynamics of UVMS

By the derivation in Sect. 2.1, the dynamic equations can be obtained as

$$\begin{aligned} &\boldsymbol{M}_{\mathrm{RB}} (\boldsymbol{q}) \dot{\boldsymbol{v}}+ \boldsymbol{C}_{\mathrm{RB}} (\boldsymbol{q},\boldsymbol{v}) \boldsymbol{v} + \boldsymbol{M}_{A} (\boldsymbol{q}) \dot{\boldsymbol{v}}_{r} + \boldsymbol{C}_{A} (\boldsymbol{q},\boldsymbol{v}_{r}) \boldsymbol{v}_{r} + \boldsymbol{D} (\boldsymbol{q}, \boldsymbol{v}_{r} )\boldsymbol{v}_{r} +\boldsymbol{g} ( \boldsymbol{q}) + \boldsymbol{\tau }_{\mathrm{Mmom}} = \boldsymbol{\tau }_{\mathrm{ctrl}}, \end{aligned}$$

where \(\boldsymbol{M}_{\mathrm{RB}} (\boldsymbol{q}) \dot{\boldsymbol{v}} + \boldsymbol{C}_{\mathrm{RB}} (\boldsymbol{q},\boldsymbol{v}) \boldsymbol{v}\) represents the force vector generated from the kinetic energy of rigid bodies, \(\boldsymbol{v}\) represents the velocity vector of UVMS, \(\boldsymbol{M}_{\mathrm{RB}} (\boldsymbol{q})\) is the system inertial and mass matrix, \(\boldsymbol{C}_{\mathrm{RB}} (\boldsymbol{q},\boldsymbol{v})\) is the Coriolis matrix, \(\boldsymbol{M}_{A} (\boldsymbol{q}) \dot{\boldsymbol{v}}_{r} + \boldsymbol{C}_{A} (\boldsymbol{q}, \boldsymbol{v}_{r} ) \boldsymbol{v}_{r} + \boldsymbol{D} (\boldsymbol{q},\boldsymbol{v}_{r} ) \boldsymbol{v}_{r}\) denotes the force vector produced from hydrodynamic effects, including hydraulic inertial forces and damping forces, \(\boldsymbol{v}_{r}\) is the velocity vector of UVMS relative to water current, \(\boldsymbol{M}_{A} (\boldsymbol{q})\) is the matrix of added mass, \(\boldsymbol{C}_{A} (\textbf{q},\boldsymbol{v}_{r})\) is the added Coriolis and centripetal contribution produced from added mass, \(\boldsymbol{D} (\boldsymbol{q},\boldsymbol{v}_{r} )\) is the dissipative drag matrix caused by fluid viscosity, \(\boldsymbol{g} (\boldsymbol{q})\) is the vector of restoring forces, \(\boldsymbol{\tau }_{\mathrm{ctrl}}\) is the force vector of control forces, and \(\boldsymbol{\tau }_{\mathrm{Mmom}}\) represents the coupling reaction forces between AUV and manipulator during manipulation. Thus, the model is composed with hydrodynamic effects, coupling forces, and restoring forces, which is different from other multibody systems such as satellite-manipulator system in space and mobile manipulator on the land.

2.2.1 Hydrodynamic effects

The hydrodynamic effects on UVMS are the summation of effects encountered by vehicle and manipulator. They include two components, the added mass forces and viscous damping. The added mass forces are the reaction forces produced by acceleration movement of the body. They can be calculated in the unbounded flow field through the panel method numerically [31]. The fluid kinetic energy produced from the \(i\mbox{th}\) link is

$$\boldsymbol{T}_{iA} = \frac{1}{2} \boldsymbol{v}^{\mathrm{T}}_{i} \boldsymbol{M}_{iA} \boldsymbol{v}_{i} . $$

Thus, the moment of momentum produced from the \(i\mbox{th}\) link is

$$\boldsymbol{B}_{i} = \frac{\partial \boldsymbol{T}}{\partial \boldsymbol{v}_{i}} = \frac{\partial ( \frac{1}{2} \boldsymbol{v}^{\mathrm{T}}_{i} \boldsymbol{M}_{iA} \boldsymbol{v}_{i})}{ \partial \boldsymbol{v}_{i}}, $$

where \(\boldsymbol{M}_{iA}\) is the \(6\times 6\) inertia matrix of added mass terms. The viscous damping forces caused by vortex shedding can be modeled as

$$\boldsymbol{f}_{i} = -\frac{1}{2} \rho C_{D} (R_{n})D(x_{i}) \mid \boldsymbol{v}_{i} \mid \boldsymbol{v}_{i} , $$

where \(\rho \) is the water density, \(D(x_{i})\) is the projected cross-sectional area of the \(i\mbox{th}\) link body. \(\boldsymbol{v} _{i}\) is the velocity vector of the \(i\mbox{th}\) link, \(C_{D} (R_{n})\) is the drag coefficient based on the representative area, and \(R_{n}\) is the Reynolds number. Since the UVMS motion speed is slow during the manipulation process, the viscosity of the fluid is mainly caused by dissipative drag and lift forces.

2.2.2 Restoring forces

Determined by the volume of the displaced fluid, the location of the center of buoyancy (CB), and the center of gravity (CG), the restoring forces affect the AUV heaving, rolling and pitching motions [13]. If we define \({}^{n} \boldsymbol{f}^{i}_{g} = [0 \ 0 \ m_{i}g]^{\mathrm{T}}\) and \({}^{n}\boldsymbol{f}^{i}_{B} = [0 \ 0 \ B_{i}]^{\mathrm{T}}\) as the gravity force and buoyancy force of the \(i\mbox{th}\) link in the inertial frame, respectively, then the vector of restoring forces and moments on the whole system is

$$ \boldsymbol{g} (\boldsymbol{q}) = \left [ \textstyle\begin{array}{c} \displaystyle {}^{\mathrm{v} }\boldsymbol{f}^{ \mathrm{v}}_{g} + {}^{\mathrm{v} }\boldsymbol{f}^{\mathrm{v}}_{B} + \sum^{4}_{i=1} ({} ^{\mathrm{v} }\boldsymbol{f}^{i}_{g} + {}^{\mathrm{v} } \boldsymbol{f}^{i}_{B} ) \\ \displaystyle {}^{\mathrm{v} }\boldsymbol{r}^{\mathrm{v}}_{g} \times {}^{\mathrm{v} }\boldsymbol{f}^{\mathrm{v}}_{g} + {}^{\mathrm{v} }\boldsymbol{r}^{ \mathrm{v}}_{B} \times {}^{0}\boldsymbol{f}^{\mathrm{v}}_{ B} + \sum^{4}_{i=1} ( {} ^{\mathrm{v} }\boldsymbol{r} ^{i}_{g} \times {}^{\mathrm{v} }\boldsymbol{f}^{i}_{g} + {}^{ \mathrm{v} } \boldsymbol{r}^{i}_{B} \times {}^{\mathrm{v} } \boldsymbol{f}^{i}_{B} ) \\ \end{array}\displaystyle \right ] , $$
(13)

where \({}^{\mathrm{v} }\boldsymbol{f}^{i}_{g} = {}^{n}\boldsymbol{R}^{\mathrm{T}}_{ \mathrm{v}} {}^{n} \boldsymbol{f}^{i}_{g}\), \({}^{\mathrm{v} } \boldsymbol{f}^{i}_{B} = {}^{n}\boldsymbol{R}^{\mathrm{T}}_{\mathrm{v}} {}^{n} \boldsymbol{f}^{i}_{B}\) denotes the restoring force of the \(i\mbox{th}\) link relative to AUV, \({}^{n}\boldsymbol{f}^{\mathrm{v}}_{g} = [0 \ 0 \ m _{\mathrm{v}}g]^{\mathrm{T}}\), \({}^{n}\boldsymbol{f}^{\mathrm{v}}_{B} = [0 \ 0 \ B_{v}]^{\mathrm{T}}\), \({}^{ \mathrm{v}}\boldsymbol{f}^{\mathrm{v}}_{g} = {}^{n}\boldsymbol{R}^{\mathrm{T}}_{ \mathrm{v}} {}^{n} \boldsymbol{f}^{\mathrm{v}}_{g}\), \({}^{\mathrm{v} } \boldsymbol{f}^{\mathrm{v}}_{B} = {}^{n}\boldsymbol{R}^{\mathrm{T}}_{\mathrm{v}} {}^{n} \boldsymbol{f}^{\mathrm{v}}_{B}\) denotes the restoring force of AUV, \({}^{\mathrm{v} } \boldsymbol{r}^{\mathrm{v}}_{g}\) and \({}^{\mathrm{v} } \boldsymbol{r}^{\mathrm{v}}_{B}\) are the AUV CB and CG position vectors relative to AUV geometric centre, respectively, and \({}^{\mathrm{v} }\boldsymbol{r}^{ i}_{g}\) and \({}^{\mathrm{v} } \boldsymbol{r}^{i}_{B}\) are the \(i\mbox{th}\) link CB and CG position vectors relative to the AUV geometric center, respectively.

2.2.3 Coupling reaction forces between AUV and manipulator

The coupling forces is the constraint reaction forces between AUV and manipulator, which can be deduced from the recursive Newton–Euler formulation by incorporating hydraulic forces. Thus, the inertial force and moment vectors exerted at the \(i\mbox{th}\) link geometric center are

$$\left \{ \textstyle\begin{array}{l} {}^{i }\boldsymbol{f}^{*}_{i} = -m _{i} {}^{i }\dot{\boldsymbol{V}}_{ci} , \\ {}^{i }\boldsymbol{n}^{*}_{i} = -\,{}^{i }\boldsymbol{I}_{i} {}^{i } \dot{\boldsymbol{\omega }}_{i} - {}^{i } \boldsymbol{\omega }_{i} \times \bigl( {}^{i }\boldsymbol{I}_{i} {}^{i }\dot{\boldsymbol{\omega}}_{i} \bigr), \end{array}\displaystyle \right . $$

where \({}^{i }\boldsymbol{I}_{i}\) is the inertial matrix of the \((i+1)\mbox{th}\) link represented in the \(\sum_{i}\) frame. Hence, the constraint reaction force and moment of the \(i\mbox{th}\) link are

$$ \left \{ \textstyle\begin{array}{l} {}^{i }\boldsymbol{f}_{i, i-1} = {}^{i }\boldsymbol{f}_{i+1,i} - {}^{i } \boldsymbol{f}^{*}_{i,i-1} - {}^{i }\boldsymbol{F}_{i,i} , \\ {}^{i }\boldsymbol{n}_{i,i-1} = {}^{i } \boldsymbol{n}_{i+1,i} + {}^{i } \boldsymbol{r}_{ci} \times {}^{i } \boldsymbol{f}_{i, i-1} + \bigl({}^{i }\boldsymbol{r}_{i} - {}^{i }\boldsymbol{r}_{ci} \bigr) \times \bigl( {}^{i }\boldsymbol{f} _{i+1} + {}^{i }\boldsymbol{F}_{i,i} \bigr) - {}^{i } \boldsymbol{n}^{*}_{i} - {}^{i }\boldsymbol{M}_{i,i}, \end{array}\displaystyle \right . $$
(14)

where \({}^{i }\boldsymbol{M}_{i,i}\) and \({}^{i }\boldsymbol{F}_{i,i}\) are the hydraulic force and moment vectors on the \(i\mbox{th}\) link. To convert \({}^{i }\boldsymbol{f}_{i,i-1}\) and \({}^{i }\boldsymbol{n}_{i,i-1}\) into the \((i-1)\mbox{th}\) link frame, we have

$$ \left \{ \textstyle\begin{array}{l} {}^{i-1}\boldsymbol{f}_{i,i-1} = {}^{i-1}\boldsymbol{R}_{i}{}^{i }\boldsymbol{f}_{i, i-1} , \\ {}^{i-1}\boldsymbol{n}_{i, i-1} = {}^{i-1}\boldsymbol{R}_{i}{}^{i }\boldsymbol{n}_{i, i-1}. \end{array}\displaystyle \right . $$
(15)

Therefore, the coupling reaction forces \({}^{\mathrm{v}} \boldsymbol{f}_{1,\mathrm{v}}\) and moment \({}^{\mathrm{v}}\boldsymbol{n}_{1,\mathrm{v}}\) between AUV and the manipulator can be deduced through equations (14) and (15) recursively.

3 Optimal motion planning algorithm

In order to execute autonomous manipulation task, motion planning is required. Since the designed UVMS is a redundant system, an infinite number of joint solutions may be available for a given task-space trajectory, which makes the planning problems more challenging. One of the objectives of motion planning algorithm is to assign additional motion DOF for secondary objective criteria. In comparison, light weight positioner can be equipped with cameras to keep the manipulator in sight, which can make far less effect on AUV than the manipulator if laid close to AUV geometrical center; the quantity of batteries can be increased, or the cruise distance can be decreased for energy consumption problem. However since UVMS is a system composed of two heterogeneous dynamic subsystem with different mass, size, and shape, the change of restoring forces, coupling reaction forces between AUV and the manipulator greatly influence the performance of AUV. Since a streamline single body is most widely applied for current AUV, an unsuccessful motion planning algorithm may even cause AUV of this shape to be capsized during manipulation. Therefore, the most important objective of motion planning is to reduce restoring forces and coupling reaction forces so as to not only maintain the AUV attitude and hovering stable, but also to realize precise manipulation. I what follows, we take precision as the priority objective and self-disturbance minimization, including restoring forces and coupling forces, as the second objective through primal dual optimization and genetic iteration.

From (13) and (15) we can obtain the self-disturbance forces including restoring forces and coupling reaction forces:

$$ \boldsymbol{F}_{\mathrm{dis}} = \left [ \textstyle\begin{array}{c} \displaystyle {}^{\mathrm{v} }\boldsymbol{f}^{\mathrm{v}}_{g} + {}^{\mathrm{v} }\boldsymbol{f}^{ \mathrm{v}}_{B} + \sum^{4}_{i=1} ({}^{\mathrm{v} } \boldsymbol{f}^{i}_{g} + {}^{\mathrm{v} }\boldsymbol{f}^{i}_{B} ) + {}^{\mathrm{v} }\boldsymbol{f}_{1,\mathrm{v}} \\ \displaystyle {}^{\mathrm{v} }\boldsymbol{r}^{\mathrm{v}}_{ g} \times {}^{\mathrm{v} }\boldsymbol{f}^{\mathrm{v}}_{ g} + {}^{\mathrm{v} }\boldsymbol{r}^{\mathrm{v}}_{B} \times {}^{0}\boldsymbol{f}^{\mathrm{v}}_{B} + \sum^{4}_{i=1} ({}^{\mathrm{v} } \boldsymbol{r}^{i}_{g} \times {}^{\mathrm{v} }\boldsymbol{f}^{i}_{g} + {}^{\mathrm{v} }\boldsymbol{r}^{i}_{B} \times {}^{\mathrm{v} }\boldsymbol{f}^{i}_{B}) + {}^{\mathrm{v} }\boldsymbol{n}_{1,\mathrm{v}} \end{array}\displaystyle \right ] . $$
(16)

Thus, we have the following primal-dual problem for optimization:

$$\begin{aligned} & \mbox{minimize} \quad \boldsymbol{F}_{\mathrm{dis}} \\ & \mbox{subject to}\ \left \{ \textstyle\begin{array}{l} \left [ \textstyle\begin{array}{c} \boldsymbol{v}_{\mathrm{end}} \\ \boldsymbol{\omega }_{\mathrm{end}} \end{array}\displaystyle \right ] = \boldsymbol{J}_{ v} \left [ \textstyle\begin{array}{c} \boldsymbol{v}_{ v} \\ \boldsymbol{\omega }_{ v} \end{array}\displaystyle \right ] + \boldsymbol{J}_{m} \dot{\boldsymbol{ \varTheta }}, \\ \bigl\lVert \boldsymbol{Y}_{\mathrm{end}} - {}^{0}{\boldsymbol{T}}_{v} {} ^{\mathrm{v}}{ \boldsymbol{T}}_{E}\bigr\rVert < e, \\ \theta _{\mathrm{imin}} \leq {\theta }_{i} \leq {\theta }_{\mathrm{imax}},\lvert \theta \rvert \leq {\theta }_{\mathrm{lim it}},\lvert \varphi \rvert \leq {\varphi }_{\mathrm{limit}}, \end{array}\displaystyle \right . \end{aligned}$$
(17)

where \({\boldsymbol{Y}}_{\mathrm{end}}\) is the planned trajectory of the manipulator end, and \(e\) is the tracking error. In order to keep AUV attitude during the manipulation process, we set \({\theta }_{\mathrm{limit}} \le 4^{ \circ }\) and \({\varphi }_{\mathrm{limit}} \le 5^{\circ }\). The desired pose of the manipulator end includes the 3-axis position and 3-axis rotation. The vehicle has been proposed with four active DOFs, for example, 3-axis position and 1-axis rotation \((x,\ y,\ z,\ \psi )\), whereas the manipulator has been proposed with 4-axis rotation \((\theta_{1}\sim \theta_{4})\). The limitation of \(\theta_{1}\) is illustrated in Table 3. The following optimization algorithm acquires the most appropriate trajectory to minimize \(\boldsymbol{F}_{\mathrm{dis}}\) during the whole manipulation process through iteration, crossover, and mutation, genetic operation of the 8 parameters group of vehicle and manipulator above.

In comparison with a deterministic SQP, the genetic algorithm is a general adaptive optimization search methodology based on a direct analogy to Darwinian natural selection and genetics in biological systems. It generates successive populations of alternate solutions that are represented by a chromosome until acceptable results are obtained or no better result is generated. Thus, this algorithm is more computationally efficient and can realize online optimization. The optimal algorithm is designed as given in Fig. 3.

  1. I.

    Initialization: a binary representation is used to encode \({\theta }_{1}\), and the total length of the binary solution vector is 1000 bits. The inputs are the AUV size and manipulator link parameters, kinematics and dynamic analysis results, joint variable limits, and so on. We can view each combination of manipulator joints and AUV position in a chromosome as a gene that contains the information of AUVMS configuration.

  2. II.

    Fitness calculation: since the optimization objective is to minimize self-disturbance forces, the fitness function is defined as

    $$ \mathrm{Fit}(f) = \frac{1}{ \lVert \boldsymbol{F}_{\mathrm{dis}} \rVert_{2}} = \frac{1}{ \sum^{6}_{i=1} \boldsymbol{F}^{2}_{\mathrm{dis}}(i)}, $$
    (18)

    which can be obtained from the combination of chromosomes. The fitness of each individual chromosome will be evaluated through (18). The optimization objective is combined through maximizing the fitness function with the trajectory constraints.

  3. III.

    Genetic operation: in these operations, new individuals are produced through selection, crossover, and mutation. Some of the population are selected and inherited according to roulette-wheel selection. Individuals are chosen at random, and crossover is operated so that new individuals are produced. The newly generated chromosome combination from genetic operation is deduced through UVMS kinematics. If the error between the trajectory result and the planned manipulator end is less than \(e\), then its fitness is calculated and compared; otherwise, it is discarded. If the optimal condition is satisfied, then the best solution is returned from a binary string to the decimal value.

Fig. 3
figure 3

Genetic optimization diagram

Full size image

4 Observer-based coordinated motion controller

This section is purposed to develop a real-time, robust and coordinate motion controller for UVMS to achieve autonomous manipulation. Such a controller can overcome the issues such as parameter uncertainties, self-disturbance, external disturbances, and internal noises. As stated before, the motion of manipulator has made great disturbance on AUV during manipulation. Since the self-disturbance varies greatly with time, it is difficult for kinematic feedback controller, which is purposed to compensate trajectory errors, to compensate self-disturbance in real-time. Therefore, a dynamic model is applied to compute self-disturbance forces based on the manipulator joint positions, AUV position, and attitude obtained in real time through dead reckoning from the sensors like gyroscopic compass, doppler velocity log (DVL), and so forth. In comparison with AUV, the manipulator is much easier to control. In the following, the manipulator is controlled through a kinematic controller, and AUV is controlled through a kinematic and dynamic controller.

4.1 Kinematic controller

In comparison with some other nonlinear control techniques, the S-surface controller not only carries on robust character of PD controller, but also possesses the advantages of fuzzy controller with detailed control volume subdivision when closing to the desired value [31]. Since S-surface control can provide quick convergence in combination with fuzzy and PD control characteristics, it has been proved successful for the AUV control. Thus, the S-surface controller is applied as a kinematic controller so as to guarantee the controller convergence. The S-surface controller is

$$ \left \{ \textstyle\begin{array}{l} \displaystyle \boldsymbol{u} = \frac{2\boldsymbol{I}}{\boldsymbol{I}+\exp( -\boldsymbol{K} _{d} \tilde{\boldsymbol{q}} -\boldsymbol{K}_{p} \dot{\tilde{\boldsymbol{q}}})} -\boldsymbol{I}+\varDelta \boldsymbol{u}, \\ \boldsymbol{f}_{T}= \boldsymbol{K}\boldsymbol{u}, \end{array}\displaystyle \right . $$
(19)

where \(\boldsymbol{q}_{d}\) represents the desired AUV position and attitude states or manipulator joint state vectors, \(\boldsymbol{q}\) represents the real AUV or manipulator state vectors, \(\tilde{\boldsymbol{q}} = \boldsymbol{q}_{d} - \boldsymbol{q}\) and \(\dot{\tilde{\boldsymbol{q}}}\) represent the input error and rate of error change in normalized form, \(\boldsymbol{u}\) is the output of the kinematic controller, which stands for the force in each degree of freedom, \(\boldsymbol{K}\) is the force coefficient matrix for the actuators, which can be obtained in the open water test in a cavitation tunnel or a towing tank [32], \(\boldsymbol{K}_{d}\) and \(\boldsymbol{K}_{p}\) are the proportional and derivative gain matrices, \(\boldsymbol{I} = [1\ 1\ \ldots \ 1]^{\mathrm{T}}\) is the identity matrix with dimension of the manipulator or AUV DOFs, \(\varDelta \boldsymbol{u}\) is the normalized compensation value of the disturbance force obtained from the dynamic controller. For the sigmoid function in Fig. 4, the controller commands are loosely considered when the deviation is comparatively large, whereas strictly treated when the deviation is comparatively small. Thus, the kinematic controller indicates the idea of fuzzy control to a certain extent.

Fig. 4
figure 4

Sigmoid-function

Full size image

Therefore, a kinematic controller can guarantee the controller convergence when confronting with external disturbance and parameter uncertainty, as long as a sufficient control force can be saved from motion planning optimization.

4.2 Observer-based dynamic controller

Although motion plan has been applied to reduce self-disturbance, it can still make AUV roll and pitch violently, and cause great effect on manipulation and subsequent cruise. Thus, we introduce a self-disturbance observer-based on the dynamic model of Sect. 2.

By using depth gauge, DVL, and gyroscopic compass, the real-time heading, roll, pitch, depth, velocity, and heave of the AUV can be obtained. Its real-time position is calculated from GPS plus extended Kalman filter (EKF):

$$ \boldsymbol{Y} = \boldsymbol{HX} + \boldsymbol{N} , $$
(20)

where \(\boldsymbol{Y}\) is the calculated position vector of AUV and manipulator DOFs, \(\boldsymbol{H}\) is the observation matrix, \(\boldsymbol{X}\) is the state variables obtained from sensors, and \(\boldsymbol{N}\) is the vector of observation noise. Therefore, the observed self-disturbance forces can be obtained from (16) and (20):

$$\begin{aligned} \hat{\boldsymbol{F}}_{\mathrm{dis}}(\boldsymbol{q}) & = {\boldsymbol{g}}( \boldsymbol{q})+ \left [ \textstyle\begin{array}{c} \displaystyle {}^{\mathrm{v}}\hat{\boldsymbol{f}}_{1,\mathrm{v}} \\ {}^{\mathrm{v}}\hat{\boldsymbol{n}}_{1,\mathrm{v}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \displaystyle {}^{\mathrm{v}}\hat{\boldsymbol{f}}^{\mathrm{v}} _{g} + {}^{\mathrm{v}}\hat{\boldsymbol{f}}^{\mathrm{v}}_{B} + \cdots \\ \sum^{4}_{i=1} ({}^{\mathrm{v}}\hat{\boldsymbol{f}}^{i} _{g} + {}^{\mathrm{v}}\hat{\boldsymbol{f}}^{i}_{B} ) + {}^{\mathrm{v}}\hat{\boldsymbol{f}}_{1,\mathrm{v}} \\ \displaystyle {}^{\mathrm{v}}\hat{\boldsymbol{r}}^{\mathrm{v}} _{g} \times {}^{\mathrm{v}}\hat{\boldsymbol{f}}^{\mathrm{v}}_{g} + {}^{\mathrm{v}}\hat{\boldsymbol{r}}^{\mathrm{v}}_{B} \times {}^{0}\hat{\boldsymbol{f}}^{\mathrm{v}}_{B} +\cdots \\ \sum^{4}_{i=1} ( {}^{\mathrm{v}}\hat{\boldsymbol{r}}^{i} _{g} \times {}^{\mathrm{v}}\hat{\boldsymbol{f}}^{i}_{g} + {}^{\mathrm{v}}\hat{\boldsymbol{r}}^{i}_{B} \times {}^{\mathrm{v}} \hat{\boldsymbol{f}}^{i}_{B}) + {}^{\mathrm{v}}\hat{\boldsymbol{n}}_{1,\mathrm{v}} \end{array}\displaystyle \right ] . \end{aligned}$$
(21)

Here \(\boldsymbol{g}(\boldsymbol{q})\) represents the reactor of gravitational and buoyant forces. The proposed dynamic controller along with self-disturbance observer is given as follows (see Fig. 5):

$$ \boldsymbol{\tau } = \hat{\boldsymbol{M}}(\boldsymbol{q}) \biggl[\ddot{ \boldsymbol{q}}_{d} + \displaystyle \frac{2\boldsymbol{I}}{\boldsymbol{I}+\exp( -\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}} )} -\boldsymbol{I} \biggr] + \hat{\boldsymbol{C}}(\dot{\boldsymbol{q}})\dot{\boldsymbol{q}} + \hat{ \boldsymbol{D}}( \dot{\boldsymbol{q}})\dot{\boldsymbol{q}} + \hat{ \boldsymbol{F}}_{\mathrm{dis}}(\boldsymbol{q}), $$
(22)

where \(\hat{\boldsymbol{M}}\) is the matrix of estimation of inertial, mass, and added mass, \(\hat{\boldsymbol{C}}\) is the matrix of Coriolis and centripetal contribution produced from mass and added mass, and \(\hat{\boldsymbol{D}}\) is the dissipative drag matrix caused by fluid viscosity. The block diagram that corresponds to the proposed controller is shown in Fig. 5. Except for the UVMS system dynamics, the proposed dynamic controller requires tracking errors of manipulator end, desired displacement and attitude vectors of UVMS, actual values of the velocity, displacement and attitude vectors of UVMS, and observed self-disturbance vectors. The task space values are transformed into desired manipulator end and AUV position values by using the trajectory planner and the UVMS inverse kinematics. The UVMS tracking errors are calculated by using UVMS kinematics and EKF block. Dynamic control vectors are calculated based on the proposed control law with the observed self-disturbance parameters. The final control vectors are the sum of the kinematic and dynamic controllers.

Fig. 5
figure 5

Observer-based coordinated motion controller

Full size image

4.3 Stability analysis

From (22) we have

$$\begin{aligned} \frac{2\boldsymbol{I}}{ \boldsymbol{I}+\exp( -\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}})} -\boldsymbol{I} & = \frac{\boldsymbol{I}-\exp( - \boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}} )}{\boldsymbol{I}+\exp( -\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}})} \\ & = \frac{ \displaystyle \exp( -\frac{1}{2} ( -\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}} ))- \displaystyle \exp( \frac{1}{2} (-\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}} ))}{ \displaystyle \exp( -\frac{1}{2} ( -\boldsymbol{K}_{d} \tilde{q} -{\boldsymbol{K}}_{p} \dot{\tilde{q}} ))+ \displaystyle \exp( \frac{1}{2} ( -\boldsymbol{K}_{d} \tilde{q} -\boldsymbol{K}_{p} \dot{\tilde{q}} ))} \\ & = \tanh\biggl( \displaystyle \frac{\boldsymbol{K}_{d} \tilde{q} +\boldsymbol{K}_{p} \dot{\tilde{q}}}{2}\biggr) \\ & = \displaystyle \frac{\boldsymbol{K}_{d} \tilde{q} +\boldsymbol{K}_{p} \dot{\tilde{q}}}{2} + \displaystyle \frac{(\boldsymbol{K}_{d} \tilde{q} +\boldsymbol{K}_{p} \dot{\tilde{q}})^{3}}{24} - \displaystyle \frac{(\boldsymbol{K}_{d} \tilde{q} +\boldsymbol{K}_{p} \dot{\tilde{q}})^{5}}{240} +\cdots \\ &\quad {} + \displaystyle \frac{2^{2n}(2^{2n}-1){\boldsymbol{B}}_{2n} (-(\boldsymbol{K}_{d} \tilde{q} +{\boldsymbol{K}}_{p} \dot{\tilde{q}})/2)^{2n-1}}{(2n)!} , \end{aligned}$$
(23)

where \(\boldsymbol{B}_{n}\) is the \(n\mbox{th}\) Bernoulli number. For the control input vector in (19), \(\hat{\boldsymbol{M}}(\boldsymbol{q}) \ddot{\boldsymbol{q}}\) is substituted by (21) for UVMS dynamics:

$$ \hat{\boldsymbol{M}}(\boldsymbol{q}) \ddot{\boldsymbol{q}} = \hat{ \boldsymbol{M}}(\boldsymbol{q}) \biggl[ \ddot{\boldsymbol{q}}_{d} + \displaystyle \frac{2\boldsymbol{I}}{\boldsymbol{I}+\exp ( -\boldsymbol{K}_{d} \tilde{\boldsymbol{q}} -\boldsymbol{K}_{p} \dot{\tilde{\boldsymbol{q}}})}- \boldsymbol{I}\biggr]. $$
(24)

Since \(\hat{\boldsymbol{M}}(\boldsymbol{q})\) is a positive definite matrix, (21) can be reduced to \(\ddot{\tilde{\boldsymbol{q}}} + \frac{2\boldsymbol{I}}{\boldsymbol{I}+( -\boldsymbol{K}_{d} \tilde{\boldsymbol{q}} -\boldsymbol{K}_{p} \dot{\tilde{\boldsymbol{q}}} )} -{\boldsymbol{I} = 0}\), where \(\ddot{\tilde{\boldsymbol{q}}} = \ddot{\boldsymbol{q}}_{d} - \ddot{\boldsymbol{q}} \) is the acceleration error:

$$ \frac{\mathrm{d}}{\mathrm{d}t} \left [ \textstyle\begin{array}{c} \tilde{{\boldsymbol{q}}} \\ \dot{\tilde{{\boldsymbol{q}}}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \dot{\tilde{{\boldsymbol{q}}}} \\ \frac{2{\boldsymbol{I}}}{{\boldsymbol{I}}+\exp( -\boldsymbol{K}_{d} \tilde{q} - \boldsymbol{K}_{p} \dot{\tilde{q}})} - \boldsymbol{I} \end{array}\displaystyle \right ] . $$
(25)

Therefore, using (23), we can linearize (25) into (26) through a certain period of control time:

$$ \frac{\mathrm{d}}{\mathrm{d}t} \left [ \textstyle\begin{array}{c} \tilde{\boldsymbol{q}} \\ \dot{\tilde{\boldsymbol{q}}} \\ \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c@{\quad}c} 0 & \boldsymbol{I} \\ -\boldsymbol{K}_{p} & - \boldsymbol{K}_{d} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \tilde{\boldsymbol{q}} \\ \dot{\tilde{\boldsymbol{q}}} \\ \end{array}\displaystyle \right ] . $$
(26)

If we neglect the higher-order term of (23), a positive definite Lyapunov function can be defined:

$$ \boldsymbol{V}(\tilde{\boldsymbol{q}},\dot{\tilde{\boldsymbol{q}}}) = \displaystyle \frac{1}{2} \tilde{\boldsymbol{q}}^{\mathrm{T}} \bigl[ \boldsymbol{K}_{p} + \varepsilon \boldsymbol{K}_{d} - \varepsilon ^{2} \boldsymbol{I}\bigr]\tilde{\boldsymbol{q}} + \displaystyle \frac{1}{2} [\dot{\tilde{\boldsymbol{q}}} + \varepsilon \tilde{\boldsymbol{q}}]^{\mathrm{T}} [\dot{\tilde{\boldsymbol{q}}} + \varepsilon \tilde{\boldsymbol{q}}] + \displaystyle \frac{1}{2} \tilde{ \boldsymbol{q}}^{\mathrm{T}} {\boldsymbol{M}}(\boldsymbol{q})\tilde{ \boldsymbol{q}} , $$
(27)

where \(\varepsilon \) is a positive constant such that \(\varepsilon \in (0,\lambda_{\min}\{ \boldsymbol{K}_{d} \})\), \(\lambda_{\min}\) is the minimum eigenvalue of the matrix \(\boldsymbol{K} _{d}\). Thus, for any nonzero vector \(\boldsymbol{U} \in \boldsymbol{R}^{n}\), we obtain

$$\boldsymbol{U}^{\mathrm{T}} \lambda _{\min} \{\boldsymbol{K}_{d} \}{\boldsymbol{U}} > \boldsymbol{U}^{\mathrm{T}} \varepsilon \boldsymbol{U},\quad \mbox{that is,}\ {\boldsymbol{U}}^{\mathrm{T}} ({\boldsymbol{K}} _{d} - \varepsilon \boldsymbol{I}) \boldsymbol{U} > 0. $$

This means that the matrix \((\boldsymbol{K}_{d} - \varepsilon {\boldsymbol{I}})\) is symmetric positive definite. On the other hand, the matrix \({\boldsymbol{K}}_{p}\) also is symmetric positive definite, so there is a constant \(\varepsilon > 0\) such that

$$ \bigl[\boldsymbol{K}_{p} + \varepsilon \boldsymbol{K}_{ d} - {\varepsilon }^{2} \boldsymbol{I}\bigr] >0 . $$

Furthermore, differentiate the Lyapunov function \(\boldsymbol{V}( \tilde{\boldsymbol{q}},\dot{\tilde{{\boldsymbol{q}}}})\) with respect to time:

$$ \dot{{\boldsymbol{V}}}\bigl(\tilde{{\boldsymbol{q}}}^{\mathrm{T}}, \dot{\tilde{{\boldsymbol{q}}}}^{\mathrm{T}}\bigr) = \dot{\tilde{{ \boldsymbol{q}}}}^{\mathrm{T}} \ddot{\tilde{{\boldsymbol{q}}}} + \dot{\tilde{{ \boldsymbol{q}}}}^{ \mathrm{T}} [{\boldsymbol{K}}_{p} + \varepsilon { \boldsymbol{K}} _{d}] \tilde{{\boldsymbol{q}}} + \varepsilon \dot{ \tilde{{\boldsymbol{q}}}}^{\mathrm{T}} \dot{\tilde{{\boldsymbol{q}}}} + \varepsilon \ddot{\tilde{{\boldsymbol{q}}}}^{ \mathrm{T}} \tilde{{ \boldsymbol{q}}} + \dot{\tilde{{\boldsymbol{q}}}}^{ \mathrm{T}} {\boldsymbol{M}} ({\boldsymbol{q}}) \ddot{\tilde{{\boldsymbol{q}}}} + \displaystyle \frac{1}{2} \dot{\tilde{{\boldsymbol{q}}}}^{\mathrm{T}} {\boldsymbol{M}} ({ \boldsymbol{q}}) \dot{\tilde{{\boldsymbol{q}}}}. $$
(28)

Since \(\ddot{\hat{{\boldsymbol{q}}}} = \ddot{{\boldsymbol{q}}}_{ d} - \ddot{\tilde{{\boldsymbol{q}}}}\), \(\dot{\tilde{{\boldsymbol{q}}}}^{\mathrm{T}}(\dot{{\boldsymbol{M}}}({\boldsymbol{q}}) - 2 {\boldsymbol{C}}(\dot{{\boldsymbol{q}}})) \dot{\tilde{{\boldsymbol{q}}}} = 0\), and \(\ddot{\hat{{\boldsymbol{q}}}} = \hat{{\boldsymbol{M}}}^{-1}({\boldsymbol{q}})(\boldsymbol{\tau } - \hat{{\boldsymbol{C}}}(\dot{{\boldsymbol{q}}})\dot{{\boldsymbol{q}}}- \hat{{\boldsymbol{D}}}( \dot{{\boldsymbol{q}}})\dot{{\boldsymbol{q}}} - \hat{{\boldsymbol{F}}}_{\mathrm{dis}}({\boldsymbol{q}}))\), substituting (23) into (25), we obtain:

$$\begin{aligned} \dot{{\boldsymbol{V}}}\bigl(\tilde{{\boldsymbol{q}}}^{\mathrm{T}}, \dot{ \tilde{{\boldsymbol{q}}}}^{\mathrm{T}}\bigr) = & - \left [ \textstyle\begin{array}{c} \tilde{{\boldsymbol{q}}} \\ \dot{\tilde{{\boldsymbol{q}}}} \\ \end{array}\displaystyle \right ] ^{\mathrm{T}} \left [ \textstyle\begin{array}{c@{\quad}c} \varepsilon {\boldsymbol{K}}_{p} & 0 \\ 0 & \boldsymbol{K}_{d} - \varepsilon {\boldsymbol{I}} \\ \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \tilde{{\boldsymbol{q}}} \\ \dot{\tilde{{\boldsymbol{q}}}} \\ \end{array}\displaystyle \right ] + \dot{\tilde{{\boldsymbol{q}}}}^{\mathrm{T}} \bigl( \hat{{ \boldsymbol{M}}}({\boldsymbol{q}}) \ddot{{\boldsymbol{q}}}_{d} + \hat{{ \boldsymbol{D}}}(\dot{{\boldsymbol{q}}})\dot{{\boldsymbol{q}}} + \hat{{ \boldsymbol{F}}}_{\mathrm{dis}}( {\boldsymbol{q}}) \bigr) \\ &{}+ \dot{\tilde{{\boldsymbol{q}}}}^{\mathrm{T}} \bigl( \hat{{ \boldsymbol{C}}}(\dot{{\boldsymbol{q}}})\dot{{\boldsymbol{q}}} + \hat{{ \boldsymbol{C}}}( \dot{{\boldsymbol{q}}})\dot{\tilde{{\boldsymbol{q}}}} \bigr) - \boldsymbol{\tau } \\ \leq & - \left [ \textstyle\begin{array}{c} \tilde{{\boldsymbol{q}}} \\ \dot{\tilde{{\boldsymbol{q}}}} \\ \end{array}\displaystyle \right ] ^{\mathrm{T}} \left [ \textstyle\begin{array}{c@{\quad}c} \varepsilon {\boldsymbol{K}}_{p} & 0 \\ 0 & {\boldsymbol{K}}_{d} - \varepsilon {\boldsymbol{I}} \\ \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \tilde{\boldsymbol{q}} \\ \dot{\tilde{\boldsymbol{q}}} \\ \end{array}\displaystyle \right ] - {\lambda }_{min} \bigl(\dot{\tilde{\boldsymbol{q}}}^{\mathrm{T}}\bigr) \boldsymbol{\tau } \\ &{}+ \bigl\lVert \dot{\tilde{\boldsymbol{q}}}^{\mathrm{T}} \bigr\rVert \bigl\lVert \hat{\boldsymbol{M}}(\boldsymbol{q}) \ddot{\boldsymbol{q}}_{d} + \hat{\boldsymbol{C}}(\dot{\boldsymbol{q}}) (\dot{\boldsymbol{q}} + \dot{\tilde{ \boldsymbol{q}}})+ \hat{\boldsymbol{D}}(\dot{\boldsymbol{q}})\dot{\boldsymbol{q}} + \hat{\boldsymbol{F}}_{\mathrm{dis}}(\boldsymbol{q}) \bigr\rVert . \end{aligned}$$
(29)

Since the matrices \((\boldsymbol{K}_{d} - \varepsilon \boldsymbol{I})\) and \(\boldsymbol{K}_{p}\) are symmetric positive definite, using the dynamic controller above to make \({\lambda }_{\min}( \dot{\tilde{\boldsymbol{q}}}^{\mathrm{T}}) \boldsymbol{\tau } \geq \lVert \dot{\tilde{\boldsymbol{q}}}^{\mathrm{T}} \rVert \lVert \hat{\boldsymbol{M}}(\boldsymbol{q}) \ddot{\boldsymbol{q}}_{d} + \hat{\boldsymbol{C}}(\dot{\boldsymbol{q}}) (\dot{\boldsymbol{q}} +\dot{\tilde{\boldsymbol{q}}})+ \hat{\boldsymbol{D}}(\dot{\boldsymbol{q}})\dot{\boldsymbol{q}} + \hat{\boldsymbol{F}}_{\mathrm{dis}}(\boldsymbol{q}) \rVert \) in (29), we get that the time derivative of \(\dot{\boldsymbol{V}}\) is globally negative definite. By Lyapunov’s stability theorem the equilibrium point \([\tilde{\boldsymbol{q}}^{\mathrm{T}}, \dot{\tilde{\boldsymbol{q}}}^{\mathrm{T}}]^{ \mathrm{T}} =\boldsymbol{0}\) is globally uniformly asymptotically stable, that is,

$$ \lim_{t \to \infty } \tilde{\boldsymbol{q}}(t) = 0, \qquad \lim _{t \to \infty } \dot{\tilde{\boldsymbol{q}}}(t) = 0. $$
(30)

Therefore, the control errors converge to zero asymptotically.

From the previous stability analysis, the manipulation process of UVMS may not be globally asymptotically stable, but we can realize an asymptotically stable manipulation by using an observer-based dynamic controller to compensate system disturbance.

5 Simulations

5.1 Simulation setup

In order to verify and make further analysis on the dynamic model of the UVMS multibody system, simulations have been established on the basis of a UVMS model through MATLAB. The diagram of simulation programs is illustrated in Fig. 5. At the beginning, a manipulation trajectory of the manipulator end is planned according to the manipulation task. In order to realize the desired trajectory of the manipulator end, the desired position of AUV and manipulator joints is obtained through the optimal motion planning algorithm in Sect. 4. Then the coupling forces and restoring forces caused by manipulators are observed through the current position and attitude of UVMS. AUV is controlled through the observer-based dynamic controller constructed in Sect. 3. After thrust allocation, propulsion forces and manipulator applied forces are added in the 6-DOF maneuverability equations [11].

The designed UVMS for autonomous manipulation is shown in Fig. 2. It is composed of a 6-DOF AUV and a 4-DOF manipulator. Although AUV is underactuated during long-distance cruising to save energy, it should be fully actuated during the manipulation process. In order to obtain stable attitude during manipulation, the AUV is equipped with a main thruster for forward and backward advance, two vertical rudders and two horizontal wings for heading and diving control during cruise, tow side thrusters, and four vertical thrusters for vehicle attitude (e.g. yaw, pitch, roll) and position control during manipulation. The max propulsive force of the main thruster is 98 N, and the others are all 49 N. Its size and inertial and hydrodynamic parameters are illustrated in Table 1 and Table 2, respectively. The location of the manipulator base joint in the coordinate of \(\sum_{\mathrm{v}}, O_{\mathrm{v}}\mbox{--}X_{\mathrm{v}}Y_{\mathrm{v}}Z_{\mathrm{v}}\) is (0.9, 0.07, 0.08). Each joint of the manipulator is equipped with a DC brushless motor. The rotation angles of the joints are defined as \({\theta }_{1}, {\theta }_{2}, {\theta }_{3}\), and \({\theta }_{4}\) is the angle from the base joint to the wrist. The added mass coefficients of the manipulator vary according to the angular displacement of the elbow (see Fig. 6). The parameters of the manipulator are illustrated in Table 3 and Table 4. Hence, the UVMS can be described by using five rigid bodies and four joints. For the designed UVMS, the motion of the manipulator \({\theta }_{4}\) joint influences little on the attitude of AUV. From equation (1), \({\theta }_{2}\) and \({\theta }_{3}\) can be directly obtained through inverse kinematics deduction. However, infinite solutions can be obtained for the value of \({\theta }_{1}\), the translation, and the attitude of AUV.

Fig. 6
figure 6

Manipulator and its added mass

Full size image
Table 1 Inertial parameters
Full size table
Table 2 Hydrodynamic parameters
Full size table
Table 3 Size parameters of the manipulator
Full size table
Table 4 Parameters of the manipulator swing and pitch joints
Full size table

5.2 Simulations and results analysis

In Fig. 7, the AUV attitude has been greatly affected by the swing and pitch motion of the manipulator without carrying out control. Although the coupling forces can be reduced through slowing down the manipulation, the restoring forces are still great and time-varying due to the change of gravity center and buoyancy center. The attitude of AUV changes greatly during the manipulation process without the effect of controller. The AUV rolls and pitches violently due to the restoring forces. Therefore, an observer-based compensation is necessary for AUV control.

Fig. 7
figure 7

Effects of manipulation without control

Full size image

In Fig. 8, the dynamic coordinate controller of Sect. 3 has been added in the simulations to realize the AUV attitude control during the manipulator motion process. During this process, the manipulator spreads out, and the base joint swings around from the preliminary attitude. The disturbance forces applying AUV are mainly composed with coupling forces and restoring forces (moments) during this process. Since the joint angular velocity is relatively slow, the restoring forces make greater effects on the AUV attitude. In comparison with the dynamic coordinate controller without disturbance force observer, the one with the observer can keep the AUV attitude more stable because it can calculate and compensate the disturbance forces in real time. From Fig. 8(c), the restoring forces are about 10 N to 15 N, which means that the thrusters have to run with the full power in order to overcome the disturbance. This not only makes the AUV being short of ability to overcome outside disturbance such as current, but also consumes the battery energy quickly and reduces the AUV cruising distance. Thus, optimal motion planning is necessary in order to realize the coordinate motions between AUV and manipulators, reduce the restoring forces, and save the electric power.

Fig. 8
figure 8

Comparison of manipulation with control

Full size image

In Fig. 9, the designed UVMS has completed a precise manipulation process. In the simulation, each step length optimization lasts 0.5 s, corresponding with the sample time of the sensors in the realization. In each step length, the base joint of manipulator finishes an optimized motion about 1–2 degrees or so. Figure 10 illustrates virtual reality simulation through Vega software with autonomous manipulation data of Fig. 9. At first 300 s, the end-effector moves downward from preliminary position. In order to reduce internal disturbance, such as restoring forces and coupling forces, AUV makes an accompanying movement. The optimal motion plan of Sect. 4 is applied according to the desired trajectory of the end-effector, the position and attitude of each manipulator joint and AUV have been obtained, and the internal disturbance has been decreased significantly. Coupling forces take the main part of the observed internal disturbance forces, whereas the restoring moment takes the main part of the observed internal disturbance. The manipulator moves downward along the desired trajectory smoothly. Then the manipulator moves upward and back. In the second 300 s, the end-effector is planned moving upward in the XOZ plane, whereas in the end of the third 300 s, the manipulator is planned moving upward in the YOZ plane. Thus, the end-effector returns to the preliminary position. This process can be treated as the manipulator moving downward, grasping an object, and moving it upward to a certain place.

Fig. 9
figure 9figure 9

Autonomous manipulation simulation

Full size image
Fig. 10
figure 10

Autonomous manipulation virtual reality simulation

Full size image

6 Conclusions

In this study, we have systematically developed a dynamic model of a vehicle-manipulator multibody system. The model is composed with hydrodynamic effects, coupling forces, and restoring forces and is different from other multibody systems such as satellite-manipulator system in space and mobile manipulator on the land. In the Newton–Euler recursive deduction, hydrodynamic forces should be considered. The restoring forces are great and time varying.

The disturbance force observer has been designed, including the coupling forces and restoring forces on the basis of dynamic analysis of Sect. 2. Through the primal dual optimal motion planning in the precise manipulation simulation, the AUV made coordinative and stable motion with the manipulator and the restoring forces was consequently minimized. The disturbance observer-based dynamic control scheme outperforms the one without observer for the AUV attitude control during manipulation. The proposed dynamic model and controller are completely general for the modeling and control of UVMS. They have been verified through precise manipulation simulations with a UVMS prototype.