1 Introduction

This study was designed to investigate and develop techniques to avoid or mitigate numerical locking phenomena associated with moderately thick absolute nodal coordinate formulation (ANCF) plate elements. A new higher order ANCF plate element is introduced to avoid Poisson thickness locking phenomena. The fully parameterized plate elements under investigation are based on an identical in-plane approximation, the only difference being the kinematics description in the transverse direction. Each plate element is based on continuum mechanics theory, and full three-dimensional strain and stress tensors are used in the formulations. As a result, these continuum elements should be applicable for thin and thick plate analyses. Any general material law based on continuum mechanics can be used. The ANCF elements do not use geometrical approximations, which is seldom the case for conventional structural finite elements.

Nonlinear continuum plate/shell elements have been the subject of active research for more than four decades. Continuum plate/shell elements often use rotation parameters instead of gradient vectors. Continuum shell elements with three-dimensional stresses and strains can be degenerated to behave as shell elements, so the kinematic and constitutive shell assumptions are acceptable. See, for example [1]. The isoparametric continuum shell element (known as the A–I–Z shell element) is based on the Mindlin/Reissner hypothesis. The element includes three translational and two rotational parameters at each nodal location. It suffers from shear locking, which can be alleviated, for example, by introducing independent linear interpolation of transverse shear deformations in a four-node shell element known as a MITCH4 shell element [13]. The original MITCH4 element was derived from the A–I–Z shell element using the same five node parameters. Its only difference is that using mixed interpolation, the MITCH4 element avoids shear locking. Another approach to avoiding shear locking is use of higher order elements; see, for example, [3].

For large strain cases, thickness deformation should be taken into account. In the thickness deformation description, the interpolation order for displacement in the thickness direction should be greater than first order, i.e., not linear. Otherwise, element types implemented with full three-dimensional elasticity will be subject to Poisson thickness locking. To avoid this problem, a 7-parameter formulation was derived in [8] that introduces two extra parameters at a node. This allows for linear stretching in the thickness direction. Furthermore, a shell element based on the MITCH4 formulation was introduced in [36]. It uses 22 degrees of freedom, including five generalized displacements at the nodal location and two degrees of freedom for linear thickness stretching.

The absolute nodal coordinate formulation was proposed by Shabana for analysis of large deformations in multibody applications [31]. This finite element approach describes beam and plate elements using absolute nodal positions and position gradients. In the formulation, gradient coordinates that are partial derivatives of the position vector are used to describe cross section or fiber orientations and deformations. All nodal coordinates are described in an inertial frame, so the ANCF is a total Lagrangian formulation.

Benefits offered by the ANCF include a simplified description for the equations of motion with a constant mass matrix [33]. Because ANCF element configuration is defined using a global description, estimating contact surfaces and describing geometric constraints, such as for a sliding joint, are straightforward—particularly when compared to the floating frame of reference formulation [34]. On the other hand, describing nonconservative forces, such as internal damping, in the formulation is cumbersome [14]. The ANCF’s use of fully parameterized elements brings about another disadvantage. Fully parameterized elements include high frequency transverse deformation modes that are, in fact, approximately two times higher than the frequencies for the common shear modes [15]. However, high frequencies due to shear deformation dominate in fine mesh refinement cases due to the different order of discretization in the transverse and axial directions [22].

The ANCF formulation can be applied to conventional as well as shear deformable beam and plate elements. In shear deformable elements, beam and plate elements can be described as a continuum. Unlike conventional beam and plate elements, the position gradients for material points within the element are displacement field derivatives. In continuum beam and plate/shell elements, the kinematic and constitutive assumptions can be relaxed. Strain and stress quantities are frame-indifferent, enabling numerical model description for large deformation problems. This can be accomplished, for example, using a nonlinear material model based on hyperelasticity [7, 19].

The first ANCF plate element was developed by Shabana and Christensen [32]. This element was based on classical (Kirchoff–Love) plate theory. Rotation parameters were used only to describe bending deformation. To account for shear and thickness deformation, a fully parameterized quadrilateral plate element was developed [25]. Full-parameterization indicates that a position vector and position vector gradients are used as variables at nodal locations. The use of fully parameterized plate/shell elements makes it possible to describe fiber deformation. However, the original fully parameterized plate element especially suffers from slow convergence due to transverse shear locking because the transverse gradient vector and in-plane gradient vectors contain different polynomial orders. This means that for the original fully-parameterized plate element, the rotation of a transverse fiber is described by linear interpolation using in-plane coordinates, and the rotation of a longitudinal fiber is described using quadratic interpolation. The unbalance of the base functions leads to overly large shear strain, which can be alleviated using mixed interpolation.

A fully parameterized quadrilateral ANCF plate element including mixed interpolation, i.e., the use of linearized shear angles, was introduced to overcome slow convergence brought about by shear locking and curvature locking [24]. In [21], which was a starting point for this study, fully parameterized plate elements are compared. Dmitrochenko et al. introduced linear shear deformable triangular and rectangular ANCF plate elements without in-plane gradient vectors [10]. Linear interpolation results in fewer degrees of freedom and simpler elastic forces; only one integration point can be used to integrate for the strain energy of bending and in-plane deformation.

Recent studies have shown that B-spline geometries can be converted to produce an ANCF plate element geometry description with simple linear mapping if polynomial order and degree of continuity are identical [23]. Converting B-spline representations to ANCF-based finite element descriptions makes it possible to control the number of degrees of freedom within the finite element model, which allows an ANCF-based finite element mesh to be constructed directly from the B-spline representation. This, in turn, can be used to develop pre- and post-processing procedures for the ANCF [28].

Higher than first-order linear interpolation for displacement in the thickness direction prevents Poisson thickness locking in the studied ANCF plate element. An accurate description of thickness deformation is important for continuum plate elements based on three-dimensional elasticity. The advantages and disadvantages of these plate elements are demonstrated here with a number of simple numerical examples. Their verification is accomplished with numerical examples of thin and thick plates. Moderately thick plate elements should be suitable for analysis where transverse shearing deformations must be considered. However, moderately thick plate elements should also be suitable for thin plate problems where the effect of transverse shearing deformations can be neglected without losing accuracy. Here, the elastic forces of the plate elements are integrated using a full Gaussian integration to show that the elements are performing properly.

The following paragraphs (Sect. 2) describe the kinematics of the fully parameterized plate elements. Section 3 introduces the updated fully parameterized plate element with linearized shear angles. Section 4 describes the higher order plate element newly introduced by this study. Section 5 offers general expressions for mass matrices, elastic forces, and external forces. Section 6 offers numerical tests for the thin plate element, and Sect. 7 covers a few thick plate numerical tests. Using a modified material model to eliminate thickness locking is discussed in Sect. 8, and numerical tests of dynamic performance are presented in Sect. 9. Finally, Sect. 10 discusses the different locking phenomena for ANCF plate elements and offers some conclusions.

2 The kinematics of a fully parameterized plate element

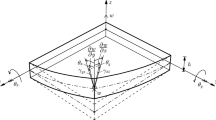
The fully parameterized plate element introduced by Mikkola and Shabana [25] is designated ANCF-P48. It is a four-node quadrilateral element with 48 degrees of freedom. Three degrees of freedom are for position and nine are for displacement gradients at each node. In ANCF elements, kinematics is expressed using spatial shape functions and global coordinates, similarly to conventional solid elements. The position of an arbitrary particle in the isoparametric fully parameterized plate element can be interpolated in the global fixed frame as follows:

$$ \boldsymbol {r}=\boldsymbol {S}_m(\boldsymbol {x}) \boldsymbol {e}, $$
(1)

where S m is a shape function matrix expressed using local element coordinates x, and e=e(t) is the vector of nodal coordinates. The kinematics of the element in the reference configuration at time t=0 can be described as r 0=S m (x)e 0, where e 0=e(0). The fully parameterized undeformed plate element in the current configuration with dimensions of width l x , length l y , and thickness l z is shown in Fig. 1.

Fig. 1
figure 1

Undeformed plate element with its dimensions in the current configuration

Full size image

The vector of nodal coordinates at node i can be written as follows:

(2)

where r is the position vector of the element, and x, y, and z are local coordinates. The following notation for partial derivatives is used here:

$$ \boldsymbol {r}_{,\alpha}^{(i)} = \left [ \begin{array}{c} r_{1,\alpha}^{(i)} \\ r_{2,\alpha}^{(i)} \\ r_{3,\alpha}^{(i)} \end{array} \right ]= \frac{\partial \boldsymbol {r}^{(i)}}{\partial\alpha}; \quad\alpha=x,y,z. $$

The interpolation functions for position are based on the following set of basis polynomials:

$$ \bigl[1,x,y,z,xz,yz,yx,{x}^{2},{y}^{2},{x}^{3},{y}^{3},{x}^{2}y,{y}^{2}x,xy z,{x}^{3}y,x{y}^{3}\bigr]. $$
(3)

Note that the basis polynomials in Eq. (3) are incomplete, so the element only has linear terms in the transverse coordinate z. Accordingly, the displacement distribution is linear in the element’s transverse direction. The interpolation for position is cubic in the in-plane coordinates x and y. The shape functions can be presented using local normalized coordinates; such as ξ,η,ζ,∈[−1…1]. The shape functions can be written as follows when the local coordinate system x,y,z is placed along the middle of the element.

$$\begin{aligned} & S_1 = \frac{ ( -1+\xi ) (1-\eta ) ( {\xi }^{2}+\xi+{\eta}^{2}+\eta-2 )}{8}, \qquad S_2 = \frac{{\it l_x} ( 1-\eta ) (1+\xi ) ( -1+\xi ) ^{2} }{16}, \\ & S_3 = \frac{{\it l_y} ( 1-\xi ) ( \eta+1 ) ( -1+\eta ) ^{2} }{16}, \qquad S_4 = \frac{{\it l_z} \zeta ( -1+\xi ) ( -1+\eta ) }{8}, \\ & S_5 = \frac{ ( 1+\xi ) ( -1+\eta ) ( {\xi }^{2}- \xi+{\eta}^{2}+\eta-2 )}{8}, \qquad S_6 = \frac{ {\it l_x} (1-\xi ) ( -1+\eta ) ( 1+\xi ) ^{2} }{16}, \\ & S_7 = \frac{{\it l_y} ( 1+\xi ) ( \eta+1 ) ( -1+\eta ) ^{2} }{16}, \qquad S_8 = \frac{{\it l_z} \zeta ( 1+\xi ) (1-\eta ) }{8}, \\ & S_9 = \frac{ ( 1+\xi ) (-\eta-1 ) ( {\xi }^{2}-\xi+{\eta}^{2}-\eta-2 )}{8}, \qquad S_{10} = \frac{{\it l_x} ( -1+\xi ) ( \eta+1 ) ( 1+\xi ) ^{2} }{16},\mbox{\quad} \\ & S_{11} = \frac{{\it l_y} ( 1+\xi ) ( -1+\eta ) ( \eta+1 ) ^{2} }{16}, \qquad S_{12} = \frac{{\it l_z} \zeta ( 1+\xi ) ( \eta+1 ) }{8}, \\ & S_{13} = \frac{ ( -1+\xi ) ( \eta+1 ) ( {\xi}^{2}+ \xi+{\eta}^{2}-\eta-2 )}{8}, \qquad S_{14} = \frac{{\it l_x} ( 1+\xi ) ( \eta+1 ) ( -1+\xi ) ^{2} }{16}, \\ & S_{15} = \frac{{\it l_y} ( -1+\xi ) ( 1-\eta ) ( \eta+1 ) ^{2} }{16}, \quad S_{16} = \frac{{\it l_z} \zeta ( \eta+1 ) (1-\xi )}{8} \end{aligned}$$
(4)

where ξ=2x/l x , η=2y/l y , and ζ=2z/l z . The shape functions can be represented in matrix form as

(5)

where I is a 3×3 identity matrix and ns is the number of shape functions. Because of the isoparametric property of the element, the kinematics (1) can also be expressed in terms of the local normalized coordinates r=S m (ξ,η,ζ)e. The strains can be obtained using the Green strain tensor E, which can be written for the plate element as

$$ \boldsymbol {E} = \frac{1}{2}\bigl(\boldsymbol {F}^T \boldsymbol {F}- \boldsymbol {I}\bigr), $$
(6)

where F is the deformation gradient. The deformation gradient can be shown in terms of the relationship of deformations between the initial r 0=S m e(t=0)=S m e 0 and current configuration r as follows:

$$ \boldsymbol {F} = \frac{\partial \boldsymbol {r}}{\partial \boldsymbol {r}_0} = \frac{\partial \boldsymbol {r}}{\partial \boldsymbol {x}} \biggl( \frac{\partial \boldsymbol {r}_0}{\partial \boldsymbol {x}} \biggr)^{-1}. $$
(7)

Using the engineering notations, the strains can be written in vector form as

$$ \boldsymbol {\varepsilon} = [E_{xx} \quad E_{yy} \quad E_{zz} \quad2E_{yz} \quad2 E_{xz} \quad2 E_{xy}]^T. $$
(8)

3 The kinematics of a plate element with linearized shear angles

The fully parameterized plate element with linearized shear angles [24], designated here as ANCF-P48lsa, leads to an improved definition of elastic forces. The use of improved definition overcomes shear and curvature locking. The updated element is based on the same in-plane interpolation functions as the original fully parameterized plate element [25]. In contrast to the ANCF-P48, however, fiber deformation of the ANCF-P48lsa plate element has been modified to linearize transverse shear deformation. This approach to alleviating shear locking has been demonstrated widely with classical MITCH shell elements [13]. Shear locking can also be avoided by applying the Hellinger–Reissner variational principle as was demonstrated with an ANCF beam element in [30]. Slow convergence as a result of shear locking also can be improved by adding shape function terms; for example, in higher order beam elements based on the ANCF [16].

The position of an arbitrary particle in the ANCF-P48lsa plate element can be expressed in the global fixed frame as follows:

(9)

The vector \(\hat{\boldsymbol {n}}\) describes the unit transverse vector of the midplane, which can be expressed with the aid of gradient vectors accordingly.

$$ \hat{\boldsymbol {n}}= \frac{\boldsymbol {r}_{,x} \times \boldsymbol {r}_{,y}}{\Vert \boldsymbol {r}_{,x} \times \boldsymbol {r}_{,y} \Vert } \biggm|_{z=0}. $$
(10)

The vector \(\hat{\boldsymbol {n}}\) is normal to the element midplane. Therefore, it is invariant with respect to transverse shear deformation. Its normalization is cumbersome, but it avoids error due to shrinking. The matrices A 1s and A 2s are used to describe transverse shear deformation. By assuming that the shear angles are small and by applying the Rodrigues rotation formula, these matrices can be obtained as follows:

$$ \boldsymbol {A}_{\mathrm {1s}}=\boldsymbol {I}+\tilde{\boldsymbol {r}}_{,x} \sin \gamma_1+2 \tilde{\boldsymbol {r}}_{,x}^2 \sin^2\frac{\gamma_1}{2} \approx \boldsymbol {I}+\tilde{ \boldsymbol {r}}_{,x} \gamma_1, $$
(11a)
$$ \boldsymbol {A}_{\mathrm {2s}}=\boldsymbol {I}+\tilde{\boldsymbol {r}}_{,y} \sin \gamma_2+2 \tilde{\boldsymbol {r}}_{,y}^2 \sin^2\frac{\gamma_2}{2} \approx \boldsymbol {I}+\tilde{ \boldsymbol {r}}_{,y} \gamma_2 $$
(11b)

where γ 1 and γ 2 are the shear angles with respect to gradient vectors r ,x and r ,y that define the direction of rotation. A skew-symmetric matrix \(\tilde{\boldsymbol {r}}_{,x}\) is determined by the unit vector \(\hat{\boldsymbol {r}}_{,x}\). And respectively, a skew-symmetric matrix \(\tilde{\boldsymbol {r}}_{,y}\) is determined by the unit vector \(\hat{\boldsymbol {r}}_{,y}\). Taking advantage of ANCF properties, the shear angles γ 1 and γ 2 can be derived from the gradient vectors as follows:

$$ \begin{gathered} \sin\gamma_1=\frac{\boldsymbol {r}_{,y}^T \boldsymbol {r}_{,z}}{\Vert \boldsymbol {r}_{,y} \Vert \Vert \boldsymbol {r}_{,z} \Vert } \approx \gamma_1 \quad\textrm{and} \quad \sin\gamma_2=- \frac{\boldsymbol {r}_{,x}^T \boldsymbol {r}_{,z}}{\Vert \boldsymbol {r}_{,x} \Vert \Vert \boldsymbol {r}_{,z} \Vert } \approx \gamma_2. \end{gathered} $$
(12)

In this case, shear angles in the element will be interpolated in-plane by fourth-order polynomials. However, nonlinear interpolations for shear deformation can lead to slow convergence, which can be alleviated by linearly interpolating the transverse shear deformations [13]. For the ANCF-P48lsa plate element, shear locking is avoided using a similar approach as in the MITC4 element [13], except the nodal values are used instead of sampling points to guarantee zero parasitic strain distribution such as in [6]. Therefore, bilinear interpolation is used for the shear angles. That is, the shear angles are interpolated linearly over the length and width of the element using the following equations:

$$ \gamma_{1}^{\operatorname {lin}} = \sum_{i=1}^4 N^{(i)} \gamma_{1}^{(i)} \quad \textrm{and} \quad \gamma_{2}^{\operatorname {lin}} = \sum_{i=1}^4 N^{(i)} \gamma_{2}^{(i)} $$
(13)

where N (i) are bilinear shape functions at the midplane. With the linearized Rodrigues rotation formula and the shear angles, the rotation matrices A 1s and A 2s take the form:

$$ \begin{gathered} \boldsymbol {A}_{\mathrm {1s}} \approx \boldsymbol {I}+\tilde{ \boldsymbol {r}}_{,x} \gamma _{1}^{\operatorname {lin}} \quad\textrm{and} \quad \boldsymbol {A}_{\mathrm {2s}} \approx \boldsymbol {I}+\tilde{\boldsymbol {r}}_{,y} \gamma _2^{\operatorname {lin}}. \end{gathered} $$
(14)

According to [24], for small displacements and when the element in the current configuration is axis-parallel to the reference configuration, unit vectors can be expressed by \(\tilde{\boldsymbol {r}}_{,x}=\left [ \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \end{array} \right ]^{T}\) and \(\tilde{\boldsymbol {r}}_{,y}=\left [ \begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0 \end{array} \right ]^{T}\). Using this simplification, the product of shear matrices can be expressed as follows:

$$ \boldsymbol {A}_{\mathrm {1s}} \boldsymbol {A}_{\mathrm {2s}} \approx \begin{pmatrix} 1 & 0 & \gamma_{2}^{\operatorname {lin}} \\ 0 & 1 & -\gamma_{1}^{\operatorname {lin}} \\ -\gamma_{2}^{\operatorname {lin}} & \gamma_{1}^{\operatorname {lin}} & 1 \end{pmatrix} , $$
(15)

where the quadratic term \(\gamma_{1}^{\operatorname {lin}}\gamma_{2}^{\mathrm {lin}}\) is neglected. The strains can be obtained using the Green strain (6). As a result, the strain components can be expressed as

$$ \begin{gathered} E_{xx}=\frac{1}{2} \bigl( \boldsymbol {r}_{e,x}^T \boldsymbol {r}_{e,x}-1 \bigr), \qquad E_{yy}=\frac{1}{2} \bigl(\boldsymbol {r}_{e,y}^T \boldsymbol {r}_{e,y}-1 \bigr), \\ E_{xy}=\frac{1}{2} \bigl(\boldsymbol {r}_{e,x}^T \boldsymbol {r}_{e,y} \bigr), \qquad E_{xz}=\frac{1}{2} \bigl( \boldsymbol {r}_{e,x}^T \boldsymbol {r}_{e,z} \bigr), \qquad E_{yz}=\frac{1}{2} \bigl(\boldsymbol {r}_{e,y}^T \boldsymbol {r}_{e,z} \bigr). \end{gathered} $$
(16)

The strain component E zz in the element thickness direction cannot be defined with the kinematics described by r e (9). However, E zz can be obtained from kinematics r of the fully parameterized plate element (1) as follows:

$$ E_{zz}=\frac{1}{2} \bigl(\boldsymbol {r}_{,z}^T \boldsymbol {r}_{,z}-1 \bigr). $$
(17)

The strain component E zz can also be interpolated using bilinear shape functions, which will prevent curvature locking (also called trapezoidal locking) [6, 17]. Therefore, the bilinear strain distribution \(E_{zz}^{\operatorname {lin}}\) along the length and width of the element is used here. The strain components can be shown in vector form ε as follows:

(18)

where kinematics with linearized shear angles is used for all strain components except \(E_{zz}^{\operatorname {lin}}\).

4 The kinematics of a higher order plate element

The first higher order ANCF elements introduced in [16] were beam elements. The higher order terms were used to prevent shear locking. The term “higher order” was used, because the nodal coordinates were defined by higher order derivatives. In [20], the trapezoidal mode with higher order terms was employed to prevent Poisson locking. Here, a new higher order four-node quadrilateral plate element is introduced to prevent Poisson thickness locking. The new element, ANCF-P60, has second derivatives with respect to z as additional nodal coordinates. The use of quadratic interpolation yields three additional nodal coordinates per node, resulting in a plate element with 60 degrees of freedom. The interpolation polynomials can be written as follows:

$$ \bigl[1,x,y,z,xz,yz,xy,xyz,x^2,y^2,x^3,y^3,x^2y,xy^2,x^3y,xy^3,z^2,xz^2,yz^2,xyz^2 \bigr], $$
(19)

where the additional terms z 2,xz 2,yz 2 and xyz 2 account for the higher order deformation mode in the thickness direction, thereby lessening Poisson thickness locking compared to the fully parameterized plate elements ANCF-P48 and ANCF-P48lsa. The vector of nodal coordinates at node i of the higher order ANCF-P60 plate element can be written as

(20)

where r is the position vector of the element and x, y, and z are the local coordinates. The ANCF-P60 shape functions are those given in (4) plus four additional shape functions given as follows:

$$ \begin{gathered} S_{17} = \frac{{{l_z}}^{2}{\zeta}^{2} ( -1+\eta ) ( -1+\xi )}{32}, \qquad S_{18} = \frac{{{ l_z}}^{2}{\zeta}^{2} ( 1-\eta ) ( \xi+1 )}{32}, \\ S_{19} = \frac{{{ l_z}}^{2}{\zeta}^{2} ( \eta+1 ) ( \xi+1 )}{32}, \qquad S_{20} = \frac{{{l_z}}^{2}{\zeta}^{2} ( \eta+1 ) ( 1-\xi )}{32} . \end{gathered} $$
(21)

As was done for the fully parameterized ANCF-P48 plate element, strains can be obtained for ANCF-60 using the Green strain tensor.

5 Elastic forces, external forces, and the mass matrix

General hyperelastic materials can be used to define elastic forces in ANCF-based elements. However, for the fully parameterized plate elements in this work, 3-D elasticity is described using the simple linear elastic St. Venant–Kirchhoff material, a valid simplification in the small strain regime. The constitutive relation in the case of the linear elastic St. Venant–Kirchhoff material can be expressed as

$$ \boldsymbol {S} = {}^4\boldsymbol {D}:\boldsymbol {E} $$
(22)

where the fourth-order tensor 4 D includes the properties of the material. For an elastic isotropic material, the relationship between the second Piola–Kirchhoff stress tensor and the Green strain tensor takes the following form:

$$ \boldsymbol {S} = \lambda \boldsymbol {I} \mathrm {tr}(\boldsymbol {E})+2 G \boldsymbol {E}, $$
(23)

where λ and G are the Lamé elastic constants. The strain energy of one plate element can be written as

$$ W_{\mathsf{int}} = \frac{1}{2} \int_V \boldsymbol {\varepsilon}^T \boldsymbol {D} \boldsymbol {\varepsilon} \, \mathrm {d}V $$
(24)

and the vector of elastic forces can be defined as follows:

$$ \boldsymbol {F}_\mathsf{e} =\frac{\partial W^T_{\mathsf{int}}}{\partial{ \boldsymbol {e}}}. $$
(25)

Externally applied forces are

$$ \boldsymbol {F}_{\mathsf{ext}} = \int_V \boldsymbol {b}^T \boldsymbol {S}_m \,\mathrm {d}V. $$
(26)

where b is the vector of body forces. In the special case of gravity, the body forces can be written as b=ρ g; where ρ is mass density, and g is the field of gravity. Using the definition for the kinematics of the ANCF plate element (Eq. (1)), the ANCF leads to a constant mass matrix:

$$ \boldsymbol {M} = \int_V \rho \boldsymbol {S}_m^T \boldsymbol {S}_m \,\mathrm {d}V. $$
(27)

For the fully parameterized plate element with linearized shear angles, the mass matrix would no longer be constant due to the kinematic description (Eq. (9)). However, the mass matrix definition (Eq. (27)) can be also used for the fully parameterized plate element with linearized shear angles without losing accuracy, because its kinematic description within the element differs slightly from the ANCF-P48 element. This influence decreases in value for finer meshes.

6 Numerical tests of thin plate elements

The three ANCF plate elements examined in this study accommodate transverse shear deformation and a nonlinear relationship between strain and displacement. Although the first numerical examples are for thin plate elements, ANCF plate elements are not restricted to thin plate structures or small displacements. All plate element types should perform properly as thin plate structures, so it is appropriate to test them using small displacement statics and eigenvalue thin plate tests. Convergence is studied by varying mesh refinement. Numerical tests used in this study, such as the cantilever plate and eigenfrequency analyses, were originally introduced by Schwab et al. to verify an ANCF thin plate element [29]. The regular meshes n×n, as shown in Fig. 2, are used.

Fig. 2
figure 2

Distributed bending moment M and distributed force F; boundaries Γ 1, Γ 2, Γ 3, and Γ 4; and uniform 4×4 mesh of a square cantilevered plate with quadrilateral elements

Full size image

6.1 Cantilever plate

The first numerical test is a linear static analysis of an infinitely wide cantilever plate under two different loading conditions. The first loading case is a distributed moment. The second is a distributed transverse force along the free edge of the structure. The numerical solutions are compared to the analytical exact solutions for transverse displacement, which in the case of static analysis are defined as follows:

$$ w_{\mathrm{exact}}=\frac{ML^2}{2D}+\frac{FL^2}{3D} \quad\textrm{and} \quad \varphi_{\mathrm{exact}}=\frac{ML}{D}+ \frac{FL^2}{2D}, $$
(28)

where M is distributed moment, F is distributed force along the loaded edge, and D is the elastic plate constant D=EH 3/(12(1−ν 2)). The results of the computations for transverse displacement w and rotation φ along the loaded edge about the y-axis are normalized with respect to the exact analytical results. The rotation angle φ, which defines the rotation due to shear and bending for ANCF plate elements, can be expressed as follows:

$$ \varphi=\arccos\frac{\boldsymbol {r}_{0,z}^T \boldsymbol {r}_{,z}}{\Vert \boldsymbol {r}_{0,z} \Vert \Vert \boldsymbol {r}_{,z} \Vert }, $$
(29)

where r 0 is defined such that e 0 is the vector of nodal coordinates in the initial configuration.

In this example, r 0,z =[0,0,1]T is the transverse gradient vector in the initial undeformed configuration. The test is modeled with the following parameters: length L=1 m, height H=0.01 m, width W=1 m, Young’s modulus E=210×109 N/m2, shear modulus \(G = \frac{E}{2(1+\nu)}\), shear correction factor k s =1, Poisson’s ratio ν=0.3, the distributed moment M=1 N m/m, and force F=1 N/m. At the clamped end, the boundary condition is defined by fixing all the nodal degrees of freedom at Γ 1. For a higher order plate element, the higher order degrees of freedom are unconstrained.

In [29], the component r 2,y was unfixed in the clamped boundary to allow in-plane deformation. However, in this study, the fixed component r 2,y did not lead to slow convergence. The analytical solutions are formulated for a cantilever plate with infinite width W. For this reason, the in-plane component r 3,y is fixed to prevent in-plane rotation along the boundaries Γ 2 and Γ 4. However, transverse shear deformation γ yz remains unconstrained to avoid slow convergence. The boundary Γ 3 is unconstrained while loaded by the distributed force F or moment M.

As can be seen from the results presented in Tables 1 and 2, the chosen boundary conditions lead to acceptable results. Errors are nearly equivalent for both loading cases. For the transverse loading force, the convergence of ANCF-P48lsa is faster than for the original fully parameterized plate element ANCF-P48. See the convergence curves in Fig. 3. ANCF-P48 converges more slowly because of shear locking, which is avoided by linearization of transverse shear angles in ANCF-P48lsa. However, because of Poisson thickness locking caused by the low order interpolation approximation in the transverse direction in full 3-D elasticity, both elements converge to an incorrect solution for both loading cases.

Fig. 3
figure 3

Convergences of the relative error of transverse displacement \(\overline{w}\) at the loaded edge for two load cases (distributed moment M and distributed force F) calculated using the ANCF-P48, ANCF-P48lsa and ANCF-P60 elements

Full size image
Table 1 Average normalized transverse displacements \(\overline{w}\) and rotations \(\overline{\varphi}\) at the loaded edge for a square cantilevered plate loaded by a distributed moment at the free edge for a number of mesh refinements and three different element types with ν=0.3—displacements and rotations are normalized with Eq. (28)
Full size table
Table 2 Average normalized transverse displacements \(\overline{w}\) and rotations \(\overline{\varphi}\) at the loaded edge for a square cantilevered plate loaded by a distributed transverse force at the free edge for a number of mesh refinements and three different element types with ν=0.3—displacements and rotations are normalized with Eq. (28)
Full size table

The higher order plate element ANCF-P60 converges to a result that agrees with the analytical solution. For all cases, except plate elements ANCF-P48 and ANCF-P60 under transverse loading, the relative error for coarse meshes is small, but becomes larger for plate elements ANCF-P48 and ANCF-P60 under transverse loading. For spatial beam elements, Poisson thickness locking can be avoided by neglecting the Poisson effect with ν=0, as explained in [27]. Correspondingly, for continuum plates and shells, different modified material laws can be used to overcome Poisson thickness locking for thin plate/shells [18].

6.2 Eigenfrequencies and Chladni figures

The second test is an eigenfrequency analysis with free boundaries, previously studied in [29]. The eigenfrequency analysis is used as a dynamics test, because it offers the advantage of coordinate free frequency and vibration mode comparison. The eigenfrequencies ω are nondimensionalized by the frequency \(\omega_{0} = \pi^{2} \sqrt{D/\rho H L^{4}}\), and the analytical results for the eigenvalue analysis were obtained from [29].

The eigenmodes will be presented as Chladni figures, where lines for nodes without displacement are shown. For a thin plate, applying the classical Kirchhoff plate element implemented in the general multibody code SPACAR can provide the reference solution [4]. The thin plate SPACAR is fully described in [29], which compares the thin plate solution for the fully parameterized ANCF plate element with SPACAR results. The same relative plate thickness of H/L=0.01 is used for this numerical example. The eigenfrequencies for the case of free boundary conditions are expressed in Tables 3, 4 and 5 where in-plane modes denoted by – are not shown.

Table 3 First ten dimensionless eigenfrequencies Ω=ω/ω 0 of the free (ffff) square plate modeled by the ANCF-P48 with a Poisson’s ratio of ν=0.3 for a number of mesh refinements—Analytic solutions are from [29] and \(\omega_{0} = \pi^{2} \sqrt {D/\rho H L^{4}}\). A relative plate thickness of H/L=0.01 is used
Full size table
Table 4 First ten dimensionless eigenfrequencies Ω=ω/ω 0 of the free (ffff) square plate modeled by the ANCFP48lsa with a Poisson’s ratio of ν=0.3 for a number of mesh refinements—Analytic solutions are from [29] and \(\omega_{0} = \pi^{2} \sqrt {D/\rho H L^{4}}\). A relative plate thickness of H/L=0.01 is used
Full size table
Table 5 First ten dimensionless eigenfrequencies Ω=ω/ω 0 of the free (ffff) square plate modeled by the ANCF-P60 with a Poisson’s ratio of ν=0.3 for a number of mesh refinements—The finite element solution is provided by commercial software with three dimensional elasticity defined using an ANSYS 45 solid element with a mesh size of 190×190×4. Analytic solutions are from [29] and \(\omega_{0} = \pi^{2} \sqrt {D/\rho H L^{4}}\). A relative plate thickness of H/L=0.01 is used
Full size table

As shown by Tables 3–4, none of the first ten dimensionless eigenfrequencies for both fully parameterized plate elements converge to the results solved using thin plate theory. This is because of Poisson thickness locking, which is avoided in the case of ANCF-P60. See Table 5. The convergence rate for ANCF-P48lsa is considerably faster than the convergence rate for ANCF-P48 or ANCF-P60. To emphasize the difference between plate elements ANCF-P48 and ANCF-P48lsa, the convergence of the first mode (see top left mode in Fig. 5) is also considered for thin plates in Fig. 4, in which the relative plate thickness is assumed to be H/L=0.001. Accordingly, for a thin plate, the convergence of the first mode does not depend on a relative plate thickness of H/L, as is the case for ANCF-P48 and ANCF-P60. This type of locking phenomenon is known as shear locking. It seems the first bending mode includes shear deformation, which results in the slow convergences for ANCF-P48 and ANCF-P60.

Fig. 4
figure 4

Convergences of the first vibration eigenmode normalized by the analytical solution for a free (ffff) square plate as calculated by SPACAR, the ANCF-P48, the ANCF-P48lsa, and the ANCF-P60 with Poisson’s ratio ν=0.3. Two different relative plate thicknesses, H/L=0.01 and H/L=0.001, are used

Full size image

Two different relative plate thicknesses, H/L=0.01 and H/L=0.001, were used in this numerical example. The eigenmodes for the ANCF-P48lsa plate element are illustrated using Chladni figures (lines of nodes) in Fig. 5. These agree with earlier reported Chladni figures based on SPACAR thin elements [29]. In [29], the in-plane modes of ANCF-P48 also are discussed. The in-plane modes for ANCF-P48 and ANCF-P48lsa are identical. Therefore, they are not shown.

Fig. 5
figure 5

First 10 transverse vibration modes together with their dimensionless frequencies for free (ffff) square plate as calculated by the ANCF-P48lsa with a mesh 32×32 and Poisson’s ratio ν=0.3—a relative plate thickness of H/L=0.01 is used

Full size image

6.3 A particular pure bending test

This section reports how each of the subject ANCF plate elements performs in pure bending. Figure 6(a) illustrates a particular case of anticlastic pure bending in response to distributed twisting moments M applied to the free edges of a plate [35]. Identical displacement fields result from application of moments M for the portion abcd (Fig. 6(a)) or nodal forces 2ML at corners a, b, c, and d (Fig. 6(b)). For this loading case, in-plane shear locking is assumed not dominant. The ANCF-P48 and ANCF-P48lsa fully parameterized ANCF plate elements are exercised here, and the results are compared to a SPACAR simulation using a three-node thin plate element (18 dofs).

Fig. 6
figure 6

Particular cases of pure bending caused by distributed twisting moment M and nodal forces 2ML from [35]

Full size image

The boundary conditions for the SPACAR element are relatively straightforward to define: All degrees of freedom at origin node O are fixed. For the ANCF-plates, all degrees of freedom at node O are fixed except for r 1,x , r 2,y , and r 3,z . The meshes for the different loading cases are shown in Fig. 7.

Fig. 7
figure 7

Square meshes 8×8 for different loading cases

Full size image

Displacement at the asymptotic line for moderately thick plates is considered in this numerical example. In the case of small deflections and moderately thick plates, deflection w in direction Z can be defined for an anticlastic surface [35] as follows:

$$ w=\frac{M}{2D(1-\nu)}\bigl(X^2-Y^2 \bigr), $$
(30)

where D=EH 3/(12(1−ν 2)). The rotation at point a about the X-axis can be defined as

$$ \varphi=\frac{M}{D(1-\nu)}Y. $$
(31)

The parameters used in the plate example are as follows: length L=1 m, Young’s modulus E=210×109 N/m2, shear modulus \(G = \frac{E}{2(1+\nu)}\), shear correction factor k s =1, Poisson’s ratio ν=0.3, and the distributed moment M=1 N m/m. The computed displacements and rotations for elements SPACAR, ANCF-P48, and ANCF-P48lsa (H/L=0.01 for thin plates, and H/L=0.2 for thick plates as shown in Table 8) are normalized by the analytical solution from Eq. (30) and the analytical solution from Eq. (31).

The results in Table 6 show that in pure bending cases with distributed moments, all elements present similar and accurately converged results for a thin structure. According to [35, p. 45], the lines ab, bc, cd, and ad for the thin structure should be linear, based on equivalence in the loading cases (Fig. 6). However, some discrepancies arise from these lines that can be seen near the corners for moderately thick plates. See Fig. 8.

Fig. 8
figure 8

Displacements at asymptotic line ad from Fig. 6. The mesh 64×64, plate element ANCF-P48lsa, and a relative plate thickness H/L=0.2 are used

Full size image
Table 6 Normalized transverse displacements \(\overline{w}\) at point a (Fig. 6) of the square thin plate modeled by SPACAR, ANCF-P48, and ANCF-P48lsa elements—displacements are normalized with Eq (30). A relative plate thickness of H/L=0.01 is used
Full size table

For alternative loading by nodal forces at corners, both plate elements based on the ANCF converge to incorrect results, whereas the SPACAR thin elements converge to correct results. Since both loading cases should produce similar displacement fields for thin plates, shear deformation is overly estimated in the ANCF plate elements. This can also be seen in Table 7, where total rotation \(\overline{\varphi}\) and shear angle \(\overline{\gamma}\) are shown.

Table 7 Normalized rotations \(\overline{\varphi}\) and shear angles \(\overline{\gamma}\) at point a (Fig. 6) of the square thin plate modeled by SPACAR, ANCF-P48 and ANCF-P48lsa elements. Displacements are normalized with Eq. (30). A relative plate thickness of H/L=0.01 is used
Full size table

Locking is not observed indicating that similar error will be observed when using a material with ν=0. In the previous test cases, the static and eigenfrequency analyses, the solutions converge to incorrect results due to Poisson thickness locking. An interesting feature of the pure bending test example is that it does not show inaccuracy due to Poisson thickness locking or slow convergence due to shear locking. On the other hand, according to eigenfrequency analysis, the second mode (saddle mode) indicates Poisson thickness locking (Tables 3 and 5). When using special material ν=0, all introduced plate elements lead to acceptable results in the studied examples where shear deformation is not a dominating factor.

7 Numerical tests of thick plate elements

Based on the numerical results of the previous thin plate tests, the SPACAR plate element performs well and fully parameterized plate elements perform acceptably only in the case of pure bending. The following paragraphs will examine the behaviors of the ANCF plate elements for thick plates. The SPACAR plate element is based on Kirchhoff theory and cannot be used for the analysis of thick plates for any other test except the pure bending test.

7.1 Pure bending test

The numerical example introduced in this section is the same as the example discussed in Sect. 6.3, except that H/L is increased to 0.2. The results from Table 8 show that for pure bending with distributed moments, fully parameterized ANCF plate elements give similar results in both the thin and thick plate examples. The displacements resulting from nodal forces at the corners using thin plate SPACAR converges to the analytical solution for thick plates subject to pure bending. For shear deformable plate elements based on the ANCF, line ad is not straight as shown by Fig. 8, where displacements are shown resulting from the nodal force loading of ANCF-P48lsa at line ad. The moment loading shows a straight line, but the alternative nodal force loading shows a nonstraight line with discrepancies at the edges. The line should be straight [35].

Table 8 Normalized transverse displacements \(\overline{w}\) and rotations \(\overline{\varphi}\) at point a (Fig. 6) of the square thick plate modeled by SPACAR, ANCF-P48, and ANCF-P48lsa elements. Displacements are normalized with Eq. (30). A relative plate thickness of H/L=0.2 is used
Full size table

7.2 Thick simply supported plate under uniform static load

In this test, a thick plate is constrained with a simply supported condition and loaded with a normal uniform force in the z-direction as shown in Fig. 9. The simply supported boundary condition is also depicted. The complete plate is modeled with identical boundary conditions as in previous examples for simply supported plates.

Fig. 9
figure 9

Simply supported plate, its subdomain Ω, and the coordinate system

Full size image

Mid-plate deflection calculated using the ANCF plate elements is compared to the analytical result based on the Reissner–Mindlin theory for a simply supported plate. This analytical formulation, presented in [37], is as follows:

$$ w_0^M = w_0^K + \frac{M^K}{k_s G H}, $$
(32)

where \(w_{0}^{K} \) is the Kirchhoff solution, and M K is the Marcus moment. The Marcus moment can be expressed as

$$ M^K = - D \nabla^2 w_0^K = \frac{1}{\pi^2} \sum_{m=1}^{\infty} \sum _{n=1}^{\infty} \frac{q_{mn}}{\frac{m^2}{L^2} + \frac{n^2}{W^2}} \sin \frac{m\pi X}{L} \sin\frac{n\pi Y}{W}. $$
(33)

In the Navier solution for a simply supported Kirchhoff rectangular plate, the deflection \(w_{0}^{K}\) is as follows. For an example, see [35].

$$ w_0^K = \frac{1}{\pi^4 D} \sum _{m=1}^{\infty} \sum_{n=1}^{\infty} \frac{q_{mn}}{\frac{m^2}{L^2} + \frac{n^2}{W^2}} \sin\frac{m\pi X}{L} \sin\frac{n\pi Y}{W}, $$
(34)

where

$$\begin{aligned} q_{mn} = & \frac{4}{LW} \int_0^W \int_0^L q(X,Y) \sin\frac{m\pi X}{L} \sin \frac{n\pi Y}{W} \, \mathrm{d}X\, \mathrm{d}Y \\ = & \frac{16 q}{\pi^2 mn}; \quad\mathrm{iff}\ m\ \mbox{and}\ n\ \mbox{odd}. \end{aligned}$$
(35)

q(X,Y) is the uniformly distributed load, which is expressed as q=−5×106 H 3 N/m3 for this example. The analytical solutions were computed using m=n=12, which resulted in an acceptable accuracy for normalized transverse displacement to within four significant digits. For a finite element solution, a uniformly distributed load is defined as a consistent load vector as follows:

$$ F_{ext} = \int_{-1}^1 \int _{-1}^1 \int_{-1}^1 \boldsymbol {b}^T \boldsymbol {S} J \, \mathrm{d} \xi\, \mathrm{d} \eta\, \mathrm{d} \zeta $$
(36)

where the body force is b=[0,0,q/H]T and the determinant of the deformation gradient tensor J=det(F). Other parameters are identical to the examples from previous sections. The normalized transverse displacements at the center of the plate, \(\overline {w}=w/w_{0}^{M}\), are shown in Tables 9, 10 and 11.

Table 9 Normalized transverse displacement \(\overline{w}\) at the center of the plate with ANCF-P48 loaded by a uniform loading—displacements are normalized with Eq. (32)
Full size table
Table 10 Normalized transverse displacement \(\overline{w}\) at the center of the plate with ANCF-P48lsa loaded by a uniform loading. Displacements are normalized with Eq. (32)
Full size table
Table 11 Normalized transverse displacement \(\overline{w}\) at the center of the plate with ANCF-P60 loaded by a uniform loading for a number of mesh refinements. The converged finite element solutions based on commercial software are found using ANSYS SHELL 181 plate and ANSYS 45 solid elements. Displacements are normalized with Eq. (32)
Full size table

To minimize the number of degrees of freedom, double symmetry for the plate under constant loading is used in the numerical example shown in Table 12. In double symmetry, the boundary conditions of subdomain Ω for boundary Γ 3 are r 1=0, r 3,x =0, and r 1,z =0. For boundary Γ 4, they are r 2=0, r 2,z =0, and r 3,y =0. The boundaries Γ 1 and Γ 2 are simply supported, therefore, r 1 and r 3 are fixed for boundary Γ 1, and r 2 and r 3 are fixed for Γ 2. Table 12 shows the displacements \(\overline{w}\) differ from those of the original problem (Table 10), where the converged displacements coincide to within three digits.

Table 12 Normalized transverse displacement \(\overline{w}\) at the center of the plate with ANCF-P48 and ANCF-P48lsa loaded by a uniform loading; the symmetry of the plate is used. H/L=0.2
Full size table

The relationship between the Reissner–Mindlin and Kirchhoff theories (Eq. (32)) is valid only when the Marcus moments are zero at the boundaries or only for “hard” simply supported conditions [37]. As shown in Fig. 10, convergence for plate elements ANCF-P48 and ANCF-P60 is slow in the beginning for the thin plate scenarios. The convergence of element ANCF-P48lsa is likely to be linear, and its relative error should be smaller than for the ANCF-P48 and ANCF-P60 elements. However, both fully parameterized plate elements converge to the same incorrect solution due to Poisson thickness locking. As can see from Table 8, when locking is neglected, shear deformation is overestimated for thick plates.

Fig. 10
figure 10

Convergences of relative error of transverse displacement \(\overline{w}\) at the center of the plate with uniform loading as calculated by the ANCF-P48, ANCF-P48lsa, and ANCF-P60 using a Poisson’s ratio of ν=0.3. Relative plate thicknesses of H/L=0.01 and H/L=0.001 are used

Full size image

8 Using a modified material model to eliminate thickness locking

Thickness locking can be prevented by applying higher order theories for the displacement field in the thickness direction or by modifying the elastic coefficients. For the newly introduced higher order ANCF plate element, a higher than first-order displacement field in the thickness direction is included in the formulation with additional nodal coordinates that are second derivatives. However, for thin plates, the assumption σ zz =0 can be used to obtain modified in-plane elastic coefficients as follows:

$$ D_{11}=\frac{E}{1-\nu^2}; \qquad D_{12} = D_{21}=\frac{\nu E}{1-\nu^2}. $$
(37)

However, this is only suitable for thin plates, and it does not produce a solution based on full 3-D elasticity. In Table 13, the first ten eigenfrequencies are shown of a free square plate for the ANCF-P48 element with modified material. The lowest eigenfrequencies correspond to analytic results, but because of slow convergence due to shear locking, the converged higher eigenfrequencies are not reached.

Table 13 First ten dimensionless eigenfrequencies Ω=ω/ω 0 of the free (ffff) square plate modeled by the ANCF-P48 with Poisson’s ratio ν=0.3 for a number of mesh refinements. Analytic solutions are from [29]. Thickness locking is neglected using plane stress assumption. A relative plate thickness of H/L=0.01 is used
Full size table

Slow convergence for transverse forces occurs when the plane stress assumption is used (Table 14). However, convergence does not depend on the Poisson effect, because the effect is neglected when using modified elasticity matrix. In the pure bending example, there were only minor differences compared to the analytical solution for 3-D elasticity. This result supports the supposition that Poisson thickness locking is not a factor in the pure bending test example. However, using the modified material does not remedy slow convergence arising from in-plane shear locking.

Table 14 Average normalized transverse displacements \(\overline{w}\) and rotations \(\overline{\varphi}\) at the loaded edge for a square cantilevered plate loaded by a distributed moment or a distributed transverse force at the free edge for a number of mesh refinements and ν=0.3. Plate element ANCF-P48 is used and Poisson thickness locking is neglected using plane stress assumption
Full size table

9 Numerical test for dynamic performance

In several previous publications related to ANCF plate elements, a rectangular plate pendulum under gravitational field has been used as a benchmark problem to validate the dynamic performance of plate/shell elements. See, for example, [11, 12, 25]. However, current research has determined that using the low Young’s modulus of 1×105 N/m2 and a mass density of 7810 kg/m3 leads to substantial elongation of the material near the pendulum joint. For this reason, the plate does not act as pendulum after ~0.4 seconds, when the number of elements is increased to obtain converged results. Rather, the plate collapses in the direction of the gravitational force. A similar result was obtained with plate elements in two commercial finite element software programs; ANSYS 12.0.1 and ABAQUS CAE 6.8. The phenomenon was not reported in the previous publications, because an overly coarse mesh was used resulting in an overly stiff plate simulation unable to depict this behavior accurately. A different dynamic example was chosen for this study to achieve results for the ANCF elements and commercial finite element software elements that are comparable.

9.1 Free flying flexible plate

The dynamic performance of the ANCF-P48 and ANCF-P48lsa elements when used to describe the behavior of a moderately thick plate is analyzed using the example shown in Fig. 11. In this example, the plate is subject to a moment and two point forces. The Young’s modulus of the material used in the analysis is E=1×106 N/m2. Poisson’s ratio is ν=0.3, and the material density is ρ=1500 kg/m3. Shear modulus is given by \(G = \frac{E}{2(1+\nu)}\), and the shear correction factor is k s =5/6. Plate length L=1.00 m, width W=0.50 m, and thickness H=0.10 m, respectively. The simulation duration for the free flying flexible plate is 3.0 s.

Fig. 11
figure 11

Free flying flexible plate

Full size image

An implicit Runge–Kutta method of order 5 is used with automatic time stepping to analyze ANCF elements. The selected initial and maximum time steps are 1×10−2 s, and the minimum time step is 1×10−5 s. During the transient analysis, the convergence of each time step solution is checked against elastic forces using an error tolerance of 1×10−5. The simulation results for the ANCF-P48 and ANCF-P48lsa elements are compared to results obtained using ANSYS, version 12.0.1. The plate is modeled with shell elements based on Mindlin–Reissner theory, i.e., ANSYS element notation SHELL181 with a consistent mass matrix. The SHELL181 is a 4-node-element, and each node has three translational and three rotational degrees of freedom. The element is suitable for large rotation and large strain nonlinear applications. Transverse shear strain is described in the element formulation using the Assumed Natural Strains (ANS) method to alleviate shear locking [13]. Stress stiffening is included with the analysis in ANSYS for transient analysis with geometrical nonlinearities [2]. Full integration with incompatible modes is chosen to prevent the propagation of zero energy modes during the analysis.

In ANSYS, implicit numerical integration (Newmark integration) is used with automatic time stepping. The integration parameters are chosen to be \(\delta= \frac{\textrm{1}}{\textrm{2}}\) and \(\alpha= \frac{\textrm {1}}{\textrm{4}}\) to render the general Newmark scheme to a constant-average-acceleration scheme. This integration scheme will retain high-frequency response. The only error caused by the time integration for displacements is period elongation [5]. The selected initial and maximum time steps are 1×10−2 s, and the minimum time step is 1×10−4 s. A maximum of 25 equilibrium iterations per time step is used. During the transient analysis, the convergence of each time step solution is checked against displacement, force, and moment using the Euclidean norm with an error tolerance of 5×10−4. The point forces and moment vary with time according to the following equations:

$$ F_{x}(t)= \left\{\begin{array}{l@{\quad}l} 0 & \text{if}\ 0\leq t \leq1.5, \\ 13.5(t-1.5) &\text{if}\ 1.5 < t \leq3.0, \end{array}\right. $$
(38)
$$ F_{y}(t)= \left\{ \begin{array}{l@{\quad}l} 0 & \text{if}\ 0\leq t \leq1.5, \\ 18(t-1.5) &\text{if}\ 1.5 < t \leq3.0, \end{array} \right. $$
(39)
$$ M_{z}(t)= \left\{ \begin{array}{l@{\quad}l} -47.5t & \mbox{if}\ 0\leq t \leq1.5,\\ 0 &\mbox{if}\ 1.5 < t \leq3.0. \end{array} \right. $$
(40)

Forces in the global x- and y-directions are applied as point loads to the node at point a in all element types. See Fig. 11. The moment around the global z-axis for the ANCF elements and ANSYS shell elements is divided among the nodes located at side ab. To illustrate the large displacement problem, the deformation of a free plate is shown in half second intervals in Fig. 12 as computed by ANSYS SHELL 181 with 32×16 mesh.

Fig. 12
figure 12

Free flying flexible plate. The deformation of a free plate computed using ANSYS SHELL 181 with 32×16

Full size image

9.1.1 Results

A separate convergence analysis was done using SHELL181 elements to determine a reference result. The maximum absolute difference of the displacements at point a was 1.31 mm with a 256 element mesh in the longitudinal direction and a 128 element mesh across the width compared to a 128×64 element mesh. The SHELL181 results are presented here for the 256×128 mesh as reference.

The convergence of the absolute displacements error in the x- and y-axis directions at point a at time=0.75 s modeled using the ANCF-P48, ANCF-P48lsa, and SHELL181 elements is shown by Fig. 13. The convergence plot shows that for a moment force applied to the plate, the ANCF-P48lsa element gives more accurate results than the ANCF-P48. The ANCF-P48 element suffers from Poisson thickness and curvature locking. The rate of convergence for ANCF-P48lsa is worse than for SHELL181, because the ANCF-P48lsa element still suffers from Poisson thickness locking. For time=2.50 s, when the two point forces are acting on the plate, the absolute displacement errors for the ANCF elements are similar, as can be seen from Fig. 14. However, the ANCF-P48lsa element, which does not suffer from shear locking, shows absolute errors that are closer to the results from the SHELL181 element when the number of elements is increased.

Fig. 13
figure 13

Convergence curves for absolute error of displacements in the x-direction (left) and y-axis direction (right) at point a calculated with ANCF-P48, ANCF-P48lsa, and SHELL181 elements for the time instance 0.75 s. Reference result calculated with SHELL181 with a 256×128 mesh

Full size image
Fig. 14
figure 14

Convergence curves of absolute error of displacements in the x-direction (left) and y-axis direction (right) at point a calculated with ANCF-P48, ANCF-P48lsa, and SHELL181 elements for the time instance 2.50 s. Reference result calculated with SHELL181 with a 256×128 mesh

Full size image

10 Discussion of locking phenomena for ANCF plate elements in the benchmarked problems

The original fully parameterized plate element ANCF-P48 with 3-D elasticity suffers from three different locking phenomena including shear, Poisson thickness, and curvature locking. In the ANCF-P48lsa fully parameterized plate element, shear and curvature locking are prevented with an improved description for kinematics and using low order interpolations for transverse shear deformations. However, according to the results, Poisson thickness locking is still problematic for the ANCF-P48lsa element.

Shear locking is caused by an imbalance of the base functions [13]. This can be avoided using the Assumed Natural Strain (ANS) technique, which is presented for shells in [13]. The ANS technique is based on strains at the sampling points. Sampling points can be either quadrature points, nodal points, or neither. In papers [6, 26], strains at the nodal points are used instead of Gaussian quadrature points, because parasitic strains are zero at the nodes [6]. To account for 3-D elasticity in the plate and shell formulations without inducing Poisson thickness locking, the transverse normal strains have to be interpolated at least linearly over the thickness direction [9]. In contrast to the other mentioned locking phenomena, the error due to Poisson thickness locking does not decrease with mesh refinements in the in-plane coordinates. In the newly introduced higher order ANCF-P60 plate element, Poisson thickness locking is prevented with a higher than first-order interpolation in the thickness direction. The ANCF-P60 plate element still suffers from shear locking; however, it can be mitigated using mixed interpolation. The ANCF-P48 plate element also suffers from curvature locking due to shrinking in the thickness direction. This locking effect is also mentioned to be problematic in other continuum plate/shell elements with coarse meshes and initially curved elements in [6]. In the ANCF-P48lsa, curvature locking is avoided using an improved description for kinematics.

When using the special case ν=0 in 3-D elasticity, or using a modified material stiffness matrix, Poisson thickness locking can be avoided. Therefore, both fully parameterized plate elements converge to the analytic solution in most thin plate cases since coupling between bending and shear deformation is neglected. In conclusion, in case of thin plates, the classical modified material, which was used for 3-D plates, can also be used to approximate a 3-D solution for thin plates modeled by fully parameterized plate elements. It shall be noted that the modified material stiffness matrix used in this study differs from the simplified material used in [24]. The same simplified material based on the diagonal material stiffness matrix D=diag(E,E,E,G,G,G) is also used for the continuum beam element [27], leading to similar results as obtained with beam theory. However, in case of plates/shells, such a simplified constitutive relation will obviously lead to an incorrect solution, which can be seen from the results in [24].

The benchmark problem results show that shear locking is strongly dependent on thickness, whereas Poisson thickness locking is independent of thickness, but strongly dependent on the Poisson effect. Numerical results differ from analytical results by about 18 %, because of Poisson thickness locking. See Tables 1–2. However, for in-plane modes in the eigenfrequency analyses, Poisson thickness locking is difficult to recognize from Tables 3, 4, and 13. The pure bending test used in this study is interesting, because it can be used to verify the accuracy of the shear deformation prediction without manifesting either shear or Poisson thickness locking (Table 7). In the pure bending test, the same amount of error for shear angles occurs for the special case of ν=0 or when the modified material is used. In other words, fully parameterized ANCF plate elements will pass all of the plate tests except for the saddle test and the simply supported plate test under uniform static load when ν=0.

11 Conclusions

In this study, rectangular plate elements based on the absolute nodal coordinate formulation were compared in terms of several numerical examples. The finite elements under investigation included a fully parameterized quadrilateral ANCF plate element, an update to this element that linearly interpolates transverse shear strains to overcome slow convergence due to transverse shear locking and a newly introduced higher order ANCF plate element designed to prevent Poisson thickness locking.

The numerical examples demonstrate the different locking phenomena that numerical solutions based on ANCF plate elements encounter. Poisson thickness locking is dominant for the fully parameterized plate elements. Because of Poisson thickness locking, both fully parameterized ANCF elements converged to the same incorrect solution in most of the numerical examples. The introduced higher order plate element with linearization of shear angles mostly overcomes the slow convergence brought about by shear locking and curvature locking. However, shear locking can be mitigated further using a mixed interpolation. Therefore, future research will concentrate on the investigation of higher order plate elements with mixed interpolation.