Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints

Abstract

In this paper, the dynamic response of a planar rigid multi-body system with stick–slip friction in revolute clearance joints is studied. LuGre friction law is proposed to model the stick–slip friction at the revolute clearance joints. This is because using this law, one can capture the variation of the friction force with slip velocity, thus making it suitable for studies involving stick–slip motions. The effective coefficient of friction is represented as a function of the relative tangential velocity of the contacting bodies, that is, the journal and the bearing, and an internal state. In LuGre friction model, the internal state is considered to be the average bristle deflection of the contacting bodies. By applying the LuGre friction law on a typical slider–crank mechanism, the friction force in the revolute joint having clearance is seen not to have a discontinuity at zero slip velocity throughout the simulation unlike in static friction models. In addition, LuGre model was observed to capture the Stribeck effect which is a phenomenon associated directly with stick–slip friction. The friction forces are seen to increase with increase in input speed. The effect of stick–slip friction on the overall dynamic behavior of a mechanical system at different speeds was seen to vary from one clearance joint to another.

1 Introduction

The dynamic modeling of multi-body systems has been recognized as a key aid in the analysis, design, optimization, control, and simulation of mechanisms and manipulators. However, clearance, friction, impact and other phenomena associated with real joints have been routinely ignored in order to simplify the dynamic model. The increasing requirement for high-speed and precise machines, mechanisms and manipulators demands that the kinematic joints be treated in a realistic way. This is because in a real mechanical joint, a clearance which permits the relative motion between the connected bodies as well as the components assemblage, is always present. Due to the relative motion of the bodies, friction at the kinematic joints will be inevitable and can lead to physical and dynamic deterioration of the mechanical system especially for poorly lubricated joints. The clearance, no matter how small it is, can lead to vibration and fatigue phenomena, premature failure and lack of precision or even random overall behavior. For instance, clearance at joints in a robot has been observed to decrease the positioning accuracy which is a key factor in achieving robotic tasks such as maintenance and assembly. This has led Wanghui et al. [1] to present a novel method based on trajectory planning to avoid the detachment of revolute and spherical joints of a manipulator with clearances. Also the clearances at joints have been observed to cause significant errors in function and path generation mechanisms due to the caused variations in mechanism performance. This has led to recent research activities [2–5] aimed at developing methodologies for optimizing performance and link parameters in path and function generation mechanisms. Using a reheat-stop-valve of a steam turbine, Dong et al. [6] demonstrated that the clearance size besides other factors leads to uncertainties in the dynamic performance of a mechanism.

There is a significant amount of available literature which discuses theoretical and experimental analysis of imperfect kinematic joints in a variety of planar and spatial mechanical systems with rigid or flexible links [2–4, 7–32]. Many of these works focus on the planar rigid-body mechanical systems in which friction is neglected, or modeled using the classical Coulomb law [7–9, 28, 29] or modeled using a modified Coulomb friction law [12, 13, 20–22, 24, 25, 30–32] for purposes of avoiding discontinuity of force at zero velocity and hence allow numerical stabilization of the integration algorithm. However, the classical Coulomb friction law does not cater for the stiction phenomenon which occurs when the relative tangential velocity of two impacting bodies, that is, the journal and the bearing (incase of a revolute clearance joint), approaches zero. But a suitable friction model must be able to detect sliding and sticking to avoid energy gains during the impact. Also, modifying the Coulomb friction law to avoid discontinuity of friction force at zero relative tangential velocity is done purely in a mathematical manner and hence this does not represent accurately the physical processes associated with the friction phenomenon at the revolute clearance joints. Hence there is a need to model the actual physical friction phenomenon in a revolute clearance joint, that is, the sliding friction, stiction friction and the stick–slip transition motion both at microscopic and macroscopic levels. There has been efforts to model stick–slip friction at lower pairs of mechanical systems, such as in [33–35], however in these works, the normal force in the joint was not considered to result from the contact-impact forces due to the clearance at the joint, and the friction models are strongly coupled with the rest of equations of motion of the system. More recently, Changkuan [36] presented a Finite Element-based approach of modeling the stick–slip friction in revolute clearance joints of a flexible multi-body system using LuGre friction law. The author presented the kinematic and unilateral contact equations (both normal and friction forces at the revolute clearance joint) in forms easier for discretization.

In this study therefore, a simple and computationally effective approach of continuously modeling and simulating the stick–slip friction in revolute clearance joints of a planar rigid multi-body system is presented. The LuGre friction law is proposed to model the stick–slip friction by calculating the effective coefficient of friction (μ) as a function of the relative tangential velocity of the contacting bodies and an internal state (z). The internal state (z) is considered to be the average bristle deflection of the contacting bodies, that is, the journal and the bearing of the revolute clearance joint. The normal force due to the impact at the revolute clearance joint is modeled using the Lankarani and Nikravesh model [37] which captures the energy dissipated during the impact. The effects of varying the static coefficient of friction, dynamic coefficient of friction, the driving crank speed, and the location of the clearance joint are numerically studied using a slider–crank mechanism as a demonstrative example.

2 Friction

The term friction comes from the Latin verb fricare, which means to rub [38]. Friction is an inevitable non-linear phenomenon that occurs in all kinds of mechanical system. It is one of the major limitations to achieve good performance in controlled mechanical systems, and hence it should be taken into account at the early stages of engineering design. One of the areas where friction is evident in a mechanical system is at the joints since it is where the bodies move relative to each other. Ideally, when modeling these kinematic joints, friction is normally neglected for purposes of simplifying the dynamic model of the mechanical system. This implies that the physical phenomenon at the joints is not realistically captured by the developed model, and hence significant differences between numerical simulation and experimental results are evident.

Friction in the kinematic joints of mechanical systems is not wanted, hence efforts are made to reduce it by design, or by control. A widely used principle of friction control is model-based friction compensation which is utilized to apply a force or torque command equal and opposite in sign to the instantaneous friction force [38]. An accurate friction model is needed for this purpose. Thus, various mathematical models have been proposed in the literature that describe the important friction phenomenon observed, most of them are still used now. The preferred model depends on its purpose, but the one that accurately describes all the observed phenomena is in general to be preferred. Other than the effectiveness and correctness of the friction model, the model efficiency, that is, the required computational time, can be of importance when the model is used in simulation studies. Due to the complexity of the physical phenomenon of friction, most models are of an empirical nature and only approximate the friction phenomenon.

2.1 Static friction models

The static friction models describe the steady-state behavior between velocity and friction force. These models are characterized by a discontinuity of friction force at zero velocity, implying that the friction force can take on an infinite number of possible values at zero velocity [39]. This discontinuity does not reflect the friction phenomenon realistically and leads to instability of the algorithms used in simulating the friction forces.

2.1.1 Coulomb friction

Devised in 1785, Coulomb friction law [40] which represents sliding friction is the most fundamental and simplest model of friction between dry contacting surfaces. During sliding between two surfaces, Coulomb law states that the frictional force is directly proportional to the magnitude of normal force at the contact point, where the constant of proportionality is termed as the kinetic coefficient of friction (μ _k ). This is mathematically represented as

(1)

where

(2)

F _N and F _C are the normal reaction force between the contacting surfaces and the Coulomb friction force, respectively. Equation (1) shows that the Coulomb friction force depends on the direction of the velocity of slip but not its magnitude as also shown Fig. 1(a), and acts in the opposite direction of the velocity of slip as indicated by the negative sign. Equation (1) has been used by several researchers [7–9, 28, 29] to model friction in revolute joints with clearance.

Fig. 1

Friction force versus tangential velocity plot for static friction models. (a) Coulomb friction. (b) Coulomb, viscous and stiction friction. (c) Coulomb friction, Viscous friction, static friction and Stribeck effect. (d) Continuous zero-velocity crossing model

Coulomb’s friction law does not model the stiction phenomenon which occurs when the relative tangential velocity of two contacting bodies approaches zero. In addition its simplicity is only apparent, and when used as it is, leads to several numerical challenges in simulation of mechanical systems. This led C. Glocker [41] to comment; “With this friction law, one has chosen one of the most complicated force laws that occur in application problems. It seems so easy and so clear at first view, however, when trying to apply it, or even just trying to write it down as a mathematical expression, one immediately encounters a lot of serious and not expected problems of different nature”.

2.1.2 Stiction friction

Stiction describes the threshold value of friction force when the contacting surfaces are at rest. Experimentally, it has been observed that friction force at rest is higher than the kinetic or Coulomb friction [42]. If the system is experiencing stiction, an externally applied force that is equal to or greater than the stiction force is needed to put the body in motion, that is, to bring the body in slipping. The force required to overcome the static friction and initiate motion is called the break-away force [43]. Transition from sticking to sliding leads to intermittent motion known as stick–slip motion. The corresponding graph of friction force and the tangential velocity when both Coulomb, viscous and stiction frictions are considered is as shown in Fig. 1(b).

2.1.3 Stribeck friction

Richard Stribeck [44] showed that at low velocities friction decreases continuously with increasing velocity when entering the slipping phase. This phenomenon contradicts the discontinuous behavior of the stiction friction (F _S as shown in Fig. 1(b)) but describes the friction force in the transition between sticking and slipping, which can be approximated by the following equation:

(3)

where v _s is the Stribeck velocity and γ is the gradient of friction decay in the velocity dependent term. This leads to a more general model of stick–slip motions that usually has the shape as depicted in Fig. 1(c).

2.1.4 Continuous zero-velocity crossing friction model

The limitations of discontinuity of force at zero velocity for static friction models as shown in Figs. 1(a), 1(b) and 1(c) have led several researchers on multi-body dynamics [45–49] to modify these models in order to avoid the discontinuity of force at zero relative velocity and to obtain a continuous-friction force–velocity relationship, such as the one shown in Fig. 1(d).

Several researchers [12, 13, 20–22, 24, 25, 30–32] on the area of multi-body systems with clearance joints have used a modified Coulomb’s friction law proposed by Ambrosio [49] which gives the tangential friction force (F _T ) as

(4)

where c _d is a dynamic correction coefficient expressed as

$$c_{d}=\left \{\begin{array}{l@{\quad}l}0 & \mbox{if\ } v_{T}\leq v_{0}\\\frac{v_{T}-v_{0}}{v_{l}-v_{0}}& \mbox{if\ } v_{0}\leq v_{T}\leq v_{l}\\1 & \mbox{if\ }v_{T}\geq v_{l}\end{array} \right .$$

(5)

in which, v ₀ and v _l are the given tolerances for the velocity. The correction factor prevents the friction force from changing direction when the value of the tangential velocity approaches zero, and allows numerical stabilization of the integration algorithm. However, it does not account for stiction phenomena of the contacting surfaces. This led Flores [32] to recommend that friction laws which account for stick–slip condition in imperfect joints of multi-body mechanical systems be included on the models.

A common practice widely advocated for in the literature is to replace Coulomb’s friction law by a continuous-friction law. However, this practice presents a number of shortcomings [50]. First, it alters the physical behavior of the system and can lead to the loss of important information such as abrupt variations in frictional forces; second, it negatively impacts the computational process by requiring very small time step sizes when the relative velocity is small; and finally it does not appear to be able to deal with systems with different values of the static and kinetic coefficients of friction. In addition, the regularization factor smoothes the discontinuity through a purely mathematical manner, but it does not represent more accurately the physical processes associated with the friction phenomenon.

2.2 Stick–slip friction

Stick–slip motion is the repeated sequence of sticking between two surfaces with static friction followed by sliding of the two surfaces. These fluctuations consist of sticking where the motion stops and slipping where the bodies suddenly accelerate again. Stick–slip motion is caused by the fact that friction is larger at rest than during motion. When the applied force reaches the break-away force the body starts to slide and friction decreases rapidly due to the Stribeck effect as shown in Fig. 1(d).

Superimposing the Coulomb, Stiction, Viscous and Stribeck models can lead to a complete static friction model which can be used to model stick–slip motions. However, the discontinuity of force at zero velocity for these static friction models poses some numerical challenges and does not model real friction phenomenon at microscopic levels. This has led researchers to develop dynamic friction models which are also called state variable models to try to model the friction phenomenon more realistically in all stages of motion. The idea in dynamic friction models is to introduce extra state variables (or internal states) that determine the level of friction in addition to velocity.

Some of the dynamic friction models include; Dahl friction model, Bristle friction model, Reset integrator friction model, Karnopp friction model, Bliman–Sorine friction model, Leuven friction model and a more recent LuGre friction model. Pennestri et al. [33] attempted to model friction in lower pairs of a planar multi-body mechanical system using the Dahl friction model. Karnopp [34] presented a friction model to simulate the stick–slip friction in planar multi-body mechanical systems. Kim [35] presented a methodology that automatically assembles dynamic equations in a matrix form according to different types of friction mode (sliding and sticking) in the lower pairs of a mechanical system. However in these three research works, the normal force in the joint was not considered to result from the contact-impact forces arising from the effect of clearance at the joint, and the friction models are strongly coupled with the rest of equations of motion of the system.

In 1995, Canudas de Wit et al. [51] through a collaboration between control groups in Lund and Grenoble, presented the LuGre (Lund–Grenoble) model which can effectively describe stick–slip motion due to its ability of capturing the Stribeck effect. The LuGre model has further been refined by Swevers et al. [52], and its characteristics and advantages reviewed by Astrom et al. [53]. Due to the advantages of LuGre friction model, such as its ability to capture the variation of friction force with slip velocity, thus making it suitable for studies involving stick–slip motions, this work uses the model with a slight modification in representation in order to include the friction force resulting from the normal contact-impact forces at the clearance of the revolute joint.

LuGre model uses the microscopic average bristle deflection z of the contacting surfaces as the internal state. In this model, friction is visualized as forces produced by bending bristles which behave like elastic springs as shown in Fig. 2. As the velocity at microscopic level increases, the number of bristles in contact progressively decrease until the bodies in contact start sliding relative to one another. LuGre model gives the dynamic friction force (F _T ) as [52]

(6)

where σ ₀ is the bristle stiffness, σ ₁ is the microscopic damping and σ ₂ is the viscous friction coefficient.

Fig. 2

Bristle interpretation of friction

For small displacements which is normally the case with mechanical systems, the bristles will behave like a spring-damping system in which the average deflection z is a function of the velocity. An appropriate model is given in [54]:

(7)

3 Modeling of revolute joints with clearance

A revolute joint can be described as an assembly of a journal and a bearing in which the journal is free to rotate inside the bearing. In the classical analysis of a revolute joint, the journal and bearing centers are considered to coincide throughout the motion, but in reality, there must be a clearance between the bearing and the journal to permit for the relative motion and the assemblage. The inclusion of the clearance allows for the separation of these centers since the bearing can translate inside the bearing, and hence two degrees of freedom are added to the system by a clearance revolute joint. However, the journal is limited to stay inside the bearing walls. In dry contact situations (without lubrication), the journal can move freely within the bearing until contact between the two bodies takes place. In modeling of a revolute clearance joint, the normal contact force together with a friction force resulting from impact of the journal and bearing are evaluated to obtain the dynamics of the real revolute joint.

3.1 Kinematic model of a revolute joint with clearance

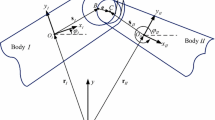
In order to simulate a real revolute joint, its necessary to develop a mathematical model for the joint in the multi-body system. Figure 3 shows two bodies i and j connected with a revolute joint with clearance. Part of body i is the bearing while part of body j is the journal. X _i Y _i and X _j Y _j are the body coordinate systems, while XY is the stationary global coordinate system. P _i is the center of the bearing and P _j is the center of the journal at the given instant.

Fig. 3

Generic revolute joint with clearance

The eccentricity vector e which connects the centers of the bearing and the journal is given as

(8)

where A _i and A _j are the transformation matrices of coordinates X _i Y _i and X _j Y _j , respectively, to coordinate XY, and u _Pi and u _Pj are the coordinates of centers of bodies i and j with respect to their coordinate systems. The magnitude of the eccentricity vector is

(9)

The indentation depth due to the impact between the journal and the bearing can be shown to be

(10)

where c is the radial clearance at the joint which is the difference between the radius of the bearing (R _B ) and the radius of the journal (R _J ). The contact points on bodies i and j during indentation are C _i and C _j , respectively, as shown in Fig. 4.

Fig. 4

Indentation depth due to impact between the bearing and the journal

The position of the contact points are given as

(11)

(12)

where n is the unit vector in the direction of indentation caused by the impact between the journal and the bearing, given as

(13)

The velocity of the contact points in the global coordinate system is found by differentiating (11) and (12) with respect to time to get

(14)

(15)

The components of the relative velocity of the contact points in the normal and tangential plane of collision are represented as v _N and v _T , and are given as

(16)

(17)

where t is obtained by rotating n anticlockwise by 90^∘.

3.2 Dynamic model of a revolute joint with clearance and friction

When the journal makes contact with the bearing, then impact occurs and the normal and friction forces are created at the joint. In reality, there are three distinct motions of the journal inside the bearing, that is, free-flight motion when the journal makes no contact with the bearing, continuous contact motion when the journal follows the bearing wall and impact motion between the journal and the bearing. In numerical analysis, there is a big challenge of contact detection, that is finding the precise moment when transition between these different motions occur, otherwise there will be a build-up of errors which make the final results to be inaccurate. The problem of contact detection is very critical in the dynamic analysis of mechanical systems as illustrated in [11, 55]. A closer inspection of (10) and Fig. 4 shows that:

• (a) When the journal is not in contact with the bearing, then e<c and the indentation depth has a negative value. In this case, the journal is in free-flight motion inside the bearing, and no impact-contact forces are created.

• (b) When contact between the journal and the bearing is established, the indentation depth has a value equal to or greater than zero. In this case, impact-contact forces at the joint are established.

Therefore the computational algorithm developed for dynamic analysis of a system with revolute clearance joint in this work ensures that impact-contact forces are generated when the depth of indentation is equal to or greater than zero. Since there are velocity components in the normal and tangential directions of the collision between the journal and the bearings as given in (16) and (17), then forces are generated in these two directions.

3.2.1 Normal force at a revolute joint with clearance: contact force models

Once the journal makes contact with the bearing, forces normal to the direction of contact are created. The non-linear continuous contact force models between two colliding bodies which include Hertz, Lankarani–Nikravesh, Dubowsky–Freudenstein and ESDU-78035 contact force models are the widely used since they represent the physical nature of the contacting surfaces.

The Hertz law of contact relates the contact force as a non-linear power function of the indentation depth as

(18)

where F _N is the normal contact force and δ is the indentation depth of the contacting bodies given in (10). For metallic surfaces n=1.5. The generalized stiffness K which depends on the material properties and the shape of the contacting surfaces is given as

(19)

where R ₁ and R ₂ are the radii of the spheres (considered negative for concave surfaces and positive for convex surfaces), σ ₁ and σ ₂ are the material parameters given by

(20)

where E _i and ν _i are the Young Modulus and Poisson ratio for each sphere.

Unfortunately, the Hertz Law as given in (18) does not account for energy dissipation during the impact process and hence cannot be used in both phases of contact (compression and restitution). Lankarani and Nikravesh [37] extended the Hertz contact force model to include a hysteresis damping function and hence represent the energy dissipated during the impact. The authors separated the normal contact force given in (18) into elastic and dissipative components as

(21)

where $\dot{\delta}$ is the relative impact velocity given in (16), and D is the hysteresis coefficient given as

(22)

where $\dot{\delta}_{i}$ is the initial impact velocity. Therefore the final normal contact force can be expressed as

(23)

Equation (23) is only valid for impact velocities lower than the propagation velocity of elastic waves across the bodies, i.e., $\dot{\delta}_{i}\leq10^{-5}\sqrt{\frac{E}{\rho}}$ where E is the Young modulus and ρ is the material mass density [56].

The contact models given by (18) and (23) are applicable for colliding bodies with spherical contact areas. Various elastic models have been put forward for the cylindrical contact surfaces, with the commonly used ones being the Dubowsky and Freudenstein model and the ESDU-78035 model, both of which are given as in (24) and (25), respectively;

(24)

and

(25)

where L is the length of the cylinder.

It has been shown by several researchers such as [13, 57–59] that the two cylindrical contact models do not present any added advantage compared to the elastic spherical contact model (that is, the Hertz contact model). However, the cylindrical models are non-linear and implicit functions, and therefore they require an iterative procedure such as Newton–Raphson algorithm to solve them which is computationally expensive. In this work therefore, Lankarani–Nikravesh contact force model represented in (21) is used to evaluate the force normal to the direction of collision (F _N ) since it accounts for energy dissipation during the impact process.

3.2.2 Friction force at a revolute joint with clearance: based on LuGre friction law

Since the normal reaction force at a revolute clearance joint can be obtained from the contact force models as illustrated in (23), then from the classical definition of friction, we have;

(26)

where μ is considered to vary as a function of the relative tangential velocity (v _T ) of the contacting bodies and an internal state z as defined in the LuGre friction model. Hence the instantaneous coefficient of friction (μ) to be used in (26) is represented as

(27)

and the evolution differential equation for the average bristle deflection being

(28)

where μ _k is the coefficient of kinetic friction which is a measure of the Coulomb friction force and μ _s is the coefficient of static friction which is a measure of the stiction friction force. Equation 28 can be substituted in (27) to solve for the instantaneous coefficient of friction (μ) as

(29)

Once the instantaneous coefficient of friction (μ) is obtained using (29), then (26) can be used to find the friction force which will capture the stick–slip motion. However, solving (29) numerically proved to be burdensome in terms of simulation time. This was overcame by writing (27) and (28) in non-dimensional forms as illustrated in [36] to get

(30)

where; $\overline{\mu}=\frac{\mu}{\mu_{k}}$; $\overline{v}_{T}=\frac{v_{T}}{v_{s}}$; $\overline{\dot{z}}=\frac{\dot{z}}{v_{s}}$; $\overline{z}=\frac{\sigma_{0}z}{\mu_{k}}$; $g(\overline{v}_{T})=\frac{g(v_{T})}{\mu_{k}}=1+(\frac{\mu_{s}}{\mu_{k}}-1)e^{|\overline{v}_{T}|^{\gamma}}$; $\overline{\beta}=\frac{\overline{v}_{T}}{g(\overline{v}_{T})}$; $\overline{\sigma}_{1}=\frac{\sigma_{1}v_{s}}{\mu_{k}}$ and $\overline{\sigma}_{2}=\frac{\sigma_{2}v_{s}}{\mu_{k}}$.

Therefore the friction force in (26) becomes

(31)

3.2.3 The friction model parameters

As already seen, LuGre friction model description is characterized by eight parameters, namely; three dynamic parameters; z, σ ₀ and σ ₁; and five static parameters; μ _k , μ _s , v _s , γ and σ ₂. The selection of these parameters is of great importance since the choice influences the outcome of the results. These parameters can be estimated more accurately by performing laboratory experiments which have been shown to be laborious and challenging. The static parameters are first estimated by performing open-loop experiments. These parameters are then used in dynamic experiments to estimate the dynamic parameters using non-linear numerical methods [60]. Swevers et al. [52] and Kermani et al. [61] presented experimental methodologies of identifying these LuGre friction model parameters for a joint of an industrial robot. The first step in identifying friction parameters of a manipulator’s joint is to obtain an experimental plot between the friction force and the velocity at the joint [61]. Then using the derived analytical LuGre model, the plot is dynamically interpreted for purposes of estimating the friction parameters. However, obtaining such friction-velocity plot by running the joint at different constant velocities and measuring friction force is not always feasible [54].

In this work, the choice of z and σ ₂ was based on the following assumptions:

• (a) Since simulations at steady-state condition are required, then the average bristle deflection (z) was assumed to be constant for a particular value of relative tangential velocity of the journal and bearing. Hence at steady state [61] we have

  $$\everymath{\displaystyle}\begin{array}{@{}rcl}\dot{z}&=&\frac{dz}{dt}=v_{T}-\frac{\sigma_{o}|v_{T}|}{\mu_{k}+(\mu_{s}-\mu_{k})e^{- |\frac{v_{T}}{v_{s}} |^{\gamma}}}z=0\\[5mm]z&=& \frac{v_{T}}{|v_{T}|}\times\frac{\mu_{k}+(\mu_{s}-\mu_{k})e^{- |\frac{v_{T}}{v_{s}} |^{\gamma}}}{\sigma_{0}}\end{array}$$

  (32)

• (b) Since this work is concerned with dry friction at the joints, then the viscous friction coefficient (σ ₂) which models the lubricant’s viscous properties was assumed to be zero.

The values of σ ₀, σ ₁, v _s , γ were chosen based on the observations made by other researchers as follows:

• (i) A lot of friction models are sufficiently described with γ=2 [54]

• (ii) σ ₀=100,000 N/m [36]

• (iii) σ ₁=400 N s/m [61]

• (iv) The characteristic Stribeck velocity v _s is usually chosen to be small compared to the maximum relative velocity encountered during the simulation. In every simulation, v _s was chosen as 1% of the maximum tangential velocity achieved.

The effects of the other parameters, that is, μ _k  and μ _s on the dynamic behavior of a mechanical system are investigated in this work.

3.2.4 Unilateral force at a revolute joint with clearance

Since the direction of the normal unit vector n is used as the working direction for the contact-impact forces, then the total unilateral contact-impact force F _Ni at body i is given by;

(33)

From Newton’s third law of motion, the contact reaction force at body j will be

(34)

These forces which act at the contact points are transferred to the center of masses of bodies i and j as shown in Fig. 5. This transfer of forces from contact points to the center of masses contributes to the moments given as

(35)

(36)

Fig. 5

Transfer of impact forces to the center of masses of the bodies

The forces in (33) and (34) and also the moments in (35) and (36) are added to the system’s equations of motion as externally applied forces and moments.

4 Results and discussions

This section contains results obtained from computational simulations of a slider–crank mechanism with a revolute clearance joint when the stick–slip friction is modeled using the LuGre friction law as described in Sect. 3.2.2. A typical slider–crank mechanism as shown in Fig. 6 is used as a demonstrative example to study the effect of stick–slip friction on a revolute joint with clearance on the dynamic response of a multi-body mechanical system. Table 1 provides the parameters which were used in simulation of the slider–crank mechanism with revolute clearance joint in either c-cr or s-cr joint.

Fig. 6

Slider–crank mechanism

Table 1 Parameters used in the dynamic simulation of the slider–crank mechanism

In the simulations, the initial configuration of the mechanism is defined when the crank and the connecting rod are collinear, and the journal and the bearing centers of the considered clearance revolute joint coincide. The initial positions and velocities necessary to start the dynamic simulation are obtained from kinematic simulation of the slider–crank mechanism in which all the joints are considered perfect. Since the equations of motion developed were numerically stiff, then an in-built MATLAB ode15s solver which is a variable order multi-step solver employing Numerical Differentiation Formulas (NDFs) and is able to handle stiff problems efficiently, was used as the integrator.

This study takes into account four main functional parameters of the slider–crank mechanism, that is, the location of the clearance joint, input crank speed, the kinetic coefficient of friction and the static coefficient of friction at the joint.

4.1 General effect of the stick–slip friction

Figure 7 shows the slider acceleration and the friction force responses when the crank-conrod (c-cr) joint is modeled with 0.5 mm radial clearance, the input speed being 2500 rev/min, μ _k =0.1 and μ _s =0.2. The results are presented for one cycle of the mechanism after the first cycle when steady state is reached.

Fig. 7

Response curves, c _A =0.5 mm, N=2500 rev/min, μ _k =0.1 and μ _s =0.2. (a) Slider acceleration and (b) friction force

When the journal moves freely inside the bearing walls, the slider moves with a constant velocity. This is replicated in the slider acceleration curve (Fig. 7(a)) as regions of zero acceleration since the slider moves with a constant velocity, and also in the friction force curve (Fig. 7(b)) as regions of zero friction force since in free-flight motion, no impact-contact forces are created. The smooth regions in the slider acceleration curve indicate that the journal and the bearing are in continuous contact motion, that is, the journal follows the bearing wall. This situation is confirmed by the purely sliding friction in the friction force curve. The sudden changes in velocity of the slider is due to the impacts and rebounds between the journal and the bearing. These impacts are visible in the acceleration curve as high peak values, and also in the friction force curve where the stick–slip motions are depicted.

Figure 8 show the slider acceleration curves for a small period of time (0.005 s) in order to show clearly how stick–slip friction at c-cr and s-cr joints affects the acceleration of the slider. It is seen that, during the transition from sliding to sticking, the acceleration of the slider increases suddenly to a maximum, while during the transition from sticking to sliding the acceleration of the slider decreases suddenly to a minimum. During pure sliding, there is a very slight difference witnessed in the slider acceleration curves in both friction and frictionless situations. However, a closer look on the curves show that the slider acceleration when friction is considered is either higher or lower than the slider acceleration for frictionless case. This scenario can be attributed to the fact that during sliding motion inside the clearance joint, the horizontal component of friction force can act on a direction similar or opposite to that of the slider motion. If the slider motion and the horizontal component of friction force are on the same direction, then the slider acceleration will be higher than that for the frictionless case. It is seen in Figs. 8(a) and 8(b) that the effect of the sliding friction force on the slider acceleration is more evident when s-cr joint is the real joint, while the effect of stiction friction on the slider acceleration is more evident in c-cr joint is the real joint.

Fig. 8

Response curves for a small period of time (0.005 s), N=2500 rev/min, μ _k =0.1 and μ _s =0.2. (a) Slider acceleration when c-cr joint is the real joint, c _A =0.5 mm. (b) Slider acceleration curve when s-cr joint is the real joint, c _B =0.5 mm

Figures 9 show the friction force and slider acceleration curves of which the time is very small (0.0002 s) in order to capture clearly the transition of friction force when the relative tangential velocity of impacting bodies in the clearance joint is zero. The transition of friction force for zero velocity when using the LuGre friction law is compared in Fig. 9(a) to when a modified Coulomb law is utilized. When the relative tangential velocity of the journal and the bearing is zero, that is at t=0.0321 s, there is no discontinuity of friction force and slider acceleration as is the case with static friction models. This shows that using the proposed representative version of LuGre friction model, the friction varies continuously throughout the simulation time and the Stribeck effect is also captured as is expected in real friction phenomenon. This is as also illustrated in Fig. 10 which shows a plot of friction force against the tangential velocity of the journal and bearing for one cycle of the mechanism when c-cr joint is the clearance joint.

Fig. 9

Response curves for a smaller period of time (0.0002 s), c _A =0.5 mm, N=2500 rev/min, μ _k =0.1 and μ _s =0.2. (a) Friction force. (b) Slider acceleration

Fig. 10

Friction force vs. tangential velocity curve, c _A =0.5 mm N=2500 rev/min, μ _k =0.1 and μ _s =0.2

Modifying the Coulomb law to a continuous-friction law only eliminates the discontinuity of friction force at zero velocity, however, this does not capture the Stribeck effect which is a phenomenon associated with stick–slip motions. In other words the curves when Lugre law is applied are comparable to Figs. 1(c) and 1(d) which capture the Coulomb, Stiction and Stribeck frictions, and at the same time ensuring that there is no discontinuity of friction force at zero relative tangential velocity. Hence the proposed representative version of LuGre friction model in this work can be said to fairly model the sliding and stiction friction as well as stick–slip transitions in a revolute clearance joint.

4.2 Influence of varying kinetic coefficient of friction

Figure 11 shows the friction force, slider acceleration and crank torque responses when c-cr joint is modeled with 0.5 mm radial clearance, the input speed being 2000 rev/min and the static coefficient of friction (μ _s ) fixed at 0.2. Since the Coulomb friction is proportional to the kinetic coefficient of friction (μ _k ), Fig. 11(a) shows that the larger the μ _k the larger the sliding (Coulomb) friction force. Also, the transition from sliding to sticking, and from sticking to sliding occurs early when the kinetic coefficient of friction is high. Figure 11(b) shows that when the slider motion and the horizontal component of the friction force are on the same direction, the slider acceleration is higher at large values of μ _k . As the value of μ _k is reduced, the slider acceleration decreases, and is minimum when friction is not considered. In addition, when the slider motion and the horizontal component of the friction force are on opposite direction, the acceleration of the slider is lower at large values of μ _k . As the value of μ _k is reduced, the slider acceleration increases, and is maximum when friction is not considered.

Fig. 11

Response curves, c _A =0.5 mm, N=2000 rev/min and μ _s =0.2: (a) Friction force. (b) Slider acceleration. (c) Crank torque

As seen in Fig. 11(c), a large torque is required to drive the crank with uniform speed when the value of μ _k is high and when sliding friction force is negative. In addition, a smaller torque is required to drive the crank with uniform speed when the value of μ _k is high and when sliding friction force is positive. According to the sign convention of friction force adopted during the modeling work [59], it implies that the moment of a negative friction force about the center of rotation of the crank acts in the opposite direction to that of the crank rotation. Therefore more torque is needed at the crank to overcome the moment of the negative friction force, and hence this torque increases as the friction force is increased, that is, as μ _k is increased. Also, the moment of a positive friction force about the center of rotation of the crank can be said to act in the same direction as that of the crank rotation, and hence less driving torque is required at the crank at larger values of positive friction forces.

Figures 12 and 13 show the effect of varying μ _k at different driving speeds of the slider–crank mechanism. Since the force of friction depends on the normal reaction force (F _N ), its clearly seen in Figs. 12(c), 12(b) and 12(a) that the higher the speed of the mechanism, the larger the friction forces at the clearance joint. This is because impact forces which determine directly the frictional force in the clearance joint are large at higher driving speeds as shown in [59]. It is also seen that, as the driving speed of the mechanism decreases, the effect of changing the kinetic coefficient of friction becomes more and more elaborate. By slightly changing μ _k from 0.01 to 0.05 at a speed of N=1500 rev/min, greater variations of the slider acceleration curves as well as the variation of times when motion changes from sliding to sticking or vice versa, become more evident unlike at a speed of N=2500 rev/min where the curves almost overlap. However, as the driving speed is reduced, the effect of stiction friction become less pronounced.

Fig. 12

Friction force response curves, c _A =0.5 mm and μ _s =0.2 at (a) N=1500 rev/min, (b) N=2000 rev/min, (c) N=2500 rev/min

Fig. 13

Slider acceleration response curves, c _A =0.5 mm and μ _s =0.2 at (a) N=1500 rev/min, (b) N=2000 rev/min, (c) N=2500 rev/min

Therefore, when the c-cr joint is modeled as the only clearance revolute joint with stick–slip friction, the effect of sliding friction on the dynamics of a mechanism is more realized at lower speeds while the effect of stiction friction is more realized at higher speeds. At low speeds the dynamic behavior of the mechanism continues been more chaotic by slightly increasing the kinetic coefficient of friction. However as seen in Figs. 14 and 15, when s-cr joint is modeled as the only clearance revolute joint with stick–slip friction, the effect of sliding and stiction friction are more realized at higher speeds. For instance, by slightly changing μ _k from 0.01 to 0.05 at a speed of N=2500 rev/min, greater variations of the slider acceleration curves as well as the variation of times when motion changes from sliding to sticking or vice versa, become more evident unlike at a speed of N=1500 rev/min where the curves almost overlap. However, the stick–slip friction in c-cr clearance joint is more sensitive to variations of the driving speeds as compared to s-cr clearance joint.

Fig. 14

Friction force response curves, c _B =0.5 mm and μ _s =0.2 at (a) N=1500 rev/min, (b) N=2000 rev/min, (c) N=2500 rev/min

Fig. 15

Slider acceleration response curves, c _B =0.5 mm and μ _s =0.2 at (a) N=1500 rev/min, (b) N=2000 rev/min, (c) N=2500 rev/min

4.3 Influence of varying static coefficient of friction

Figure 16 shows the friction force, slider acceleration and crank torque response curves when c-cr joint is modeled with 0.5 mm radial clearance, the input speed been 2000 rev/min and the kinetic coefficient of friction (μ _k ) fixed at 0.05.

Fig. 16

Response curves, c _A =0.5 mm, N=2000 rev/min and μ _k =0.05 for a smaller period of time (0.0002 s). (a) Friction force. (b) Slider acceleration. (c) Crank torque

The static coefficient of friction (μ _s ) determines the stiction frictional force, that is, the peak value of the friction force during the transition from pure sliding to pure sticking motion, and also from pure sticking to pure sliding motion. Therefore as seen in Fig. 16(a), the larger the value of μ _s the large the stiction frictional force. Also the Stribeck effect is high for large values of μ _s . This implies that for large values of μ _s , the continuous increase and decrease of friction force when entering sticking and slipping phase, respectively, is high. This explains why in Figs. 16(b) and 16(c), the slider deceleration and crank torque are large for large values of μ _s when entering the sticking phase, and the slider acceleration and crank torque are less for large values of μ _s when entering the slipping phase.

In addition, during pure sliding motion the change in the value of μ _s does not affect significantly the responses of the mechanism since all the curves at a constant μ _k =0.05 and varying μ _s are seen to overlap. This is because during pure sliding motion, only the Coulomb friction which is determined by the kinetic coefficient of friction (μ _k ) is present. Hence the static coefficient of friction (μ _s ) only affects the stiction and Stribeck frictional forces.

5 Conclusions

From the numerical simulations presented in this work, the proposed representative version of LuGre friction law has been to capture both the sliding and stiction friction together with stick–slip motions inside a revolute clearance joint. The developed algorithm is capable of capturing the frictional forces developed in a clearance revolute joint during all motion modes of the journal inside the bearing. During the periods of impacts and rebounds between the journal and the bearing, stick–slip motion at microscopic levels is witnessed. The microscopic transitions from pure sticking to pure sliding and vice versa have been shown to significantly affect the dynamic responses of a mechanical system in a non-linear and unpredictable manner. This poses a challenge in controlled mechanical systems in which the effective controllers should be able to follow closely these non-linear and sudden changes on the dynamics of the system introduced by the stick–slip friction.

Unlike the case when Coulomb law is mathematically modified to a continuous law, the LuGre friction law has been shown to eliminate the discontinuity of friction force at zero velocity while at the same time capturing the Stribeck effect which is a phenomenon entirely attributed to the stick–slip friction. The elimination of the discontinuity of friction force at zero velocity is very vital since it ensures that the friction force varies continuously throughout the simulation time as is expected in real life. Also, the LuGre friction law shows major dynamic effects on the responses of the mechanical system.

The effects of varying the static coefficient of friction, the kinetic coefficient of friction, the driving speed of the mechanical system and the location of the imperfect revolute joint have also been numerically studied. As expected, it has been seen that the larger the kinetic coefficient of friction the larger the sliding (Coulomb) friction force, and the large the static coefficient of friction, the large the stiction and Stribeck friction. Increasing the driving speed has been shown to increase the frictional forces, however, the effect of friction on the overall dynamic behavior of a mechanical system at different speeds varies from one kinematic joint to another.