Time-frequency analyses of fluid–solid interaction under sinusoidal translational shear deformation of the viscoelastic rat cerebrum

Abstract

During normal extracellular fluid (ECF) flow in the brain glymphatic system or during pathological flow induced by trauma resulting from impacts and blast waves, ECF–solid matter interactions result from sinusoidal shear waves in the brain and cranial arterial tissue, both heterogeneous biological tissues with high fluid content. The flow in the glymphatic system is known to be forced by pulsations of the cranial arteries at about 1 Hz. The experimental shear stress response to sinusoidal translational shear deformation at 1 Hz and 25% strain amplitude and either 0% or 33% compression is compared for rat cerebrum and bovine aortic tissue. Time-frequency analyses aim to correlate the shear stress signal frequency components over time with the behavior of brain tissue constituents to identify the physical source of the shear nonlinear viscoelastic response. Discrete fast Fourier transformation analysis and the novel application to the shear stress signal of harmonic wavelet decomposition both show significant 1 Hz and 3 Hz components. The 3 Hz component in brain tissue, whose magnitude is much larger than in aortic tissue, may result from interstitial fluid induced drag forces. The harmonic wavelet decomposition locates 3 Hz harmonics whose magnitudes decrease on subsequent cycles perhaps because of bond breaking that results in easier fluid movement. Both tissues exhibit transient shear stress softening similar to the Mullins effect in rubber. The form of a new mathematical model for the drag force produced by ECF–solid matter interactions captures the third harmonic seen experimentally.

1 Introduction

The mechanical behavior of brain tissue is nonlinear viscoelastic in its response to internal deformations, whether due to normal internal functions or due to external mechanical insults. Brain tissue contains about 20% by volume extracellular fluid (ECF) (Verkman 2013), which plays an important role in the glymphatic system, so that ECF interaction with solid matter including axons, glial processes or blood vessels, may significantly influence the bulk mechanical response of brain tissue. The fluid–solid interaction in brain tissue has rarely been studied in depth (Haslach et al. 2014, 2015b, 2017).

A deformation wave is composed of sinusoidal compressive and translational shear waves that permeate the brain tissue. Compressive force is supported primarily by the ECF, but the shear force may generate an internal drag force from the ECF–solid interaction that must be supported by the network structure of axons, dendrites, and glial processes.

To investigate the drag force, sinusoidal translational shear deformation applied to heterogeneous cerebrum specimens from rat brains models the brain shear stress response. A larger than normal physiological shear deformation amplitude is employed to magnify the ECF–solid interaction. Unconfined compression of a hydrated soft tissue redistributes the internal fluid so that fixed unconfined compression during translational shear deformation may modify the internal fluid–solid interaction.

Further insight into the brain ECF–solid interaction is obtained from comparison of similar translational shear deformation of a different structural type of hydrated soft biological tissue. The aorta is a naturally force bearing material, while brain tissue does not experience regular mechanical insults. Aortic tissue is mainly comprised of layers of smooth muscle cells, of elastin sheets, and of collagen fibers that reinforce against excessive deformation of the tissue in vivo (Clark and Glagov 1985; Davis 1993; Dingemans et al. 2000; Holzapfel et al. 2000; Humphrey and Na 2002). In contrast, the brain tissue configuration depends on a mechanical balance of a network of neurons and glial cells held in tension by the hydrostatic pressure of the extracellular fluid (Van Essen 1997). Aortic tissue has a circumferentially layered structure, while the structure of brain tissue is a mechanically balanced cellular network.

Because the in vivo frequency of the shear deformation of aortic tissue is about 1 Hz, the rat brain tissue and the bovine descending aortic tissue are deformed in sinusoidal translational shear at 1 Hz to compare their internal fluid–solid interactions. The aortic tissue, which is naturally force bearing in vivo, is loaded within the normal physiological range of deformation of an aorta so that damage to aortic tissue is not a factor. The deformation frequency of 1 Hz also naturally occurs within the brain in the glymphatic system; the cranial arteries, pumping at 1 Hz, create a pressure differential in the brain which drives the flow of extracellular fluid through the tissue to remove waste (Iliff et al. 2012).

A set of discretely sampled experimental shear stress data is viewed as a time series whose frequency content is to be determined. Before the 1960s, correlation functions provided approximate estimates of the spectrum of frequencies composing a time series set of data. In that decade, newly developed efficient algorithms to compute the fast Fourier transform (FFT) allowed direct calculation of the frequency components of periodic functions. The invention of wavelets two decades later facilitated analysis of the frequency content of non-periodic functions. Harmonic wavelets improve standard wavelets because they produce not only the frequency components but also the times at which they occur and because the computations are simpler (Newland 1993b).

Decompositions by the fast Fourier transform and by harmonic wavelets (Newland 1993a) identify the frequency components of the shear stress response of each tissue. The goal of this novel application of frequency analysis is to determine whether a frequency component of the shear stress response corresponds with any internal mechanical behavior of the tissue, such as the fluid–solid interaction. In addition, a three-parameter mathematical model fits the transient stress response peaks on each cycle of both aortic tissue and brain tissue. The stress–strain curve over multiple cycles indicates whether the brain shear response tends to a periodic cycle under sinusoidal deformation. The drag force is hypothesized to significantly affect the morphology of the mechanical shear viscoelastic response in brain tissue to an applied sinusoidal translational shear deformation, and a dimensional analysis of the ECF flow produces the form of a new mathematical model proposed for the shear drag force.

2 Methods and materials

Similar translational shear deformation applied to both brain and to aortic specimens allows comparison of their shear stress response by a frequency component analysis. This component analysis also produces a possible measure of the drag force induced by the ECF–solid interaction in the brain tissue.

2.1 Specimen preparation

The whole rat brains harvested from freshly euthanized healthy Sprague Dawley rats (6–9 months) are approximately 2 cm long and 1.2 cm wide. After excision, each half cerebrum is carefully dissected using a scalpel, guided by a specially built fixture, to slice four sagittal planar slabs of thickness 3 mm and surface $12\times6$ mm, two from each hemisphere. The shear deformation is applied on this sagittal surface in the 12 mm direction from the anterior to the posterior of the rat brain. Tissue slices are placed in Phosphate Buffered Saline (PBS) to maintain hydration until they are tested within 2 hours of harvest. These heterogeneous cerebrum specimens composed of white and gray matter contain the deep brain sub-regions believed to be most involved in mild traumatic brain injury. It is currently not possible to determine the proportion of white and gray matter in a given cerebrum specimen non-destructively. The heterogeneous rat brain specimens allow room for ECF redistribution and include the interactions of regions of the cerebrum. The tests approximate the average mechanical response of the full rat brain because the $12\times6\times3$ mm specimens are nearly the length of the cerebrum.

The aortic samples are taken from bovine descending aortas obtained from a local slaughterhouse (J.W. Treuth & Sons, 328 Oelle Ave. Baltimore, MD 21228) and are tested the same day. Once all significant fat is removed from the aorta surface, a ring that is approximately 6 mm in width is cut from the middle section of the aorta, where the internal diameter is about 20 mm. The thickness of the sample varies by location on the aorta. After the ring is cut open by making a longitudinal incision along the convex side, a grooved pattern fixture guides a cut along the circumferential direction to width and length of approximately 6 mm. Blue dye is used to mark one of the two circumferential sides, the cross-sectional face normal to the dominant direction of the collagen fibers. The aorta specimens are $6\times 6\times h$ mm, where $h$ is the aortic wall thickness, to avoid introducing residual stresses by flattening the circumferential curvature of the specimen. The specimen is sheared in the circumferential direction.

Both the rat brain and the bovine aorta specimens have a 6 mm width perpendicular to the shear direction. All specimens are tested in the laboratory environment of 21 C and 30% relative humidity. No specimen is preconditioned in any of these tests because the transient mechanical response is of interest.

2.2 Apparatus

All aortic and brain tissue specimens are deformed in an apparatus that applies translational shear with a chosen initial fixed unconfined compression and is mounted on a Bose-Electroforce test machine. The LM-1 Bose-Electroforce Testbench 250N materials testing system (Bose-Electroforce, Eden Prairie, MN) is electromagnetically controlled so that no wave artifacts at frequencies other than the desired deformation frequency occur in the sinusoidal displacement curve, when displacement is controlled, as happens with some hydraulic testing machines. The Bose-Electroforce uses a linear motor design that is modified from a Bose sub-woofer. A permanent magnet suspended in an electromagnetic field produces translational motion as the electromagnetic field changes and so the design reduces friction by avoiding bearings or seals (Chan and Rodriguez 2008). The Bose proprietary control software, WinTest 4.1, allows the mover to translate at a set constant rate up to $3.2~\mbox{m}/\mbox{s}$ and to a set final displacement or sinusoidally at a constant frequency up to 200 Hz with fixed amplitude up to 6 mm. Throughout a test, WinTest 4.1 records the elapsed time, displacement, and the reactive force induced in the load cell. The scan time interval between recorded data points is set to the shortest programmable time of 0.0002 seconds to maximize the number of points collected during a test.

A shear fixture (Fig. 1) to accommodate specimens of dimensions up to 25 mm × 25 mm with thicknesses up to 8 mm was designed and built to apply translational shear to flat rectangular plate specimens between two parallel 25 mm long flat grips or to apply fixed normal compression during the shear deformation. The top test grip is mounted to the mover of the Bose test machine and drives the shear deformation. Inertial effects were minimized by reducing the mass of the aluminum top grip to 8.12 g, a much smaller mass than the Bose specified allowable 1600 grams inertial load. The bottom grip is mounted to a 250 gram load cell (Interface WMCP-250G-567) and rests on top of a linear bearing (Del-tron M-1 linear ball slide), with manufacturer specified 0.003 coefficient of friction, which ensures that the bottom test grip remains parallel to the top grip with negligible friction detected by the load cell. The other end of the load cell is secured to a support bracket that is essential to the design because one end of the load cell must be fixed at all times in order to deflect due to the applied force. The support bracket is connected to a spring-loaded displacement stage (ThorLabs T12X) that enables the bottom plate and load cell to move up and down as a unit to increase or decrease the compression on the specimen and to adjust for different specimen thicknesses. This assembly is fastened to a mounting bracket that is screwed into a stationary stand.

Fig. 1

Combined translational shear and unconfined compression apparatus

2.3 Protocol

The same sinusoidal deformations are applied to both the brain and the aorta specimens to allow comparison of their shear stress responses. In each case, the amplitude is chosen as 25% of the length of the specimen in the direction of the shear deformation. The sinusoidal translational shear frequency is 1 Hz and each specimen is deformed for 40 cycles. A fixed unconfined compression of either 0% or 33% of the thickness of the specimen is applied prior to the sinusoidal translational shear test. The unconfined compression of 33% is chosen to ensure a large enough deformation for the fluid to move internally due to the applied compression. Six specimens are tested for each of the two types of compression, either no compression or 33% compression, for each material, for a total of 24 tests. Variation between the brain tissues from different rats and between the aortas from different cows requires multiple repetitions of each type of test to conduct statistical analysis.

To address the possibility that the observed morphology of the brain shear stress response is an artifact of the 1 Hz frequency or the 25% amplitude, specimens are deformed at another frequency and amplitude. A further six rat brain tissue specimens of size $10 \times 6$ mm with a thickness of 3 mm are tested at 25 Hz, and 25% amplitude and another six rat brain tissue specimens are also tested at 25 Hz and 10% deformation amplitude for 40 cycles to investigate whether any phenomena found in the 1 Hz stress response are characteristic of other frequencies or if these phenomena only occur with a 1 Hz applied shear deformation.

The shear specimens are attached to the grips by Vetbond glue (3M: 1469SB) with setting time of 15 seconds on aluminum and shear strength on metal of about 16.55 MPa to prevent specimen slip. The glue is allowed to set for 90 seconds before the test. The T12X stage is adjusted to raise the bottom plate to either 0% or 33% compression of the specimen.

2.4 Methods of analysis

Any spurious frequency components other than 1 Hz produced by the Bose displacement are computed from the discrete fast Fourier transform decomposition of the recorded displacement versus time signal to determine whether their magnitude is negligible.

The shear stress is computed by dividing the load cell measurement by the specimen surface area to which the translational shear deformation is applied. The translational shear strain is, by definition, $d/L$, the deformation magnitude, $d$, divided by the length, $L$, of the specimen in the direction of shear deformation. The translational shear stretch would be $1+d/L$. These strain measures are used, as discussed in detail in Haslach et al. (2017), because the specimen may not be in pure shear under zero compression since it would not be incompressible if internal fluid is lost due to shear deformation, as observed in aortic tissue (Haslach et al. 2015a).

The morphology of the shear stress versus time response curves for aortic tissue and brain tissue depends on the internal fluid–solid interaction as well as the applied deformation frequency (1 Hz or 25 Hz) and the transverse unconfined compression (0% or 33%). The analysis of the shear stress response as a function of time, $t$, to sinusoidal translational shear deformation of large amplitude employs techniques from signal analysis to detect the frequency components of the shear stress and the possible existence of a limit cycle.

2.4.1 Frequency analysis of the shear stress response

A frequency filter determines the main frequencies that exist in the rat cerebrum stress response. The magnitudes of each frequency component of the shear stress response from both tissues are further examined by a discrete fast Fourier transform (FFT) decomposition by Matlab fft, and by a harmonic wavelet decomposition. Because of its algorithm, the program fft works most efficiently if the number of sample points $N=2^{\bar{m}}$, for some integer $\bar{m}$. Usually $\bar{m}$ is taken as the largest integer such that $2^{\bar{m}}$ is less than or equal to the actual number of data points recorded, and the data points numbered above $2^{\bar{m}}$ are neglected. This procedure is simpler than trying to collect exactly $2^{\bar{m}}$ data points. The total time of the shear stress signal evaluated is therefore $T=2^{\bar{m}}(0.0002)$ for the FFT computations. Thus, the analysis is applied to the number of 1 Hz deformation cycles that occur in time $T$. The use of the program fft on data with a time step of 0.0002 s between sample points over 40 cycles requires a total evaluated time of $T=26.2142$ since $2^{18}$ is the largest power of 2 less than the 200,000 recorded data points.

The strength of a frequency component identified by the FFT analysis is measured by the power. By definition, the power of a frequency component in a signal $\sigma (t)$ of a frequency, $f$, is computed in the frequency domain and is $P_{\sigma }(f) = 2|H(f)|^{2}$, where $H(f)$ is the complex-valued Fourier transform of a time signal $\sigma (t)$ at frequency $f$ (Press et al. 1992, p. 492). Alternatively, the strength is measured at the value of the frequency in the single-sided amplitude spectrum, whose magnitude is proportional to $|H(f)|$, in the Matlab program fft. Two-factor Analysis of Variance (ANOVA) tests are computed to determine the dependence of the strength for 0 Hz, 1 Hz, and 3 Hz on material (brain or aorta) and compression magnitude (0 or 33%). Each ANOVA computation assumes a critical $p$-value of $\alpha =0.05$, and all ANOVAs are with replication.

When the shear stress function is not periodic, a more complex technique is required to compute functions whose sum approximates the function. The transient response, which is not cyclic, and the response to the remaining deformation cycles in time $T$ are decomposed into components that are a type of non-periodic functions, called wavelets. The wavelet, in contrast to the sine that oscillates over infinite time, represents a brief wave-like oscillation that is nearly zero as time approaches plus or minus infinity. Many popular wavelets, such as the Daubechies, do not have a simple mathematical expression. A type of wavelet that has a simple continuous mathematical expression, the harmonic wavelet defined by Newland (1993a, 1993b), has the functional form,

$$ w\bigl(2^{j}x-k\bigr)=\bigl\{ \exp \bigl[i4\pi \bigl(2^{j} x-k\bigr)\bigr]- \exp \bigl[i2\pi \bigl(2^{j} x-k\bigr) \bigr]\bigr\} /i2 \pi \bigl(2^{j}x-k\bigr). $$

(1)

A wavelet series is the representation of a function by a series of wavelet functions that are mutually orthonormal. The real-valued function, $\sigma (t)$, is expressed as a sum of terms that are a complex-valued coefficient times a complex-valued harmonic wavelet. The harmonic wavelet is orthogonal to its own unit translations and octave dilations and its frequency spectrum lies in one octave. Because of these properties, the coefficients and frequencies of the harmonic wavelet decomposition of any function represented by discrete points may be relatively simply computed in terms of the discrete fast Fourier transform (fft in Matlab) (Newland 1993a), a key reason to use this type of wavelets. The integer $0\leq k\leq 2^{j}$ translates the center of the wavelet, to locate it in time, and the integer $j \geq 0$ dilates the wavelet. The frequency range doubles with each sequential $j$ level increase and the frequency range at any $j$ level is

$$ \frac{(2 \pi ) 2^{j}}{T} \leq f < \frac{(2 \pi ) 2^{j+1}}{T}. $$

(2)

Therefore the wavelet decomposition allows determination of the location $k$ of frequencies $2\pi 2^{j}/T$ to $4\pi 2^{j}/T$, where $T=26.2142$. This method is very dependent on the number of data points; the more data points over a given time frame, the more frequencies that can be analyzed and the more tightly defined time intervals can be examined at a given $j$ level (Eq. (2)). A shorter programmed sampling time gives more points in a test, but again the shortest sampling interval on the Bose test machine is 0.0002 s. The harmonic wavelet decomposition in this way gives the frequency composition of the non-periodic transient region of the shear stress signal. The coefficient of the wavelet determines the magnitude of the corresponding frequency component.

A binning technique orders the components by significance and outputs the $j$ and $k$ values in each bin. The wavelets are organized into 20 bins in order of their magnitudes. The bin magnitude ranges are determined by the step size of $(\max-\min)/20$ where the maximum, max, and minimum, min, wavelet magnitudes are obtained from the wavelet decomposition. The bins capture the highest magnitude wavelet in bin number 1 and decreasing magnitude wavelets are placed in a bin with higher number so that an increase in bin number corresponds to a decrease in wavelet amplitude. The classical magnitude versus time and frequency contour plot typically used for other types of wavelet decompositions is not needed because the values of $j$ and $k$ locate the time at which various frequencies occur.

2.4.2 Transient response

The transient shear stress response is expected to be initially stress softening. To quantify whether this assumption is valid, a three-parameter nonlinear curve, using Matlab lsqcurvefit, is fit through the maximum shear stress response on each deformation cycle. Two-factor ANOVA tests examine the statistical dependence of each of the three parameters fitting the shear stress response on the factors compression magnitude (0 or 33%) and material (brain or aorta).

3 Results

Brain tissue, a naturally non-force bearing material, and aortic tissue, a naturally force bearing material in vivo, exhibit qualitative and quantitative differences when tested under sinusoidal translational shear deformation and fixed unconfined compression. Qualitatively, several characteristics of the morphology of the shear stress response of the bovine aorta and the rat brain tissue are similar (Figs. 2, 3, 4, 5). The peak shear stress response occurs at the end of the initial quarter cycle of the first deformation cycle. Both have a transient region lasting about 10 deformation cycles, and then the shear stress response tends to approach a periodic orbit. The magnitude of the shear stress response for both materials is increased by the application of constant unconfined compression as compared to shearing under zero compression.

Fig. 2

Stress versus time response of aortic tissue under 0% compression and 1 Hz, 25% translational shear strain

Fig. 3

Stress versus time response of aortic tissue under 33% compression and 1 Hz, 25% translational shear strain

Fig. 4

Stress versus time response of brain tissue under 0% compression and 1 Hz, 25% translational shear strain

Fig. 5

Stress versus time response of brain tissue under 33% compression and 1 Hz, 25% translational shear strain

The morphology of the aortic tissue shear stress curve appears nearly symmetric about the near-zero mean value, but the brain tissue shear stress response morphology exhibits asymmetry that is repeated on each deformation cycle (asymmetry is particularly noticeable under compression). Each deformation cycle has four regions, deform and un-deform in one direction, followed by deform and un-deform in the opposite direction. The shear stress versus time curve for brain tissue, in its local morphology near-zero stress, displays shoulders, asymmetric changes in concavity from concave down to concave up and then back to concave down at the beginning of the deform region in each direction (Fig. 6). So at the beginning of deformation, the stress change rate initially slows. The upper grip attached to the Bose mover (Fig. 1) controls the specimen deformation while the stress reading from the load cell is proportional to the displacement of the lower grip driven by the specimen. During the time interval of the shoulder, the lower grip moves very little because a force within the specimen resists its motion. The frequency analyses provide information about this force. No shoulder appears on the first deformation of the brain (Figs. 4, 5).

Fig. 6

Shoulder shown on a stress versus time curve for brain tissue under 0% compression and 1 Hz, 25% translational shear strain

The aortic tissue stress response is nearly symmetric with respect to the point at which the first un-deform becomes deform, or alternatively in a single half cycle with respect to the vertical line that passes through the peak value. No shoulders are visible in the aortic tissue response (Figs. 2, 3); this difference indicates that some component of the brain tissue significantly influences its shear stress response.

The shoulder in the brain shear stress versus time curve is not an artifact of the 1 Hz applied deformation or of the strain magnitude because it also occurs in the shear stress response to an applied deformation with frequency 25 Hz and amplitudes of either 10% or 25% of the length under no compression (Figs. 7a, 7b).

Fig. 7

(a) Shoulder shown on a stress versus time curve for brain tissue under 0% compression and 25 Hz, 10% translational shear strain. (b) Shoulder shown on a stress versus time curve for brain tissue under 0% compression and 25 Hz, 25% translational shear strain

The sinusoidal shear stress response exhibits a small phase shift compared to the deformation at the end of each deformation cycle. The brain tissue stress versus time response is quasiperiodic in the sense that the time shift slightly increases and eventually stabilizes over time. For example, the time shift in the brain tissue is about 0.1 s on the first three transient cycles and is slightly larger under compression. The time shift increases with the repetition through three cycles in both cases. The aortic tissue has a nearly constant time shift.

3.1 Frequency analysis

Decomposition of the shear stress versus time responses for rat brain tissue and bovine aortic tissue into their frequency components characterizes the source of the shoulders in the brain tissue response. The harmonic wavelet decomposition also determines how each frequency component changes through time during the signal.

3.1.1 Frequency components of the applied 1 Hz sinusoidal deformation

The Bose displacement mover is electromagnetically controlled, which allows the mover to move nearly friction-free as compared to hydraulic testing machines. Further, sometimes during testing with hydraulic machines, spurious waves are induced in the hydraulic fluid that can add other frequency components to the controlled displacement. Discrete fast Fourier transform decomposition verifies the shape and frequency of the mover displacement amplitude and ensures that no artifacts in the controlled displacement can account for some characteristics of the shear stress response.

The frequencies extracted from the Bose displacement versus time data for the programmed displacement amplitude of 3 mm at 1 Hz are 0, 1, and 3 Hz with fast Fourier transform amplitudes, respectively, 0.1547, 2.9916, and 0.0129. The most significant frequency is 1 Hz with very small amplitude frequencies of 0 and 3 Hz so that the applied displacement is nearly a pure 1 Hz signal.

3.1.2 Frequency filter

A pass filter provides a first approximation of the components of the uncompressed brain stress response data by isolating the part of the stress versus time signal with a frequency response within a chosen frequency range. Expanding and constricting the pass filter from 0–1 Hz, 2–3 Hz and 0–3 Hz, shows that the shear stress response of brain tissue to an applied 1 Hz sinusoidal deformation has a 1 Hz component, which is equal to the applied deformation frequency, and a 3 Hz component which captures the shoulders in the stress response (Fig. 8a). The fit by the sum of 1 and 3 Hz components imperfectly reconstructs the majority of the response (Fig. 8b). Other higher frequency components also exist to account for the rest of the signal response.

Fig. 8

(a) Frequency decomposition using two pass filters for 1 Hz and 3 Hz, of an original stress versus time curve (red) for brain tissue under 0% compression and 1 Hz, 25% translational shear strain. (b) Sum of 1 Hz and 3 Hz curves detected from pass filters and original stress versus time curve (red) for brain tissue under 0% compression and 1 Hz, 25% translational shear strain (Color figure online)

3.1.3 Periodic frequency analysis of the shear stress spectrum

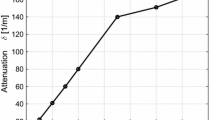
A discrete fast Fourier transform analysis provides the strength of the frequency components of the shear stress response for each material at 0% and 33% compression. For brain tissue, the significant frequencies for brain tissue are 0, 1, and 3 Hz (Figs. 9a, 9b). In contrast, the shear stress response of the aorta under 1 Hz deformation is dominated by a 1 Hz component with a small 3 Hz component (Table 1). However, negligibly small 2 Hz and 4 Hz components appear in some tests. The brain tissue shear stress response has a non-negligible 5 Hz component under both 0 and 33% compression whose strength is about 25% of the 3 Hz component. In contrast, the artery tissue shear stress exhibits no such 5 Hz component under either compression magnitude. The reproducibility factor, the standard deviation divided by the average, for the component magnitudes is less than 1 for all of the 1 Hz and 3 Hz components that are most significant. By convention, in hydrated soft biological tissue a reproducibility factor of less than 1 indicates that the response is reproducible.

Fig. 9

(a) Fourier coefficient magnitudes versus frequency for brain tissue under 1 Hz, 0% compression, 25% translational shear strain. The magnitudes are computed by the Matlab program fft. (b) Fourier decomposition curve versus time (blue) and original stress versus time (red) curve for brain tissue under 1 Hz, 25% translational strain. The Fourier decomposition curve has magnitude of approximately 1000 (Pa) throughout time and does not capture the much larger transient response (Color figure online)

Table 1 Two-factor ANOVA $p$-values and averages for the strength of 0, 1 and 3 Hz measured by the single-sided amplitude spectrum in fft

A two-factor ANOVA with replication determines the significance of tissue and compression on the power for each dominant frequency (0, 1, and 3 Hz). The magnitude of the 0 Hz component corresponds to a magnitude shift or the average stress value and is not statistically different from tissue type ($p=0.109$) or compression ($p=0.629$). The 1 Hz strength is higher in aortic tissue ($p=1.2\mbox{E-}05$, Table 1) and under 33% compression is higher than 0% compression in both materials ($p=0.051$, Table 1). The 3 Hz strength is higher in brain tissue ($p=8.87\mbox{E-}07$, Table 1) and is not statistically affected by compression, however visually the shoulders are influenced by compression as a shift toward the negative stress side with respect to the horizontal axis (Fig. 5). Compression increases the ratio of the 1 Hz strength to the 3 Hz strength.

Likewise, for the 25 Hz applied frequency tests on brain tissue, a third harmonic exists (Fig. 10). In preliminary tests, some samples for higher frequency sinusoidal deformation of brain tissue, additional higher odd integer harmonics exist in the signal and are visible in the distortion of the shoulder.

Fig. 10

Fourier coefficient magnitudes versus frequency for brain tissue under 25 Hz, 0% compression, 25% translational shear strain. The magnitudes are computed by the Matlab program fft

3.1.4 Harmonic wavelet frequency analysis of the shear stress signal

A Fourier series decomposition cannot model the transient portion of either set of data; for example the sum of the 1, 3 and 5 Hz sine components does not capture the transient portion of the brain shear stress response (Fig. 9b). Further, the brain tissue shear stress response is quasiperiodic and so cannot be fit by the periodic Fourier series summands, each of which has a fixed phase shift. Harmonic wavelet analysis (Sect. 2.4.1) provides information about the change in amplitude and the location of the frequency components with respect to time.

The harmonic wavelet analysis with a time interval of 0.0002 s between sample points over the 40 seconds of 40 cycles requires restriction to a total evaluated time of $T=26.2142$ seconds to have $2^{\bar{m}}$ data points. The harmonic wavelet decomposition frequency ranges are given in (2). Level $j=4$ corresponds to the frequency range of $0.6\mbox{--}1.2$ Hz, which is interpreted as the 1 Hz frequency response because the FFT power spectrum contains dominant 1 Hz and 3 Hz components. A $j=6$ level is interpreted as the 3 Hz frequency response by the same argument (Table 2). The coefficient magnitude for the $j=-1$ level corresponds to a vertical shift in the signal at all points (much like the Fourier series coefficient for the 0 Hz component).

Table 2 Frequency ranges for $j$ levels from Eq. (2)

The dominant $j$-levels are 4 and 6 in the harmonic wavelet decomposition for brain tissue under no compression (Table 3) and under 33% compression (Table 4) and 4 for aortic tissue (Table 5). In these Tables, the computed significant harmonic wavelet components are ranked by magnitude in bins. Recall that an increase in bin number corresponds to a decrease in wavelet amplitude, with the highest magnitude wavelet in bin number 1. An increase in $k$ level corresponds with a further shift to a later time. If a bin contains many wavelets (greater than 50), then the bin is not considered for analysis (which only happens for the shear stress wavelets in the smallest magnitude bins, 19 and 20). Exclusion of any other bin from the tables is due to the lack of any wavelets in that particular magnitude range. For all tests, bin 20 contains a large amount of wavelets with the bottom 5% magnitudes. Figures 11 and 12 present the reconstruction of the stress signal from the dominant wavelets given in Tables 3 and 5 along with the original stress data to show that little significant information is lost in the aortic shear stress decomposition by neglecting bin 20. The brain tissue shear stress reconstruction requires some of the small wavelets in bins 19 and 20 to complete the shoulders and peaks at later times in the 40 cycles. However, the goal is not to produce a complete reconstruction of the original signal by wavelets, but it is to identify the most significant wavelets within the response.

Fig. 11

Harmonic wavelet decomposition curve (including only the binned wavelets from Table 3) and the original stress curve for brain tissue under 0% compression and 1 Hz, 25% translational shear strain

Fig. 12

Harmonic wavelet decomposition curve (including only the binned wavelets from Table 5) and the original stress curve for aortic tissue under 0% compression and 1 Hz, 25% translational shear strain

Table 3 Brain tissue 40 cycles at 0% compression

Table 4 Brain tissue 40 cycles at 33% compression

Table 5 Aortic tissue 40 cycles at 0% compression

The dominant frequency throughout the harmonic wavelet analysis of the shear stress signal for both brain tissue and aortic tissue is 1 Hz ($j=4$), the applied deformation frequency. In the brain shear stress under zero compression, the 1 Hz component magnitude decreases with time from initial deformation, as indicated by the $k$ values in the first four non-empty bins. The brain shear stress analysis also detects a significant 3 Hz ($j=6$) component throughout the signal that is responsible for capturing the shoulder phenomenon. In the transient region composed of the first few cycles, the 3 Hz component decreases in magnitude with respect to time. The $k$ values 0, 1, and 2 appear in bins 13–16, and so these wavelets are centered at the beginning of the response in the first few cycles. The lowest $k$ values (wavelets at the beginning of the signal in time) have the largest magnitude of all of the 3 Hz wavelets in the signal. The magnitude of the 3 Hz wavelet for higher $k$ values places these wavelets in bins 17 and 18 indicating that the 3 Hz magnitude tends to a steady state over time. More 3 Hz components may exist within the many more small magnitude wavelets in bin 20. Wavelets also interact and may overlap to create a 3 Hz signal at times where the $k$ values are not dominant. Compression during shear of the brain tissue moves the 3 Hz wavelets to higher numbered bins because compression increases the ratio of the magnitude of the 1 Hz wavelet to that of the 3 Hz wavelets (Table 4).

The harmonic wavelet decomposition of the aortic shear stress under no compression (Table 5) contains only 1 Hz ($j=4$) wavelets in bins 1–8. The 3 Hz component only appears in bins 19 and 20 so that the 3 Hz component is not significant in the aortic tissue and exists only in the initial few cycles as indicated by its associated $k$ values. The average shear stress response is not exactly zero because bin number 18 contains the $j=-1$ wavelet. Compression during the shear deformation has little influence on either the $j$-levels obtained from the harmonic wavelet decomposition of the aortic shear stress response or their pattern of distribution into bins, as compared to analysis of the aortic shear stress under zero compression.

3.2 Drag force model

The 3 Hz component identified by the frequency analysis of the shear stress response of rat brain cerebrum tissue is likely induced by an internal interaction that the shear stress must overcome in response to an applied sinusoidal translational shear deformation. The drag force induced by the ECF–solid interaction in brain tissue is a candidate for the source of the 3 Hz signal. The remainder of the stress response that is not drag gives information about the solid phase brain tissue shear stress behavior or about other forces exerted on the solid phase.

The shoulder morphology in the brain tissue response appears in each deformation cycle throughout the signal with respect to time and exists even as some test variables change. Compression does not significantly affect the morphology of the shoulders, the deformation frequency levels of 1 Hz and 25 Hz display a shoulder in the stress response, and the shoulder persists even as the peak magnitude stress drops on subsequent cycles. The total force detected by the load cell is probably the sum of the solid phase response and the drag force exerted by the extracellular fluid on the solid phase in the rat brain tissue. The third harmonic is unlikely to be produced by axon deformation because axons are commonly modeled with linear viscoelastic models, including the Zener model (e.g. Dennerll et al. 1989), which does not display a third harmonic component within its response to sinusoidal strain.

A new mathematical model for the drag force that generates the third harmonic provides evidence that the third harmonic in the shear stress response is a consequence of internal ECF–solid interaction. Since the goal is to identify the cause of the shoulder, only the steady state portion of the shear stress versus time curves, and not the region where the transient stress softening occurs, is analyzed in this model.

Dimensional analysis and the Buckingham $\varPi$ theorem generate a possible model for the drag force between the ECF and the solid matter that reproduces a 3 Hz (third harmonic) response to 1 Hz sinusoidal shear deformation. The Buckingham $\varPi$ theorem allows selection of a non-unique set of dimensionless parameters that characterize the ECF flow. The chosen three fundamental units are force ($F$), length ($L$), and time ($T$); the FLT system is more convenient than the MLT system of fundamental units that replaces force by mass (Munson et al. 2009). The seven assumed physical quantities are (1) translational shear strain, $\epsilon$, which is dimensionless; (2) tortuosity, $\tau$, which is dimensionless; (3) drag force, $F_{d}$ ($F$); (4) fluid density, $\rho$ ($FT^{2}/L^{4}$); (5) kinematic fluid viscosity, $\mu$ ($L ^{2}/T$), which is the dynamic viscosity divided by density; (6) fluid velocity with respect to solid matter, $v$ ($L/T$); (7) area of solid, $A= \varPhi_{o} A_{c}$ ($L^{2}$), where $\varPhi_{o}$ is the initial solid volume fraction and $A_{c}$ is the specimen cross-sectional area. Tortuosity is the average resistance to flow as compared to the resistance in an obstacle free path (Hrabe et al. 2004) and is a measure commonly used in analyses of diffusion in the brain. We use it here as a measure of the resistance to forced ECF flow in the brain glymphatic system.

Since there are 7 physical parameters and 3 fundamental units, the Buckingham $\varPi$ theorem guarantees that 4 dimensionless parameters describe the fluid flow. One set of four dimensionless parameters, $\pi_{i}$, is (1) $\pi_{1} = F_{d}/(A v^{2} \rho )$; (2) $\pi_{2} = v \sqrt{A}/\mu =R$, the Reynolds number; (3) $\pi_{3} = \epsilon$; (4) $\pi_{4}=\tau$. An unknown function $f(F_{d}, v, \epsilon, \rho, A, \mu, \tau )=0$ relates all physical parameters. The dimensionless parameters are related by the equivalent unknown function $g(\pi_{1}, \pi_{2}, \pi_{3}, \pi_{4})=0$. Solving for $\pi_{1}$ and replacing $\pi_{1}$ by its physical quantities yields the shear drag force in terms of an unknown function $g_{1}$,

$$ F_{d}=\rho A v^{2} g_{1}(\pi_{2}, \pi_{3}, \pi_{4}). $$

(3)

To capture the third harmonic, assume that $g_{1}$ takes the form $\epsilon g_{2}(R, \tau )$, where $g_{2}$ is an unknown function. The term $\epsilon$ in $g_{1}$ accounts for structural deformation that influences the path for the ECF while the velocity squared term in (3) accounts for fluid damping (see Balachandran and Magrab 2004, p. 227).

Further assume that the applied deformation is $\epsilon = a \sin (2 \pi \omega t)$, and that the velocity of the fluid takes the form $v = a_{1} 2 \pi \omega \cos (2 \pi \omega t)$, where $a_{1}$ accounts for the unknown uniform ECF velocity. Presumably, a larger Reynolds number, which is proportional to the ECF velocity, implies a smaller tortuosity because the ECF velocity and the tortuosity are expected to be inversely correlated. Assume, further, that $g_{2}(\pi_{2}, \pi _{4})$ is a constant to simplify the model.

Under these assumptions, the drag force becomes $F_{d} = \rho A v^{2} \epsilon g_{2}(R, \tau )$. The application of trigonometric identities to the term $v^{2} \epsilon$ yields the third harmonic.

$$\begin{aligned} v^{2} \epsilon =& a(a_{1} 2\pi \omega )^{2} \cos^{2}(2\pi \omega t) \sin (2\pi \omega t) \\ = & a(a_{1} 2\pi \omega )^{2} \bigl[\sin (2\pi \omega t) - \sin^{3}(2 \pi \omega t)\bigr] \\ =& a(a_{1} 2\pi \omega )^{2}\bigl[\sin (2\pi \omega t) - 0.75 \sin (2 \pi \omega t) + 0.25 \sin (6\pi \omega t)\bigr]. \end{aligned}$$

(4)

The last equality follows from the standard trigonometric identity, $\sin^{3}(2\pi \omega t) = 0.75 \sin (2\pi \omega t) - 0.25 \sin (6 \pi \omega t)$. So this model produces the experimentally required third harmonic. Because the fluid velocity squared term $v^{2}$ and $\epsilon$ both contribute to $\sin^{3}(2\pi \omega t)$ and therefore to the third harmonic, the average shear drag force, $F_{d}$, is induced by a combination of both structural deformation and fluid damping.

$$ F_{d} = \rho A g_{2}(\pi_{2}, \pi_{4}) \bigl\{ a(a_{1} 2\pi \omega )^{2}\bigl[ 0.25 \sin (2\pi \omega t) + 0.25 \sin (6\pi \omega t)\bigr]\bigr\} . $$

(5)

An increase in tortuosity would result in an increase in the drag force. An increase in deformation amplitude (translational shear strain) and frequency is predicted to increase the drag force, as expected.

The magnitude of the drag force is computed directly from the amplitude, $\sigma_{3}$, of the third harmonic since in the drag force expression (5) the coefficients of the deformation frequency term and the third harmonic are equal.

$$ \sigma_{3} A_{p} = 0.25 \rho A g_{2}(R, \tau ) a (a_{1} 2 \pi \omega )^{2}, $$

(6)

where $A_{p}$ is the area of the specimen surface to which the shear deformation is applied.

The mathematical technique to compute the coefficients of a Fourier series decomposition determines the unknown value, $\sigma_{3}$ in the drag force equation. For period, $\bar{T}$, the magnitude of the third harmonic of a frequency $\omega$, is $2\bar{T}^{-1}\int_{0}^{\bar{T}} \sigma (t)\sin (6\pi \omega t) \,dt$ since $3\omega$ Hz is $6\pi \omega~\mbox{radians}/\mbox{s}$. Because the shear stress data $\sigma (t)$ is discrete, the integral is computed by the Matlab program, trapz. The magnitude of the third harmonic for 1 Hz sinusoidal deformation is typically less than 300 Pa, and the sign of the coefficient of the 3 Hz component is negative. The influence that the fluid has on the stress response contains equal magnitudes of a 1 Hz component and of a 3 Hz component. Therefore, the drag reduces the magnitude of the 1 Hz response while also resisting the fluid flow according to this model. The discrete fast Fourier transform decomposition analysis shows a stronger 1 Hz component than the 3 Hz component. The remainder of the 1 Hz component is assumed to be a result of the solid phase response.

The model is not complete because $a_{1}$ and $g_{2}$ are unknown, and so the model is only defined up to a multiplicative constant. These constants, $a_{1}$ and $g_{2}$, are related by (6) to $\sigma_{3}$. However, the dimensional analysis shows that fluid interaction with solid matter can account for the third harmonic.

3.3 Transient response of the shear stress

The graphs of 40 cycles of the shear stress response to sinusoidal deformation at 1 Hz as well as the harmonic wavelet decomposition suggest that the shear stress passes through a softening transient region and eventually after about 10 cycles, the response becomes nearly cyclic, i.e. approaches a possible limit cycle, in both the brain and the aortic tissue. The drop in each cycle of the peak stress magnitude with respect to time appears exponential (Figs. 2, 3, 4, 5). The elastomer damage theory (e.g. Zuñiga and Beatty 2002), which assumes chain rupture, slipping of molecules, and cross-link ruptures, proposes an exponential model passing through the peaks of each cycle that captures the decrease in peak stress. A similar model applied to these biological tissues is $Y(t)$, the positive envelope for the peak stress values on each deformation cycle with respect to time,

$$ Y(t) = A \exp (-b t) +c. $$

(7)

In this model, $A$ is the magnitude of drop from the peak shear stress at the end of the initial deformation to the shear stress amplitude, $c$, of the limit cycle, and $b$ is the rate of peak shear stress amplitude decrease. The Matlab program lsqcurvefit fits each curve and computes the empirical coefficients (Table 6).

Table 6 Two-factor ANOVA $p$-values and averages for the exponential fit coefficients

A two-factor ANOVA with replication evaluates the effect of the tissue material and compression on each coefficient in the decay equation (7). The coefficient, $A$, for brain tissue is significantly larger than that for the aortic tissue ($p=1.3\mbox{E-}06$, Table 6). The compression causes a significant increase in $A$ for both tissues ($p=0.020$, Table 6). The coefficient, $b$, which measures the quickness of the drop in stress is also larger for brain tissue than for aortic tissue ($p=0.0009$, Table 6). Compression causes an increase in the coefficient, $b$, for both tissues ($p=0.005$, Table 6). The coefficient, $c$, corresponds to the steady state shear stress magnitude which is higher for the compressed tests for both materials as compared to their uncompressed test ($p=0.0125$, Table 6). The coefficient, $c$, is lower for brain tissue than aortic tissue ($p=6.13\mbox{E-}05$, Table 6).

Direct measurement of the maximum shear stress at the end of the first quarter cycle (Table 7) indicates the accuracy of the fit by the magnitude of the difference of the sum $A+c$ and the average maximum stress. In each of the cases, the two values are within 1.6% for no compression and 12.5% for compression, where the error equals the difference divided by $A+c$.

Table 7 Two-factor ANOVA $p$-values and averages for the maximum initial stress value

A two-factor ANOVA shows that the initial peak stress magnitude does not depend on material ($p= 0.27$), but does depend on compression ($p=0.014$). However, the application of compression does not modify the overall morphology of the shear stress curves.

The shear stress versus translational strain graph is another technique to visualize the possible limit cycle. In this representation for the brain tissue under zero compression (Fig. 13), the nearly horizontal sections near the origin capture the shoulders. Under compression, the stress at the origin is clearly non-zero; the curves tend to slightly shift down. It should be noted for the brain tissue stress response that, although the stress magnitude changes through time and reaches a steady state, the shoulder exists throughout the entire signal. A steady state cycle also exists for the aortic shear stress.

Fig. 13

Stress versus strain curve for the rat cerebrum under 0% compression and 1 Hz, 25% translational shear strain showing the possible limit cycle

4 Discussion

The frequency analyses of the brain shear stress response to sinusoidal shear deformation verify that the magnitude and frequency of the components of the signal vary through time. The morphology of the shear stress response curve to large amplitude sinusoidal translational shear deformation reflects changes in the tissue structure or the fluid–solid interaction during deformation. Therefore, in particular, the frequency components correspond to either ECF–solid matter interaction or solid matter-solid matter interactions. The drag force mathematical model (5) strongly suggests that the third harmonic component of the brain shear stress signal should be interpreted as shear stress required to overcome the shear drag induced by the ECF–solid interaction produced by fluid motion under deformation control.

4.1 Influence of tissue structure

The third harmonic of the shear deformation appears in the decomposition for the shear stress response of the brain but not of the aorta. The aortic tissue, although high in fluid content, does not exhibit a shoulder or a significant third harmonic in its shear stress response. The drastic difference in the structures of these tissues likely explains whether the third harmonic of the deformation frequency appears in the decomposition of their shear stress responses.

The aorta is a naturally load bearing, soft biological tissue with high interstitial fluid content and is comprised of three main layers called the intima (inner), media (middle) and adventitia (outer). The media, which extends over almost the full wall thickness, is comprised of many circumferential layers of smooth muscle cells, elastin sheets and collagen fibers (Clark and Glagov 1985). The interstitial fluid in the extracellular matrix of the media transports nutrients to the cells and removes waste. The source of the interstitial fluid is the capillaries in the wall that normally deliver a net gain of water to the aorta because the heart systolic pressure forces plasma through the wall at the arterial end, even though smaller osmotic pressure induces some flow back into the capillary at the other end. Versican proteoglycans which bond to water are a main filler substance in between cells and allow for diffusion of nutrients to the cells. Mechanical deformation of the aorta forces a different type of interstitial fluid flow. Translational shear deformation moves the interstitial fluid within the aortic wall as shown by weight loss of about 7% measured during translational shear deformation of $6\times 6\times h$ mm specimens under 10% compression, where $h$ is the wall thickness, in the circumferential direction parallel to the layers (Haslach et al. 2015a). In these specimens, the flow is probably parallel to the circumferential layers in the media. Therefore, the lack of a third harmonic component in the shear stress of the aorta reflects minimal drag because the sinusoidal shear deformation induced interstitial fluid flow is along the circumferential layers with negligible drag force between the fluid and the solid matter.

The network structure of brain tissue interacts differently with ECF flow. Brain cerebrum tissue is a heterogeneous soft biological tissue comprised of many subsections of both white and gray matter and is not a natural load bearing material. Brain tissue does not have a layered structural framework supporting the tissue as does the aorta. The neuronal axons and dendrites, with the synapses, have a structural role as well as signaling functions and along with the glial cells form a network that maintains the configuration of the brain. When brain tissue is not subjected to external forces or deformations in vivo, hydrostatic pressure in the ECF is balanced by tension in axons, dendrites and glial processes to maintain the tissue morphology, and neurites adjust their length accordingly to remain under steady tension (Van Essen 1997). Such a configuration persists even with the normal slow movement of waste matter through the glymphatic system.

The process of fluid redistribution, nutrient transport and waste removal within the brain is referred to as the glymphatic system. The source of the ECF is the cerebrospinal fluid (CSF) that is produced in the four ventricles of the brain and that moves through the subarachnoid compartment. Therefore the ECF may be considered part of the glymphatic system and as such normally is not static. The flow of CSF and the ECF is driven by the pulsing arteries in the brain that cause a pressure change between the para-arterial and paravenous pathways, and flows in channels between cells provide low-resistance pathways for fluid movement between the paravascular spaces system as reported by Iliff et al. (2012), who imaged the normal glymphatic flow in mice by introducing markers into the CSF. A paravascular space for flow in the glymphatic system is a continuous sheath surrounding a blood vessel that lies between vascular cells and astroglial end-foot processes. Due to the gaps between the astrocyte endfeet in the astroglial sheath that surround brain blood vessels (Mathiisen et al. 2010), the nutrient filled fluid is able to flow between the dendrites, but the exchange of fluid between the blood and brain is controlled by the size of the narrow clefts between overlapping endfeet of the astrocytes which may restrict free flow of the fluid. Astrocytes are star-shaped glial cells that provide biochemical support of the blood-brain barrier, provide nutrients to the neurons, maintain the extracellular ion balance, and help repair the brain after traumatic injury. Due to the low-resistant pathways between the paravascular spaces, under loading pathological motion of the ECF is possible. A mechanical insult might accelerate the ECF flow or increase the ECF hydrostatic pressure to disrupt axonal and glial connections or disrupt the flow so that some waste products are not removed from the brain interstitium.

In a tissue with a network structure, such as the brain, the drag force of the fluid–solid interaction results from shear deformation transverse to the network. Therefore, the network structure of the brain is more likely to produce a drag force, and the 3 Hz component of the shear stress, than aortic tissue. The network structure in brain tissue is somewhat analogous mechanically to the collagen network in cartilage. The support of forces by cartilage depends on proteoglycan swelling from their glycosaminoglycan (GAG) chains that bond water and on a network of collagen fibers. However, no bonding exists between the proteoglycans and the collagen. The proteoglycans and water held in place by the collagen network support compressive forces as verified by the fact that degradation of the GAGs induced by hyaluronidase removes much of the compression resistance of cartilage (Broom and Silyn-Roberts 1990). However, the collagen fiber network supports shear forces by fiber to fiber linking. This mechanical behavior is likely similar to that of the brain for which the ECF supports compressive loads, perhaps with the aid of the proteoglycans in the extracellular space, but the network of neuron axons and dendrites, along with glial, connections supports shear forces and holds the ECF in place. The extracellular space in the brain tissue also contains glycosaminoglycans, proteoglycans, as well as lecticans that form barriers to cell migration and signaling. The lecticans, which include aggrecan, versican, neurocan and brevican, easily bond with hyaluronan docked to the plasma membrane that encloses a cell (McRae and Porter 2012). So in both materials a network tends to support forces. Further, forces on cartilage lead to breakage of proteoglycan bonds with water and fluid loss from the tissue, a process that is also observed in brain tissue. This analogy suggests that shear deformation may reconfigure the brain tissue more, and thus to be more dangerous, than compressive deformation. Pathological ECF flow in the brain would likely shear the network structure of linked axons, dendrites, and glial processes.

4.2 Transient stress response mechanism

Stress softening characterizes the initial shear stress response because the peak stress magnitude on subsequent deformation cycles decreases exponentially. On the initial loading, the material exhibits a relatively stiff response, but when the material is unloaded and then reloaded so that the deformation of the current cycle is less than or equal to the maximum stretch previously applied, the stress–strain curve softens significantly, in the sense that the stress required to achieve the same stretch in re-deformation is smaller than the stress required on the previous deformation.

In cyclic tensile tests, some biological tissues also exhibit stress softening (Horný et al. 2010). Such stress softening phenomenon in elastomers is referred to as the Mullins effect. The phenomenon is typically attributed to bond breaking involving chain breakage, slipping of molecules, and cross-link ruptures, although the exact physical explanation of the Mullins effect has not been generally agreed upon (e.g. Diani et al. 2009; Blanchard and Parkinson 1952; Bueche 1960). Zuñiga and Beatty (2002) describe the material as having a selective memory of only the maximum of the previous strains ever experienced and represent the Mullins effect with a 3 parameter damage model that fits the exponential stress softening in rubber, which has a molecular network structure. Inspired by their model, a similar approach to their enriched form of the linear vibrations damping envelope equation for the brain and artery tests, the decreasing trend of the peaks on subsequent cycles is fit to the three-parameter model (7). The exponential decrease in peak shear stresses is by analogy attributed to bond breaking within the brain or aortic tissue.

The stress softening Mullins effect also appears in cyclic uniaxial compression (Rickaby and Scott 2013) and in torsional shear (Mars and Fatemi 2004). Mars and Fatemi (2004) observe that the majority of the softening in rubber occurs in the first 10 cycles of loading and that under constant-amplitude cyclic loading, as in our tests, the stress–strain curve exhibits some additional softening. In some cases, Mars and Fatemi also describe, without explanation, a healing effect in which, after several cycles, the stress–strain response remains relatively constant and then starts to slightly stiffen. Such healing might involve bond reformation that could strengthen the tissue and explain the slight increase in peak stress magnitudes in some aorta specimens towards the end of the set of deformation cycles.

Franceschini et al. (2006) have argued that brain tissue under slow ($5.5\mbox{--}9.3 \times 10^{-3}/\mbox{s}$) cyclic uniaxial tension–compression tests deforms similarly to filled elastomers because both their brain tests and the elastomers produce S-shaped stress curves. They also observe changes in stiffness in tension and compression of the brain tissue that is characteristic of the Mullins effect. However, the analogy between elastomers and brain tissue should not be overstated. Rubber is not hydrated, and brain tissue is not elastic (nor even pseudo-elastic as Franceschini et al. suggest). No evidence exists that an elastic model for rubber such as that of Rickaby and Scott (2013) applies to brain tissue, and in fact a nonlinear viscoelastic model is very accurate for constant deformation rate translational shear and for unconfined compression (Haslach et al. 2015b).

The aortic tissue shear stress drop during the transient region, as measured by the parameter $A$ in (7), is significantly smaller than that for the brain tissue, possibly because the bonds broken are those between circumferential layers. The initial 3 Hz component found in bin 19 the harmonic wavelet decomposition of the aortic shear stress under zero fixed compression may indicate a temporary drag force that quickly becomes zero on subsequent deformation cycles.

No shoulder appears in the shear stress response to the first quarter cycle deformation of the brain tissue. A possible explanation is that during the first deformation, bonds must be broken between the GAGs and water in the extracellular space (ECS). Once free water exists in the ECS, then drag is possible between the ECF and solid matter.

The drag force induced by fluid movement within the brain tissue generates a major contribution to the shear stress response as a shoulder. In the brain shear stress response, the magnitude of the 3 Hz component from the harmonic wavelet decomposition shown in the bin classification decreases over the initial few cycles and may correlate with initial bond breaking that decreases the drag force. Further, if the transient is due to bond breaking, the drag force must not depend on the transient bond breaking because the shoulder persists appears throughout the shear stress signal, and therefore bond breaking does not explain the shoulder. The possible limit cycle (Fig. 13) is likely due to cessation of bond breaking on the later deformation cycles.

4.3 The influence of compression on the shear stress response in the brain tissue

Fixed compression through one third of the thickness of a brain specimen under translational shear deformation is not sufficient to close all pathways for ECF flow since the power of the third harmonic component in the fast Fourier transform decomposition is statistically the same for the zero and 33% compression tests. Compression does not eliminate the third harmonic but rather increases the ratio of the magnitude of the first harmonic to that of the third harmonic. Since the brain tissue maximum initial shear magnitude is about 12% less than $A+c$ in (7), mechanisms in addition to bond breaking occur under compression. Fixed compression makes the drag force due to the ECF a smaller portion of the total measured shear stress, perhaps because compression increases additional solid on solid shear contact that induces friction that must be overcome by the shear stress.

4.4 Frequency components and their physical source

To summarize, four results provide evidence that the shoulder in the shear stress response for the brain is due to a 3 Hz third harmonic component and that the third harmonic is generated by ECF–solid matter interaction.

The filter applied to the shear stress data shows that the superposition of the 1 Hz and 3 Hz components produces the shoulder geometry in the graph (Fig. 8b). The resulting inflection points on the shear stress graph therefore need not arise from some critical event within the solid matter. This fact raises the question of whether the ECF–solid interaction or some solid substructure generates the 3 Hz stress component.

The shoulder exists in the brain tissue shear stress response but not in that of the aortic tissue. Structural differences in the brain tissue probably generate the significant 3 Hz component to create the shoulder. About 20 percent of the volume of the brain tissue is ECF, and so the fluid is a prime candidate for the source of the 3 Hz component. The aortic tissue also contains fluid, but its internal flow pattern differs from that in the brain.

The dimensional analysis of the ECF flow within the brain tissue suggests the form of a possible model (5) for the drag force due to ECF–solid interaction. The form involves a third harmonic term and so is consistent with the hypothesis that the third harmonic represents ECF–solid drag. The first harmonic component of the model form reduces the 1 Hz response of the solid matter.

The exponential fit (7) to the transient peaks that agrees with the Mullins effect model suggests significant bond breaking during the initial cycling that creates the transient region. According to the harmonic wavelet analysis, the magnitude of the third harmonic component decreases during the transient stress and reaches a nearly constant magnitude during the more periodic motion on later deformation cycles. The decrease in magnitude of this component is consistent with the third harmonic representing drag force because bond breaking suggested by the Mullin damage model may lower the drag interaction between the solid and ECF.

While this evidence is not conclusive, the frequency components of the shear stress response must be generated by the response of substructures or ECF within the tissue. The largest such structural component is the ECF and the most significant frequency component other than the first (1 Hz) is the third harmonic (3 Hz).

The above analysis does not address the 5 Hz component observed in the brain tissue shear stress response. While it may be a coincidence, the theta waves emitted by the hippocampus as measured by electroencephalography (EEG) are in the range of 4 to 7 Hz. These waves clearly occur in physically active rats, but their frequency decreases slightly in inactive rats. Neurons are known to be oscillators because they generate oscillatory electrical voltage signals (Izhikevich 1999), but neurologists have not deeply examined the mechanics involved. The governor for the theta waves is unknown. One possibility is that the layered structural arrangement of the neurons in the hippocampus governs the theta wave by its control of the electrical resistance (Buzsáki 2002). Deformation is well known to modify the resistance of materials, a mechanical property commonly used in the design of electrical strain gages. This layered structure may induce the small strength 5 Hz component of the brain shear stress response. In vivo, the deformation could be generated by the glymphatic system 1 Hz pulse that is produced by the blood flow in the cranial arteries. Verification would require a different and clever experiment. However, we do expect the frequency component induced by the solid matter to be of lower strength than that induced by the fluid because the axonal and glial network connections should reduce local oscillations.

5 Conclusion

A frequency analysis of the shear stress response of hydrated biological tissue investigates the idea that each frequency component is physically induced by a particular tissue substructure behavior. The focus here is on the 3 Hz component because this third harmonic has the greatest strength observed. The shoulders in the shear stress signal for the rat cerebrum are captured by the third harmonic of the deformation frequency. The results strongly suggest that the third harmonic component represents the shear stress required to overcome the drag induced by the ECF–solid interaction. The frequency content of the rat cerebrum and the bovine descending aorta shear stress response differ because the brain network solid matter structure is more likely than the aortic layered solid matter structure to involve drag. The drag force likely plays an important role in the nonlinear viscoelastic behavior of the rat cerebrum. In contrast, the aorta is commonly modeled as hyperelastic (e.g. Holzapfel et al. 2000).

We have presented the first, to our knowledge, application of harmonic wavelet analysis to a frequency decomposition of the shear stress response of hydrated biological tissue. The harmonic wavelet analysis has several advantages over the standard derivation of the frequency spectrum of the shear stress time series by the fast Fourier transform. First, the series need not be assumed periodic by viewing it as one period of a longer series. Primarily, rather than merely measuring the presence of a particular frequency component, the wavelet analysis identifies how the component changes in magnitude at various times during the time series. For example, the wavelet analysis verifies that the third harmonic decreases in magnitude during the transient region consistent with an expected decrease in drag because the transient response of brain tissue apparently involves bond breaking similar to the Mullins effect in elastomers.

The proposed form of the mathematical model for the magnitude of the interaction force between the ECF and the solid matter offers a basis for an estimate of the drag force magnitude that could help cell specialists to relate the force to the amount of released biochemicals in vivo measured by physicians following brain trauma. Under higher shear deformation frequencies, due to blast or impact, the drag force could be an immediate mechanical cause of mild traumatic brain injury by disrupting axon and dendrite synapses.