1 Introduction

Information security has become a major concern in to- day’s world since our lives depend on technology and information transmission. Images as one of the most transmitted data are the interest of many researchers.

Among different image security metrics like Watermark [30], and Steganography [26], image encryption is a straight- forward one with concerns in encrypting an image to an unrecognized one. The rapid advancement of chaos theory and its excellent properties present an opportunity for researchers to improve several traditional encryption schemes and build new ones [4, 18, 20, 21, 29]. R. Matthews [23] was the first who presents and published the chaotic map encryption. Following that, many researchers developed image encryption techniques based on chaotic maps. Beginning with the one-dimensional chaotic maps to the n-dimensional chaotic maps our related work is illustrated as follows: Authors in [9] proposed an encryption-compression algorithm. The encryption is done with the Chiricov standard map and the compression with the SPIHIT coding.. Zahmoul et all in [24] proposed a new one-dimensional chaotic map called Beta chaotic map(1D-BCM) based on the Beta equation and the Beta wavelet [34]. This map is then used in image encryption. In the same manner as [9] this new map is then used by Elkhalil et all in [7] to build a robust compression-encryption algorithm. Results show the effectiveness of the BCM in the encryption algorithm and also the flexibility of this map to adapt to the compression part. In ref. [27] another type of 1D-BCM called Wide Range Beta Chaotic Map is presented with the lifting wavelet transform and the Latin square to prove for more time its strengths.

Belazi et all in [1] suggested a new image encryption permutation substitution algorithm based on a chaotic map. Also, Elghandour et all proposed in [6] a new encryption algorithm based on a two-dimensional piecewise smooth nonlinear chaotic map. Their results have proved the high-level protection of images. Hua and Zhou proposed in [12] new two- dimensional Sine Logistic modulation map (2D-SLMM) and used this map in the image encryption process. In this scheme, the authors designed a mechanism to add random values in the images to increase the encryption probability. According to the testing results, the suggested technique can protect images with a good level of security and low time complexity. Another work was reported by Sharm in [28] using a new 2D chaotic map-based encryption technique. The idea behind the new 2D chaotic map is to split the outputs of a 2D logistic map into two distinct 1D logistic maps. Gao in [8] proposed a 2D hyperchaotic map which is derived from 1D-chaotic map. Results show that the 2D hyperchaotic map has more complexity, and randomness than a 1D hyperchaotic map. Moreover, the security analysis has good results. In [22] authors proposed a new image encryption scheme based on three-dimensional Lorenz chaotic system. A 3D chaotic economic map was used in [15]. In [17] authors proposed an optical encryption scheme based on hybrid 3D chaotic maps and discrete cosine transform. The original images was converted to an indexed formats using their color maps. The 3D-logistic chaotic map is used to generate a chaotic sequence (key stream) that will be used to shuffle the indexed images. The encrypted image is obtained after separating the amplitude and phase part of the signal. The experimental results prove that the proposed scheme is resistant to the chosen plain-text attacks.

Authors in [5] proposed a hybrid chaos image encryption scheme. Two-dimensional ecological chaotic map, Free and Lawton (BFL) map was combined with logistic map and Chebyshev map to generate a pseudo-random sequence for image encryption key. Results show that the proposed scheme has good immunity against several cryptography attacks.

As can be observed, seemingly little changes in the mathematical formulation result in considerably innovative and successful encryption algorithms [2, 3, 10, 11, 13, 32, 33]. The current work was inspired by the work of Zahmoul et all in [25] and Wu et all in [31].

2 Our contribution

To further ameliorate the performance of the 1D Beta chaotic map, we create new 2D Beta chaotic map based on 1D Beta chaotic map function.

Our new map has a large range of bifurcation parameters, strong chaotic behavior and high number of parameters.

Our map is used to generate pseudo-random sequences. Those chaotic sequences are used to generate the encryption key, furthermore, they were used in the permutation and substitution process.

This paper is organized into the following sections. Section 2: Displays the review of 2D chaotic maps. Section 3: Devoted to introducing the new 2D-BCM; the mathematical definition and the bifurcation diagram. The encryption algorithm is detailed in Section 4. Section 5: details the security analysis and results and Section 6: Gives a general conclusion.

3 Review of 2D chaotic maps

The 2D chaotic maps lead to 2D iterate xi + 1, yi + 1 from the previous xi and yi. Here, we will present some of the proposed 2D chaotic maps.

3.1 2D logistic map

The 2D logistic map (2D-LM) was suggested by Wu et all in [31] and used for image encryption. Security analysis results reflect its performance and efficacity. The 2D-LM is defined as

$${x}_{i+1}=r\left({3}_{y_i}+1\right){x}_i\left(1-{x}_i\right)$$
(1)
$$\kern0.5em {y}_{i+1}=r\left({3}_{x_{i+1}}+1\right){y}_i\left(1-{y}_i\right)$$
(2)

3.2 2D sine logistic modulation map

The 2D Sine Logistic Modulation Map (2D-SLMM) proposed by Hua et all in [13] is defined as follows:

$$xi+1=\mu \left[\mathit{\sin}\left(\pi yi\right)+3\right] xi\left(1- xi\right)$$
(3)
$$yi+1=\mu \left[\mathit{\sin}\left(\pi xi+1\right)+3\right] yi\left(1- yi\right)$$
(4)

4 New 2D Beta chaotic

Derived from the 1D Beta chaotic map proposed by Zahmoul et all in [24, 31] and defined as follow:

$${x}_{n+1}=k\times Beta\ \left( yn;x1,x2,p,q\right)$$
(5)

where

$$p={b}_1+{c}_1\times a\kern0.5em$$
(6)
$$q={b}_2+{c}_2\times a$$
(7)

b1,c1,b2 and c2 adequately chosen constants.

a: bifurcation parameter.

k: amplitude control parameter.

We created a new 2D Beta chaotic map. The 2D-BCM has more chaotic behavior and large bifurcation diagram than the 1D-BCM.

4.1 Mathematical definition

The mathematical definition of our map is as follows:

$${x}_n+1=k\times Beta\ \left({y}_{n+1};x1,x2,p,q\right)$$
(8)
$${y}_n+1=k\times Beta\ \left( xn;y1,y2,p,q\right)$$
(9)

where

$$p=b1+c1\times a\kern0.5em$$
(10)
$$q=b2+c2\times a\kern0.5em$$
(11)

b1,c1,b2 and c2 adequately chosen constants.

a: bifurcation parameter.k: amplitude control parameter.

4.2 Bifurcation diagram of the 2D-BCM

A bifurcation diagram illustrates a qualitative change in dynamics as a result of a simple change in one of parameters. The dotted line in the bifurcation diagram generally relates to the system’s chaotic behavior; the solid line, on the other hand, indicates that the system’s behavior has been adjusted to be periodic [16]. Figure 1 shows the different 2D Beta Chaotic maps. Our maps characterized by strong chaotic behavior, better pseudo random sequences, wide range of bifurcation parameters, and a large number of parameters.

Fig. 1
figure 1

Different shapes of the 2D-BCM

Full size image

As result, encryption process become more efficient and could stand up to most attacks.

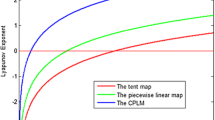
4.3 The Lyapunov exponent

Lyapunov exponent represents a quantitative measure of chaos. It is commonly used to determine whether the given system has a chaotic behavior or not.

The Lyapunov exponent of the Beta chaotic map is positive as indicated in ref. [27]. Our present work is based on the Beta map, thus the 2D Beta chaotic map is an extended version of 1D chaotic map. Thus we can conclude that the Lyapunov exponent of 2D Beta chaotic map has a large number of positive values.

5 Proposed encryption algorithm

  1. Step 1:

    Resizing the plain text image to a square dimension.

  2. Step 2:

    We employed the 2D-BCM with its parameters and initial values to create the encryption key. Weused the initial values ×0, y0, and k to generate a sufficiently long chaotic sequence, whose length equals to the number of pixels in the plaintext image P. The encryption key control the pseudo random sequences generated from the 2D-BCM. Xseq and Yseq be the 2D- BCM x and y coordinate sequences, respectively.

  3. Step 3:

    The rows and columns of the plaintext image are now shuffled using the Beta chaotic maps’ generated sequences. We sorted the Xseq and the Yseq in a matrix form, to obtain 2 matrices M1 and M2. Per- mute the plain text images pixels within columns, using the position of M1 elements. After the column permutation, we permute the resulting matrix using the M2 rows positions.

  4. Step 4:

    The substitution step is done, by first: dividing the resulting matrix of the permutation step into four equal-sized blocks B. After that, each 4*4 block B will be changed using the functions below:

    $${f}_N(d)=T(d) modG\kern1.25em$$
    (12)
    $$R(d)=T\left\lfloor \left(\sqrt{d}\right)\right\rfloor \mathrm{modG}\kern1.25em$$
    (13)
    $${f}_s(d)=T\left({d}^2\right) modG\kern0.5em$$
    (14)
    $${f}_D(d)=T(2d) modG$$
    (15)

    And the matrix function is given below:

    $$W=\left[\begin{array}{ccc}{f}_N\left({B}_{1,1}\right)& {f}_R\left({B}_{1,2}\right)&\ {f}_S\left({B}_{1,3}\right)\kern1.25em {f}_D\kern0.5em \left({B}_{1,4}\right)\\ {}{f}_R\left({B}_{2,1}\right)& {f}_S\left({B}_{2,2}\right)& {f}_D\left({B}_{2.3}\right)\kern1.5em {f}_N\left({B}_{2.4}\right)\\ {}{f}_N\left({B}_{3.1}\right)& {f}_D\left({B}_{3.2}\right)& \kern0.5em {f}_N\left({B}_{3.3}\right)\kern2em {f}_R\left({B}_{3.4}\right)\kern0.75em \\ {}{f}_D\left({B}_{4.1}\right)& {f}_N\left({B}_{4.2}\right)& {f}_R\left({B}_{4.3}\right)\kern1.75em {f}_S\left({B}_{4.4}\right)\end{array}\right]$$
    (16)

    Function T: is a truncation of a decimal to form an integer for every number of the resulting matrix W. G: represents the image type. For 8-bit gray images G = 256 and for the binary images G = 2.

    Here we got a new random integer matrix I. So, we can now determine the encrypted image C using the following equation:

    $$C=\left(P+I\right)\mathit{\operatorname{mod}}\ G\kern0.75em$$
    (17)

    And the decrypted image P by:

    $$P=\left(C-I\right)\mathit{\operatorname{mod}}\kern1.5em$$
    (18)
  5. Step 5:

    The last step in our algorithm is the diffusion stage. In this stage we aim to eliminate the redundancy in the statics and information contained in the original image in the ciphered one. It is done by changing each pixel in the original image over the finite field GF(28). Figure 2 illustrates the steps mentioned above, and Fig. 3 represents the flowchart of the hole process.

    Fig. 2
    figure 2

    Detailed Steps of the encryption algorithm

    Full size image
    Fig. 3
    figure 3

    Diagram of the encryption process

    Full size image

6 Experimentation and results

Noise and data loss can easily affect digital images through transmission over the network and computer storage, which is normally done by changing one or more bits.

Furthermore, an efficient encryption algorithm should be resistant to all known attacks and its performance should not be dependent on the original image or the encryption key. Our experiments were carried out using different images from the USC-SIPI Image Database as plaintext images and various security tests. A comparison is made with different published algorithms. The next paragraphs go over the findings.

6.1 Histogram analysis

Histogram bars for a plain image are uneven, indicating that some information is carried in the plain image [14]. Also, The randomness of pixel values is indicated by the flatness of histogram bars. Thus the encrypted image’s histogram bars should be flat in order to resist to differential attack. The histograms of the encrypted images are shown in Fig. 4, whereas the plain image ones are shown in Fig. 5. Evidently, the encrypted images can be considered random-like images and have no discernible characteristics.

Fig. 4
figure 4

Respectively from left to right: Encrypted images and their histograms Cameraman, Boat, Chemical plant, Airplane

Full size image
Fig. 5
figure 5

Respectively from left to right: original images and their histograms: Cameraman, Boat, Chemical plant, Airplane

Full size image

6.2 Information entropy

Information entropy can be used to show the random- ness of the cipher image. It can be calculated as follows:

$$H(S)=\sum \limits_{i=1}^{2^n-1}P\left({S}_i\right)\log \left(\frac{1}{P\left({S}_i\right)}\ \right)$$
(19)

Where

  • 2n: the total states of the information source Si,

  • P (Si): the probability of symbol Si.

The information entropy for the encrypted images using our method is presented in Table 1. Also, a comparison with algorithms in [12, 25, 31] is established in Table 2.

Table 1 Entropy average of our approach
Full size table
Table 2 Entropy average of our approach and algorithm in [12, 25, 31]
Full size table

Results prove that the entropy of the encrypted images using our algorithm is extremely near to the theoretical value 8. Our entropy average 7.99% is the closest to the expected one than [5, 12, 25, 31]. As a result, we can conclude that the randomness is achieved and our proposed method is strong against differential attack.

6.3 Sensitivity analysis

In the field of image encryption, sensitivity analysis are crucial metrics. They are often used to test the sensitivity of the plain image and the secret key. A few changes to any one of them results in a nonidentical

Cipher image in the efficient algorithm [8].

6.3.1 Key sensitivity analysis

Key sensitivity has a significant impact on the security of a cryptosystem. As a result, a single bit variation in the key should result in different ciphered images. As demonstrated in Figs. 6 and 7, the suggested approach demonstrates the encryption key’s high sensitivity. It also proves the key sensitivity in consideration of encryption and decryption, where K1,K2 and K3 re different by only one bit.

Fig. 6
figure 6

Key sensitivity results: Encrypted image C2 = Encryption(I,K1),Encrypted image C3 = Encryption(I,K2); Encrypted image difference C3 C2; Decrypted image DI=Decryption(C2,K1); decrypted image D2 = Dec(C2,K2); decrypted image D3 = Decryption(C2,K3); decrypted image difference D3-D2(K1 and K2 are different only in one bit; K2 and K3 are also different only in one bit; and K1 K3)

Full size image
Fig. 7
figure 7

Number of pixel change rate (NPCR) in the plain and encrypted images of Cameraman

Full size image

6.3.2 Plain image sensitivity

The sensitivity test is done by changing the value of one pixel in the original image, after that comparing the encrypted images of the original image with the en crypted images of the modified one. The sensitivity to the plain image will be measured using two metrics. The first one is the Number of Pixels Change rate (NPCR) and the second one is the unified average changing Intensity (UACI).NPCR and UACI are calculated as follows:

$$NPCR\kern1.25em =\kern0.5em \frac{\sum_{i,j}D\left(i,j\right)}{M\times N}\times 100\%\kern0.75em$$
(20)
$$UACI=\frac{1}{M\times N}\left[{\sum}_{i,j}\frac{\mid {C}_1\left(i,j\right)-{C}_2\left(i,j\right)\mid }{255}\right]\times 100\%\kern0.5em$$
(21)

Where

$$D\left(i,j\right)=\left\{\begin{array}{c}0\kern3em if\kern0.75em {C}_1\left(i,j\right)={C}_2\left(i,j\right)\\ {}\kern0.75em 1\kern3em if\kern0.5em {C}_1\left(i,j\right)\ne {C}_2\left(i,j\right)\kern1em \end{array}\right.$$
(22)

M and N: the height and the width of the original and the cipher images, C1 and C2 are the encrypted images before and after one pixel is modified from the original image, respectively. Tables 3 and 4 rep- resent the NPCR and UACI of the tested images by applying our algorithm and the suggested in literature [11, 19, 25, 28, 31]. Our NPCR and UACI average is about 99.6236%,33.49337%, respectively. For comparison, among all the encryption schemes as listed in Tables 3 and 4, our algorithm achieves the expected average of NPCR and UACI (99.6094%, 33.4635%) . Thus, we can conclude that the proposed algorithm is very sensitive to changes in the plain image and that even small changes in the plain image result in completely different cipher images. As a result, the proposed technique can overcome differential attacks.

Table 3 NPCR results of our approach and other approaches
Full size table
Table 4 UACI results of our approach and other approaches
Full size table

6.4 The mean square error analysis

The Mean Square Error (MSE) is a metric that de- scribes the difference between the original image and the encrypted one. Pixels are represented by numbers between 0 and 255.

$$MSE=\frac{1}{MN}\sum \limits_{i=1}^N\sum \limits_{j=1}^M\left[C\left(i,j\right)-{C}^{\prime}\left(i,j\right)\right]$$
(23)

  • M, N: the size of the original or the ciphered image.

  • C(i, j): original image pixel.

  • C′(i, j): encrypted image pixel

MSE should be as high as possible while encrypting images. A higher MSE value between the original and encrypted image indicates more attack resistance Table 5 shows that the MSE values of our method is better than other in [25, 31].

Table 5 MSE values of our method and those in [25, 31]
Full size table

6.5 Peak signal to noise ratio analysis

Peak Signal to Noise Ratio (PSNR) define the ratio of the noise and the highest achievable power that influences image representation. It is mostly used as a metric for image reconstruction quality. PSNR defined by the following formula:

$$PSNR=10{\log}_{10}\left(\frac{Ma{x}_I^2}{MSE}\right)\kern0.75em$$
(24)

where:

MaxI: the highest pixel value of the image I.

A high PSNR value indicates good image quality. To ensure the efficiency of the suggested method, the difference between two images PSNR should be as little as possible. Table 6 shows the difference in PSNR values between the original and encrypted images. Our method yields a lower PSNR than the one calculated in [25, 31]. We conclude that the proposed approach is more resistant to statistical attacks.

Table 6 PSNR of encrypted image using our approach and those in [25, 31]
Full size table

6.6 Key space analysis

It is well noun that a good encryption scheme is characterized by a large key space which enhance its immunity to several attacks.

Our encryption key composed of different parameters of the two coordinate x and y, about 512 bit is sufficient enough to overcome the brute force attacks.

Our encryption key is comparable and even better than other state of the art methods. Thus, the key has high immunity against brute force attacks.

7 Real implementation and future work

All Experimental tests and implementations were realized under the same conditions on the same machine, PC HP; an Intel(R) Core-i7–2.5GHz processor, RAM: 6 Go.

In the future, we hope to take the new 2D-BCM a step further by incorporating it into steganography, watermarking also in other cryptography techniques.

8 Conclusion

In order to improve the results achieved by the one dimensional Beta Chaotic map, we created a new 2 dimensional beta chaotic map. The bifurcation diagram and the sensitivity to initial conditions of our new 2D- BCM indicate that our map have a good chaotic behavior. The 2D-BCM is then used in an image encryption scheme to better prove its efficiency.

The suggested image encryption method adopts the permutation-substitution network structure and a diffusion step. Results obtained for information entropy, histogram analysis, sensitivity analysis, MSE and PSNR prove that the encryption algorithm has successfully been able to prevent various existing cryptography attacks and cryptanalysis techniques.