A chaotic framework and its application in image encryption

Abstract

A novel image encryption framework is proposed in this article. A new chaotic map and a pseudorandom bit generator are proposed. Apart from this, a novel image encryption system is designed based on the proposed map and the proposed pseudorandom bit generator. These three are the major contributions of this work that makes a complete cryptosystem. The proposed new chaotic map is proposed which will be known as the ‘RCM map’ and its chaotic property is studied based on Devaney’s theory. The proposed pseudorandom bit generator is tested using the NIST test suite. The proposed method is simple to implement and does not involve any highly complex operations. Moreover, the proposed method is completely lossless, and therefore cent percent of data can be recovered from the encrypted image. The decryption process is also simple to implement i.e. just reverse of the encryption procedure. A scrambling algorithm is also proposed to further enhance the security of the overall system. The simulation, detailed analysis, and comparative studies of the proposed overall image encryption framework will help to understand the strengths and weaknesses of it. The experimental results are very promising and show the prospects of chaos theory and its usage in the field of data security.

1 Introduction

The theory of chaos is an important and interesting field of study for a long time. Various applications of chaotic systems can be observed in different domains like physics, mathematics, computer science, etc. [4, 5, 10, 35]. The research in the field of chaos is evolving since the seventieth century and gradually progressing and its advantages are exploited by various domains. The field of data security is no exception and is continuously trying to exploit the advantages of chaos theory in various ways. In recent years, the field of image security is a very attractive topic of interest and becomes a hotspot in the study of data security. A huge number of images are transmitted every second over various networks. The advent of various social media platforms brings a sudden growth in the transmission of images and other multimedia content over the internet. Images and other multimedia data may contain various sensitive and personal information that needs to be preserved and communicated confidentially [45]. Data can be preserved in both online and offline modes. Online storages are available nowadays at a very cheap rate which increases its popularity and many people can afford them [8, 9]. Therefore, in another sense, the advancements and growth in science and technology increase the chance of data leakage from various sources. Therefore, data security is an active and prominent challenge and is to be defeated. This is the main reason behind the continuous effort of the researchers who are engaged to solve this problem, to secure the data communication process, and to make the data safe at the storage locations. It is necessary to protect privacy and confidential data because sometimes, unintentional data leakage can be very costly and can reveal various precious information about a person or an organization. So, data confidentiality and integrity must be maintained to ensure reliable and secure communication.

Steganography is considered as one of the most important topics that are to be discussed in the context of the secured data communication. Typically, image-based steganography approaches conceal an image into another image or in more than one image. The image or the set of images in which an actual confidential file is made hidden is typically not a secret file. Sometimes, steganography can be associated with the encryption process to make the overall system stronger. The encrypted digital image is kept inside of another image that can be shared publicly. Steganography is in active use for many centuries and it covers various techniques that provide a protective cover or a safeguard for the original messages. Two payload distribution strategies are developed for the steganographic purposes in [34]. These two approaches can effectively distribute the original content into multiple images and these approaches are based on texture-based features. Both approaches can be combined applied for image steganographic purposes. Experimental results prove that the performance of this approach can outperform some of the standard approaches. A convolutional neural network-based operation-chain detection mechanism is proposed in [33]. In this work, a novel framework is proposed to detect various tampering that has been performed on an image. This work is helpful in forensic investigations and can detect two image operations without knowing anything about the operations beforehand. This work proves to be efficient in detecting various operations automatically and also capable to detect the order to some extent. A comprehensive detail about steganography and its recent advancements can be found in [1].

Various methods and frameworks are available in the literature that can be used to secure images and videos [11, 12, 38, 44, 46, 49, 63]. Several traditional methods and their variants like, DES [13], AES [16], IDEA [32] etc. and other modern methods like chaotic system based techniques [11, 51, 63, 75], DNA computing based security methods [14, 19, 49, 56] and many more advanced methods can be found in literature. Chaotic systems are frequently used in various applications including cryptography. A large number of methods are available in the literature that exploits different properties of chaotic systems like ergodicity, sensitivity to the initial conditions, pseudorandom behavior, mixing features, etc. [17]. Some chaotic properties and their mapping in the cryptography are given in Table 1. Some of the recent developments in the chaotic cryptosystems are discussed here. A chaos-based image encryption method is presented in [2] where a larger keyspace can be obtained with a single round of encryption. The correlation among the pixels is removed with the help of the chaotic sequences. This algorithm is tested by performing various experiments and proves the strength of various attacks. Different properties make this method suitable for various real-life applications. An integrated chaotic system based image encryption system is proposed in [30] where a complex chaotic map is generated and some of the existing problems are overcome. The efficiency of the chaotic map is proved using an image encryption system which is proved to have a large keyspace and robust against various attacks. A discrete chaotic map called 2D-TFCDM is proposed in [36]. This map is based on the discrete fractional calculus. Chaotic properties are numerically analyzed. Elliptic curves and the chaos are applied for the image encryption purpose. Chaotic map and the bitplane decomposition method are applied simultaneously in [41]. A one-dimensional chaotic map is used for the diffusion process and the beta map is used to scramble the bit planes. The key space is large enough and the execution time of this method is also low. A piecewise linear chaotic map-based image encryption method is proposed in [60]. A couple of binary sequences are generated using the bitplane decomposition method and then the diffusion procedure is applied in such a way so that the sequences become sensitive to a small change in the actual image. The piecewise linear chaotic map is used to control the confusion process. This algorithm is tested using many standard validation parameters and found to be robust against various types of attacks. A symmetric key image encryption system is developed in [6] which is based on the mixed chaotic map. A one-dimensional chaotic map is mixed up with a distinctive chaotic map to use in the image encryption process. Various experiments prove that the proposed method is highly resilient against various types of attacks and highly complex to provide better security. A multi-image encryption method based on piecewise linear chaotic map is proposed in [69]. This method can encrypt more than one image simultaneously. The proposed algorithm outperforms some of the established methods in terms of various standard parameters. A color image encryption method is proposed in [25]. This method is based on the well-known logistic map and the double random-phase encoding. The logistic map is used for the diffusion purpose and the double random-phase encoding system is used to combine all scrambled images into one encrypted image. Different experiments prove the efficiency of this method. An image encryption system is proposed in [67] which is based on the lifting scheme and chaotic maps. This method overcomes some security problems which are associated with the permutation-substitution models. At first, the input image divided into high and low-frequency components, and then chaos theory is used to disturb these components. After that, the lifting scheme is used for the image encryption purpose. Experiments show the superiority of this method compared to some other methods. An image encryption method based on a one-dimensional sine powered chaotic system is proposed in [39]. A one-dimensional sine powered chaotic system is used to enhance security by performing the sequence addition. This method is tested and compared with some other methods and its performance is found to be satisfactory. A novel image encryption strategy is proposed in [43] based on chaos theory. In this work, the expand-shrink operation is incorporated in the chaotic environment for confusion and diffusion purposes. The confusion and the diffusion mechanism are applied at the pixel level. The actual image is expanded depending on the biplanes. The Hilbert scan approach is adopted to implement the confusion and diffusion approach. The experimental outcomes show that this approach performs well compared to some of the existing approaches. An another novel image encryption approach is proposed in [18]. This approach involves fractional Fourier transform and DNA sequence operation along with the chaotic environment. A chaotic Lorenz map is used to generate the random phase masks. This approach is proved to be efficient enough and proved to be resilient against different types of attacks. Experimental results show that this approach is reliable enough for real-life digital image encryptions. A chaos-based satellite image encryption system is proposed in [7]. This approach incorporates Fridrich’s scheme to encrypt multispectral images. The experimental outcome show that this approach can achieve a good level of security with lesser hardware requirements and can get a throughput of120mbit/s. Some of the recent chaotic environment based image encryption approaches are discussed in detail in [22, 29, 40]. A data security approach is designed in [28] for the cloud environment that is based on hierarchal identity. This approach is useful to protect the cloud data from unauthorized persons and also helps in securing the cloud data from getting tampered with. This approach ensures the security of the cloud data storage and also takes care of the delivery of the data to legitimate users. A novel image encryption mechanism is proposed in [71] to provide security to the railway cloud services. This approach is based on the combination of the S-box coupled map lattice and chaotic environment. This approach overcomes some of the drawbacks of some of the previous approaches and experimental results prove the efficiency of this combined approach. A secured data communication and storage framework is proposed in [74]. This proposes a novel attribute-based image encryption method to secure the contents of the cloud as well as helping to maintain data integrity throughout the communication process. Experimental results provide proof of the effectiveness and efficiency of the proposed approach. A data security and encryption scheme is designed in [62] that is specifically designed to provide security to the data in the DaaS or database as a service cloud model. This work uses the DSP re-encryption method to design the new encryption framework besides developing an efficient access control mechanism. Experiments prove the efficiency and correctness of this approach. Elliptic-curve cryptography-based authentication mechanism is proposed in [52]. This approach is primarily designed for IoT based networks. Promela model and SPIN tool are used to validate the security and authentication approach.

Table 1 Mapping of some chaotic properties and their corresponding cryptographic properties

In this article, a new chaotic map is proposed (which will be known as the ‘RCM map’ and in the rest of the article, the proposed map is referred to with this name) along with a pseudorandom bit generation method which is based on the proposed chaotic map. The proposed chaotic map and the pseudorandom bit generator is used to construct an image encryption method. The proposed new image encryption method is robust, resilient against different types of attacks, and useful for both grayscale and color images. This approach is completely independent of any external image and the core part of the proposed image encryption method is designed using the proposed RCM chaotic map and the pseudorandom bit generator. The proposed algorithm involves a dimension transformation phase that generates a color encrypted image if the input image is in grayscale mode. If the input image has more than one channel (e.g. color images) then multiple encrypted images will be generated. The number of encrypted images is equivalent to the number of channels present in the encrypted image. The correlation of the pixels is disturbed using a new scrambling algorithm which is proposed in this work, however, the proposed scrambling method is flexible enough and can be easily modified and any permutation of the chaotic sequence can be used for a certain channel (please refer Section 4 for detailed description). The decryption method is completely lossless, easy to implement, and can be easily executed by performing the exactly reverse operations of the encryption method. The efficiency and the effectiveness of the proposed image encryption method are established via simulation and different experiments in both visual and quantitative manner.

This article contributes to the existing literature in three different ways. First of all, a new chaotic map called RCM is proposed in this work. The second one is, A pseudorandom bit generator is proposed that is based on the proposed RCM map. And the last one is, a novel image encryption system is designed based on the proposed RCM map and the proposed pseudorandom bit generator. These three are the major contributions of this work that makes a complete cryptosystem. Each individual contribution is analyzed separately and their advantages are depicted. For example, the proposed RCM map is analyzed in Section 2. Similarly, the proposed pseudorandom bit generator is analyzed in Section 3. The proposed encryption scheme is also analyzed and compared in Section 5. Therefore, the superiority of the proposed approach is established individually for three different contributions. The large keyspace makes the proposed approach resilient against exhaustive search-based attacks. Moreover, the experimental results show that the proposed approach can withstand different possible attacks that make it secured and acceptable for different real-life applications. Theoretical and experimental analysis build the foundation of the practical applicability of the proposed cryptosystem.

1.1 Motivation

No method can be claimed as a cent percent secured against various attacks. In most of the works, standard chaotic maps like logistics, tent, etc. are used for encryption purposes. Some traditional approaches like DES, AES are suitable for independent and identically distributed data. Typically, the distribution of multimedia data is not independent and identically distributed. Hence, the traditional approaches are not always suitable for multimedia data [5]. Although the strength of these approaches is already proved on different types of data but, the non-independent and non-identical nature of the multimedia data can often cause some serious problems [5]. It is well-known that AES should not be used in a block-wise fashion, but, the effect of AES in ECB mode on a digital image is not satisfactory at all and can be visualized in [4].

With the ever-increasing need for image communications, it is required to design sophisticated image encryption schemes to make the image communication system efficient. It is always challenging to design Chaotic systems that possess some properties like ergodicity, sensitivity to the initial conditions, pseudorandom behavior, mixing features, etc. that are lucrative from the perspective of the cryptosystem because these features can significantly increase the security of the overall encryption mechanism. Therefore, the main motivation of this proposed work is to design a new resilient and reliable cryptosystem for the images because many traditional data security approaches are not suitable. Apart from this, an effort is paid to design a novel chaotic map and a pseudorandom bit generator that can support the proposed image encryption system. To enhance the security of the proposed approach image encryption system, a scrambling algorithm is also proposed and incorporated in the image encryption system. So, the proposed image encryption system is beneficial for real-life image communications. The benefits and the performance of the different components of the proposed framework are tested and discussed elaboratively in respective sections.

The remainder of this article is organized as follows: Section 2 describes the proposed RCM chaotic map. Section 3 illustrates the proposed pseudorandom bit generation method. Section 4 describes the proposed image encryption method which is based on the proposed RCM map and the proposed pseudorandom bit generation method. Section 5 shows the results of the simulation and a detailed performance analysis along with the security analysis of the proposed image encryption method can be found in Section 6. Section 7 concludes the article.

2 The proposed new chaotic map

The proposed chaotic map is defined in Eq. 1. The proposed map will be known as the ‘RCM’ chaotic map and in the remaining article, this map will be referred to by this name.

$$ {s}_i=\psi \sin \left({e}^{-{s}_{i-1}}\times \left(1-{s}_{i-1}^3\right)\right) $$

(1)

Here, s₀ ∈ [0, 1] is the initial value or the seed and ψ ∈ [1, 4] is the control parameter or the bifurcation parameter. The proof of the chaotic nature of the above equation can be done using the definition given by the Devaney [54] and in the similar way as given in [68]. The definition of Devaney is given in definition 1 and the definition of the topological mixing map is given in the definition 2 [20].

Definition 1:

Assume S is a set (metric space) and f : S → S is the continuous transformation of the metric space S. fcan be called chaotic if it satisfies the following criteria:

• i. f should be sensitive and have a high dependency on the initial conditions i.e. a small change in the initial condition results in a huge change in the output. Let us assume a constant α > 0 which is known as the sensitivity constant. Now, for every $\hat{s}\in S$and for every open interval I about $\hat{s}$, there is some $\hat{i}\in I$ and p > 0 such that, $\left|{f}^p\left(\hat{s}\right)-{f}^p\left(\hat{i}\right)\right|>\alpha$.

• ii. f should be topologically transitive in nature. A dynamical system (S, f) can be called the topological transitive if for every non-empty pair (x, y) ∈ S, there must exist a non-negative integer a such that f^a(x) ∩ y ≠ ϕ.

• iii. Periodic points of f should be dense in S. Mathematically, every point that belongs to the attractor should be arbitrarily close to some particular point that belongs to a periodic orbit. Theoretically, if someone chose a point and a distance value σ > 0, there must be a periodic orbit, irrespective of the small value of σ, from the chosen point.

Definition 2:

A continuous map f : S → S can be called as the topologically mixing map if for every non-empty subset (u, v) ∈ S, there must exist a non-negative integer K such that f^k(u) ∩ v ≠ ϕ where k > K.

Proposition 1:

If a map is a topologically mixing map then it must be a topologically transitive map.

• Proof. Expansion maps of S¹ are inherently topologically mixing maps.

Proposition 2:

If an orbit is dense then it implies the transitivity property.

• Proof. Every open subinterval can be visited by a dense orbit.

Proposition 3:

If the space has more than one points then, every topologically mixing map is dependent on and sensitive to the initial conditions.

• Proof. Assume that f : S → Sis a topologically mixing map and |S| > 1. Now consider two separate points ${\hat{s}}_1,{\hat{s}}_2\in S$ and a set $\omega =\frac{1}{4}d\left({\hat{s}}_1,{\hat{s}}_2\right)>0$. If k ≫ K then, for every object $O\left(\hat{s},\varepsilon \right)\subseteq S$, ${f}^k\left(O\left(\hat{s},\varepsilon \right)\right)\cap O\left({\hat{s}}_1,\omega \right)\ne \phi$ and similarly ${f}^k\left(O\left(\hat{s},\varepsilon \right)\right)\cap O\left({\hat{s}}_2,\omega \right)\ne \phi$. Therefore, there exists ${\hat{t}}_1,{\hat{t}}_2\in O\left(\hat{s},\varepsilon \right)$ and ${f}^k\left({\hat{t}}_i\right)\in O\left({\hat{s}}_i,\omega \right)$. Therefore, the following inequality can be written: $d\left({f}^k\left({\hat{t}}_1\right),{f}^k\left({\hat{t}}_2\right)\right)\ge d\left({\hat{s}}_1,{\hat{s}}_2\right)-d\left({\hat{s}}_1,{f}^k\left({\hat{t}}_1\right)\right)-d\left({\hat{s}}_2,{f}^k\left({\hat{t}}_2\right)\right)>4\omega -\omega -\omega =2\omega$. So, either $d\left({f}^k\left({\hat{t}}_1\right),{f}^k\left(\hat{s}\right)\right)>\omega$ or $d\left({f}^k\left({\hat{t}}_2\right),{f}^k\left(\hat{s}\right)\right)>\omega$.

2.1 Analysis of the proposed new chaotic map

In this section, the dynamics of the proposed chaotic map along with some other properties are discussed. The response of the chaotic map for 5000 iterations and the bifurcation diagram is given in Figs. 1 and 2 respectively.

Fig. 1

Response of the proposed RCM chaotic map for 5000 iterations

Fig. 2

Bifurcation diagram of the proposed RCM map

In Fig. 1, the response value is plotted on the y-axis and the number of iterations is plotted on the x-axis. From Fig. 1, it can be observed that the response values are plotted for 5000 iterations and the range of the response values in the y axis is from −4 to +4. This figure helps to understand the fluctuations and the randomness of the proposed RCM chaotic map.

In Fig. 2, the value of the state parameter s is plotted on the y-axis and the value of the controlling parameter or the bifurcation parameter is plotted in the x-axis.

2.2 Lyapunov exponent

Lyapunov exponent or the Lyapunov characteristic exponent is a property of the dynamical systems. This parameter explains the divergence rate of the adjacent trajectories [50]. This property is helpful to understand the chaotic behavior of a chaotic map. The larger value of this parameter shows the more chaotic behavior of the corresponding chaotic map. The Lyapunov exponent λ can be calculated using Eq. 2.

$$ \lambda =\underset{N\to +\infty }{\lim}\frac{1}{S}\sum \limits_{p=1}^S\log \left|\frac{dx_{p+1}}{dx_p}\right| $$

(2)

The Lyapunov exponent of the proposed chaotic map is given in Fig. 3. A comparative study is presented in Table 2 where the Lyapunov exponent of the proposed chaotic map is compared with some other chaotic maps. From this table, it is clear that the value of the Lyapunov exponent for the proposed RCM map is higher than the other chaotic maps including the well-known logistic map.

Fig. 3

Lyapunov exponents for proposed RCM map

Table 2 Comparison of the Lyapunov exponents

In Fig. 3, the value of the Lyapunov exponent or the Lyapunov characteristic exponent is plotted on the y-axis and the value of the control parameter or the bifurcation parameter is plotted on the x-axis. Figure 3 helps to visualize the Lyapunov exponent.

2.3 System complexity analysis

Approximate entropy is one of the important parameters that are useful to understand the complexity of the system. It is helpful for quantitative analysis of the system complexity [42].

Larger approximate entropy value indicates higher complexity of the system. Let us assume that D is the number of data points {d(i)} taken from vector sequences v(1) to v(D − m + 1) and it is defined in Eq. 3.

$$ v(i)=\left[d(i),\dots d\left(i+m-1\right)\right] $$

(3)

Here, m represents the dimension of the vector.

The distance between two vectors v(i) and v(j) dist(v(i), v(j)) can be calculated using Eq. 4.

$$ dist\left(v(i),v(j)\right)=\underset{t=0\sim m-1}{\max}\left|d\left(i+t\right)-d\left(j+t\right)\right| $$

(4)

Now, let us assume a threshold value th, (th > 0), ${\eta}_i^m$ can be calculated using Eq. 5.

$$ {\eta}_i^m(th)=\frac{The\kern0.17em count\kern0.17em of\kern0.17em dist\left(v(i),v(j)\right)}{\left(M-m+1\right)} $$

(5)

From Eq. 5, the value of the ${\eta}_i^m$ can be obtained which can be further used to compute the value of Φ^m(th). This value can be computed using Eq. 6.

$$ {\Phi}^m(th)=\frac{1}{D-m+1}\sum \limits_{i=1}^{D-m+1}{\log}_e{\eta}_i^m(th) $$

(6)

The approximate entropy AE can be obtained using Eq. 7.

$$ AE\left(m, th,D\right)={\Phi}^m(th)-{\Phi}^{m+1}(th) $$

(7)

A comparative study is presented in Table 3 where the approximate entropy of the proposed chaotic map is compared with some of the chaotic maps. From this table, it is clear that the value of the approximate entropy for the proposed RCM map is higher than the other chaotic maps including the well-known logistic map.

Table 3 Comparison of the approximate entropy

The autocorrelation of the proposed RCM map is given in Fig. 4. The orbits of the proposed chaotic maps can be observed in Fig. 5.

Fig. 4

Auto correlation of the proposed RCM map

Fig. 5

Orbits of the proposed RCM map (a) s(i) vs. s(i + 1), (b) s(i) vs. s(i + 3)

3 The proposed new pseudorandom bit generator

The proposed chaotic map is used to generate a pseudorandom bit sequence and it is described in this section. First of all, two chaotic sequences of equal length n are generated using the proposed chaotic map with two different seed values using Eqs. 8 and 9. Here s₀ and t₀ are the initial seed values and ψ and ψ^′ are the controlling or the bifurcation parameters of the system. The seed values that is s₀ and t₀should not be same i.e. s₀ ≠ t₀ and (s₀, t₀ ∈ [0, 1]).

In Fig. 4, the autocorrelation values are plotted on the y-axis corresponding to the time values that are plotted on the x-axis. This plot helps in visualizing the autocorrelation of the proposed RCM map.

Figure 5 depicts the orbits of the proposed RCM map i.e. the plot of the different states. It can be shown that Fig. 5a, 5b visually illustrate the state movements s(i) vs. s(i + 1), and s(i) vs. s(i + 3) respectively.

$$ {s}_i=\psi \sin \left({e}^{-{s}_{i-1}}\times \left(1-{s}_{i-1}^3\right)\right) $$

(8)

$$ {t}_i={\psi}^{\prime}\sin \left({e}^{-{t}_{i-1}}\times \left(1-{t}_{i-1}^3\right)\right) $$

(9)

In this specific experiment the seed values are considered as s₀ = 0.5 and t₀ = 0.8. Experiments can also be performed by taking any other seed values provided s₀ ≠ t₀ condition is satisfied. One thing should be noted that the system parameter or the controlling parameter should be the same for both equations i.e. ψ = ψ^′. It is necessary to make both the map surjective in a specific interval. Moreover, the value of the controlling parameter should be large enough, preferably near 4.0. The basic reason behind this concept is to obtain a significantly large interval for the initial seed values (i.e. s₀ and t₀).

Elements of each sequence must be between 0 and 1. Now, each value is converted into the IEEE 754 double-precision binary representation. Therefore, for each member of a particular sequence, there are corresponding 64 bits are generated [21] as shown in Fig. 6 where, the first bit or the MSB is the sign bit, next 11 bits are exponent and rest of the bits i.e. last 52 bits are mantissa. Now, these 64 bits are divided into 8 groups with 8 bits each.

Fig. 6

IEEE 754 double precision floating point number representation format

Now for each group, 8 bits are represented by a single bit. To get a single bit representative GR_b for the group, the following method is proposed. At first, the number of ones and number of zeros is counted to perform a majority voting i.e. if the number of ones is greater than the number of zeros then that particular group will be represented by 1 otherwise if the number of zeros is greater than the number of ones then that particular group will be represented by 0. For example, if a group is consisting of the following 8 bits i.e., then this group will be represented by 0 because of the majority of the number of zeros. Now, if a particular group contains an equal number of ones and zeros then, for that group, the representative bit GR_bis computed using Eq. 10 where GR_i represents the i^th bit of a group. For example, if a group is consisting of the following 8 bits i.e. 10110001the representative bit GR_b for this group will be 0. Now, by following the above procedures, 64 bits are reduced to 8 bits.

$$ {GR}_b= remainder\left(\left|\sum \limits_{i=1}^4{GR}_{2i}-\sum \limits_{i=0}^3{GR}_{2i+1}\right|,2\right) $$

(10)

The major problem which is associated with the aforementioned method is that there is a possibility to get a chain of the same bits to represent multiple groups. In the worst case, all representative 8 bits can be 0 or 1. To eliminate this possibility, one method is proposed that takes care of the consecutive three same bits i.e. the proposed methods eliminate the possibility of being similar consecutive three bits. Now to understand this method, let us assume three consecutive bits b₋₂, b₋₁ and b. These three bits can have 8 possibilities but the third bit i.e. b is going to be determined on the basis of the previous two bits. It can be easily understood from Fig. 7a and if these three bits are going to be the same then, Y is the bit which is used to replace the third bit i.e. b. Figure 7b is the elaborated version of Fig. 7a that shows all possible 8 combinations and the required value of Y. From Fig. 7, it is clear that if b₋₂ and b₋₁ become same then, there is no option except to place the complementary bit of b₋₂ and b₋₁ at the third position i.e. b. Otherwise, the value of b can be kept as it is. Now, to achieve this, Fig. 7b is used to simplify the truth table using the Karnaugh map [27]. The simplification process can be visualized in Fig. 8. From this simplification, the logical expression for Ycan be obtained and it is given in Eq. 11. Here, · and + represents the standard Boolean AND and OR operators respectively and $\overline{x}$ represents the complement of x (i.e. the Boolean NOT operation).

$$ {\displaystyle \begin{array}{l}Y={\overline{b}}_{-2}\cdotp {\overline{b}}_{-1}+{\overline{b}}_{-2}\cdotp b+{\overline{b}}_{-1}\cdotp b\\ {}\kern0.6em ={\overline{b}}_{-2}\cdotp \left({\overline{b}}_{-1}+b\right)+{\overline{b}}_{-1}\cdotp b\end{array}} $$

(11)

Fig. 7

Possible combinations of the consecutive three-bit sequence a dependency of the third bit on the previous two bits, b elaborated table that shows the possible output value for all combinations of the consecutive three bits so that, no consecutive three bits can have the same value

Fig. 8

Karnaugh map simplification of the truth table which is given in Fig. 7b

Now, each element of both the sequences can be represented by 8 bits. In each sequence of length n, there are n ∗ 8 bits are present. Therefore, if a pseudorandom bit sequence of length n is to be generated then, the mapping ratio i.e. the number of bits which is to be mapped into a single bit in the pseudorandom bit sequence will be $mapRatio=\frac{number\kern0.17em of\kern0.17em bits\kern0.17em in\;a\; sequence}{n}$ which is nothing but 8 in this case. Now, each sequence is divided into k number of groups with 16 elements in each group (because here, 2 ∗ mapRatio = 16). Now, perform XOR operation between the first 8 bits of the first sequence and the last 8 bits of the second sequence. Similarly, perform XOR operation between the first 8 bits of the second sequence and the last 8 bits of the first sequence. It is explained in Fig. 9 where, ${b}_i^1$ and ${b}_i^2$ are the i^th bit of the obtained groups from the first and second sequence respectively.

Fig. 9

Illustration of the XOR operation

After this operation, two-bit sequences of length 8 bits can be obtained. Now, to convert each of them into a single bit, just perform an XOR operation with the consecutive bits as given in Eq. 12. Here, rb^k is the representative bit of the k^th sequence and ${x}_j^k$ is the j^th bit of the k^th sequence. m represents the total number of bits present and for this experiment this value is 8.

$$ {rb}^k=\left(\left(\left(\left(\left({x}_{m-1}^k\oplus {x}_{m-2}^k\right)\oplus {x}_{m-3}^k\right)\oplus {x}_{m-4}^k\right)\oplus ..\dots \dots \oplus {x}_1^k\right)\oplus {x}_0^k\right) $$

(12)

The above procedure generates a pseudorandom bit sequence of length n. Now, to test the proposed pseudorandom bit generator, the well-known National Institute of Standards and Technology (NIST) statistical test suit is used [47]. As per the recommendation given in [48] 15 subtests are performed with the pseudorandom bit sequences of the length 1,000,000. The decisions are at the 1% level i.e. if the calculated P − value < 0.01 the sequence can be considered as non-random otherwise random. The result of the tests is given in Table 4. From the obtained results, it is clear that the proposed pseudorandom bit generator passes all the tests and therefore the proposed method is suitable enough for cryptographic applications.

Table 4 NIST test results for the proposed pseudorandom bit generator

4 The proposed image encryption method

In this section, one image encryption method is proposed which is based on the proposed RCM map and the proposed pseudorandom bit generator. The proposed method is tested on different types of images including grayscale, biomedical, biometric, color, and some other standard images. The proposed encryption algorithm is efficient enough to encrypt different types of images and the proposed method has no dependency on any extra image. The efficiency of the proposed method is illustrated in Section 6 by both visual and quantitative analysis. The encryption process begins with the transformation of the pixel dimension. Let us assume that an image I of size M × N is being encrypted and a pseudorandom bit sequence prbs of length M × N × 8 is generated using the proposed pseudorandom bit generator and with the initial parameters (s₀, t₀, ψ₀). At first, every pixel of the image is converted into 8 bits binary representation. Now take the binary representation of two consecutive pixels I(i, j) and I(i, j + 1)where 1 ≤ i ≤ M, 1 ≤ j ≤ N and reverse each of them individually. Now, divide each sequence into two halves where each of them consists of a nibble. Find the positions of the ones in the first half of the first sequence and the positions of the zeros in the second half of the first sequence considering LSB as the 0^th position. Again, find the positions of the ones in the second half of the second sequence and the positions of the zeros in the first half of the second sequence considering LSB as the 0^th position. The searching for both cases should begin from the LSB. The searched indexes are simply added by multiplying with the decimal positional weights. Therefore, in this method, a nibble can generate a maximum of a four-digit decimal number dVal using Eq. 13 where n is the count of either 0 or 1 as per the above description and c_k is the k^th counting value from LSB.

$$ dVal=\sum \limits_{k=1}^n{c}_k\cdotp {10}^{k-1} $$

(13)

Now take the first 16 bits from the pseudorandom bit sequence and divide them into four blocks each consisting a nibble. Find the positions of the zeros in the first half of the first nibble and the positions of the ones in the second nibble. Again, find the positions of the ones in the third nibble and the positions of the zeros in the fourth nibble considering LSB as the 0^th position for each nibble. The searched indexes for every nibble are simply added separately by multiplying with the decimal positional weights using Eq. 13. The corresponding decimal value for every nibble of the pseudorandom bit sequence is to be added with the obtained decimal value of the corresponding nibbles of the pixels. Now every digit of the obtained sum is converted into binary. One important point that can be observed from this discussion is the obtained sum can be a maximum of 8642 (i.e. 4321*2). So, a maximum of 12 bits is sufficient to store the binary form of each digit sequentially. The 12 bits are divided in such a way so that the first digit from the left i.e. Most Significant Digit (MSD) gets 4 bits, the next two digits get 3 bits each and the last digit i.e. Least Significant Digit (LSD) gets 2 bits. The bit reservation pattern is shown in Fig. 10.

Fig. 10

Bit reservation pattern

In this figure, the MSD indicates the first four bits i.e. (bit₁₂, bit₁₁, bit₁₀, bit₉), MSD-1 indicates the next three bits i.e. (bit₈, bit₇, bit₆), MSD-2 indicates the next three bits i.e. (bit₅, bit₄, bit₃), and LSD denotes the last three bits MSD-2 indicates the last two bits i.e. (bit₂, bit₁).

In this way, four decimal values are generated from two pixels which in turn generate 48 bits (i.e. 4*12 bits). Now, these 48 bits and 16 bits of the chaotic sequence are taken to perform the XOR operation. Chaotic 16 bits are replicated to make it 48 bits equivalent where the 16 bits of the middle are reversed. The obtained 48 bits are divided into 6 groups with 8 bits each. Each group is now converted into its decimal equivalent. So, we have 6 decimal values where each decimal value ranges from 0 to 255. Two sets are formed 〈DecVal₁, DecVal₃, DecVal₅〉 and 〈DecVal₂, DecVal₄, DecVal₆〉 where DecVal_i ∈ {0, 1, 2...255} represents the corresponding decimal value of the i^th binary group. These sets represent a new pixel. Each members of the set are representing the values of three channels i.e. 〈red, green, blue〉.

So, the input image is transformed from two dimensions to three dimensions. The discussed method is very simple to implement and cost-effective because it involves some basic operations only. In this context, Fig. 11 can be helpful to understand the proposed method for dimension transformation. One important point can be observed here, a pixel of a grayscale image is transformed into a pixel that consists of three-color channels. It is worth mentioning that the proposed procedure is completely reversible. The process can be reversed and the original pixel can be regenerated by following the exactly reverse procedure of the proposed method. Therefore, the proposed transformation incurs zero loss, and a hundred percent of data can be retrieved. This transformation process is dependent on the pseudorandom bit sequence which is generated using the proposed chaotic map and the proposed pseudorandom bit generator. The process will continue until all pixels of the input image is processed accordingly. The proposed transformation method can also be applied to color images. In that case, three channels can be processed separately using the same method and three different color images can be obtained. If the total number of pixels in the input image is odd then the last pixel will be alone and cannot find a pixel to form a pair. But to execute this algorithm, simply take the last pixel and execute all the steps and form the set at the last stage as 〈DecVal₁, DecVal₂, DecVal₃〉. At the time of decryption, the last pixel can be processed accordingly.

Fig. 11

Diagram to illustrate the proposed dimension transformation technique of a pixel

The obtained image will go through a scrambling process. The proposed pixel scrambling process is discussed next. The scrambling algorithm can efficiently shuffle the positions of the pixels. The proposed scrambling algorithm is also completely reversible i.e. the actual arrangements of the pixels can be retrieved from the scrambled image hence, there is no provision of data loss. Algorithm 1 describes the proposed scrambling method. The proposed scrambling algorithm works on every channel separately and each channel incurs a significant shuffling of the pixel positions which in turn modifies the whole image and disturbs the correlation among the pixels. If the color image is considered for encryption purposes then, all three transformed images are to be processed separately. The proposed scrambling algorithm is very useful to enhance the security of the encrypted image and makes the proposed encryption system resilient against differential attacks.

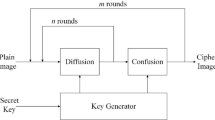
Now choose another two seed values and a value for the control parameter and use the set $\left({s}_0^{{\prime\prime} },{t}_0^{{\prime\prime} },{\psi}^{{\prime\prime}}\right)$ to generate new pseudorandom bit sequence prbs^′ of length Len = M × N × 3 × 8 and generate three dimensional matrix $Mat\left(p,q,r\right)= prb{s}_{\left(p-1\right)\cdotp N+q+\left(r-1\right)\cdotp Len/64}^{\prime }$ where the size of each channel is M × N and each pixel consist of 8 bits. Now, every pixel (i^′, j^′) of the k^th channel of TI^′ is converted into 8 bit binary equivalent and XORed with the corresponding pixel (p, q) in the r^th channel of Matwhere i^′ = p, j^′ = q, r = kand store the resultant image in an another matrix Mat^′. The obtained image Mat^′can be again scrambled using the algorithm 1. A value Itr is to be chosen that determines the number of iterations for which these steps are to be repeated. Figure 12 illustrates the proposed image encryption method in detail. For multiple iterations, there is no need to choose different seed values all the time. Instead of that, the last value of every chaotic sequence can be saved for the next iteration and can be treated as the new seed in the next iteration.

Fig. 12

Flow diagram of the proposed image encryption method

Some of the advantages of the proposed image encryption method is given as follows:

• 1. The proposed image encryption algorithm has no dependency on any additional image. The proposed method is efficient enough to encrypt different types of images using the proposed chaotic map and the pseudorandom bit generator.

• 2. The proposed encryption method is completely based on the proposed RCM chaotic map and the proposed pseudorandom bit generator. The efficiency of the proposed pseudorandom bit generator is already discussed earlier. The chaotic sequence as well as the pseudorandom bit sequence can be changed by varying the input parameters of the chaotic map. Therefore, it is very difficult to guess the pseudorandom bit sequence and the initial parameters of the chaotic map. These properties make the proposed encryption system safe and resilient against various types of attacks.

• 3. The proposed scrambling method can be easily modified. For example, the rows and columns may not be sorted instead that, any other permutations can be used.

• 4. The keyspace of the proposed method is sufficiently large that can prevent brute force attacks.

• 5. As discussed earlier, the proposed image encryption method is completely lossless in nature, and therefore, 100% of information can be recovered from the encrypted image.

• 6. The decryption process is very simple. The reverse operations are to be performed accordingly.

• 7. In the case of a grayscale image, the proposed image encryption method generates a color encrypted image which increases the confusion.

• 8. In case of a color image, the proposed image encryption method will generate three color encrypted images. So, at the time of decryption, all three encrypted images are necessary to get back the actual image.

5 Results of the simulation

This section presents the results which are obtained by applying the proposed image encryption method on different types of images. From this section, an idea about the proposed method can be obtained and a detailed analysis of the proposed image encryption system is given in the next section. The obtained results after applying the proposed image encryption algorithm are given in Fig. 13. As discussed earlier, the proposed method will generate a color encrypted image when the input image is in grayscale format. For the color images, the proposed encryption method will generate three different color encrypted images. At the time of decryption, all three images are necessary. From the given results, it is clear that the proposed image encryption method encrypts an image in such a way so that no one can understand or even guess the original image by interpreting the encrypted image(s). The encrypted images are given in Fig. 13b. Figure 13c shows the decrypted images and it can be clearly observed by the visual inspection that the decrypted images in Fig. 13c are quite similar to the corresponding original images under consideration, which are displayed in Fig. 13a. The lossless nature of the proposed image encryption method is analyzed and proved in the next section.

Fig. 13

Results of the propose image encryption a Actual Images (From top to bottom: Cameraman, Fingerprint (biometric image), CT Scan (biomedical image), Lake, Peeper (Color Image), Baboon (color image), watch (color image), and tulips (color image); b Encrypted Images; c Decrypted Images

All experiments are performed in a computer that is equipped with an Intel i3 processor with 1.8GHz clock speed, 4 gigabytes of RAM, 500 GB hard disk, and Microsoft Windows 7 operating system. All simulations and experiments are performed in the MatLab R2014a environment.

The results of research work can be validated with the help of the obtained results by the similar work performed by various researchers. In this work, the proposed approach is compared with various standard image encryption procedures. The comparative analysis of the proposed approach is useful to establish the quality and efficiency of the proposed work. Moreover, the comparative analysis of the proposed work is helpful to validate the proposed work from the context of the other established works. The obtained experimental results are promising and proven to be better enough compared to other approaches. Both qualitative and quantitative analysis helps to investigate the performance of different components with greater details. The lossless property of the proposed RCM map-based image encryption system is also proven by using both qualitative and quantitative manner. The NIST test results for the proposed pseudorandom bit generator is indicating the effectiveness of the method. Similarly, the detailed analysis of the proposed RCM map is depicting the applicability of this map in different domains.

The proposed image encryption method involves a parameter Itr which is used to determine the number of iterations is to be performed (please refer the Fig. 12). This Itrparameter has a major influence on the final quality of the encrypted images and the impact of this parameter is visually demonstrated in Fig. 14. The Itris a very important parameter to be known to generate the original images from the decrypted image. If someone knows the other security keys except the value of Itr then also, the correct image is not possible to reconstruct. This feature is demonstrated in Fig. 15. So, the value of the Itrcan be considered as a key.

Fig. 14

The impact of the parameter Itr on the encryption a Original image; (b)-(d) The output of the proposed encryption algorithm after the b first, c second, d third iterations respectively; e histogram of the original image; (f)-(h) histograms of the encrypted output which is obtained after the f first, g second and h third iterations respectively

Fig. 15

The impact of the iterations on the decryption process (a) Original image; (g) histogram of the original image; (b) encrypted image; (h) histogram of the encrypted image; (c)-(f) The output of the decryption process after the (c) first, (d) second, (e) third and (f) fourth iterations respectively; (i)-(l) histograms of the decrypted output which is obtained after the (i) first, (j) second, (k) third and (l) fourth iterations respectively

6 Performance and security analysis

On most occasions, visual investigations are may not be sufficient to test the quality of an image encryption system. In this section, various security aspects and performance of the proposed cryptosystem is analyzed in detail. Several relevant parameters like directional correlation coefficients, histogram analysis, strength against differential attacks, efficiency, etc. are evaluated and analyzed. Moreover, the keyspace and the sensitivity of the keys are also discussed.

6.1 Key space and strength against brute force attacks

The keyspace of a cryptographic system is a very important parameter from the security perspective. It is defined as the count of all possible combinations of a key or set of keys that are applied in various stages of an image cryptosystem. If the range of values or the set of possible values for the keys is known then it is possible to discover the original key or the set of keys by testing all possible combinations. This type of attack is the naïve approach by an intruder to break a cryptosystem and known as a brute-force attack.

It can be easily understood from the above discussion that, small keyspace is not at all desirable, and small keyspace is always vulnerable against brute force attacks which makes the overall cryptosystem weaker. It is necessary to design a cryptosystem with sufficiently large key space so that the encryption algorithm can withstand the brute force attacks and other exhaustive search-based attacks. It is difficult to search a large key space exhaustively because modern-day computers also not very efficient to search a large key space and therefore it is hard for the intruders to guess or retrieve the actual key or the set of keys from the ocean of the possible keys.

The key space of the proposed image encryption system is composed of the following segments:

• 1. The input parameters (s₀, t₀, ψ₀) to generate a chaotic sequence which is required for the dimension transformation phase.

• 2. The input parameters $\left({s}_0^{\prime },\hat{\psi}\right)$ for the scrambling algorithm.

• 3. The input parameters $\left({s}_0^{{\prime\prime} },{t}_0^{{\prime\prime} },{\psi}^{{\prime\prime}}\right)$ for the channel wise XOR operation.

• 4. The number of iterations i.e. Itr.

To determine the key space of the proposed method, these four segments should be taken into account. For the sake of explanation, consider a gray scale image of size M × N. The input parameters (s₀, t₀, ψ₀) are required to perform the dimension transformation where s₀ and t₀ are the seeds of the chaotic maps and can take any values in the range (0, 1) i.e. s₀, t₀ ∈ (0, 1). From the theoretical point of view, these two parameters can be assigned infinite number of values. But for the sake of analysis, let us consider the precision up to two decimal points then the range of these two parameters are 0.01 ≤ s₀ ≤ 0.99and 0.01 ≤ t₀ ≤ 0.99. ψ₀is the controlling parameter or the bifurcation parameter of the proposed RCM map and can take any value between 1 to 4? So, this parameter can also take infinite number of values. Therefore, the analysis of the key space is possible under certain assumptions. Suppose, an attacker tries to generate the pseudorandom bit sequence without involving the chaotic maps then, for the dimension transformation phase, there are P₁ = 2^{M × N × 8} number of possibilities which are needs to be investigated. The input parameters $\left({s}_0^{\prime },\hat{\psi}\right)$ are required to perform the scrambling operation. Scrambling operation shuffles the position of the pixels. This operation can also be performed without involving the chaotic maps. A scrambling algorithm can modify the pixel positions in P₂ = M !  × N !  × 3! ways. Now, the input parameters $\left({s}_0^{{\prime\prime} },{t}_0^{{\prime\prime} },{\psi}^{{\prime\prime}}\right)$ are required to perform the channel wise XOR operation. These input parameters are required to generate a chaotic pseudorandom bit sequence of length M × N × 3 × 8 which is in turn used to generate the synthetic channels. This operation can also be performed without involving the chaotic maps in P₃ = M !  × N !  × 3 !  × 2⁸ ways. Itr is an another important parameter for the proposed method. As discussed earlier, without knowing the exact value of Itr, it is impossible to decrypt an encrypted image.

Therefore, the key space P for the proposed image cryptosystem can be expressed as P = Itr × P₁ × P₂ × P₃ i.e. P = Itr × 2^{M × N × 8} × M !  × N !  × 3 !  × M !  × N !  × 3 !  × 2⁸ = Itr × 2^{(M × N × 8) + 8} × (M !  × N !  × 3!)². To explain it further and to get an essence of the actual key space for a real image, let us consider an grayscale image of size 128 × 128 is to be encrypted by using the proposed image encryption method. Assume that the value of the Itr is 5. Then the total possible key space for the proposed image encryption system which needs to be explored to perform a brute force attack is P = 5 × 2^{(128 × 128 × 8) + 8} × (128 !  × 128 !  × 3!)² ≈ 4.0902 × 10⁴⁰³²³, which is significantly large and makes the proposed image encryption system resilient against exhaustive search-based attacks.

6.2 Key sensitivity analysis

A good cryptosystem should have high sensitivity to the key or the set of keys. It is one of the fundamental requirements of any image cryptosystem to ensure the security of the encrypted image. The actual image should not get revealed due to a tiny change in the key. Therefore, it is necessary to study the sensitivity of the keys for both encryption and the decryption process. As discussed earlier, the initial parameters of the chaotic systems are the keys of the proposed system along with the value of the Itr. The effect of the Itr is already discussed earlier. Fig. 16 shows the effect of small change in the parameter(s₀, t₀, ψ₀) which are required for the dimension transformation phase. Figure 17 demonstrates the impact of a tiny change in the parameter(s₀, t₀, ψ₀) on the decryption process.

Fig. 16

The impact of the small change in the key for the dimension transformation phase for encryption (a) Actual image (peppers.png), (b) Encrypted image with s₀ = 0.5, t₀ = 0.8, ψ₀ = 3.5; (c) Encrypted image with s₀ = 0.6, t₀ = 0.7, ψ₀ = 3.5, (d) difference between (b) and (c)

Fig. 17

The impact of the small change in the key for the dimension transformation phase for decryption (a) Decrypted Image (Same as Actual image peppers.png), (b) Encrypted image withs₀ = 0.5, t₀ = 0.8, ψ₀ = 3.5, (c) Decrypted image withs₀ = 0.6, t₀ = 0.7, ψ₀ = 3.5, (d) difference between (a) and (c)

Figure 16a shows the actual image. Figure 16b shows the encrypted image with the key values s₀ = 0.5, t₀ = 0.8, ψ₀ = 3.5. This combination of the key values is used for the demonstration purposes in this work. Figure 16c shows the encrypted image with the key values s₀ = 0.6, t₀ = 0.7, ψ₀ = 3.5. So, the s₀ and t₀ experienced slight modification but the controlling parameter i.e. ψ₀ kept unchanged. The encrypted image in Fig. 16c is significantly different from Fig. 16b and their difference can be observed from Fig. 16d. The sensitivity of the keys in the decryption process is illustrated in Fig. 17. Figure 17a is the decrypted image and it is completely the same as the actual image because the proposed image encryption method is completely lossless in nature. Figure 17b is the encrypted image with the key values s₀ = 0.5, t₀ = 0.8, ψ₀ = 3.5. The decryption method takes the encrypted image and tries to find out the actual image with a slightly different set of key values s₀ = 0.4, t₀ = 0.7, ψ₀ = 3.5 and the result is given in Fig. 17c. It can be easily observed that the decrypted image in Fig. 17c is significantly different and the difference can be observed in Fig. 17d.

One important point about the chaotic system that can be observed from the above discussion is that the changes in the encrypted or the decrypted images are obtained by slightly changing the seed values only. The system parameter ψ remains unchanged during the experiments. Therefore, a small change in the initial parameters of the chaotic map can bring a significant change in both encrypted and decrypted images which are significantly different from the actual encrypted and decrypted images respectively. As discussed earlier, the effect of the Itr parameter on encryption and the decryption process can be observed from Figs. 14 and 15 respectively.

6.3 Analysis of the histogram

The intensity distribution of an image can be understood from the analysis of the histogram. In general, meaningful images do not have a uniform intensity distribution. It is desirable to have a uniform distribution in the encrypted image to resist various statistical attacks. A comparative study of the histograms is presented in this work where the proposed method is compared with some of the standard methods [11, 72, 73, 75] in the literature to test the effectiveness of the proposed method and the obtained results are given in Fig. 18. The popular Lena image is considered for comparison purposes which are shown in Fig. 18a along with its histogram. Figure 18b to f are the results of the encryption procedure along with their corresponding histograms. The result of the histogram analysis is given in Fig. 18f. It can be observed that the histogram of the encrypted image has three channels in the proposed method because of the dimension transformation phase. From the histogram, it can be observed that all three channels have almost uniform intensity distribution in the encrypted image. This analysis and comparison prove that the proposed image encryption method is resilient against different statistical attacks.

Fig. 18

a Actual Lena image and its histogram; (b)-(f) encrypted images and their corresponding histograms which are obtained using b Zhu’s Method [75], c Chakraborty’s Method [11] d Zhou’s Method [72] e Zhou’s Method [73] f Proposed Method

6.4 Analysis of the correlation coefficients

Typically, a meaningful image is constructed with highly correlated pixels. It is one of the fundamental requirements for any image encryption method to break such a high correlation. It is necessary to prevent unintentional data leakage. Therefore, the study of the correlation is very important from the security perspective. To analyze the correlation of various pixels, 2500 randomly chosen pairs of the adjacent pixels are taken into consideration and these pixels are considered in the horizontal, vertical, and diagonal directions for all three planes separately. Intensity values of these pair of pixels are plotted in a two-dimensional graph which is shown in Fig. 19. All three directions are considered and the corresponding intensity values of the pair of pixels are plotted. If two pixels are highly correlated then the diagonal line will be highly dense [23]. It can be easily observed from Fig. 19 that most of the pixel values are plotted near the diagonal line for the original image which signifies the high correlation whereas the pixel values for the encrypted images are plotted throughout the possible range of the intensity values which indicates a lesser correlation.

Fig. 19

Obtained correlations in various directions using the proposed image encryption algorithm. The top and bottom rows are showing the correlations of the (a) Original Cameraman image and the corresponding encrypted image and correlation of (b) Horizontal, (c) Vertical, (d) Diagonal directions, respectively

Figure 19 can only be used for visual inspection purposes. But as discussed earlier, a visual inspection may not always reveal the actual scene because it can vary from observer to observer. Therefore, a quantitative analysis is performed using Eq. 14.

$$ CorCoef\left(m,n\right)= COV\left(m,n\right)/\sqrt{D(m)}\sqrt{D(n)} $$

(14)

Here, (m, n) represents the intensity values of a pair of adjacent pixels. COV(m, n) can be computed using Eq. 15 and D(x) can be computed using Eq. 16.

$$ COV\left(m,n\right)=\frac{1}{Count_{pairs}}\sum \limits_{i=1}^{Count_{pairs}}\left(\left({m}_i-E(m)\right)\left({n}_i-E(n)\right)\right) $$

(15)

$$ D(x)=\frac{1}{Count_{pairs}}\sum \limits_{i=1}^{Count_{pairs}}{\left({x}_i-E\left({x}_i\right)\right)}^2 $$

(16)

In Eqs. 15, and 16, the total number of randomly chosen pairs are represented by the Count_pairs. The value of E(y) can be computed using Eq. 17.

$$ E(y)=\frac{1}{Count_{pairs}}\sum \limits_{j=1}^{Count_{pairs}}{z}_j $$

(17)

The CorCoef can take any value from the range [−1, 1]. The absolute value of the CorCoef is important here and if it is close to 1 then it indicates a high correlation among the pixels [66]. Therefore, a good encryption mechanism must generate a correlation value close to 0. Figure 19 demonstrates the correlation coefficient and shows the effect of the proposed image encryption method on the cameraman standard image. The quantitative analysis is performed using Eq. 14 and numerical results are reported in Table 5. It can be observed from Table 5 that, the values of the correlation coefficients for the encrypted images are nearly zero that proves the efficiency of the proposed image encryption method.

Table 5 Correlation Coefficients of various images and corresponding encrypted images using the proposed image encryption algorithm in different directions

6.5 Strength against differential attacks

The differential attack is a variant of the chosen-plaintext attacks. A tiny change is performed on the plain image and then an intruder studies the original and the encrypted images and tries to find out the relation between the original and the encrypted images to get some hint about the encryption process as well as about the keys. This kind of attack can be prevented if a small change in the actual image produces a huge deviation in the encrypted image. The proposed image encryption method is tested against the differential attacks using the Lena image and compared with some standard algorithms and the results are reported in this subsection. The actual image of Lena is encrypted two times using the same set of keys but with a difference in one bit. Four algorithms are involved in this experiment. These are DecomCrypt [72], Zhu’s Method [75], Zhou’s method [73] and the proposed image encryption method. A small change in the actual image does not have any significant effect on the encrypted images for the Zhu’s Method [75] and Zhou’s method [73]. However, a small change produces a good amount of deviation in the encrypted images which are obtained using DecomCrypt [72] and the proposed image encryption system. It can be easily observed in Fig. 20. As discussed earlier, visual verification is not enough always. Therefore, two popular parameters are used to analyze the impact of a small change in the actual image on the encrypted image. The number of Pixel Change Rate (NPCR) and the Unified Average Changing Intensity (UACI) are the two parameters that are considered in this work. NPCR can be computed using Eq. 18 and UACI can be computed using Eq. 19.

Fig. 20

Illustration of the differential attacks: (a) Original Lena images with a single-pixel variation and the difference between them; (b)-(e) obtained encrypted images and the difference between them after applying (b) DecomCrypt [72], (c) Zhou’s algorithm [73], (d) Zhu’s algorithm [75], (e) Proposed image encryption algorithm

$$ NPCR=\frac{\sum \limits_{i=1}^{\dim_1}\sum \limits_{j=1}^{\dim_2} Difr\left(i,j\right)}{\dim_1\times {\dim}_2}\times 100\% $$

(18)

$$ UACI=\frac{1}{\dim_1\times {\dim}_2}\sum \limits_{i=1}^{\dim_1}\sum \limits_{j=1}^{\dim_2}\frac{\left|{IMG}_1\left(i,j\right)-{IMG}_2\left(i,j\right)\right|}{255} $$

(19)

In Eq. 18 and 19, dim₁ and dim₂ are the dimensions of the images IMG₁and IMG₂. These two images are the encrypted images corresponding to the original images and these images are slightly different. Difr(i, j)is an array with dimension dim₁ × dim₂consist of only binary elements. It stores the count of the different pixels in IMG₁and IMG₂. Difr(i, j)is defined in Eq. 20.

$$ Difr\left(i,j\right)=\left\{\begin{array}{c}1\kern0.48em if\;{IMG}_1\left(i,j\right)={IMG}_2\left(i,j\right)\\ {}0\kern0.48em Otherwise\kern3.839998em \end{array}\right. $$

(20)

Ten images are chosen randomly from this web repository [15] to analyze the strength of the proposed method against the differential attacks. The proposed method is compared with four standard algorithms and the comparative results are presented in Table 6. The image ids which are given in the first column of Table 6 corresponds to the image ids which are given in the specified web repository. It can be easily observed that the proposed image encryption method achieves 97.384% NPCR and 33.235% of UACI on an average over the ten test images. The obtained results are satisfactory compared to some other standard algorithms. This analysis proves that the proposed image encryption method is resilient against differential attacks. The effect of the parameter Itr in the proposed method on NPCR and UACI can be observed in Figs. 21 and 22 respectively (two separate figures are used for better understanding).

Table 6 Comparison of the computed NPCR and UACI values

Fig. 21

Effect of Itr on the value of NPCR (Image with id 1 in Table 6 is used for this experiment)

Fig. 22

Effect of Itr on the value of UACI (Image with id 1 in Table 6 is used for this experiment)

From Table 6, it can be observed that the proposed approach achieves the NPCR value 0.8963 to 0.9993 with the average NPCR value 0.97384. Although, the ideal value of NPCR is 96.6094% [57] still, the proposed approach achieves significant overall NPCR score of 97.384% which is very close to the ideal value. The performance of the encryption approaches is not same for different images and therefore, three state-of-the-art approaches are compared to establish the effectiveness of the proposed approach.

6.6 Analysis of the time complexity

The time complexity of the proposed image encryption algorithm is analyzed in this subsection. For the sake of this analysis, let us assume a grayscale image of size M × N. The first operation i.e. the dimension transformation requires a pseudorandom bit sequence of length M × N × 8. The pseudorandom bit sequence can be generated using the proposed RCM map in two phases. In the first phase, the same chaotic map is used twice with different seed values to generate chaotic sequences, and then the proposed pseudorandom bit generation method is used to generate the pseudorandom bit sequence. The proposed pseudorandom bit generation method can be implemented in polynomial time because it is directly and linearly related to the number of elements to be generated. So, a pseudorandom bit sequence of length n can be generated using the proposed method in O(n) time. The dimension transformation phase requires an O(M × N)time.

The scrambling algorithm changes the position of the pixels in a three-dimensional matrix and produces a scrambled image. The operations which are associated with the scrambling process can be easily performed in O(M × N × 3) times because positions of each pixel in a channel can be modified in constant time and the required chaotic sequence can be generated in O(M × N × 3) time. The last phase i.e. the channel wise XOR operation can also be implemented in O(M × N × 3) time considering XOR operation takes a constant amount of time. Therefore, the proposed image encryption method can be implemented in polynomial time. The required time is completely dependent on the size and type of the input image i.e. the required time will increase in case of a color image to treat three channels separately. Now, if the scrambling procedure and the channel wise XOR method is repeated for Itr number of times then the overall time complexity of the proposed image encryption procedure will be O(itr × M × N × 3) (because the function and the number of steps does not change and can be assumed as constant).

6.7 Analysis of the information entropy

The information entropy is one of the important parameters which is helpful in evaluating an image encryption method. The information entropy can be computed using Eq. 21.

$$ InfEntr(d)=\sum \limits_{i=0}^{2^{len}-1}P\left({d}_i\right)\log \frac{1}{P\left({d}_i\right)} $$

(21)

Here, InfEntr(d) denotes the information entropy of a message source d. len represents the length of the bit sequence of a symbol d_i ∈ d and the P(d_i) represents the probability of occurrence for a specific symbol d_i.

For a strong, robust, and reliable cryptographic system, the desired value of the information entropy is close to 8 [61]. Table 7 shows the values of information entropy after applying the proposed image encryption system. A comparative study of the information entropy is presented in Table 8 using the Lena image where the proposed method is compared with 7 standard methods of the literature. It can be easily observed that the proposed image encryption method produces satisfactory results and outperforms some of the standard methods.

Table 7 Obtained values of the information entropy using the proposed image encryption system

Table 8 Comparison of the proposed image encryption method with some other standard methods in terms of information entropy (lena image is considered for the comparison)

6.8 Quantitative analysis of the average change in distance

The confusion characteristics of an encryption scheme can be well-understood by finding the average change in distance. The change in the average distance for a pixel (k, l) in an image of size d₁ × d₂ is denoted as ${\Phi}_{avg}^{d_1,{d}_2}$ and defined in Eq. 22 [26]. In this equation, d_E(i, j) represents the simple Euclidean distance between two points i and j. Equation 23 mathematically expresses the average change in the whole image. In this equation, the permuted pixel corresponding to the original pixel (k, l), is denoted using $\left(\overset{\frown }{k},\overset{\frown }{l}\right)$.

$$ {\Phi}_{avg}^{d_1,{d}_2}=\frac{1}{4}\left[\begin{array}{l}{d}_E\left(\left(\overset{\frown }{l}-1,\overset{\frown }{k}\right),\left(l-1,k\right)\right)+{d}_E\left(\left(\overset{\frown }{l}+1,\overset{\frown }{k}\right),\left(l+1,k\right)\right)+\\ {}{d}_E\left(\left(\overset{\frown }{l},\overset{\frown }{k}-1\right),\left(l,k-1\right)\right)+{d}_E\left(\left(\overset{\frown }{l},\overset{\frown }{k}+1\right),\left(l,k+1\right)\right)\end{array}\right] $$

(22)

$$ {\Phi}_{avg}=\frac{1}{\left({d}_1-2\right)\cdotp \left({d}_2-2\right)}\sum \limits_{i=1}^{d_1-2}\sum \limits_{j=1}^{d_2-1}{\Phi}_{avg}^{d_1,{d}_2} $$

(23)

Higher value of the average change in the distance denotes greater confusion.

6.9 Quantitative analysis of the change in graylevel intensity values

The change in the graylevel intensity values in the cipher image is measured to quantitatively analyze the quality of cipher image. Typically, the deviation of the graylevel intensity values in the encrypted image from the original image is measured using the approach proposed in [3, 37]. Equation 24 can be used to quantitatively analyze the cipher image using this criterion.

$$ Q=\frac{\sum \limits_{k=0}^{\mathrm{N}-1}\left|{\varphi}_k\left({O}_{img}\right)-{\varphi}_k\left({E}_{img}\right)\right|}{\mathrm{N}} $$

(24)

In Eq. 24, the count of the graylevels is represented by Ν and the original image and its corresponding cipher images are denoted using Ο_img and E_img respectively. The number of the k^th graylevel intensity present is denoted with φ_k(·). Equation 25 helps to mathematically express the relative error [37].

$$ {Error}_{avg}^{rel}=\frac{1}{d_1\times {d}_2}\sum \limits_{i=0}^{d_1-1}\sum \limits_{j=0}^{d_2-1}\frac{\left|{O}_{img}\left(i,j\right)-{E}_{img}\left(i,j\right)\right|}{\left|{O}_{img}\left(i,j\right)\right|} $$

(25)

6.10 Analysis of the degree of scrambling

Equation 26 can be used to compute the degree of scrambling that investigates the relatively closed pixels. This parameter can be computed using the approach developed in [64]. The range of this parameter can be 0 to 1 i.e. DoS ∈ [0, 1]) can be evaluated using the method proposed in.

$$ DoS=\frac{\sum \limits_{i=0}^{d_1-2}\sum \limits_{j=0}^{d_2-2}{\Psi}_{ij}}{{\left(\mathrm{N}-1\right)}^2\times \left({d}_1-2\right)\times \left({d}_2-2\right)} $$

(26)

In this equation, the term Ψ_ij is mathematically expressed in Eq. 27.

$$ {\Psi}_{ij}={\lambda}_1\left(i,j\right)+{\lambda}_2\left(i,j\right)+{\lambda}_3\left(i,j\right)+{\lambda}_4\left(i,j\right) $$

(27)

In Eq. 27, four functions i.e. λ_q(i, j), q = 1, . …, 4 are mathematically defined in Eq. 28.

$$ \left\{\begin{array}{c}\begin{array}{c}{\lambda}_1\left(i,j\right)=\mid {\left\{{O}_{img}\left(i-1,j\right)-{E}_{img}\left(i,j\right)\right\}}^2-{\left\{{E}_{img}\left(i-1,j\right)-{O}_{img}\left(i,j\right)\right\}}^2\mid \\ {}{\lambda}_2\left(i,j\right)=\mid {\left\{{O}_{img}\left(i+1,j\right)-{E}_{img}\left(i,j\right)\right\}}^2-{\left\{{E}_{img}\left(i+1,j\right)-{O}_{img}\left(i,j\right)\right\}}^2\mid \end{array}\\ {}{\lambda}_3\left(i,j\right)=\mid {\left\{{O}_{img}\left(i,j-1\right)-{E}_{img}\left(i,j\right)\right\}}^2-{\left\{{E}_{img}\left(i,j-1\right)-{O}_{img}\left(i,j\right)\right\}}^2\mid \\ {}{\lambda}_4\left(i,j\right)=\mid {\left\{{O}_{img}\left(i,j+1\right)-{E}_{img}\left(i,j\right)\right\}}^2-{\left\{{E}_{img}\left(i,j+1\right)-{O}_{img}\left(i,j\right)\right\}}^2\mid \end{array}\right. $$

(28)

In implementing these concepts, specifically for the Eqs. 23 and 26, 2 is subtracted from the actual dimension d₁ and d₂ to avoid the zero padding. Some images are selected from this web repository [39] to test the performance of the proposed system using the three evaluation parameters i.e. average change in distance, change in graylevel intensity values, degree of scrambling and the quantitative results are reported in Table 9. From Table 9, it can be observed that the proposed approach performs well and produces satisfactory results.

Table 9 Quantitative results of average change in distance, change in graylevel intensity values, degree of scrambling

6.11 Analysis of the SSIM index

The structural similarity index is first proposed in [53]. Let us assume that, two images IMG and IMG^′ are two images from which, two windows ω₁ and ω₂ are extracted respectively. The value of the SSIM can be computed using Eq. 29 where, μ and σ denote the average and variance respectively and α₁ and α₂ are the two constants.

$$ SSIM\left({\omega}_1,{\omega}_2\right)=\frac{\left(2\cdotp {\mu}_{\omega_1}\cdotp {\mu}_{\omega_2}+{\alpha}_1\right)\cdotp \left(2\cdotp {\sigma}_{\omega_1{\omega}_2}+{\alpha}_2\right)}{\left({\mu}_{\omega_1}^2+{\mu}_{\omega_2}^2+{\alpha}_1\right)\cdotp \left({\sigma}_{\omega_1}^2+{\sigma}_{\omega_2}^2+{\alpha}_2\right)} $$

(29)

The quantitative results obtained using the proposed approach on some of the selected images from this repository [39] are reported in Table 10.

Table 10 Obtained SSIM values

6.12 Analysis of the cyclic length of the proposed RCM map

Typically, the cycle length of continuously-realized and ergodic chaotic systems can be infinite. It can be hold for almost every orbit that begins with any seed or initial condition. In case of discrete realization with finite-precision can cause some short-length cycles [31]. In this subsection, the cycle length is analyzed with different seed values and with different values of the controlling parameter.

Here, the first experiment is performed by varying the seed values. The value of the controlling parameter ψ is made fixed at 3.5. The value of the initial seed is started with 0.01 and runs upto 0.99. It is observed that the maximum cyclic length obtained is 3,445,575 and it is obtained when the seed value is 0.96. The fluctuations in the cycle lengths can be visualized from Fig. 23.

Fig. 23

Fluctuations in cyclic lengths when ψ = 3.5

In this figure, the seed values are plotted in the x-axis and the cyclic lengths are plotted in the y-axis. It is worth noting that for the seed value 0.96 the cyclic length becomes maximum. It should also be noted that for some seeds the cyclic length is very low, and hence those combinations may not be used direct. But this experiment is performed for only one value of the controlling parameter. In the second experiment, the effect of changing the value of the controlling parameter can be observed. The value of the initial seed is made fixed at 0.5 and the value of ψ varied ranging from 2.5 to 3.99. The maximum cyclic length obtained is 2,527,205 and this value is obtained for ψ = 3.54. Fluctuations in the cyclic length can be visualized from Fig. 24. In this figure, the different values of ψ are plotted in the x-axis and corresponding of cyclic lengths are plotted in y-axis. It is worth noting that for the cyclic length becomes maximum when ψ = 3.54.

Fig. 24

Fluctuations in cyclic lengths when seed value = 0.5

7 Conclusion

This article proposed a novel chaotic map called RCM and a new method to produce pseudorandom bit sequences. The proposed chaotic map and the pseudorandom bit generator is applied in an image cryptosystem. The proposed RCM map and the pseudorandom bit generator is tested by various standard testing procedures to prove the strength and usefulness of it for various practical and real-life applications. The results which are produced by the proposed cryptosystem are tested and validated using both visual and quantitative methods which proves the effectiveness of the proposed method. The proposed image encryption method has no dependency on any external image in any phase of the whole process. The proposed method involves a significantly large keyspace and can easily withstand any exhaustive search-based attacks and statistical attacks. The scrambling method is flexible enough and can be easily modified by changing the rule of permutation. The proposed image encryption method is completely lossless and therefore, a cent percent of data can be recovered from the encrypted image. Simulation of the proposed method shows some aspiring results and encourages further experiments. This image encryption system is completely dependent on the proposed RCM map and proposed pseudorandom bit generation method and hence, highly sensitive to the initial conditions. Moreover, the i.e. number of iterations is another important parameter that serves as an additional layer of security. The proposed image encryption method is applied to various types of images and both visual and quantitative results speak itself about the strength and efficiency of the proposed approach. Therefore, the proposed image encryption system along with the proposed RCM map and the pseudorandom bit generator can be applied to secure real-life digital communications and can be further extended for various other types of data. The proposed image encryption system, the proposed RCM chaotic map, and the pseudorandom bit generator is found to be effective in securing digital images. However, in this work, only a single dimension is explored i.e. the application in the domain of image encryption. But the proposed approach can be applied in different other domains. For example, the proposed RCM map can be applied in the domain of non-linear dynamics, image segmentation, optimization problems, different industrial applications, neural networks, etc. Similarly, audio, video, text, and different other types of data can be encrypted with the proposed image encryption system with little or no modification. The proposed approach can further be extended by combining the metaheuristics with the proposed system. Moreover, the proposed scrambling approach can also be modified further the proposed system is flexible enough to adopt any new scrambling approach. Hence, there are lots of research directions on this topic is open that can be supported by this work.