1 Introduction

With the development of internet and information communication technique, a large number of image and video data including various information are distributed and stored, so the safe storage and distribution of the data has a vital importance. In particular, compared to text data, some intrinsic features of image data, such as big size, high redundancy of data and strong correlation among neighboring pixels require the strong real-time property in communication. For this reason, the traditional block encryptions (DES, IDEA, AES) being widely used now is found to be inefficient for image encryption [14].

To prevent the loss of image information, a large number of algorithms, such as fractional wavelet transform [3, 4], p-Fibonacci transform [29], gray code [28], vector quantization [5] and chaos [1, 2, 6,7,8,9,10,11,12,13, 15,16,17,18,19,20,21,22,23,24,25,26,27, 30, 31], have been proposed and among them the image encryption based on the chaotic map is being widely used.

The chaotic map is distinguished by the sensitivity to initial conditions and system parameters and the excellent random distribution. In particular, in the image encryption by chaotic map, some property coefficients of encryption result depend on the property of the chaotic map, so it needs the better distribution of chaotic map used in the encryption. Compared to the multi-dimensional chaotic map, the 1D chaotic map has some disadvantages in the chaotic range and distribution, but, because of the advantage of easiness of implementation by hardware and software, the 1D chaotic map is being widely used now. But the 1D chaotic systems have some disadvantages such as limited range of chaotic behaviors and non-uniform data distribution of output chaotic sequences [1, 12, 19]. Many researches are being done to overcome the disadvantages of 1D chaotic map, obtain the chaotic distribution with improved properties and apply it to image encryption [7, 10, 13, 16, 18, 20, 24, 30].

The bit-level image encryption has different advantages in image encryption. The permutations in the bit-level image encryption have an advantage that the position and value of a pixel can be changed simultaneously, but little research on it is being made now. Some bit-level encryption algorithms are being proposed [6, 9, 15, 17, 21, 22, 25,26,27, 31]. One pixel of image is composed of 8 bits, the amount of information occupied by the 8 bits is different from position to position. The computation shows that the 4 upper-level bits have about 94 percent of a pixel information, for this reason, the method of encryption using the 4 upper-level bits is proposed.

The encryption system consists of a pair of linear (permutation)-nonlinear(diffusion) conversion and some encryption systems repeat this process to raise the strength of encryption. But the repetition of this linear-nonlinear process requires a large number of computation time, so that it gives an influence on the performance of whole encryption system.

On the basis of analysis of above mentioned problems, we propose the improved Logistic map and Sine map and evaluate their performance in this paper. The simulation and analysis of bifurcation property of chaotic map and Lyapunov exponent and information entropy evaluating chaotic performance demonstrate the accuracy of the improved chaotic map. And, on the basis of analysis of existing encryption systems, a bit-level image encryption system of linear-nonlinear-linear conversion structure is proposed. Simulation and experiment evaluate key space and key sensitivity, correlation and resistance to attack.

The paper is organized as follows. Section 2 briefly reviews the performance of existing Logistic map and Sine map. Section 3 makes an improved 1D chaotic map by using above mentioned existing 1D chaotic map and demonstrate its accuracy. Section 4 proposes a bit-level image encryption algorithm of linear-nonlinear-linear structure. Section 5 shows the results of simulation and analysis. Section 6 shows the conclusion.

2 1D chaotic maps

Because of the simplicity of structure, the 1D chaotic maps are being widely used in image encryption. In this section, 1D chaotic maps: Logistic map and Sine map will be briefly discussed.

2.1 Logistic map

The logistic map is one of simple 1D chaotic maps with complex chaotic behavior and it is expressed in the following equation.

$$ x_{n + 1} = F_{L}(u, x_{n}) = u \times x_{n} \times (1 - x_{n}) $$
(1)

where u is a control parameter with the range of (0,4] and x0 is the initial value of chaotic map, xn is the output chaotic sequence.

The bifurcation diagram and Lyapunov Exponent diagram are shown in Figs. 1a and 2a. There are two problems in the Logistic map. Two problems are that its chaotic range is limited and the data distribution of output chaotic sequences is non-uniform. As shown in the bifurcation diagram and Lyapunov Exponent diagram, its chaotic range is limited only within [3.57,4] and the control parameter beyond the range can’t have chaotic behaviors. The Lyapunov Exponent is a value for the quantitative evaluation of the chaotic performance. When the Lyapunov Exponent has a positive value, the chaotic map has a good performance and the larger the value is, it has a better chaotic performance. In other words, when parameter u < 3.57, the Lyapunov Exponents of the Logistic map are smaller than zero and it means that they have no chaotic behaviors. On the other hand, the data range of the chaotic sequences is smaller than [0,1], showing the non-uniform distribution in the range of [0,1]. In the encryption system, the generated chaotic sequences are used in the process of permutation and diffusion of pixels or bits of the original image. Therefore, the non-uniform output chaotic sequences have some influences not only on the distribution of encrypted image data, but also on the performance of the encryption system. And, the encrypted image should have close correlation with the security key, so that it is important to use a good key generation algorithm. These problems narrow down the applications of Logistic map.

Fig. 1
figure 1

The bifurcation diagrams of the (a) Logistic map; (b) Sine map; (c) improved Logistic map; (d) improved Sine map

Full size image
Fig. 2
figure 2

The Lyapunov exponent diagram of the (a) Logistic map; (b) Sine map; (c) improved Logistic map; (d) improved Sine map

Full size image

2.2 Sine map

The Sine map is one of 1D chaotic maps and has a similar chaotic behavior with the Logistic map. The definition can be described by the following equation.

$$ x_{n + 1} = F_{S}(r, x_{n}) = r \times sin(\pi \times x_{n}) $$
(2)

where parameter r ∈ (0,1] and xn is the output chaotic sequence.

As shown in bifurcation diagram and Lyapunov Exponent diagram of Figs. 1b and 2b, it has a similar property with the Logistic map.

3 The improved chaotic system

In this section, an improved 1D chaotic map is proposed to solve the problems mentioned in Section 2. To verify its accuracy, above-mentioned Logistic map and Sine map are used.

3.1 The structure of chaotic map

The new chaotic map is defined by the following equation.

$$ \begin{array}{ll} x_{n + 1}=F(u, x_{n}, k)=mod((F_{chaos}(u, x_{n}) - F^{\prime}_{chaos}(u, x_{n})) \times G(k), 1) \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} \begin{array}{ll} where \ \ \ \ \ \ G(k)= 2^{k}, 9 \leq k \leq 16 \end{array} \end{array} $$

where Fchaos(u,xn) is one of the existing 1D chaotic maps mentioned above and F(u,xn,k) is a newly made chaotic map. \(F^{\prime }_{chaos}(u, x_{n})\) is the function where u of the function Fchaos(u,xn) is replaced with (4 − u). u is a control parameter with the range of \([0,2) \bigcup (2, 4]\).

From equation [4], it can be seen that the proposed system does not have a chaotic property when u = 2, and the all values of output sequences become zero.

In other words, F(u,xn,k) still has a chaotic property in the expanded range of \([0,2) \bigcup (2, 4]\) lager than the range of the existing 1D chaotic maps. The output chaotic sequences surely are to be in the range of (0,1) by the ’mod’ operation. xn is the sequence of the chaotic map, n is the iteration number, and G(k) is an adjustable function with parameter k. k has a good chaotic performance in the range of [9,16]. In Fig. 3, it can be seen that the larger k means the better chaotic performance in the range. The value range of k has been confirmed in the experiment. In the paper, the control parameter k is set to 12. The new proposed chaotic system has a simple structure, so it is easy to implement by software and hardware. Lots of new chaotic sequences can be made by using the proposed chaotic system.

3.2 The improved 1D chaotic maps

To verify the performance of the proposed chaotic system, two existing 1D chaotic maps discussed above are used.

3.2.1 The improved logistic map

The Logistic map are combined by using the equation [4]. It can be expressed in the following equation.

$$ x_{n + 1}=mod((u \times x_{n} \times (1 - x_{n}) - (4 - u) \times x_{n} \times (1 - x_{n})) \times 2^{12}, 1) $$
(4)

where the parameter \(u \in [0,2) \bigcup (2, 4]\) and x0 is the initial value of the sequence.

The bifurcation diagrams and Lyapunov exponent of the improved Logistic map are shown in Figs. 1c and 2c. As shown in Figs. 1c and 2c, the chaotic range is \([0,2) \bigcup (2, 4]\) and it is much larger than that of the existing Logistic map, and it has a good chaotic performance.

3.2.2 The improved sine map

The Sine map are combined by using the equation [4], it can be expressed in the following equation.

$$ x_{n + 1}=mod((u \times sin(\pi \times x_{n}) - (4 - u) \times sin(\pi \times x_{n})) \times 2^{12}, 1) $$
(5)

where the parameter \(u \in [0,2) \bigcup (2, 4]\) and x0 is the initial value of the sequence.

The bifurcation diagrams and Lyapunov exponent of the improved Sine map are shown in Figs. 1d and 2d. Like the improved Logistic map, its chaotic range and performance is much better than the previous Sine map’s.

3.2.3 Information Entropy of the improved chaotic maps

The information entropy (IE) is designed to evaluate the uncertainty in a random variable and its ideal value is 8. The evaluation equation is as follows.

$$ H(R)=-\sum\limits_{i = 0}^{F-1} P(R = i) \times log_{2} P(R = i) $$
(6)

where F is the gray level, F = 256 and P is a discrete probability density function.

The information entropy has a maximum when all signal values have random distributions. We made a comparison analysis between the information entropy of output sequences of the existing 1D chaotic maps and that of the output chaotic sequences of the proposed chaotic system. The results are shown in Fig. 3. As shown in Fig. 3, the more the value of k is, the information entropy of the output sequences of the proposed chaotic map has a value closer to 8 in the range of \([0,2) \bigcup (2, 4]\). This means that its distribution has a higher randomness compared to the existing 1D chaotic output sequences.

Fig. 3
figure 3

The Information entropy diagram of the (a) Logistic map and improved Logistic map with k = 12; (b) Sine map and improved Sine map with k = 12

Full size image

4 A new encryption algorithm

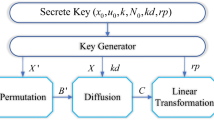
In the section, a new bit-level image encryption algorithm is proposed and its application in information security by using the above-mentioned improved Logistic map is verified. Bitplane decomposition adopts BBD(binary bitplane decomposition) method [26]. The encryption algorithm uses six parameters of (x0,u,k,N0,kd,rp) as the security key. The diagrams of the proposed cryptosystem are shown in Fig. 4.

Fig. 4
figure 4

The block diagram of the proposed cryptosystem

Full size image

4.1 Encryption process

  1. Step 1:

    The color image with the size of M × N is divided into 3 images with R, G and B channels respectively, and then the 3 images is linked to make a grayscale image with the size of M × 3N. In case of the Grayscale image with the size of M × N, it will be used without conversion.

  2. Step 2:

    The grayscale image obtained above is converted into the 1D image pixel matrix and then it is converted into 1D image bit matrix B = {b1,b2,...bM×24N} again.

  3. Step 3:

    The chaotic sequence X used in the encryption system is obtained in the above-mentioned improved chaotic map. where x0, u and k are initial values of the chaotic system and are used as the security keys.

    Iterate the improved chaotic map (M × 24N + N0) times and discard the former N0 elements to make a new sequence with M × 24N elements. where N0 is a constant used as the security key.

  4. Step 4:

    Obtain the permutation position matrix \(X^{\prime }=\{x_{1}^{\prime },x_{2}^{\prime }...x_{M \times 24N}^{\prime }\}\) by sorting the chaotic sequence X in ascending order.

  5. Step 5:

    Obtain the permuted image bit matrix \(B^{\prime }=\{b_{1}^{\prime },b_{2}^{\prime },...b_{M \times 24N}^{\prime }\}\) by using the permutation position matrix X′ and the image bit matrix B. Permutation equation can expressed in the following equation.

    $$ B^{\prime}(i)= B(X^{\prime}(i)); $$
    (7)
  6. Step 6:

    Obtain the diffusion matrix \(D^{\prime }=\{d_{1}^{\prime }, d_{2}^{\prime }, ... d_{M \times 24N}^{\prime }\}\) by the following equation.

    $$ D^{\prime}(i)=mod(floor(X(i) \times kd), 2); $$
    (8)

    where kd is a positive integer and are used as the security keys, the diffusion matrix D′ consists of 0 and 1.

  7. Step 7:

    Obtain the encrypted image bit matrix C = {c1,c2,...cM×24N} from the diffusion matrix D′ and the matrix B′ by the following diffusion equation.

    $$ C(i) = bitxor(B^{\prime}(i), D^{\prime}(i)); $$
    (9)
  8. Step 8:

    Obtain a new encrypted image bit matrix \(C^{\prime }=\{c_{1}^{\prime }, c_{2}^{\prime },...c_{M \times 24N}^{\prime }\}\) by rotating the above obtained matrix C to the right by the amount of rp. where rp is used as a security key and rp ∈ [1,M × 24N].

    The new image bit matrix C′ is obtained in the following equation.

    $$ \left\{\begin{array}{ll} C^{\prime}(i+rp)=C(i); & \quad i+rp \leq M \times 24N\\ C^{\prime}((i+rp)-M \times 24N)=C(i); & \quad i+rp > M \times 24N \end{array}\right. $$
    (10)

    The step 8 not only avoid the repetition of linear(permutation)-nonlinear(diffusion) conversion to shorten the encryption time, but also increase the strength of encryption.

  9. Step 9:

    Convert the C′ into the R, G and B color image with the size of M × N.

    The obtained color image is a noise-like encrypted image.

4.2 Decryption process

The decryption is the inverse process of encryption.

The encryption and decryption algorithms are simple but they are enough to increase the strength of encryption. They can be applied not only to color image, but also to grayscale image.

5 Experimental results and discussion

To evaluate the performance of our encryption algorithm, we made a simulation experiment with Matlab 2013a. The above-mentioned improved Logistic map and color images with the size of 256 × 256 are used. The parameters are set as follows. The initial value of the chaotic map x0 = 0.34, the control parameter u = 2.56, k = 12, N0 = 1000, kd = 654321 and rp = 1000 and the results of encryption and decryption are shown in Fig. 5. As shown in Fig. 5, all encrypted images are noise-like ones and can be efficiently applied to images of various forms such as grayscale images, color images and binary images.

Fig. 5
figure 5

Encryption result of some images. a the original images; b the histogram of the original images; c the encrypted images; d the histogram of the encrypted images

Full size image

5.1 Security key space

For the good security performance of an encryption algorithm, it should be very sensitive to any change of its security key and have a larger space than 2100 enough to withstand the brute force attack. The encryption algorithm has 6 security keys: u,x0,k,N0,kd and rp. where \(u \in [0,2) \bigcup (2, 4], x_{0} \in (0, 1), k \in [9,6], rp \in [1, M \times 24N]\) and kd a positive integer. Here we compute the u and x0 in the accuracy of 10− 15, set the size of image to 256 × 256, set N0 = 103, so the total key space is 1015 × 1015 × (256 × 256 × 24) × 103 ≈ 2130. When k and kd is considered, the maximum key space is much greater than 2130.

This means that the algorithm can withstand any blute force attack.

5.2 Statistical analysis

5.2.1 Histogram analysis

Image histogram reflects the distribution of pixel values of an image. To resist statistic attacks, the image histogram should be flat. Figure 5b, d shows the histograms of the some images and the histograms of their encrypted images. As shown in Fig. 5b, d, the histogram of the encrypted image has a good uniform distribution, so that it is enough to resist statistic attacks. The distribution scale of the encrypted images are calculated by equation [5] and the results are shown in Table 1.

Table 1 Information entropy of the some encrypted images
Full size table

Table 2 shows the performance comparison with the reference [22]. As shown in Table 2, the information entropy of a image encrypted by the proposed system is equally distributed in channels of R, G and B. As a result, it can be seen that the performance of entropy is superior to that of the system proposed by the preceding literature.

Table 2 Information entropy performance
Full size table

5.2.2 Correlation of two adjacent pixels

Image data generally has high redundancy of data and strong correlation among neighboring pixels, so it can be used as attacking information. In the experiment, we randomly selected 1000 pairs of adjacent pixels from the original image and the encrypted image and analyzed the correlations at 3 directions. The correlation coefficient is calculated by the following equation [2].

$$ r_{xy}={\frac{cov(x,y)}{\sqrt {D(x)} \times \sqrt {D(y)}}} $$
(11)
$$\begin{array}{@{}rcl@{}} \begin{array}{ll} where \ \ cov(x,y)={\frac{1}{N}}\sum\limits_{i = 0}^{N}{(x_{i}-E(x))(y_{i}-E(y))}\\ D(x)={\frac{1}{N}}\sum\limits_{i = 0}^{N}{(x_{i}-E(x))^{2}}, E(x)={\frac{1}{N}}\sum\limits_{i = 0}^{N}{x_{i}} \end{array} \end{array} $$

where x and y are values of two adjacent pixels in the image.

The correlation diagram among adjacent pixels at horizontal, vertical and diagonal directions of R channel in the Lena.bmp image is shown in Fig. 6 and the correlation coefficients according to each direction of R channel of some images are shown in Table 3. As seen in Table 3, the correlation coefficient of the original images comes near to 1, but the correlation coefficient of the encrypted images comes near to 0.

Fig. 6
figure 6

Correlation analysis of image Lena in R channel. a horizontal correlation of original and encrypted images; b vertical correlation of original and encrypted images; c diagonal correlation of original and encrypted images

Full size image
Table 3 Correlation coefficient of the some encrypted images in R channel
Full size table

This means that the encrypted image has no correlation property of the original image.

Table 4 shows the performance comparison with the reference [22]. As seen in Table 4, the correlation coefficient of the encrypted image has the value near zero similar to that in the preceding literature.

Table 4 Correlation coefficient performance
Full size table

5.2.3 Sensitivity analysis

A good encryption system should be sensitive to tiny differences in key and plain image and the sensitivity can be quantitatively evaluated by NPCR(number of pixels change rate) and UACI(unified average changing intensity). It is expressed in the following equation.

$$ NPCR={\frac{1}{W \times H}}\sum\limits_{i = 0}^{H}\sum\limits_{j = 0}^{W}D(i,j) \times 100(\%) $$
(12)
$$\begin{array}{@{}rcl@{}} where D(i, j) = \left\{\begin{array}{lll} 0 & \quad \text{if} \ c_{1}(i,j) = c_{2}(i,j)\\ 1 & \quad \text{if} \ c_{1}(i,j) \neq c_{2}(i,j) \end{array}\right. \end{array} $$
$$ UACI={\frac{1}{W \times H}}\sum\limits_{i = 0}^{H}\sum\limits_{j = 0}^{W}{\frac{|c_{1}(i,j) - c_{2}(i,j)|}{255}} $$
(13)

where c1 and c2 are encrypted images corresponding to two security keys.

Table 5 shows NPCR and UACI of 8 images. The results of encryption and decryption of two security keys x0 and k with tiny difference are shown in Fig. 7. As shown in Table 5 and Fig. 7, it can be seen that the proposed chaotic system is very sensitive to tiny differences of initial condition.

Table 5 The mean NPCR and UACI of the some encrypted images
Full size table
Fig. 7
figure 7

Encryption results with closed initial values and their difference. a, f, k The original images; b the encrypted image(c1) with u = 2.56; c the encrypted image(c2) with u = 2.560000000000001; d, e the pixel-to-pixel difference (|c1 − c2|) and its histogram; g the encrypted image(\(c^{\prime }_{1}\)) with x0 = 0.34; h the encrypted image(\(c^{\prime }_{2}\)) with x0 = 0.340000000000001; i, j the pixel-to-pixel difference (\(|c^{\prime }_{1} - c^{\prime }_{2}|\)) and its histogram; l the encrypted image(\(c^{\prime }_{1}\)) with k = 12; m the encrypted image(\(c^{\prime }_{2}\)) with k = 12.000000000000001; n, o the pixel-to-pixel difference (\(|c^{\prime }_{1} - c^{\prime }_{2}|\)) and its histogram

Full size image

Table 6 shows the performance comparison with the reference [22]. As shown in Table 6, it can be seen that the sensitivity also has the superior performance to the previous systems.

Table 6 The NPCR and UACI performance
Full size table

5.2.4 Data loss and noise attack

Digital images can be easily influenced by noise and data loss in different conditions. An image encryption algorithm should have an ability of resisting these abnormal phenomena. To test the ability of resisting the noise, we did some experiments on cutting attack of image data with the size of 64 × 64 and noise attack with 3% ′salt&pepper′.

The restoring ability of an image after the decryption is evaluated by PSNR(Peak Signal to Noise Ratio) and is expressed in the following equation.

$$ PSNR= 10 \times lg{\frac{255^{2}}{MSE}} (dB) $$
(14)
$$\begin{array}{@{}rcl@{}} where \ \ MSE={\frac{1}{W \times H}{\sum\limits_{i = 0}^{H}\sum\limits_{j = 0}^{W}(OI(i,j) - DI(i,j))^{2}}} \end{array} $$

where H × W is the size of image, OI(i,j) a pixel of the original image and DI(i,j) a pixel of the decrypted image.

In general, the larger the value of PSNR is, the breakdown coefficient of image gets smaller, and when the value of PSNR is above 35dB, it is very difficult to distinguish the decrypted image and the original image. Figure 8 shows the results of decryption and the Table 7 shows the PSNR coefficients in some images. As shown in the experimental results, the proposed encryption algorithm has excellent performance in noise and attacks.

Fig. 8
figure 8

Data loss and noise attack (a) the encrypted original image and its decrypted image; (b) the encrypted image with 64 × 64 data loss and its decrypted image; (c) the encrypted image added with 3% \('salt \& pepper^{\prime }\) noise and its decrypted image

Full size image
Table 7 The PSNR of the some encrypted images
Full size table

Table 8 shows the performance comparison with the reference [18]. As shown in Table 8, the proposed encryption system has the better superior performance to a noise attack, but has a little bad performance to a data loss, compared to previous systems.

Table 8 The PSNR performance
Full size table

6 Conclusion

In the paper, the improved 1D Logistic map and Sine map made by the output sequences of two same existing 1D chaotic maps were proposed. The experiments verified the chaotic behavior and the chaotic range of the improved chaotic systems. And it also verified that our new chaotic system has a better chaotic performance than existing 1D chaotic systems. We propose a bit-level image encryption algorithm to verify the applications in image encryption of the proposed chaotic system and our simulation and experiments demonstrated that the proposed algorithms have the efficiency in image encryption.