1 Introduction

Over the last few years, a variety of geometry-based proposals have been made to calibrate projectors, a procedure which is crucial for some applications, like multi-projector visualization on large screens [1, 5, 6], videogrammetry [13], and 3D object reconstruction in structured light scanning [11, 12, 18, 19]. The most extended calibration methods make use of planar homographies supported by physical planar surfaces with known patterns (e.g. checkerboards, grids of dots) [14, 15, 17, 20]. In these methods, the geometric correction and alignment is carried out by means of planar homography transformations between the planar surface, the projector frame buffers and the images of one or more cameras observing the surface. To that end, some physical and projected set of points are considered, whose 2D-to-3D coordinates are previously known or computed during the calibration procedure. The image-based recognition of the known patterns, either alone or in combination with other planar surfaces, are used to automatically measure 2D points and then establish 2D-to-3D correspondences. Therefore, in this kind of methods the physical surface with the known pattern has to be moved and rotated into different spatial positions (at least 10 different positions are recommended) to complete the calibration procedure.

Nevertheless, the use of planar surfaces is not always feasible, specially when some space or environment restrictions arise. For instance, a case where the projector to be calibrated is located at 3 meters high would require a planar surface of equivalent dimensions (of that of the projected image at the working distance) than could be moved to 10 different positions, making impractical this kind of calibration methods. In order to avoid this kind of restrictions, other calibration methods using cylindrical surfaces have been proposed, such as the ones described in [7, 25, 26]. Nevertheless, the calibration method is still an open issue, since the restrictions encountered in real scenarios often require ad-hoc solutions.

In this paper, we propose a new calibration method based on the well-known Direct Linear Transformation (DLT) equations to calibrate projectors making use of cylindrical surfaces. For evaluation purposes, we have dealt with a real case scenario that has specific restrictions. It consist of a typical “Visionarium”, a room for 3D environments visualization with a cylindrical projection screen at University of Valencia premises. In these facilities, the curved image is composed from the projections of three projectors, which are located at a height of 5 m. The image of the central projector is completely projected onto the screen. The image of the two side projectors is only partially projected onto the screen. First we show the application of this method on cylindrical surfaces. The calibration results show that with the minimum configuration of 6 control points (CPs), the standard deviation in the projector positioning yielded by the calibration process is less than one per cent of the position values. Also, we show the application of the proposed method to some real application examples.

The rest of the paper is organized as follows: Section 2 presents some related work. Section 3 introduces the proposed calibration method. Next, Section 5 describes some real use cases of the proposed method. Finally, Section 6 shows some conclusion remarks.

2 Related work

Projectors are key elements in many different applications like scientific visualization, virtual and augmented reality, structured light techniques and other visually intensive applications. The geometric calibration of a projector can be based on either a mechanical and electronic alignment, or by vision-based indirect methods, involving one or more cameras that observe a set of projected images [2]. Since the latter strategy requires no special infrastructure and/or resources except one or two cameras, many vision-based techniques have been proposed in the last years for the geometrical calibration of projectors. Many of these techniques use planar screens as physical surfaces. In these cases, the automated geometric correction and alignment are simplified through the use of planar homographic transformations between the physical surface, the projector frame buffers, and the images of one or more cameras focusing on the surface [3, 16, 22].

Some other works can be found where non-planar surfaces are used to achieve calibration. One of the first works found in the literature made use of a 3D calibration pattern with spatially-known control points (CPs) and two cameras, which were fully calibrated by means of projective geometry [23]. Other authors incorporate structured light techniques in the process of calibration. As an example, an approach that allows one or more projectors to display an undistorted image on a surface of unknown geometry is presented in [27]. In this case, patterns which are commonly used in techniques based on structured light are considered for computing the relative geometric relationships between camera and projector, thus avoiding an explicit calibration. A different method for projecting images without distortion onto a developable surface (producing a wall-paper effect) is presented in [7]. In this case, the correspondences between a camera and a projector are computed by projecting a sequence of bar code images (they use between 8 and 12 images) of increasingly fine spatial frequency, in such a way that projector coordinates corresponding to various camera pixels can be temporarily encoded.

It is also worth citing the approach introduced in Sajadi and Majumder [24, 25], where some spatial geometric relationships are established to derive the exterior orientation of a camera (the interior orientation is considered as already known) and from this one, the interior and exterior orientation of a projector is computed.

Finally, our previous work [21] proposes a calibration method which results from the combination of surveying, photogrammetry and image processing approaches, and has been designed by considering the spatial restrictions of virtual reality simulators. However, that method needs a previous laboratory work to obtain the internal calibration of the camera. Also, the camera usually needs the re-calibration periodically, and the method requires that the optical zoom is the same used in the internal calibration of the camera.

In the next sections, we present a projector calibration method that can greatly simplify the calibration process and can be applied to cylindrical surfaces. The proposed method eliminates the need for the previous laboratory work and fully exploits the advantages of the DLT, as shown in the next section. Together with a fixed calibration bench whose points are measured with a topographic total station, they allow the calibration of an unlimited number of projectors.

3 Six Control Points Method (SCPM)

The aim of our research is to design a fast and easy-to-use method to provide both camera and projector geometric calibration with the smallest set of input data as possible, in order to reduce the calibration time. Our method combines the easiness of establishing 2D-3D correspondences with checkerboards-based patterns from only two images (one with the background and the other with a projected pattern), with the facility of its mathematical formulation. The Direct Linear Transformation has been traditionally used in camera calibration, and our previous experience with the DLT [21] shows that it yields several advantages: first, it defines a linear relationship between the points in the image and the real world, which in turn implies a simple mathematical formulation. Second, the focal length may be unknown and it can vary between different images. This feature is specially advantageous when several projectors (with different characteristics) should be calibrated simultaneously, like in spatial augmented reality applications. Third, the position of the system coordinates of the image can be arbitrary. This feature implies that the system can be calibrated even with only part of the image. In projectors, this feature means calibrating with zoom. Thus, we propose the DLT also for projector calibration. Moreover, we propose the double application of the DLT, once for calibrating the camera and once for calibrating the projector. In this way, the SCPM duplicates the advantages of the DLT. In the end, we have two optical devices calibrated almost simultaneously, without needing to know in advance the internal calibration of neither of them (unlike other calibration methods), with a very simple mathematical formulation and reducing the required time (since we only need to select six points in a semi-automatic way).

The proposed method is based on projective geometry similar to the one presented in [23], but using one instead of two cameras, and assuming that geometry of the projection surface is a vertical cylinder, a common case in many virtual reality systems. The mathematical background makes use of the Direct Linear Transformation (DLT) model [4, 9], which gives both simplicity and robustness to our implementation because the model is easy to implement and the results can be refined through a least square procedure if redundancies (more CPs than the minimum required) are available.

Our method assumes that the camera and the projector are linear devices with no radial distortion and the projector can be considered as equivalent to a pin-hole camera. Then, the mathematical formulation that lies on the background is the DLT that is twice applied, one to derive camera parameters and the other one to derive projector parameters. The formulation of the DLT is shown in (1) and (2), where x and y denote the observable 2D image coordinates of a given point, the parameters X, Y, Z denote the 3D spatial coordinates of that point, and the terms ai, bi, and ci denote the 11 DLT parameters for a particular image. Since a single observed point yields 2 equations, a minimum of 6 points are needed to solve the equations and find the 11 unknown DLT parameters.

$$ x = \frac{a_{1}X+a_{2}Y+a_{3}Z+a4}{c_{1}X+c_{2}Y+c_{3}Z + 1} $$
(1)
$$ y = \frac{b_{1}X+b_{2}Y+b_{3}Z+b4}{c_{1}X+c_{2}Y+c_{3}Z + 1} $$
(2)

In order to solve the 11 unknowns of the DLT, a matrix system can be built as shown in (3), which can be solved by a Least Square fitting. The elements of the matrix A and the vector k are given in (4) and (5), respectively, for the first CP; r is the vector of residuals and x is the vector of unknowns, i.e. the 11 DLT parameters.

$$ A x = k + r $$
(3)
$$ \small A = \left[\begin{array}{ccccccccccc} X_{1}&Y_{1}&Z_{1}&1&0&0&0&0&-x_{1}X_{1}&-x_{1}Y_{1}&-x_{1}Z_{1}\\ 0&0&0&0&1&X_{1}&Y_{1}&Z_{1}&-y_{1}X_{1}&-y_{1}Y_{1}&-y_{1}Z_{1}\\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots \end{array}\right] $$
(4)
$$ \small k = \left[\begin{array}{c} x_{1}\\ y_{1}\\ \cdots \end{array}\right] $$
(5)

Solving these equations makes the computing of the projector orientation straightforward, since the 11 DLT parameters are related to the six parameters of exterior orientation (coordinates X0, Y 0, Z0, and angles κ, φ, ω), and to the five elements of interior orientation (principal point coordinates x0, y0, focal length c, relative y-scale λ and shear d) [4, 10]. Since each observed point (with 2D-3D correspondences) gives two equations and there are 11 unknowns, solving these equations for a minimum of 6 observed points leads to the computation of the interior and exterior sensor (camera or projector) orientation. In case that more points are available, the system can be solved with a minimum squares procedure. Finally, it is worth mentioning that the DLT fails if all CPs lie in a single plane. However, this situation cannot occur in our case, because the projection surface is a vertical cylinder, which is non-planar.

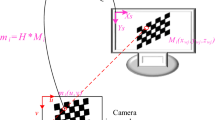
The input data of the SCPM calibration method are: four measured distances (a, b, c and h in Fig. 1, from which the coordinates of the six required CPs are obtained), an image of a checkerboard pattern, an image acquired by the camera of the projected checkerboard pattern and an image acquired by the camera of the projection screen. It is assumed that the screen has a cylindrical shape which is vertically aligned.

Fig. 1
figure 1

Spatial arrangement of six control points on the cylinder and definition of object reference system (XYZ)

Full size image

The first step in this method is to compute the 2D-3D camera correspondences of a minimum of six CPs. From the four measured distances, the radius r of the cylinder and the 3D coordinates of the six CPs are computed. In order to achieve this goal, the six CPs must be located as shown in Fig. 1, being vertically aligned in pairs and horizontally aligned in threes. In this way, the triangles formed by the three upper and the three lower points are equal, and the relative vertical distance between pairs is a constant value, h. From the triangle, the radius r of the vertical cylinder is calculated. Then, a coordinates system with the origin at the central point of the circle defining the cylinder and at the same horizontal plane than the three lower CPs is established, with the Y coordinate in the vertical direction. At this point, the computation of the 3D coordinates of the CPs and the vertical distance h is straightforward. On other hand, the CPs’ image coordinates are measured from the image acquired by the camera. This procedure can be either automatic or manual. The implementation includes a method to automatically find round shaped CPs, but for those cases where artificial CPs cannot be placed on the screen, the manual selection of any physical feature that can act as a control point is allowed.

The second step consist of computing the interior and exterior orientation parameters of the camera. In this step, the DLT (1) and (2) are applied to the 2D-3D correspondences of CPs derived in the first step. From the 11 obtained parameters, the relationship between them and the equations of central projection is straightforward, and therefore the interior and exterior orientation parameters are computed.

The third step is to compute the camera image coordinates of a projected checkerboard pattern. The image of the checkerboard pattern is projected and recovered by the camera. The background of the recovered image is subtracted, in order to avoid the visualization of the CPs or other artifacts, and then it is thresholded. The corners of the squares are automatically detected with sub-pixel accuracy by an image-processing algorithm based on the OpenCV library [8]. Figure 2 illustrates how the background image and the projected checkerboard-like pattern showing detected points are displayed. These points constitute the array of camera image coordinates of the checkerboard which will be used in the following step to derive their corresponding 3D coordinates.

Fig. 2
figure 2

Processed images during point detection: a background image and b projected checkerboard with point detection after applying background subtraction and thresholding

Full size image

Figure 3 illustrates the spatial positioning of devices and 3D points. In this figure, the black dots represent the camera projection center; the cyan dot represents the projector projection center; the red dots represent the CPs at the cylindrical surface; the green dots represent the checkerboard points at Z = 0, and finally the blue dots represent the checkerboard points at the cylindrical surface. The fourth step consists of obtaining the 3D coordinates of the projected checkerboard on the cylinder.

Fig. 3
figure 3

Spatial positioning of devices and 3D points of the projected checkerboard

Full size image

As Fig. 3 shows, the projected points belong to the spatial rays that start in the camera projection center, intersect the checkerboard in the image plane of the camera, and intersect the vertical cylinder (that we have previously defined in a mathematical way). Thus, the fourth step is to obtain 3D coordinates of the projected checkerboard. Since at this point we have computed the intrinsic calibration of the camera and the 3d coordinates of the camera, we can trace rays going from the 3d coordinates of the camera, and passing through the image plane of the camera. The points of intersection between these rays and the vertical cylinder are the 3D coordinates of the projected checkerboard on the cylinder that we are looking for. Equations (1) and (2) can be rearranged as the equation system (6) to trace rays from the camera origin to a certain spatial direction. This system can be solved assuming e.g. Z = 0, and being the X and Y the unknown variables. This will produce the green dots in Fig. 3.Then, tracing spatial rays from the camera projection center to each of them, the rays will intersect the cylinder as the blue dots in Fig. 3.

$$ \left[\begin{array}{cc} a_{1}-xc_{1} & a_{2}-xc_{2}\\ b_{1}-yc_{1} & b_{2}-yc_{2} \end{array}\right] \left[\begin{array}{c} X\\ Y \end{array}\right] = \left[\begin{array}{c} -Za_{3}-a_{4}+xZc_{3}+x\\ -Zb_{3}-b_{4}+yZc_{3}+y \end{array}\right] $$
(6)

The fifth step in this method is to compute the 2D-3D projector correspondences of the checkerboard points. In order to achieve this goal, we propose a similar approach as the one given in the third step described above. However, in this step there is no need to apply background extraction and thresholding. Figure 4 depicts an example of the result of this step.

Fig. 4
figure 4

Detected image points of the projected checkerboard

Full size image

Finally, the last step consists of computing the interior and exterior parameters of the projector. The same approach as the one followed in the second step can be used acquire the interior and exterior parameters of the projector. In this case, the 2D-3D correspondences are the ones derived in steps 4 and 5, with a total of 60 points (as shown in Fig. 4). It must be noted that in this case the number of equations (60x2) is much higher than the number of unknowns variables (11), and a least-square procedure can be applied.

4 Method validation

In order to validate the proposed method (SCPM), we have conducted some experiments to check how stable the system is in computing the interior and exterior orientation parameters of the projector for different camera positions. We have conducted two representative experiments, one carried out in a laboratory and the other one carried out on a real Visionarium available at IRTIC, University of Valencia. We have denoted the latter one as the professional setup.

The laboratory setup consists of a 1800 home-made cylindrical surface with a radius of 0.48 m and 1.0 m height, a Logitech webcam of 640×480 pixel resolution, and a 1280×800 pixel resolution Vivitek multimedia projector with integrated DLP technology. A total of six black circular shaped control points have been attached to the surface. Distances a, b, c and h (from which the coordinates of 6 CPs are derived, see Fig. 1) have been manually measured with a measuring tape.

The camera was moved into 6 different positions, leading to a total of 6 different probes. The obtained results are shown in Tables 1 and 2. These tables include the values obtained for parameters X, Y and Z, measured in meters; the values for parameters κ, φ, ω measured in [gon]; and the values for parameters x0, y0, and c measured in pixels. As a measure of variability, the standard deviation for each parameter is included in both tables. It must be noted that the exterior orientation parameters of the camera are also given with the purpose of showing the camera locations in the different probes.

Table 1 Results of camera calibration in the laboratory setup
Full size table
Table 2 Results of projector calibration in the laboratory setup
Full size table

Tables 1 and 2 show that the highest variability when moving the camera to different positions is reached in the projector calibration, for the Z direction (14 mm), κ parameter (0.0214 gon) and y0 parameter (9.2 pixels). Nevertheless, these values of standard deviation represent 2.8%, 0.36%, and 0.91% of the maximum values shown in the corresponding column. Therefore, these results show that SCPM yields a low level of variability and require a minimum effort for calibration.

The professional setup consists of a 180 sgi Silicon Graphics cylindrical surface with a radius of 3.75 m and 3.0 m height, and a CanonⒸPowerShot G12 camera. The camera has up to 10 MP resolution (2816x2112 resolution setup was used) and integrated optics with varying focal lengths from 6.1 to 30.5 mm (the minimum value was used in order to have a greater field of view). Although the cylindrical surface commercial system has its own projectors, we used for the professional setup the same projector as in the laboratory setup, in order to achieve comparable results. The surface had a 40×9 grid of small white circular shaped control points (ca. 2.5 mm of radius) that were sensitive (and thus visible) under black light conditions. Six of those points where taken as control points. Distances a, b, c and h were measured in the same way as in the laboratory setup.

Like in the laboratory setup, the camera was moved into 6 different positions, leading to a total of 6 different probes. The obtained results are shown in Tables 3 and 4. These tables show that the results for the projector calibration obtained with the professional setup are not better than those of the laboratory setup. This is an expected result, because the professional surface (and thus the working volume) is greater than the one considered for the laboratory setup, although the camera of the professional setup has a greater resolution. In the professional setup, the major variability also is achieved in the Z direction (31 mm) and κ (0.0049 gon), whereas x0 and y0 give similar results (4.7 and 4.5 pixels, respectively). It also draws the attention the fact that a greater variability is obtained for the IO parameters of the camera in the professional setup. A way of reducing this variability could be to increase the number of control points.

Table 3 Results of camera calibration in the professional setup
Full size table
Table 4 Results of projector calibration in the professional setup
Full size table

5 Application examples

5.1 Image warping

Once the projector orientation parameters have been obtained, it is possible to project on the cylindrical surface (whose geometry is known) any point in a 3D known position. In the same way, images can be mapped into any known surface. As an example, Fig. 5 shows the implementation of three different mappings: Fig. 5a shows a wallpaper-like mapping, Fig. 5b shows an orthogonal-like mapping, and Fig. 5c shows a perspective-like mapping.

Fig. 5
figure 5

Schematics of a wallpaper-like mapping; b orthogonal-like mapping; c perspective-like mapping

Full size image

In all cases, the original image i is first scaled to i’ in order to fit the size ratio of the surface area where it should be mapped. Then, the mapping transformation is applied. The name of the wallpaper-like mapping comes from the fact that it produces the same effect as if the image was printed on a paper and attached to the cylindrical surface following its curvature. Figure 5a shows how first the cylindrical surface is straightened to form a planar surface, and the image is orthogonally mapped. Next, the surface with the attached image is again bended. In our implementation, the user can choose the height of the projection on the cylindrical surface and the horizontal angle (w) that has to be covered.

The orthogonal-like mapping represented in Fig. 5b produces the same effect as if the projection surface was planar when viewed at a certain distance to the surface. This kind of projection can be used to project planar images to non-regular surfaces by producing the effect that they are not distorted because of the surface geometry. The user can choose the height and width that the projection has to cover on the cylindrical surface. Finally, the perspective-like mapping shown in Fig. 5c tries to reproduce the human viewing, and it is commonly used in virtual reality simulations. In this case, the user has to specify the coordinates of the projection center, the distance to a virtual projection plane, and the dimensions of that plane. In Fig. 5c two different projection planes that are at different distances from the projection center (d and d’). In this way, this Figure shows how different the projections on the cylindrical surface can be, depending on this parameter.

Next, we have used the laboratory setup described in Section 3 to compute the distortions to be applied to an image in order to be projected on the cylindrical surface. As an example, Fig. 6 shows the warped images and their projections on a cylindrical surface of a checkerboard image. The images on the left side of this Figure show photographs of the laboratory setup. In the case of wallpaper-like mapping, the projection covers a vertical distance of 0.3 m., and it is 120 horizontally opened. In the case of orthogonal-like mapping, the projection is 0.3 m. high and 0.4 m. width. Finally, in the perspective-like mapping, the projection center is located at coordinates (0.0, 0.3, 2.0), the projection plane is located at a distance of 1.5 m. from the projection center and it is 0.3 m. high by 0.4 m. wide.

Fig. 6
figure 6

Warped (left) and projected (right) images, where: a and b wallpaper-like mapping; c and d orthogonal-like mapping; e and f perspective-like mapping

Full size image

5.2 3-D object reconstruction

Once the camera and the projector have been calibrated, the projector-camera pair can act as a stereoscopic system. That means that for any point projected onto any surface and recovered by the camera, its 3D coordinates can be computed.

Equation (7) can be used in turn to derive the 3D object coordinates of each image point. These equations are derived from (1) and (2) assuming that two rays intersect at XYZ, where XYZ are the unknown object coordinates of a point, \(a_{1c} {\dots } c_{3c}\) are the 11 DLT calculated parameters for the camera, \(a_{1p} {\dots } c_{3p}\) are the 11 DLT parameters for the projector, xc, yc are the image coordinates of the principal point of the camera and xp, yp are the image coordinates of the principal point of the projector.

$$ \left[\begin{array}{lll} a_{1c}-x_{c}C_{1c} & a_{2c}-x_{c}C_{2c} & a_{3c}-x_{c}C_{3c}\\ b_{1c}-y_{c}C_{1c} & b_{2c}-y_{c}C_{2c} & b_{3c}-y_{c}C_{3c}\\ a_{1p}-x_{c}C_{1p} & a_{2p}-x_{p}C_{2p} & a_{3p}-x_{p}C_{3p}\\ b_{1p}-y_{c}C_{1p} & b_{2p}-y_{p}C_{2p} & b_{3p}-y_{p}C_{3p} \end{array}\right] \left[\begin{array}{l} X \\ Y \\ Z \end{array}\right] =\left[\begin{array}{l} -a_{4c}+x_{c}\\ -b_{4c}+y_{c}\\ -a_{4p}+x_{p}\\ -b_{4p}+y_{p} \end{array}\right] $$
(7)

Therefore, the proposed calibration method can be applied to recover the 3D shape of any object by projecting a grid of points, and then using an automatic approach that identifies correspondences between each projected point and the imaged point by the camera. Nevertheless, this can be tricky if the 3D surface is complex, as the grid recovered by the camera may be quite different from the projected grid (regular or not), and thus some correspondences may be erroneously established. However, correspondences can be unequivocally assigned if the projector is used to sequentially illuminate point after point and the camera is synchronized to recover those points. While the first strategy is fast because only one image is needed, the second one is much slower as it needs to recover as many images as projected points. Therefore, the first strategy can be used in real-time applications where usually the object and/or the camera-projector system are moving and the accuracy is not critical. The second strategy can be used to reconstruct static objects with greater accuracy. Apart from these techniques, other structured light techniques can be applied, which are out of the scope of this paper.

As an example, Fig. 7 shows the 3D reconstruction of a mannequin body by using the technique of illuminating point after point and using the laboratory setup as described in Section 3. A total of 5,000 points were recovered, which were afterwards triangulated (as shown in Fig. 7b) and meshed for visualization purposes (as shown in Fig. 7c).

Fig. 7
figure 7

3D object reconstruction: a registration procedure with a single projected point; b triangulated cloud of points; c mesh with shadows

Full size image

6 Conclusions

In this paper, we have proposed a fast and easy-to-use projector calibration method needing a minimum set of input data, which reduces the required calibration time. The method is based on the Direct Linear Transformation (DLT) mathematical model, which makes it simple and fully automatic. We have shown the application of this method on cylindrical surfaces. The results show that with the minimum configuration of 6 control points (CPs), the standard deviation in the projector positioning yielded by the calibration process is less than one per cent of the position values. Also, we have used the proposed method in some real application examples, validating it as an efficient method for real cases.